Пять удивительных математических фактов / Хабр
Для начала небольшой спойлер
Да я знаю, что если написать фамилию с заглавной буквы, казуса не получится. Дальше перевод.
Математика – одна из немногих областей знаний, которая может быть объективно названа истинной, потому что ее теоремы основаны на чистой логике. Но в то же время эти теоремы часто оказываются очень странными и противоречащими интуиции.
Некоторые люди считают математику скучной. Следующие примеры показывают, что она какая угодно, но не такая
5. Случайные наборы данных
Как это ни странно, случайные данные на самом деле не такие уж и случайные. В приведенных данных, представляющих собой все от биржевых курсов до населения городов, высот зданий и протяженностей рек, около 30 процентов всех чисел начинаются с единицы. Меньшее количество начинается с 2, еще меньше с 3 и так далее, с 9 начинается только каждое двадцатое число.
И чем больше набор данных, чем шире порядок охватываемых величин, тем сильнее проявляется эта закономерность.
4. Спирали простых чисел
В силу того, что простые числа неделимы (кроме как на единицу и самого себя), и того, что все остальные числа могут быть представлены в виде их произведения, простые числа часто рассматриваются как «атомы» в мире математики. Несмотря на свою важность, распределение простых чисел до сих пор остается тайной. Нет такого правила, которое бы однозначно говорило, какие числа будут простыми и через сколько встретится следующее простое число.
Кажущаяся случайность простых чисел делает факты, обнаруженные в «Скатерти Улама» очень странными.
В 1963 году математик Станислав Улам, обнаружил удивительную закономерность, когда разрисовывал свою записную книжку во время презентации: если записывать целые числа по спирали, простые числа выстраиваются вдоль диагональных линий. Само по себе это не очень удивительно, если помнить, что все простые числа, кроме двойки, нечетные, а диагональные линии в спиралях целых чисел поочередно являются нечетными.
Более необычной была тенденция простых чисел лежать преимущественно на одних диагоналях и практически отсутствовать на других. Причем закономерность наблюдалась вне зависимости от того, с какого числа начиналась спираль (с единицы или любого другого).
Даже если масштабировать спираль, чтобы она вмещала гораздо большее количество чисел, можно увидеть, что скопление простых чисел на одних диагоналях гораздо плотнее, чем на других. Существуют математические предположения, объясняющие эту закономерность, но пока они не доказаны.
3. Выворачивание сферы
В одной важной области математики, которая называется топология, два объекта считаются эквивалентными или гомеоморфными, если один из них может быть преобразован в другой путем скручивания или растягивания поверхности. Объекты считаются разными, если для преобразования требуются разрезы или изломы поверхности.
В качестве примера рассмотрим тор – объект в форме пончика. Если поставить его вертикально, расширить одну сторону и вдавить верхушку этой же стороны, то получится цилиндрический объект с ручкой.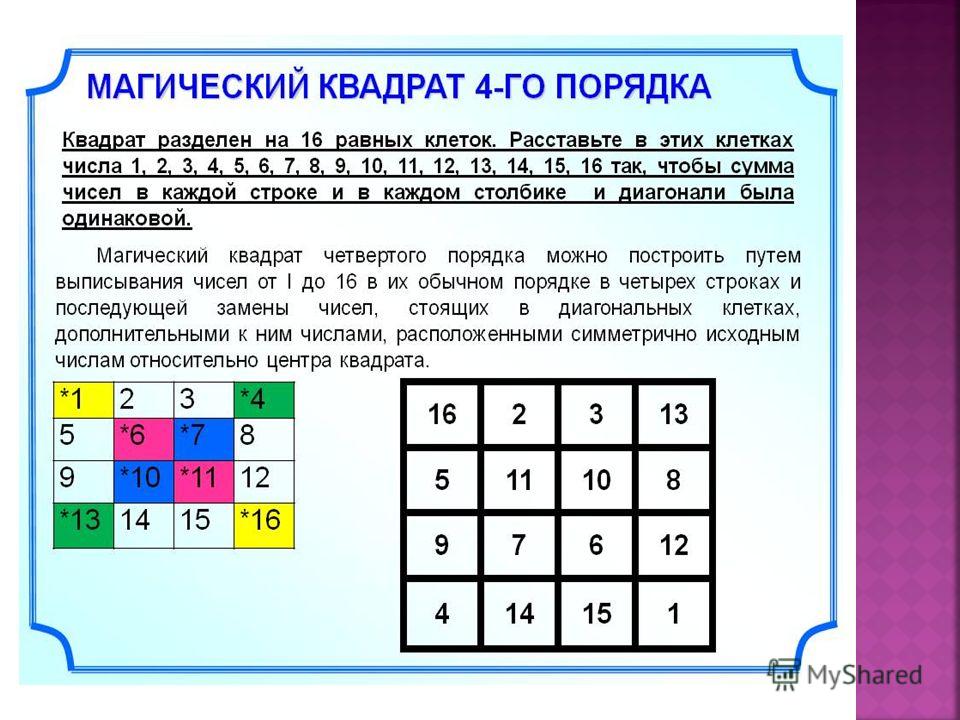
В среде математиков существует классическая шутка, что топологи не могут отличить пончика от чашки с кофе.
С другой стороны, ленты Мебиуса – петли с единственным перегибом не являются гомеоморфными петлями без перегибов (цилиндры), потому что нельзя распрямить ленту Мебиуса, без того чтобы разрезать ее, перевернуть одну сторону и склеить заново.
Топологов давно интересует вопрос, будет ли сфера гомеоморфной самой себе, будучи вывернутой наизнанку? Другими словами, можно ли выворачивать сферу? На первый взгляд это кажется невозможным, потому что нельзя проткнуть дырку в сфере. Но, оказывается, выворачивание сферы возможно. Как это делается, показано на видео
.
Поражает тот факт, что тополог Бернард Морин, который является главным разработчиком приведенного метода выворачивания сферы, слеп.
2. Математика стен
Несмотря на то, что стены могут быть украшены бесконечным количеством завитушек, говоря математическим языком, существует конечное число отдельных геометрических шаблонов.
1. Сонет
«Как сонет Шекспира схватывает саму суть любви, или картина показывает внутреннюю красоту человека, уравнение Эйлера проникает в самые глубины существования.»
Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?
Во-первых, буква «e» представляет собой иррациональное число (с бесконечным количеством цифр), которое начинается с 2.71828… Открытое в контексте непрерывно начисляемого сложного процента, оно описывает темпы экспоненциального роста от колоний популяций насекомых до радиоактивного распада. В математике число обладает рядом неожиданных свойств, например, оно равняется сумме обратных факториалов от нуля до бесконечности.
В конечном счете константа e оккупировала математику, взявшись вроде бы ниоткуда, но оказавшись в большом числе важных уравнений.
Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.
Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.
Константа e, возведенная в степень мнимая единица, умноженная на Пи равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль.
Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.
интересные математические задачи и задания
Советы родителям и примеры увлекательных заданий по математике. Занимательные задачи, головоломки, упражнения и тесты с ответами и решениями.
Попробуйте курс ЛогикЛайк в игровой форме!
Выберите возраст для старта
4-5 лет
6-7 лет
1-2 класс
3-5 класс
15+ для себя
Почему дети и родители выбирают ЛогикЛайк?
ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ!
- Гибкий ум
и уверенность Когда дети решают
задачи и головоломки на LogicLike, они развивают смекалку и
уверенность в своих силах.
- Фундамент
для IT
- Глоток «свежего воздуха» Можно потратить 20-30 минут на себя, пока ребёнок развивается. Кстати, заниматься на ЛогикЛайк интересно и взрослым.
Начать занятия!
Польза занятий логикой и математикой
Элементарные математические представления помогают сформировать в детском саду.
Базовые
математические способности развивают в школе.
А чтобы ребёнок научился рассуждать логически, мыслить нестандартно — обычных арифметических и геометрических задач недостаточно.
Уже в дошкольном возрасте желательно выработать привычку ежедневно выполнять задания и упражнения на развитие логического мышления.
Благодаря регулярным тренировкам:
- ребёнок учится рассуждать, анализировать и делать правильные выводы;
- развивает сообразительность, память, внимание и интеллект;
- успехи повышают самооценку, интерес к обучению в школе, вдохновляют на победы в математических олимпиадах и конкурсах.
Дети 5-12 лет с удовольствием проходят
курс ЛогикЛайк в игровой форме.
Тем временем они учатся рассуждать,
развивают логику, способности к математике и познавательный интерес.
Математические задачи по возрасту
Заинтересовать дошкольников 5-7 лет, учащихся начальных классов проще всего. Главное — предложить разнообразные занимательные задания, сделать процесс решения задач увлекательным, с элементами игры, и обеспечить умеренную сложность задач.
Примеры заданий по возрасту
- Логика для детей 5-6 лет
- Логика для детей 6-7 лет
- Математика для дошкольников
- 1 класс
- 2 класс
- 3 класс
- 4 класс
К 3-4 классу мотивация у школьника часто снижается.
Родителям важно не упустить этот момент и
объяснить ребёнку, зачем вообще заниматься
математикой и учиться решать задачи.
Логические и математические примеры
- для дошкольников
- для первоклассников
- примеры для 2 класса
- для 3 класса
- для 4 класса
- примеры для 5 класса
Логико-математические и другие развивающие игры по возрасту
4 — 5 лет
Занимательные задачи по типу
В плане регулярных тренировок в любом возрасте должно быть выполнение заданий минимум 5-7 типов.
Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических
способностей.
Среди самых интересных и популярных категорий заданий на логику и смекалку:
- Классические логические задачи. Учат детей анализировать текст, выделять главное, рассуждать и делать выводы.
- Арифметические ребусы. Отличная отработка ключевых мыслительных операций: абстрагирование, анализ и синтез, сравнение и другие.
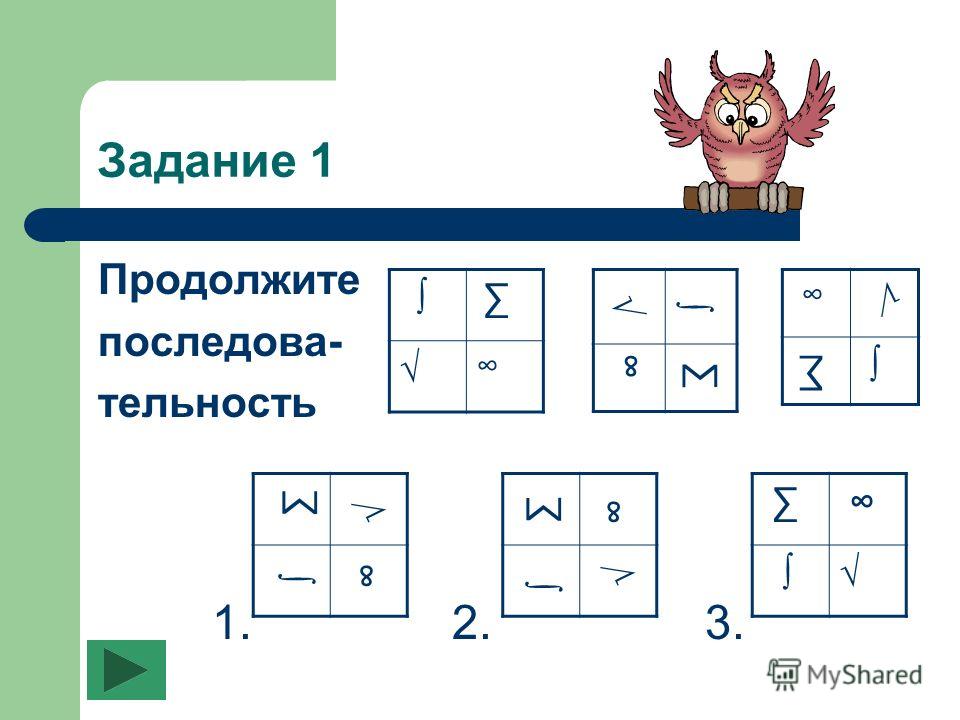
- Задачи на закономерности, последовательности. Помогают развить аналитические способности и творческое мышление.
Примеры заданий по типу
Логические задачи
Математические ребусы
Задачи на поиск закономерностей
Правда и ложь
Найди лишнее в каждой группе
Магические квадраты
Шахматные задачи для начинающих
Загадки на логику
Головоломки со спичками, перестановки
Ребусы с буквами и цифрами
Загадка математики: 5 красивых математических явлений
Фракталы — узоры, которые повторяются в меньших масштабах — часто можно увидеть в природе, например, в снежинках.
Кредит: Unsplash.Математика видна в природе повсюду, даже там, где мы ее не ожидаем. Это может помочь объяснить, как галактики закручиваются по спирали, изгибаются морские раковины, повторяются узоры и изгибаются реки.
Даже субъективные эмоции, такие как то, что мы находим красивым, могут иметь математическое объяснение.
«Математика считается не только красивой — красота также математическая», — говорит доктор Томас Бритц, преподаватель Школы математики и статистики Университета Нового Южного Уэльса. «Эти два взаимосвязаны».
Доктор Бритц работает в области комбинаторики, которая занимается сложным счетом и решением головоломок. В то время как комбинаторика находится внутри чистой математики, доктора Бритца всегда привлекали философские вопросы математики.
Он также находит красоту в математическом процессе.
«С личной точки зрения заниматься математикой очень весело. Я любил ее с тех пор, как был маленьким ребенком.
«Иногда красота и удовольствие от математики заключаются в концепциях или результатах или в пояснениях.
В других случаях это мыслительные процессы, которые заставляют ваш разум переключаться в нужное русло, эмоции, которые вы получаете, или просто работа в потоке — например, погружение в хорошую книгу».
Здесь доктор Бритц делится некоторыми из своих любимых связи между математикой и красотой.
1. Симметрия — но с оттенком неожиданности
Куда ни глянь, везде симметрия. 1 кредитВ 2018 году доктор Бритц выступил на TEDx с докладом о математике эмоций, в котором он использовал недавние исследования по математике и эмоциям, чтобы рассказать о том, как математика может помочь объяснить эмоции, такие как красота.
«Наш мозг вознаграждает нас, когда мы распознаем закономерности, будь то видение симметрии, организация частей целого или решение головоломок», — говорит он.
«Когда мы замечаем что-то, отклоняющееся от шаблона — когда есть что-то неожиданное — наш мозг снова вознаграждает нас. Мы чувствуем восторг и волнение».
Например, люди считают симметричные лица красивыми. Однако особенность, которая нарушает симметрию небольшим, интересным или неожиданным образом, например, красивым пятном, добавляет красоты.
«Эту же идею можно увидеть и в музыке», — говорит доктор Бритц. «Узорчатые и упорядоченные звуки с оттенком неожиданности могут добавить индивидуальности, очарования и глубины».
Многие математические концепции демонстрируют подобную гармонию между закономерностью и неожиданностью, элегантностью и хаосом, правдой и тайной.
«Сплетение математики и красоты само по себе прекрасно для меня», — говорит доктор Бритц.
Каждая ветвь папоротника отбрасывает меньшие версии самих себя. Иногда узор в виде вайи можно увидеть даже на листьях. 1 кредит2. Фракталы: бесконечные и призрачные
Фракталы — это самореферентные паттерны, которые до некоторой степени повторяются в меньших масштабах. Чем внимательнее вы смотрите, тем больше повторений вы увидите — как ветки и листья папоротника.
«Эти повторяющиеся узоры повсюду в природе», — говорит доктор Бритц. «В снежинках, речных сетях, цветах, деревьях, ударах молнии — даже в наших кровеносных сосудах».
Фракталы в природе часто могут воспроизводиться только несколькими слоями, но теоретически фракталы могут быть бесконечными. Многие компьютерные симуляции были созданы как модели бесконечных фракталов.
«Вы можете продолжать фокусироваться на фрактале, но вы никогда не доберетесь до его конца», — говорит доктор Бритц.
«Фракталы бесконечно глубоки. Они также бесконечно призрачны.
«У вас может быть целая страница, заполненная фракталами, но общая площадь, которую вы нарисовали, по-прежнему равна нулю, потому что это просто набор бесконечных линий.»
Множество Мандельброта, пожалуй, самый известный фрактал, сгенерированный компьютером. При увеличении откроется точно такое же изображение в меньшем масштабе — головокружительный и гипнотический бесконечный цикл. 1 кредит 3.
Пи: непостижимая истина
Пи (или «π») — это число, которое часто впервые учат в средней школе по геометрии. Проще говоря, это число чуть больше 3,9.0003
Пи в основном используется при работе с кругами, например, при вычислении длины окружности, используя только ее диаметр. Правило состоит в том, что для любого круга расстояние вокруг края примерно в 3,14 раза больше расстояния поперек центра круга.
Но число Пи намного больше.
«Если вы посмотрите на другие аспекты природы, вы вдруг обнаружите число Пи повсюду», — говорит доктор Бритц. «Мало того, что оно связано с каждым кругом, но Пи иногда появляется в формулах, которые не имеют ничего общего с кругами, например, в вероятности и исчислении».
Несмотря на то, что это самое известное число (Международный день числа Пи отмечается ежегодно 14 марта, 3.14 по американским датировкам), вокруг него много загадок.
«Мы много знаем о Пи, но на самом деле ничего не знаем о Пи», — говорит доктор Бритц.
«В этом есть красота — прекрасная дихотомия или напряжение.»
Пи связано с океаном и звуковыми волнами через ряд Фурье, формулу, используемую в ритмах и циклах. 1 кредитПи бесконечно и по определению непознаваемо. Никакой закономерности в его десятичных точках пока не выявлено. Понятно, что любая комбинация цифр, например, ваш номер телефона или день рождения, где-то появится в Pi (вы можете найти это с помощью онлайн-инструмента поиска первых 200 миллионов цифр).
В настоящее время мы знаем 50 триллионов цифр числа Пи, что является рекордом, побитым ранее в этом году. Но поскольку мы не можем вычислить точное значение числа Пи, мы никогда не сможем полностью вычислить длину окружности или площадь круга, хотя приблизиться к этому можно.
«Что здесь происходит?» говорит доктор Бритц. «Что такого в этом странном числе, которое каким-то образом связывает воедино все круги мира?
«В Пи есть какая-то скрытая правда, но мы ее не понимаем. Эта загадочность делает его еще более прекрасным».0003
4. Золотое и древнее сечение
Золотое сечение (или «ϕ») — пожалуй, самая популярная математическая теорема о красоте. Это считается наиболее эстетичным способом пропорционировать объект.
Отношение можно сократить примерно до 1,618. В геометрическом представлении соотношение создает Золотой прямоугольник или Золотую спираль.
«На протяжении всей истории отношение рассматривалось как эталон идеальной формы, будь то в архитектуре, произведениях искусства или человеческом теле», — говорит доктор Бритц. «Это называлось «Божественная пропорция».0003 Золотая спираль часто используется в фотографии, чтобы помочь фотографам создать эстетически приятную композицию изображения. 1 кредит
«Многие известные произведения искусства, в том числе работы Леонардо да Винчи, основаны на этом соотношении».
Золотая спираль сегодня часто используется, особенно в искусстве, дизайне и фотографии. Центр спирали может помочь художникам создать эстетически привлекательные фокусные точки изображения.
5. Парадокс ближе к магии
Непостижимая природа математики может сделать ее ближе к магии.
Знаменитая геометрическая теорема, называемая парадоксом Банаха-Тарского, утверждает, что если у вас есть шар в трехмерном пространстве и вы разделите его на несколько конкретных частей, то есть способ собрать эти части так, чтобы получилось два шара.
«Это уже интересно, но становится еще страннее», — говорит доктор Бритц.
«Когда будут созданы два новых шара, они оба будут того же размера, что и первый шар.»
С математической точки зрения эта теорема работает — можно собрать части так, чтобы шары удвоились.
Дублировать шары невозможно, верно? 1 кредит«Вы не можете сделать это в реальной жизни», — говорит доктор Бритц. «Но вы можете сделать это математически.
«Это своего рода магия. Это волшебство».
Фракталы, парадокс Банаха-Тарского и Пи — это только поверхность математических понятий, в которых он находит красоту.
«Чтобы испытать на себе множество прекрасных частей математики, вам нужно много фоновых знаний», — говорит доктор Бритц. «Вам нужно много базовых — и часто очень скучных — тренировок. Это немного похоже на миллион отжиманий перед тем, как заняться спортом.
«Но оно того стоит. Я надеюсь, что больше людей получат удовольствие от математики. Впереди еще столько прекрасного».
Предоставлено Университет Нового Южного Уэльса
Цитата : Мистика математики: 5 красивых математических феноменов (20 мая 2020 г.) получено 20 января 2023 г. с https://phys.org/news/2020-05-mystique-mathematics-beautiful-math-phenomena.html
Этот документ защищен авторским правом. Помимо любой добросовестной сделки с целью частного изучения или исследования, никакие
часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в ознакомительных целях.
5 удивительных способов увидеть математику в мире
Вы когда-нибудь останавливались, чтобы оглянуться и заметить все удивительные формы и узоры, которые мы видим в окружающем нас мире? Математика формирует строительные блоки мира природы, и ее можно увидеть потрясающим образом. Вот несколько из моих любимых примеров математики в природе , но есть и много других примеров.
Последовательность Фибоначчи:Названная в честь известного математика Леонардо Фибоначчи, эта числовая последовательность представляет собой простой, но глубокий узор.
На основе «задачи о кролике» Фибоначчи эта последовательность начинается с чисел 1 и 1, а затем каждое последующее число находится путем сложения двух предыдущих чисел. Следовательно, после 1 и 1 следует число 2 (1+1). Следующее число 3 (1+2), затем 5 (2+3) и так далее.
Что примечательно, так это то, что числа в последовательности часто встречаются в природе .
Несколько примеров включают количество спиралей в сосновой шишке, ананасе или семенах подсолнуха или количество лепестков на цветке.
Числа в этой последовательности также образуют уникальную форму, известную как спираль Фибоначчи, которую мы снова видим в природе в виде раковин и в форме ураганов.
Фракталы в природе:Фракталы — еще одна интригующая математическая форма, которую мы видели в природе. Фрактал — это самоподобная, повторяющаяся форма, то есть одна и та же базовая форма снова и снова видна в самой форме.
Другими словами, если вы увеличите или уменьшите масштаб, везде будет видна одна и та же форма.
Фракталы составляют многие аспекты нашего мира, включая листья папоротников, ветви деревьев, разветвления нейронов в нашем мозгу и береговые линии.
Узнайте больше о фракталах и о том, как мы видим и применяем их в нашем мире сегодня, в Fractal Foundation.
Шестиугольники в природе: Еще одно геометрическое чудо природы — шестиугольник. Правильный шестиугольник имеет 6 сторон одинаковой длины, и эта форма снова и снова встречается в окружающем нас мире.
Самый распространенный пример использования шестиугольников в природе — пчелиный улей.
Пчелы строят улей, используя мозаику из шестиугольников. Но знаете ли вы, что каждая снежинка также имеет форму шестиугольника?
Мы также видим шестиугольники в пузырях, которые составляют пузырь плота. Хотя мы обычно думаем о пузырьках как о круглых, когда многие пузырьки сталкиваются друг с другом на поверхности воды, они принимают форму шестиугольников.
Концентрические круги в природе:Еще одна распространенная форма в природе — набор концентрических кругов. Концентричность означает, что все круги имеют один и тот же центр, но разные радиусы. Это означает, что все круги разных размеров, один внутри другого.
Типичным примером является рябь пруда, когда что-то ударяется о поверхность воды. Но мы также видим концентрические круги в слоях лука и кольцах деревьев, которые формируются по мере его роста и старения.
Если вы живете рядом с лесом, вы можете поискать упавшее дерево, чтобы сосчитать кольца, или найти паутину-шар, которая состоит из почти идеальных концентрических кругов.
Математика в космосе:Удаляясь от планеты Земля, мы также можем увидеть многие из этих же математических особенностей в космосе.
Например, наша галактика имеет форму спирали Фибоначчи. Планеты вращаются вокруг Солнца по концентрическим траекториям. Мы также видим концентрические круги в кольцах Сатурна.
Но мы также видим уникальную симметрию в космическом пространстве, которая уникальна (насколько могут судить ученые), и это симметрия между Землей, Луной и Солнцем, которая делает возможным солнечное затмение.
Каждые два года Луна проходит между Солнцем и Землей таким образом, что кажется, что она полностью закрывает Солнце. Но как это возможно, если Луна намного меньше Солнца?
Из-за математики.
Видите ли, Луна примерно в 400 раз меньше Солнца, но и примерно в 400 раз дальше.
Эта симметрия допускает полное солнечное затмение, которого не бывает ни на одной другой планете.
Разве природа не прекрасна??
Хотите узнать еще больше об этих темах и глубже изучить их со своими детьми? Попробуйте мою дополнительную программу по математике: Математика в природе.
Посмотрите, что ваши дети изучат в этом коротком видео:
Эта учебная программа, разработанная для классов 3-6 , предлагает практические уроки, чтобы посмотреть на математику в реальном мире, а также отработать важные математические навыки.
Включает списков книжек с картинками по каждой теме, подробное руководство для учителя , раздаточные материалы для учащихся к урокам, сводные страницы с «забавными фактами» и список математических художественных проектов по каждой теме.
Купить «Математика в природе» ЗДЕСЬ
Я также рекомендую вам приобрести БЕСПЛАТНЫЙ набор плакатов «Математика в природе» , чтобы показать своим детям математику в реальном мире.
