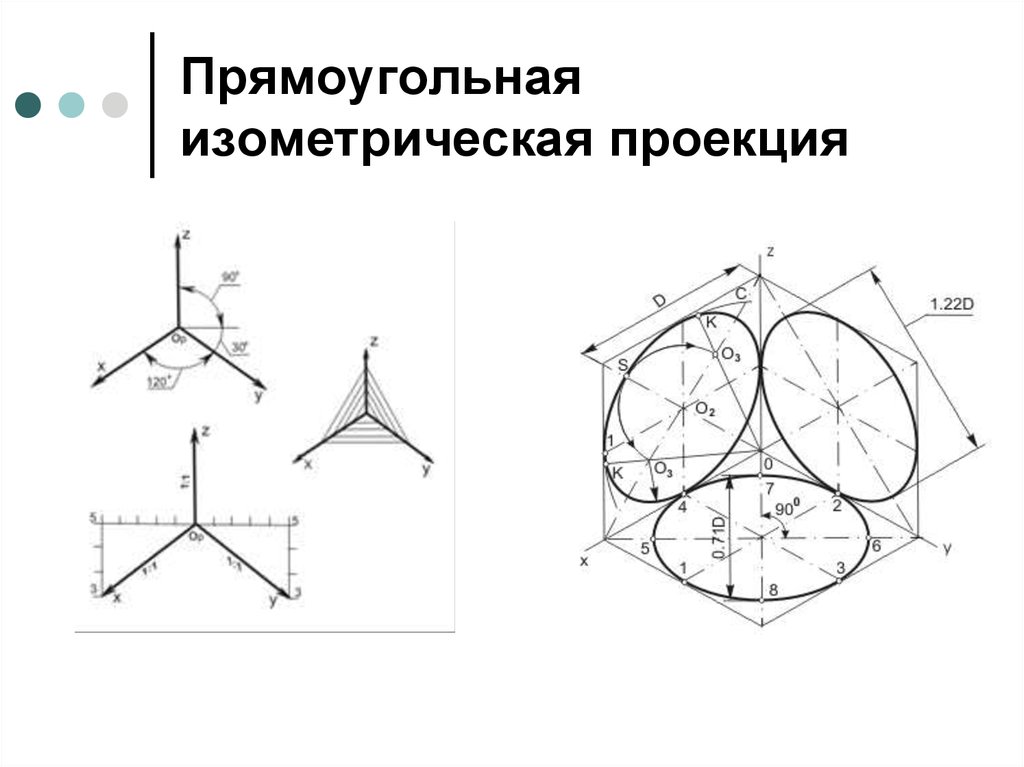
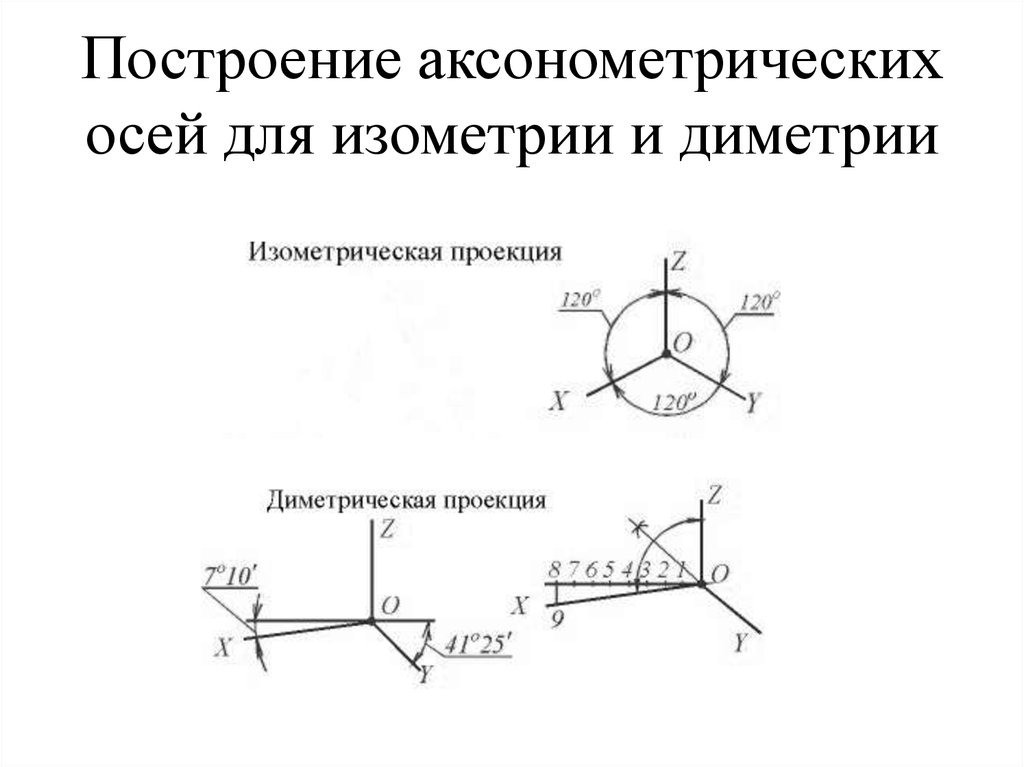
Изометрия правила построения: Построение третьего вида и изометрии с вырезом четверти — Независимое театральное объединение "Зрительские симпатии"

Разное

Содержание

Изометрия. Способы построения изометрических осей

Похожие презентации:

Основы архитектуры и строительных конструкций. Основы проектирования

Конструктивные схемы многоэтажных зданий

Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)

Правила выполнения архитектурно-строительных чертежей

ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)

задачи на построение (геометрия 7 класс)

Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)

Параллельность в пространстве. (Графическая работа 2)

Строительное черчение. Графическое оформление и чтение строительных чертежей

Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты

900igr.net
Содержание
Немного теории
Способы построения изометрических осей
Порядок построения изометрии
Точки и отрезки
Изометрия плоских фигур
Геометрические тела
Деталь изнутри
Практика
Проверь себя
Используемая литература

3.

Немного теорииЧертеж механизма или детали не дает полное представление о его
форме. Поэтому чертежи сложных изделий сопровождают наглядными
изображениями (аксонометрическими проекциями).
Аксонометрия — слово греческое, в переводе означает измерение по осям.
При построении аксонометрических проекций размеры откладывают
вдоль осей X,Y,Z. Аксонометрические проекции отличаются наглядностью:
Изометрия – это одна из аксонометрических проекций.
Изометрия(греч.) — равное измерение.
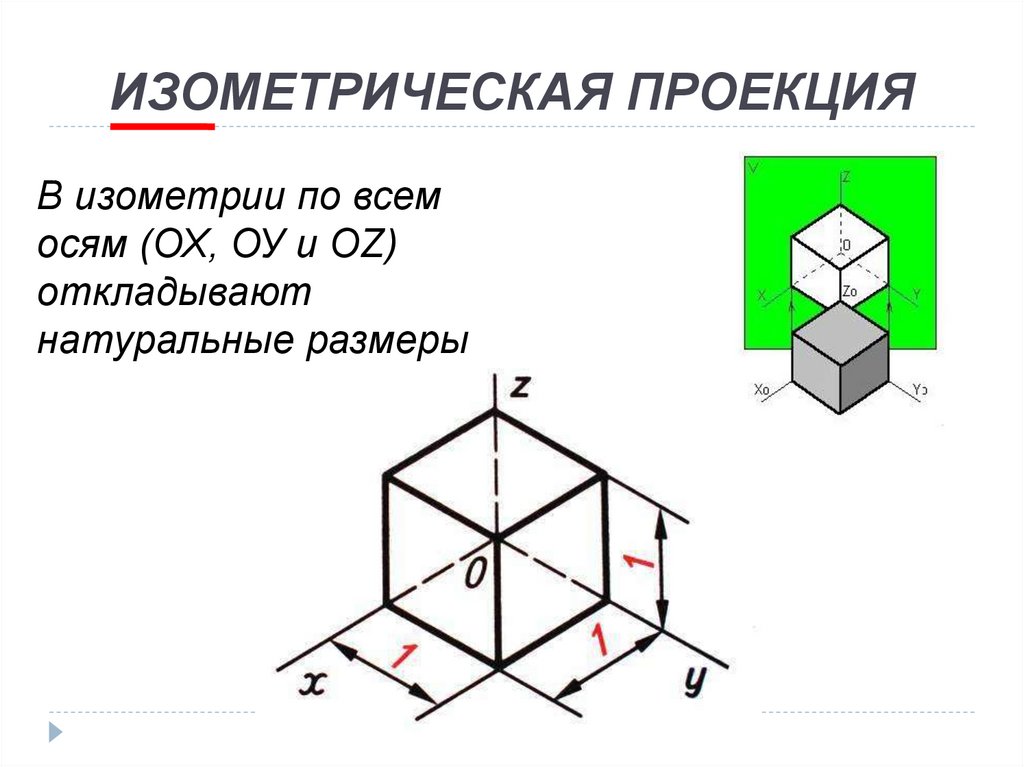
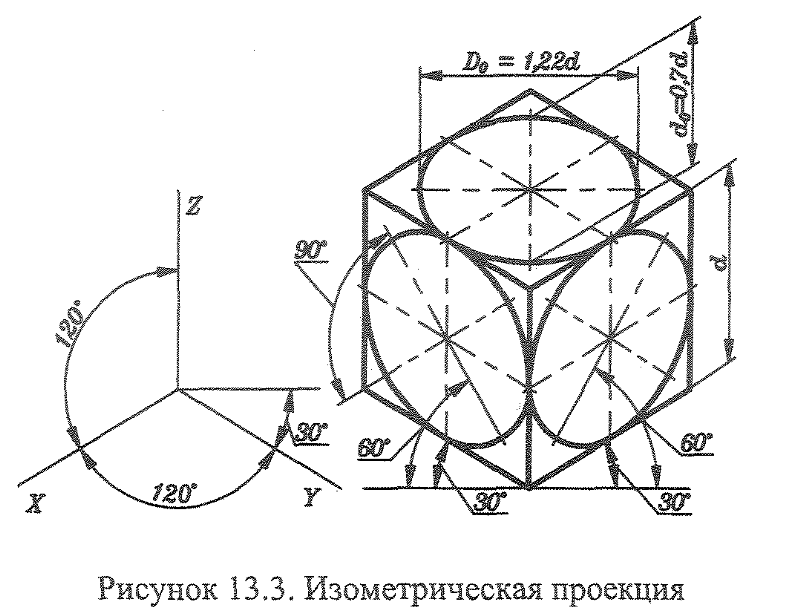
При вычерчивании изометрической проекции (изометрии)
размеры по всем трем осям откладывают натуральные, а
сами оси выглядят так:
Содержание
x
z
y

4. Способы построения изометрических осей

Содержание

5. Порядок построения изометрии

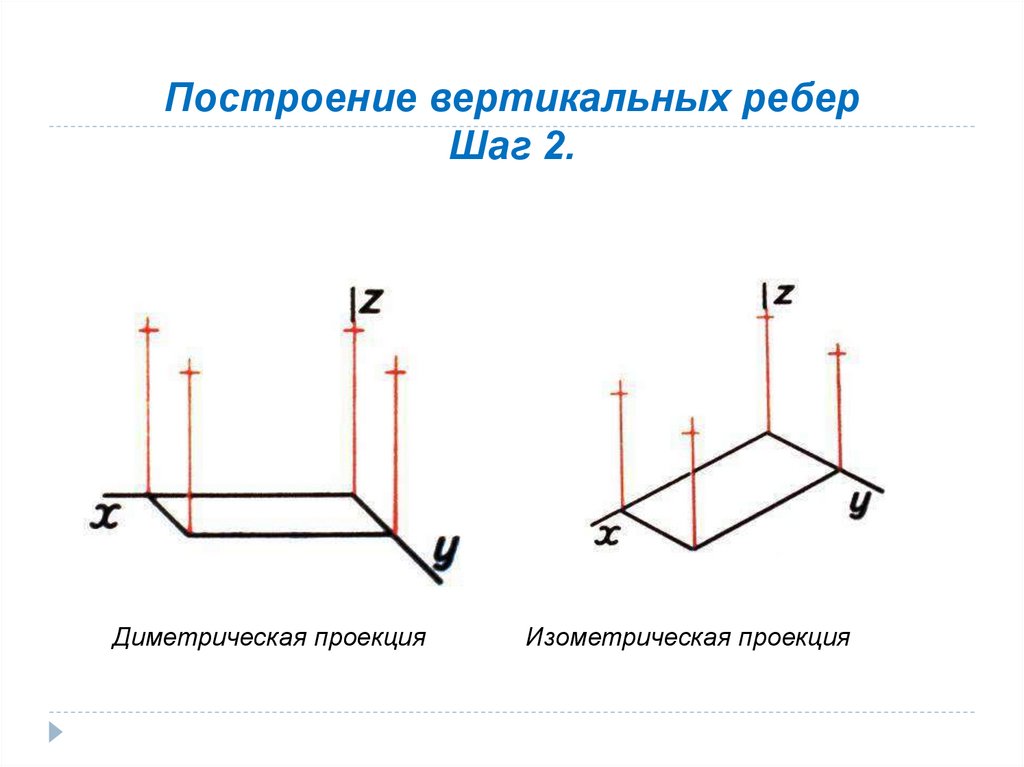
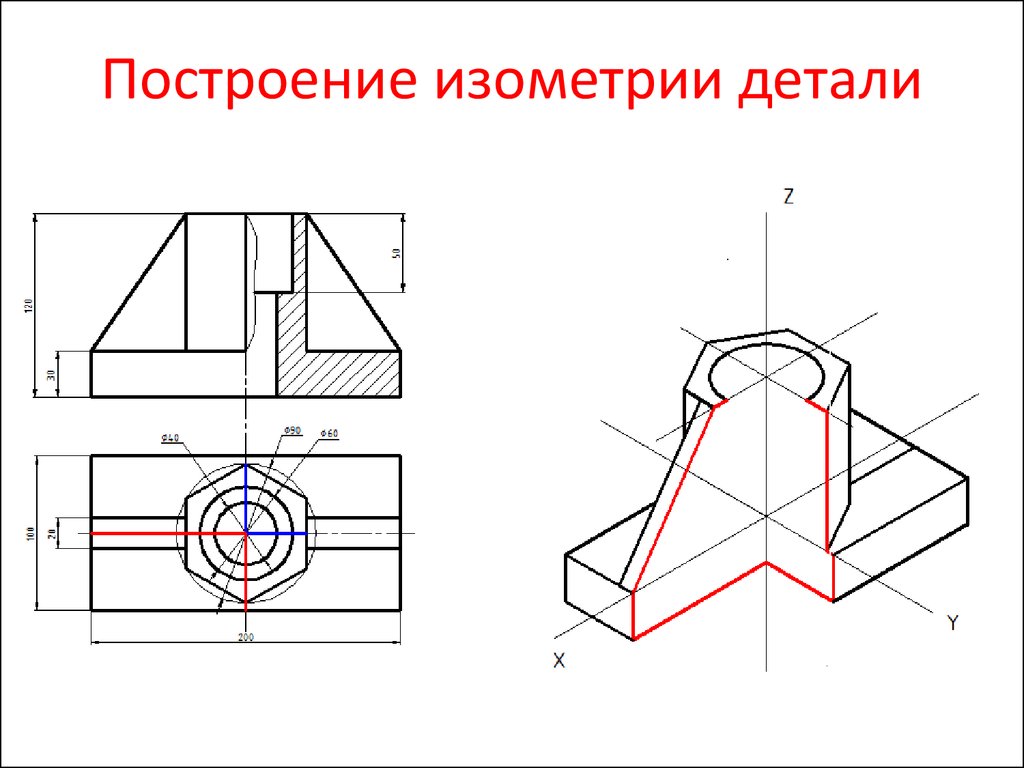
1. Проводят оси. Строят переднюю грань детали, откладывая
действительные величины высоты — вдоль оси Z, ширины – вдоль оси X.
2. Из вершины полученной фигуры параллельно оси Y проводят ребра, уходящие
вдаль.

Вдоль них откладывают действительную толщину детали.
3. Через полученные точки проводят прямые, параллельные ребрам передней
грани.
4. Удаляют лишние линии, обводят видимый контур и наносят размеры.
Вы познакомились с общими правилами построения изометрических проекций. На
следующих слайдах эти проекции представлены более детально.
Содержание

6. Точки и отрезки

Все детали можно мысленно разделить на геометрические тела,
которые состоят из вершин (точек), ребер (отрезков) и граней
(плоских фигур).
Чтобы построить изометрию точки, необходимо знать ее
координаты X, Y, Z и откладывать их по соответствующим
осям:
Аналогично строят изометрию отрезка.
Содержание

7. Изометрия плоских фигур

Правильный шестиугольник в плоскости XOY:
из точки О1 по оси X откладывают отрезки О111 и О141,
равные размеру отрезков О1 и О4. По этой же оси
откладывают отрезки О171 и О181, равные отрезкам О7 и
О8. Через полученные точки 71 и 81 проводят
параллельно оси Y прямые линии.

На них откладывают
отрезки 71-21, 81-31 и т. д ., равные отрезкам 7-2, 8-3 и т. д.
Найденные шесть точек последовательно соединяют
прямыми.
Аналогично строят изометрию правильного шестиугольника
в плоскостях ZOX и ZOY.
Правильный пятиугольник:
Для упрощения работы построения выполняют по двум
координатам вершин, откладывая их по
соответствующим осям.
Содержание
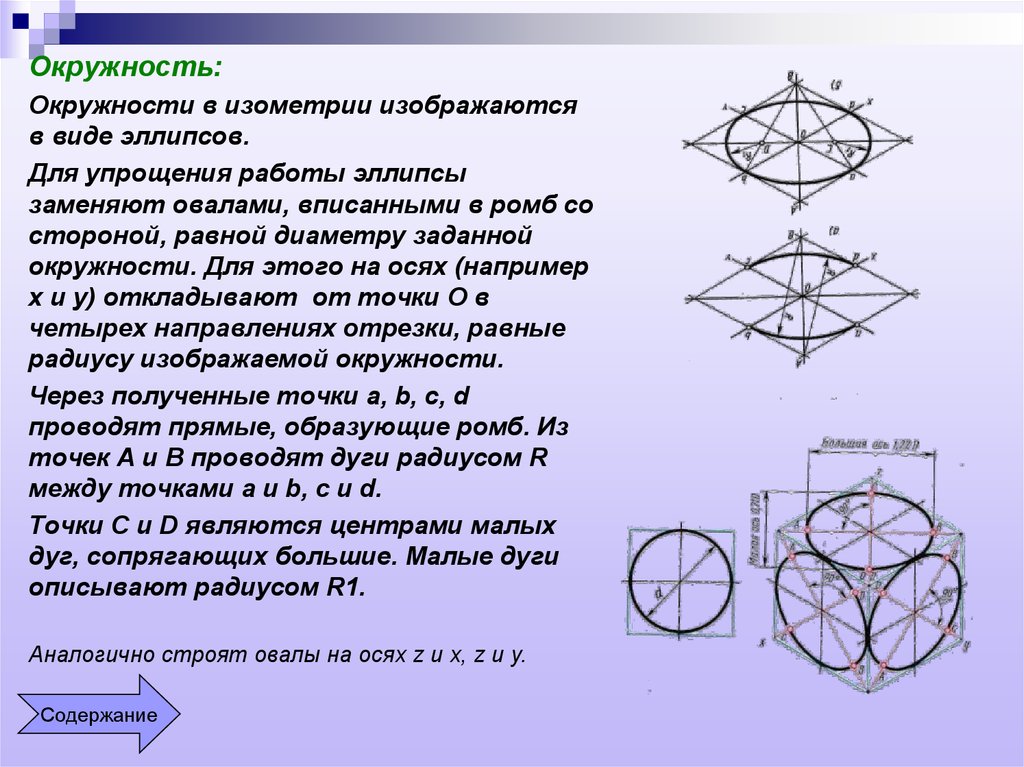
Окружность:
Окружности в изометрии изображаются
в виде эллипсов.
Для упрощения работы эллипсы
заменяют овалами, вписанными в ромб со
стороной, равной диаметру заданной
окружности. Для этого на осях (например
x и y) откладывают от точки О в
четырех направлениях отрезки, равные
радиусу изображаемой окружности.
Через полученные точки a, b, c, d
проводят прямые, образующие ромб. Из
точек А и В проводят дуги радиусом R
между точками a и b, c и d.
Точки C и D являются центрами малых
дуг, сопрягающих большие. Малые дуги
описывают радиусом R1.

Аналогично строят овалы на осях z и x, z и y.
Содержание

9. Геометрические тела

Пирамида.
На рисунке а показан комплексный
чертеж(рисунок а) неправильной пятиугольной
пирамиды. По этому чертежу определяем
координаты всех точек основания пирамиды.
Затем по координатам x и y строим изометрию
пяти точек-вершин основания
пирамиды(рисунок б).
Пример.
По оси х от точки О откладываем координату
ХА=a‘ d. Из конца ее проводим прямую,
параллельную оси y,на которой откладываем
вторую координату этой точки YA=a‘ a.
Далее строят по координатам высоту
пирамиды и получают точку S-вершину
пирамиды. Соединяя точку S с
Точками A, B, C, D и E, получают
изометрическую проекцию пирамиды.
Содержание
Призма:
Если основание призмы – правильный
многоугольник (например, шестиугольник), то
построение вершин основания по координатам
можно упростить, проводя одну из осей
координат через центр основания.

Оси x, y и z
проводят через центры правильных
шестиугольников призмы. Далее из вершин
шестиугольника основания проводим прямые,
параллельные соответственно осям x, y и z (для
каждой из рассматриваемых на рисунке призм). На
этих прямых от вершин основания откладывают
высоту призмы и получают точки 1, 2, 3, 4, 5, 6
вершин другого основания призмы.
Соединив эти точки прямыми, получают
изометрическую проекцию призмы. В заключение
видимые ребра проводят сплошными толстыми
линиями, а невидимые ребра — тонкими
штриховыми.
Содержание

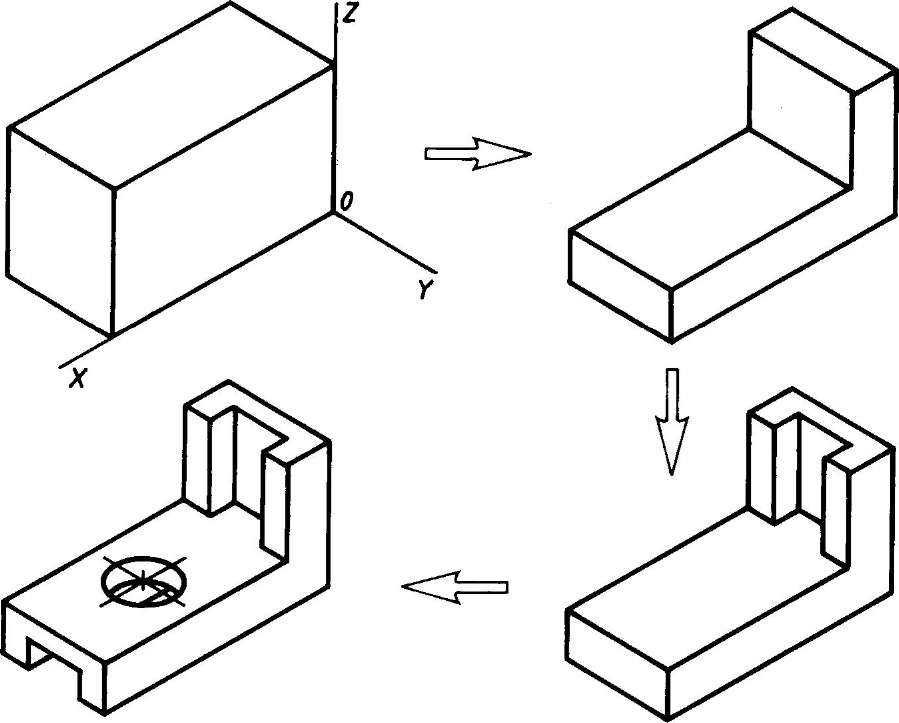
11. Деталь изнутри

Для выявления внутренней формы
предмета применяют вырез одной
четверти детали.
Вначале строят в тонких линиях
изометрию (см. рисунок а). Затем
выполняют вырез, направляя две
вертикальные секущие плоскости
по осям x и y (см. рисунок б).
Удаляют часть изображаемого
предмета (см. рисунок в), после чего
штрихуют сечения и обводят
изображение сплошными толстыми
линиями (см.

рисунок г).
Содержание

12. Практика

Эти упражнения помогут Вам попробовать свои силы
(проверить и закрепить знания).
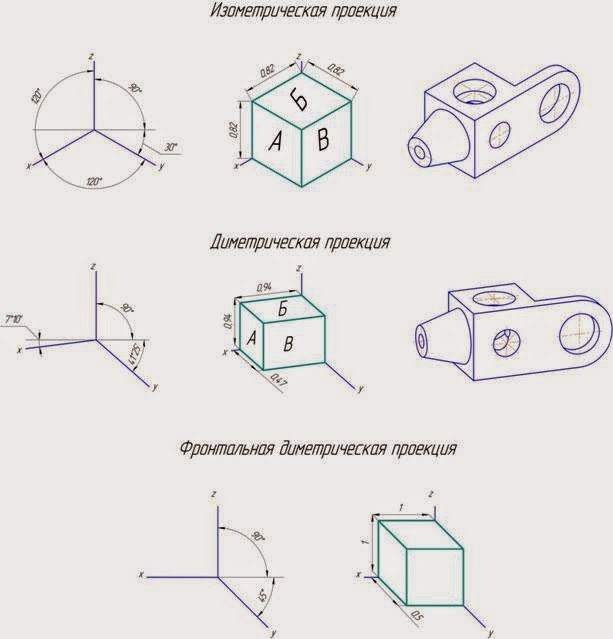
Упражнение 1.
1. Какое наглядное изображение представлено на
чертеже?
2. Чему равны углы между осями изометрической
проекции?
3. В какую фигуру проецируются окружности в
изометрии?
4. Чему равны габаритные размеры детали?
5. Есть ли в изделии отверстия? Сколько их и какова
их форма?
Упражнение 2.
Постройте изометрическую проекцию детали по ее
комплексному чертежу.
Содержание

13. Проверь себя

Эталон к упражнению 1:
1. Изометрическая проекция.
2. 120°.
3. Эллипс.
4. 90; 40; 50 мм.
5. Да. 3. Цилиндр.
Содержание
Эталон к упражнению 2:

14. Используемая литература

1.Боголюбов С.К. Черчение, М.: Машиностроение,1989г.
2.Вышнепольский И.С. Техническое черчение, М.: Высшая школа,
2005г.
3.Вышнепольский И.С. Черчение для техникумов, М.: АСТ,
Астрель, 2002г.

4.Бахнов Ю.Н. Сборник заданий по техническому черчению,
М.: Высшая школа, 1988г.
Содержание
Благодарю за
внимание!
Содержание
В начало

English Русский Правила

Понятие об аксонометрических проекциях • Блог архитектора

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Рис. 103

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).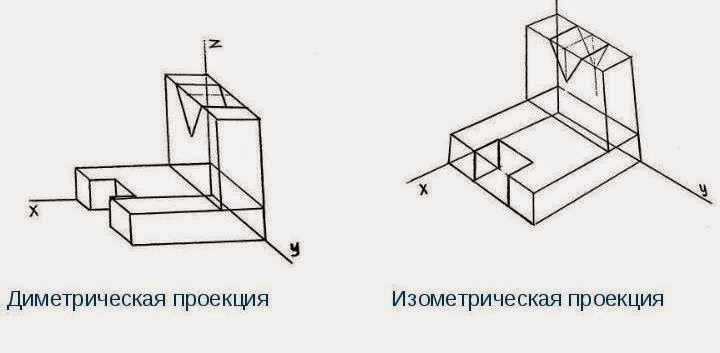

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

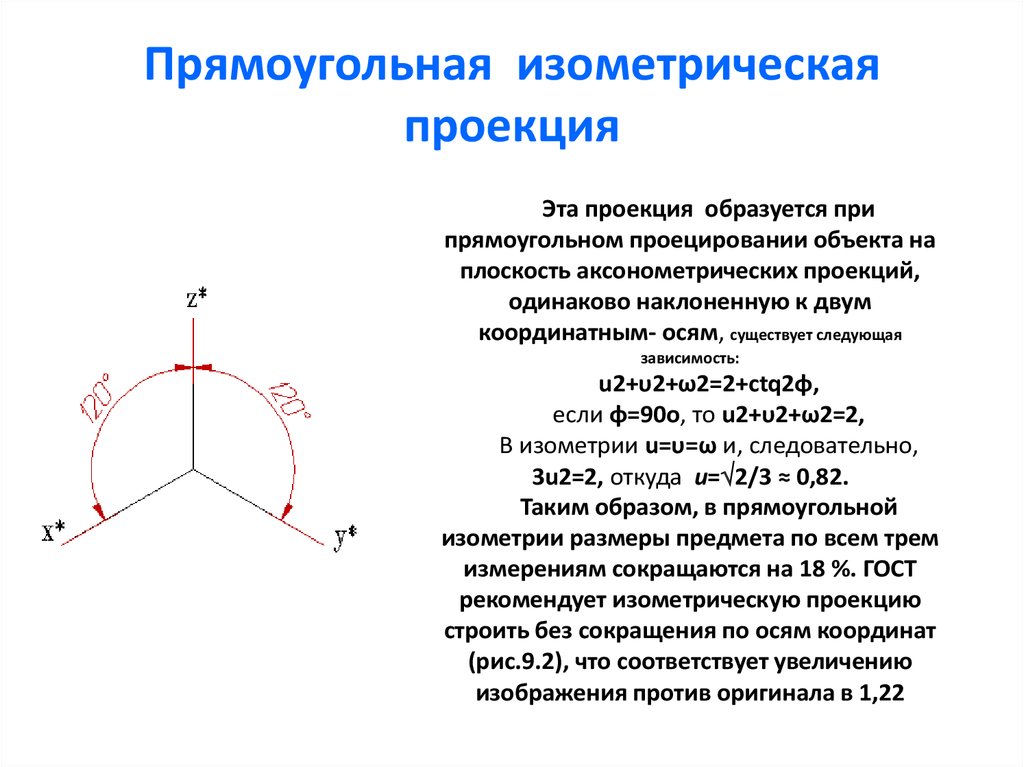
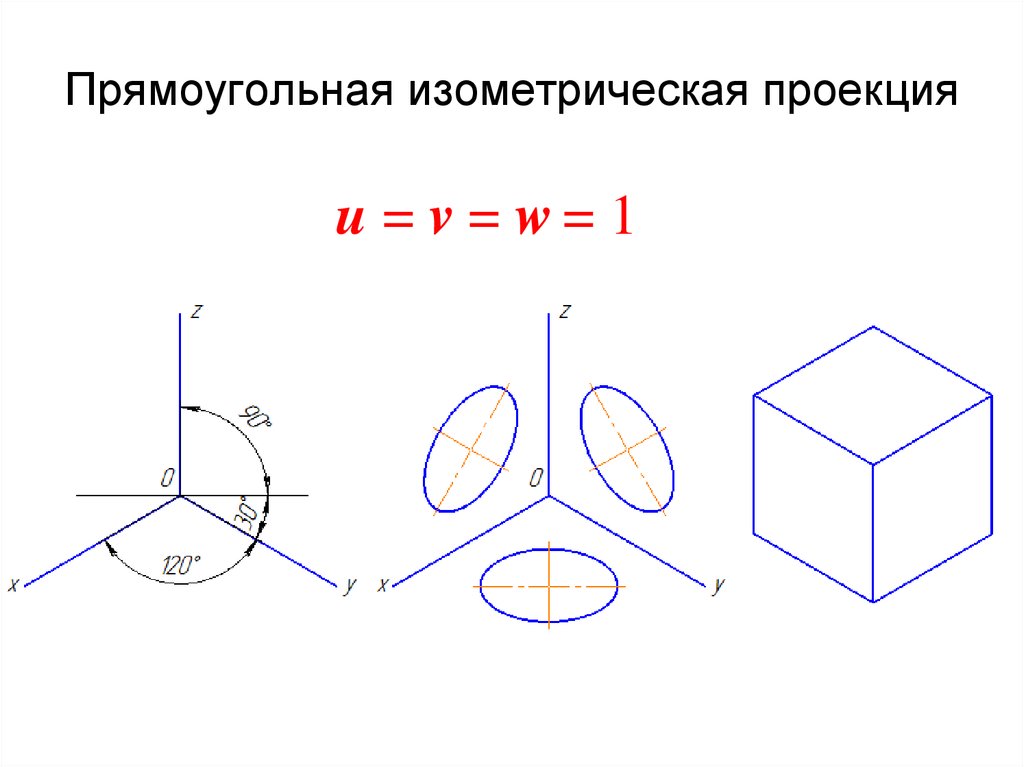
Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Рис. 104

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.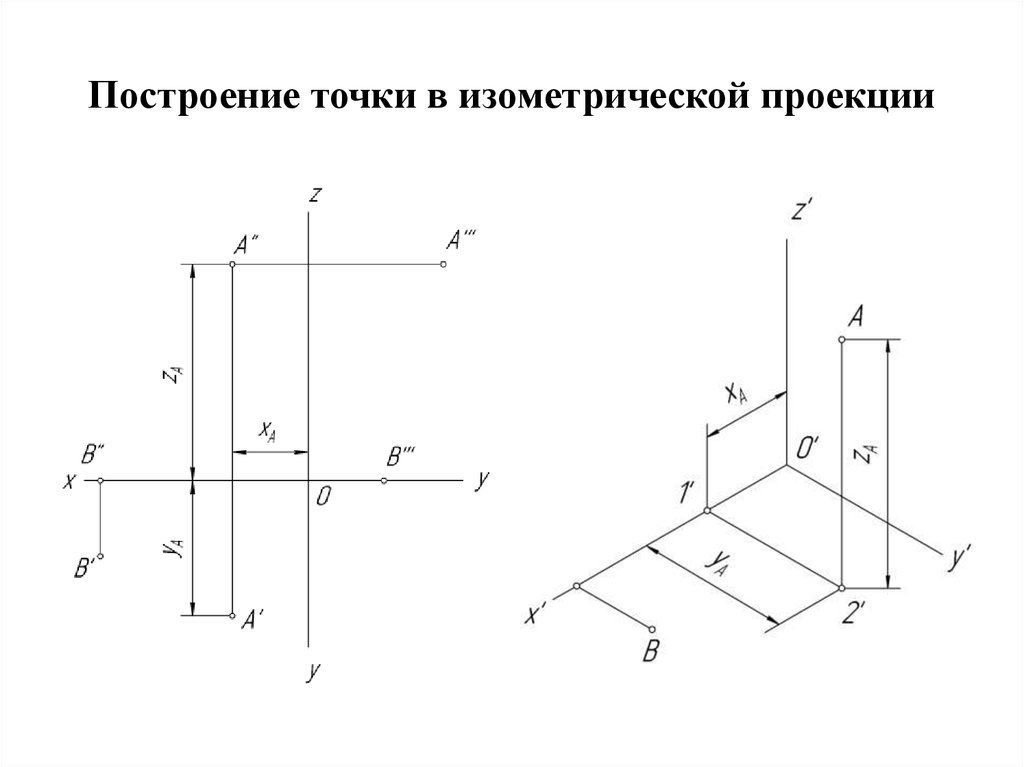

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

Рис. 105

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

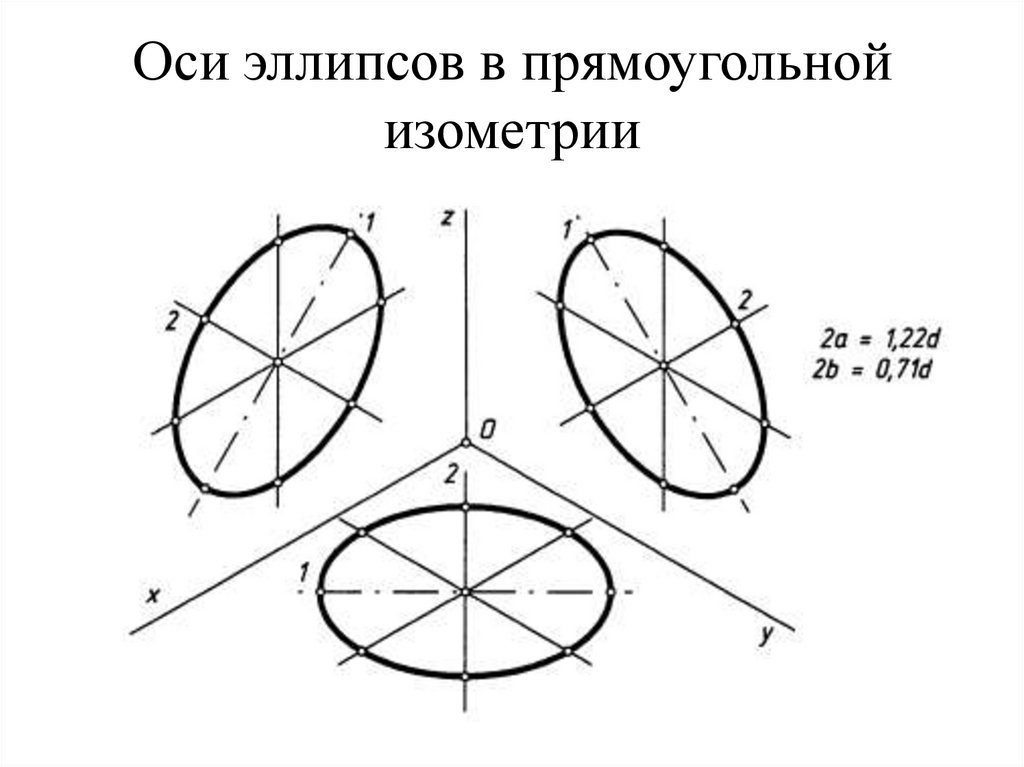
Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Рис. 106

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

Рис. 107

Этот способ заключается в построении изометрии квадрата, описанного вокруг окружности. Точки N_p и L_p (вершины квадрата) являются центрами для дуг радиуса R 1 . Соединив точку N_p с точками 2_р и 3_р, получим точки О₁ и О₂ – центры дуг радиуса R₂.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Рис. 108

Диметрия. Окружности, расположенные в горизонтальной и профильной плоскостях, проецируются в эллипсы с большой осью, равной 1,06Dокp , а малой – 0,35Dокр (рис. 109).

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Рис. 109

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Рис. 110

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

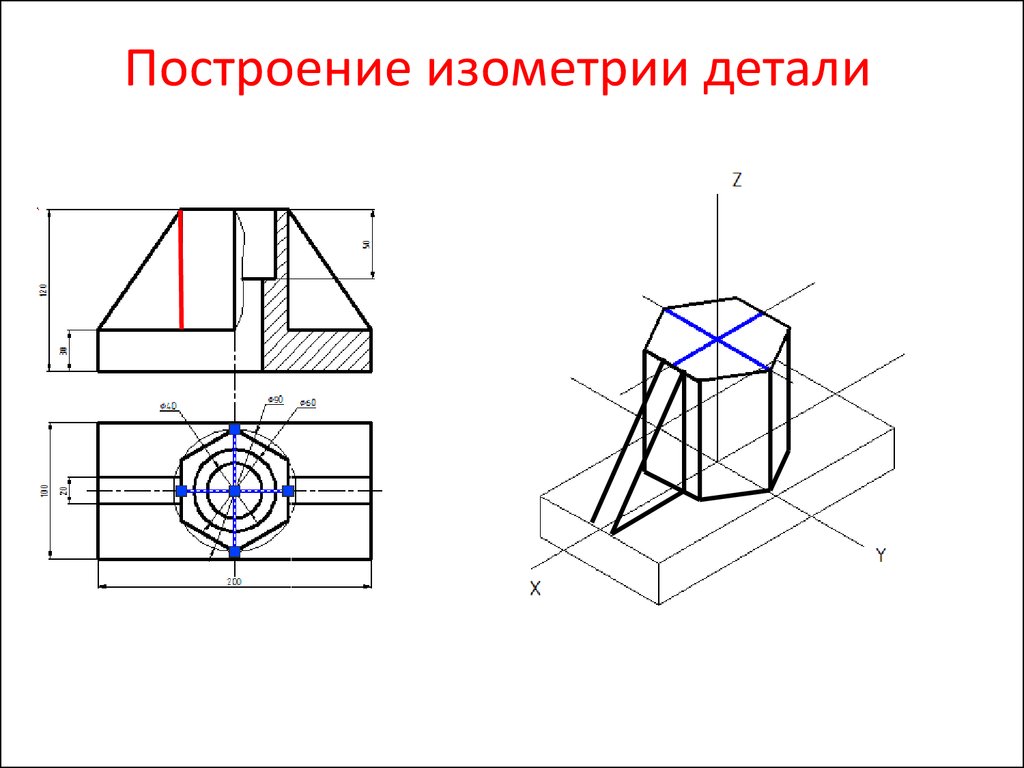
На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111рис. 112рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Рис. 114

СПЛАЙН

Благодаря своим знаниям и программы 3d max профессионалы создают интересные грамотные проекты за короткие сроки.

Изометрический архитектурный чертеж в разобранном виде — Tejjy Inc

Архитектура — это изучение эстетики здания или сооружения. Говорят, что он был изобретен около 10 000 лет до нашей эры. С момента своего создания чертежи и эскизы были неотъемлемой частью архитектуры. Архитектурные чертежи изображают архитектуру строительной конструкции.

Однако представить полный архитектурный вид здания на одном чертеже достаточно сложно. Поэтому позже было изобретено несколько типов рисунков, которые могли представлять архитектуру здания, каждый с разных точек зрения и видов. Некоторые из них широко используются: – изометрический, орфографический, развертка, сечение, вырез, деталь и вспомогательный вид. В этой статье мы сосредоточимся на изометрических архитектурных чертежах для архитектуры и подробно рассмотрим их.

Содержание [TOC]

📑Что такое изометрический рисунок?
- 📑benefits изометрических рисунков для проектов AEC
- 📑limitions of Isometric Design

📑Types изометрических архитектурных чертежей

- WHOMETRICE ENGINIGHTER DRAWING
999999999999999999999999999999999999 гг.
- 📑Преимущества изометрических чертежей для проектов AEC
- 📑Ограничения изометрического проектирования
Используйте автоматизацию BIM для автоматизации моделирования и проектирования
📑types изометрических архитектурных рисунков
- - Правила для создания изометрического инженерного рисунка

Это типичный рисунок. объект рисуется в полном масштабе, чтобы можно было четко увидеть взаимосвязь между различными частями объекта. Этот тип чертежа часто используется в архитектуре для точного представления объекта или конструкции.

Изометрические чертежи помещений можно создавать вручную или с помощью компьютерных программ, таких как AutoCAD или Revit. После завершения чертежа его можно использовать для создания трехмерной модели объекта или конструкции. Изометрические инженерные чертежи также могут быть созданы из 3D-модели конструкции BIM.

📑Преимущества изометрических чертежей для проектов AEC

Изометрические чертежи в архитектуре и строительстве обеспечивают отличную визуализацию с точным и подробным представлением здания и его компонентов. Профессионалы AEC могут использовать широкий спектр преимуществ изометрического дизайна, а именно:

Изометрические чертежи чрезвычайно ценны для дизайнеров, особенно архитекторов, промышленных дизайнеров и дизайнеров интерьеров, а также инженеров, поскольку они позволяют им визуализировать помещения, товары и инфраструктуру. Это отличный способ быстро протестировать различные концепции дизайна.
Изометрическая проекция также может быть полезна во множестве других сценариев. В системах навигации, таких как те, которые используются в музеях или галереях, изометрические настенные карты могут указывать посетителям, где они находятся в здании, что еще происходит и как ориентироваться.
Некоторые из лучших инфографиков используют изометрическую проекцию, чтобы показать больше информации, чем позволяет 2D-рисунок. Эта стратегия также используется некоторыми из лучших логотипов для создания эффекта.
Изометрический архитектурный чертеж облегчает передачу замысла проекта клиенту и специалистам по строительству, а также лучше объясняет сложности проекта.

📑Ограничения изометрической проекции

Есть несколько ограничений изометрической проекции для AEC. Давайте рассмотрим недостатки изометрических конструкций, приведенные ниже.

Из-за отсутствия ракурса изображение выглядит искаженным.
Больше подходит для прямоугольных форм, чем для изогнутых.
Форма и глубина искажены.
Он просто обеспечивает 2D-вид вместо подлинного.

📑Типы изометрических архитектурных чертежей

Услуги по изометрическому рисованию широко используются инженерами, архитекторами и другими специалистами в области строительства и инженерами, архитекторами и другими специалистами в области строительства для различных целей. Использование изометрических инженерных чертежей приведено ниже.

Изометрические чертежи сантехники позволяют сантехникам и инженерам-сантехникам визуализировать свои системы до их установки.
Электрические изометрические чертежи используются инженерами-электриками для представления фактического положения и расположения электрических систем и компонентов в здании.
С помощью механических изометрических чертежей инженеры-механики и инженеры по ОВКВ могут обеспечить точные размеры компонентов механических систем и систем ОВКВ.
Точно так же изометрические чертежи трубопроводов обеспечивают отличную визуализацию системы на этапе планирования для эффективного и бесконфликтного исполнения.

Правила создания изометрических чертежей

Существует несколько правил создания изометрических чертежей помещений в строительстве. Правила создания изометрического рисунка следующие: –

Вертикальная и горизонтальная линии обычно используются для изображения изометрического объекта. В изометрическом архитектурном чертеже горизонтальные линии создаются под углом 30° к горизонтальной плоскости, а вертикальные линии остаются вертикальными.
Три оси координатной плоскости должны образовывать друг с другом угол 120°.
Три грани объекта отображаются в изометрической проекции, и каждая грань равномерно расширена.

Заключение

Изометрические чертежи — это тип аксонометрического чертежа, в котором три оси представлены воображаемыми линиями, отстоящими друг от друга на 120 градусов. Изометрические чертежи проектов часто используются инженерами, архитекторами и дизайнерами интерьеров для проектов AEC. Они представляют собой отличный способ представления трехмерных объектов в двухмерном формате и могут использоваться для различных целей, включая проектирование зданий и других сооружений. Изометрические инженерные чертежи помогают архитекторам более эффективно и точно передавать свои проекты, предлагая глубокое понимание конструкции здания. Если вы хотите узнать больше об изометрических архитектурных чертежах или изучить наши комплексные услуги по архитектурным чертежам. Чтобы получить бесплатную консультацию и индивидуальное ценообразование, свяжитесь с командой консультантов по BIM Tejjy Inc. сегодня.

Архитектура — это изучение эстетики здания или конструкции. Говорят, что он был изобретен около 10 000 лет до нашей эры. С момента своего создания чертежи и эскизы были неотъемлемой частью архитектуры. Архитектурные чертежи изображают архитектуру строительной конструкции.

Это тип изобразительного рисунка, в котором три стороны объекта нарисованы в полном масштабе, так что можно ясно увидеть отношения между различными частями объекта. Этот тип чертежа часто используется в архитектурном проектировании для точного представления объекта или конструкции.

📑Преимущества изометрических чертежей для проектов AEC

Изометрические чертежи в архитектуре и строительстве обеспечивают отличную визуализацию с точным и подробным представлением здания и его компонентов. Специалисты по проектированию зданий и сооружений могут использовать широкий спектр преимуществ изометрического проектирования, а именно: –

Изометрические чертежи чрезвычайно ценны для дизайнеров, особенно архитекторов, промышленных дизайнеров и дизайнеров интерьеров, а также инженеров, поскольку они позволяют им визуализировать помещения, товары и инфраструктура. Это отличный способ быстро протестировать различные концепции дизайна.
Изометрическая проекция также может быть полезна во множестве других сценариев. В системах навигации, таких как те, которые используются в музеях или галереях, изометрические настенные карты могут указывать посетителям, где они находятся в здании, что еще происходит и как ориентироваться.
Некоторые из лучших инфографиков используют изометрическую проекцию, чтобы показать больше информации, чем позволяет 2D-рисунок. Эта стратегия также используется некоторыми из лучших логотипов для создания эффекта.
Изометрический архитектурный чертеж облегчает передачу замысла проекта клиенту и специалистам по строительству, а также лучше объясняет сложности проекта.

📑Ограничения изометрической проекции

Из-за отсутствия ракурса изображение выглядит искаженным.
Больше подходит для прямоугольных форм, чем для изогнутых.
Форма и глубина искажены.
Он просто обеспечивает 2D-вид вместо подлинного.

Использование BIM-автоматизации для автоматизации моделирования и проектирования

Позвоните намЗапросите бесплатную цитату

📑Типы изометрических архитектурных чертежей

Услуги по изометрическому рисованию широко используются инженерами в строительных проектах и проектных чертежах MEP (механических, сантехнических, электрических). архитекторы и другие специалисты в области строительства для различных целей. Использование изометрических инженерных чертежей приведено ниже.

Изометрические чертежи сантехники позволяют сантехникам и инженерам-сантехникам визуализировать свои системы до их установки.
Электрические изометрические чертежи используются инженерами-электриками для представления фактического положения и расположения электрических систем и компонентов в здании.
С помощью механических изометрических чертежей инженеры-механики и инженеры по ОВКВ могут обеспечить точные размеры компонентов механических систем и систем ОВКВ.
Точно так же изометрические чертежи трубопроводов обеспечивают отличную визуализацию системы на этапе планирования для эффективного и бесконфликтного исполнения.

Правила создания изометрических чертежей

Вертикальная и горизонтальная линии обычно используются для изображения изометрического объекта. В изометрическом архитектурном чертеже горизонтальные линии создаются под углом 30° к горизонтальной плоскости, а вертикальные линии остаются вертикальными.
Три оси координатной плоскости должны образовывать друг с другом угол 120°.
Три грани объекта отображаются в изометрической проекции, и каждая грань равномерно расширена.

Заключение

Изометрии треугольников и сегментов

Изометрия треугольника | Сохранение ориентации из сегмента | Ориентация-реверс с сегмента

1.

Как построить данные изометрии по изображению треугольника

Для данных двух треугольников ABC и A’B’C’ мы говорим, что преобразование T принимает ABC в A’B’C’, если T(A) = A’ и T(B) = B’ и T(C) = C’. Если ABC и A’B’C’ являются конгруэнтными треугольниками, мы знаем из фундаментальной теоремы об изометриях, что существует ровно одна изометрия T, которая переводит ABC в A’B’C’.

Примечание: Этот оператор учитывает порядок вершин. Если T переводит ABC в A’B’C’, то он не переводит ABC в C’A’B’.

Однако в конкретных случаях нужно точно определить по двум треугольникам что такое изометрия Т. Какой это тип изометрии и каковы ее определяющие данные.

Метод построения 1: (Используйте доказательство основной теоремы)

Доказана фундаментальная теорема о том, что треугольник ABC можно преобразовать в конгруэнтного треугольника A’B’C’ композицией одно-, двух- или трехпрямых отражений. Таким образом, изометрия T, которая переводит ABC в A’B’C’, и есть эта композиция. Доказательство представляет собой пошаговое построение до трех линий отражения. Можно сделать эту конструкцию, а затем использовать теоремы о композиции изометрий точно определить, что такое изометрия Т. Однако этот метод долгий и косвенный, особенно для скользящих отражений.

Способ построения 2: (использовать средние точки)

Даны два конгруэнтных треугольника ABC и A’B’C’, постройте их середины A». AA’, B» из BB’, C» из CC’.

Тогда расположение средних точек покажет, какую изометрию принимает Т. от АВС до А’В’С’.

Если T является тождеством или переводом, A»B»C» является конгруэнтным треугольником к АВС.
Если T — это поворот на угол x, но не на пол-оборота, то A»B»C» является треугольником аналогично ABC (коэффициент масштабирования cos(x/2).
Если T — половина оборота, все 3 средние точки — это одна и та же точка, т. е. центр полуоборота.
Если T является отражением линии, 3 средние точки коллинеарны и не более 2 совпадают, так как A, B, C не лежат на одной прямой*. Таким образом, через середины проходит одна линия, а это зеркальная линия Т.
Если T является скользящим отражением, 3 средние точки коллинеарны и не более 2 совпадают, так как А, В, С не лежат на одной прямой*. Таким образом, есть одна линия через середины, и это инвариантная линия T.

Перевод
Полуоборота
Вращение
Отражение линии
Скользящее отражение
* Доказательство того, что точки A», B» и C» не могут быть одинаковыми для прямой отражение или скользящее отражение следует из определения этих преобразований. Для T = отражение линии в линии m, A», B», C» являются основаниями перпендикуляров. к m через A, B, C. Таким образом, они могут совпадать только в том случае, если A, B, C находятся на той же прямой, перпендикулярной m. Для T = отражение скольжения с вектором скольжения v, тогда если A*, B*, C* основания перпендикуляров к m, проходящих через точки A, B, C, тогда A», B», C» — переносы этих точек на вектор (1/2)v. Таким образом середины A», B», C» совпадают тогда и только тогда, когда совпадают ножки A*, B*, C*, что снова означает, что A, B, C лежат на одной прямой, перпендикулярной m.
Эти случаи позволяют нам вывести характер изометрии по средним точкам А»В»С».
Если точки совпадают с точкой P, T является полуоборотом с центром P.
Если точки лежат на одной прямой, но не все совпадают, то Т является ориентацией реверсивный Полное построение геометрических данных прописано в этом разделе ниже: Метод построения: линейное отражение или скользящее отражение из 2 равных сегментов
Если точки образуют треугольник, то T сохраняет ориентацию, а данные могут быть построены по описанию в этом разделе ниже: Строительство Метод: вращение или перемещение из 2 конгруэнтных сегментов
2.
Как построить данные поворота или перевода с изображения отрезка или точки
Основная теорема | Из изображения сегмента | Из изображения точки, зная угол
Имея два отрезка AB и CD, мы говорим, что преобразование T переводит AB в CD, если T(A) = C и T(B) = D .
Примечание: Этот оператор учитывает порядок конечных точек. Если T переводит AB в CD, то он не переводит AB в DC.
Теорема (Фундаментальная теорема для сохранения ориентации Изометрии)
Для двух конгруэнтных отрезков AB и CD существует ровно один сохраняющий ориентацию отрезок. изометрия T, переводящая AB в CD.
Доказательство (также конструкция):
Это состоит из первых двух шагов второй фундаментальной теоремы изометрий.
Если A и C различны, пусть m ₁ будет серединным перпендикуляром переменного тока. В частном случае, когда A = C, пусть m ₁ = линия AB (на самом деле, подойдет любая линия через А). Пусть R ₁ обозначает отражение линии в m ₁ .
Для этого отражения R ₁ (A) = C. Пусть B’ = R ₁ (B). Отрезок CD конгруэнтен CB’, так как R ₁ является изометрией.
Если B’ не D, пусть m ₂ будет серединным перпендикуляром к B’D. Так как |CB’| = |CD|, точка C находится на m ₂ . В особом случае B’ = D, пусть m ₂ = линия CD. Пусть R ₂ — отражение в м ₂ .
В любом случае 9 р.0306 2 (B’) = D и R ₂ (C) = C. Так установка T = R ₂ R ₁ , T(A) = C и T(B) = D.
T — композиция двух линейных отражений. T — вращение с центром O если две прямые m ₁ и m ₂ пересекаются в одной точке O; Это является переводом, если m ₁ и m ₂ параллельны. Если линии одинаковы, то Т тождественно.
Наконец, утверждается, что Т является единственной сохраняющей ориентацию изометрией, которая переводит AB в CD. Чтобы убедиться в этом, предположим, что S = R ₄ R ₃ также переводит AB в CD. Тогда S ^-1 = R ₃ R ₄ берет CD жаба. Таким образом, S ^-1 T = R ₃ R ₄ R ₂ R ₁ переводит AB в AB.
Это означает, что S ^-1 T (A) = A и S ^-1 T (B) = B являются двумя неподвижные точки изометрии. Но изометрия S ^-1 Т — сохраняющая ориентацию изометрия, так как это произведение 4-х линейных отражений. Это означает, что это является вращением, переводом или тождеством. Но единственная из этих изометрий с двумя неподвижными точками — тождество, поэтому S ^-1 T = I, и поэтому T = S.
Таким образом, существует только одна сохраняющая ориентацию изометрия, которая переводит AB в CD.
Метод построения: вращение или перемещение от 2 конгруэнтные сегменты
Учитывая два конгруэнтных отрезка AB и CD, как можно построить единственный сохраняющий ориентацию отрезок? изометрия T, которая переводит AB в CD?
На практике представляют интерес случаи, когда T представляет собой вращение или перемещение, поскольку, если A = C и B = D, для тождества не требуется построения.
Общий случай: Предположим, что A не C, а B не D. Постройте линии m = биссектриса AC и n = биссектриса BD.
Если T — вращение, прямые m и n пересекаются в точке O, центре вращение. Ведь в этом случае A и C = T(A) лежат на одной окружности. с центром O, так что биссектриса m хорды AC проходит через O. Для по той же причине n проходит через O. Угол поворота равен углу АОС.
В особом случае полуоборота O также является средней точкой AC и BD. а также пересечение m и n.
Если T является переносом, то AC и BD параллельны, поэтому m и n также параллельно. Вектор трансляции AC.
Особые случаи: Предположим, что A = C, но B и D различны. В таком случае, A уже является центром вращения, которое приведет B к D. Вращение угол это угол БАД. Аналогично обрабатывается случай, когда B = D. Если А = C и B = D, тогда T = тождество.
Метод построения: Вращение изображения одной точки плюс угол поворота
Предположим, что T является поворотом на угол x. Если нам даны два различных точки A и C, такие, что T(A) = C, достаточно ли этого для определения T?
Поскольку угол поворота T задан, если можно построить центр O, тогда Т будет известно полностью.
Из данной информации T(A) = C следует, что O находится на прямой m, серединный перпендикуляр к АС. Кроме того, угол AOC = x.
Угол x является ориентированным, или углом со знаком. Есть несколько корпусов:
Угол x = 0 градусов. Это означает, что T = I и, следовательно, A = T(A) = C. Это нарушает предположение, что A и C различны.
Угол х = 180 градусов. В этом случае T является полуоборотом, а O = середина AC. На этом строительство завершено.
Для угла x 0 < x < 180. Это будет обсуждаться ниже
Для угла x: -180 < x < 0. Это очень похоже на случай 3, и будет обсуждаются ниже.
Случаи 3 и 4: В каждом случае 0 < |x| < 180 - неориентированный угол АОС.
Представьте, что O построен. Тогда OA = OC, так как T — вращение с центром O. Кроме того, угол AOC = x. Это означает, что треугольник OAC равнобедренный треугольник с (неориентированным) углом O = |x|, а угол A = угол С = у = (180-|х|)/2 = 90 (|х|/2).
Итак, чтобы построить такой треугольник, нужно только построить луч AD так, что угол CAD = y. Пересеките этот луч с m, чтобы получить P.
Отразите P от линии AC, чтобы получить Q. Тогда оба треугольника PAC и QAC равнобедренные. треугольники с (неориентированными) углами |x|, y, y. Один из углов APC или AQC равно +|х| а другой — |x|. Таким образом, одно является решением случая 3, а другое решение случая 4.
Из этой конструкции видно, что для каждого (ориентированного) существует только одна Т. Икс.
Для построения угла y необходимо только построить равнобедренный треугольник с углами |x|, y, y и скопируйте угол y. Например, предположим этот угол FGH = |x| дано. Затем выберите точку K на луче GF и пусть точка L на GH будет той точкой, где |GL| = |ГК|. Это значит, что GKL — равнобедренный треугольник с углами |x|, y, y.
Это завершает построение, а также доказывает теорему о том, что для любые различные A и C и любой ориентированный ненулевой угол, существует единственный вращение, которое переводит A в C с этим углом поворота
Другие построения: Перенос или полуоборот от изображения одной точки
Для двух различных точек A и C существует единственный полуоборот H, который занимает от А до С.
Конструкция центра O полуоборота проста. О — середина переменного тока. Для любой другой точки B H (B) — это точка D, для которой O — середина. БД.
Для двух различных точек A и C существует уникальный перевод T, который принимает от А до С.
Вектор трансляции AC. Таким образом, для любого B, не лежащего на прямой AC, T(B) есть точка D такое, что ACDB — параллелограмм. Если B находится на линии AC, то эта альтернатива Критерий параллелограмма все еще работает. D — точка, так что середина AD = середина BC.

3. Как построить данные линии отражения или скользящее отражение от изображения сегмента или точки
Основная теорема | Из изображения сегмента | Из изображения точки, знающей вектор
Вспомним наше определение: для двух отрезков AB и CD мы говорим, что преобразование T переводит AB в CD, если T(A) = C и T(B) = D.
Примечание: Этот оператор учитывает порядок конечных точек. Если T переводит AB в CD, то он не переводит AB в DC.
Теорема (Фундаментальная теорема для обращения ориентации Изометрии)
Для двух конгруэнтных отрезков AB и CD существует ровно один отрезок, меняющий ориентацию. изометрия U, переводящая AB в CD.
Доказательство: Это следует из теоремы для сохраняющих ориентацию изометрий
Для заданных AB и CD существует ровно одна сохраняющая ориентацию изометрия T, которая переводит AB в CD. Пусть R = отражение линии в AB. Тогда U = RT — изменяющая ориентацию изометрия, переводящая AB в CD. Это показывает, что U существует.
Чтобы увидеть, что существует только одна такая U, предположим, что V — это еще одна изменяющая ориентацию изометрия, переводящая AB в CD. Тогда RV — сохраняющая ориентацию изометрия который переводит AB в CD, поэтому RV должно = T. Тогда V = RRV = RT. Но по определению, РТ = U.
КЭД
Метод построения: линейное отражение или скользящее отражение из 2 конгруэнтных сегментов
Имея два конгруэнтных отрезка AB и CD, как можно построить единственный изменяющий ориентацию изометрия U, которая переводит AB в CD?
Из определения линейного отражения и теоремы о скользящем отражении, для любого изменяющего ориентацию U и для любых точек A и C = U (A) середина AC находится на зеркальной линии (если U — отражение линии) или инвариантной линии (если U — скользящее отражение).
Таким образом, если U переводит AB в CD, пусть M = середина AC и N = середина BD.
Пусть A’ и B’ будут отражениями A и B в линии MN.
Если U является отражением линии, то отрезки AC и BD оба перпендикулярны к MN, и фактически MN является серединным перпендикуляром к этим двум отрезкам. В этом случае A’ = C и B’ = D.

Если U — скользящее отражение, то MN — инвариантная линия. Ни один из отрезки AC и BD будут перпендикулярны MN. Вектор скольжения = A’C = Б’Д.
Чтобы построить образ некоторой другой точки P, отразите P от линии MN до получить P’ и затем перевести на вектор скольжения.
Метод построения: линейное отражение или скользящее отражение по изображению одной точки плюс вектор скольжения
Предположим, что известно, что U является либо (а) линейным отражением, либо (б) скользящим отражением с заданным вектором планирования EF.
No related posts.