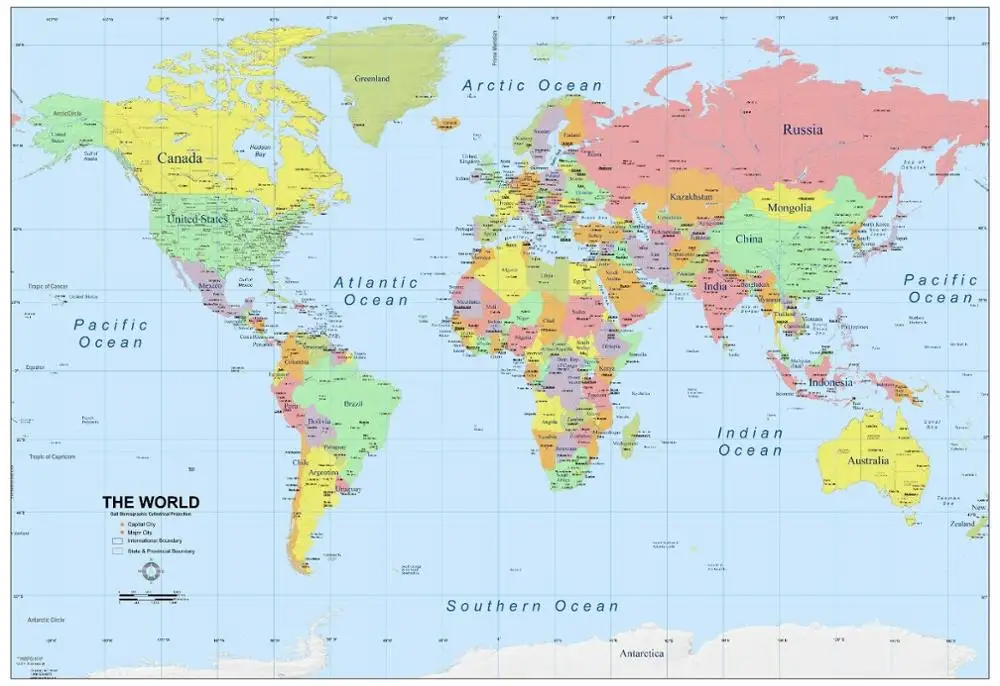
Вот почему плоские карты мира не нарисованы в масштабе
В тренде > Видео
Всякий раз, когда вы смотрите на плоскую карту мира, вы должны воспринимать то, что видите, с долей скептицизма. В частности, одна из них, известная как проекция Меркатора, искажает реальные размеры массивов суши, таких как Аляска и Гренландия, и заставляет их казаться больше по сравнению с Африкой или Северной Америкой, чем они есть на самом деле. Но почему это происходит?
Как оказалось, изобразить поверхность круглой планеты на плоском листе бумаги — задача не из легких. Взяв гипотетическую скалку на Землю, чтобы расплющить ее, вы можете разложить ее на листе бумаги несколькими способами.
Некоторые проекции, такие как проекция Робинсона, проекция Гуда-Гомолосина и проекция Галла-Питерса, гораздо точнее отображают размеры земных массивов, но они оставляют контурные пробелы или визуальные аномалии по всей карте.
Проекция Меркатора просто закрашивает не очень красивые участки карты, растягивая части земной поверхности по плоской поверхности для более эстетичного вида для читателя карты.
Итак, в следующий раз, когда вы посмотрите на проекцию Меркатора и удивитесь, почему Гренландия выглядит такой большой, теперь вы знаете, почему.
Поделиться
Об авторе
Энтони Бушар
Очарованный научными открытиями и средствами массовой информации, Энтони нашел свой путь сюда, в LabRoots, где он мог попробовать себя в обеих областях. Энтони — технологический наркоман, который имеет большой опыт работы с компьютерными системами и автомобильной механикой, как бы это ни звучало.
Вам также может понравиться
15 декабря 2020 г.
Химия и физика
15 декабря 2020 г.
Беспроводная зарядка — насколько мы близки к реализации видения Tesla?
Когда изобретатель и провидец Никола Тесла построил свою башню Уорденклиф, чудовищную башню высотой 186 футов и шириной 68 футов.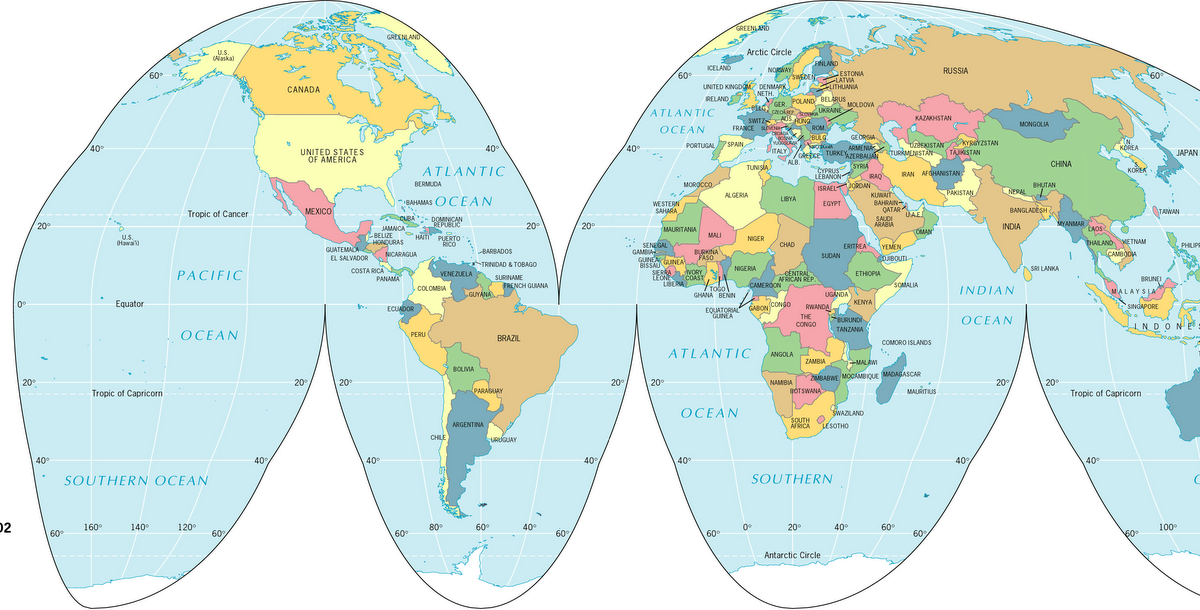
…
Автор:
10 февраля 2021 г.
Растения и животные
10 февраля 2021 г.
Является ли нано-хамелеон самым маленьким видом рептилий в мире?
Скажи «привет!» до нано-хамелеона, главного претендента на звание самой маленькой рептилии в мире. Согласно …
Автор: Тиффани Дазет
15 мая 2021 г.
15 мая 2021 г.
Ученые нашли жидкую воду внутри метеорита
Ученым известно, что вода в изобилии содержится в Солнечной системе, существующей в кольцах Сатурна и на его спутнике Энцеладе.
…
Автор: Энни Леннон
04 июня 2021 г.
Растения и животные
04 июня 2021 г.
Что хоботы слонов учат науке о всасывании
То, как слон поднимает чипсы из тортильи, может вдохновить на создание технологии всасывания следующего поколения.
Автор: Энн Медина
05 июня 2021 г.
Космос и астрономия
05 июня 2021 г.
Предоставило ли тепло астероидов строительные блоки для жизни на Земле?
Исследователи из Университета Кобе в Японии обнаружили, что тепло, выделяемое при столкновении небольших астрономических тел, может
.
Автор: Энни Леннон
17 октября 2022 г.
микробиология
17 октября 2022 г.
Это панрезистентный Candida auris? Теперь вы можете знать наверняка
Candida auris представляет собой глобальную проблему, классифицированную CDC как неотложная угроза. Согласно последним данным CDC 2 …
Автор: Сара Хоффман
2.3: Масштаб карты и проекция
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2238
- К.
Эллисон Ленкейт-Мизан - Колледж Футхилл
Эллисон Ленкейт-МизанМасштаб карты определяется как: Отношение расстояния на карте к расстоянию на земле
Один из способов визуализации масштаба карты, который я считаю полезным, — это представить себе карту мира. Длина экватора в разных масштабах — это хороший способ оценить фактический размер карты в этом масштабе. В таблице ниже указано расстояние на карте (как если бы вы проложили линейку по карте и измерили экватор) для каждого масштаба карты. Как видите, карта масштаба 1:400 000 000, вероятно, уместилась бы на двух страницах вашего учебника, а карта масштаба 1:10 000 000 заняла бы стену вашего класса. В масштабе 1:1000 карта мира растянулась бы на всю округу!
| 1:400 000 000 | |
| 1:40 000 000 | 1. 0002 |
| 1:10 000 000 | 4.0008 |
| 40.008 | |
| 1:100 000 | 400.078 |
| 1:10 000 | 4000,78 |
| 1:1000 |
«Большой масштаб» Маленькие детали большие
| «Малый масштаб» Крупные детали маленькие
|
Разрешение определяется как: Наименьший объект, представленный на карте
- Такой город, как Лос-Альтос-Хиллз, вероятно, не будет представлен на карте США (в масштабе 1:10 000 000). Таким образом, разрешение этой карты слишком грубо для представления нашего города.
- Такой город, как Лос-Альтос-Хиллз, вероятно, будет представлен на карте залива (масштаб 1:500,000). Таким образом, разрешение этой карты достаточно хорошо, чтобы представить наш город.
Таким образом, разрешение этой карты слишком грубо для представления нашего города. Картографическая проекция — это способ, которым мы изображаем сферическую Землю на плоской карте (см. ниже). Возможно, вы захотите выполнить поиск, чтобы найти различные типы картографических проекций. Однако самое важное, что следует помнить о картографических проекциях, это то, что всегда будет некоторое искажение . Некоторые картографические проекции сохраняют относительные площади, некоторые проекции сохраняют форму (например, форму береговых линий), некоторые пытаются делать и то, и другое, но в конечном итоге не делают ни того, ни другого. Но в результате будет всегда может быть какая-то ошибка в проецируемой карте.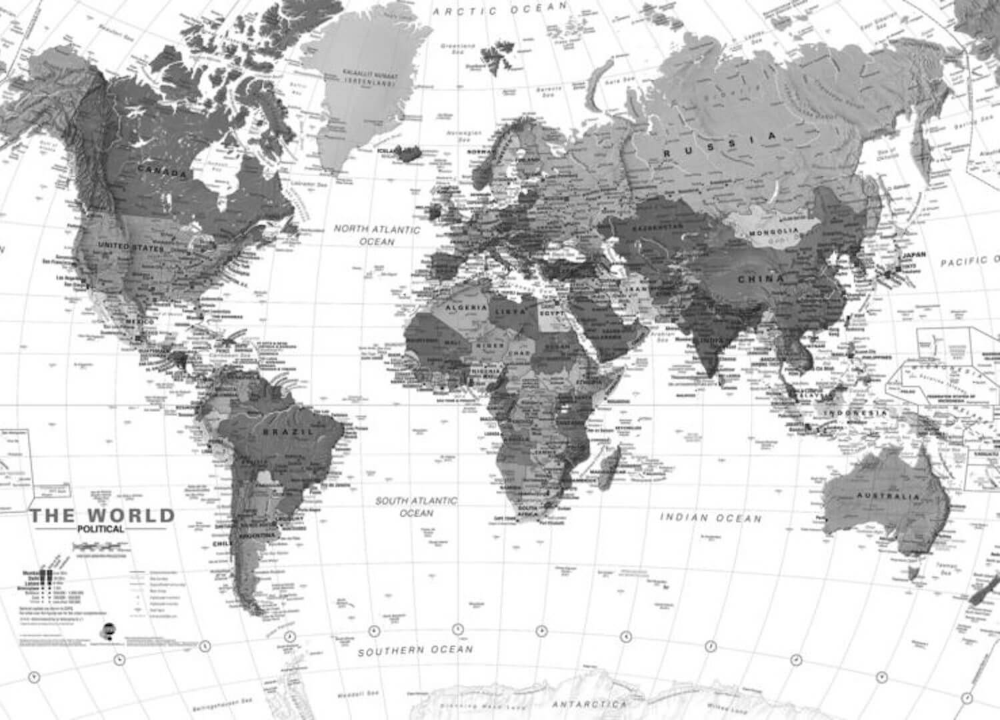
Один пример ошибки в картографической проекции можно увидеть на картах Соединенных Штатов. На приведенном ниже рисунке показаны три различные проекции Соединенных Штатов, наложенные друг на друга. Обратите внимание, что чем дальше вы уходите от центра проекции (ярко-розовая точка в середине рисунка ниже), тем больше становится искажение. Посмотрите, в частности, на Флориду, Вашингтон и Мэн.
Рисунок 2.4.2 Картографическая проекция СШАДругим примером искажения, вызванного картографической проекцией, является представленная территория Австралии и Гренландии. Площадь Гренландии составляет 1/3 территории Австралии. То есть Австралия в три раза больше Гренландии. Карта слева представляет собой равновеликую проекцию Моллвейде, которая сохраняет относительную площадь форм рельефа. Проекция справа — это проекция Галла (очень похожая на проекцию Меркатора), и она сохраняет форму рельефа, но не площадь.
Рисунок 2.4.3 Другие картографические проекции Эта страница под названием 2.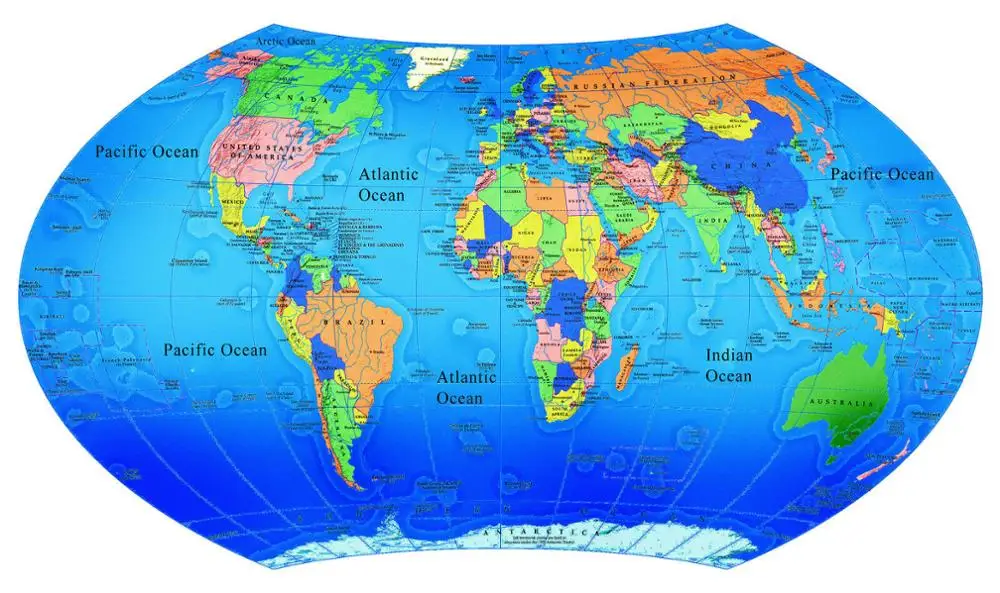
3: Масштаб и проекция карты распространяется под лицензией CC BY-NC 4.0, ее автором, ремиксом и/или куратором является К. Эллисон Ленкейт-Мизан.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- К. Эллисон Ленкейт-Мизан
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
