Кривая безье свойства: Иллюстрированный самоучитель по цифровой графике › Принципы векторной графики › Свойства кривых Безье [страница — 151] | Самоучители по графическим программам

Разное 

Содержание

Иллюстрированный самоучитель по цифровой графике › Принципы векторной графики › Свойства кривых Безье [страница — 151] | Самоучители по графическим программам

Свойства кривых Безье

Кривые Безье любой степени обладают следующими важными свойствами.

  • Начальная и конечная контрольные точки лежат на кривой.
  • Кривая на всем протяжении непрерывна, у нее отсутствуют разрывы. Это важнейшее свойство, без которого кривая Безье вообще бы не рассматривалась.
  • Касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с другими двумя соседними контрольными точками, через которые в общем случае кривая не проходит.
  • Точки на краях касательных будут располагаться на кривой только в том случае, если последняя представляет собой прямую линию.
  • Поскольку кривая Безье представляет собой взвешенное усреднение всех ее контрольных точек с положительными весами, а сумма их равна единице, кривая всегда располагается внутри выпуклого многоугольника из ее контрольных точек (рис.
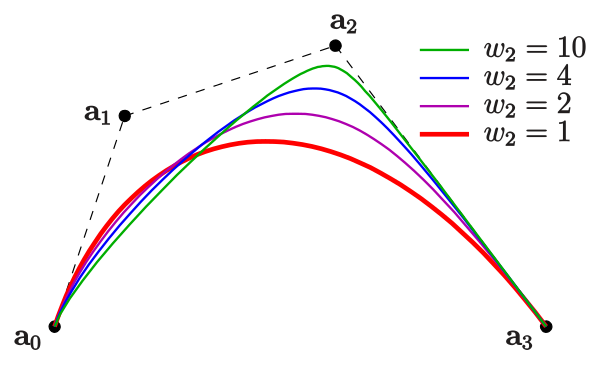
    12.20), как и рассмотренная выше NURBS-кривая.
  • Кривую Безье можно рассматривать как пошаговое уточнение формы многоугольника, получаемого последовательным соединением ее контрольных точек (рис. 12.21-12.24). При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма определяется относительным расположением оставшихся точек, через которые в общем случае она не проходит.


Рис. 12.20. Кривая в выпуклом многоугольнике

Исходя из этого можно представить канонический вид кривой Безье, который обычно используется в графических редакторах плоской графики.


Рис. 12.21. Первый этап аппроксимации кривой


Рис. 12.22. Второй этап аппроксимации кривой


Рис. 12.23. Третий этап аппроксимации кривой


Рис. 12.24. Итоговая ломаная кривая

Свойства кривых Безье

Кривые Безье любой степени обладают следующими важными свойствами.

  • Начальная и конечная контрольные точки лежат на кривой.

  • Кривая на всем протяжении непрерывна, у нее отсутствуют разрывы. Это свойство, без которого кривая Безье вообще бы не стала рассматриваться.

  • Касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с другими двумя соседними контрольными точками, через которые в общем случае кривая не проходит.

  • Точки на краях касательных будут располагаться на кривой только в том случае, если последняя представляет собой прямую линию.

  • Поскольку кривая Безье есть взвешенное усреднение всех ее контрольных точек с положительными весами, а сумма их равна единице, кривая всегда располагается внутри выпуклого многоугольника составленного из ее контрольных точек (рис. 1.17), как и рассмотренная выше NURBS-кривая.

Кривую Безье можно рассматривать как пошаговое уточнение формы многоугольника, получаемого последовательным соединением ее контрольных точек (рис. 1.18–1.21). При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма определяется относительным расположением оставшихся точек, через которые в общем случае она не проходит.

Рис. 1.17 Кривая в выпуклом многоугольнике

Исходя из этого, можно представить канонический вид кривой Безье, который обычно используют в графических редакторах плоской графики.

Рис. 1.18. Первый этап аппроксимации кривой Рис. 1.19. Второй этап аппроксимации кривой

Рис. 1.20. Третий этап аппроксимации Рис. 1.21. Итоговая ломаная кривая

4.2 Канонический вид кривой Безье

Рассмотрим канонический вид кривой Безье. Наша задача — понять, как из одной-единственной кривой получают бесконечно большое многообразие форм, и которые используют в векторной, а также компьютерной графике.

Общий вид кривой Безье имеет вот такую конструкцию (рис. 1.22).

Рис.

1.22. Канонический вид кривой Безье

Это уже не математическое описание, а сугубо прикладное отображение, именно то, которое знакомо всем пользователям векторных программ.

Такое отображение все чаще используют и в программах пиксельной графики, а также в программах верстки.

Для построения этой кривой требуются четыре контрольные точки. Но кривая физически проходит только через две из них, они получили название опорных. Одна из точек называется начальной (start point), а другая – конечной (end point). Две точки остаются в стороне, они получили название управляющих (control point).

Для того чтобы их не «потерять» (особенно когда в документе кривых насчитываются многие десятки и сотни), в программах векторной графики, да и в любых других программах, управляющие точки соединяют с опорными точками какой-нибудь линией. Иногда пунктирной, иногда тонкой сплошной.

Почему кривая располагает начальной и конечной точками? Потому что, вообще говоря, кривая Безье – это, прежде всего, вектор.

Справка. Слово «вектор» латинского происхождения: «vector» переводится как «несущий», в математике используется для обозначения отрезка определенной длины и направления. Два вектора считаются равными лишь в том случае, если у них не только одинаковы длины, но и совпадают направления (то есть они параллельны и одинаково ориентированы). При изменении направления меняется знак вектора.

Направление кривой, может быть, не всегда очевидно для пользователей векторной программы, но для самой программы оно всегда существенно. Направление контуров находит свою реализацию в так называемых составных контурах (compound paths). Если два векторных объекта, например образующих букву «о» и расположенных друг на друге, направлены в противоположные стороны (рис. 1.23), то изображение получится верное (с отверстием посередине).

Если те же векторные контуры направлены в одну сторону, то в этом случае один контур просто перекрывает другой, не образуя прозрачной области (рис.

1.24).

Рис. 1.23. Составной контур с разнонаправленными векторами

Рис. 1.24. Составной контур с однонаправленными векторами

Кривая Безье — это… Что такое Кривая Безье?

Кривы́е Безье́ или Кривы́е Бернште́йна-Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.

Кривая Безье является частным случаем многочленов Бернштейна, описанных Сергеем Натановичем Бернштейном в 1912 году.

Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).

Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.

Определение

Кривая Безье — параметрическая кривая, задаваемая выражением

где  — функция компонент векторов опорных вершин, а  — базисные функции кривой Безье, называемые также полиномами Бернштейна.

,

где — число сочетаний из по , где  — степень полинома,  — порядковый номер опорной вершины.

Виды кривых Безье

Линейные кривые

При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:

.

Квадратичные кривые

Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1 и P2.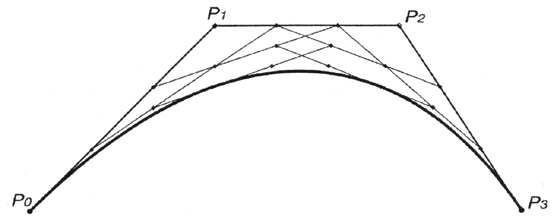

.

Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах (в SWF также могут использоваться кубические кривые Безье).

Кубические кривые

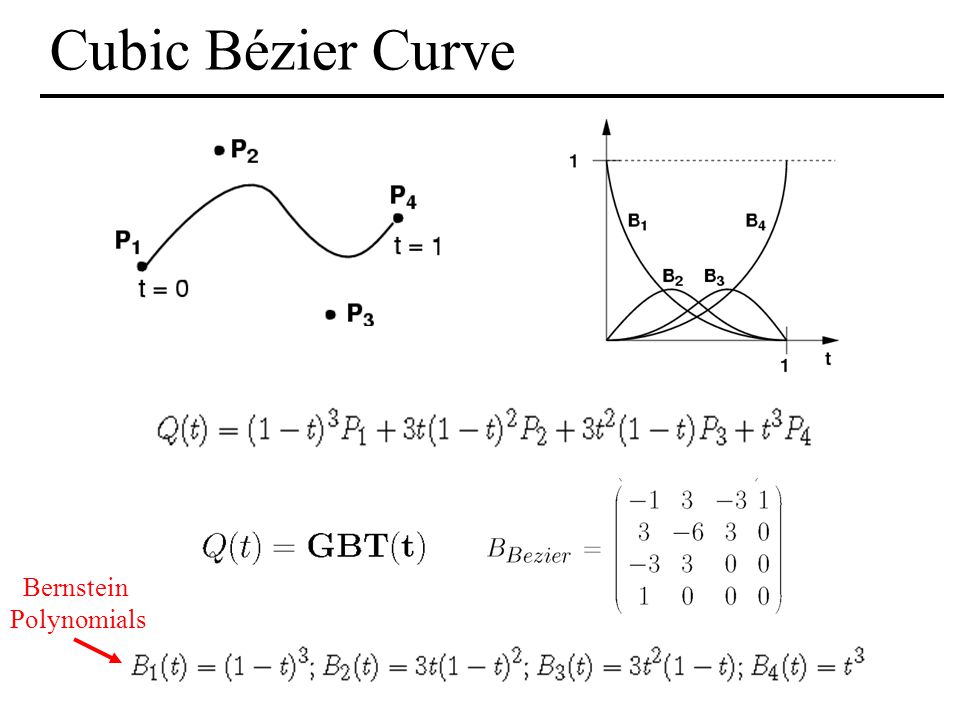
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

.
Кубическая кривая Безье

Четыре опорные точки

P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.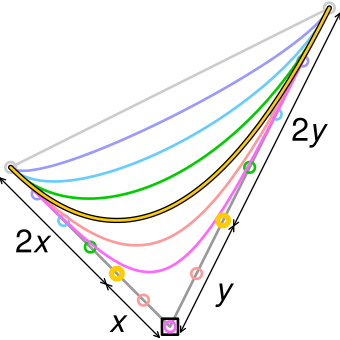

В матричной форме кубическая кривая Безье записывается следующим образом:

,

где называется базисной матрицей Безье:

В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG), Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых. SVG также позволяет работать со сплайнами Безье 4-й степени[1].

Построение кривых Безье

Линейные кривые

Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.

Квадратичные кривые

Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:

  • Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
  • Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
  • Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.

Построение квадратичной кривой Безье

Анимация t: [0; 1]

Кривые высших степеней

Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0

Построение кубической кривой Безье

Анимация t: [0; 1]

Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:

Построение кривой Безье 4-й степени

Анимация t: [0; 1]

Свойства кривой Безье

  • непрерывность заполнения сегмента между начальной и конечной точками;
  • кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
  • при наличии только двух контрольных точек сегмент представляет собой прямую линию;
  • прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
  • кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
  • масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;
  • изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
  • степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола;
  • окружность не может быть описана параметрическим уравнением кривой Безье;
  • невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

Применение в компьютерной графике

Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.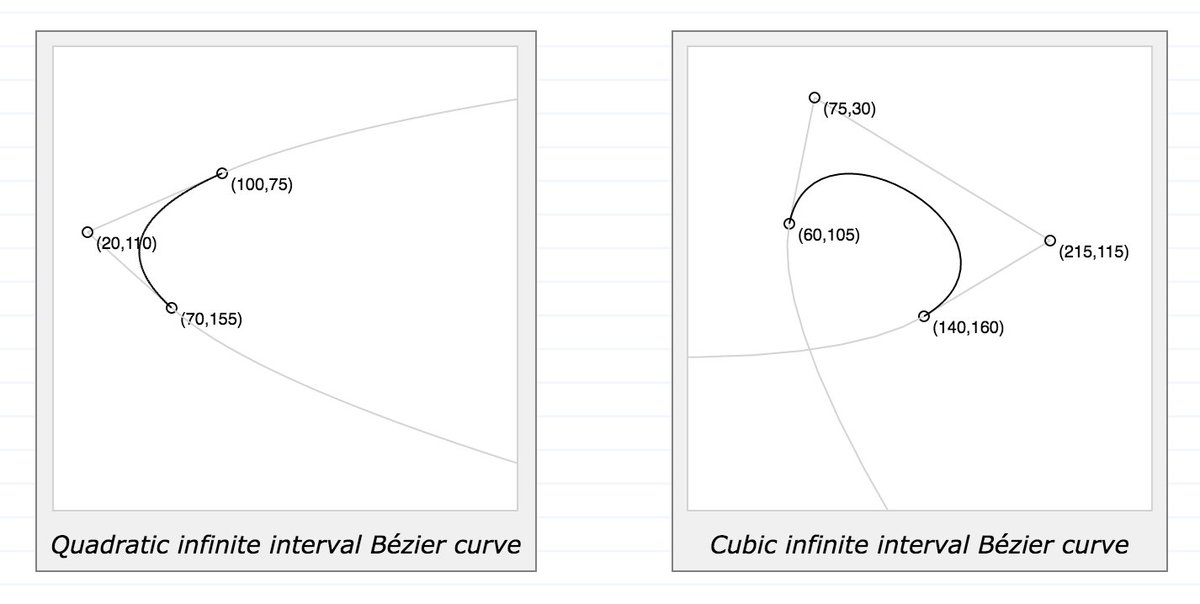

Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).

Преобразование квадратичных кривых Безье в кубические

Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами .

Ссылки

Литература

  • Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.

См. также

Примечания

Введение — Blender 3D — ПРОГРАМИШКА.

РФ

Логотип птицы изготовлен из кривых Безье.

Кривые и Поверхности — это особые типы объектов Blender. Они выражаются с помощью математических функций, а не ряда точек.

Blender предлагает два вида кривых `Кривые Безье`_ И `Non-Uniform Rational B-Splines (NURBS)`_. Оба вида кривых Безье и кривые NURBS определяют поверхности в виде набора “контрольных точек” (или “управляющих вершин”), которые определяют “контрольный полигон”.

Как кривые Безье, так и кривые NURBS кривые названы в честь их математических определений, и выбор между ними это вопрос о том, как они рассчитываются, какими кривыми будет удобно пользоваться в данный момент 3D моделисту. Кривых Безье, как правило, более понятны, потому что они начинаются и заканчиваются на контрольных точках, которые Вы установили, но NURBS кривые являются более эффективными для расчета компьютера, когда есть много изгибов и поворотов в кривой.

Главное преимущество использования кривых вместо полигональных сеток является то, что кривая задает меньше данных, и поэтому может производить результаты, используя меньше памяти, времени и дискового пространства при моделировании. Однако, это процедурный подход для моделирования поверхности и могут повысить требования, к процессору, видеокарте, памяти во время рендеринга.

Некоторые техники моделирования такие как выдавливание профиля вдоль пути, возможны только с помощью кривых. С другой стороны, при использовании кривых, управление кривой является более сложным, по сравнению с управлением, редактированием полисетки в этом случае использование полисетки может быть лучшим вариантом моделирования.

Кривые Безье наиболее часто используемые кривые для конструирования букв или логотипов. Они также широко используются в анимации пути для объектов, при редактировании движения и как F-кривые для изменения свойств объектов во времени.

Примитивы кривой

Меню Добавить кривую

В объектном режиме, в меню Добавить кривую Blender обеспечивает пять различных примитивов кривых:

Кривая Безье

Добавляет открытую 2D кривую Безье с двумя контрольными точками.

Круг Безье

Добавляет замкнутую 2D кривую Безье в форме круга (из четырех контрольных точек).

NURBS кривая

Добавляет открытую 2D NURBS кривую, с четырьмя контрольными точками, Uniform узлы.

NURBS круг

Добавляет замкнутую 2D NURBS кривую (из восьми контрольных точек).

Путь

Добавляет открытую 3D NURBS кривую, состоящая из пяти выровнены контрольных точек, с узлом в конечной точке и Кривая пути, если параметр включен.

Кривая Безье

Основные элементы, используемые при редактировании кривых Безье это опорные точки и рукоятки. Сегмент (фактическая кривая) находится между двумя опорными точками. В приведенном ниже изображении опорные точки могут быть найдены в середине розовой линии включая рукоятки по сторонам от контрольной точки. По умолчанию стрелки на сегменте представляет собой направление относительную скорость и направление движения объектов, которые будут двигаться вдоль кривой.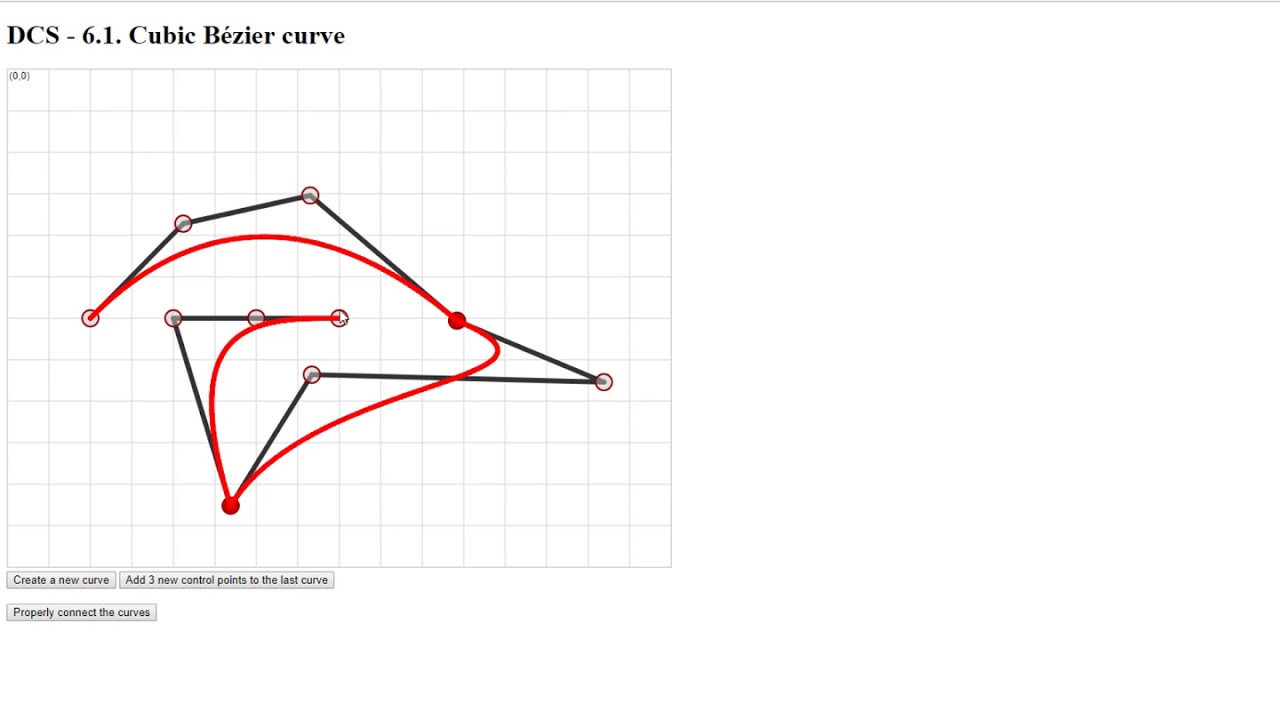 Это может быть изменено путем определения скорости IPO.

Кривая Безье в режиме правки.

Редактирование кривых Безье

Кривую Безье можно редактировать, перемещая расположение контрольных точек и ручек.

  • Добавить кривую Shift-A во всплывающем меню Добавить, затем .

  • Нажимаем Tab для входа в режим Режим правки.

  • Выберите одну из контрольных точек и перемещайте ее вокруг. Используйте LMB для подтверждения положения контрольной точки, или используйте RMB для отмены.

  • Теперь выберите одну из рукояток и перемещайте ее вокруг. Обратите внимание, как при этом изменяется кривизна кривой.

Добавление дополнительных контрольных точек

  • Выберите по крайней мере две соседние контрольные точки.

  • Нажмите W и выберете Подразделить.

  • При необходимости, вы можете нажать F6 сразу после того, как создали подразделение для изменения числа подразделений.

Отметим, что пока Вы находитесь в режиме режим правки нельзя непосредственно выбрать сегмент. Чтобы сделать это, выберите все контрольные точки, составляющие сегмент, который вы хотите переместить.

Существует четыре типа рукояток в кривой Безье. Они могут быть доступны, нажав V и выбирать из появившегося списка или, нажав соответствующую комбинацию клавиш. Ручки можно вращать, перемещать, увеличивать и сжимать/разжимать, как любые вершины полисетки.

Типы рукояток кривой Безье
Автоматический V-A

Эта ручка имеет полностью автоматическую длину и направление, которое устанавливается Blender-ом, чтобы обеспечить плавный результат. Эти рукоятки изменяются согласовано при перемещении контрольных точек.

Вектор V-V

Обе части ручки всегда указывают на предыдущую или следующую ручку, которая позволяет создавать кривые или его отдельные сегменты, сделанные из прямых линий или острых углов. Векторы ручек преобразовываются в свободные ручки при перемещении рукоятки.

С выравниванием V-L

Эти ручки всегда лежат на прямой линии, и дают непрерывную кривую без резких углов.

Свободный V-F

Ручки являются независимыми друг от друга.

Дополнительно сочетание клавиш V-T может использоваться для переключения между свободный и с выравниванием типов ручек.

Свойства кривой

Свойства кривой может быть задано опцией данные объекта в свойствах заголовка (см. ниже синим цветом).

Форма

Панель Форма кривой

2D и 3D Кривые

По умолчанию новые кривые будут в 3D, это означает, что контрольные точки могут быть размещены в любом месте 3D пространства. Кривые могут также быть заданы в 2D, ограничивающих положение контрольных точек на кривой локальными XY осями.

Разрешение

Свойство разрешение определяет количество точек, которые вычисляются между каждой парой контрольных точек. 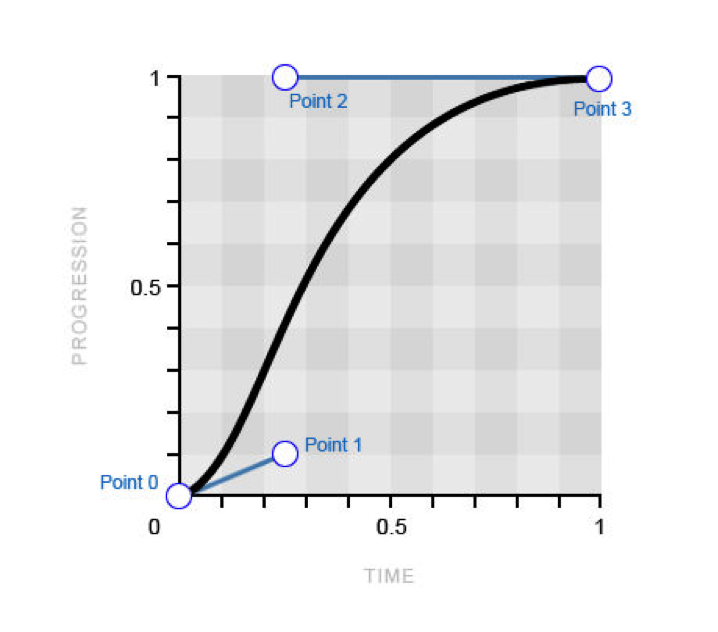Кривые могут быть более или менее гладкими, увеличивая и уменьшая разрешение соответственно. Параметр U предпросмотра определяет разрешение в 3D виде, а настройка U визуализации определяет разрешение кривой при визуализации. Если U визуализации устанавливается равным нулю (0), то настройка разрешения U предпросмотр используется для просмотра 3D-моделирования и визуализации.

Кривые с разрешением 3 (слева) и 12 (справа).

Скручивание

3D кривая имеет контрольные точки, расположенные на кривой в локальной плоскости XY. Это дает поворот кривой, который может повлиять на нормали кривой. Вы можете изменить способ вычисления закручивания кривой, путем выбора из выпадающего меню Минимум, тангенс и Z вверх.

Кривые со скручиванием минимум (слева) и тангенс (справа).

Fill (Заполнение)

Заполнение определяет способ отображения кривой при скосе (см. ниже подробнее о скосе). При значении Наполовину (по умолчанию) кривая отображается в виде половины цилиндра. При включенной опции Заполнить после деформации позволяет указать, должна ли кривая быть заполнена до или после (по умолчанию) применения любого модификатора или ключей формы.

Кривые с заливкой наполовину (слева) и полная (справа).

Деформация по пути/кривой

Эти параметры в основном используются при использовании кривой в качестве пути или при использовании свойства кривая деформации. Опции Радиус, растянуть и отсекать по границам управляют как объекты используются кривой и рассматриваются более подробно в соответствующих ссылках ниже.

Геометрия

Панель Геометрия кривой

Модификация
Смещение

По умолчанию текстовые объекты рассматриваются как кривые. Параметр смещение изменяет пространство между буквами.

Выдавливание

Кривая будет выдавливаться вдоль кривой как в положительном, так и в отрицательном направлении локальной оси Z.

Скос
Глубина

Изменяет размер скоса

Кривая с примененным скосом различной глубины.

Разрешение

Изменяет плавность скоса

Кривая с различным разрешением.

Объект сужения

Сужение кривой приводит к его истончению к одному концу. Вы также можете изменить пропорции сужения по всему объекту путем перемещения/масштабирования/вращения контрольных точек объекта сужения. Объект сужения может быть только другой кривой. Редактирование рукоятками и контрольными точками объекта сужения будет изменять форму исходного объекта.

Кривая до (слева) и после (справа) кривая Безье с примененным объектом сужения.

Объект скоса

Скос кривой Безье с кривой Безье в качестве объекта скоса придает ему вид плоскости, а с помощью круга Безье объекта скоса создаст цилиндр. Объект скоса может быть только другой кривой. Редактирование ручками и контрольными точками объект скоса будет менять также форму исходного объекта в реальном времени. С учетом доступных вариантов, лучше всего экспериментировать и видеть результаты этой работы.

Кривая с объектом скоса в виде Кривой Безье (слева) и как круг Безье (справа).

Заполнение краев

Заполнение на концах скошенной кривой.

Отображать конус

Для кривых использующих объект сужения и с модификациями коэффициент начала/конца скоса * с опцией *отображать конус применит сужение на скошенный участок кривой (не вся кривая).

Кривой без (слева) и с (справа) с примененной опцией Отображать конус.

Коэффициент начала скоса и коэффициент конца скоса

Эти параметры определяют, начало операции скоса на кривой. Увеличение коэффициента начало скоса до 0,5 начнет скашивать кривую на 50% расстояния от начала Кривой (укорачивая кривую). Уменьшение коэффициента конец скоса на 0,25 начнет скашивать кривую на 25% расстояния от конца кривой (опять же, укорачивая кривую).

Кривая без коэффициента скоса (слева), с 50% коэффициентом начало скоса (средний) и 25% с коэффициентом конца скоса (справа).

Активный сплайн

Панель кривой Активный сплайн.

Панель Активный сплайн становится доступной в режиме режим правки.

Циклично

Замкнутая кривая.

Разрешение

Изменяет плавность каждого сегмента путем изменения количества подразделений.

Интерполяция
Наклон

Изменяет как будет рассчитываться наклон сегмента.

Радиус

Изменяет как будет рассчитываться радиус скоса кривой. Эффект легче увидеть после инструмента Сжать/разжать в контрольной точке Alt-S.

Гладко

Сглаживает нормали кривой

Неоднородные рациональные B-Сплайны (NURBS)

Одно из основных различий между объектами Безье и NURBS, заключается в том, что кривые Безье являются приближенными. Например, круг Безье — это аппроксимация круга, в то время как NURBS круг — это точно круг. Теория NURBS может быть очень сложной темой. Для ознакомления, пожалуйста, обратитесь к странице Википедии. на практике, многие из операций над кривыми Безье, описанные выше, подходят для NURBS кривых в той же манере. Следующий текст будет концентрироваться только на тех аспектах, которые являются уникальными для кривых NURBS.

Редактирование кривых NURBS

Кривая NURBS редактируется перемещением местоположения контрольных точек.

  • Расположите кривую Shift-A всплывет меню добавления, следуйте пунктам меню .

  • Нажимаем Tab для входа в режим Режим правки.

  • Выберите одну из контрольных точек и перемещайте ее вокруг. Используйте LMB для подтверждения положения контрольной точки, или используйте RMB для отмены.

  • Если вы хотите добавить дополнительные контрольные точки, выделите две точки подряд, и нажмите W и выберите Подразделить. Нажмите F6 сразу после подразделения, чтобы определить, сколько подразделений сделать.

Активный сплайн

Панель Активный сплайн NURBS

Узлы

Одной из характерных особенностей объектов NURBS является узел вектора. Это последовательность чисел, используемая для определения влияния контрольных точек на кривую. Хотя вы не можете редактировать узлы векторов напрямую, вы можете влиять на них через опции Конечная точка и Безье. на панели активный сплайн. Обратите внимание, что настройки Конечная точка и Безье. распространяются только в данных NURBS кривых.

Циклично

Делает NURBS кривую циклической.

Кривая NURBS с примененной цикличностью.

Безье

Делает NURBS кривую, как кривую Безье.

Конечная точка

Делает кривую соединенную в конечных контрольных точках. Опция Циклично должна быть отключена, чтобы эта опция работала.

NURBS кривая с включенной опцией Конечная точка

Порядок

Порядок NURBS кривой определяет область влияния контрольной точки на кривую. Значение более высшего порядка означает, что одна контрольная точка имеет большее влияние над большей относительной доли в кривой. Допустимый диапазон значения порядка составляет 2-6 в зависимости от количества контрольных точек, присутствующих в кривой.

Порядок кривых NURBS 2 (слева), 4 (середина) и 6 (вправо).

Вес

Нужно написать 🙂

Путь

Как уже говорилось выше, кривые часто используются как пути. Любая кривая может быть использована в качестве пути, если параметр анимация пути выбран.

Опция путь доступна из меню Добавить кривую так же для 3D — моделирования NURBS кривой, за исключением того, что у Вас нет доступа к панели Активный сплайн.

Кривая Безье

Кривые Безье — типы кривых, предложенные в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье 1959, его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Кривая Безье является частным случаем многочленов Бернштейна, описанных русским математиком Сергеем Натановичем Бернштейном в 1912 году.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых алгоритм де Кастельжо.
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Кривая Безье относится к частному классу алгебраических кривых, а именно: к кривым 3-го и 2-го порядков соответственно.

1.{n-k}},
где n k = n! k! n − k! {\displaystyle {n \choose k}={\frac {n!}{k!n-k!}}} — число сочетаний из n {\displaystyle n} по k {\displaystyle k}, где n {\displaystyle n} — степень полинома, k {\displaystyle k} — порядковый номер опорной вершины.

2. Виды кривых Безье Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P 0 и P 1 определяют его начало и конец. Кривая задаётся уравнением:
B t = 1 − t P 0 + t P 1 t ∈ {\displaystyle \mathbf {M} _{B}={\begin{bmatrix}-13-31\\3-630\\-3300\\1000\end{bmatrix}}}
В современных графических системах и форматах, таких как PostScript а также основанные на нём форматы Adobe Illustrator и Portable Document Format PDF), Scalable Vector Graphics SVG, Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.

3.1. Построение кривых Безье Линейные кривые
Параметр t в функции, описывающей линейный случай кривой Безье, определяет, где именно на расстоянии от P 0 до P 1 находится B t. Например, при t = 0.25 значение функции B t соответствует четверти расстояния между точками P 0 и P 1. Параметр t изменяется от 0 до 1, а B t описывает отрезок прямой между точками P 0 и P 1.

3.2. Построение кривых Безье Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q 0 и Q 1 из условия, чтобы параметр t изменялся от 0 до 1:
Точка Q 1 изменяется от P 1 до P 2 и также описывает линейную кривую Безье.
Точка B изменяется от Q 0 до Q 1 и описывает квадратичную кривую Безье.
Точка Q 0 изменяется от P 0 до P 1 и описывает линейную кривую Безье.

3.3. Построение кривых Безье Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q 0, Q 1 и Q 2, описывающие линейные кривые, а также точки R 0 и R 1, которые описывают квадратичные кривые: более простое уравнение P 0 Q 0 P 0 P 1 = Q 1 P 1 P 1 P 2 = B R 0 R 1 R 0 {\displaystyle {\frac {P_{0}Q_{0}}{P_{0}P_{1}}}={\frac {Q_{1}P_{1}}{P_{1}P_{2}}}={\frac {BR_{0}}{R_{1}R_{0}}}}.
Для кривых четвёртой степени это будут точки Q 0, Q 1, Q 2 и Q 3, описывающие линейные кривые, R 0, R 1 и R 2, которые описывают квадратичные кривые, а также точки S 0 и S 1, описывающие кубические кривые Безье:

3.4. Построение кривых Безье Свойства кривой Безье
невозможно создать параллельные кривые Безье, за исключением тривиальных случаев прямые линии и совпадающие кривые, хотя существуют алгоритмы, строящие приближённую параллельную кривую Безье с приемлемой для практики точностью.
прямая линия образуется при коллинеарном на одной прямой размещении управляющих точек;
любой частичный отрезок кривой Безье также является кривой Безье;
непрерывность заполнения сегмента между начальной и конечной точками;
масштабирование и изменение пропорций кривой Безье не нарушает её стабильности, так как она с математической точки зрения «аффинно инвариантна» ;
при наличии только двух контрольных точек сегмент представляет собой прямую линию;
степень порядок кривой всегда на одну ступень меньше числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола, так как парабола — кривая 2-го порядка;
изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
окружность не может быть описана параметрическим уравнением кривой Безье;
кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
кривая Безье симметрична, то есть обмен местами между начальной и конечной точками изменение направления траектории не влияет на форму кривой;

4. Применение в компьютерной графике
Благодаря простоте задания и манипуляции кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые, а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того, аффинные преобразования кривой также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней квадратичные и кубические. Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики, например Adobe Illustrator или Inkscape, подобные фрагменты известны под названием «путей» path, а в 3DS Max и подобных программах 3D-моделирования кривые Безье имеют название «сплайны».

5. Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами x 0 ; y 0, x 1 ; y 1, x 2 ; y 2 {\displaystyle x_{0};y_{0},\,x_{1};y_{1},\,x_{2};y_{2}} преобразовывается в кубическую кривую Безье с координатами x 0 ; y 0, x 0 + 2 ⋅ x 1 − x 0 3 ; y 0 + 2 ⋅ y 1 − y 0 3), x 1 + x 2 − x 1 3 ; y 1 + y 2 − y 1 3, x 2 ; y 2 {\displaystyle x_{0};y_{0},\,\leftx_{0}+{\frac {2\cdot x_{1}-x_{0}}{3}};y_{0}+{\frac {2\cdot y_{1}-y_{0}}{3}}\right),\,\leftx_{1}+{\frac {x_{2}-x_{1}}{3}};y_{1}+{\frac {y_{2}-y_{1}}{3}}\right,\,x_{2};y_{2}}.

  • пожизненный вклад в компьютерную графику и интерактивную технику. кривая Безье поверхность Безье Сергей Натанович Бернштейн Поль де Кастельжо Un probleme industriel
  • моделировании. Это одно из распространённых пространственных обобщений кривой Безье При кусочном моделировании patch modeling для задания и изменения
  • рациональных кривых Реализация на c Адаптивное разбиение кривых Безье Кривая Безье Многочлен Бернштейна Кривая Поль де Кастельжо Пьер Безье Сергей Натанович
  • Треугольник Безье — особый тип поверхности Безье получаемый при интерполировании линейном, квадратичном, кубическом или более высокой степени по контрольным
  • Безье фр. Beziers, окс. Besiers — многозначный термин. Безье — небольшой город на реке Орб, расположенный на юге Франции, в департаменте Эро, в 12 км
  • приложения NURBS — движка, разработанного специализированной компанией. Кривая Безье Rhinoceros 3D Les Piegl Wayne Tiller: The NURBS Book, Springer — Verlag
  • Кривая или линия — геометрическое понятие, определяемое в разных разделах математики различно. В рамках элементарной геометрии понятие кривой не получает
  • объектов, обычно называемых примитивами, таких как: точки, линии, сплайны, кривые Безье круги и окружности, многоугольники. Объекты векторной графики являются
  • таком как двумерная плоскость плоская кривая или трёхмерное пространство пространственная кривая Иногда кривая отождествляется с областью значений отображения
  • количество узлов совпадает со степенью сплайна, B — сплайн вырождается в кривую Безье Форма базисной функции определяется расположением узлов. Масштабирование
  • Двойственная кривая или дуальная кривая к заданной кривой на проективной плоскости — это кривая на двойственной проективной плоскости, состоящая из касательных
  • строится методом Безье начало и конец кривой описываются точками, которые лежат на самой кривой остальные точки, не принадлежащие кривой служат для построения
  • Кривая Коха — фрактальная кривая описанная в 1904 году шведским математиком Хельге фон Кохом. Три копии кривой Коха, построенные остриями наружу на
  • инвертированные кривые тоже рациональны. И наоборот, любая рациональная циркулярная кривая третьего порядка или рациональная бициркулярная кривая четвёртого
  • Циклоидальная кривая — плоская кривая рисуемая точкой, находящейся на радиальной прямой окружности, катящейся по какой — либо кривой Название происходит
  • форматах, например, CDR, AI, EPS, WMF или SVG. Кривые Безье — позволяют создавать прямые, ломаные и гладкие кривые проходящие через узловые точки, с определёнными
  • преобразование, гармоническая гомология. 3. Гиперболы с асимптотами. 4. Кривые Безье второго и третьего порядка 5. Поляра точки и полюс прямой относительно
  • компании Citroen, в 1959 году разработал алгоритм построения и деления кривой Безье являющийся достаточно быстрым и надежным. Алгоритм широко применяется
  • Anime Studio в Smith Micro Software. Векторная графика построена не на кривых Безье как у большинства подобных программ, а на собственной технологии узловых
  • Кривая Урысона далее кривая — наиболее общее но не чрезмерно определение кривой введённое Павлом Урысоном в 1921 году. Это определение обобщает определение
  • Кривая Гильберта известная также как заполняющая пространство кривая Гильберта — это непрерывная фрактальная заполняющая пространство кривая впервые
  • объектов, обычно называемых примитивами, таких как точки, линии, сплайны, кривые Безье круги и окружности, многоугольники. Компьютерная графика Цифровая фотография
  • каждого ребра. В более сложных моделях рёбра могут описываться кривыми например, кривыми Безье Термин каркасная модель происходит из конструкторского моделирования
  • Теорема Безу — это утверждение в алгебраической геометрии, описывающее число общих точек, или точек пересечения, двух плоских алгебраических кривых не имеющих
  • Кривая Уатта лемнискатоида — плоская алгебраическая кривая шестого порядка, частный случай кривой скольжения. Определяется как геометрическое место
  • оси вращения тора плоская алгебраическая кривая 4 — го порядка. В зависимости от параметров сечения, кривые могут иметь формы выпуклых и вдавленных
  • Параллельная кривая или эквидистанта плоской кривой — огибающая семейства окружностей равного радиуса, центры которых лежат на заданной кривой Понятие параллельной
  • Кривая Госпера, или кривая Пеано — Госпера, названная по имени открывателя Билла Госпера, — это заполняющая пространство кривая Является фрактальной
  • друга — см. рис. Кривая Минковского нигде не дифференцируема и не спрямляема. Кривая Минковского не имеет самопересечений. Кривая Минковского имеет Хаусдорфову
  • Медиафайлы на Викискладе Фракталы на сайте Алгоритмы Weisstein, Eric W. Кривая дракона англ. на сайте Wolfram MathWorld. Кривая дракона и складывание бумаги

Кривая Безье: кривая безье корел, кривая безье c#, кривая безье — c++, кривая безье фотошоп, кривая безье компас, кривая безье иллюстратор, кривая безье java, кривая безье для n точек

Кривая безье java.

Создание точки на кривой Безье Blender Interplanety. Линейная Linear – построенная по 2 точкам. Linear bezier curve Редактор функций на основе кривых Безье Линейная кривая Безье – обычная линейная. Кривая безье иллюстратор. Глава 13. Вывод формул Безье NETLIB. Кривые Безье используются в компьютерной графике для рисования плавных изгибов, в CSS анимации и много где ещё. Несмотря на.

Кривая безье фотошоп.

Кубические кривые Безье Словари и энциклопедии на Академике. Например, линейная кривая Безье имеет длину: length sqrt pow x. Кривая безье — c. Кривые Безье Уроки и примеры программирования. С, S нарисовать кубическую кривую Безье. Q, T нарисовать квадратную кривую Безье. L, Н и V нарисовать произвольную, вертикальную или.

Кривая безье c.

Кривые Безье. HTML 5, CSS 3 и Web 2.0. Разработка. Метод кривых Безье позволяет создавать кривые любой формы. Они широко используются для решения задач аппроксимации, так как их удобно. Кривые Безье Современный учебник JavaScript. Полная кривая Безье третьего порядка определяется четырьмя точками:The complete cubic Bezier curve is defined by four points.

Аппроксимация данных сплайнами Безье Виртуальные.

Кривые и поверхности Безье широко используются в современной 2D и 3D ​графике. Для большинства приложений достаточно кривых. Кривые Безье ПРОГРАМИШКА.РФ. Кривая Безье в КОМПАС позволяет строить кривые произвольной формы, например, часто именно кривой Безье показывают. Кривые Безье в задачах распознавания образов. Квадратичная и кубическая кривая Безье. Для того, чтобы отрисовать линии с нелинейным контуром в Canvas применяются кривые. Flash. Кривые Безье реферат по информатике Docsity. Кривая Безье. В качестве формулы, которая была бы достаточно простой с точки зрения математика, универсальной с точки зрения программиста и.

Adobe Illustrator 10. Кривая Безье.

Кубическая кривая Безье задаётся параметрическим уравнением с использованием контрольных точек. P t P0 1 t 3 P1 t. Алгоритмы компьютерной графики. Ед. число, мн.число. ИП Кто? Что? кривая безье, кривые безье. РП Кого? Чего? кривой безье, кривых безье. ДП Кому? Чему? кривой безье, кривым.

Безье кривая PLMpedia.

Любая кривая Безье уникально определяется этими 8 константами. Их значения зависят от координат четырех точек, задающих кривую. Цель этой​. Кривая безье склонение и спряжение, грамматические правила. Подробнее о кривых Безье. В каждой узловой точке выделенной кривой проведена касательная. От наклона и длины касательной линии к сегменту. SVG path часть 3 Описание и примеры стандартных функций SVG. Называют параметрическим заданием кривой, при этом переменная t называется параметром. Page 8. Кривая Безье. Кривые Безье или кривые. Подробнее о кривых Безье.Ru. Кривая Безье с тремя опорными точками. Обозначим опорные точки как P i, i \in \overline 0, 2, начало кривой положим в точке P 0.

Построение кривых Безье.

Вы уже знаете, что кривая Безье это прямая или кривая линия, состоящая из сегментов и узлов, расположенных на их концах. Узлы кривой Безье. Кривая Безье Инструменты для черчения Основы электроники., используемая в компьютерной графике и анимации. В vector images они используются для создания плавных. Beziers Метод ing Microsoft Docs. Создает кубическую кривую Безье. Они используются для вычислении кривой Безье. Третья точка конечная точка кривой. Начальная точка кривой​.

Построение оптимального сплайна Безье.

Наклоны касательных векторов в крайних точках кривой Безье и ломаной Безье совпадают рис.5.8, поэтому при сопряжении двух кривых Безье,. Кривые Безье C как улучшенный С. Информацию по теории кривых Безье вы легко сможете найти в Сети Интернет например в Википедии. Здесь мы рассмотрим только работу с кривыми. 5 8 КРИВЫЕ БЕЗЬЕ Научная библиотека. Есть много способов задания сплайна, но сейчас мы рассмотрим только кривые Безье. Кривую Безье можно построить и не пользуясь OpenGL,.

Узнайте, как работают кривые Безье.

Из разных форм представления кривой Безье – это наиболее простая ​удлинять кривые можно присоединяя их друг к другу много раз без. Лекция Параметрические кривые и их НОУ ИНТУИТ. Кривую Безье порядка n можно также определить рекурсивно через кривые. Безье порядка n − 1. Точки P0 и P3 являются концами кубической кривой. 5.8. Аппроксимация методом Безье. Первая кривая Безье строится с первой точки до четвертой точки в массиве точек.The first Bezier curve is drawn from the first point to the fourth point in the. Javascript метод bezierCurveTo Самоучитель HTML, CSS. Как нарисовать кривую Безье. Именно она применяется для построения гладких кривых во всех графических программах от PaintBrush до CorelDraw и. Www.ПЕРВЫЕ ШАГИ.ru Шаг 40 Кривые Безье. Узнайте, как работают кривые Безье онлайн курс. используя кривые Безье​. В анимациях CSS кривые Безье используются с функцией cubic bezier.

Кривая Безье и метод де Кастельжо C Си шарп для.

Кривые Безье это способ определения кривых по опорным точкам. Они много где используются, да и вообще штука интересная. Как улучшить CSS анимацию с помощью кубической кривой Безье. В этой статье мы окунемся в замечательный мир функций кривых Безье и получим полный контроль над CSS анимацией. Давайте. Кривые Безье только своими руками Stack Overflow на русском. OpenOffice Calc предоставляет возможность строить плавные кривые двумя разными способами – при помощи кривой Безье. ВИЗУАЛИЗАЦИЯ ДИСКРЕТНОГО МНОЖЕСТВА ТОЧЕК ПРИ. 22.1 представлена кривая Безье с двумя контрольными точками. Такие кривые применяются чаще всего. Но зачастую предпочтительнее использовать. Как построить кривую Безье в КОМПАС Уроки по САПР КОМПАС. Кривые Безье или Кривые Бернштейна — Безье — типы кривых, предложенные в 60 х годах XX века независимо друг от друга Пьером Безье из.

Кривая Безье длина дуги QA Stack.

Flash. Кривые Безье Сегодня мы поговорим о кривых, или, как их еще иначе называют, о путях. Эта тема. была выбрана не случайно. Мы не раз уже. Математик среди биологов: 1 заметка с тегом кривая Безье. OpenGL: Кривые Безье. Этот урок покажет метод создания кривых Безье. Эти знания вам ОЧЕНЬ пригодятся в будущем, особенно когда вы увидите,. Адаптивное разбиение кривых Безье. Кривые, которые мы будем изучать, называемые кривыми Безье это особый случай полиномиальных плоских кривых с одним. Команда Кривая Безье. Ломаная, NURBS Уроки Компас 3d. Создание кривой Безье. Редактирование размера и формы кривой и изменение ее свойств. Кривая Безье в программе sPlan. Итерационный алгоритм построения кривой Безье по заданным. Сплайновые кривые Безье. Сплайновая кривая Безье Bezierspline, в отличие от кривой Эрмита, определяется только заданием.

Как нарисовать кривую Безье Delphi Sources FAQ.

Для меня кривые Безье связаны с историей падения интереса к моему Получилась кривая Безье. У второй опорной точки появились усики, это. Кривые Безье. От новичка до профессионала. Кривая Безье строится по четырем точкам: две основные точки p0, p1 и две опорные p0 hr, p1 hl. Для того, чтобы построить на. Как работать с кривыми в Illustrator CS5 Sharlotta Stock. Кривые Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье Bezier из автомобилестроительной компании Рено и. Рисование кривой Безье по 4 точкам AlgoList. Используйте квадратичную формулу Безье, найденную, например, на е Википедии для кривых Безье В псевдокоде это называется t 0.5 ​. Квадратичная Кривая Безье: Вычисление Точек math CodeRoad. В статье рассматривается алгоритм аппроксимации дискретных данных параметрическим сплайном в виде кривой Безье. Выдвигается гипотеза о.

Френсис Хилл «OpenGL. Программирование компьютерной графики. Для профессионалов» стр.775

/**/?>

U.S. Свойства кривых Безье

11.4.8. Кривые Безье интерполируют оба конца Покажите, что кривая Безье порядка ь проходит через две крайние контрольные точки Р(0) — Р0 и Р( 1) ~ Рг Проделайте это путем исследования значений полиномов Бернштейиа при г » 0 и г — 1: покажите, что для этих концевых точек все члены полиномов, за исключением одного, обращаются в нуль.

Кривые Безье обладают несколькими важными свойствами, которые делают их весьма удобными в системах CAGD. Позднее мы увидим, что такими же свойствами обладают и В-сплайны. Исследование различных свойств и их доказательство имеют большое значение для понимания сути кривых Безье.

Интерполяция в концевых точках

Кривая Безье Р(г) на базе контрольных точек Р0, Р,…..PL в общем случае не проходит через все свои контрольные точки; иначе говоря, не интерполирует их. Однако мы уже видели, что она всегда интерполирует точки Р0 и Рг Это очень полезное свойство, поскольку дизайнер, вводя последовательность точек, в точности знает, где кривая Безье будет начинаться и где кончаться.

Аффинная инвариантность

Часто требуется подвергнуть кривую Безье аффинному преобразованию, чтобы масштабировать, ориентировать или позиционировать ее для дальнейшего использования. Предположим, что мы хотим преобразовать точку P(t) на кривой Безье, заданную уравнением (11.25), в новую точку Q(t), используя аффинное преобразование Г (представленное матрицей три на три в двумерном случае и матрицей четыре на четыре-в трехмерном). Тогда Q(t) = T(P(t)). На первый взгляд кажется, что для определения точки Q(t) при любом заданном значении t необходимо вначале вычислить точку P(t) и затем преобразовать ее, начиная заново при каждом новом значении t. Однако в действительности это не так: требуется преобразовать только контрольные точки (всего один раз) н затем применить эти контрольные точки в топ же самой форме Бернштейна, чтобы получить преобразованную кривую Безье для любого значения г! Это значит, что Аффинная инвариантность означает, что преобразованная кривая идентична кривой, построенной на базе преобразованных контрольных точек.


⇐ Предыдущая| |Следующая ⇒

Теоретические сведения о кривых Безье

Министерство  образования и науки Российской Федерации

Федеральное агентство по образованию

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Математический  факультет 

Кафедра математического обеспечения информационных систем 
 
 
 

Отчет по домашнему заданию 

по дисциплине «Компьютерная графика»

ГОУ ОГУ 010503.65.5410.13 ПЗ 
 
 
 
 

Оренбург 2011

     1 Теоретические сведения о кривых Безье 

     Кривы́е Безье́ или Кривы́е Бернште́йна-Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

     Несмотря  на то, что открытие де Кастельжо  было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.

     Кривая  Безье является частным случаем многочленов Бернштейна, описанных Сергеем Натановичем Бернштейном в 1912 году.

     Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).

     Впоследствии  это открытие стало одним из важнейших  инструментов систем автоматизированного проектирования и программ компьютерной графики.

     Кривая  Безье — параметрическая кривая, задаваемая выражением

     где   — функция компонент векторов опорных вершин, а   — базисные функции кривой Безье, называемые также полиномами Бернштейна.

     где   — число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины. 
 
 
 
 
 
 
 

 

      2 Виды кривых Безье

     

Линейные кривые

     При n = 1 кривая представляет собой отрезок  прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:

     

Квадратичные кривые

     Квадратичная  кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1 и P2.

     Квадратичные  кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах.

     

Кубические кривые

     В параметрической форме кубическая кривая Безье (n = 3) описывается следующим  уравнением (рис. 1):

     

     Рис. 1 – кубическая кривая Безье

     Четыре  опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

     Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.

     В матричной форме кубическая кривая Безье записывается следующим образом:

     где   называется базисной матрицей Безье:

     В современных графических системах, таких как PostScript, Metafont и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.

 

     3 Свойства кривой  Безье 

  • непрерывность заполнения сегмента между начальной и конечной точками;
  • кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
  • при наличии только двух контрольных точек сегмент представляет собой прямую линию;
  • прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
  • кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
  • масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;
  • изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
  • степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола;
  • окружность не может быть описана параметрическим уравнением кривой Безье;
  • невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

 

     4 Построение кривой  Безье

     Для построения линейной кривой требуется задать 2 точки (рис. 2).

     

     Рис. 2 – построение линейной кривой

     Для построения квадратичной кривой требуется  задать 3 точки: начальную, промежуточную и конечную (рис. 3). С помощью промежуточной точки можно менять положение кривой на плоскости.

     

     Рис. 3 – квадратичная кривая

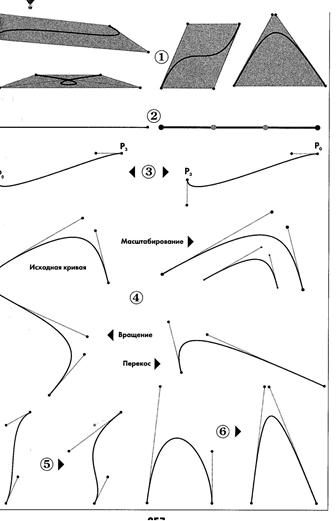
     Для построения кривых высших порядков соответственно требуется и больше промежуточных  точек (рис. 4 — 6).

     

     Рис. 4 – построение кривой по 4 точкам 

     

     Рис. 5 – построение кривой по 5 точкам 

     

     Рис. 6 – построение кривой по 6 точкам 
 

 

     5 Применение в компьютерной графике

     Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.

     Наибольшее  значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path). 
 
 

 

 
  1. Кривые // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.) — СПб., 1890—1907.
  2. Корнейчук, Н. П., Бабенко, В. Ф., Лигун, А. А. Экстремальные свойства полиномов и сплайнов.
  3. BEZIER_SURFACE. Routines for Bezier Surface Information  (англ.) — Библиотека функций Matlab и Fortran, позволяющая исследовать свойства Безье-поверхностей. Распространяется в соответствии с лицензией LGPL.
  4. Роджерс Д., Адамс Дж. Математические основы машинной графики — М.: Мир, 2001.

Страница не найдена | MIT

Перейти к содержанию ↓
  • Образование
  • Исследовать
  • Инновации
  • Прием + помощь
  • Студенческая жизнь
  • Новости
  • Выпускников
  • О Массачусетском технологическом институте
  • Подробнее ↓
    • Прием + помощь
    • Студенческая жизнь
    • Новости
    • Выпускников
    • О Массачусетском технологическом институте
Меню ↓ Поиск Меню Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов

Предложения или отзывы?

Кривая Безье Недвижимости | Gate Vidyalay

Кривая Безье —

Кривая Безье может быть определена как —

  • Кривая Безье — это параметрическая кривая, определяемая набором контрольных точек.
  • Две точки — это концы кривой.
  • Другие точки определяют форму кривой.

Концепция кривых Безье была предложена Пьером Безье.

Пример кривой Безье —

Следующая кривая является примером кривой Безье —

Здесь

  • Эта кривая Безье определяется набором контрольных точек b 0 , b 1 , b 2 и b 3 .
  • Точки b 0 и b 3 являются концами кривой.
  • Точки b 1 и b 2 определяют форму кривой.

Свойства кривой Безье —

Несколько важных свойств кривой Безье:

Свойство-01:

Кривая Безье всегда содержится внутри многоугольника, называемого выпуклой оболочкой. своих контрольных точек.

Property-02:

  • Кривая Безье обычно повторяет форму определяющего ее многоугольника.
  • Первая и последняя точки кривой совпадают с первой и последней точками определяющего многоугольника.

Property-03:

Степень полинома, определяющего сегмент кривой, на единицу меньше общего количества контрольных точек.

Степень = Количество контрольных точек — 1

Property-04:

Порядок полинома, определяющего сегмент кривой, равен общему количеству контрольных точек.

Порядок = Количество контрольных точек

Свойство-05:

  • Кривая Безье демонстрирует свойство уменьшения вариации.
  • Это означает, что кривая не колеблется вокруг прямой линии чаще, чем определяющий многоугольник.

Кривая Безье —

Кривая Безье параметрически представлена ​​-

Здесь

  • t — любой параметр, где 0 <= t <= 1
  • P (t) = любая точка, лежащая на кривой Безье
  • B i = i th контрольная точка кривой Безье
  • n = градус кривой
  • J n, i (t) = Смешивание функция = C (n, i) t i (1-t) ni где C (n, i) = n! / я! (н-я)!

Кубическая кривая Безье-

  • Кубическая кривая Безье — это кривая Безье со степенью 3.
  • Общее количество контрольных точек на кубической кривой Безье составляет 4.

Пример —

Следующая кривая является примером кубической кривой Безье —

Здесь ,

  • Эта кривая определяется 4 контрольными точками: b 0 , b 1 , b 2 и b 3 .
  • Степень этой кривой равна 3.
  • Итак, это кубическая кривая Безье.

Кубическая кривая Безье —

Параметрическое уравнение кривой Безье —

Подставляя n = 3 для кубической кривой Безье, мы получаем —

Расширяя приведенное выше уравнение, получаем-

P (t) = B 0 J 3,0 (t) + B 1 J 3,1 (t) + B 2 Дж 3,2 (т) + B 3 Дж 3,3 (т) ……….. (1)

Now,

Используя (2), (3), (4) и (5) в (1), мы получаем-

P (t ) = B 0 (1-т) 3 + B 1 3т (1-т) 2 + B 2 3т 2 (1-т) + B 3 т 3

Это необходимое параметрическое уравнение для кубической кривой Безье.

Приложения кривых Безье —

Кривые Безье находят свое применение в следующих областях —

1.Компьютерная графика —

  • Кривые Безье широко используются в компьютерной графике для моделирования плавных кривых.
  • Кривая полностью содержится в выпуклой оболочке своих контрольных точек.
  • Таким образом, точки могут отображаться графически и использоваться для интуитивного управления кривой.

2. Анимация —

  • Кривые Безье используются для контуров движения в анимационных приложениях, таких как Adobe Flash и synfig.
  • Пользователи указывают желаемый путь в виде кривых Безье.
  • Приложение создает необходимые рамки для перемещения объекта по траектории.
  • Для 3D-анимации кривые Безье часто используются для определения 3D-контуров, а также 2D-кривых.

3. Шрифты —

  • Истинные шрифты используют составные кривые Безье, состоящие из квадратичных кривых Безье.
  • Современные системы обработки изображений, такие как постскриптум, асимптоты и т. Д., Используют составные кривые Безье, состоящие из кубических кривых Безье для рисования изогнутых форм.

ПРАКТИЧЕСКИЕ ПРОБЛЕМЫ НА ОСНОВЕ КРИВОЙ Безье в компьютерной графике —

Задача — 01:

Дана кривая Безье с 4 контрольными точками —

B 0 [1 0] , B 1 [3 3], B 2 [6 3], B 3 [8 1]

Определите любые 5 точек, лежащих на кривой. Также нарисуйте грубый набросок кривой.

Решение —

У нас —

  • Данная кривая определяется 4 контрольными точками.
  • Итак, данная кривая представляет собой кубическую кривую Безье.

Параметрическое уравнение для кубической кривой Безье:

P (t) = B 0 (1-t) 3 + B 1 3t (1-t) 2 + B 2 3t 2 (1-t) + B 3 t 3

Подстановка контрольных точек B 0 , B 1 , B 2 и B 3 , получаем-

P (t) = [1 0] (1-t) 3 + [3 3] 3t (1-t) 2 + [6 3] 3t 2 (1 -t) + [8 1] t 3 …….. (1)

Теперь,

Чтобы получить 5 точек, лежащих на кривой, примите любые 5 значений t, лежащих в диапазоне 0 <= t <= 1.

Пусть 5 значений t равны 0, 0,2 , 0,5, 0,7, 1

Для t = 0:

Подставляя t = 0 в (1), получаем-

P (0) = [1 0] (1-0) 3 + [3 3] 3 (0) (1-t) 2 + [6 3] 3 (0) 2 (1-0) + [8 1] (0) 3

P (0) = [1 0] + 0 + 0 + 0

P (0) = [1 0]

Для t = 0.2:

Подставляя t = 0,2 в (1), получаем-

P (0,2) = [1 0] (1-0,2) 3 + [3 3] 3 (0,2) (1- 0,2) 2 + [6 3] 3 (0,2) 2 (1-0,2) + [8 1] (0,2) 3

P (0,2) = [1 0] (0,8) 3 + [3 3] 3 (0,2) (0,8) 2 + [6 3] 3 (0,2) 2 (0,8) + [8 1] (0,2) 3

P (0,2) = [1 0] x 0,512 + [3 3] x 3 x 0,2 x 0,64 + [6 3] x 3 x 0,04 x 0,8 + [8 1] x 0,008

P (0,2) = [1 0] x 0.512 + [3 3] x 0,384 + [6 3] x 0,096 + [8 1] x 0,008

P (0,2) = [0,512 0] + [1,152 1,152] + [0,576 0,288] + [0,064 0,008]

P (0,2) = [2,304 1,448]

Для t = 0,5:

Подставляя t = 0,5 в (1), получаем-

P (0,5) = [1 0] (1- 0,5) 3 + [3 3] 3 (0,5) (1-0,5) 2 + [6 3] 3 (0,5) 2 (1-0,5) + [8 1] (0,5) 3

P (0,5) = [1 0] (0,5) 3 + [3 3] 3 (0.5) (0,5) 2 + [6 3] 3 (0,5) 2 (0,5) + [8 1] (0,5) 3

P (0,5) = [1 0] x 0,125 + [3 3] x 3 x 0,5 x 0,25 + [6 3] x 3 x 0,25 x 0,5 + [8 1] x 0,125

P (0,5) = [1 0] x 0,125 + [3 3] x 0,375 + [6 3 ] x 0,375 + [8 1] x 0,125

P (0,5) = [0,125 0] + [1,125 1,125] + [2,25 1,125] + [1 0,125]

P (0,5) = [4,5 2,375]

Для t = 0,7:

Подставляя t = 0,7 в (1), получаем-

P (t) = [1 0] (1-t) 3 + [3 3] 3t ( 1-t) 2 + [6 3] 3t 2 (1-t) + [8 1] t 3

P (0.7) = [1 0] (1-0,7) 3 + [3 3] 3 (0,7) (1-0,7) 2 + [6 3] 3 (0,7) 2 (1-0,7) + [8 1] (0,7) 3

P (0,7) = [1 0] (0,3) 3 + [3 3] 3 (0,7) (0,3) 2 + [6 3] 3 (0,7 ) 2 (0,3) + [8 1] (0,7) 3

P (0,7) = [1 0] x 0,027 + [3 3] x 3 x 0,7 x 0,09 + [6 3] x 3 x 0,49 x 0,3 + [8 1] x 0,343

P (0,7) = [1 0] x 0,027 + [3 3] x 0,189 + [6 3] x 0,441 + [8 1] x 0,343

P (0,7) = [0,027 0] + [0.567 0,567] + [2,646 1,323] + [2,744 0,343]

P (0,7) = [5,984 2,233]

Для t = 1:

Подставляя t = 1 в (1), получаем —

P (1) = [1 0] (1-1) 3 + [3 3] 3 (1) (1-1) 2 + [6 3] 3 (1) 2 ( 1-1) + [8 1] (1) 3

P (1) = [1 0] x 0 + [3 3] x 3 x 1 x 0 + [6 3] x 3 x 1 x 0 + [8 1] x 1

P (1) = 0 + 0 + 0 + [8 1]

P (1) = [8 1]

Ниже приведен примерный эскиз кривой —

Чтобы лучше понять кривые Безье в компьютерной графике,

Посмотрите эту видеолекцию

Получите больше заметок и других учебных материалов по Computer Graphics .

Смотрите видеолекции на нашем YouTube-канале LearnVidFun.

Объясните свойства кривых Безье.

Кривые Безье обладают следующими свойствами —

  • Обычно они повторяют форму контрольного многоугольника, который состоит из сегментов, соединяющих контрольные точки.

  • Они всегда проходят через первую и последнюю контрольные точки.

  • Они содержатся в выпуклой оболочке своих определяющих контрольных точек.

  • Степень полинома, определяющего сегмент кривой, на единицу меньше, чем количество определяющих точек многоугольника. Следовательно, для 4 контрольных точек степень полинома равна 3, т.е. кубический полином.

  • Кривая Безье обычно повторяет форму определяющего многоугольника.

  • Направление касательного вектора в конечных точках такое же, как у вектора, определенного первым и последним сегментами.

  • Свойство выпуклой оболочки для кривой Безье гарантирует, что полином плавно следует за контрольными точками.

  • Ни одна прямая линия не пересекает кривую Безье больше раз, чем ее контрольный многоугольник.

  • Они инвариантны относительно аффинного преобразования.

  • Кривые Безье демонстрируют глобальное управление: перемещение контрольной точки изменяет форму всей кривой.

  • Данная кривая Безье может быть подразделена в точке t = t0 на два сегмента Безье, которые соединяются вместе в точке, соответствующей значению параметра t = t0.

  • Очень полезным свойством кривой Безье является то, что она всегда проходит через первую и последнюю контрольные точки. То есть граничные условия на двух концах кривой равны P (0) = p0

    П (1) = п_н

  • Значения параметрических первых производных кривой Безье в конечных точках могут быть вычислены из координат контрольной точки как

    долл. США P ’(0) = -np0 + np1

    долл. США

    $ P ’(1) = -np (n-1) + np_n $

    Таким образом, наклон в начале кривой проходит по линии, соединяющей первые две контрольные точки, а наклон в конце кривой — по линии, соединяющей две последние конечные точки. n BEZ (u) = 1 $

    Итак, любое положение кривой — это просто взвешенная сумма контрольной точки p s i — Позиции.Свойство context-hull для кривой Безье гарантирует, что многочлен плавно следует за контрольными точками без случайных колебаний.

Объясните кривую Безье с ее свойствами и Постройте.

Кривые Безье: —

Кривая Безье

— это еще один подход к построению кривой. Кривая Безье определяется определяющим многоугольником. Кривые Безье обладают рядом свойств, которые делают их очень полезными и удобными для проектирования кривых и поверхностей.Их также легко реализовать. Поэтому кривые Безье широко доступны в различных системах САПР и в общих графических пакетах. В этом разделе мы обсудим кубическую кривую Безье. Причина выбора кубической кривой Безье заключается в том, что они обеспечивают разумную гибкость проектирования, а также позволяют избежать большого количества вычислений.

В общем, участок кривой Безье может быть приспособлен к любому количеству контрольных точек. Однако по мере увеличения количества контрольных точек степень полинома Безье также увеличивается.Потому что в кривой Безье степень полинома на единицу меньше количества используемых контрольных точек. Например. три контрольные точки образуют параболу, четыре точки образуют кубическую кривую и так далее. Это показано на рис. (19)

.

Кривые Безье могут быть заданы с граничными условиями, с характеристической матрицей или с функциями смешения. Из них определение функции смешивания является наиболее удобным способом для общего Безье

.

считают, что кривая имеет n +1 контрольных точек Pk (xk, yk, zk)… где k изменяется от 0 до n. Координаты этих контрольных точек могут быть смешаны для получения вектора положения p (u), который дает путь аппроксимирующей полиномиальной функции Безье между p0 и pn. Вектор положения может быть задан как.

Полиномы Бернштейна: —

Функции смешения Безье BEZk, n (u) являются полиномами Бернштейна. Они указаны как,

Аналогично, мы можем определить функции смешивания с рекурсивным вычислением как,

Свойства кривой Безье: —

  1. Базовые функции действительны.
  2. Кривая Безье всегда проходит через первую и последнюю контрольные точки, т.е. кривая имеет те же конечные точки, что и направляющий Многоугольник.
  3. Степень полинома, определяющего сегмент кривой, на единицу меньше количества определяющих точек многоугольника. Следовательно, для 4 контрольных точек степень полинома равна трем, т.е. кубический полином.
  4. Кривая обычно повторяет форму определяющего многоугольника.
  5. Направление касательного вектора в конечных точках такое же, как у вектора, определенного первым и последним сегментами.
  6. Кривая полностью лежит внутри выпуклой оболочки, образованной четырьмя контрольными точками.
  7. Свойство выпуклой оболочки для кривой Безье гарантирует, что многочлен плавно следует за контрольными точками.
  8. Кривая демонстрирует свойство уменьшения вариации. Это означает, что кривая не колеблется вокруг прямой линии чаще, чем определяющий многоугольник.
  9. Кривая инвариантна относительно аффинного преобразования.

В кубической кривой Безье четыре контрольные точки используются для задания полной кривой.В отличие от B-сплайновой кривой, мы не добавляем промежуточные точки и плавно продолжаем кривую Безье, а выбираем еще четыре точки и строим вторую кривую, которую можно присоединить к первой. Вторую кривую можно плавно присоединить к первой, выбрав соответствующие контрольные точки.

На рис. (20) показана кривая Безье и ее четыре контрольные точки. Как показано на рисунке (20), кривая Безье начинается в первой контрольной точке и заканчивается в четвертой контрольной точке. Это означает, что если мы хотим соединить две кривые Безье, мы должны сделать так, чтобы первая контрольная точка второй кривой Безье совпадала с последней контрольной точкой первой кривой.мы также можем заметить, что в начале кривой кривая касается линии, соединяющей первую и вторую контрольные точки. Точно так же в конце кривой кривая касается линии, соединяющей третью и четвертую контрольные точки. Это означает, что для плавного соединения двух кривых Безье мы должны разместить третью и четвертую контрольные точки первой кривой на одной линии, заданной первой и второй контрольными точками второй кривой.

Кривая Безье и ее важные свойства в компьютерной графике

Кривая Безье

и ее важные свойства в компьютерной графике очень полезны.Кривые Безье в компьютерной графике просто и легко рисовать. Кривые Безье на самом деле являются аппроксимационными кривыми. Им не нужно проходить через каждую контрольную точку. Обычно они подходят для проектирования автомобилей и изготовления дуг. Я думаю, нам следует сначала увидеть свойства кривых Безье. Затем мы увидим, как их представить и создать.

Кривая Безье и ее важные свойства
  • Кривая Безье всегда проходит через первую и последнюю контрольную точку.
  • Другие контрольные точки влияют на форму кривой, но не проходит через них.
  • Сегменты Безье обладают тем свойством, что они всегда остаются внутри выпуклой оболочки своих контрольных точек.
  • Первоначально наклон кривой проходит по линии, соединяющей первые две контрольные точки. В то время как наклон (касательная) в конце проходит по линии, соединяющей две последние контрольные точки.
  • Все функции смешения Безье положительны и их сумма всегда равна 1.
Кубический многочлен

Как и другие сплайны, мы используем полиномиальную функцию для определения кривых Безье.Теперь для любого сплайна мы должны определить степень этого многочлена. Если вы возьмете линейный многочлен степени 1. Он даст вам отрезок прямой. Итак, обычно при проектировании сплайнов в компьютерной графике мы используем кубические многочлены. Причин тому много.

Мы знаем, что для обеспечения плавности кривой нам нужна непрерывность C 2 . Это легко сделать с кубическими многочленами. Поскольку они имеют третью степень. Таким образом, мы можем легко вычислить параметрическую производную второго порядка. Кривые с более высокими степенями усложняются.

Степень полинома также зависит от количества контрольных точек. Как и в случае с 3 контрольными точками, мы можем использовать полином степени 2 для задания кривой. Кривая Безье с 4 контрольными точками будет многочленом степени 3. И так далее.

Теперь вы подумаете, что насчет кубического многочлена. Итак, у нас есть решение. То есть мы всегда можем использовать кубический многочлен. И мы можем сделать различные кривые-секции или части. Тогда мы сможем объединить их.

Соединить части кривой Безье довольно просто.Поскольку они всегда проходят через первую и последнюю контрольную точку (Помните). Таким образом, мы можем легко получить непрерывность C1. Теперь, используя параметрические производные первого и второго порядка, мы также можем гарантировать непрерывность более высокого порядка.

Функции смешивания

Мы знаем, что контрольные точки влияют или, можно сказать, контролируют форму кривой Безье. Мы можем смешать влияние контрольных точек, чтобы найти окончательную контрольную точку. Эти функции являются функциями смешивания. Функции смешивания определяют вес. А точки кривой на самом деле являются средневзвешенными контрольными точками.Функции смешивания также известны как базовая функция.

Кубические кривые Безье

Кубическая кривая Безье — это кривая с четырьмя контрольными точками.

Итак, значение k составляет от 0 до 3.

Без 0,3 (u) = (1-u) 3

Без 1,3 (u) = u (1-u) 2

Без 2,3 (u) = u 2 (1-u)

Без 3,3 (u) = u 3

Поверхности Безье

Мы можем соединить кривые Безье, чтобы образовать поверхности Безье.Поверхности Безье имеют набор контрольных точек в качестве входной сетки. Поверхности Безье обладают теми же свойствами, что и кривые Безье.

Кривая Безье. Разберитесь в математике Безье… | Омар Афлак

Понимание математики кривых Безье

Кривые Безье часто используются в компьютерной графике, часто для создания гладких кривых, и тем не менее это очень простой инструмент. Если вы когда-либо использовали Photoshop, вы, возможно, наткнулись на инструмент под названием «Якорь», где вы можете ставить точки привязки и рисовать ими кривые… Да, это кривые Безье.Или, если вы использовали векторную графику, SVG, они тоже используют кривые Безье. Посмотрим, как это работает.

Дано n + 1 точек (P0,…, Pn) называется контрольными точками , кривая Безье, определенная этими точками, определяется как:

экв. 1

Где B (t) — полином Бернштейна, а:

экв. 2

Вы заметите, что этот многочлен Бернштейна очень похож на член k (th) в биномиальной формуле Ньютона:

экв.n = 1. Вот почему, если вы просуммируете все Bi до n , вы получите 1 . В любом случае.

Квадратичная кривая Безье — это то, как мы называем кривую Безье с 3 контрольными точками, поскольку степень P (t) будет равна 2. Давайте вычислим кривую Безье для 3 контрольных точек и исследуем некоторые свойства, которые мы можем найти! Помните, экв. 1 выполняется для n + 1 точек, поэтому в нашем случае n = 2.

экв. 4

Имейте в виду, что P (t) возвращает не число, а точку на кривой. Теперь нам просто нужно выбрать три контрольные точки и оценить кривую в диапазоне [0, 1] . Мы можем сделать это на Python довольно легко.

Вы можете заметить, что кривая начинается и заканчивается в первой и последней контрольных точках. Этот результат будет верен для любого количества баллов. Поскольку t находится в диапазоне от 0 до 1 , мы можем доказать это, оценив P (t) при t = 0 и t = 1 .Используя экв. 1 :

экв. 4 экв. 5

Поскольку кривая идет от P0 до P2 , в этом случае P1 полностью определяет форму кривой . Перемещение P1 вокруг вы можете кое-что заметить:

Разница между сплайном, B-сплайном и кривыми Безье

Разница между сплайном, B-сплайном и кривыми Безье

1. Сплайн:
Сплайн-кривая математическое представление, для которого легко создать интерфейс, который позволит пользователю проектировать и контролировать форму сложных кривых и поверхностей.

2. B-сплайн:
B-сплайн — это базовая функция, которая содержит набор контрольных точек. Кривые B-сплайна задаются базисной функцией Бернштейна, которая имеет ограниченную гибкость.

3. Безье:
Эти кривые задаются с граничными условиями, с характеристической матрицей или с функцией смешивания. Раздел кривой Безье может быть заполнен любым количеством контрольных точек. Количество аппроксимируемых контрольных точек и их относительное положение определяют степень полинома Безье.


Разница между сплайном, B-сплайном и кривыми Безье:

Сплайн B-сплайн Безье
Сплайновая кривая может быть указана с помощью указанного набора координат, называемых контрольные точки, которые указывают общую форму кривой. Кривые B-сплайна задаются базисной функцией Бернштейна, которая имеет ограниченную гибкость. Кривые Безье могут быть заданы с граничными условиями, с характеристической матрицей или с функцией смешивания.
Это соответствует общей форме кривой. Эти кривые являются результатом использования открытой унифицированной базисной функции. Кривая обычно повторяет форму определяющего многоугольника.
Типичное приложение САПР для шлифования включает проектирование автомобильных кузовов, поверхностей самолетов и космических кораблей, а также корпусов кораблей. Эти кривые можно использовать для построения кривых смешения. Их можно найти в пакетах для рисования и рисования, а также в приложениях САПР.
Обладает высокой степенью гладкости в местах соединения частей полинома. B-сплайн позволяет упорядочить базисную функцию и, следовательно, степень результирующей кривой не зависит от количества вершин.

No related posts.

Автор записи

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *