Как начертить изометрию?
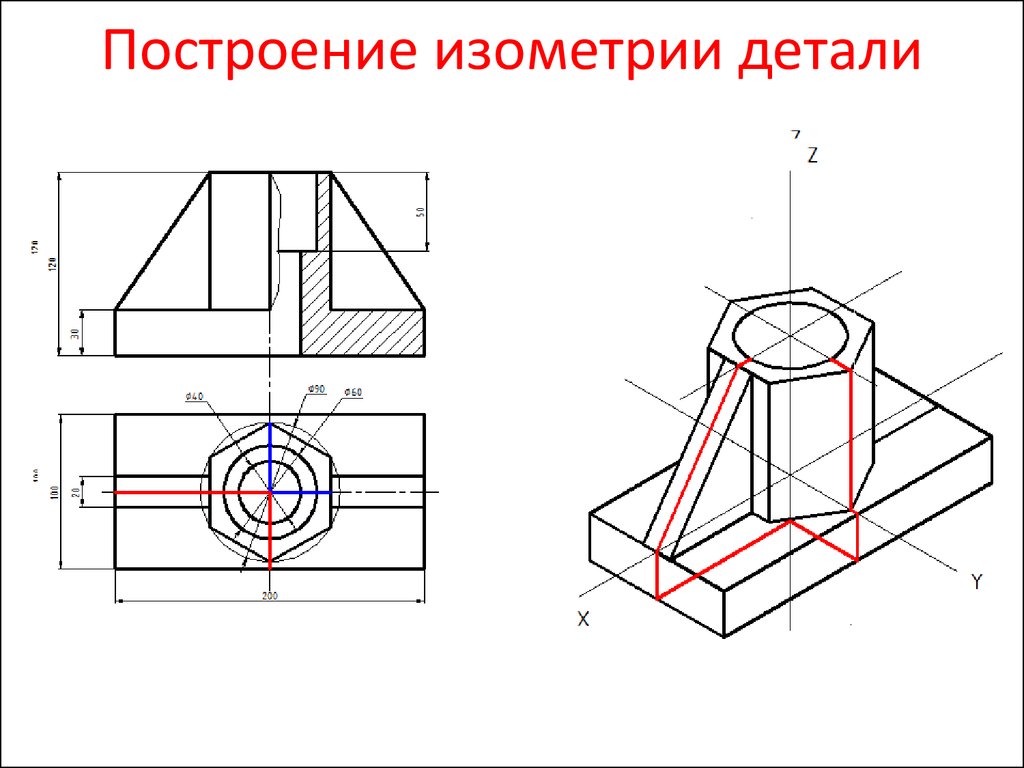
Начнем с того, что определимся с направлением осей в изометрии.
Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.
Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.
Мы получили верхнюю грань фигуры.
Не
хватает только отверстия диаметром 20
мм. Построим это отверстие. В изометрии
окружность изображается особым образом
— в виде эллипса. Это связано с тем, что
мы смотрим на нее под углом. Изображение
окружностей на всех трех плоскостях я
описал в  Эллипсы,
обозначающие окружности на горизонтальных
плоскостях в изометрии изображаются с
осью а расположенной горизонтально, а
ось b — вертикально. При этом расстояние
между точками расположенными на оси Х
или У равно диаметру окружности (смотри
размер 20 мм).
Эллипсы,
обозначающие окружности на горизонтальных
плоскостях в изометрии изображаются с
осью а расположенной горизонтально, а
ось b — вертикально. При этом расстояние
между точками расположенными на оси Х
или У равно диаметру окружности (смотри
размер 20 мм).
Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра — по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена — не хватает только прямоугольного сквозного отверстия.
Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия — по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.
На
этом простая изометрическая проекция
может считаться завершенной. Но как
правило, в курсе инженерной графики
выполняется изометрия с вырезом одной
четверти.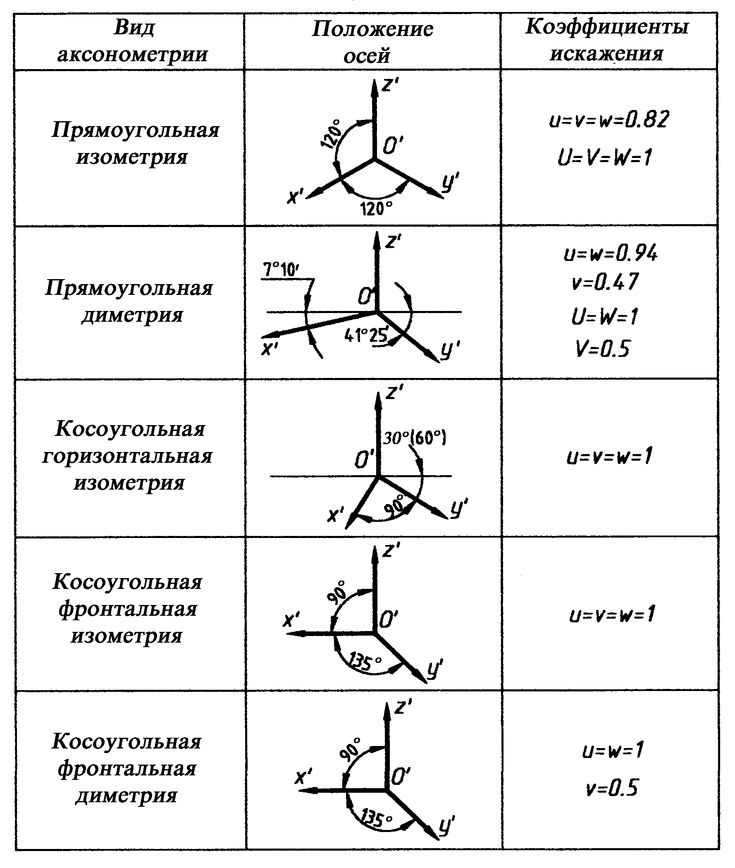 Чаще всего, это четверть нижняя
левая на виде сверху — в этом случае
получается наиболее интересный с точки
зрения наблюдателя разрез (конечно же
все зависит от изначальной правильности
компоновки чертежа, но чаще всего это
так). На нашем примере эта четверть
обозначена красными линиями. Удалим
ее.
Чаще всего, это четверть нижняя
левая на виде сверху — в этом случае
получается наиболее интересный с точки
зрения наблюдателя разрез (конечно же
все зависит от изначальной правильности
компоновки чертежа, но чаще всего это
так). На нашем примере эта четверть
обозначена красными линиями. Удалим
ее.
Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).
Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!
Как начертить окружность в изометрии?
Как
вы наверняка знаете, при построении
изометрии окружность изображается в
виде эллипса.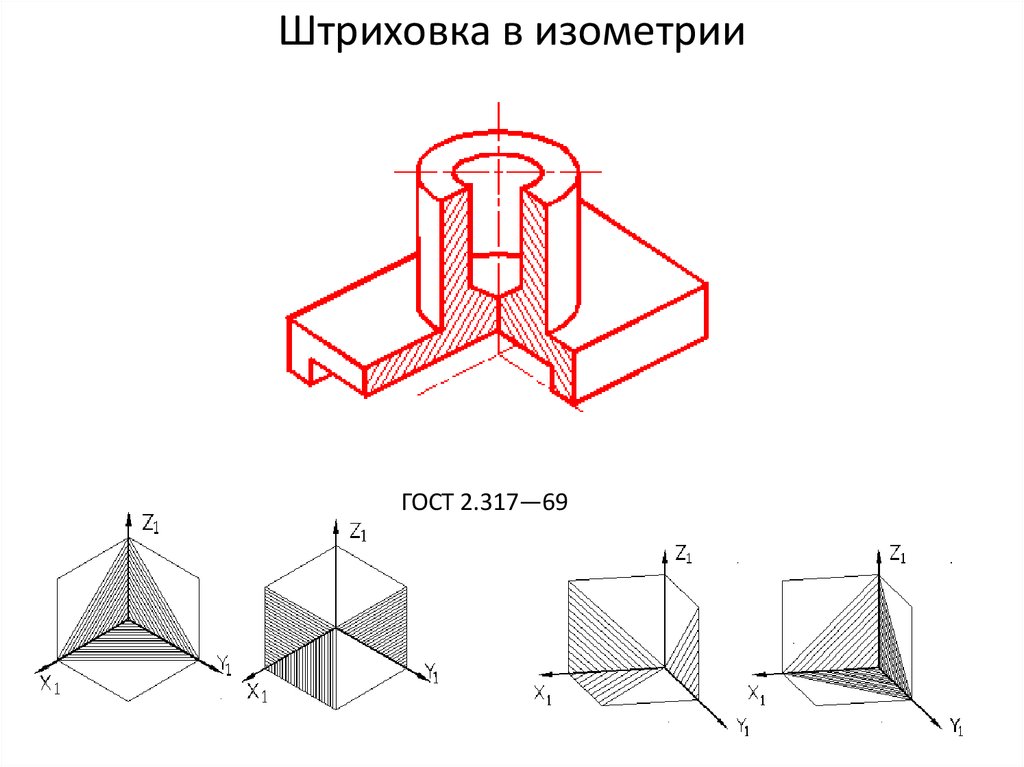 Причем вполне конкретного:
длина большой оси эллипса AB=1.22*D, а длина
малой оси CD=0.71*D (где D — диаметр той самой
исходной окружности, которую мы хотим
начертить в изометрической проекции).
Как начертить эллипс зная длину осей?
Об этом я рассказывал в отдельном уроке.
Там рассматривалось построение больших
эллипсов. Если же исходная окружность
имеет диаметр где-то до 60-80 мм, то скорее
всего мы сможем начертить ее и без лишних
построений, используя 8 опорных точек.
Рассмотрим следующий
рисунок:
Причем вполне конкретного:
длина большой оси эллипса AB=1.22*D, а длина
малой оси CD=0.71*D (где D — диаметр той самой
исходной окружности, которую мы хотим
начертить в изометрической проекции).
Как начертить эллипс зная длину осей?
Об этом я рассказывал в отдельном уроке.
Там рассматривалось построение больших
эллипсов. Если же исходная окружность
имеет диаметр где-то до 60-80 мм, то скорее
всего мы сможем начертить ее и без лишних
построений, используя 8 опорных точек.
Рассмотрим следующий
рисунок:
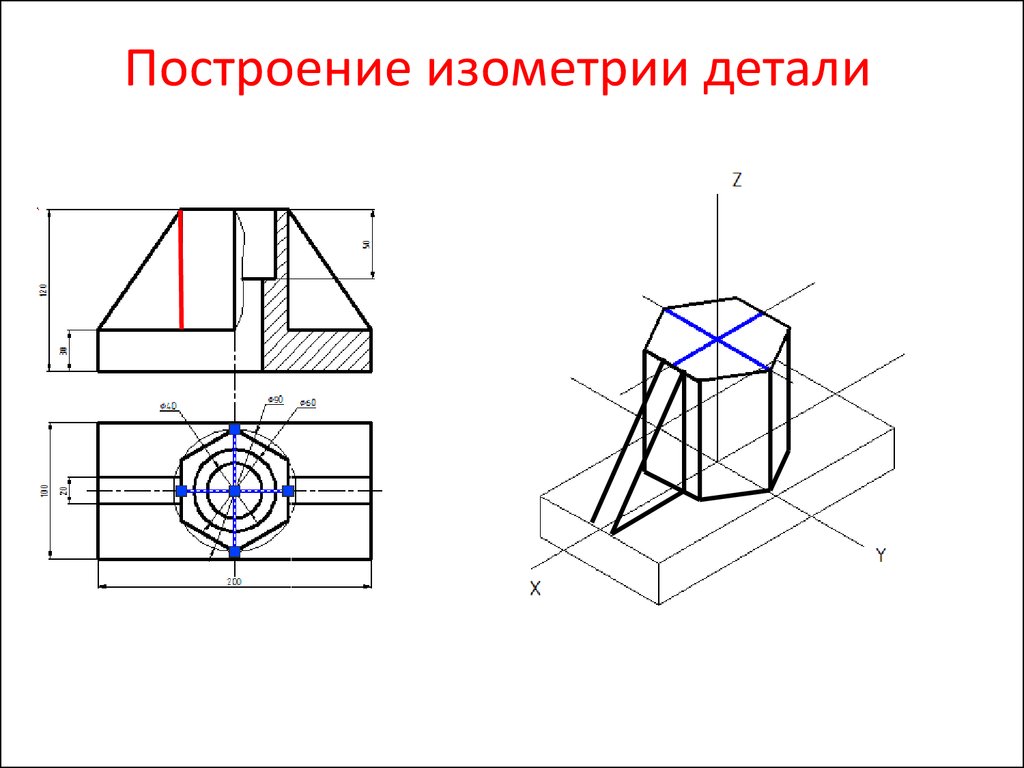
Это
фрагмент изометрии детали, полный чертеж
которой можно увидеть ниже. Но сейчас
мы говорим о построении эллипса в
изометрии. На данном рисунке AB — большая
ось эллипса (коэффициент 1.22), CD — малая
ось (коэффициент 0.71). На рисунке половина
короткой оси (ОD) попала в вырезанную
четверть и отсутствует — используется
полуось СО (не забудьте об этом, когда
будете откладывать значения по короткой
оси — полуось — имеет длину равную половине
короткой оси).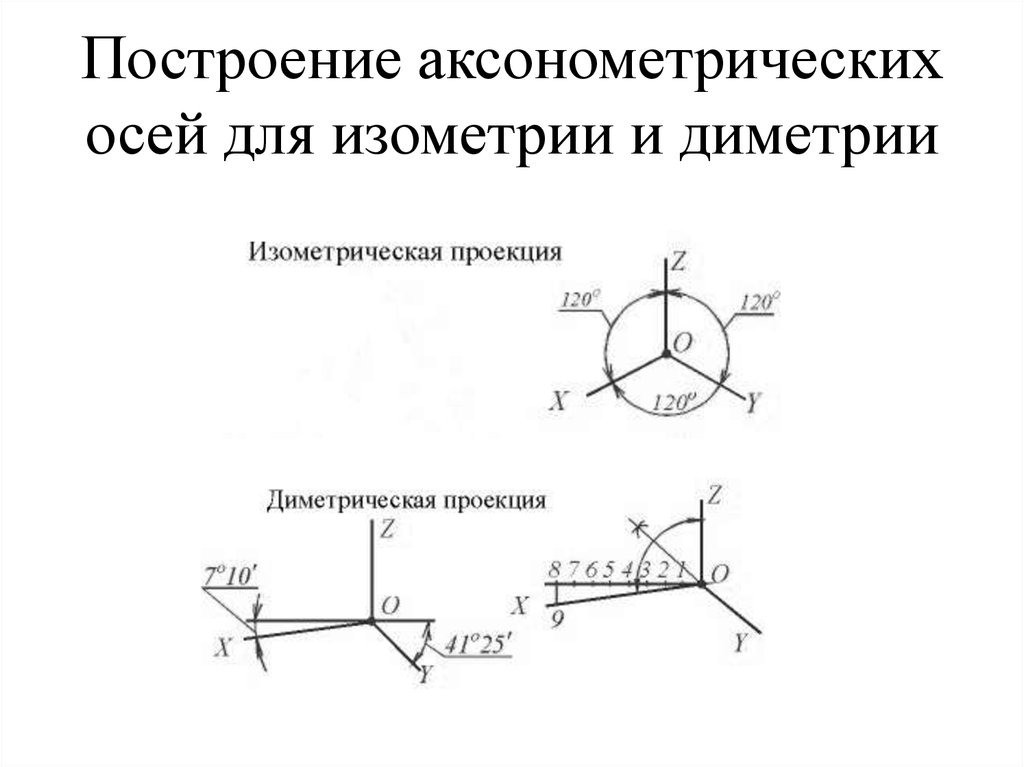
Для лучшего понимания направления осей эллипсов в зависимости от того, какое направление имеет циллиндр, рассмотрим три разных отверстия в детали, имеющей форму параллелепипеда. Отверстие — тот же цилиндр, только из воздуха 🙂 Но для нас это особого значения не имеет. Полагаю, что ориентируясь на эти примеры вы без труда сможете правильно расположить оси своих эллипсов. Если же обобщить, то получится так: большая ось эллипса перпендикулярна той оси, вокруг которой образован цилиндр (конус).
Изометрия. Способы построения изометрических осей
Похожие презентации:
Основы архитектуры и строительных конструкций.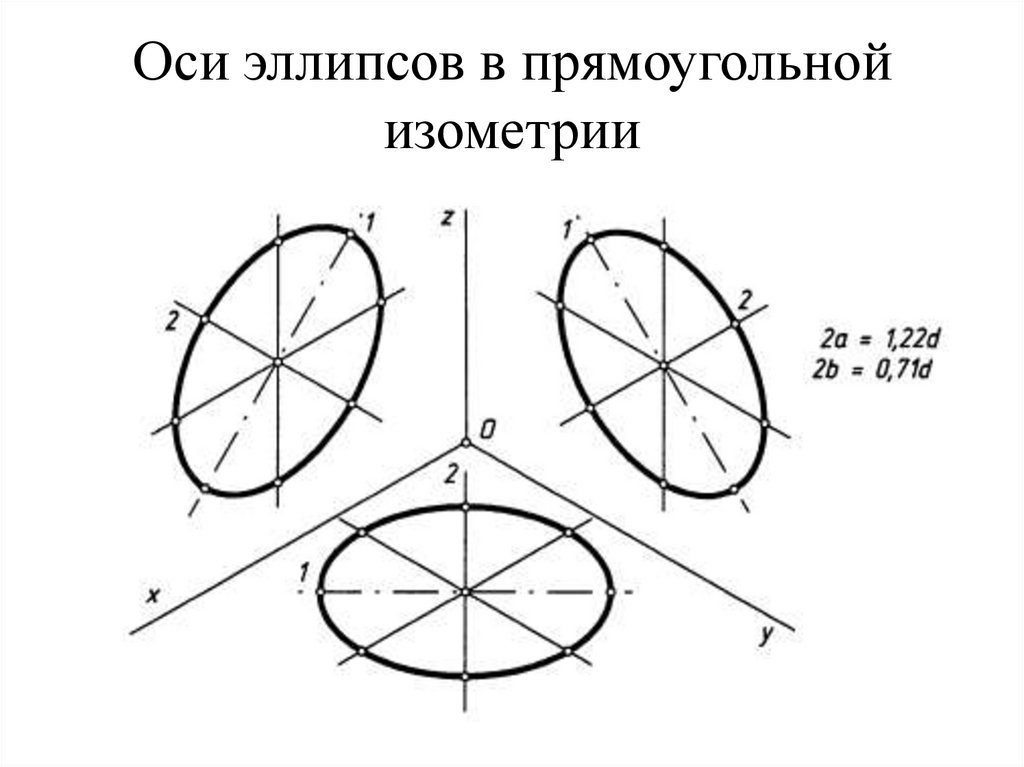 Основы проектирования
Основы проектирования
Конструктивные схемы многоэтажных зданий
Стадии проектирования зданий. Маркировка строительных чертежей (лекция №2)
Правила выполнения архитектурно-строительных чертежей
ЕСКД. Общие правила оформления чертежей. (Лекция 1.1)
задачи на построение (геометрия 7 класс)
Выполненный вариант контрольной работы по разделу «Техническое черчение». (Приложение 3)
Параллельность в пространстве. (Графическая работа 2)
Строительное черчение. Графическое оформление и чтение строительных чертежей
Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты
900igr.net
Содержание
Немного теории
Способы построения изометрических осей
Порядок построения изометрии
Точки и отрезки
Изометрия плоских фигур
Геометрические тела
Деталь изнутри
Практика
Проверь себя
Используемая литература
3. Немного теории
Чертеж механизма или детали не дает полное представление о егоформе.
 Поэтому чертежи сложных изделий сопровождают наглядными
Поэтому чертежи сложных изделий сопровождают нагляднымиизображениями (аксонометрическими проекциями).
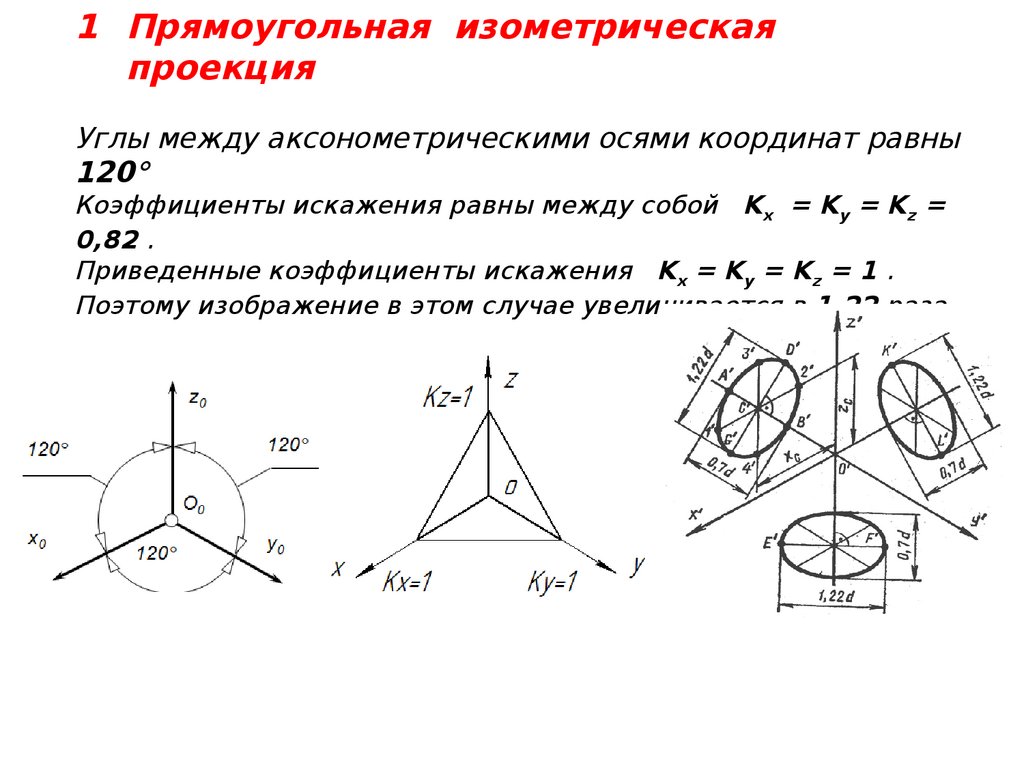
Аксонометрия — слово греческое, в переводе означает измерение по осям.
При построении аксонометрических проекций размеры откладывают
вдоль осей X,Y,Z. Аксонометрические проекции отличаются наглядностью:
Изометрия – это одна из аксонометрических проекций.
Изометрия(греч.) — равное измерение.
При вычерчивании изометрической проекции (изометрии)
размеры по всем трем осям откладывают натуральные, а
сами оси выглядят так:
Содержание
x
z
y
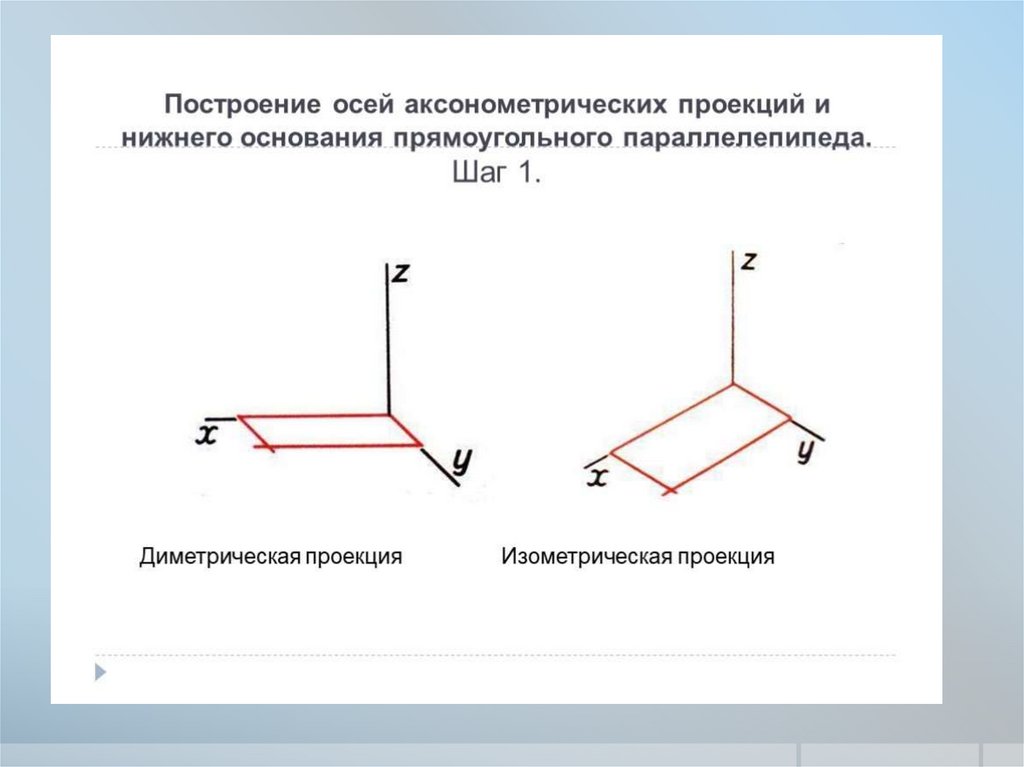
4. Способы построения изометрических осей
Содержание5. Порядок построения изометрии
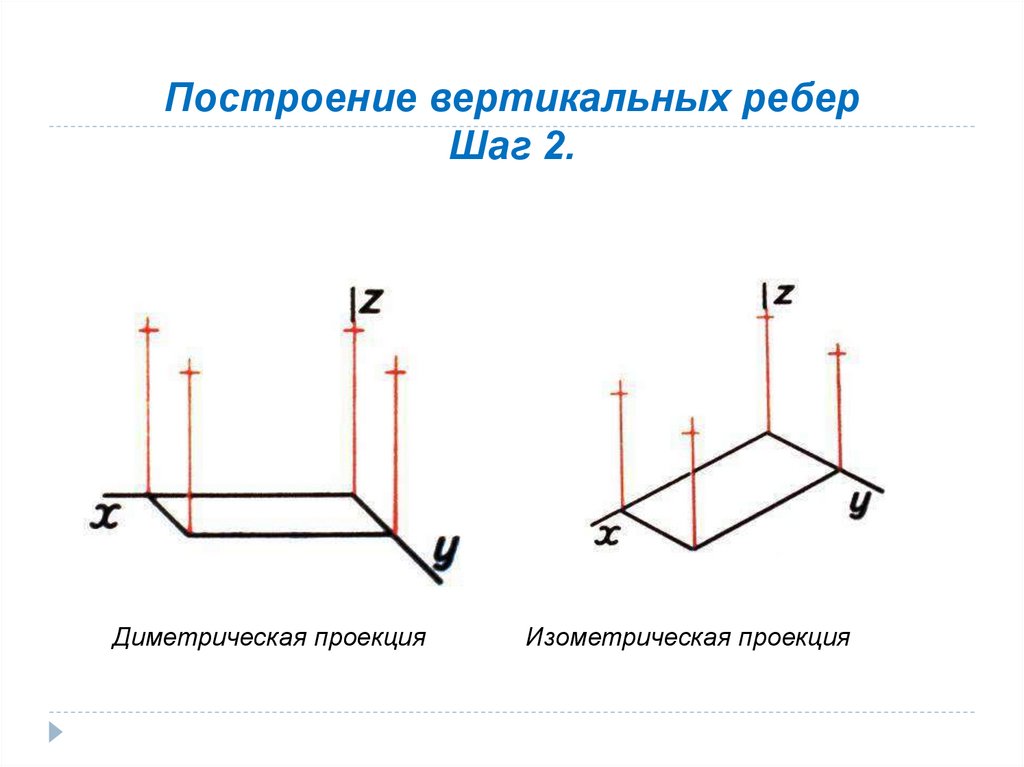
1. Проводят оси. Строят переднюю грань детали, откладываядействительные величины высоты — вдоль оси Z, ширины – вдоль оси X.
2. Из вершины полученной фигуры параллельно оси Y проводят ребра, уходящие
вдаль. Вдоль них откладывают действительную толщину детали.
3. Через полученные точки проводят прямые, параллельные ребрам передней
грани.
4. Удаляют лишние линии, обводят видимый контур и наносят размеры.
Вы познакомились с общими правилами построения изометрических проекций. На
следующих слайдах эти проекции представлены более детально.
Содержание
6. Точки и отрезки
Все детали можно мысленно разделить на геометрические тела,которые состоят из вершин (точек), ребер (отрезков) и граней
(плоских фигур).
Чтобы построить изометрию точки, необходимо знать ее
координаты X, Y, Z и откладывать их по соответствующим
осям:
Аналогично строят изометрию отрезка.
Содержание
7. Изометрия плоских фигур
Правильный шестиугольник в плоскости XOY:из точки О1 по оси X откладывают отрезки О111 и О141,
равные размеру отрезков О1 и О4. По этой же оси
откладывают отрезки О171 и О181, равные отрезкам О7 и
О8. Через полученные точки 71 и 81 проводят
параллельно оси Y прямые линии. На них откладывают
отрезки 71-21, 81-31 и т. д ., равные отрезкам 7-2, 8-3 и т.
 д.
д.Найденные шесть точек последовательно соединяют
прямыми.
Аналогично строят изометрию правильного шестиугольника
в плоскостях ZOX и ZOY.
Правильный пятиугольник:
Для упрощения работы построения выполняют по двум
координатам вершин, откладывая их по
соответствующим осям.
Содержание
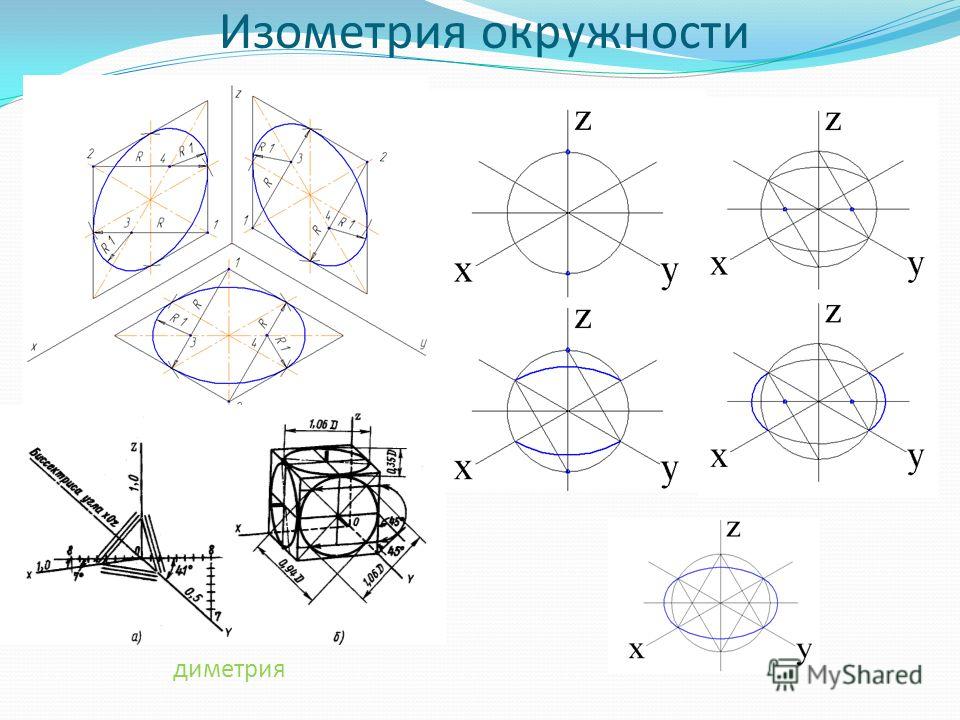
Окружность:
Окружности в изометрии изображаются
в виде эллипсов.
Для упрощения работы эллипсы
заменяют овалами, вписанными в ромб со
стороной, равной диаметру заданной
окружности. Для этого на осях (например
x и y) откладывают от точки О в
четырех направлениях отрезки, равные
радиусу изображаемой окружности.
Через полученные точки a, b, c, d
проводят прямые, образующие ромб. Из
точек А и В проводят дуги радиусом R
между точками a и b, c и d.
Точки C и D являются центрами малых
дуг, сопрягающих большие. Малые дуги
описывают радиусом R1.
Аналогично строят овалы на осях z и x, z и y.
Содержание
9.
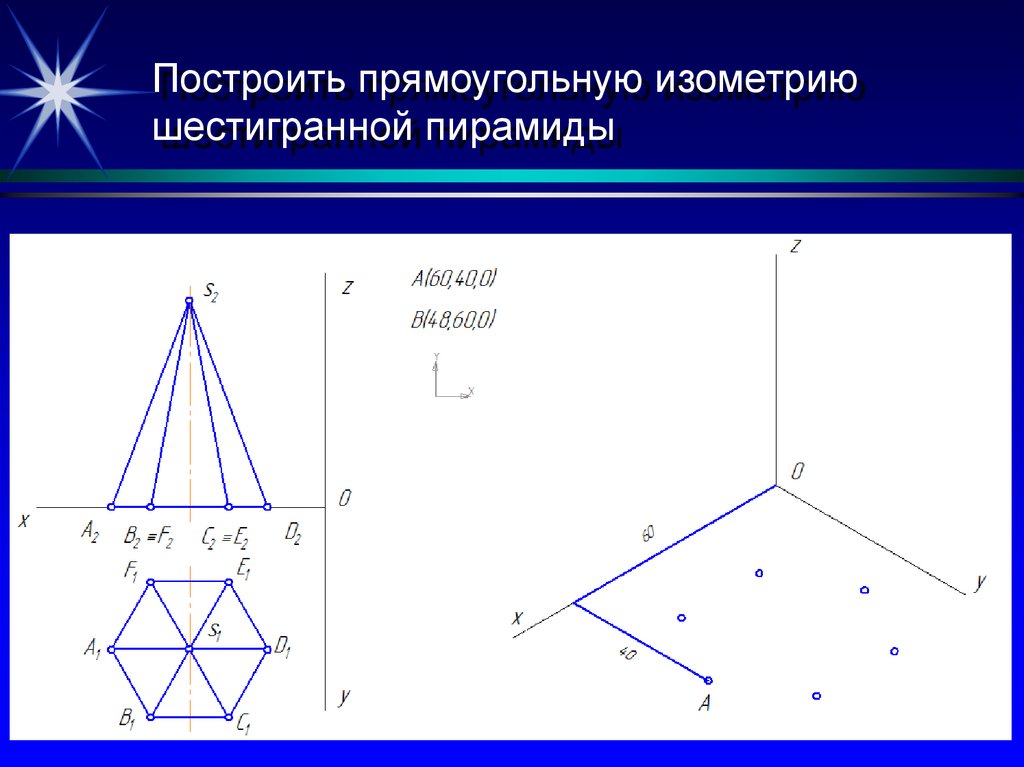
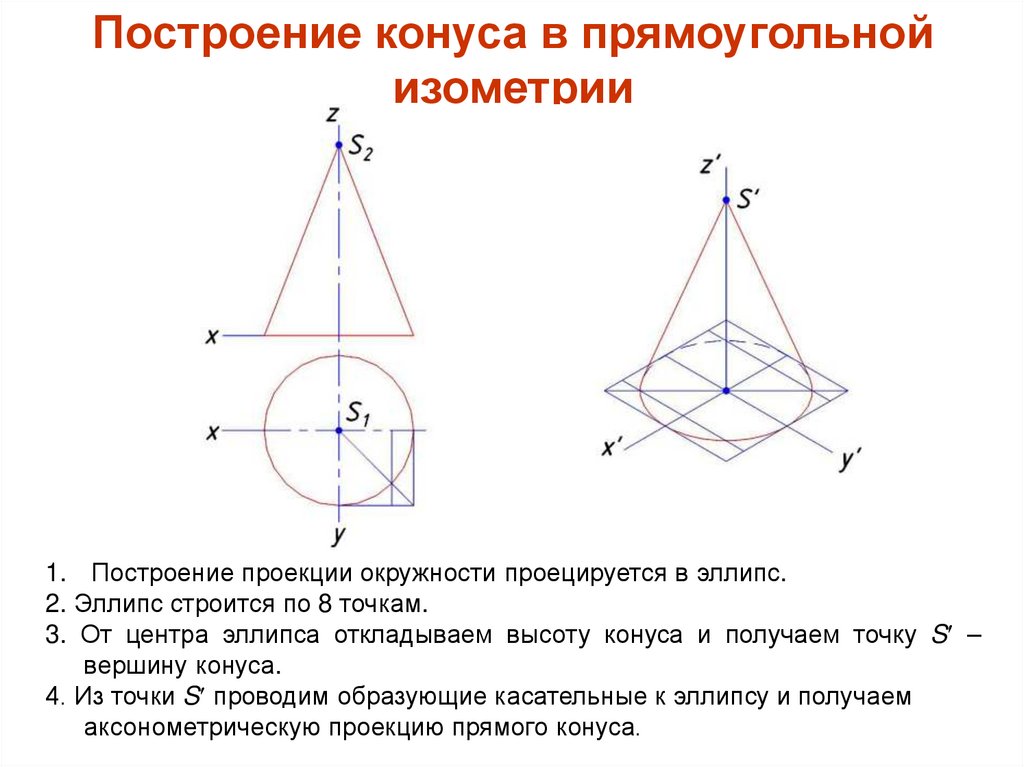 Геометрические телаПирамида.
Геометрические телаПирамида.На рисунке а показан комплексный
чертеж(рисунок а) неправильной пятиугольной
пирамиды. По этому чертежу определяем
координаты всех точек основания пирамиды.
Затем по координатам x и y строим изометрию
пяти точек-вершин основания
пирамиды(рисунок б).
Пример.
По оси х от точки О откладываем координату
ХА=a‘ d. Из конца ее проводим прямую,
параллельную оси y,на которой откладываем
вторую координату этой точки YA=a‘ a.
Далее строят по координатам высоту
пирамиды и получают точку S-вершину
пирамиды. Соединяя точку S с
Точками A, B, C, D и E, получают
изометрическую проекцию пирамиды.
Содержание
Призма:
Если основание призмы – правильный
многоугольник (например, шестиугольник), то
построение вершин основания по координатам
можно упростить, проводя одну из осей
координат через центр основания. Оси x, y и z
проводят через центры правильных
шестиугольников призмы.
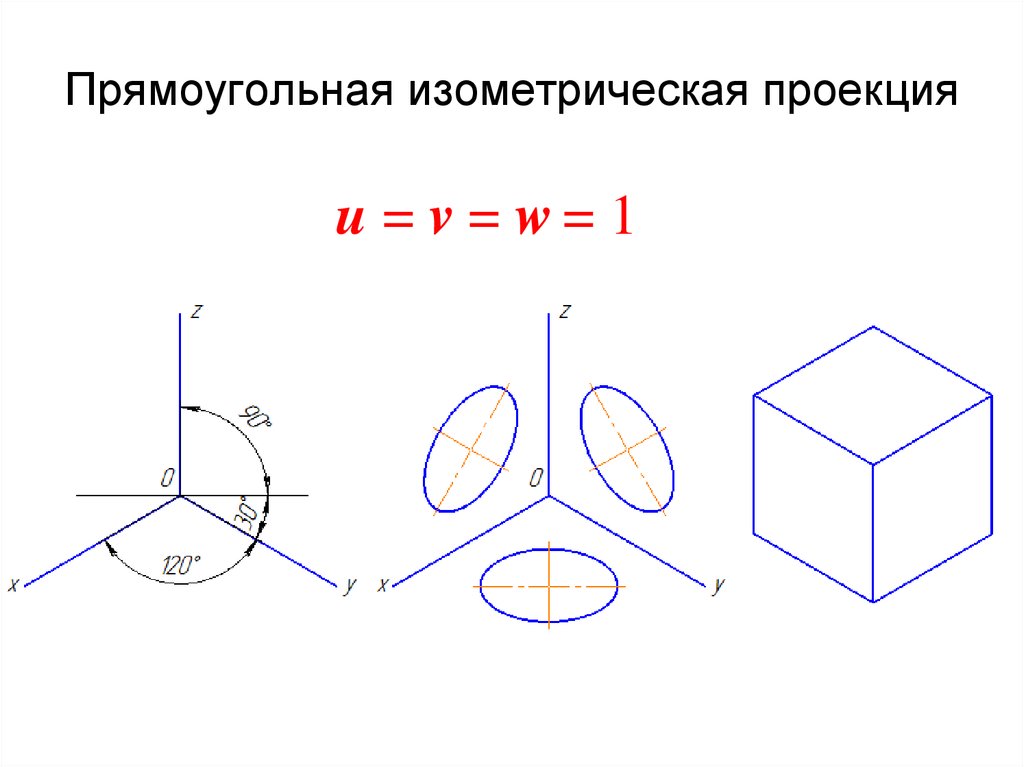 Далее из вершин
Далее из вершиншестиугольника основания проводим прямые,
параллельные соответственно осям x, y и z (для
каждой из рассматриваемых на рисунке призм). На
этих прямых от вершин основания откладывают
высоту призмы и получают точки 1, 2, 3, 4, 5, 6
вершин другого основания призмы.
Соединив эти точки прямыми, получают
изометрическую проекцию призмы. В заключение
видимые ребра проводят сплошными толстыми
линиями, а невидимые ребра — тонкими
штриховыми.
Содержание
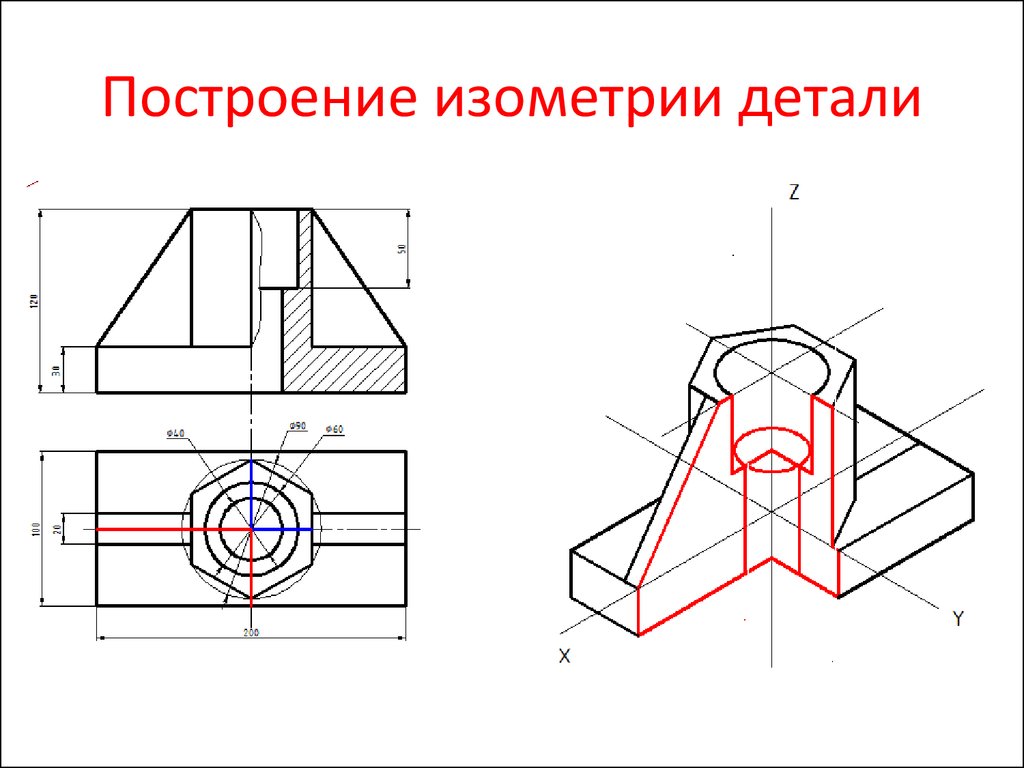
11. Деталь изнутри
Для выявления внутренней формыпредмета применяют вырез одной
четверти детали.
Вначале строят в тонких линиях
изометрию (см. рисунок а). Затем
выполняют вырез, направляя две
вертикальные секущие плоскости
по осям x и y (см. рисунок б).
Удаляют часть изображаемого
предмета (см. рисунок в), после чего
штрихуют сечения и обводят
изображение сплошными толстыми
линиями (см. рисунок г).
Содержание
12. Практика
Эти упражнения помогут Вам попробовать свои силы(проверить и закрепить знания).
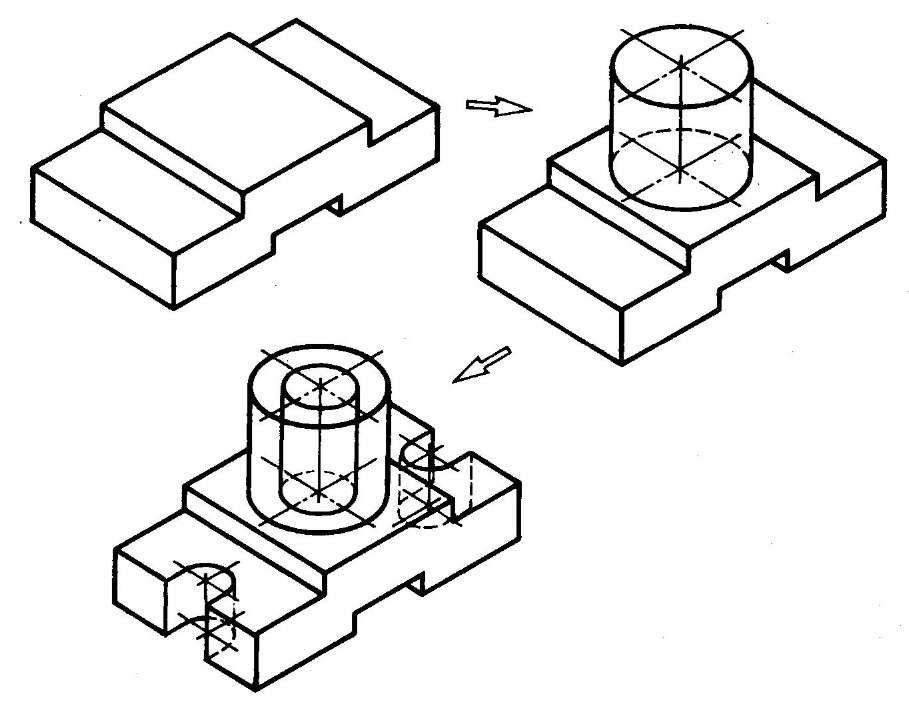
Упражнение 1.
1. Какое наглядное изображение представлено на
чертеже?
2. Чему равны углы между осями изометрической
проекции?
3. В какую фигуру проецируются окружности в
изометрии?
4. Чему равны габаритные размеры детали?
5. Есть ли в изделии отверстия? Сколько их и какова
их форма?
Упражнение 2.
Постройте изометрическую проекцию детали по ее
комплексному чертежу.
Содержание
13. Проверь себя
Эталон к упражнению 1:1. Изометрическая проекция.
2. 120°.
3. Эллипс.
4. 90; 40; 50 мм.
5. Да. 3. Цилиндр.
Содержание
Эталон к упражнению 2:
14. Используемая литература
1.Боголюбов С.К. Черчение, М.: Машиностроение,1989г.2005г.
3.Вышнепольский И.С. Черчение для техникумов, М.: АСТ,
Астрель, 2002г.
4.Бахнов Ю.Н. Сборник заданий по техническому черчению,
М.: Высшая школа, 1988г.
Содержание
Благодарю за
внимание!
Содержание
В начало
English Русский Правила
изометрий треугольников и сегментов
изометрий треугольников и сегментовИзометрия треугольника | Сохранение ориентации из сегмента | Ориентация-реверс с сегмента
1.
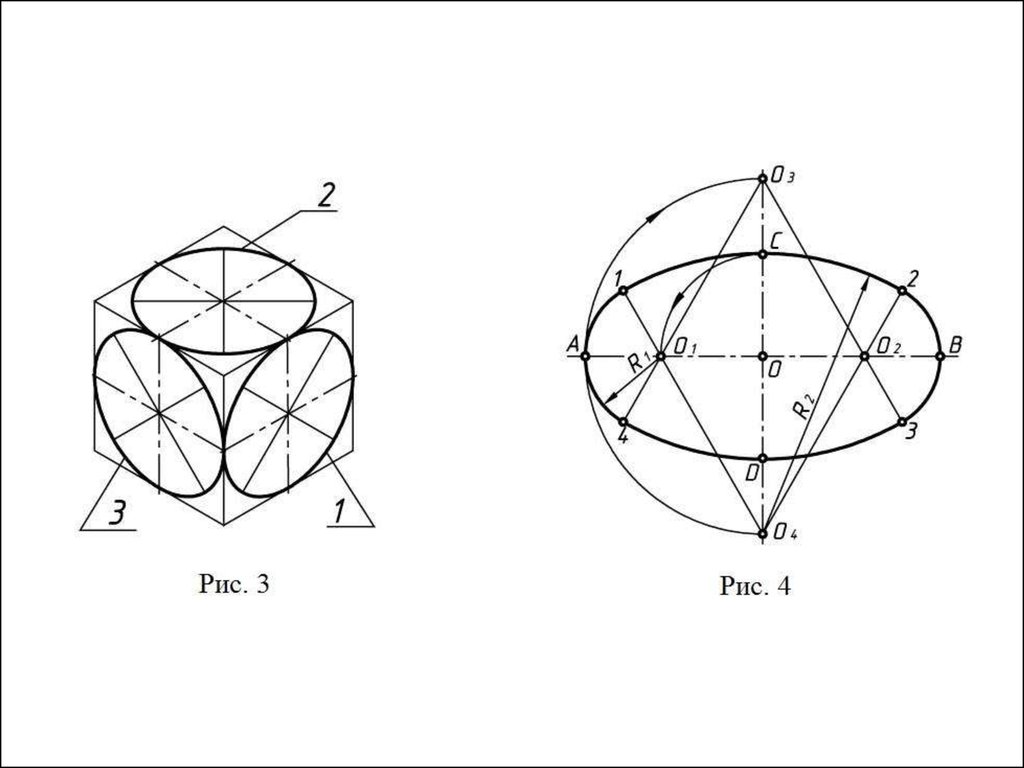
Имея два треугольника ABC и A’B’C’, мы говорим, что -преобразование T принимает ABC в A’B’C’, если T(A) = A’ и T(B) = B’ и T(C) = C’. Если ABC и A’B’C’ являются конгруэнтными треугольниками, мы знаем из фундаментальной теоремы об изометриях, что существует ровно одна изометрия T, которая переводит ABC в A’B’C’.
Примечание: Этот оператор учитывает порядок вершин. Если T переводит ABC в A’B’C’, то он не переводит ABC в C’A’B’.
Однако в конкретных случаях нужно точно определить по двум треугольникам что такое изометрия Т. Какой это тип изометрии и каковы ее определяющие данные.
Метод построения 1: (Используйте доказательство основной теоремы)
 Доказательство
представляет собой пошаговое построение до трех линий отражения. Можно
сделать эту конструкцию, а затем использовать теоремы о композиции изометрий
точно определить, что такое изометрия Т. Однако этот метод долгий и косвенный,
особенно для скользящих отражений.
Доказательство
представляет собой пошаговое построение до трех линий отражения. Можно
сделать эту конструкцию, а затем использовать теоремы о композиции изометрий
точно определить, что такое изометрия Т. Однако этот метод долгий и косвенный,
особенно для скользящих отражений.Метод построения 2: (Используйте средние точки)
Даны два конгруэнтных треугольника ABC и A’B’C’, постройте их середины A». AA’, B» из BB’, C» из CC’.
Тогда расположение средних точек покажет, какую изометрию принимает Т. от АВС до А’В’С’.
- Если T является тождеством или переводом, A»B»C» является конгруэнтным треугольником к АВС.
- Если T — это поворот на угол x, но не на пол-оборота, то A»B»C» является треугольником аналогично ABC (коэффициент масштабирования cos(x/2).
- Если T представляет собой пол-оборота, все 3 средние точки являются одной и той же точкой, т.е.
центр полуоборота.
- Если T является скользящим отражением, 3 средние точки коллинеарны и не более 2 совпадают, так как А, В, С не лежат на одной прямой*. Таким образом, есть одна линия через середины, и это инвариантная линия T.
Перевод Полуоборота | Вращение |
Отражение линии | Скользящее отражение |
* Доказательство того, что точки A», B» и C» не могут быть одинаковыми для прямой
отражение или скользящее отражение следует из определения этих преобразований.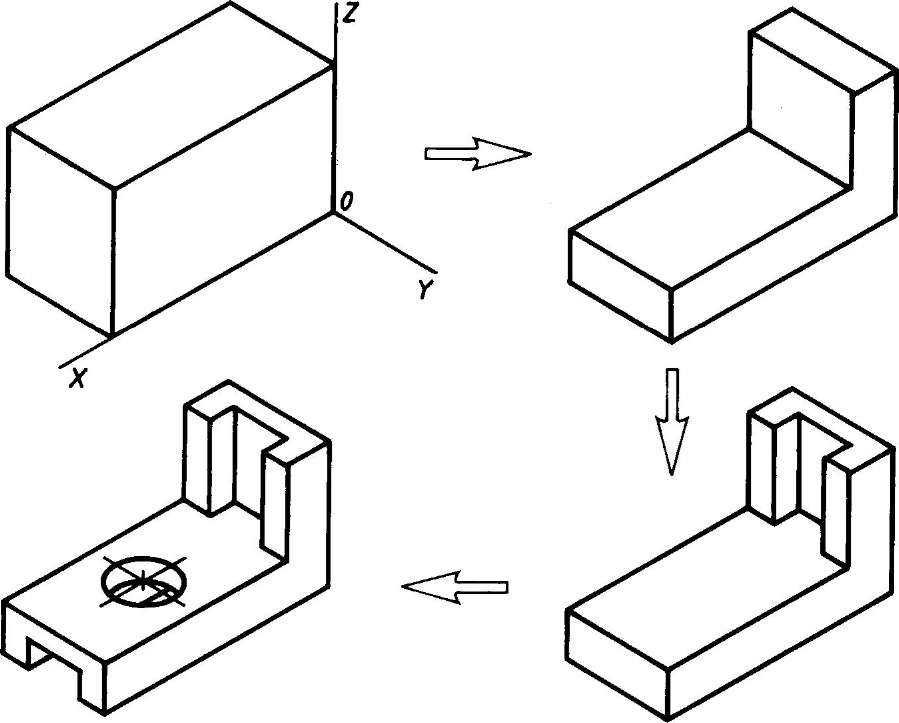 Для T = отражение линии в линии m, A», B», C» являются основаниями перпендикуляров.
к m через A, B, C. Таким образом, они могут совпадать только в том случае, если A, B, C находятся на
той же прямой, перпендикулярной m. Для T = отражение скольжения с вектором скольжения v,
тогда если A*, B*, C* основания перпендикуляров к m, проходящих через точки A, B, C,
тогда A», B», C» — переносы этих точек на вектор (1/2)v. Таким образом
середины A», B», C» совпадают тогда и только тогда, когда совпадают ножки A*, B*, C*,
что снова означает, что A, B, C лежат на одной прямой, перпендикулярной m.
Для T = отражение линии в линии m, A», B», C» являются основаниями перпендикуляров.
к m через A, B, C. Таким образом, они могут совпадать только в том случае, если A, B, C находятся на
той же прямой, перпендикулярной m. Для T = отражение скольжения с вектором скольжения v,
тогда если A*, B*, C* основания перпендикуляров к m, проходящих через точки A, B, C,
тогда A», B», C» — переносы этих точек на вектор (1/2)v. Таким образом
середины A», B», C» совпадают тогда и только тогда, когда совпадают ножки A*, B*, C*,
что снова означает, что A, B, C лежат на одной прямой, перпендикулярной m.
Эти случаи позволяют нам вывести характер изометрии по средним точкам А»В»С».
- Если точки совпадают с точкой P, T является полуоборотом с центром P.
- Если точки лежат на одной прямой, но не все совпадают, то Т является ориентацией реверсивный Полное построение геометрических данных прописано в этом разделе ниже: Метод построения: линейное отражение или скользящее отражение из 2 равных сегментов
- Если точки образуют треугольник, то T сохраняет ориентацию, а данные могут быть построены по описанию в этом разделе ниже: Строительство Метод: вращение или перемещение из 2 конгруэнтных сегментов
2.
 Как построить данные поворота или перевода
с изображения отрезка или точки
Как построить данные поворота или перевода
с изображения отрезка или точкиОсновная теорема | Из изображения сегмента | Из изображения точки, зная угол
Имея два отрезка AB и CD, мы говорим, что преобразование T переводит AB в CD, если T(A) = C и T(B) = D .
Примечание: Этот оператор учитывает порядок конечных точек. Если T переводит AB в CD, то он не переводит AB в DC.
Теорема (Фундаментальная теорема для сохранения ориентации Изометрии)
Для двух конгруэнтных отрезков AB и CD существует ровно один сохраняющий ориентацию отрезок. изометрия T, переводящая AB в CD.
Доказательство (также конструкция):
Это состоит из первых двух шагов второй фундаментальной теоремы изометрий.
Если A и C различны, пусть m 1 будет серединным перпендикуляром
переменного тока. В частном случае, когда A = C, пусть m 1 = линия AB (на самом деле,
подойдет любая линия через А).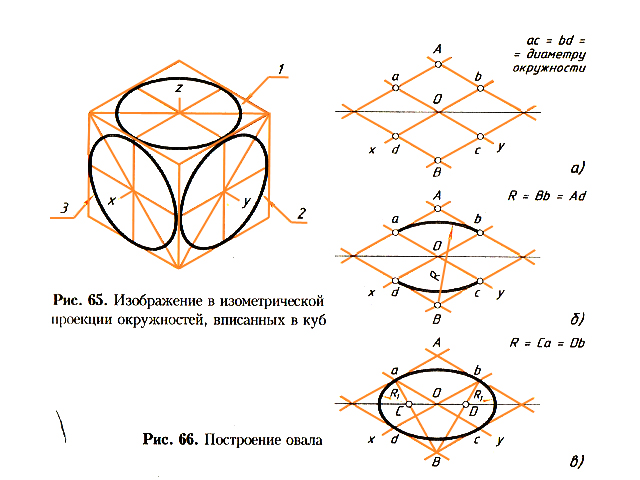 Пусть R 1 обозначает отражение линии в m 1 .
Пусть R 1 обозначает отражение линии в m 1 .
Для этого отражения R 1 (A) = C. Пусть B’ = R 1 (B). Отрезок CD конгруэнтен CB’, так как R 1 является изометрией. Если B’ не D, пусть m 2 будет серединным перпендикуляром к B’D. Так как |CB’| = |CD|, точка C находится на m 2 . В особом случае B’ = D, пусть m 2 = линия CD. Пусть R 2 — отражение в м 2 . В любом случае 9 р.0122 2 (B’) = D и R 2 (C) = C. Таким образом, настройка T = R 2 R 1 , T(A) = C и T(B) = D. |
T – это композиция двух линейных отражений. T — вращение с центром O
если две прямые m 1 и m 2 пересекаются в одной точке O; это
является переводом, если m 1 и m 2 параллельны.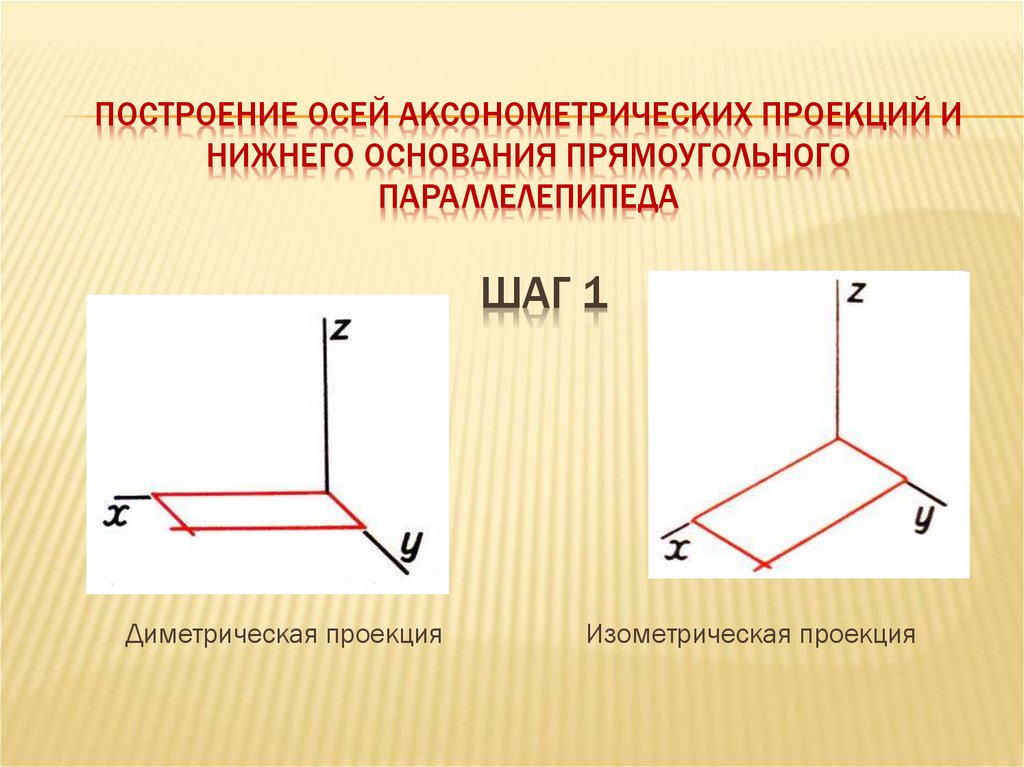 Если линии
одинаковы, то Т тождественно.
Если линии
одинаковы, то Т тождественно.
Наконец, утверждается, что Т является единственной сохраняющей ориентацию изометрией, которая переводит AB в CD. Чтобы убедиться в этом, предположим, что S = R 4 R 3 также переводит AB в CD. Тогда S -1 = R 3 R 4 берет CD жаба. Таким образом, S -1 T = R 3 R 4 R 2 R 1 переводит AB в AB.
Это означает, что S -1 T (A) = A и S -1 T (B) = B являются двумя неподвижные точки изометрии. Но изометрия S -1 Т — сохраняющая ориентацию изометрия, так как это произведение 4-х линейных отражений. Это означает, что это является вращением, переводом или тождеством. Но единственная из этих изометрий с двумя неподвижными точками является единицей, поэтому S -1 T = I, и, следовательно, T = S.
Таким образом, существует только одна сохраняющая ориентацию изометрия, которая переводит AB в CD.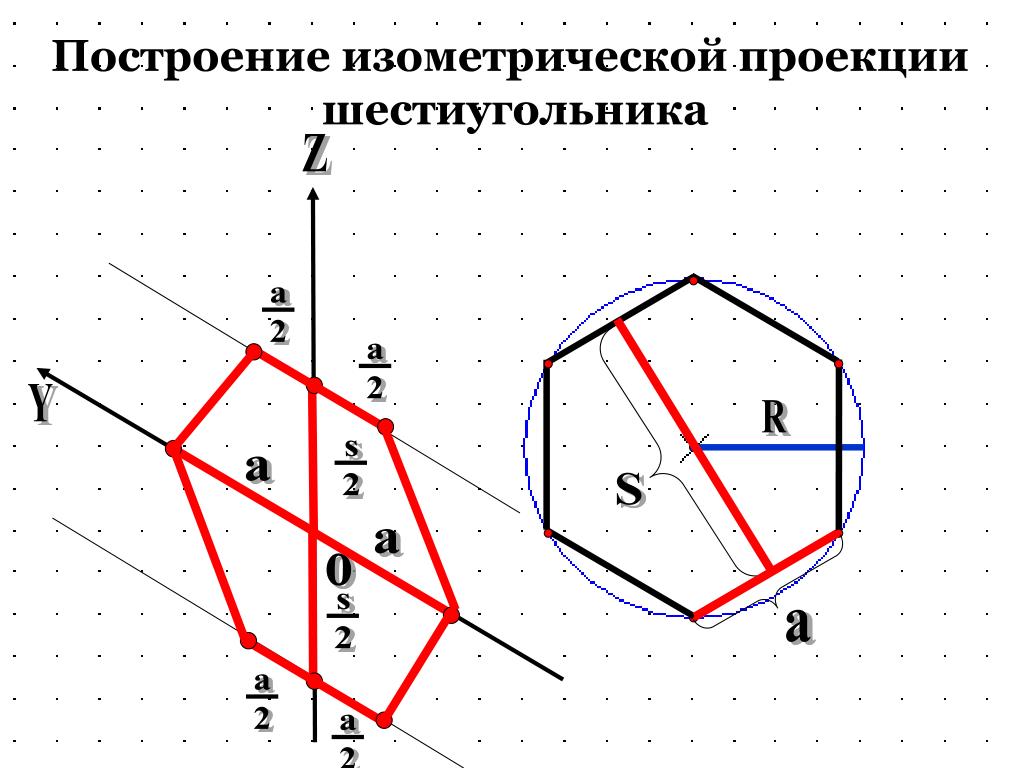
Метод построения: вращение или перемещение от 2 конгруэнтные сегменты
Учитывая два конгруэнтных отрезка AB и CD, как можно построить единственный сохраняющий ориентацию отрезок? изометрия T, которая переводит AB в CD?
На практике представляют интерес случаи, когда T представляет собой вращение или перемещение, поскольку, если A = C и B = D, для тождества не требуется построения.
Общий случай: Предположим, что A не C, а B не D. Постройте линии m = биссектриса AC и n = биссектриса BD.
Если T — вращение, прямые m и n пересекаются в точке O, центре вращение. Ведь в этом случае A и C = T(A) лежат на одной окружности. с центром O, так что биссектриса m хорды AC проходит через O. Для по той же причине n проходит через O. Угол поворота равен углу АОС. В особом случае полуоборота O также является средней точкой AC и BD. Если T является переносом, то AC и BD параллельны, поэтому m и n также параллельно. Вектор трансляции AC. |
Особые случаи: Предположим, что A = C, но B и D различны. В этом случае, A уже является центром вращения, которое приведет B к D. Вращение угол это угол БАД. Аналогично обрабатывается случай, когда B = D. Если А = C и B = D, тогда T = тождество.
Метод построения: Вращение изображения одной точки плюс угол поворота
Предположим, что T является поворотом на угол x. Если нам даны два различных точки A и C, такие, что T(A) = C, достаточно ли этого для определения T?
Поскольку угол поворота T задан, если можно построить центр O, тогда Т будет известно полностью.
Из данной информации T(A) = C следует, что O находится на прямой m,
серединный перпендикуляр к АС.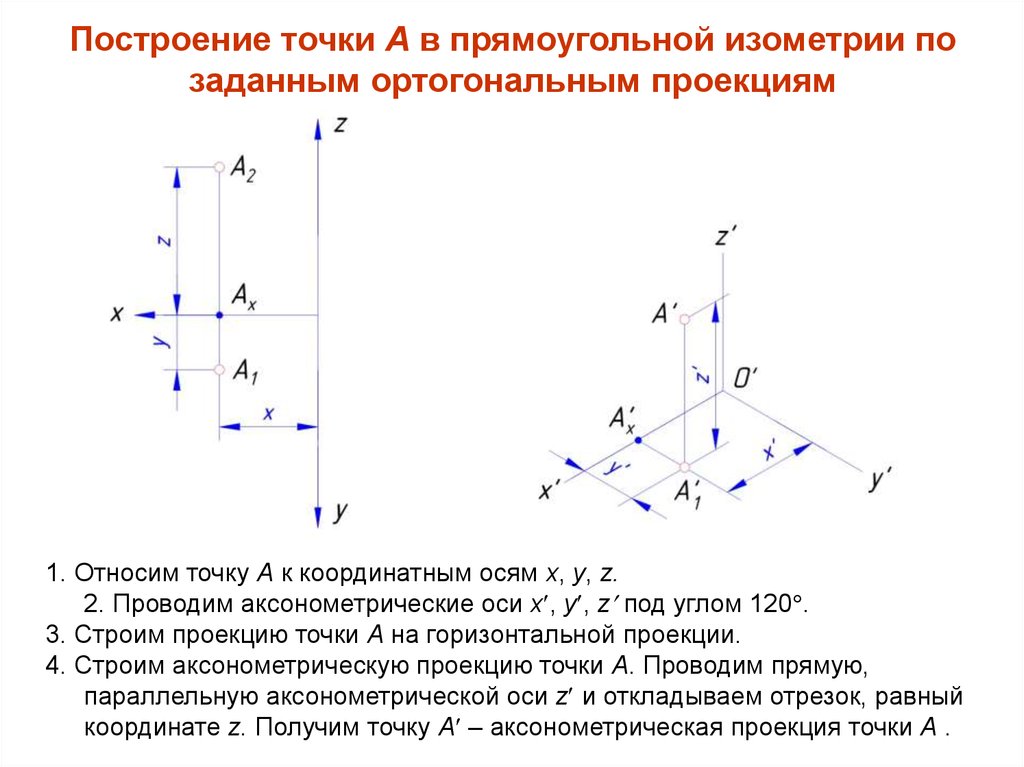 Кроме того, угол AOC = x.
Кроме того, угол AOC = x.
Угол x является ориентированным, или углом со знаком. Есть несколько корпусов:
- Угол x = 0 градусов. Это означает, что T = I и, следовательно, A = T(A) = C. Это нарушает предположение, что A и C различны.
- Угол х = 180 градусов. В этом случае T является полуоборотом, а O = середина AC. На этом строительство завершено.
- Для угла x 0 < x < 180. Это будет обсуждаться ниже
- Для угла x -180 < x < 0. Это очень похоже на случай 3 и будет обсуждаются ниже.
Случаи 3 и 4: В каждом случае 0 < |x| < 180 - неориентированный угол АОС.
Представьте, что O построен. Тогда OA = OC, так как T — вращение
с центром O. Кроме того, угол AOC = x. Это означает, что треугольник OAC
равнобедренный треугольник с (неориентированным) углом O = |x|, а угол A = угол
С = у = (180-|х|)/2 = 90 (|х|/2). Итак, чтобы построить такой треугольник, нужно только построить луч AD так, что угол CAD = y. Пересеките этот луч с m, чтобы получить P. |
Отразите P от линии AC, чтобы получить Q. Тогда оба треугольника PAC и QAC равнобедренные. треугольники с (неориентированными) углами |x|, y, y. Один из углов APC или AQC равно +|х| а другой — |x|. Таким образом, одно является решением случая 3, а другое решение случая 4.
Из этой конструкции видно, что для каждого (ориентированного) существует только одна Т. Икс.
Для построения угла y необходимо только построить равнобедренный
треугольник с углами |x|, y, y и скопируйте угол y. Например, предположим
этот угол FGH = |x| дано. Затем выберите точку K на луче GF и
пусть точка L на GH будет той точкой, где |GL| = |ГК|. Это завершает построение, а также доказывает теорему о том, что для любые различные A и C и любой ориентированный ненулевой угол, существует единственный вращение, которое переводит A в C с этим углом поворота |
Прочие конструкции: перенос или полуоборот от изображения одной точки
Для двух различных точек A и C существует единственный полуоборот H, который занимает от А до С.
Конструкция центра O полуоборота проста. О — середина переменного тока. Для любой другой точки B H (B) — это точка D, для которой O — середина. БД.
Для двух различных точек A и C существует уникальный перевод T, который принимает от А до С.
Вектор трансляции AC. Таким образом, для любого B, не лежащего на прямой AC, T(B) есть точка
D такое, что ACDB — параллелограмм. Если B находится на линии AC, то эта альтернатива
Критерий параллелограмма все еще работает. D — точка, так что середина
AD = середина BC.
Если B находится на линии AC, то эта альтернатива
Критерий параллелограмма все еще работает. D — точка, так что середина
AD = середина BC.
3. Как построить данные линии отражения или скользящее отражение от изображения сегмента или точки
Основная теорема | Из изображения сегмента | Из изображения точки, знающей вектор
Вспомним наше определение: для двух отрезков AB и CD мы говорим, что преобразование T переводит AB в CD, если T(A) = C и T(B) = D.
Примечание: Этот оператор учитывает порядок конечных точек. Если T переводит AB в CD, то он не переводит AB в DC.
Теорема (Фундаментальная теорема для обращения ориентации Изометрии)
Для двух конгруэнтных отрезков AB и CD существует ровно один отрезок, меняющий ориентацию. изометрия U, переводящая AB в CD.
Доказательство: Это следует из теоремы для сохраняющих ориентацию изометрий
Для заданных AB и CD существует ровно одна сохраняющая ориентацию изометрия T, которая
переводит AB в CD. Пусть R = отражение линии в AB. Тогда U = RT — изменяющая ориентацию
изометрия, переводящая AB в CD. Это показывает, что U существует.
Пусть R = отражение линии в AB. Тогда U = RT — изменяющая ориентацию
изометрия, переводящая AB в CD. Это показывает, что U существует.
Чтобы увидеть, что существует только одна такая U, предположим, что V — это еще одна изменяющая ориентацию изометрия, переводящая AB в CD. Тогда RV — сохраняющая ориентацию изометрия который переводит AB в CD, поэтому RV должно = T. Тогда V = RRV = RT. Но по определению, РТ = U.
КЭД
Метод построения: линейное отражение или скользящее отражение из 2 конгруэнтных сегментов
Имея два конгруэнтных отрезка AB и CD, как можно построить единственный изменяющий ориентацию изометрия U, которая переводит AB в CD?
Из определения линейного отражения и теоремы о скользящем отражении, для любого изменяющего ориентацию U и для любых точек A и C = U (A) середина AC находится на зеркальной линии (если U — отражение линии) или инвариантной линии (если U — скользящее отражение).
Таким образом, если U переводит AB в CD, пусть M = середина AC и N = середина BD.
Пусть A’ и B’ будут отражениями A и B в линии MN. Если U является отражением линии, то отрезки AC и BD оба перпендикулярны к MN, и фактически MN является серединным перпендикуляром к этим двум отрезкам. В этом случае A’ = C и B’ = D. |
|
Если U — скользящее отражение, то MN — инвариантная линия. Ни один из отрезки AC и BD будут перпендикулярны MN. Вектор скольжения = A’C = Б’Д. Чтобы построить образ некоторой другой точки P, отразите P от линии MN до получить P’ и затем перевести на вектор скольжения. |
Метод построения: линейное отражение или скользящее отражение из изображения одной точки плюс вектор скольжения
Предположим, что известно, что U является либо (а) линейным отражением, либо (б) скользящим отражением
с заданным вектором планирования EF.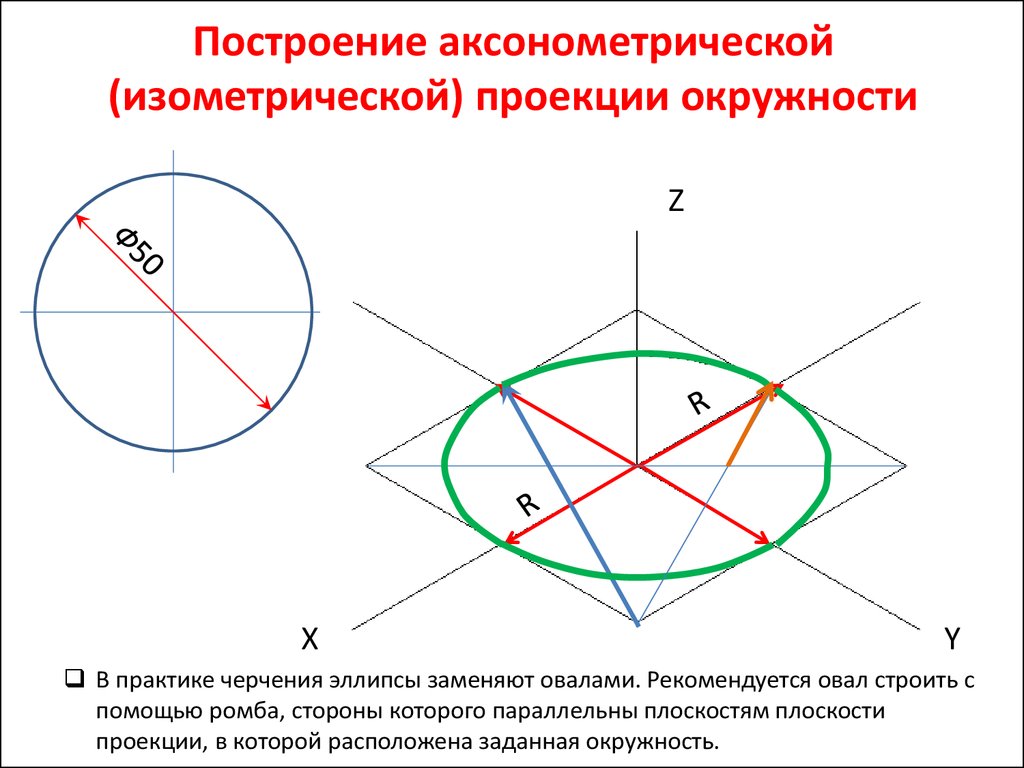 Имея две различные точки A и C, как можно построить
уникальная изменяющая ориентацию изометрия U, которая переводит A в C?
Имея две различные точки A и C, как можно построить
уникальная изменяющая ориентацию изометрия U, которая переводит A в C?
Во-первых, если U — отражение линии, то пусть m — серединный перпендикуляр переменного тока. Тогда U — отражение линии в м.
Во-вторых, если задан EF, пусть A’ будет переводом C на вектор FE = -EF. По определению вектора скольжения, тогда серединный перпендикуляр n к AA’ должна быть инвариантной линией U и U = T EF R n .
Джейсон Хоппе — Инфографический блог
29.07.2019
4 комментария
Изометрический рисунок это способ представления проектов/чертежей в трех измерениях. Для того, чтобы дизайн казался трехмерным, к его сторонам применяется угол 30 градусов. Вот как легко это настроить и создать! |
Чтобы упростить создание изометрических чертежей, установите направляющие для построения под углом 30°. | С помощью инструмента «Линия» нарисуйте линию и поверните ее на -30° на панели «Преобразование» или «Свойства». | Выберите линию, затем щелкните OPTION (ALT) и перетащите линию немного вниз. Используйте COMMAND + D, чтобы продублировать строку несколько раз. |
Выберите все линии и используйте значок «Перевернуть» на панели «Свойства», чтобы перевернуть набор. Переместите линии друг над другом, чтобы создать сетку 30°. | Выберите все линии и выберите «Просмотр»> «Направляющие»> «Создать направляющие». Это берет все линии и превращает их в структуру сетки, чтобы точки и линии могли привязываться к ним. | Проще всего рисовать изометрические панели или фигуры с помощью инструмента «Перо». Точки будут привязываться прямо к сетке, и подсказки Smart Guide покажут вам, когда точки привязываются. |
Чтобы нарисовать что-либо плоское, следуйте сетке и завершите форму. | Чтобы нарисовать вертикальную панель, вам нужно будет провести линии сверху и снизу, а затем создать вертикальные линии. | Эти основные горизонтальные и вертикальные формы будут использоваться для создания множества различных конструкций. |
При создании панелей, если применяется Обводка, углы будут острыми и создадут странные точки. | На панели «Обводка» задайте для фигур закругленные углы. Это относится только к штриху, а не к форме. | Это относится только к обводке, а не к форме, и решает проблему с обведенным объектом, имеющим нечетные перекрывающиеся угловые точки. |
Дублируйте панели и отправьте их назад, чтобы создать внешние задние панели. | Дублируйте боковые панели, чтобы создать панели крыши. Нарисуйте вертикальную линию от центра передней панели вверх за точку основания. | Инструментом «Прямое выделение» выберите верхний путь панели крыши и переместите его, пока угол не коснется вертикальной линии. |
Инструментом «Прямое выделение» выберите верхний путь задней панели крыши и переместите его, пока угол не коснется вертикальной линии. Удалите строку, когда закончите. | Выберите фигуры и выберите Инструмент «Создание фигур» (Shift+M). С помощью инструмента «Создание фигур» перетащите три фигуры, чтобы создать одну фигуру. | Залейте фигуру цветом, и у вас получится торцевая панель дома. |
Другой способ создания фигур — нарисовать их форму, а затем использовать инструмент «Наклон», чтобы наклонить ее на 30° по горизонтали или вертикали. |

 а также пересечение m и n.
а также пересечение m и n.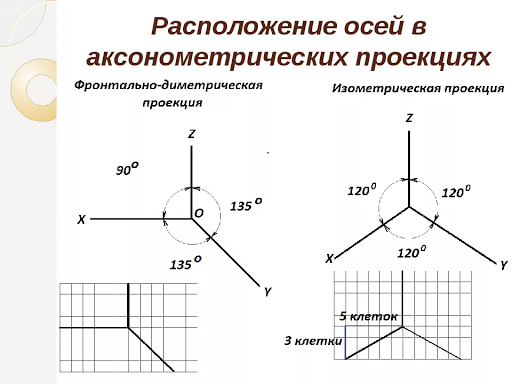
 Это значит, что
GKL — равнобедренный треугольник с углами |x|, y, y.
Это значит, что
GKL — равнобедренный треугольник с углами |x|, y, y.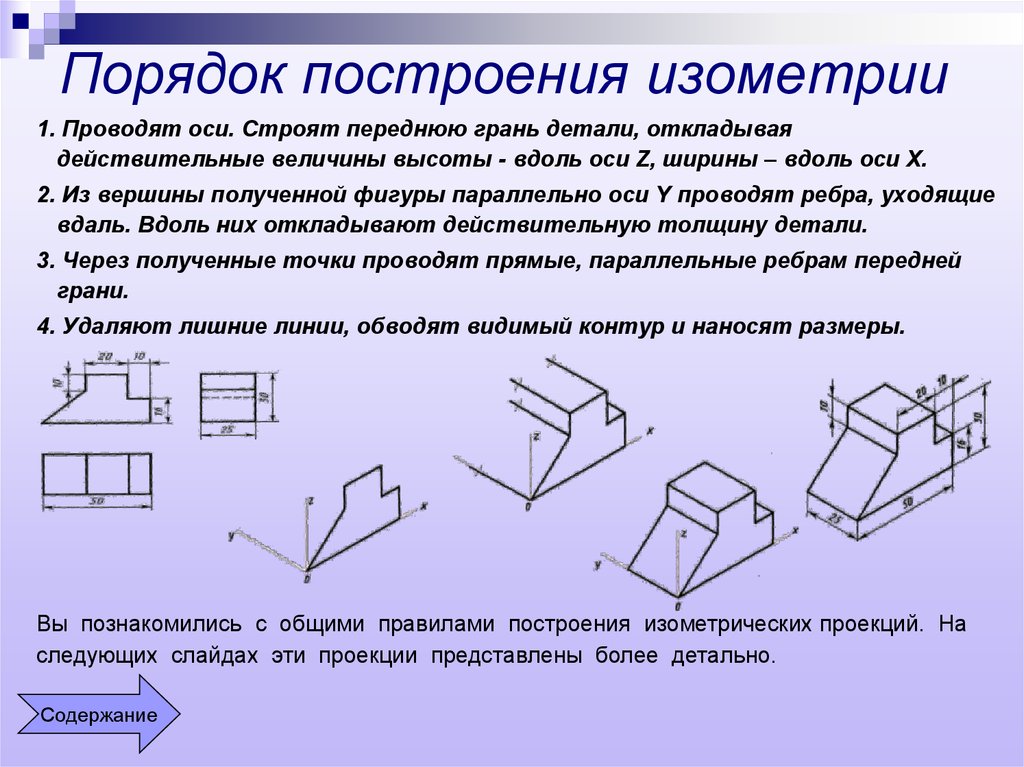 Сделайте это в разделе «Настройки»> «Smart Guides». Включите флажок Construction Guides и добавьте 30 и -30 в поля.
Сделайте это в разделе «Настройки»> «Smart Guides». Включите флажок Construction Guides и добавьте 30 и -30 в поля.