Правила построения изометрия: Как построить чертеж в изометрии. Построение аксонометрического изображения детали

Как по 3 видам построить изометрию. Черчение

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис.

110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Построение аксонометрических проекций начинают с проведения аксонометрических осей.

Положение осей. Оси фронтальной ди-метрической проекции располагают, как показано на рис. 85, а: ось х — горизонтально, ось z — вертикально, ось у — под углом 45° к горизонтальной линии.

Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.

Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис.

85, д).

Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.

При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».

При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».

На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3: 5 (3 и 5 клеток).

Построение фронтальной диметрической и изометрической проекций . Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.

Порядок построения проекций следующий (рис. 87):

1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты — вдоль оси z, длины — вдоль оси х (рис. 87, а).

2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной ди-метрической проекции — сокращенную в 2 раза; для изометрии — действительную (рис. 87, б).

3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).

4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).

Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?

Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

Построение аксонометрической проекции квадрата показано на рис. 88, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

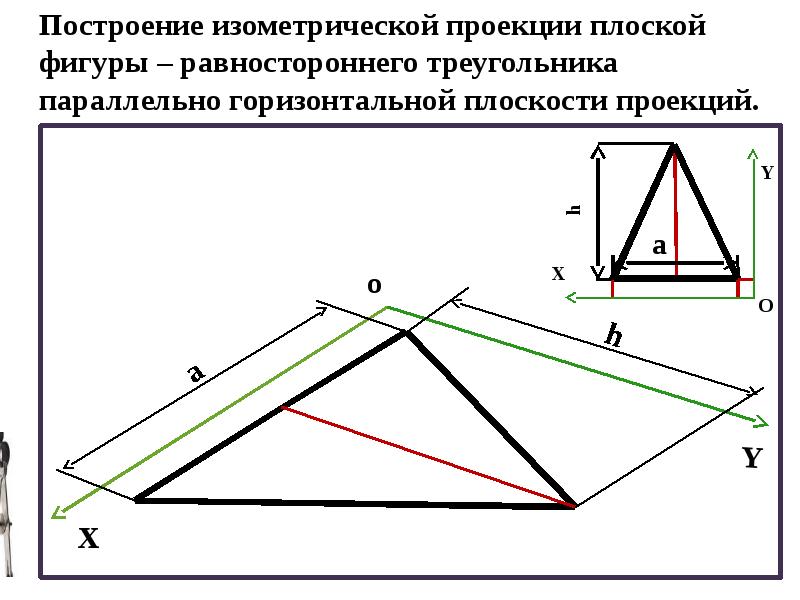
Построение аксонометрической проекции треугольника показано на рис. 89, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Построение аксонометрической проекции правильного шестиугольника показано на рис.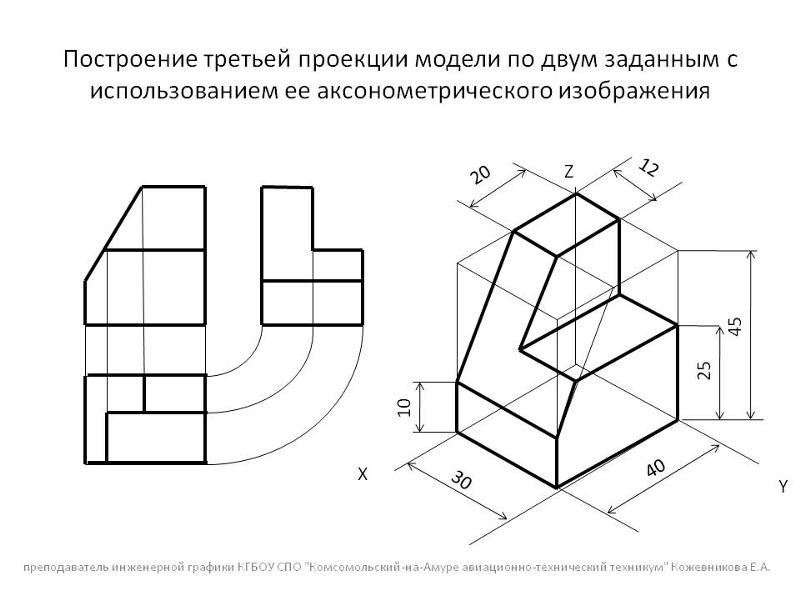

90.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Ответьте на вопросы

1. Как располагают оси фронтальной диметрической и изометрической проекций? Как их строят?

Прямоугольной изометрией называется аксонометрическая проекция, у которой коэффициенты искажения по всем трём осям равны, а углы между аксонометрическими осями 120. На рис. 1 представлено положение аксонометрических осей прямоугольной изометрии и способы их построения.

Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) циркуля; в) угольников или транспортира.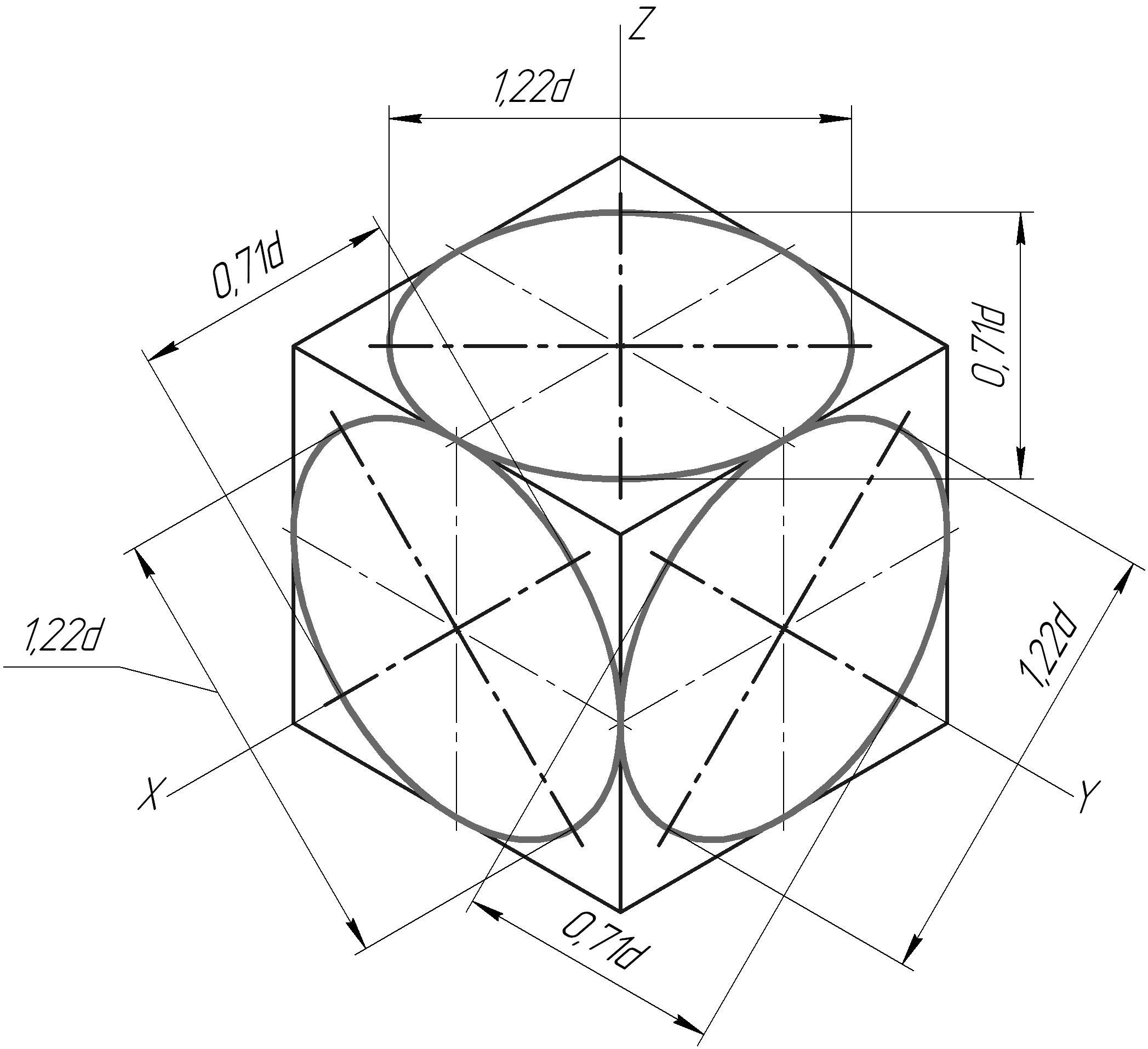

При практических построениях коэффициент искажения (К) по аксонометрическим осям согласно ГОСТ 2.317- 2011 рекомендуют равный единице. При этом изображение получают более крупным по сравнению с теоретическим или точным изображением при коэффициентах искажения 0,82. Увеличение равно 1,22. На рис. 2 приведён пример изображения детали в прямоугольной изометрической проекции.

Рис. 2. Изометрия детали.

Построение в изометрии плоских фигур

Задан правильный шестиугольник АВСDЕF, расположенный параллельно горизонтальной плоскости проекций Н (П 1).

а) Строим изометрические оси (рис.3).

б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О 0 по осям откладываем натуральные величины отрезков: А 0 О 0 = АО; О 0 D 0 = ОD; К 0 О 0 = КО; О 0 Р 0 = ОР.

в) Линии, параллельные координатным осям, проводятся в изометрии также параллельно соответствующим изометрическим осям в натуральную величину.

В нашем примере стороны ВС и FЕ параллельны оси Х .

В изометрии они вычерчиваются также параллельно оси Х в натуральную величину В 0 С 0 = ВС; F 0 Е 0 = FЕ.

г) Соединяя полученные точки, получим изометрическое изображение шестиугольника в плоскости Н (П 1).

Рис. 3. Изометрическая проекция шестиугольника на чертеже

и в горизонтальной плоскости проекции

На рис. 4 представлены проекции наиболее распространенных плоских фигур в различных плоскостях проекций.

Наиболее распространённой фигурой является окружность. Изометрическая проекция окружности в общем случае представляет собой эллипс. Эллипс строят по точкам и обводят по лекалу, что в практике черчения весьма неудобно. Поэтому эллипсы заменяют овалами.

На рис. 5 построен в изометрии куб с окружностями, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается изобразить окружность. Как видно на рис. 5 большие оси овалов располагаются по большей диагонали ромбов, в которые спроецировались грани куба.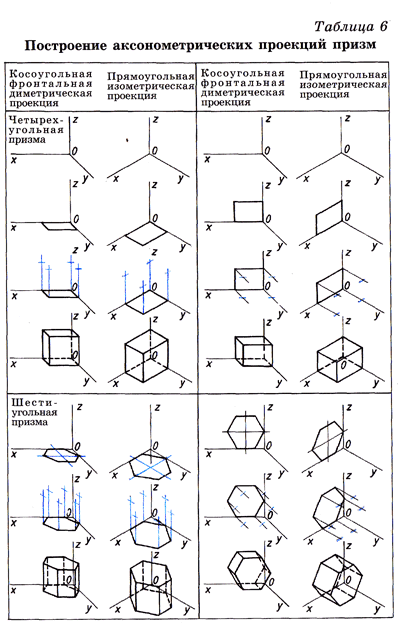

Рис. 4 Изометрическое изображение плоских фигур

а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскостиW.

Для прямоугольной аксонометрии любого вида правило определения главных осей эллипса овала, в который проецируется окружность, лежащая в какой-либо плоскости проекции, может быть сформулировано следующим образом: большая ось овала располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая совпадает с направлением этой оси. Форма и размеры овалов в каждой плоскости изометрических проекций одинаковы.

Все точки окружности, проецируемой на плоскость, обязаны быть параллельны этой плоскости. Потому что все плоскости в изометрической проекции находятся под наклоном, окружность принимает форму эллипса. Для облегчения работы эллипсы в изометрической проекции заменяются овалами.

Вам понадобится

• – карандаш;
• – угольник либо линейка;
• – циркуль;
• – транспортир.

Инструкция

1. Построение овала в изометрии начинается с определения расположения его малой и крупной оси, которые пересекаются в его центре. Следственно вначале определите расположение центра окружности на надобной плоскости изометрической проекции. Обозначьте центр окружности точкой O.

2. Начертите малую ось овала. Малая ось параллельна отсутствующей в плоскости оси изометрической проекции и проходит через центр окружности O. Скажем, в плоскости ZY малая ось параллельна оси X.

3. С поддержкой угольника либо линейки с транспортиром постройте огромную ось овала. Она перпендикулярна малой оси овала и пересекает ее в центре окружности O.

4. Проведите через центр окружности O две линии параллельные осям плоскости, в которой строится проекция.

5. С поддержкой циркуля подметьте на малой оси овала и на линиях параллельных осям проекции по две точки в противоположных от центра сторонах. Расстояние до всякой точки на всех линиях откладывается из центра O и равно радиусу проецируемой окружности.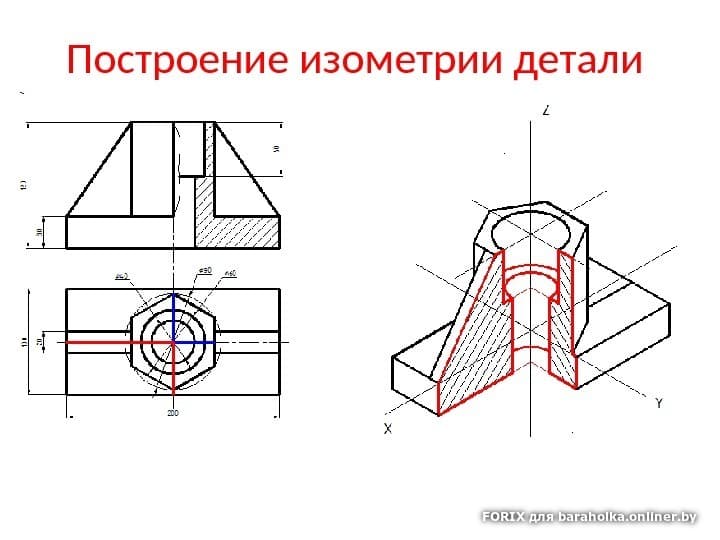 Каждого у вас должно получиться 6 точек.

6. Обозначьте на малой оси овала точки A и B. Точка A располагается ближе к началу координат плоскости, чем точка B. Предисловие координат плоскости соответствует точке пересечения осей изометрической проекции на чертеже.

7. Обозначьте подмеченные точки на линиях параллельных осям проекции как точки C, D, E и F. Точки C и D обязаны располагаться на одной линии. Точка C располагается ближе к началу координат оси проекции, которой параллельна выбранная линия. Схожие правила действуют для точек E и F, которые обязаны быть расположены на 2-й линии.

8. Объедините точки A и D, а также точки BC отрезками, которые обязаны пересекать крупную ось овала. Если получившиеся отрезки не пересекают огромную ось, обозначьте точку E как точку C, а точку C как точку E. Подобно измените обозначение точки F на D, а точки D на F. И объедините получившиеся точки A и D, B и C отрезками.

9. Обозначьте точки, в которых отрезки AD и BC пересекают огромную ось овала как G и H.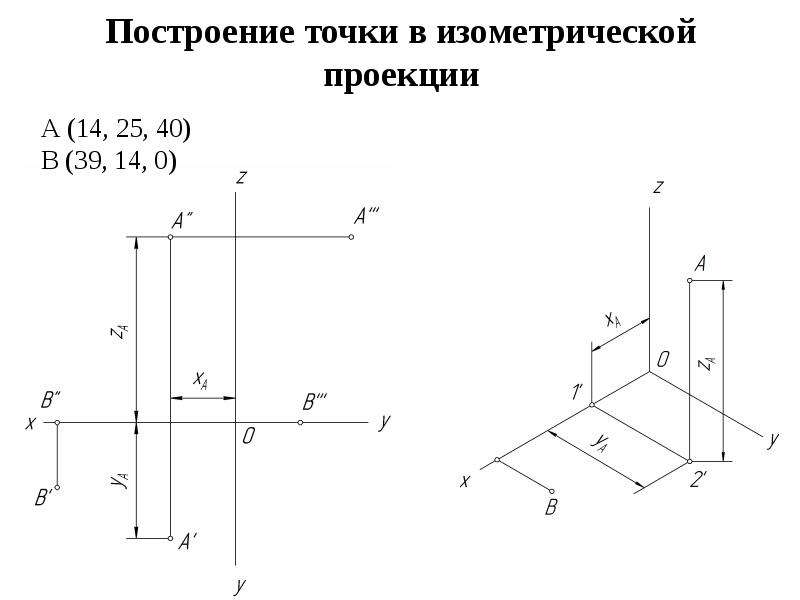

10. Задайте циркулю радиус, тот, что равен длине отрезка CG, и начертите дугу между точками C и F. Центр дуги должен быть размещен в точке G. Аналогичным методом начертите дугу между точками D и E.

11. Из точки A начертите дугу радиусом равным длине отрезка AD между точками F и D. Аналогичным методом начертите вторую дугу между точками C и E. Построение овала на первой плоскости готово.

12. Повторите аналогичным образом построение овалов для остальных плоскостей изометрической проекции.

Соотношение углов и плоскостей всякого предмета визуально меняется в зависимости от расположения объекта в пространстве. Именно следственно деталь на чертеже обыкновенно выполняется в 3 ортогональных проекциях, к которым добавлено пространственное изображение. Традиционно это изометрическая проекция. При ее выполнении не применяются точки схода, как при построении общей перспективы. Следственно размеры по мере удаления от наблюдателя не меняются.

Вам понадобится

• – линейка;
• – циркуль;
• – лист бумаги.

Инструкция

1. Изометрическая проекция строится в системе 3 осей – X, Y и Z. Точку их пересечения пометьте как О. Ось ОZ неизменно идет сурово вертикально. Остальные располагаются к ней под некоторым углом.

2. Определите направления осей. Для этого начертите из точки О окружность произвольного радиуса. Центральный угол ее равен 360?. Поделите окружность на 3 равные часть, использовав в качестве базового радиуса ось ОZ. При этом угол всякого сектора будет равен 120?. Два новых радиуса как раз и представляют собой необходимые вам оси ОX и OY.

3. Представьте себе, как будет выглядеть окружность, если ее разместить к зрителю под некоторым углом. Она превратится в эллипс, у которого есть огромный и малый диаметры.

4. Определите расположение диаметров. Поделите углы между осями напополам. Объедините точку О с этими новыми точками тонкими линиями. Расположение центра окружности зависит от условий задания. Подметьте его точкой и проведите к ней в обе стороны перпендикуляр.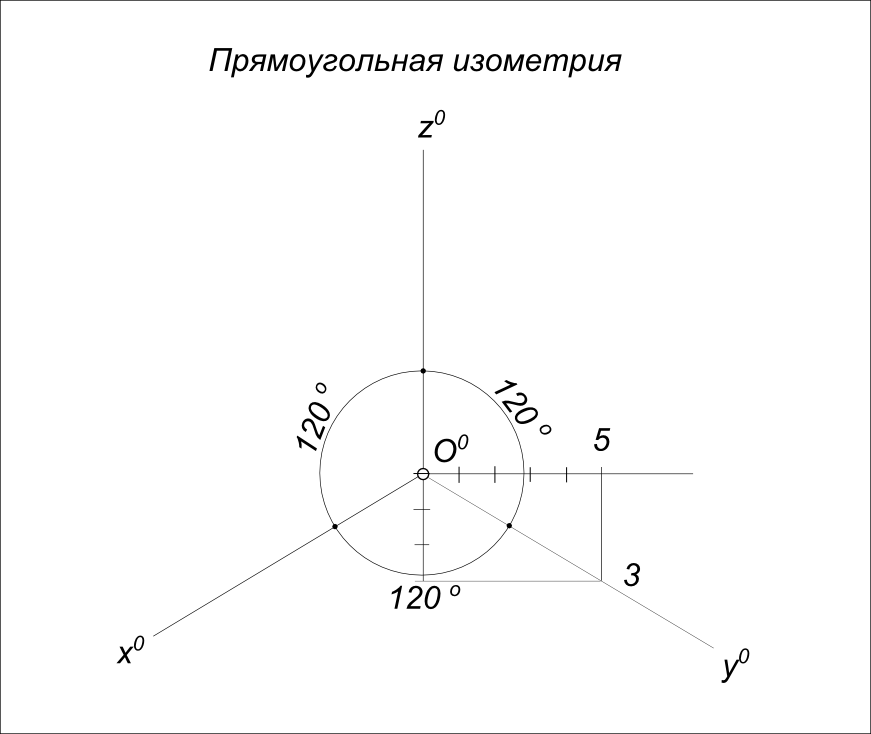 Эта линия определит расположение большого диаметра.

5. Вычислите размеры диаметров. Они зависят от того, применяете вы показатель искажения либо нет. В изометрии данный показатель по каждым осям составляет 0,82, но достаточно зачастую его округляют и принимают за 1. С учетом искажения огромный и малый диаметры эллипса составляют соответственно 1 и 0,58 от начального. Без использования показателя эти размеры составляют 1, 22 и 0, 71 диаметра изначальной окружности.

6. Поделите весь диаметр напополам и отложите от центра окружности огромные и малые радиусы. Начертите эллипс.

Видео по теме

Обратите внимание!
Для создания объемного изображения дозволено возвести не только изометрическую, но и диметрическую проекцию, а также фронтальную либо линейную перспективу. Проекции применяются при построении чертежей деталей, а перспективы – в основном в архитектуре. Окружность в диметрии тоже изображается как эллипс, но там другое расположение осей и другие показатели искажения. При выполнении разных видов перспектив учитываются метаморфозы размеров при удалении от наблюдателя.

Окружность еще древние греки считали самой идеальной и слаженной из всех геометрических фигур. В их ряду окружность является примитивной косой, а ее безупречность заключается в том, что все составляющие ее точки располагаются на идентичном расстоянии от ее центра, вокруг которого она “скользит сама по себе”. Неудивительно, что методы построения окружности начали волновать математиков еще в древности.

Вам понадобится

• * циркуль;
• * бумага;
• * лист бумаги в клеточку;
• * карандаш;
• * веревка;
• * 2 колышка.

Инструкция

1. Самый легкой и знаменитый с древности и по сей день – построение окружности при помощи особого инструмента – циркуля (от лат. “circulus” – круг, окружность). Для такого построения сперва надобно подметить центр грядущей окружности – скажем, пересечением 2х штрихпунктирных линий под прямым углом, и выставить шаг циркуля, равный радиусу грядущей окружности. Дальше установите ножку циркуля в подмеченный центр и, поворачивая ножку с грифелем вокруг него, проведите окружность.

2. Без циркуля окружность возвести тоже допустимо. Для этого понадобится карандаш и лист бумаги в клеточку. Подметьте предисловие грядущей окружности – точку А и запомните примитивный алгорифм: три – один, один – один, один – три. Для построения первой четверти окружности продвиньтесь из точки А на три клетки вправо и на одну вниз и зафиксируйте точку В. Из точки В – на одну клетку вправо и одну вниз и подметьте точку С. И из точки С – на одну клетку вправо и три вниз в точку D. Четверть окружности готова. Сейчас для комфорта дозволено развернуть лист супротив часовой стрелки так, дабы точка D оказалась вверху, и по тому же алгорифму достроить оставшиеся 3/4 окружности.

3. Но что делать, если нам необходимо возвести окружность большего размера, чем разрешает тетрадный лист и шаг циркуля – скажем, для игры? Тогда нам понадобится веревочка длины, равной радиусу желаемой окружности, и 2 колышка. Колышки привяжите к концам веревки. Один из них воткните в землю, а иным при натянутой веревке начертите окружность.Абсолютно допустимо, что одним из этих методов построения окружности воспользовался и изобретатель колеса – по сей день одного из самых талантливых изобретений общества.

Видео по теме

Построение изометрической проекции детали разрешает получить максимально подробное представление о пространственных колляциях объекта изображения. Изометрия с вырезом части детали добавочно к внешнему виду показывает внутреннее устройство предмета.

Вам понадобится

• – комплект чертежных карандашей;
• – линейка;
• – угольники;
• – транспортир;
• – циркуль;
• – ластик.

Инструкция

1. Для построения чертежа в изометрии выберите такое расположение изображаемой детали либо устройства, при котором будут максимально видны все пространственные колляции.

2. Позже выбора расположения решите, какой вид изометрии вы будете исполнять. Существует два вида изометрии : прямоугольная изометрия и горизонтальная косоугольная изометрия (либо военная перспектива).

3. Начертите оси тонкими линиями так, дабы изображение разместилось по центру листа. В прямоугольной изометрии углы между осями составляют сто двадцать градусов. В горизонтальной косоугольной изометрии углы между осями X и Y составляют девяносто градусов. А между осями X и Z; Y и Z — сто тридцать пять градусов.

4. Начните исполнять изометрию с верхней поверхности изображаемой детали. От углов горизонтальных поверхностей проведите вниз вертикальные линии и отложите на этих линиях соответствующие линейные размеры с чертежа детали. В изометрии линейные размеры по каждому трем осям остаются кратными единице. Ступенчато объедините полученные точки на вертикальных линиях. Внешний силуэт детали готов. Исполните изображения имеющихся на гранях детали отверстий, пазов и пр.

5. Помните, что при изображении предметов в изометрии видимость криволинейных элементов будет искажаться. Окружность в изометрии изображается как эллипс. Расстояние между точками эллипса по осям изометрии равно диаметру окружности, а оси эллипса не совпадают с осями изометрии .

6. Если у предмета имеются спрятанные полости либо трудное внутреннее строение, исполните изометрическую проекцию с вырезом части детали. Вырез может быть простым либо ступенчатым в зависимости от трудности детали.

7. Все действия обязаны выполняться с поддержкой чертежных инструментов — линейки, карандаша, циркуля и транспортира. Используйте несколько карандашей различной твердости. Крепкий — для тонких линий, твердо-мягкий — для пунктирных и штрихпунктирных линий, мягкий — для основных линий. Не позабудьте начертить и заполнить основную надпись и рамку в соответствии с ГОСТ. Также построение изометрии дозволено исполнять в специализированном программном обеспечении, таком как Компас, AutoCAD.

Эллипс – это изометрическая проекция окружности. Овал строят по точкам и обводят по лекалам либо фигурным линейкам. Проще каждого возвести эллипс в изометрии , вписав фигуру в ромб, напротив изометрическую проекцию квадрата.

Вам понадобится

• – линейка;
• – угольник;
• – карандаш;
• – бумага для черчения.

Инструкция

1. Разглядим, как возвести эллипс в изометрии , лежащий в горизонтальной плоскости. Постройте перпендикулярные оси X и Y. Точку пересечения обозначьте O.

2.

3. От точки O отложите на осях отрезки, равные радиусу окружности. Обозначенные точки обозначьте цифрами 1, 2, 3, 4. Через эти точки проведите параллельные осям прямые.

4. Проведите дугу из вершины тупого угла, объединив точки 1 и 4. Подобно объедините точки 2 и 3, проведя дугу из вершины D. Объедините точки 1,2 и 3,4 из центров мелких дуг. Таким образом построен эллипс в изометрии , вписанный в ромб.

5. 2-й метод возвести эллипс в изометрии заключается в отображении окружности с показателем искажения. Начертите оси X и Y, из точки O проведите две вспомогательные окружности. Диаметр внутренней окружности равен малой оси эллипса, внешней – крупной оси.

6. В одной четверти постройте вспомогательные лучи, исходящие из центра эллипса. Число лучей произвольное, чем огромнее, тем вернее чертеж. В нашем случае довольно будет 3 вспомогательных лучей.

7. Получите добавочные точки эллипса. Из точки пересечения луча с малой окружностью проведите горизонтальную линию параллельную оси X в сторону внешней окружности. Из верхней точки, лежащей на пересечении луча и огромный окружности, опустите перпендикуляр.

8. Полученную точку обозначьте цифрой 2. Повторите операции по нахождению 3 и 4 точек эллипса. Точка 1 находится на пересечении оси Y и малой окружности, точка 5 на оси X в месте прохождения внешней окружности.

9. Проведите кривую через полученные 5 точек эллипса. В точках 1 и 5 кривая сурово пропорциональна осям. Проведите схожие построения эллипса в изометрии на оставшихся? чертежа.

Все объекты окружающей реальности существуют в трехмерном пространстве. На чертежах их доводится изображать в двухмерной системе координат, и это не дает зрителю довольного представления о том, как предмет выглядит в действительности. Следственно в техническом черчении используются проекции, разрешающие передать объем. Одна из них именуется изометрической.

Вам понадобится

• – бумага;
• – чертежные принадлежности.

Инструкция

1. Построение изометрической проекции начните с расположения осей. Одна из них неизменно будет вертикальной, и на чертежах она традиционно обозначается как ось Z, Исходную ее точку принято обозначать как О. Продолжите ось ОZ вниз.

2. Расположение остальных 2-х осей дозволено определить двумя методами, в зависимости от того, какие чертежные инструменты у вас есть. Если у вас имеется транспортир, отложите от оси ОZ в обе стороны углы, равные 120?. Проведите оси X и Y.

3. Если в вашем распоряжении только циркуль, начертите окружность произвольного радиуса с центром в точке О. Продолжите ось ОZ до ее второго пересечения с окружностью и поставьте точку, скажем, 1. Разведите ножки циркуля на расстояние, равное радиусу. Проведите дугу с центром в точке 1. Подметьте точки ее пересечения с окружностью. Они и обозначают направления осей Х и Y. В левую сторону от оси Z отходит ось Х, вправо – Y.

4. Постройте изометрическую проекцию плоской фигуры. Показатели искажения в изометрии по каждом осям принимаются за 1. Дабы возвести квадрат со стороной а, отложите это расстояние от точки О по осям Х и Y и сделайте засечки. Проведите через полученные точки прямые, параллельные обеим указанным осям. Квадрат в этой проекции выглядит как параллелограмм с углами в 120? и 60?.

5. Дабы возвести треугольник, нужно продолжить ось Х так, дабы новая часть луча расположилась между осями Z м Y. Поделите сторону треугольника напополам и отложите полученный размер от точки О по оси Х в обе стороны. По оси Y отложите высоту треугольника. Объедините концы отрезка, расположенного на оси X, с полученной точкой на оси Y.

6. Схожим методом строится в изометрической проекции и трапеция. На оси Х в одну и в иную сторону от точки О отложите половину основания этой геометрической фигуры, а по оси Y – высоту. Через засечки на оси Y проведите прямую, параллельную оси Х, и отложите на ней в обе стороны половину второго основания. Объедините полученные точки с засечками на оси Х.

7. Окружность в изометрии выглядит как эллипс. Ее дозволено возвести как с учетом показателя искажений, так и без. В первом случае огромный диаметр будет равен диаметру самой окружности, а малый составит 0,58 от него. При построении без контроля этого показателя оси эллипса будут равняться соответственно 1,22 и 0,71 диаметра начальной окружности.

8. Плоские фигуры могут располагаться в пространстве как горизонтально, так и вертикально. За основу дозволено брать всякую ось, тезисы построения остаются теми же, что и в первом случае.

Полезный совет
Объемный объект трудной формы проанализируйте и мысленно поделите на больше примитивные, отличнее каждого всякую строну представить в виде близкой по форме геометрической фигуры. При этом может появиться надобность откладывать размеры не на самих осях, а на параллельных им линиях. Расстояния между этими линиями зависят от формы детали. Скажем, дозволено по одной из осей отложить расстояние от края детали до выемки либо выступа и провести линии, параллельные двум иным осям. Изометрическая проекция фрагмента в этом случае строится не на стержневой координатной сетке, а на дополнительной.

Окружность земли принято оценивать по самой длинной параллели – экватору. Впрочем последние итоги измерений этого параметра показывают, что общепризнанное представление о нем не неизменно оказывается правильным.

Вопрос о том, чему равна величина окружности планеты Земля, волновал ученых дюже давным-давно. Так, первые измерения этого параметра были осуществлены еще в Старинной Греции.

Измерение окружности

О том, что наша планета имеет форму шара, ученым, занимающимся изысканиями в области геологии, было знаменито довольно давным-давно. Именно следственно первые измерения величины окружности земной поверхности касались самой длинной параллели Земли – экватора. Эту величину, предполагали ученые, дозволено считать верной для всякого иного метода измерения. Скажем, считалось, что если измерить окружность планеты по самому длинному меридиану, полученная цифра будет верно такой же.Такое суждение существовало вплотную до XVIII столетия. Впрочем ученые ведущего научного учреждения того времени – Французской академии – придерживались суждения о том, что эта догадка неверна, и форма, которую имеет планета, не вовсе положительна. Следственно, по их суждению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.В подтверждение в 1735 и 1736 годах были предприняты две научные экспедиции, которые подтвердили истинность этого предположения. Позднее была установлена и величина отличия между этими двумя длинами – она составила 21,4 километра.

Длина окружности

В реальное время длина окружности планеты Земля многократно измерена теснее не посредством экстраполяции длины того либо другого отрезка земной поверхности на ее полную величину, как это делалось прежде, а с использованием современных высокоточных спецтехнологий. Вследствие этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину отличия между этими параметрами.Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть особенно длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом подобный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра. Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Помимо того, такое отличие обозначает, что один градус географического меридиана несколько короче, чем один градус географической параллели.

Что такое диметрия

Диметрия представляет собой один из видов аксонометрической проекции. Благодаря аксонометрии при одном объемном изображении можно рассматривать объект сразу в трех измерениях. Поскольку коэффициенты искажений всех размеров по 2-м осям одинаковы, данная проекция и получила название диметрия.

Прямоугольная диметрия

При расположении оси Z» вертикально, при этом оси Х» и Y» образуют с горизонтального отрезка углы 7 градуса 10 минут и 41 градус 25 минут. В прямоугольной диметрии коэффициент искажения по оси Y будет составлять 0,47, а по осям Х и Z в два раза больше, то есть 0,94.

Чтобы осущесвить построение приближенно аксонометрические оси обычной диметрии, необходимо принять, что tg 7 градусов 10 минут равен 1/8, а tg 41 градуса 25 минут равен 7/8.

Как построить диметрию

Для начала необходимо начертить оси, чтобы изобразить предмета в диметрии. В любой прямоугольной диметрии углы, находящиеся между осями Х и Z, равны 97 градусов 10 минут, а между осями Y и Z – 131 градусов 25 минут и между Y и Х – 127 градусов 50 минут.

Теперь требуется нанести оси на ортогональные проекции изображаемого предмета, учитывая выбранное положение предмета для вычерчивания в диметрической проекции. После того, как завершите перенос на объемное ихображение габаритных размеров предмета, можете приступать к чертежу незначительных элементов на поверхности предмета.

Стоит запомнить, что окружности в каждой плоскости диметрии изображаются соответствующими эллипсами. В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет составлять 1,06 диаметра нарисованной окружности. А малая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY – 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях. В плоскости ХОZ малая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.

Чтобы получить более детально изображение, необходимо выполнить вырез через детали на диметрии. Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции выбранного квадрата на необходимую плоскость.

Что такое изометрия

Изометрия является одним из видов аксонометрической проекции, где расстояния единичных отрезков на всех 3-х осях одинаковые. Изометрическая проекция активно используется в машиностроительных чертежах, чтобы отобразить внешний вид предметов, а также в разнообразных компьютерных играх.

В математике изометрия известна как преобразование метрического пространства, которое сохраняет расстояние.

Прямоугольная изометрия

В прямоугольной (ортогональной) изометрии аксонометрические оси создают между собой углы, которые равны 120 градусам. Ось Z находится в вертикальном положении.

Как начертить изометрию

Построение изометрии предмета дает возможность получить наиболее выразительное представление о пространственных свойствах изображаемого объекта.

Перед тем, как начать построение чертежа в изометрической проекции, необходимо выбрать такое расположение изображаемого предмета, чтобы были максимально видны его пространственные свойства.

Теперь вам требуется определиться с видом изометрии, которую будете чертить. Существует два ее вида: прямоугольная и горизонтальная косоугольная.

Нарисуйте оси легкими тонкими линиями, чтобы изображение получилось по центру листа. Как уже раньше говорилось, углы в прямоугольном виде изометрической проекции должны составлять 120 градусов.

Начинайте рисовать изометрию с именно верхней поверхности изображения предмета. От углов получившейся горизонтальной поверхности нужно провести две вертикальные прямые и отложить на них соответствующие линейные размеры предмета. В изометрической проекции все линейные размеры по всех трем осям будут оставаться кратны единице. Затем последовательно требуется соединить созданные точки на вертикальных прямых. В результате получиться внешний контур предмета.

Стоит учитывать, что при изображении любого предмета в изометрической проекции видимость криволинейных деталей будет обязательно искажаться. Окружность должна изображаться эллипсом. Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.

Если изображаемый объект имеет скрытые полости ли сложные элементы, постарайтесь выполнить заштриховку. Она может быть простой либо ступенчатой, все зависит сложности элементов.

Запомните, что все построение должно выполнять строго с применением чертежных инструментов. Применяйте несколько карандашей с разными видами твердости.

Как нарисовать изометрию в Adobe Illustator ~ Записки микростокового иллюстратора

Делай изометрию в Adobe Illustrator в один клик с новым скриптом
Magic Isometry — НАЖМИ МЕНЯ

Всем привет! Сегодня у нас в гостях Александр Сераков, преподаватель Школы цифровых искусств Юниверс. Александр преподаёт с 2008 года, является официальным спикером Adobe, и имеет внушительный опыт в сфере полиграфии, дизайна и обработки цифровых изображений. Поэтому спешу представить вашему вниманию урок Александра, в котором он поделится своими знаниями.

Речь пойдёт об изометрии. Из урока вы узнаете, как переводить плоские объекты в изометрическую проекцию, как автоматизировать этот процесс с помощью Actions, и как делать бесшовные паттерны в изометрии.

Итак, если вы готовы окунуться в удивительный мир изометрии, то передаю слово Александру.

Ничто так не возбуждает фантазию как борьба с невозможным. Применительно к двухмерной графике одним из таких моментов, является добавление еще одного измерения. Проще говоря — создание объемных фигур без привлечения 3D. Обходя преграды на этом пути, художники открывали целые миры изобразительных средств, обладающих удивительными свойствами и эстетикой. Мы знаем, что объем можно передать: тоном, перспективой, перекрытием объекта объектом, сочетанием размеров одинаковых объектов (меньше кажется дальше), тональной перспективой (дальше — светлее) и так далее. При этом мы не должны забывать о геометрии, ведь любое изображение объемного предмета на плоскости должно следовать определенным геометрическим правилам — проекциям. И вот на стыке геометрии и рисунка вдруг появляется гадкий утенок — изометрическая проекция. То есть, изображение трехмерного объекта, но без учета перспективы. Попав в заботливые руки дизайнеров изометрия выросла в прекрасного лебедя, крылья которого могут вас перенести в удивительные миры. Если вы, сможете справится с управлением, конечно.

Иллюстратор: Coen Pohl

Изометрия — удивительное дело. Мало того, что в ней есть характерная эстетика, мало того, что она обладает мощным изобразительным потенциалом, она еще является необыкновенно притягательной из-за целого ряда визуальных эффектов и оптических иллюзий, которые возникают при построении изометрических композиций. У этого есть ряд причин, главная из которых — отсутствие перспективы. То есть понятно, что эти объекты объемные, но что дальше, что ближе, что выше, что ниже однозначно определить невозможно. И это развязывает нам руки для самых немыслимых визуальных провокаций.

Это невероятно ярко продемонстрировал голландский художник Мауриц Эшер:

А в компьютерной игре echoсhrom эти визуальные эффекты были возведены в главный принцип игры: «В этом мире то, что ты видишь, становится реальностью». Идея в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией.

Строить изображения в изометрии легко, и Adobe Illustrator, обладает необходимым набором инструментов для этого. Давайте разберемся как это делать и создадим вот такой симлес из изометрических коробочек:

Прежде всего нам нужна коробочка, а еще раньше — ее стороны. Не забудьте сгруппировать объекты из которых состоит каждая из стенок:

1. Выделим всё, перейдём в меню Object > Transform > Scale. В появившемся окне в секции Non-Uniform задайте значение Vertical = 86,6%.

Вы можете спросить, что это за число такое и почему оно часто встречается при работе с изометрией? Так уж получается, что все наши трансформации в этой проекции нередко обыгрывает идею равностороннего треугольника. А 0,866 — это соотношение ширины к высоте этой фигуры. Это корень из трех пополам — иррациональное число, что-то вроде 0,866025… и далее до бесконечности. И тут есть одна проблема — Illustrator всё время норовит округлить это число и в некоторых случаях это создает проблемы, так как округление происходит в большую сторону. Из практики выясняется, что меньше всего ошибок возникает, когда мы используем такой «укороченный» вариант этого числа — 0,866.

2. Выделим всё и выполним команду Object > Transform > Reset Bounding Box.

Это действие стало необходимым в последних версиях программы, так как сейчас Illustrator помнит угол на который вы поворачивали объект. Это конечно круто, но в нашем уроке вы можете запутаться в углах, если не сбросите значения габаритной рамки.

3. Снимем выделение.

4. Выделим грани поочередно и при помощи панели Transform выполним следующие трансформации именно в таком порядке (сначала скос, потом поворот):

Верхняя грань: Shear +30º, Rotate 330º;
Левая грань: Shear -30º, Rotate 330º;
Правая грань: Shear +30º, Rotate 30º.

Для частого использования этот процесс можно автоматизировать. Просто выполните эти действия для каждой грани, включив запись сценария в окне Actions.

Если вы не имели ещё дело с Actions в Иллюстраторе, то посмотрите этот видео урок: Actions в иллюстраторе, или как свернуть горы нажатием одной кнопки.

5. Включим «умные направляющие» View > Smart Guides.

6. Аккуратно соединим коробочку

7. Перейдем к созданию симлеса, бесшовного паттерна. Для этого перетащите коробочку в панель Swatches, снимите выделение.

8. Настроим паттерн. Дважды кликните по иконке паттерн в панели Swatches. Установите Type в режим Brick by Row и настройте ширину и высоту ячейки. Нажмите Done, в верхней части окна.

При желании в этот паттерн можно добавить и другие элементы, для этого просто нарисуйте их, скопируйте, перейдите снова в редактор паттернов и вставьте их. Паттерн будет сохранён в панели Swatches в виде образца бесшовной текстурной заливки. То есть вы можете применять этот паттерн к любой фигуре в качестве заливки.

Конечно, мы рассмотрели самый простой пример, как раз такой, чтобы вы смогли разобраться в вопросе. Тема изометрии просто бесконечная и безбрежная. Вот, еще один пример работы с изометрией и снова паттерны:

Если вы еще не очень уверенно чувствуете себя в работе с паттернами, а эта тема вам интересна — посетите мой специальный курс, посвященный исключительно теме создания паттернов, использования и подготовки их к печати и продаже на стоках.

Александр Сераков специально для блога Записки микростокового иллюстратораЧитать дальше…

Подпишитесь на нашу рассылку, чтобы не пропустить ничего нового:

Предлагаю ознакомиться с аналогичными статьями:

Как начертить фигуру по черчению. Изометрическая проекция с вырезом передней четверти

Начнем с того, что определимся с направлением осей в изометрии.

Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.

Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.

Мы получили верхнюю грань фигуры.

Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом — в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. Изображение окружностей на всех трех плоскостях я описал в отдельном уроке , а пока лишь скажу, что в изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b — вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм).

Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра — по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена — не хватает только прямоугольного сквозного отверстия.

Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия — по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.

На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху — в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.

Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).

Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!

Как начертить окружность в изометрии?

Как вы наверняка знаете, при построении изометрии окружность изображается в виде эллипса. Причем вполне конкретного: длина большой оси эллипса AB=1.22*D, а длина малой оси CD=0.71*D (где D — диаметр той самой исходной окружности, которую мы хотим начертить в изометрической проекции). Как начертить эллипс зная длину осей? Об этом я рассказывал в отдельном уроке . Там рассматривалось построение больших эллипсов. Если же исходная окружность имеет диаметр где-то до 60-80 мм, то скорее всего мы сможем начертить ее и без лишних построений, используя 8 опорных точек. Рассмотрим следующий рисунок:

Это фрагмент изометрии детали, полный чертеж которой можно увидеть ниже. Но сейчас мы говорим о построении эллипса в изометрии. На данном рисунке AB — большая ось эллипса (коэффициент 1.22), CD — малая ось (коэффициент 0.71). На рисунке половина короткой оси (ОD) попала в вырезанную четверть и отсутствует — используется полуось СО (не забудьте об этом, когда будете откладывать значения по короткой оси — полуось — имеет длину равную половине короткой оси). Итак, мы уже имеем 4 (3) точки. Теперь отложим по двум оставшимся изометрическим осям точки 1,2,3 и 4 — на расстоянии равном радиусу исходной окружности (таким образом 12=34=D). Через полученные восемь точек уже можно провести достаточно ровный эллипс, либо аккуратно от руки, либо по лекалу.

Для лучшего понимания направления осей эллипсов в зависимости от того, какое направление имеет циллиндр, рассмотрим три разных отверстия в детали, имеющей форму параллелепипеда. Отверстие — тот же цилиндр, только из воздуха:) Но для нас это особого значения не имеет. Полагаю, что ориентируясь на эти примеры вы без труда сможете правильно расположить оси своих эллипсов. Если же обобщить, то получится так: большая ось эллипса перпендикулярна той оси, вокруг которой образован цилиндр (конус).

Инструкция

Постройте с помощью линейки и транспортира или циркуля и линейки для прямоугольной (отрогональной) изометрической проекции. В этой разновидности аксонометрической проекции все три оси — OX, OY, OZ — между собой углы в 120°, при этом ось ОZ имеет вертикальную направленность.

Для простоты чертите изометрическую проекцию без искажений по осям, так как принято изометрический коэффициент искажения приравнивать к единице. Кстати, само «изометрический» в переводе «равный размер». На самом деле при отображении трехмерного объекта на плоскость отношение длины любого спроецированного отрезка, параллельного координатной оси, к действительной длине этого отрезка равно для всех трех осей 0,82. Поэтому линейные размеры предмета в изометрии (при принятом коэффициенте искажения) увеличиваются в 1,22 раза. При этом изображение остается правильным.

Начните проецировать предмет на аксонометрическую плоскость с его верхней грани. Отмерьте по оси OZ от центра пересечения осей координат высоту детали. Проведите тонкими линиями оси Х и Y через эту точку. Из этой же точки отложите половину отрезка длины детали по одной оси (например, по оси Y). Проведите через найденную точку отрезок нужного размера (ширина детали) параллельно другой оси (OX).

Теперь вдоль другой оси (OX) отложите половину ширины. Через эту точку проведите отрезок нужной величины (длина детали) параллельно первой оси (OY). Два начерченных отрезка должны пересечься. Достройте оставшуюся часть верхней грани.

Если в этой грани имеется круглое отверстие, начертите его. В изометрии окружность изображается в виде эллипса, потому что мы смотрим на нее под углом. Размеры осей этого эллипса рассчитайте исходя из диаметра окружности. Они равны: a = 1,22D и b = 0,71D. Если окружность располагается на горизонтальной плоскости, ось а эллипса всегда горизонтальная, ось b — вертикальная. При этом расстояние между точками эллипса на оси Х или Y всегда равно диаметру окружности D.

Начертите из трех углов верхней грани вертикальные ребра, равные высоте детали. Соедините ребра через их нижние точки.

Если у фигуры есть прямоугольное отверстие, начертите его. Отложите из центра ребра верхней грани вертикальный (параллельно оси Z) отрезок нужной длины. Через полученную точку начертите отрезок требуемого размера параллельно верхней грани, а значит и оси X. Из крайних точек этого отрезка начертите вертикальные ребра нужной величины. Соедините их нижние точки. Проведите от нижней правой точки нарисованного ромба внутреннее ребро отверстия, которое должно быть параллельно оси Y.

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

В этом уроке я вам покажу, как поместить на чертеж изометрическую проекцию модели с вырезом передней четверти. Как это делается я покажу на примере выполнения задания, взятого из учебного пособия С.К. Боголюбова «Индивидуальные задания по курсу черчения». Задание звучит так: по двум данным проекциям построить третью проекцию с применением разрезов, указанных в схеме, изометрическую проекцию учебной модели с вырезом передней четверти.

Приступим к созданию модели. Создайте новую деталь, выполнив команду Файл – Создать.

Присвойте ей наименование. Для этого выполните команду Файл — Свойства модели. На вкладке Список свойств в графе Наименование введите Стойка.

Установите ориентацию Изометрия XYZ.

Для создания первого эскиза выберите плоскость ZX и нажмите на панели инструментов Текущее состояние . Создайте эскиз, как показано на рисунке ниже. Нанесите размеры.

Выдавите эскиз в прямом направлении на 10 мм.

XY.

Выдавите его от средней плоскости на 50 мм.

Создайте следующий эскиз на плоскости XY.

Выдавите его от средней плоскости на 35 мм.

Выберите указанную поверхность и создайте на ней эскиз.

Вырежьте выдавливанием в прямом направлении через все.

На указанной поверхности создайте эскиз отверстия.

Создайте отверстие с помощью команды Вырезать выдавливанием .

Создайте эскиз для последнего элемента на плоскости XY.

Выполните команду Вырезать выдавливанием по двум направлениям. Через все в каждом направлении.

И так деталь готова. Но пока все еще нет возможности показать ее в изометрии с вырезом одной четверти. Для этого создадим новое исполнение детали. Что такое исполнения и для чего их применяют я рассказывал в одном из прошлых уроков . До появления в Компас-3D исполнений для показа на чертеже изометрии с вырезом приходилось создавать копию модели, в копии делать вырез и уже с нее создавать вид, что не совсем удобно. Сейчас можно обойтись без этого. И так, откройте Менеджер документа и создайте зависимое исполнение. Назначьте его текущим и нажмите ОК.

На плоскости ZX создайте эскиз.

Выполните Сечение по эскизу в обратном направлении.

Исполнение готово. Текущее исполнение можно сменить в окне на панели Текущее состояние.

Создайте новый чертеж. В Менеджере документа установите формат А3, горизонтальную ориентацию. Нажмите кнопку Стандартные виды на панели инструментов Виды. В окне открытия выберите сохраненную модель. Обратите внимание, что окно Исполнение должно быть пустым, это означает что виды будут создаваться с базового исполнения. Ориентацию главного вида установите Спереди.

Укажите точку привязки вида. После этого необходимо создать вид с исполнения. На панели Виды нажмите кнопку Произвольный вид . В окне Исполнение выберите исполнение -01, в качестве ориентации главного вида выберите Изометрия XYZ

Останется только нанести штриховку, размеры и создать необходимые разрезы, в соответствии со схемой в задании.

P.S. Для тех, кто хочет стать Мастером КОМПАС-3D! Новый обучающий видеокурс позволит вам легко и быстро освоить систему КОМПАС-3D с нуля до уровня опытного пользователя.

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 35) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.

 

 

Рис. 35. Прямоугольная и изометрические проекции квадрата

 

При построении изометрической проекции треугольника (рис. 36) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.

Рис. 36. Прямоугольная и изометрические проекции треугольника

 

При построении изометрической проекции шестиугольника (рис. 37) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой – H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками.

Рис. 37.Прямоугольная и изометрические проекции шестиугольника

При построении изометрической проекции круга (рис. 38) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.

 

Рис. 38. Прямоугольная и изометрические проекции круга

 

Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел.

Способы построения изометрической проекции детали:

1) Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:

— построение осей изометрической проекции;

— построение изометрической проекции формообразующей грани;

— построение проекций остальных граней посредством изображения ребер модели;

— обводка изометрической проекции (рис. 39).

Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 40).

 

Рис. 39. Построение изометрической проекции детали,

начиная от формообразующей грани

 

 

Рис. 40. Построение изометрической проекции детали на основе

последовательного удаления объемов

 

2) Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 40).

 

Рис. 41.Построение изометрической проекции детали на основе

последовательного приращения объемов

 

3) Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построе­ния.

4) Аксонометрическую проекцию детали можно выполнять с изображением и без изображения невидимых частей формы.

 

 

Построение объемных геометрических фигур

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Geogebra — наилучшее он-лайн геометрическое приложение для рисования геометрических фигур.
Подождите. Идёт загрузка (прим. 1-2 минуты).
Открыть в полный экран

Открыть в полный экран
Это он-лайн приложение позволяет рисовать геометрические фигуры — точки, линии, углы, треугольники, многоугольники, круги.
Вы можете создавать анимиционную геометрию и слайды.
Если Вам не нужна система координат по умолчанию, Вы можете скрыть ее.

Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.

Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.

Основные геометрические фигуры:

Двухмерные плоские фигуры

Трехмерные фигуры, у которых есть объем

Абсолютно все предметы в основе своего построения имеют эти фигуры.

Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина. В самом кубе заложено понятие рисунка в целом.

Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы. Для большего понимания и анализа рисунка есть несколько упражнений.

Упражнения

Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет). Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.

Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…

Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов. Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.

Чтобы нам чувствовать пространство, нужно придать рисунку плавности. То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.

Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.

Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке.

Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.

Технологическая карта урока в 7 классе «Построение аксонометрических проекций. Изометрия».

Федеральное государственное казенное общеобразовательное учреждение

«Ставропольское президентское кадетское училище»

Преподаватель изобразительного искусства: Малахова Е.А.

Урок №4.

Тема урока: «Построение аксонометрических проекций. Изометрия».

Тип урока: изучения новых знаний.

Наглядные пособия: презентация.

Цели урока как планируемые результаты обучения, планируемый уровень достижения целей:

1. Когнитивные: дать воспитанникам основные понятия об аксонометрической проекции и ее разновидности – изометрии, при которой объект в трёхмерном отображении на плоскость имеет  коэффициент искажения, правилах их выполнения. Освоить построение предмета в прямоугольной изометрической проекции.

2. Операциональные: Развивать графические и композиционные навыки воспитанников, способствовать формированию навыков самостоятельной работы при выполнении чертежно-графических работ. Развивать пространственное мышление, познавательный интерес.

3. Аксиологические: способствовать формированию навыков самостоятельной работы при выполнении чертежно-графических работ.

Методы: наглядные методы обучения.

Форма урока: урок-практикум.

Преподаватель: Малахова В.М.

Руководитель ОД (Искусство, МХК и технология) Катаева В.М

Вид планируемых учебных действий	Учебные действия	Планируемый уровень достижения результатов обучения
Предметные	— Рассмотреть правила построения аксонометрических проекций; познакомить кадет с получением изображений и с расположением осей в аксонометрии; — познакомить с последовательностью построения аксонометрических проекций плоских фигур; — познакомить с последовательностью построения аксонометрических проекций плоскогранных фигур; — освоить построение предмета в прямоугольной изометрической проекции; — научить применять последовательность построения видов на чертеже детали с учётом анализа; — умение использовать графические приемы оформления в черчении; — приобретение чертежно-графических навыков.	1 уровень — узнавание
Регулятивные	— Умение решать аналитические задачи при помощи чертежно-графических приемов. — Умение планировать собственную деятельность, ориентируясь во времени, контролировать и оценивать результаты своей учебной деятельности. — Умение оценивать правильность выполнение учебной задачи, собственные возможности ее решения. — Воспитывать аккуратность в графических представлениях; — Развивать образное представление и пространственное мышление.	2 уровень — самостоятельное выполнение действий с опорой на известный алгоритм
Познавательные	Выдвигать версии образно-художественной осмысленности простейших плоскостных аксонометрических проекций.	2 уровень — умение выражать структуру задачи разными средствами
Коммуникативные	Умение формулировать собственную позицию относительно предмета изучения.	1 уровень — уметь формулировать и задавать вопросы, владеть вербальными и невербальными способами общения
Личностные	— активизировать познавательную деятельность и развивать творческий потенциал кадет; — создавать условия для раскрытия интеллектуальных и духовных возможностей кадет; — продолжать формировать способность к художественно-образному познанию мира, умению применять полученные знания в своей собственной художественно-творческой деятельности;	2 уровень — чувство необходимости учения, осознание необходимости самосовершенствования
Этап урока, время этапа	Задачи этапа	Методы, приемы обучения	Формы учебного взаимодей-ствия	Деятельность учителя	Деятельность воспитанников	Формируемые УУД и предметные действия
Мотивационно-целевой этап	Орг. момент 2 мин.	Организовать самоопределение кадет к деятельности на уроке.	фронтальная	Приветствует кадет. Проверяет готовность к уроку.	Воспринимают на слух, визуально контролируют готовность к уроку.	Личностные: доброжелательность, эмоционально-нравственная отзывчивость. Регулятивные: уметь организовать место занятий; правильность выбора учебных принадлежностей
Актулиза-ция знаний	Целеполагание и постановка задач. Систематизировать имеющиеся у кадет знания	Наглядные методы обучения. Беседа по уточнению и конкретиза-ции имеющихся у кадет знаний	Фронтальная и групповая	— Чертежи, схемы и другие конструкторские документы содержат необходимые надписи: названия изделий, размеры, данные о материале, обработке поверхностей детали, технические требования, характеристики. По указанным данным мы можем построить три вида и более детали. Рассмотрите слайд. Сколько на нем изображено предметов различной формы? Вы видите один предмет, изображенный по-разному. А можете ли вы ответить, как называются изображения а, б, в? Как изобразить ее в три четверти, под углом с наименьшим искажением размеров и формы? Предложите свои варианты. Подведение к теме урока. Преподаватель: — Оказывается, на этот вопрос уже давно найден ответ инженерами прошлого. Они придумали способ изображения плоских и объемных тел в пространстве с наименьшим искажением, который называется аксонометрическим проецированием. ось Z всегда вертикальна; — все измерения выполняются только по аксонометрическим осям или прямым, параллельным им; — все прямые линии, параллельные друг другу или осям координат на комплексном чертеже, в аксонометрических проекциях остаются параллельными между собой и соответствующим аксонометрическим осям. Закрепление: Чаще всего построение аксонометрической проекции происходит с построения основания. Рассмотрим алгоритм построения аксонометрических проекций предмета на примере прямоугольного параллелепипеда.	Кадеты предлагают варианты выполнения решения проблемного вопроса . Организация поискового решения выдвинутых познавательных задач. Слушают, отвечают на поставленный вопрос, осмысливают цель урока. Самостоятельно формулируют тему, цели урока выбор материалов план пути достижения цели. — Тема урока: «Аксонометрические проекции». Цель: познакомиться с изометрией как простейшим способом построения аксонометрической проекции, особенностями чертежного построения тел в проекции, приобрести практические навыки. .	Личностные: осознание своих возможностей. Регулятивные:  умение наблюдать, анализировать, осуществлять сравнение. Осознание необходимости получения новых знаний. Познавательные: целеполагание, Умение анализировать, выделять и формулировать учебную задачу; Коммуникативные: умение осознанно строить речевое высказывание.
Изучение новых знаний	Подготовка кадет к получению новых знаний	Рассказ учителя о различных видах народных промыслов, показ учителя способов изображения эскиза по мотивам народной росписи	фронтальная	Предлагает воспитанникам просмотр видеоряда. Просмотр видеоряда. Обсуждение содержания фильма, что нового из него узнали. 1.Рассказ преподавателя на тему: “Правила построения аксонометрии: изометрическая проекция простых плоских фигур по осям». Аксонометрической проекцией называют изображение, полученное при параллельном проецировании предмета вместе с осями прямоугольных координат на плоскость. Аксонометрическая проекция включает в себя два вида проекций: фронтальную диметрическую и прямоугольную изометрическую. Изометрическая проекция (др.-греч. ἴσος «равный» + μετρέω «измеряю») — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так. Изометрическая проекция используется в машиностроительном черчении для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам. Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. Коэффициент искажения по осям x, y, z равен 0,82. Для упрощения изометрическую проекцию, как правило, выполняют без искажения, т.е. приняв коэффициент искажения равным 1. Ось Z всегда вертикальна; — все измерения выполняются только по аксонометрическим осям или прямым, параллельным им; — все прямые линии, параллельные друг другу или осям координат на комплексном чертеже, в аксонометрических проекциях остаются. По всем аксонометрическим осям (X, Y, Z) и параллельно им откладывают натуральные размеры! Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.	Воспринимают на слух информацию. Кадеты рассматривают презентацию, записывают важные моменты и определения в рабочую тетрадь, делают зарисовки, задают вопросы.	Познавательные: самостоятельное  выделение и формулирование познавательной цели; Рефлексивные: — планировать свои действия в соответствии с поставленной задачей и условиями её реализации, в том числе во внутреннем плане; Коммуникативные: — допускать возможность существования у людей различных точек зрения, в том числе не совпадающих с его собственной, и ориентироваться на позицию партнера в общении и взаимодействии;
Практическая работа	Здоровье сберегающие технологии знания	Практически закрепить полученные кадетами знания	индивидуальная	Преподаватель предлагает воспитанникам перейти к приобретению практических навыков создания чертежа простых плоских фигур в изометрической проекции. Дает указания. Соблюдать расположение осей по 120°, а так же натуральные размеры объекта изображения. Все надписи на чертеже должны быть аккуратными. Преподаватель предлагает кадетам создать изометрическую проекцию заданной детали.	Кадеты самостоятельно выполняют чертежно-графические проекционные чертежи с соблюдением требований ЕСКД; работают над овладением приемами работы в чертежной графике ее техническими средствами.	Познавательные: классифицируют по заданным основаниям учебный материал, сравнивают по заданным критериям, делают выводы. Личностные: самоорганизация, осознание своих возможностей. Регулятивные: планировать свои действия в соответствии с поставленной задачей и условиями её реализации, в том числе во внутреннем плане;
Закрепление материала	Рефлексия	Устный опрос кадет. Проверка систематизации учебного материала кадетами в рабочих тетрадях	фронтальная	Преподаватель задает вопросы: Что нового вы сегодня узнали? — Зачем нужны знания о способах проецирования? С каким из видов проецирования мы познакомились на уроке? — Для чего нужны разнообразные способы проецирования? — Для чего их используют? -Что было интересно? -Что теперь помимо учебного задания вы можете изобразить? -Какие новые чертежно-графические приемы вы приобрели? Какие практические знания для жизни дал вам урок?	Кадеты отвечают на вопросы учителя и товарищей: Я сегодня я узнал… было трудно… я понял, что… теперь я могу… я приобрел… я научился… у меня получилось …  я смог… я попробую… мне захотелось…	Коммуникативные: умение аргументированно защитить свою точку зрения;
Подведение итогов урока		Технология критического мышления	фронтальная	Анализ ошибок кадет и подведение итогов урока. Выставление оценок.	Кадеты осуществляют самооценку собственной учебной деятельности, сопоставляют цель и результаты, степень их соответствия. Сравнивают, что сделали за отведенное время, оцениваем по следующим критериям: целостность композиции; выразительность исполнения цвета, рисунка, объема; умение согласовать между собой детали для объединения их в целостный ансамбль; декоративность композиции; аккуратность. исполнения	Коммуникативные: формулировать собственное мнение и позицию; Регелятивные: выделение и осознание того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения. Умение соотносить результаты собственной деятельности Коммуникативные: излагают свое мнение в диалоге. Личностные:  доброжелательность, эмоционально-нравственная отзывчивость; приобретение ценностно-смысловых ориентиров
Задание на самоподготовку		Учебно- познавательная компетенция.	фронтальная	Выполнить чертеж параллелепипеда с произвольными размерами в изометрической проекции.	Запись домашнего задания уборка рабочих мест, художественных инструментов	Кадеты выстраивают самостоятельно траекторию самостоятельной учебной деятельности.

Как начертить куб в изометрической проекции поэтапно. Прямоугольная изометрия

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.

Рис. 3.16.

Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а ). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.

Рис. 3.17.

Из вершин тупых углов (точек А и В ) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б ).

Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.

Малые дуги описывают радиусом R, равным отрезку Са (Db ).

Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.

Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б ) и окружности (рис. 3.18, в).

Рис. 3.18.

Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б ). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.

На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).

Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г ).

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а ). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б ). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19.

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20.

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

В изометрической проекции все коэффициенты равны между собой:

к = т = п;

3 к 2 = 2,

k = yj 2УЗ — 0,82.

Следовательно, при построении изометрической проекции размеры предмета, откладываемые по аксонометрическим осям, умножают на 0,82. Такой перерасчет размеров неудобен. Поэтому изометрическую проекцию для упрощения, как правило, выполняют без уменьшения размеров (искажения) по осям х, у, I, т.е. принимают приведенный коэффициент искажения равным единице. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры, чем в действительности. Увеличение в этом случае составляет 22% (выражается числом 1,22 = 1: 0,82).

Каждый отрезок, направленный по осям х, у, z или параллельно им, сохраняет свою величину.

Расположение осей изометрической проекции показано на рис. 6.4. На рис. 6.5 и 6.6 показаны ортогональные (а) и изометрические (б) проекции точки А и отрезка Л В.

Шестигранная призма в изометрии. Построение шестигранной призмы по данному чертежу в системе ортогональных проекций (слева на рис. 6.7) приведено на рис. 6.7. На изометрической оси I откладывают высоту Н, проводят линии, параллельные осям хиу. Отмечают на линии, параллельной оси х, положение точек / и 4.

Для построения точки 2 определяют координаты этой точки на чертеже — х 2 и у 2 и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.

Построенные точки верхнего основания соединяют между собой, проводят ребро из точки / до пересечения с осью х, затем —

ребра из точек 2 , 3, 6. Ребра нижнего основания проводят параллельно ребрам верхнего. Построение точки Л, расположенной на боковой грани, по координатам х А (или у А) и 1 А очевидно из

Изометрия окружности. Окружности в изометрии изображаются в виде эллипсов (рис. 6.8) с указанием величин осей эллипсов для приведенных коэффициентов искажения, равных единице.

Большая ось эллипсов расположена под углом 90° для эллипсов, лежащих В ПЛОСКОСТИ хС>1 к ОСИ у, В ПЛОСКОСТИ у01 К ОСИ X, в плоскости хОу К ОСИ?.

При построении изометрического изображения от руки (как рисунка) эллипс выполняют по восьми точкам.G до пересечения с большой осью эллипса в точках О у Проводя через точки О р 0 3 прямую, находят в пересечении с дугой CGC точку К, которая определяет 0 3 К — величину радиуса замыкающей дуги овала. Точки К являются также точками сопряжения дуг, составляющих овал.

Изометрия цилиндра. Изометрическое изображение цилиндра определяется изометрическими изображениями окружностей его основания. Построение в изометрии цилиндра высотой Н по ортогональному чертежу (рис. 6.9, слева) и точки С на его боковой поверхности показано на рис. 6.9, справа.

Предложено Ю.Б. Ивановым.

Пример построения в изометрической проекции круглого фланца с четырьмя цилиндрическими отверстиями и одним треугольным приведен на рис. 6.10. При построении осей цилиндрических отверстий, а также ребер треугольного отверстия использованы их координаты, например координаты х 0 и у 0 .

Для трёхмерных объектов и панорам.

Ограничения аксонометрической проекции

Изометрическая проекция в компьютерных играх и пиксельной графике

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

Примечания

1. По ГОСТ 2 .317-69 — Единая система конструкторской документации. Аксонометрические проекции.
2. Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z»).
3. Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM , декабрь 1978. — Т. 10. — № 4. — С. 465-502. — ISSN 0360-0300 . — DOI :10.1145/356744.356750
4. Jeff Green. GameSpot Preview: Arcanum (англ.) . GameSpot (29 февраля 2000).(недоступная ссылка — история ) Проверено 29 сентября 2008.
5. Steve Butts. SimCity 4: Rush Hour Preview (англ.) . IGN (9 сентября 2003). Архивировано
6. GDC 2004: The History of Zelda (англ.) . IGN (25 марта 2004). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
7. Dave Greely, Ben Sawyer.

Изометрическая и наклонная проекция — Обмен идеями — Edexcel — Дизайн и технология GCSE — Edexcel

Изометрические чертежи

Изометрические чертежи обычно используются в технических чертежах, чтобы показать объект в 3D на странице 2D. Изометрические чертежи, иногда называемые изометрическими проекциями, являются хорошим способом показать измерения и то, как компоненты сочетаются друг с другом. В отличие от перспективных рисунков, они не становятся меньше по мере того, как линии уходят вдаль.

Есть три основных правила для изометрического рисования:

Изометрическая бумага может использоваться для рисования трехмерных фигур — например, куб ниже нарисован с использованием точек в качестве ориентира.Вертикальные линии всегда остаются вертикальными, а горизонтальные — под углом.

Изометрические чертежи можно использовать для отображения масштаба продукта, а также для трехмерного представления.

Пример

Ниже представлены два куба, нарисованные в изометрии:

Масштабный коэффициент = меньшая длина ÷ большая длина

= 30 ÷ 60

= 0,5

Это означает, что второй куб нарисован в половинном масштабе , также записывается как 1: 2.

Вопрос

Определите масштабный коэффициент меньшего кубоида ниже:

Показать ответ

Масштабный коэффициент = 30 ÷ 40 или 60 ÷ 80

= 0.75

Также представлен как множитель ³ ⁄ ₄ или как соотношение 3: 4.

Изометрический чертеж: руководство дизайнера

Изометрический чертеж: быстрые ссылки

Изометрический чертеж — это форма трехмерного чертежа, который выполнен под углом 30 градусов. Это тип аксонометрического рисунка, поэтому для каждой оси используется один и тот же масштаб, что приводит к неискаженному изображению. Поскольку изометрические сетки довольно легко настроить, как только вы поймете основы изометрического рисования, создать изометрический эскиз от руки будет относительно просто.

Этот пост объясняет все, что вам нужно знать об изометрическом чертеже. Вы узнаете, что именно определяет изометрический рисунок, чем он отличается от одноточечной перспективы, что нужно сделать, чтобы приступить к созданию собственной изометрической проекции, и многое другое.

Повысьте свои художественные навыки, следуя инструкциям в нашем руководстве по рисованию (которое научит вас рисовать практически все), а также вы можете использовать этот обзор художественных техник, о которых вы должны знать.

Что такое изометрический чертеж?

Изометрический чертеж — это трехмерное представление объекта, комнаты, здания или конструкции на двухмерной поверхности.Одной из определяющих характеристик изометрического чертежа по сравнению с другими типами трехмерного представления является то, что конечное изображение не искажается. Это связано с тем, что ракурс осей одинаковый. Слово «изометрический» происходит от греческого языка и означает «равная мера».

Изометрические чертежи построены под углом 30 градусов (Изображение предоставлено: Кристоф Данг Нгок Чан, Майк Хорват)

Изометрические чертежи отличаются от других типов аксонометрических чертежей, включая диметрические и триметрические проекции, в которых для разных осей используются разные масштабы чтобы получить искаженное окончательное изображение.

На изометрическом чертеже объект выглядит так, как если бы он просматривался сверху с одного угла, причем оси были вынесены из этой угловой точки. Изометрические чертежи начинаются с одной вертикальной линии, вдоль которой определяются две точки. Любые линии, проведенные из этих точек, должны быть построены под углом 30 градусов.

Изометрические чертежи и одноточечная перспектива

Как изометрические чертежи, так и одноточечные перспективные чертежи используют геометрию и математику для представления трехмерных представлений на двумерных поверхностях.Одноточечные перспективные рисунки имитируют то, что воспринимает человеческий глаз, поэтому объекты кажутся меньше, чем дальше они находятся от зрителя. Напротив, в изометрических чертежах используется параллельная проекция, что означает, что объекты остаются одного размера, независимо от того, как далеко они находятся.

Одноточечная перспектива имитирует то, что воспринимает человеческий глаз (Изображение предоставлено Оливером Харрисоном — CC BY 2.5)

По сути, изометрический рисунок не использует перспективу при визуализации (т. зритель).Изометрические рисунки более полезны для функциональных рисунков, которые используются для объяснения того, как что-то работает, в то время как рисунки с одноточечной перспективой обычно используются, чтобы дать более чувственное представление об объекте или пространстве.

Как нарисовать изометрический куб

Нарисовать куб с помощью изометрической проекции очень просто. Вам понадобятся лист бумаги, линейка, карандаш и транспортир (или для более быстрой версии, используя бумагу с сеткой, перейдите к следующему разделу).

С помощью линейки нарисуйте вертикальную линию на странице и отметьте на ней три точки с равным интервалом.Проведите горизонтальную линию через самую низкую точку и с помощью транспортира отметьте угол в 30 градусов вверх от линии с обеих сторон. Проведите линию через самую низкую точку под углом 30 градусов с каждой стороны.

Повторите этот шаг через среднюю точку и то же самое через верхнюю точку, но с верхней точкой отметьте угол вниз. Линии из второй и третьей точек пересекутся в определенной точке, и от этого пересечения проведите вертикальную линию вниз к наклонным линиям, идущим из нижней точки.Вы должны увидеть форму куба в месте пересечения всех линий.

Использование изометрической сетки

Для всех читеров, у которых нет необходимых инструментов (или наклона) для создания изометрической проекции, есть надежный способ разбить ваш аксонометрический рисунок: просто используйте изометрический сетка. Выкройку можно скачать в Интернете, и это сэкономит вам много времени и усилий.

Вы также можете узнать, как настроить собственную сетку в Illustrator, следуя приведенному ниже видеоуроку.

Как только ваши глаза привыкнут к хитрости треугольного узора, вы сразу заметите, как работает изометрия. Самое удобное в сетке то, что для вас уже настроены все 30-градусные углы. В этом руководстве вы узнаете, как нарисовать куб с помощью изометрической сетки.

Преимущества изометрического чертежа

Изометрические чертежи очень полезны для дизайнеров, особенно для архитекторов, промышленных дизайнеров, дизайнеров интерьеров и инженеров, поскольку они идеально подходят для визуализации помещений, продуктов и инфраструктуры.Это отличный способ быстро проверить различные дизайнерские идеи.

Существует ряд других ситуаций, в которых полезно использовать изометрическую проекцию. В системах навигации, например в музеях или галереях, изометрические настенные карты могут показывать посетителям, где они находятся в здании, что происходит в других местах и ​​как передвигаться.

В некоторых лучших инфографиках используется изометрическая проекция, позволяющая отображать больше информации, чем это было бы возможно в двухмерном чертеже. Некоторые дизайны логотипов также используют этот подход для создания впечатления.

Представления мест, таких как это, созданное Цзин Чжаном, — это всего лишь одно из применений техники изометрического рисования (Изображение предоставлено Цзин Чжан).

Разнесенные изометрические чертежи полезны для выявления частей продукта, которые могут быть скрыты или скрыты внутри. Они используются архитекторами, инженерами и дизайнерами по всему миру, чтобы лучше объяснить тонкости дизайна. Чтобы создать изометрию с разнесенными частями, вам нужно знать детальное внутреннее устройство того, что вы рисуете, поэтому они обычно используются на заключительном этапе проектирования для презентаций клиентам.

Примеры изометрических чертежей

Щелкните значок в правом верхнем углу, чтобы увеличить изображение (Изображение предоставлено Mauco)

Иллюстратор и арт-директор Mauco создали эту изометрическую карту, чтобы представить районы, окружающие здание SPECTRUM в Лондоне. На нем показаны только основные дороги и ориентиры, чтобы помочь людям сориентироваться.

Щелкните значок в правом верхнем углу, чтобы увеличить изображение (Изображение предоставлено: Jing Zhang)

Цзин Чжан — иллюстратор, работающий в основном с клиентами из рекламной индустрии.Она заработала особую репутацию благодаря своим детальным взорванным изометрическим проектам, включая это творение для Slack. Это часть серии статей, посвященных историям бренда, с акцентом на такие элементы, как счастливые мобильные сотрудники (см. Выше).

Щелкните значок в правом верхнем углу, чтобы увеличить изображение (Изображение предоставлено Тимом Пикоком, The California Sunday Magazine)

Этот дизайн был создан для статьи в The California Sunday Magazine под названием The Tech Revolt и изучения политической активности в технологическая индустрия.В нем иллюстратор Тим Пикок использует изометрическую проекцию как способ раскрыть внутреннее устройство офисного блока Кремниевой долины.

Щелкните значок в правом верхнем углу, чтобы увеличить изображение (Изображение предоставлено М.С. Эшером)

М.С. Эшер, возможно, был королем в использовании изометрических проекций в своих работах. Его использование параллельной геометрии для изображения умопомрачительных лестниц, ведущих в никуда, будет знакомо большинству. В «Цикле» (1938) ясно, как изометрическая проекция входит в его работу, от узора на земле до использования кубиков, которые превращаются в ступеньки.

Подробнее:

Изометрический чертеж и изометрическая проекция

Термин «изометрический» происходит от греческого слова «равная мера», отражая, что масштаб вдоль каждой оси проекции одинаков, что неверно для некоторых других форм графической проекции. Одним из преимуществ изометрической перспективы на инженерных чертежах является то, что углы в 60 градусов легко построить, используя только циркуль и линейку.

Изометрический рисунок чаще всего используется в его истинной форме, дающей «равные размеры» и вид в ракурсе трех сторон объекта.Изометрический рисунок — это одна из форм графического рисунка. Скрытые линии обычно не вставляются. Изометрический рисунок — это метод визуального представления трехмерных объектов в двух измерениях, в котором три оси координат выглядят одинаково укороченными, а углы между любыми двумя из них составляют 120 градусов. Изометрическая проекция, как и ортогональная проекция. используется в инженерных чертежах. Изометрический чертеж можно легко построить с помощью треугольника 30–60–90 градусов и Т-образного квадрата или с помощью программирования САПР.На рис. 5.17A и B показаны два примера изометрических чертежей в архитектурном контексте. На рис. 5.17C приведен пример архитектурного чертежа с использованием как ортогональной проекции (высота), так и изометрической проекции (детали).

ИЗОМЕТРИЧЕСКАЯ ДИМЕТРИЧЕСКАЯ ТРИМЕТРИЧЕСКАЯ ПЕРСПЕКТИВА

Рис. 5.16. Различные типы аксонометрических проекций (изометрические, диметрические и триметрические) и перспективные. В большей части Европы аксонометрия использует угол 45 градусов, в отличие от углов 30/60 градусов, используемых в изометрическом чертеже.

ИЗОМЕТРИЧЕСКАЯ ДИМЕТРИЧЕСКАЯ ТРИМЕТРИЧЕСКАЯ ПЕРСПЕКТИВА

Рис. 5.16. Различные типы аксонометрических проекций (изометрические, диметрические и триметрические) и перспективные. В большей части Европы аксонометрия использует угол 45 градусов, в отличие от углов 30/60 градусов, используемых в изометрическом чертеже.

Рис. 5.17A. Пример использования изометрических чертежей в архитектуре и проектировании (источник: North American Steel Framing Alliance).

Продолжить чтение здесь: Общие типы кирпичных облигаций

Была ли эта статья полезной?

ИЗОМЕТРИЧЕСКИЕ ЧЕРТЕЖИ И КОНСТРУКТОРЫ

Изометрический рисунок — это способ представления дизайна / чертежей в трех Габаритные размеры.Для того чтобы дизайн выглядел трехмерным, необходимо поднять угол 30 градусов. к его сторонам приложен угол. Куб напротив нарисован в изометрическая проекция.
СВОБОДНЫЙ ЭСКИЗ В ИЗОМЕТРИИ: Дизайн, нарисованный в изометрии проекции обычно рисуются точно с помощью чертежного оборудования. Тем не мение, дизайнеры считают полезным рисование «от руки» в изометрической проекции. Мобильный телефон / музыкальный проигрыватель напротив, был нарисован бесплатно. рука изометрической проекции.Позволяет дизайнеру быстро рисовать в 3D. и с разумной степенью точности. Дизайн все еще отрисовывается на Угол 30 градусов, хотя это оценочно, а не нарисовано с помощью графическое оборудование. Добавлен ограниченный цвет / оттенок меню телефона. Это означает, что эскиз не полностью представлен как «незамысловатый» дизайн. Эти рисунки представляют собой быстрые наброски, которые позволяют дизайнер, чтобы быстро изложить свои мысли на бумаге.Это помогает он / она быстро разработает идею или концепцию дизайна без необходимости сложные чертежи на ранней стадии проектирования. В начале встречи с клиентом, дизайнер может показать 3D чертежи этого типа чтобы убедиться, развивается ли дизайн так, как заказчик хочет.
Рисование в изометрической проекции обычно означает очень точное рисование. с использованием традиционного чертежного оборудования.Это включает в себя использование T-Square, установите квадраты и измерения точно. Виден изометрический чертеж противоположность была нарисована точно, с использованием навыков, полученных за часы упражняться. Когда эти навыки будут развиты, рисование в изометрической становится второй натурой.
РАЗБОРНЫЙ ИЗОМЕТРИЧЕСКИЙ ПРОЕКЦИОН
Дизайнеры используют «покомпонентные» виды, часто нарисованные в изометрической проекции, чтобы показать скрытые от глаз части продукции.Например, все части пера, изображенные ниже, можно увидеть, потому что оно было снято кроме того, используя технику рисования, называемую «Изометрические разнесенные детали Проекция ». В разобранной изометрической проекции все части расположены на одной линии по центральной линии. Это нарисовано точно через центр вытягиваемого продукта. с обычный изометрический чертеж, все детали в сборе позиции. Это означает, что невозможно увидеть важные скрытые детали.
Дизайнеры также используют покомпонентные изображения для объяснения своих проектов. клиенты / заказчики и производители. Кроме того, покомпонентные изображения продукты часто поставляются клиентам, которые, в свою очередь, собирают продукт. Хороший пример — «разобранная» мебель. Когда квартира упаковка открыта, инструкция или буклет объясняют, как мебель собирается, часто в виде изометрии в разобранном виде.
Рисунки, показанные ниже, поставлялись с инструкциями. Они две из многочисленных диаграмм, нарисованных в изометрической проекции. Они помогают объяснить, как собирается шкаф и все его составные части, формируют готовое изделие. Это точные чертежи разработанные дизайнером, которые объясняют, как продукт, который он / она имеет спроектирован собран.
ССЫЛКИ
Изометрическая проекция — An Пояснение Изометрическая проекция — сводка Изометрические круги и цилиндры Упражнение с изометрическим кубом 1 Упражнение с изометрическим кубом 2 Изометрические персональные стереоупражнения 2 Печать в изометрическом упражнении 3 Упражнение с изометрической дискетой 4 Рисование мобильного телефона в изометрии Проекция — Первая страница Рисование мобильного телефона в изометрии Проекция — Вторая страница
НАЖМИТЕ ЗДЕСЬ, чтобы увидеть УКАЗАТЕЛЬ ДИЗАЙНА ПРОДУКЦИИ, СТРАНИЦА

Что такое изометрический чертеж? — Определение и примеры — Видео и стенограмма урока

Третье измерение

Нарисовать двухмерный объект на бумаге просто, потому что бумага имеет два измерения: высоту и ширину.Но у объектов в реальной жизни есть третье измерение, глубина, которую нужно представить на чертеже. На изометрических чертежах все три измерения представлены на бумаге.

Три измерения представлены в виде трех осей: одна вертикальная ось и две горизонтальные оси.

Все дело в углах

Так чем же изометрический чертеж отличается от других трехмерных чертежей? Оси нарисованы так, что две горизонтальные оси нарисованы под углом 30 градусов.Как будто вертикальная ось находится в своем истинном положении, но горизонтальные оси согнуты на 30 градусов от своего истинного положения.

Примеры

Вот несколько примеров изометрических чертежей. Обратите внимание, что на каждом изображении показаны три оси для представления каждого измерения объекта: вертикальная ось синего цвета, а две горизонтальные оси нарисованы оранжевым и зеленым.

Бумага для изометрических чертежей

Как вы понимаете, создание изометрических чертежей сложных конструкций может оказаться довольно сложной задачей.Доступны программные приложения, позволяющие точно создавать изометрические изображения. Но если вы хотите нарисовать его вручную, можно приобрести или загрузить бумагу для изометрического рисования, чтобы сделать это намного проще. Он похож на миллиметровую бумагу, за исключением того, что горизонтальные линии рисуются под углом 30 градусов к вертикальным линиям.

Резюме урока

Изометрические чертежи обеспечивают систематический способ рисования трехмерных объектов.Изометрические чертежи включают три оси: одну вертикальную ось и две горизонтальные оси, которые нарисованы под углом 30 градусов от их истинного положения. Применение этого типа чертежа распространяется на многие области, такие как инженерия, механика, физика и архитектура.

Свойства изометрических чертежей

Изометрические чертежи …

• Используются инженерами, иллюстраторами и другими техническими художниками
• : две горизонтальные оси под углом 30 градусов плюс вертикальная ось
• Можно нарисовать на специальной миллиметровой бумаге или с помощью программных приложений

Результаты обучения

По завершении урока попробуйте сделать следующее:

• Различать изометрические и неизометрические 3D-эскизы
• Используйте изометрическую миллиметровку или другие инструменты для создания изометрического чертежа

Руководство дизайнера по изометрической проекции | Александр | Gravit Designer

Термин «изометрический» — одно из самых неверных слов в индустрии дизайна.Мы склонны называть любой трехмерный рисунок без перспективы «изометрическим».

Одним из недавних примеров псевдоизометрических произведений искусства является старый логотип Medium, который использовался с 2015 по 2017 год. Он был разработан на параллельной (аксонометрической) сетке, но совсем не изометричен.

Старый логотип Medium был разработан на триметрической сетке.

В этой статье я собираюсь объяснить разницу между изометрической проекцией и другими типами проекций.

Графические рисунки

Способность визуализировать трехмерные формы — это навык, которым должен овладеть каждый дизайнер и инженер.Это особенно важно в 3D-моделировании. Однако существует явная разница между рисованием вида, который выглядит как трехмерный, и созданием настоящей трехмерной модели.

Реальные 3D-модели можно поворачивать на экране для просмотра под любым углом. Компьютер вычисляет точки, углы и поверхности объекта в космосе. Затем он отображает результат на плоском экране в виде так называемых графических рисунков.

Слово «» изобразительное «» означает «как изображение». Это относится к любому реалистичному типу рисунка, изображающему высоту, ширину и глубину объекта.Графические рисунки чрезвычайно полезны, когда нам нужно передать дизайн людям, не имеющим технической подготовки по интерпретации многоракурсных проекций.

Иллюстрированное изображение с мультиэкранными рисунками. Источник изображения sites.google.com/site/multiviewdrawings/home.

В дизайне и технических чертежах используются несколько форм графических проекций:

• Перспектива — наиболее реалистичные рисунки. Наши глаза видят объекты в перспективе. Есть три типа перспективных проекций: одно-, двух- и трехточечная перспектива.

Три типа перспективы. Изображение из гамильтониана дизайна (hamiltonianofdesign.wordpress.com).

• Наклон — наименее реалистично. Только одна или две грани в наклонных проекциях имеют истинную форму и размер. Наклонные выступы бывают трех типов: кабинетные, кавалерийские и общие.

Три типа наклонных выступов.

• Аксонометрические проекции более реалистичны, чем наклонные. Горизонтальные края объекта в аксонометрических проекциях параллельны друг другу и наклонены к плоскости.Существует три типа аксонометрических проекций: изометрическая, , диметрическая и триметрическая.

Три типа аксонометрических проекций. Изображение из гамильтониана дизайна (hamiltonianofdesign.wordpress.com).

Аксонометрические проекции

Аксонометрические проекции — наиболее распространенный способ изображения трехмерных объектов без использования перспективы. В отличие от перспективных чертежей, все оси в аксонометрических проекциях не сходятся и всегда остаются параллельными.

Перспектива и изометрия.Источник изображения: vitorials.net

Нет точек схода, нет линии горизонта. С расстоянием объект не становится меньше. Это было очень важно для игровой индустрии между 1980 и 1990 годами, потому что компьютеры той эпохи с ограниченными ресурсами должны были визуализировать объект только один раз.

Основная цель аксонометрических проекций — показать форму и размер объекта. Они спроектированы таким образом, что прямо с этих проекций можно снимать измерения объектов.

Все три типа аксонометрических проекций построены на сетке, где оси X и Z наклонены к горизонтальной плоскости.Ось Y всегда остается перпендикулярной горизонтальной плоскости.

Оси X и Z наклонены к горизонтальной плоскости. Источник изображения: vitorials.net.

Угол между «горизонтальными» осями X и Z и горизонтальной плоскостью определяет тип аксонометрической проекции.

Изометрическая проекция

Изометрическая (что означает «равная мера») — это тип параллельной (аксонометрической) проекции, при которой оси X и Z наклонены к горизонтальной плоскости под углом 30⁰. Угол между аксонометрическими осями равен 120⁰.

30/120/30 также называется истинной изометрической сеткой.

Идеальный куб в изометрической проекции выглядел бы как идеальный шестиугольник.

В Gravit Designer вы можете построить истинную изометрическую сетку прямо из коробки.

Вы можете настроить размер изометрической сетки по умолчанию в Gravit Designer.

Поскольку все края изометрического объекта наклонены под одинаковым углом, они имеют одинаковый ракурс. Это позволяет вам измерять каждую сторону объекта, используя один и тот же масштаб.

Изометрическая длина и истинная длина. Источник изображения: ed-zon.blogspot.com/2013/05/isometric-projection-and-isometric.html.

Большинство дизайнеров игнорируют ракурс на этапе создания эскиза и строят изометрические виды объекта с фактической длиной. Конечным результатом будет изометрический эскиз, а не проекция.

Изометрический эскиз иногда называют изометрическим видом или изометрическим рисунком. Источник изображения: ed-zon.blogspot.com/2013/05/isometric-projection-and-isometric.html.

Как построить изометрию без сетки

Использование изометрической сетки — не единственный способ рисования изометрических произведений искусства в Gravit Designer.

Их можно строить прямо из многовидовых проекций (верхних, передних, боковых и т. Д.). Наиболее распространенные и простые методы — это SR45⁰ и SSR30⁰ .

Это очень удобные методы, когда вам нужно создать анизометрический макет вашего дизайна с помощью нескольких щелчков мышью:

Создание изометрического актива с использованием метода SSR в Gravit Designer.

SR45⁰ техника

SR45⁰ обозначает масштаб и поворот на 45⁰. Масштабное соотношение составляет 0,577 или, что более важно, tan (30⁰) .

Вы можете строить изометрические проекции через SR45⁰, используя панель преобразования Gravit Designer в два простых шага.

Шаг 1: повернуть объект на 45⁰

Шаг 2: масштабировать объект

SSR30⁰ техника

SSR30⁰ — это больше популярный и гибкий метод создания изометрических работ. С SSR30⁰ вы можете быстро создавать изометрические виды сверху, слева и справа.

SSR30⁰ обозначает масштабирование, наклон и поворот на 30⁰.

Использование метода SSR в Gravit Designer.Источник изображения: vitorials.net.

Создание других аксонометрических проекций с помощью Gravit Designer

В диметрических проекциях только две стороны имеют одинаковый ракурс. Оси X и Z по-прежнему находятся под одинаковым углом к ​​горизонтальной плоскости, но не на 30 °. Углы между осями не равны.

Обычная диметрическая сетка 15⁰ в Gravit Designer.

Триметрические выступы

Все углы триметрических выступов разные, поэтому все стороны (ребра) и оси укорочены неодинаково.

Вы можете настроить триметрическую сетку в Gravit Designer за несколько секунд.

Вы можете использовать широкий спектр углов для создания триметрических и диметрических изображений, но старайтесь избегать маленьких. На мой взгляд, это делает проекцию слишком плоской:

Маленькие углы делают ваши работы слишком плоскими.

Анатомия логотипа Medium

Исходный логотип Medium был разработан на неизометрической сетке, где оси X и Y наклонены к горизонтальной плоскости под углом -27⁰ и 60⁰ соответственно. Итак, логотип Medium построен на триметрической сетке.

Средний предыдущий логотип был триметрическим

Поздравляем, если вы дошли до этого места! Я надеюсь, что все GIF и JPG не заставили ваш браузер (или даже вас ) переборщить. Я также надеюсь, что вы получили некоторую ценность для себя и несколько новых инструментов, которые можно использовать в своих изометрических рисунках.

Веб-сайт | Facebook | Twitter | Forum

Система координации трубопроводов — изометрические, изометрические и ортогональные виды трубопроводов

В отличие от орфографии, изометрия трубопровода позволяет рисовать трубу таким образом, чтобы длина, ширина и глубина отображались на одном виде.Изометрия обычно строится на основе информации, содержащейся на видах плана и фасада. Символы, обозначающие фитинги, клапаны и фланцы, изменены для адаптации к изометрической сетке. Обычно изометрия трубопроводов рисуется на заранее распечатанной бумаге с линиями равносторонних треугольников в форме 60 °.

Iso, как обычно называют изометрические, ориентирована на сетке относительно стрелки севера на чертежах плана. Поскольку ISO не нарисованы в масштабе , размеры требуются, чтобы указать точную длину участков трубопровода.

Длины труб определяются путем расчетов с использованием координат и отметок. Длина трубы по вертикали рассчитывается с использованием отметок, а длина по горизонтали рассчитывается с использованием координат север-юг и восток-запад.

Изометрия трубопроводов обычно создается на основе орфографических чертежей и является важной информацией для инженеров. В очень сложных или больших системах трубопроводов изометрия трубопроводов имеет важное значение на этапах проектирования и производства проекта.
Изометрические параметры трубопроводов часто используются проектировщиками перед анализом напряжений, а также используются чертежниками для создания заводских чертежей катушек. Изометрические чертежи являются наиболее важными чертежами для подрядчиков по установке во время полевой части проекта.

Большое изображение нарисованной вручную изометрии

Как читать изометрические данные трубопровода?

Труба в изометрической проекции всегда рисуется одной линией. Эта единственная линия является центральной линией трубы, а от этой линии — измеренными размерами.Так что не снаружи трубы или фитинга.
На изображении ниже показан ортогональный вид трубы, сваренной встык, трех размеров (A, B, C).

• Размер A измеряется от передней части до центральной линии колена / трубы.
• Размер B измеряется от средней до средней линии.
• Размер C аналогичен размеру A и измеряется от передней части до центральной линии колена / трубы.

Ортогональный вид
(двухстрочное представление)

Изометрический вид

Изометрический вид показывает ту же трубу, что и ортогональный вид.

Как видите, этот рисунок очень прост и быстро реализуется. Красные линии показывают трубу, черные точки — стыковые швы, а A, B и C — размеры от передней до центральной линии и от центральной линии до центральной линии.

Простота, с которой можно нарисовать изометрию трубы, является одной из причин создания ISO.

Вторая причина делать изометрию; если труба должна быть нарисована в нескольких плоскостях (с севера на юг, затем вниз, затем на запад и т. д.), ортогональные виды действительно не подходят.В ортогональном виде это не проблема, если труба проходит в одной плоскости, но когда труба должна быть нарисована в двух или трех плоскостях, ортогональный вид может быть нечетким.

Еще одна причина, по которой предпочтение отдается исо, — это количество рисунков, которые необходимо сделать для ортогональных видов.
Например: для сложной трубопроводной системы необходимо нарисовать 15 изометрий. Я никогда не пробовал, но думаю, что для орфографических видов потребуется 50 рисунков, чтобы показать то же, что и на Iso.

Изометрические, плановые и вертикальные представления трубопроводной системы

На изображении ниже показана презентация, использованная при редактировании.Изометрический вид ясно показывает расположение трубопроводов, но на виде сверху не видны байпасный контур и клапан, и необходим дополнительный вид в вертикальной проекции.

Изометрические изображения в нескольких плоскостях

Ниже приведены несколько примеров изометрических чертежей. Вспомогательные линии в форме куба обеспечивают лучшую визуализацию трассы трубопровода.

На рисунке 1 показан трубопровод, проходящий через три плоскости. Трубопровод начинается и заканчивается фланцем.
Начальная точка маршрута X

• трубопровода на восток
• трубопроводов
• трубопровода на север
• трубопроводов на запад
• Трубопровод

Рисунок 2 почти идентичен рисунку выше. Показана другая перспектива, и труба, идущая сверху, длиннее.
Поскольку эта труба в изометрии проходит за другой трубой, это должно быть обозначено разрывом на линии.
Начальная точка маршрута X

• трубопроводов на юг
• трубопроводов
• трубопроводов на запад
• трубопровода на север
• Трубопровод

На рисунке 3 показана труба, которая проходит в трех плоскостях и в двух плоскостях образует дугу.
Начальная точка маршрута X

• трубопроводов на юг
• трубопроводов
• труба идет вверх и на запад
• трубопроводов
• трубопроводов на запад
• трубопровода на северо-запад
• трубопровода на север

На рис. 4 показана труба, проходящая через три плоскости, от одной плоскости к противоположной.
Начальная точка маршрута X

• трубопроводов на юг
• трубопроводов
• труб вверх и на северо-запад
• трубопровода на север

Люки на изометрическом чертеже

Нанесение штриховки на изометрических чертежах для обозначения того, что труба проходит под определенным углом и в каком направлении идет труба.

Иногда, небольшие изменения в люке, трасса трубы уже не на восток, а, например, внезапно на север.

Рисунок 5 показывает трубу, где штриховка указывает на то, что средняя ветвь идет на восток.
Начальная точка маршрута X

• трубопроводов
• труба идет вверх и на восток
• трубопроводов

На рис. 6 показана труба, где штриховка указывает на то, что средняя ветвь идет на север.
Начальная точка маршрута X

• трубопроводов
• труба идет вверх и на север
• трубопроводов

На двух вышеприведенных рисунках показано, что при переходе только от люка трубопровод принимает другое направление.Люки особенно важны в изометрических проекциях.

Рисунок 7 показывает трубу, где штриховкой обозначено, что средняя опора идет вверх и на северо-запад.
Начальная точка маршрута X

• трубопроводов
• труб вверх и на северо-запад
• трубопровода на север

.

No related posts.