Что такое «золотое сечение»?. На протяжении веков «золотое сечение»… | by Сергей Базанов | Paradox Review
На протяжении веков «золотое сечение» считается самым прекрасным соотношением в искусстве и архитектуре.
«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».
Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».
Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения».
Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:
Что эквивалентно пропорции:
Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».
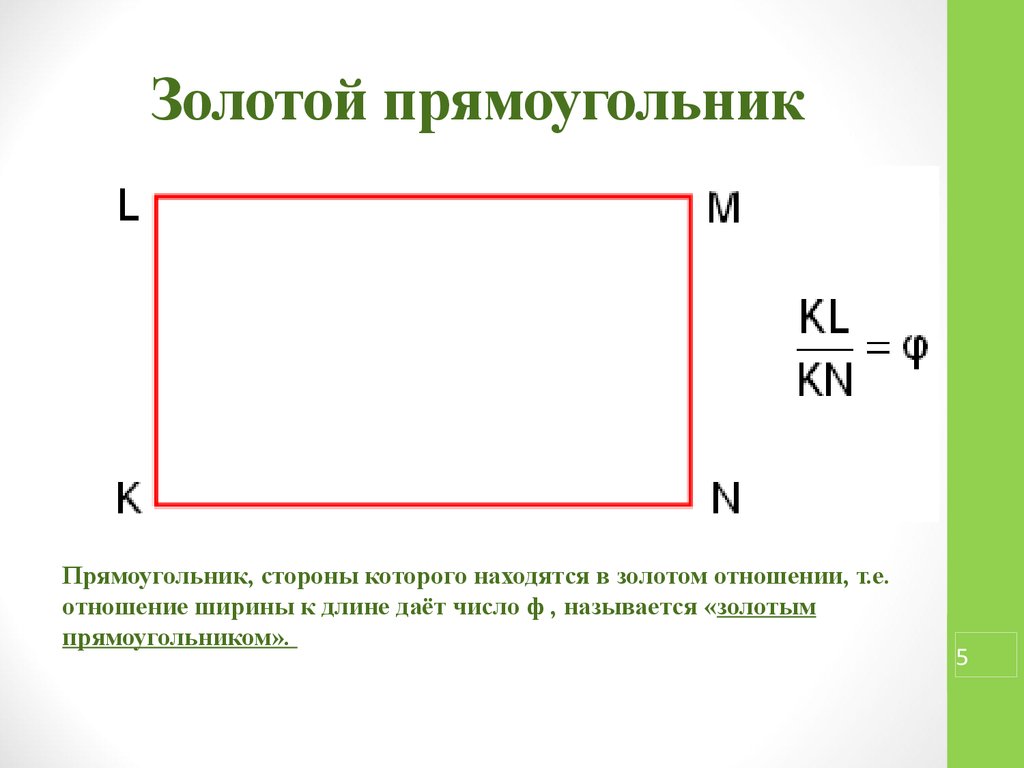
«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.
Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.
Золотой прямоугольник.На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.
е. бесконечная десятичная дробь, не имеющая периода.
Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.
Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.
a = x, b = 1Шаг 1. Сделаем перекрестное умножение:
Шаг 2. Приведем уравнение к 0:
Шаг 3. Решим квадратное уравнение:
Поскольку мы работаем с длинами, нам нужно только положительное решение:
Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:
Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя.
Это потрясающе!
Что эквивалентно:
Пойдем дальше… Заменим φ = 1 + 1 / φ для φ в знаменателе:
И еще дальше!
Мы могли бы продолжать делать это бесконечно. Оказывается, «Золотое сечение» может быть записано как бесконечная цепная дробь.
Мы можем использовать непрерывную дробь, чтобы раскрыть связь «золотого сечения» с последовательностью Фибоначчи.
Для начала мы немного изменим нашу бесконечную дробь — добавим индексы, чтобы показать, как следующее значение φ(n+1) может быть получено из предыдущего значения φ(n).
Так как это бесконечная цепная дробь, с ростом n искомое значение приближается к истинному значению φ.
Теперь допустим, что φ(0) = 1 и найдем φ(1).
Продолжим вычислять следующеезначение — φ(2)
И далее… φ(3), φ(4)…
Посмотрите! Это же последовательность Фибоначчи! Каждое приближение — это отношение двух соседних чисел Фибоначчи.
По мере продвижения к каждому новому последовательному вычислению мы обнаруживаем, что наше искомое значение все ближе и ближе приближается к его истинному «Золотому сечению».
На девятом члене последовательности Фибоначчи мы уже получаем значения «золотого сечения», с тремя верными цифрами после запятой.
В самом деле, limit F(n+1)/F(n) при n→∞ (где F(n) и F(n+1) представляют n и n+1 числа в последовательности Фибоначчи) сходится к φ.
Если визуализировать этот процесс, то мы увидим, как последовательность Фибоначчи создает прямоугольники всё ближе и ближе к «Золотому прямоугольнику».
Прямоугольник Фибоначчи.Хотя в мире дизайна продолжаются споры о том, является ли «золотое сечение» оптимальной пропорцией или нет, можно с уверенностью сказать, что оно математически совершенно и не перестает нас удивлять.
What is the Golden Ratio?
You know you’re truly geeking out when you’re gushing about how beautiful a number is, but hey this number is pretty…
medium.
com
Нереализованное влияние золотого сечения
Математика на службе у искусства
medium.com
Лучшая книга о Биткоине для начинающих
Всё, что вы хотели знать о Биткоине, но стеснялись спросить, найдете в книге «Биткоин для всех»
medium.com
Основные построения золотого сечения — Записки недизайнера — LiveJournal
На практике при выборе формата листа (картины) часто используют «классические» пропорции сторон прямоугольника, в котором отношение меньшей стороны к большей составляет число 0,6180339, а большей к меньшей — 1,6180339. Эти числа с древнейших времён называют золотыми, а отношение величин, необходимое для их получения, известно как золотая пропорция или золотое сечение.
Основа учения о гармонии мира, выраженная в числовых отношениях, была заложена древнегреческим учёным-математиком Пифагором (VI в до н.э). Им представлено золотое сечение как одна из закономерностей, математически точно определяющая наиболее красивое и гармоничное соотношение частей целого, разделённого на две неравные половины.
На соотношении частей отрезка в пропорциях золотого сечения основано построение прямоугольника. С помощью диагоналей осуществляется членение его на составные части, при котором образуется динамика пропорциональных фигур — квадрата, прямоугольника, а также прямоугольного и равнобедренного треугольников.
Т.о., используя диагонали можно получить последовательный ряд увеличивающихся прямоугольников, с соотношением сторон — 1:√ 2, 1:√3, 1:√4, 1:√5, производных от квадрата.
При стороне √4 образуется прямоугольник с удвоенным квадратом. При стороне √3 образуется два прямоугольных треугольника, у которых общая гипотенуза является диагональю прямоугольника, равная удвоенной величине меньшего катета (т.е. стороне квадрата), и они имеют острые углы 30 и 60 градусов.
Диагональ используется и в построении последовательно увеличивающихся квадратов, создающих «динамическое» развитие их величины.
В этом построении сторона каждого последующего квадрата относится к стороне предыдущего, как диагональ квадрата к его же стороне.
Эти преобразования иногда называют «активным квадратом».
Геометрическая система динамических пропорций квадрата, прямоугольника и треугольника были основой в создании архитектурных сооружений в ранний период Древнего Египта. Кроме того, в условиях примитивной техники архитектурного строительства в те далёкие времена постоянно требовалось восстановление перпендикуляра к прямой, которое осуществлялось тогда при помощи верёвки с 12 узлами. С использованием такого приспособления получался прямоугольный треугольник с отношением строно — 3:4:5, который впоследствии стали называть египетским. В настоящее время на его основе строят прямые углы и проводят перпендикуляры к концу отрезка.
С древнейших времён золотое сечение используется в практике построения различных изображений. Это способствует созданию гармоничных образов и уравновешенности пропорций во всём, что на окружает. Пропорции золотого сечения присутствуют в мамематике, и особенно в геометрии, в изобразительном искусстве, в быту и в природе, в растительном и животном мире.
Золотое сечение получило широкое развитие в математике. Так, в XVI веке итальянский учёный Фибоначчи выстроил математический ряд цифр, при котором последующее число определяет сумму двух предыдущих — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Кроме того, устанавливается и другая зависимость этих чисел, при которой отношение каждого последующего к предыдущему выражается числом 1,618…, а предыдущего к последующему — 0,618. Таким образом, в этом математическом ряду образуется взаимосвязь чисел, содержащая пропорции золотого сечения.
Особенно часто золотое сечение используется в геометрии при делении окружности на равные части и построении правильных многоугольников.
В звёздчатом многоугольнике — пятиконечной звезде, каждая точка пересечения её сторон делит их на две неравные части в пропорциях золотого сечения.
С древнейших времён золотое сечение применялось в различных видах изобразительного искусства — в архитектуре, вкульптуре, живописи. Парфенон — классический пример применения золотого сечения в архитектуре.
Особенно широко использовал в своём творчестве соотношение величин золотого сечения Леонардо да Винчи, которое он назвал «божественная пропорция».
Числовой гармонии золотого сечения подчиняются также античные статуи греческого искусства, отражающие пропорции идеально сложённого человеческого тела.
Золотое сечение применяют в начертании букв и цифр различного шрифта.
Золотое сечение часто используют в определении величины прямоугольника при заданной его большей или меньшей стороне. Если у прямоугольной картины задана длина (АВ), то её высоту (АС) определяют следующим построением:
Сначала из конца отрезка (В) проводят дугу, равную его половине до пересечения с перпендикуляром (АО=ОВ=ВД). Полученную точку Д соединяют прямой с другим концом отрезка (А). Затем из точки Д проводят дугу радиусом ВД до пересечения с этой прямой и отмечают точку Е. Дуга, проведённая из конца отрезка А радиусом АЕ определяет по вертикальной прямой точку С и искомую высоту картины АС.
Если задана высота картины (АС), то её длину (АВ) определяют другим построением. Сначала строят квадрат АСДЕ со стороной равной АС. Затем из середины стороны квадрата (О) проводят дугу радиусом ОД и получают на горизонтальной прямой точку В, которая определит искомую длину стороны прямоугольной картины АВ.
По прямоугольнику с золотыми пропорциями можно построить любой величинны подобный формат листа.
Для этого его накладывают на лист бумаги в один из его углов (А) и проводят в нём диагональ. Затем от точки А откладывают заданный размер горизонтальной или вертикальной стороны формата листа и через его конец проводят перпендикуляр до пересечения с диагональю, которая определит вторую сторону прямоугольника.
Источник: М.Н. Макарова «Практическая перспектива»
Tags: Золотое сечение
Золотое сечение породило новую красивую кривую: спираль Харриса | Алекс Беллос
Математики любят придумывать что-то новое. Теорема, может быть, лемма или даже просто следствие.
Эдмунд Харрис открыл кривую.
Харрисс преподает математику в Университете Арканзаса. Он также художник, и его интеллектуальные поиски начались с формы, которая, как известно, принадлежит как науке, так и искусству: золотой прямоугольник:
Золотой прямоугольник делится на квадрат и меньший золотой прямоугольник.Золотой прямоугольник — это прямоугольник, стороны которого пропорциональны золотому сечению, равному 1,618. Другими словами, длинная сторона в 1,618 раза больше короткой.
Что особенно интересно в золотом прямоугольнике, так это то, что если вы нарисуете внутри него квадрат, как показано выше, оставшаяся часть (синий) будет меньшим золотым прямоугольником.
Продолжим. Мы можем разделить меньший прямоугольник на квадрат и еще меньший золотой прямоугольник:
Разрезание золотого прямоугольника. Мы можем продолжать до тех пор, пока нам нравится делить прямоугольники. А если в каждом квадрате нарисовать четверть круга, то получится спираль.
Иллюстрация ниже, вероятно, является одним из самых известных изображений в математике, если не во всей науке. Кривая называется «золотой спиралью».
Вдохновленный классической конструкцией золотой спирали, Харрис, англичанин, начал экспериментировать с процессом разделения прямоугольников. в надежде, что он сможет создать другие эстетически приятные кривые.
Таким образом, вместо того, чтобы начать с прямоугольника, а затем вырезать квадрат, который оставил бы такой же прямоугольник, как мы сделали выше с золотым прямоугольником, он сделал что-то подрывное.
«Вместо того, чтобы вырезать квадрат, я вырезал прямоугольник», — сказал он.
Он сделал следующее: он нашел прямоугольник, который разделился бы на два подобных прямоугольника и квадрат, как показано ниже.
Синий прямоугольник и оранжевый прямоугольник имеют те же пропорции, что и весь прямоугольник, то есть соотношение между сторонами равно 1,325.
Прямоугольник рождает двух одинаковых детей разного размера и квадрат.Так как у нас есть два таких прямоугольника, мы можем продолжить разделение.
При делении мы получаем больше прямоугольников с коэффициентом 1,325.И снова. И опять.
Давайте устроим прямоугольную вечеринку!Еще раз в путь.
Наконец, исходный прямоугольник делится на 34 одинаковых прямоугольника и 33 квадрата.Помните, что для получения золотой спирали мы добавили к квадратам четверть круга? Харрис сделал это и здесь:
Четверть круга идет от угла к соседнему углу каждого квадрата.Глядь, еще одна спираль! Но есть и другие квадраты, которые мы пропустили. Давайте заполним их.
Спирали разветвляются фрактальным узором.А теперь удалите самую большую дугу, чтобы открыть… фигуру, которую я назову «спираль Харриса».
Спираль Харриса.
Харрис был вне себя от радости, когда впервые увидел спираль, потому что она была эстетически привлекательной. Одной из его основных целей было нарисовать разветвляющиеся спирали, которые можно найти в исламском искусстве или работах Густава Климта. Но особенно он был в восторге, потому что пришел к спирали с помощью очень простого математического процесса.
«Нетрудно сделать что-то, чего никто раньше не видел», — сказал он. «Сложнее сделать что-то математически удовлетворительное, чего люди не видели раньше».
Его первым беспокойством было то, что, возможно, кто-то другой на самом деле нарисовал спираль «Одна вещь, связанная с математическими открытиями и математическим искусством, заключается в том, что даже если процесс совершенно новый, нет гарантии, что кто-то еще не исследовал его. ”
Оказалось, что отношение 1,325, которое дает вам прямоугольник, образующий спираль Харриса, было написано — оно известно как «пластическое число», — но Харрис не смог найти предыдущих рисунков спирали.
(На самом деле отношение — это число, которое начинается с 1,32472… и продолжается вечно).
Теперь кривая стала его визитной карточкой, напечатанной на футболках:
Спиральное племя: Эдмунд Харрис, Джесси Хортон, Элла Ван Хорн и Эзра Ван Хорн (по часовой стрелке от бородатого). Они держат экран для печати футболок.На картах.
Если вы друг Эдмунда, возможно, вы получили одну из этих великолепных открыток.И на номер его машины.
Особое отделение.Еще одним мотивом Харрисса было привнести золотое сечение в более широкое семейство того, что он называет «системами пропорций».
«Золотое сечение — это невероятно хорошо изученный уголок целого города», — сказал он. «Я хотел дать указатели на другие места в этом городе».
Системы пропорций Харриса представляют собой прямоугольники, которые можно разделить только на квадраты и подобные прямоугольники.
В соответствии с этим правилом есть только три возможности для прямоугольников, которые можно разделить на две части.
Первый (разделенный на два одинаковых прямоугольника) представляет собой пропорцию листа бумаги формата А4 (или любого другого числа А) с отношением √2.
Второй (разделенный на квадрат и такой же прямоугольник) представляет собой золотой прямоугольник, а третий (два квадрата) имеет форму домино.
Существует 16 вариантов прямоугольников, которые можно разделить на три части.
Вот шесть вариантов, где вы отрезаете большой квадрат и кладете два квадрата/прямоугольника в столбец. Помните, что в любом случае, если есть мини-прямоугольник, он должен иметь те же пропорции, что и весь прямоугольник.
Соотношения прямоугольников и соответствующие уравнения отмечены для каждого прямоугольника. Вот шесть вариантов, где можно отрезать похожий прямоугольник и поместить два квадрата/прямоугольника в столбец.
А вот четыре варианта, в которых все квадраты/прямоугольники выстраиваются в линию.
Математики узнают соотношения, представленные системой пропорций Харриса, как «алгебраические числа» — числа, являющиеся решениями простых уравнений. Харрисс считает, что геометрический подход к алгебраическим числам может привести к их более глубокому пониманию.
«Соотношения уже встречаются в математике и искусстве, что говорит о том, что системы пропорций отражают некоторую идею простоты этих чисел», — сказал Харрис, добавив, что он работает над доказательством того, что каждое алгебраическое число является отношением прямоугольника. принадлежность к системе пропорций.
Я спросил, искал ли Харрис красивые спирали с каким-либо другим соотношением? — Да, но с ограниченным успехом, — вздохнул он. «Проблема в том, чтобы получить набор квадратов, совпадающих в правильном порядке».
Вот что он пока придумал:
Спирали из систем пропорций.
Читателям предлагается построить свои собственные спирали, а затем прислать мне футболку.
Чтобы поддерживать связь с этим блогом, подпишитесь на меня в Twitter, нажмите «Нравится» на Facebook или добавьте меня в Google+.
Блог Эдмунда Харриса называется «Демон Максвелла».
Чтобы узнать больше о золотом сечении, вот мой пост о том, что оно было обнаружено в матке, и вот проект, в котором я участвовал, в котором 55 дизайнеров попросили интерпретировать это число. 9Калькулятор золотого прямоугольника Калькулятор золотого прямоугольника рассчитает длину любой стороны и площадь золотого прямоугольника, если вы укажете другую сторону. Прежде чем использовать этот калькулятор, вы должны понять, что такое золотой прямоугольник, как вообще рассчитывать отношения и формулу золотого сечения. Золотой прямоугольник — это прямоугольник, стороны которого находятся в золотом сечении, то есть Калькулятор коэффициентов является эффективным инструментом для помощи в расчете коэффициентов в целом. Напротив, калькулятор золотого сечения будет делать то же самое, что и калькулятор золотого прямоугольника, за исключением нахождения площади прямоугольника. Вот шаги: Интересным аспектом золотого прямоугольника является то, что после удаления квадратной части остается еще один золотой прямоугольник. Кроме того, добавление еще одного квадрата к прямоугольнику со стороной Знаете ли вы, что можно использовать периметр прямоугольника, чтобы найти его длину и ширину? Наш калькулятор длины и ширины прямоугольника с учетом периметра научит вас, как это легко сделать! Чтобы построить золотой прямоугольник с помощью циркуля и линейки: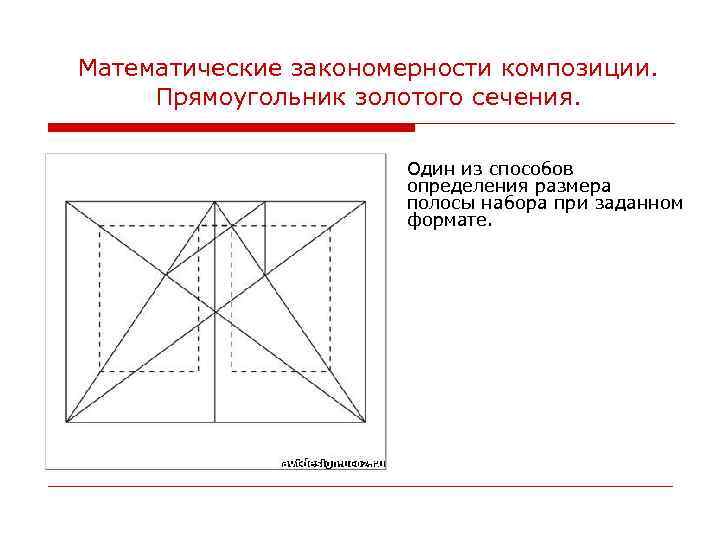
Что такое золотой прямоугольник?
(a + b)/a = a/b = φ , где a — ширина, a + b — длина прямоугольника, а φ — золотое сечение: φ = (1+√5)/2 . Как использовать наш калькулятор золотого прямоугольника?
a . a + b или сегмент b a × (a + b) 
a + b — еще один золотой прямоугольник. Калькулятор золотого прямоугольника проверит это. Как нарисовать золотой прямоугольник?
