Разложение цвета на цвета: Дисперсия света — урок. Физика, 9 класс.

Разложение белого света на цвета. Дисперсия света

Конспект по физике для 9 класса «Разложение белого света на цвета. Дисперсия света». Каков состав белого света. Как зависит преломление света от цвета светового луча. Чем обусловлен цвет тела. Что такое дисперсия света.

Конспекты по физике    Учебник физики    Тесты по физике

---

Мы привыкли видеть окружающий нас мир красочным и обычно не задумываемся над вопросами: а что же такое цвет тел? Можем ли мы рассматривать цвет как одно из основных свойств материальных объектов?

ОПЫТЫ НЬЮТОНА

До Ньютона вопросами о природе цвета занимались в основном художники, поэты и философы. Их рассуждения, как правило, касались пропорции смешения различных цветов, и на этой основе строились те или иные теории цвета. В частности, ещё в IV в. до н. э. древнегреческий учёный Аристотель выдвинул свою теорию цветов, согласно которой солнечный свет является простым, а все остальные цвета получаются из него в результате смешивания с различным количеством тёмного цвета.

В 1666 г. Ньютон, занимаясь усовершенствованием телескопов, обратил внимание на тот факт, что изображение, получаемое с помощью объектива телескопа, окрашено по краям. Предполагая, что это может быть связано с преломлением света, он направил узкий пучок солнечного света, образованного малым отверстием в ставне, на грань стеклянной призмы, установленной в затемнённой комнате. При этом на противоположной стене комнаты, выполнявшей роль экрана, появилось удлинённое изображение щели, состоящее из ряда цветных полос.

Результаты опыта озадачили Ньютона и породили ряд вопросов. Во-первых, почему белый свет, входящий в призму, выходил из неё в виде цветной полосы, содержащей семь цветов: фиолетовый, синий, голубой, зелёный, жёлтый, оранжевый и красный? Во-вторых, почему круглый в сечении пучок после преломления в призме оказался существенно растянутым в длину? Влияет ли вещество самой призмы на окрашивание белого света? Располагая цвета в определённой последовательности, Ньютон, по-видимому, учитывал последовательность цветов в радуге.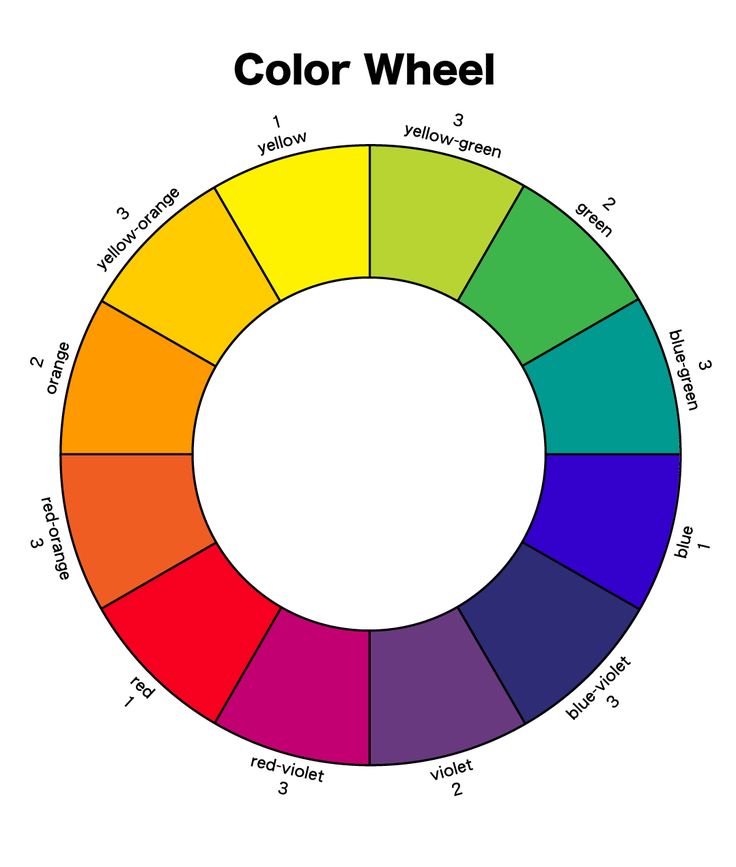 Получившуюся на экране цветную полоску Ньютон назвал спектром (от лат. spectrum — изображение). Из опыта следовало, что белый свет является сложным: пройдя через призму, он разлагается на пучки различных цветов.

Однако далеко не все современники Ньютона согласились с этим выводом: слишком уж необычным казалось это предположение.

Между тем Ньютон нашёл простой и убедительный способ доказательства справедливости своей теории. Для этого он на пути пучка, прошедшего через призму, поместил вторую призму, повёрнутую на 180 относительно первой. При этом вторая призма действовала как собирающая линза: вышедший из неё пучок в точке схождения лучей становился белым.

ДИСПЕРСИЯ СВЕТА

Таким образом, опыты Ньютона убедительно свидетельствовали о том, что белый свет имеет сложную структуру.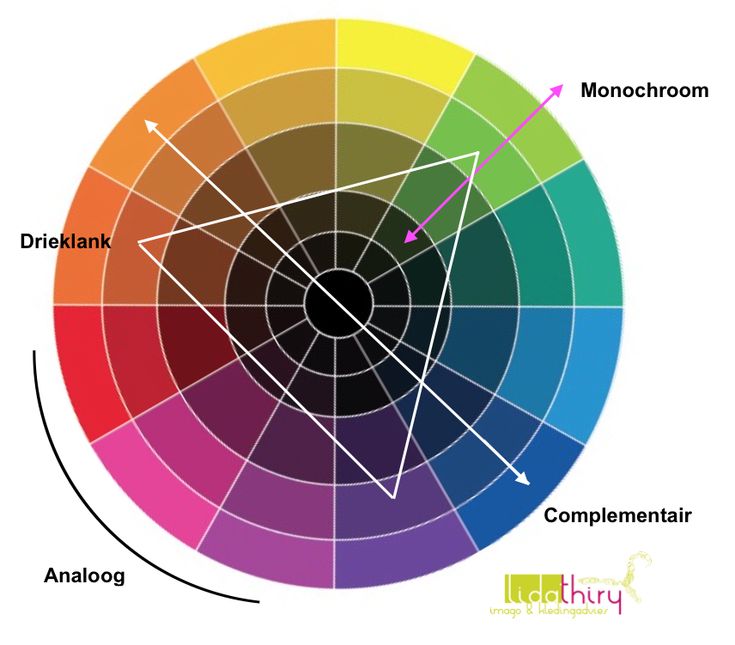 Вместе с тем Ньютона интересовал вопрос: оказывает ли влияние вещество призмы на характер окрашивания пучка? Для ответа на этот вопрос он закрывал отверстие в ставне поочерёдно синим и красным стеклом и наблюдал при этом синее и соответственно красное пятно на стене. Это означало, что призма не может влиять на цвет пучка.

Опытным путём Ньютон нашёл ответ и на другой важный вопрос: почему пучки разных цветов по-разному отклоняются призмой? В своём фундаментальном трактате «Оптика» Ньютон так сформулировал полученный им вывод: «Световые пучки, отличающиеся по цвету, отличаются по степени преломляемости». В наибольшей степени преломляются фиолетовые пучки, в наименьшей — красные.

Как известно, показатель преломления среды зависит от скорости света и в веществе: n = с/υ, где с — скорость света в вакууме. Следовательно, пучок фиолетового цвета преломляется в большей степени потому, что фиолетовый цвет имеет в веществе наименьшую скорость. Красные же лучи преломляются меньше других потому, что их скорость в веществе наибольшая.

Зависимость показателя преломления среды от цвета световых лучей Ньютон назвал дисперсией (от лат. dispersion — рассеяние).

ЦВЕТ ТЕЛА

Окружающий нас мир является красочным именно потому, что солнечный свет является сложным. Но всё же пока непонятно, почему траву и листья растений мы видим зелёными, мак — красным, одуванчик — жёлтым, а мел — белым? Почему различные предметы, освещённые одним и тем же солнечным светом, имеют разный цвет?

Чтобы разобраться в этом, будем освещать, например, синим светом поочерёдно синие, зелёные, жёлтые и красные листы бумаги из набора для изготовления аппликаций. Мы увидим, что только при освещении синей бумаги она будет казаться нам яркой. При освещении же синим светом бумаги других цветов она будет выглядеть тёмной.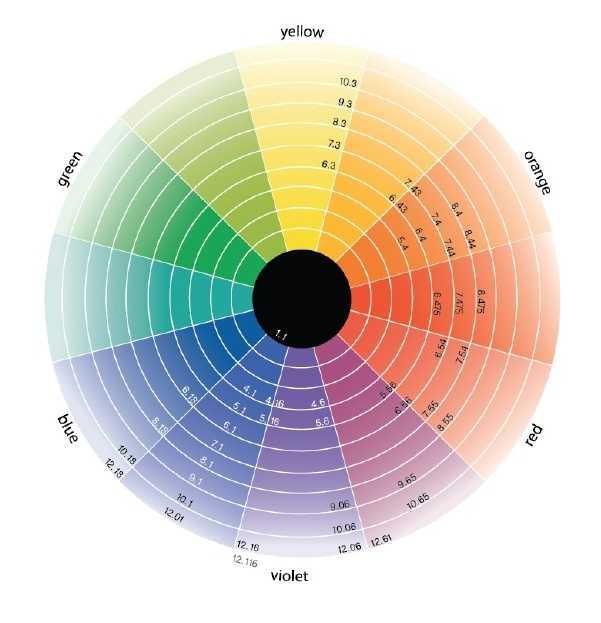 Это означает, что тела, имеющие синюю окраску, рассеивают в основном синие лучи, а остальные поглощают. Аналогично тела, имеющие красную окраску, в основном рассеивают красные лучи.

Белые тела, которые освещаются дневным светом, в равной степени рассеивают лучи всех цветов, поэтому мы их видим белыми. Чёрные же тела представляются нам чёрными потому, что они поглощают практически все падающие на них лучи.

Среди палитры цветов красный, синий и зелёный цвета относятся к основным.

Даже много позднее, в начале XIX в. великий немецкий поэт Гёте, обладавший исключительным авторитетом, выступил против теории цвета Ньютона. Одним из его аргументов было то, что любой цветной свет темнее белого и, следовательно, яркость не может быть получена из темноты.

 

---

Вы смотрели Конспект по физике для 9 класса «Разложение белого света на цвета. Дисперсия света»: Каков состав белого света. Как зависит преломление света от цвета светового луча. Чем обусловлен цвет тела. Что такое дисперсия света.

Вернуться к Списку конспектов по физике (Оглавление).

Разложение белого света на цвета и образование цветов в физике с примерами

Разложение белого света на цвета и образование цветов:

Вам не раз приходилось видеть, как после дождя в солнечный день на небе возникает разноцветная полоса — радуга. А если вы наблюдательны, то могли заметить такие радужные цвета не только на небе. Посмотрите, например, на водяной фонтан, освещенный Солнцем, и вы увидите, как радуга, подобная небесной, играет в каплях воды.

Опыт 1. Возьмите линзу и посмотрите сквозь нее на пламя свечи. Вы увидите, что вокруг пламя свечи наблюдаются цветные кольца.

Предупреждаем! В любом случае нельзя смотреть сквозь линзу на Солнце. Так вы можете испортить себе зрение.

Откуда же появляются на небе, в каплях воды или линзах такие разноцветные полосы?

То, что солнечный свет состоит из цветных лучей, установил Исаак Ньютон. Совершенствуя телескопы, он обратил внимание на то, что изображение объектов, которое дает объектив, по краям окрашено.

В 1754 г. Ньютон выполнил гениально простой опыт. Он пропустил солнечный (белый) свет через маленькое отверстие в ставне в затемненную комнату, а на пути луча поместил стеклянную призму (рис. 151). Призма преломила солнечные лучи и направила их на стену, на которой появилась многоцветная полоса.

Эту многоцветную полосу разложенного белого света Ньютон назвал спектром (лат. spectrum — «видимый»).

Он пришел к заключению, что:

1. Солнечный (белый) свет — это свет, состоящий из семи цветов.
2. Разложение солнечного света трехгранной призмой объясняется тем, что отдельные цветные лучи преломляются в ней неодинаково. Менее всего преломляются лучи красного цвета, а больше всего — фиолетового.
3. Порядок цветов в спектре всегда одинаков (рис. 152).

Опыт 2. Возьмем диск Ньютона — круг, на котором нанесены цвета спектра, — (рис. 153) и будем вращать его с определенной скоростью. В результате опыта мы увидим, что диск имеет белый цвет. Если на пути солнечных лучей поставить две призмы, то на выходе получим белый свет (рис. 154).

В 1807 г. английский ученый Томас Юнг сделал еще одно важное открытие: белый свет можно получить путем смешивания только трех цветов — красного, зеленого и синего.

Оказывается, остальные цвета спектра, а также их оттенки можно получить, смешивая красный, зеленый и синий цвета. Но ни одним смешиванием других цветов нельзя получить красный, зеленый и синий цвета.

Опыт 3. Направим от трех одинаковых источников света на экран свет красного, синего и зеленого цветов так, чтобы они накладывались друг на друга (рис.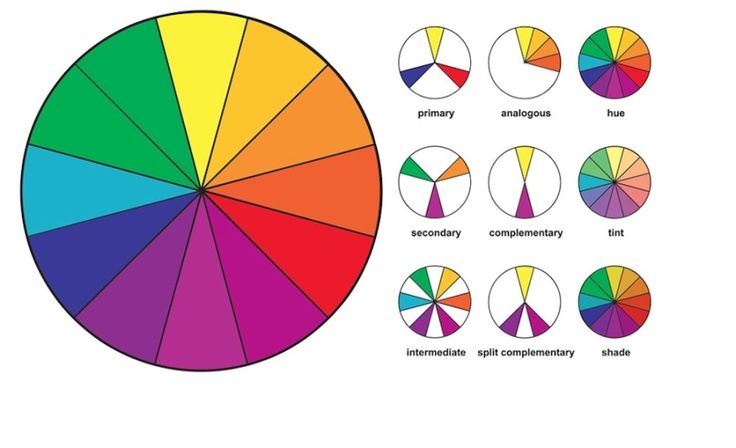 155, а). Там, где накладываются все три цвета, мы увидим белый цвет (рис. 155, б).

Красный, зеленый и синий цвета — это основные, или первичные, цвета спектра.

Почему предметы имеют разные цвета

Цвет любого непрозрачного тела зависит от света, который оно отражает (рис. 156). Предмет имеет красный цвет, потому что он отражает красный свет и поглощает все другие цвета. Другой предмет имеет синий цвет, потому что он отражает синий свет и поглощает все другие цвета. Предмет белого цвета отражает свет всех цветов, а предмет черного цвета, напротив, вообще не отражает свет, а полностью его поглощает.

Тело может поглощать и отражать одновременно несколько цветов.

Отраженные цветные лучи смешиваются между собой, и цвет тела зависит от того, в каком соотношении они от него отражаются. Благодаря этому и возникает разноцветная гамма красок, которую мы наблюдаем в природе.

Цвет прозрачных тел зависит от того, какие лучи света проходят сквозь них.

Например, красное стекло пропускает только красные лучи, а зеленое — только зеленые, что и предопределяет их цвет. С помощью таких стеклышек можно получить однородный по цвету пучок лучей. Прозрачные пластинки, применяемые для получения однородного по цвету светового пучка, называют светофильтрами. Их широко применяют в оптических приборах.

Предметы могут изменять свой цвет, если на них падает свет какого-либо другого цвета. Например, красное платье будет иметь вид черного в лучах синего или зеленого цвета.

• Заказать решение задач по физике

Тремя основными цветами, которые используют в живописи, являются красный, желтый и синий. Они не совпадают с основными цветами света. Смешивая эти цвета, можно получить практически любой цвет, кроме белого. Если смешать все три основных цвета в равных пропорциях, то получим черный цвет (рис. 157).

Интересным природным явлением является радуга. Как же она возникает?

Радуга возникает в результате преломления и отражения света, например в каплях дождя (рис.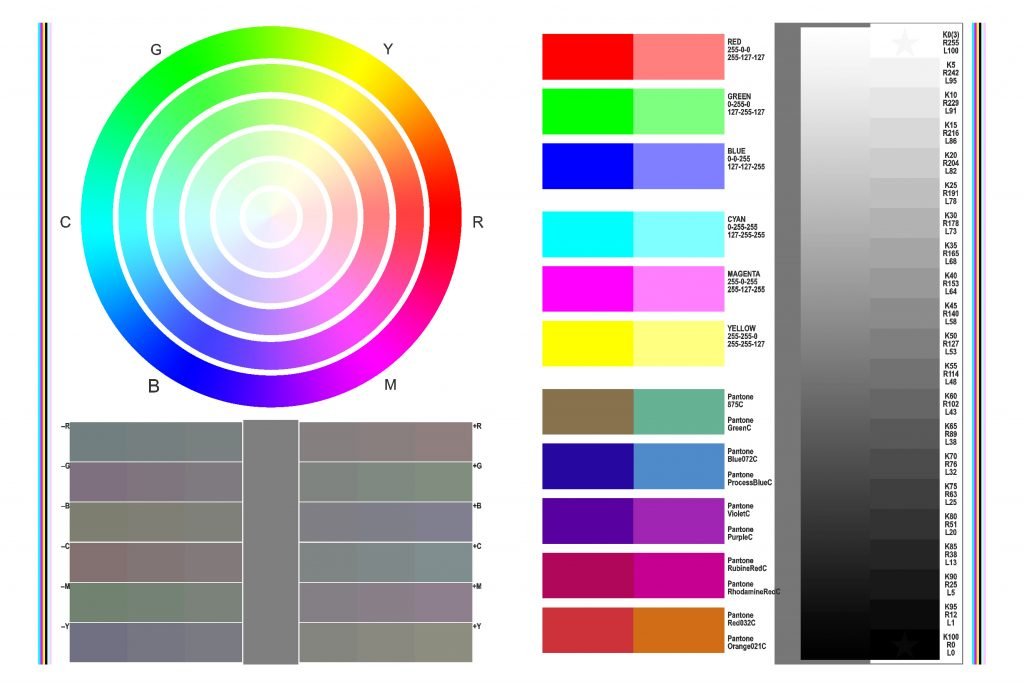 158). В капле воды свет раскладывается на цвета.

Капля воды словно маленькая призма, а ее внутренняя поверхность выполняет роль зеркала, направляя лучи, которые проникают в каплю, в обратную сторону — к наблюдателю. При этом наибольшее количество света выходит под углом 42° к начальному направлению солнечных лучей. Как раз этот свет мы и видим.

Цвета радуги расположены в таком порядке: фиолетовый, синий, голубой, зеленый, желтый, оранжевый, красный. Дальше идет полоса, в которой глаз не различает цветов, иногда она даже кажется темнее, чем вся остальная часть неба, на фоне которого видна радуга. За этой полосой начинается верхняя радуга: в ней порядок цветов обратный — от красного к фиолетовому.

Но почему вы иногда видите радугу ярких цветов, а иногда — неярких?

Оказывается, яркость цветов в радуге зависит от размеров дождевых капель. Если они большие (1-2 мм), фиолетовая и зеленая полосы очень яркие, красная тоже хорошо заметна, а голубую видно слабо. С уменьшением размеров капель радуга расширяется и бледнеет, а когда капли совсем маленькие (0,05 мм), она исчезает.

Кстати:

Из рассказа первого космонавта Юрия Гагарина о пребывании в космосе: «…Небо имеет совершенно черный цвет. Звезды на этом небе выглядят несколько ярче и четче видны на фоне этого черного неба. Земля имеет очень характерный, очень красивый голубой ореол. Этот ореол хорошо просматривается, когда наблюдаешь горизонт, плавный переход от нежно-голубого цвета через голубой, синий, фиолетовый и совершенно черный цвет неба. Очень красивый переход! При выходе из тени попало Солнце, и оно просвечивало земную атмосферу. И здесь этот ореол принял немного другой цвет. У самой поверхности, у самого горизонта земной поверхности можно было наблюдать ярко-оранжевый цвет, который затем переходил во все цвета радуги: к голубому, синему, фиолетовому и черному цвету неба.

Вход в тень Земли осуществляется очень быстро. Сразу наступает темнота и ничего не видно.

..».

Первый космонавт Украины Леонид Каденюк так описал свое впечатление от вида Земли из космоса: «…Нет таких слов, с помощью которых можно описать увиденное. Чрезвычайно большое количество самых разнообразных цветов, но основной оттенок — голубой».
 

Пример №1

После дождя в солнечную погоду иногда можно наблюдать радугу. Почему именно после дождя? Почему в солнечную погоду?

Ответ: в воздухе содержатся дождевые капли, которые являются своеобразными призмами и в которых преломляются солнечные лучи.

Пример №2

Почему для запрещающих сигналов на транспорте (в светофорах, семафорах, стоп-сигналах и т. п.) используют именно красный, а не какой-либо другой цвет?

Ответ: красные лучи меньше рассеиваются в воздухе и хорошо видны при любой погоде.

Разложение белого света на цвета. 8-й класс

Цели:

• Ввести понятие дисперсии света и закрепить основные законы геометрической оптики.
• Развить умения обобщать, вступать в речевое общение, выражать результаты своей деятельности в письменном виде, внимательность, навыки работы с физическим оборудованием.
• Воспитать аккуратность, самостоятельность, волю и настойчивость для достижения конечного результата при выполнении лабораторной работы.

Тип урока: комбинированный.

Оборудование: компьютер, экран, миллиметровая бумага, прозрачная пластина со скошенными гранями, пластиковый коврик, иголки.

План урока:

1. Орг.момент.
2. Повторение домашнего задания.
3. Фронтальная лабораторная работа.
4. Изучение нового материала.
5. Обобщение и систематизация знаний.
6. Итог урока.

Ход урока

1. Орг. Момент

Проверка готовности учащихся.

2. Повторение домашнего задания

Для изучения новой темы нам необходимо повторить изученный материал.

В работе используется презентация (Приложение 1).

Краткий фронтальный опрос учащихся:

• вспомните законы отражение света? (слайд 1)
• вспомните законы преломления света? (слайд 2)

3. Фронтальная лабораторная работа (слайд 3-4)

Тема: Измерение показателя преломления вещества

Цель работы: научиться измерять показатель преломления вещества при помощи призмы.

Оборудование: миллиметровая бумага, прозрачная пластина со скошенными гранями, пластиковый коврик, иголочки.

Ход работы

1. Очертите остро отточенным карандашом на листе бумаги контур основания пластины.
2. С помощью иголок указать падающий луч и луч преломленный, провести перпендикуляр.
3. Указать угол падения и угол преломления.
4. Измерить эти углы с помощью транспортира.
5. Вычислить показатель преломления вещества, из которого сделана прозрачная пластина.

4. Изучение нового материала

Закон преломления, который мы сейчас с вами использовали при выполнении опыта, рассматривается в очень интересном и необычном явлении, благодаря которому можно видеть наш окружающий мир цветным. Это явления называется дисперсией света. Поэтому сегодня на уроке мы с вами будем изучать следующую тему «Разложение света на цвета» (слайд 5)

На данном уроке мы с вами познакомимся с понятием дисперсия, а в дальнейшем будем изучать это явление подробнее.

Сейчас посмотрим опыт на преломление света через призму, которое было открыто И. Ньютоном. (слайд 6)

Видео «Разложение белого света с помощью призмы» (Приложение 2).

– Итак, что же сделал Ньютон?

– Что же такое дисперсия света?

(учащиеся высказывают мнение по поводу дисперсии света)

Дисперсия – зависимость показателя преломления от частоты колебаний.

– Как понять это явление? (слайд 8-11)

Свет различного цвета характеризуется различными показателями преломления света в данном веществе.

Есть простые цвета, не разлагающиеся при прохождении через призму (например, красный цвет) и сложные, представляющие совокупность простых, имеющих разные показатели преломления (белый солнечный свет). Но это не нужно понимать слишком буквально: белый или вообще сложный свет, разлагаемый призмой, есть нечто целое. Разложение белого света призмой – есть результат действия прибора на свет, но не доказывает, что он – смесь простых цветов.

Наш глаз – для анализа света. При помощи глаза мы получаем знание обо всем многообразии цветов в окружающем мире. Свет проходит через тела, частично преломляясь, частично поглощаясь ими и частично отражаясь от их поверхности. Спектральный состав цвета, дошедший до нашего глаза, значительно изменен и различен.

(Учащиеся слушают учителя)

Тела (вещества), у которых поглощение велико – черные, непрозрачные; у которых велико отражение – белые; у которых велико пропускание (преломление) – прозрачные. (слайд 12)

(Учащиеся записывают в тетради  материал,  данный на экране)

А теперь давайте рассмотрим “цвет” с точки зрения предмета “Технология”. (слайд 13)

Вы увидели, что красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый цвета похожи один на другой. Это позволило расположить спектральные цвета по кругу. (слайд 14)

Цветовой круг обычно делится на две части: теплую и холодную.

Теплые цвета: красный, оранжевый, желтый и все другие, которые содержат эти цвета.

Холодные цвета: синие, голубые, зеленые, сине-фиолетовые, сине-зеленые.

Из основных цветов мы можем получить составные цвета. (слайд 15-18)

Примеры дисперсии света (слайд 19-20)

(Учащиеся рассматривают дисперсию света на примерах)

– Ребята, как можно запомнить расположение цветов? (слайд 21)

5. Обобщение и систематизация знаний

Вернемся к теме урока и ответим на вопросы:

– Какое применение своих знаний вы видите в жизни?  

– Где используют это явление?

6. Итог урока

Учащимся предлагается поставить галочку около выбранного утверждения.

1. Мне все понравилось____________
2. Мне ничего не понравилось______
3. Мне ничего не понятно__________
4. Мне было интересно____________
5. Мне было скучно_______________
6. Мне было легко________________
7. Мне было трудно_______________
8. Я узнал много нового____________
9. Я не узнал ничего нового_________

Домашнее задание: повторить законы отражения и преломления света, подготовиться к самостоятельной работе.

Что такое свет, цвет и спектральные цвета

Как всякая волна, свет излучается и поглощается физическими телами. Свет излучается нагретыми или иначе находящимися в возбужденном состоянии телами и веществами.

Как физическое явление, Свет изучается в физике, в разделе оптика. Причем Свет это не одиночная волна с определенными характеристиками, а поток волн, разной длины и частоты.

Из школьного курса физики мы знаем, что как всякие другие волны, свет может быть разложен на составляющие его волны при помощи дифракционной решетки (дифракция) или при помощи призмы (дисперсия). После такого разложения мы получаем спектр волн разной длины, при этом большой участок этого спектра будет невидим человеческим глазом.

Дифракционный и дисперсионный спектры имеют некоторые различия.

Дифракция, это явление отклонения от прямолинейного направления движения волны при прохождении ее через препятствия (щель, отверстие, стержень), размер которого соизмеримы с длиной волны. В случае дифракции, мы получаем картинку, имеющую несколько максимумов, не растянутую ни в какой из областей спектра (нормальный дифракционный спектр).

Нормальный дифракционный спектр равномерный во всех областях и располагается в порядке возрастания длин волн.

Дисперсия это физическое явление, связанное с распространением волн разной длины с разной скоростью в данном веществе. Коэффициент, полученный в результате таких опытов, называют коэффициентом преломления среды.

Дисперсионный спектр сильно сжат в области волн имеющих большую длину, и сильно растянут в области волн имеющих меньшую длину волны. Дисперсионный спектр располагается в порядке убывания длин волн.

Видимая часть спектра называется оптическим диапазоном спектра.

Цвет и спектральные цвета

Что такое цвет? Физика дает следующий ответ на этот вопрос: Цвет, это качественная субъективная характеристика электромагнитного излучения оптического диапазона, определяемая на основании возникающего физиологического зрительного ощущения, и зависящая от ряда физических, физиологических и психологических факторов.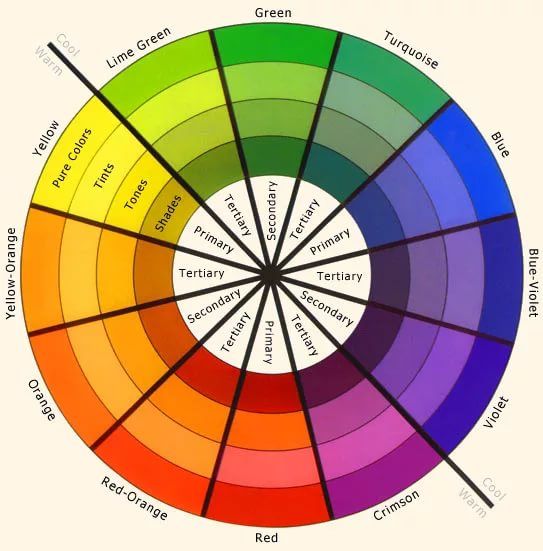 [1.1]

Индивидуальное восприятие цвета определяется его спектральным составом, а также цветовым и яркостным контрастом с окружающими источниками света и не светящимися объектами. [1.1]

В непрерывном световом спектре, в котором одни цвета плавно переходят в другие так, что определить точно границы каждого цвета и связь его с определенной длиной волны сложно принято различать следующие цвета в зависимости от длины волны [3.1]:

№ п/п	Название цвета		Длина волны (нм)
		От	До
1	Фиолетовый	380	440
2	Синий	440	480
3	Голубой	480	510
4	Зеленый	510	550
5	Желто-зеленый	550	575
6	Желтый	575	585
7	Оранжевый	585	620
8	Красный	620	780

Диапазон волн от 0 нм до 380 нм, принято считать невидимым и называть ультрафиолетовой областью оптического излучения.

Диапазон волн от 780 нм до 1 мм, принято считать невидимым и называть инфракрасной областью оптического излучения.

Непрерывный оптический спектр

На рисунке 1 приведен главный максимум дифракционного цветового спектра.

Органы зрения живых существ воспринимают свет, отраженный от физических объектов и предметов. Цвет предмета, воспринимаемый органами зрения будет соответствовать длинам волн, отражаемых данными объектами. На пример, листва нам кажется зеленой по тому, что зеленую составляющую спектра лист отражает, а все другие составляющие, наоборот, поглощает. Или другой пример: апельсин оранжевый, по тому, что именно оранжевая составляющая светового спектра отражается апельсином.

Чувствительность органов зрения живых существ не постоянна в зоне видимого светового спектра. Для человека, на пример, на основании данных [3.2] чувствительность органов зрения приведена на Рисунке 2.

Спектральная чувствительность палочкового зрения (рисунок 2, кривая 2 — глаз адаптирован к ночным яркостям) характеризует работу глаза при столь малом количестве света, что его не хватает даже для частичного возбуждения колбочек. Кривая относительной спектральной чувствительности глаза имеет максимум на длине волны в 507 нм.

Для глаза, адаптированного к дневным яркостям V(λ) (рисунок 2, кривая 1), на длинах волн 510 нм и 610 нм характерно двукратное снижение чувствительности. Если же глаз адаптирован к ночным яркостям V’(λ) (рисунок 2, кривая 2), то снижение чувствительности в два раза наблюдается на длинах волн 455 нм. и 550 нм.

Рисунок 2. Относительная спектральная чувствительность глаза человека

Максимумы на кривых 1 и 2 на рисунке 2, равные единице, относительны. Дело в том, что палочковый аппарат ночного зрения человека намного чувствительнее, и для восприятия предельно малого светового сигнала (например, едва видимой точки на темном фоне) палочкам необходима примерно в пятьсот раз меньшая мощность, чем колбочкам. При этом палочки, действующие при периферическом (боковом) зрении, не позволяют определить цвета точки, в то время как колбочки, фиксирующие точку при прямом зрении, дают возможность увидеть и ее цвет [3.3].

Кроме этого, чувствительность человеческого глаза неодинакова к разным цветовым компонентам света. Чувствительность максимальна при 555 нм (желто-зеленый свет) и сводится к минимуму при более длинных (красный свет) и коротких (синий свет) длинах волн. Чувствительность человеческого глаза к воздействию красного излучения (650 нм) составляет всего 10% от максимальной чувствительности. Иными словами, чтобы добиться ощущения той же яркости, что и у желто-зеленого света, интенсивность красного света должна быть в десять раз больше [4.1].

Если соединить видимые красный и синий диапазон спектра, то мы получим цветовой круг Рисунок 3. Цветовой круг это способ представления непрерывности цветовых переходов в видимой части спектра. Сектора круга окрашены в различные цветовые тона, размещенные в порядке расположения спектральных цветов, причем пурпурный цвет связывает крайние красный и фиолетовый цвета.

Рисунок 3. Цветовой круг и триады цветов, дающие при смешивании белый цвет.

Цветовой круг впервые был предложен Исааком Ньютоном в 1704 году. Цветовой круг имеет большое значение для понимания законов смешивания спектральных цветов. Так на пример, вершины треугольника, вписанного в цветовой круг, однозначно указывают на триады цветов, которые при смешивании дадут белый цвет.

Рисунок 4. Цветовое поле видимого спектра.

В общем случае, оттенки цветов получаемые при смешивании простых спектральных цветов представлены на Рисунке 4.

Не спектральные цвета и смешивание цвета

Для восприятия цвета очень важно такое явление, как метамерия, особенности глаза и психики. [1.2]. Метамерия, это свойство зрения, при котором свет различного спектрального состава может вызывать ощущение одинакового цвета. Иначе метамерией можно назвать восприятие двух окрашенных образцов одинаково окрашенными под одним источником освещения, но различно окрашенными под другим источником освещения. Это можно объяснить разными спектральными характеристиками источников освещения и разными наполняющими цветами в красочных покрытиях рассматриваемых образцов.

Физиологически метамерия зрения основана на строении периферического отдела зрительного анализатора биологического объекта. В соответствии с теорией происхождения видов, предки человека получили органы зрения от рыб. Эта гипотеза получила в настоящее время, как множество подтверждений, так и не меньшее число опровержений.

У человека, как и у карпа, роль периферического отдела зрительного анализатора выполняет сетчатка, в которой за восприятие цвета отвечают особые клетки, называемые колбочками.

В общем случае, можно создать такие условия, при которых пучок оранжевого спектрального цвета, пучок оранжевого не спектрального цвета (полученный смешением желтого и красного спектральных цветов) и пучок пурпурного не спектрального цвета (полученный смешением синего и красного спектральных цветов) могут восприниматься зрительным анализатором наблюдателя, как пучки одинакового цвета.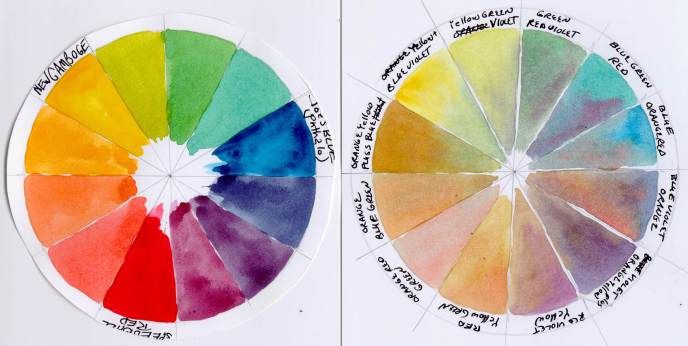

Однако если пропустить эти три пучка через дисперсионную призму, то мы получим:

Для оранжевого спектрального цвета: одну полоску, соответствующую длине волны первичного светового пучка.

Для оранжевого не спектрального цвета (полученного смешением желтого и красного спектральных цветов): две полоски, соответствующие длинам волн составляющих желтого и красного спектральных цветов первичного светового пучка.

Для пурпурного не спектрального цвета (полученного смешением синего и красного спектральных цветов): две полоски, соответствующие длинам волн составляющих синего и красного спектральных цветов первичного светового пучка.

В общем случае, результирующие цвета получаемые при смешивании цветов иллюстрирует Рисунок 5.

Рисунок 5. Результирующие цвета, получаемые при смешивании спектральных цветов

Данное наблюдение представляется мне важным при создании цвета красителя для окрашивания насадки.

Теории восприятия цвета

На сегодняшний день, существуют несколько теорий восприятия цвета. Пожалуй, самой распространенной из них является Трехкомпонентная теория, предложенная тремя авторами: М.В. Ломоносовым, Т. Юнгом и Г. Гельмгольцем. Согласно этой теории, в органе зрения человека существуют три цветоощущающих аппарата: красный, зеленый и синий. Каждый из них возбуждается в большей или меньшей степени, в зависимости от длины волны излучения. Затем возбуждения суммируются аналогично тому, как это происходит при суммируемом смешении цветов. Суммарное возбуждение ощущается человеком как тот или иной цвет. В своей работе «Цветовое зрение» авторы Л.Н. Миронова, И.Д. Григорьевич отмечают: «…Трехкомпонентная теория хорошо объясняет важнейшие закономерности цветового зрения: адаптацию, индукцию, цветовую слепоту, спектральную чувствительность глаза, зависимость цвета от яркости и другие, Однако, следует заметить, что в наше время известны факты, свидетельствующие о более сложной картине функционирования органа зрения. ..» [2.1].

Другой, очень распространенной и имеющей множество подтверждений, теорией является теория оппонентных цветов Э. Геринга. Геринг выдвинул предположение, что в колбочках сетчатки могут существовать три вида гипотетических веществ: бело-черные, красно-зеленые и желто-синие. Световой поток влечет их разрушение (одни световые лучи) с образованием белого, красного или желтого цветов или синтез (другие световые лучи) чорного, зеленого или синего цвета. Геринг предполагал, что имеются четыре основных цвета красный, желтый, зеленый и синий, и что они попарно связаны с помощью двух антагонистических механизмов зелено-красного механизма и желто-синего механизма. Постулировался также третий оппонентный механизм для ахроматически дополнительных цветов белого и черного. Из-за полярного характера восприятия этих цветов Геринг назвал эти цветовые пары «оппонентными цветами». Из его теории следует, что не может быть таких цветов, как зеленовато-красный и синевато-желтый. Таким образом, теория оппонентных цветов постулирует наличие антагонистических цветоспецифических нейронных механизмов. Например, если такой нейрон возбуждается под действием зеленого светового стимула, то красный стимул должен вызывать его торможение. Предложенные Герингом оппонентные механизмы получили частичное подтверждение после того, как научились регистрировать активность нервных клеток, непосредственно связанных с рецепторами. Так, у некоторых позвоночных, обладающих цветовым зрением, были обнаружены красно-зеленые и желто-синие горизонтальные клетки. У клеток красно-зеленого канала мембранный потенциал покоя изменяется и клетка гиперполяризуется, если на ее рецептивное поле падает свет спектра 400-600 нм, и деполяризуется при подаче стимула с длиной волны больше 600 нм. Клетки желто-синего канала гиперполяризуются при действии света с длиной волны меньше 530 нм и деполяризуются в интервале 530-620 нм.

Множество проводимых исследований подтвердили предположения этих двух теорий, так например колбочки у приматов существуют всего трех типов: воспринимающие цвет в фиолетово-синей, зелено-жёлтой, в желто-красной частях спектра. Каждый вид колбочек интегрирует поступающую лучистую энергию в довольно широком диапазоне длин волн, и диапазоны чувствительности трех видов колбочек перекрываются, различаясь лишь диаграммой величины чувствительности.

Человеческое зрение, таким образом, является трёхстимульным анализатором, то есть спектральные характеристики цвета выражаются всего в трех значениях. Если сравниваемые потоки излучения с разным спектральным составом производят на колбочки одинаковое действие, цвета воспринимаются как одинаковые.

В животном мире известны четырёх- и даже пятистимульные цветовые анализаторы, так что цвета, воспринимаемые человеком одинаковыми, животным могут казаться разными так, хищные птицы видят следы грызунов на тропинках к норам исключительно благодаря ультрафиолетовой люминисценции компонентов их мочи.

Характеристика органов зрения карпа

Как уже говорилось выше, в соответствии с теорией происхождения видов, предок человека унаследовал органы зрения от низших позвоночных, или от рыб, что вызывает большое сомнение у некоторых, уважаемых в научных кругах, авторов [5]:

«. ..Если принять как факт, что цветовое зрение мы унаследовали от низших позвоночных (рыб), что доказывается анатомическим, физиологическим, химическим и структурным сходством строения сетчатки, то эволюцию цветового зрения следует изучать не на приматах, а начиная с рыб. Тогда рассуждения об эволюции цветового зрения от протонопии до тритонопии (С.В.Кравков) нельзя признать обоснованной. Ведь уже у карпа имеются все три типа колбочек и даже детекторов оппонентного типа, хотя и находятся эти детекторные клетки еще в самой сетчатке, а не в латеральном коленчатом теле, как у приматов и человека (Пэдхем Ч., Сондерс Ж., 1978). Хотя карп обладает повышенной чувствительностью в красно-оранжевой, а не зелено-желтой области спектра, диапазоны частот реагирования рецепторов карпа и человека почти не различаются по ширине.

Таким образом, эволюция цветового анализатора шла параллельно с развитием анатомических и функциональных отделов центральной нервной системы (промежуточного, среднего мозга, коры), по „вертикали“, а не в сторону дифференциации цветочувствительных клеток периферического отдела анализатора (колбочек сетчатки), по горизонтали. Сохранение (даже небольшое расширение) диапазона чувствительности при усовершенствовании структуры цветового анализатора в ходе наземной эволюции высших позвоночных свидетельствует, что цвет играл существенную роль в их жизнедеятельности. Но только у той биологической линии, которая привела к возникновению человека. О центральном значении цветоразличения для человека свидетельствует хотя бы тот факт, что все 6,5 миллиона колбочек как у карпа, так и у человека, располагаются в фовеа-центральной зрительной ямке, области максимально четкого зрения …».

Далее автор делает вывод [5]: «…Итак, мы видели, что для видов, значительно уступающих человеку в психическом развитии (растения, насекомые, рыбы, пресмыкающиеся, птицы), цвет не отделим от функций размножения, питания и выживания, т.е. от всего биологического цикла …».

Из сказанного становится ясным, что максимум цветового восприятия карпа обыкновенного лежит в красно-оранжевой области светового спектра, что находит свое подтверждение в большом количестве работ других авторов.

Автор считает, что диапазон чувствительности в области видимого спектра карпа обыкновенного и человека почти не различается по ширине, что противоречит данным некоторых других источников.

Автор подчеркивает подобность строения органов зрения карпа и человека не только качественно: «…колбочки как у карпа, так и у человека располагаются в фовеа-центральной зрительной ямке» но и количественно: «все 6,5 миллиона колбочек как у карпа, так и у человека…».

Кроме этого, автор считает функцию распознания цвета, в частности карпом, не отделимой от функций размножения, питания и выживания, то есть от всего биологического цикла. Это пожалуй самый ценный для нас вывод, для нас — рыбаков, осуществляющих ловлю этой умной рыбы, маскируя насадку под привлекающую ее, рыбу, пищу.

Справедливости ради, нужно отметить, что в результате биофизических исследований органов зрения рыб, пресноводных, пресмыкающихся, приматов, человека, были получены другие, очень интересные факты, способные поставить под сомнение приведенные выше заключения.

Так на пример, в своей статье «О зрении животных», опубликованной в электронном журнале «LiveJournal» некий Евгений [6], приводит интересные факты, касающиеся возможностей органов зрения различных животных, птиц, рыб, ссылаясь на результаты научных исследований, опубликованные в научных изданиях. Так на пример, относительно золотых рыбок, относящихся к карповидным, Евгений пишет: «… 14. Золотые рыбки — тетрахроматы и видят длины волн от 300 нм (и даже ниже) до примерно 730 нм — то есть весь человеческий диапазон, плюс хороший кусок ультрафиолета, плюс пограничную с инфракрасным область… ». Ссылаясь на статью известных биологов Shozo Yohoyama, Huan Zhang, Z. Bernhard Radlwimmer, Nathan S. Blow «Adaptive Evolution of Color Vision of the Commoran Coclacanth (Latimeria Chalumnae)» [6.1], опубликованную в 26 марта 1999 года в Ню-Йорке, и перепечатанную журналом «Evolution» в мае 1999 года, Евгений пишет: «…15. Латимерия (целакант) — древняя, долгое время считавшаяся вымершей рыба, обитающая на глубине около 200 м. Света там почти нет, а те его остатки, что все-таки туда просачиваются — исключительно синие. Тем не менее, она тоже обладает цветным зрением, с нашей точки зрения весьма уникальным. Латимерия — дихромат, но все богатство воспринимаемой ею гаммы укладывается, по нашим меркам, в почти неотличимые оттенки синего в узеньком диапазоне длин волн возле 480 нм. Максимумы цветового восприятия её рецепторов отстоят друг от друга всего на 7 нанометров: 478 и 485 нм. …». Относительно карпа обыкновенного, ссылаясь на статью [6.2] «The eyes of the common carp and Nile tilapia are sensitive to near-infrared» японских авторов Taro MATSUMOTO and Gunzo KAWAMURA, Евгений пишет: «…16. Обыкновенный карп может видеть в ближнем инфракрасном диапазоне (865 нм) — там же, где работают пульты управления телевизором и где рассеяние света в воде и воздухе существенно ниже».

Учитывая эти данные, мы можем усомниться в утверждении о равенстве ширины светового спектра воспринимаемого органами зрения карпа и человека.

Интересным представляется мнение А.М. Черноризова, высказанное им в его докторской диссертации на тему «Нейронные механизмы цветового зрения».

Проведя опыты на речном карпе, Carpio Cyprims L.; на 13 карпах in vivo (живых карпах) и более чем 200 карпах in vitro, и проанализировав другие, известные ему работы, автор пришел к заключению [7.1]: «…Исследование и моделирование процессов передачи информации о цвете в нейронных сетях зрительной системы является одной из главных задач психофизиологии цветовосприятия в рамках современной психофизиологии как науки о нейронных механизмах психических процессов и состояний. Адекватной экспериментальной моделью для этого является сетчатка глаза, которая по сложности строения и возможностям интегральной обработки параметров зрительных образов напоминает мозг (Jasper, Raynauld, 1975; Хьюбел, 1990). На уровне нервных элементов сетчатки осуществляется переход от кодирования цвета цо принципам трехкомпонентной теории Ломоносова-Юнга-Гельмгольца (слой фоторецепторов) к кодированию цвета по принципам теории оппонентных цветов Геринга (слой горизонтальных и биполярных клеток). В сетчатке происходит формирование цветооппонентных („красно-зеленых“, RG-типа; „сине-желтых“, YB-типа) и ахроматических (нецветооппонентных „яркостных“, В-типа, и „темновых“, D-типа) нейронных систем, которые, по нашим данным, обладают разной функцией в процессе цветокодирования. …».

Далее автор отмечает [7.1]: «…В поведенческих опытах Wolf (1925) показано, что рыбы из одного с карпом семейства Cyprinidae могут различать до 20 различных цветов в диапазоне от 340 до 760 нм. При этом рыбы отличают пурпурный цвет (смесь синего и красного спектральных излучений) от любого другого цвета. Hamburger (1926) выявил существование дополнительных цветов для рыб {Phoxinus laevisAG, семейство Cyprinidae), а также способность отличать белый цвет от какого-либо спектрального цвета. Таким образом, всю гамму цветов для рыб, как и для человека, можно представить в виде замкнутой круговой диаграммы (круга Ньютона) (Herter, 1953). Herter (1953) констатировал явления одновременного и последовательного яркостного и цветового контрастов для цветового зрения рыб. Horio (1938) в опытах на карпах показал, что при различении зрительных стимулов рыбы чаще ориентируются на цвет, чем на форму. Способность рыб, в частности, карпа, правильно оценивать цвет предметов независимо от условий освещения (константность восприятия цвета) продемонстрирована в поведенческих и Электрофизиологических исследованиях (Oyama, Jitsumori, 1974; Диментман и др., 1975; Максимова и др., 1975; Crawford et.al., 1990). Наконец, цветовое зрение рыб, как и у человека, трихроматично. На это указывают данные микроспектрофотометрических, нейрофизиологических и поведенческих экспериментов (для обзора см.: Измайлов и др., 1989).

Имеются данные о наличии в сетчатке костистых рыб фоторецепторов с пиком чувствительности в ультрафиолетовой области спектра (Neumeyer, Arnold, 1989). Не ясна роль этих рецепторов в цветовом зрении рыб ввиду того, что оптическая система камерного глаза этих животных не пропускает ультрафиолетовые лучи. Однако, имеются данные о влиянии активности рецепторов этого типа в различение цветов в синей области спектра (400-480 нм) (Neumeyer, Arnold, 1989).

У рыб и амфибий хорошо развита система ретино-тектальных зрительных проекций, что обусловливает сложный характер обработки цветового сигнала уже на уровне нейрональных структур сетчатки. В этой ситуации сетчатка этих животных может служить моделью для изучения принципов цветокодирования, реализуемых у приматов центральными отделами зрительного анализатора. …»

Подводя итог проведенным исследованиям, автор замечает [7.1]: «…Достоверность результатов достигалась большим объемом выборки и использованием современных статистических методов многомерного анализа (метрическое многомерное шкалирование). Представленные в работе данные получены в более чем 500 опытах на 26 моллюсках, 40 лягушках, 13 карпах in vivo и более чем 200 карпах in vitro. На изолированной сетчатке карпа внутриклеточно исследованы спектральные реакции 538 горизонтальных клеток и 45 биполярных клеток. …».

Анализируя приведенные выше исследования, с высокой степенью достоверности, можем предположить следующее:

Сетчатки глаза карпа и человека очень похожи по функционированию и строению, и «.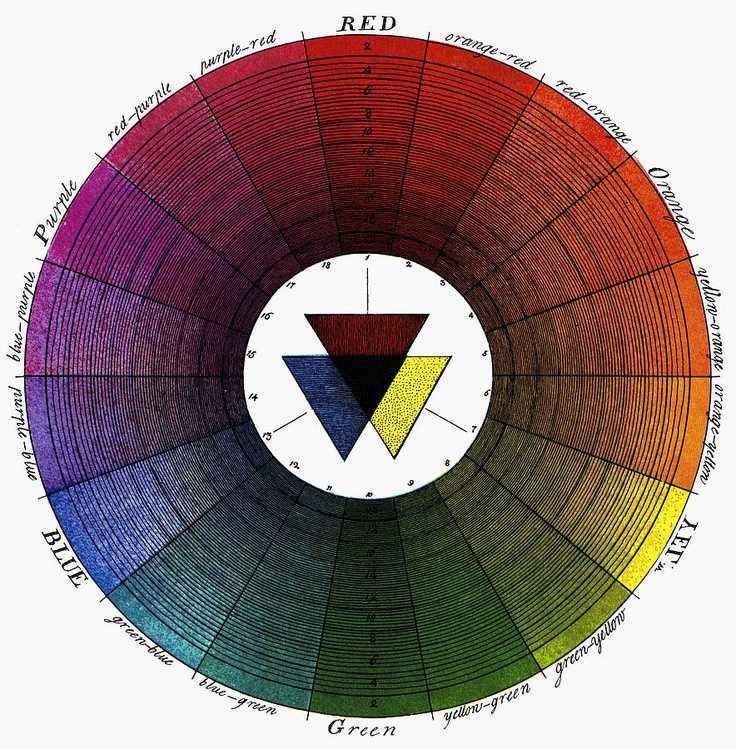 ..по сложности строения и возможностям интегральной обработки параметров зрительных образов напоминают мозг…».

Имеются данные о наличии у рыб рецепторов, помогающих им различать цвета в области синего цвета, а также в значительном диапазоне инфракрасной зоны спектра.

Особое внимание нужно обратить на то, что максимальная активность нейронов мозга карпа зарегистрирована при раздражении его фоторецепторов пурпурным цветом, который является не спектральным цветом, а результатом суммирующего действия двух спектральных цветов: синего и красного.

Выводы

1. Сетчатки глаза карпа и человека очень похожи по функционированию и строению, а по сложности строения и возможностям интегральной обработки параметров зрительных образов напоминают мозг.

2. Диапазон чувствительности в области видимого спектра органов зрения карпа и человека значительно различается по ширине, что дает карпу возможность видеть объекты в синей части спектра и в невидимой области инфракрасного цвета, предположительно до длин волн около 865 нм. Это, в свою очередь, объясняет то, как карп может найти пищу в условиях практически полной темноты, например, ночью.

3. Максимум цветового восприятия карпа лежит в красно-оранжевой области светового спектра.

4. Максимальная активность нейронов мозга карпа зарегистрирована при раздражении его фоторецепторов пурпурным цветом, который является не спектральным цветом, а результатом суммирующего действия двух спектральных цветов: синего и красного.

5. Карп способен отличать белый спектральный цвет от какого-либо другого цвета.

6. Во время распознавания объекта, карп более склонен ориентироваться на цвет объекта, чем на его форму.

7. Функцию распознания цвета у карпа не отделима от функций размножения, питания и выживания, то есть от всего биологического цикла.

Заключение

Сделанные мною и приведенные выше, выводы, не претендуют на научную ценность и вполне могут быть ошибочными. Но в своих экспериментах с окрашиванием насадок я придерживаюсь следующих, изложенных мною ниже правил.

Мои насадки имеют преимущественно оранжевый спектральный цвет, оранжевый не спектральный цвет, пурпурный не спектральный цвет и белый не спектральный цвет. Они обязательно яркие и отчетливо выделяются на фоне окружающих предметов.

Насадки дают обильное, легко различимое облако мути имеющее тот же цвет, что и насадка.

В свои насадки я пытаюсь включать энзимы, способные поднять температуру поверхности насадки, по сравнению с температурой окружающей среды, хотя бы на один градус. Это позволяет выделить насадку на фоне окружающих ее объектов (заставляет насадку светиться изнутри) и делает ее более привлекательной и легко распознаваемой рецепторами инфракрасного зрения зрительного аппарата рыбы.

Литература:

1. Википедия. Свободная энциклопедия.

1.1. Цвет: http://ru. wikipedia.org/wiki/%D0%A6%D0%B2%D0%B5%D1%82

1.2. Метамерия: http://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D0%B0 %D0%BC%D0%B5%D1%80%D0%B8%D1%8F_(%D1%86%D0%B2%D0%B5%D1%82)

2. Л.Н. Миронова, И.Д. Григорьевич, «Цветовое зрение», 2004 — 2008 годы.

2.1. Трех компонентная теория восприятия цвета. http://www.mironovacolor.org/theory/color_vision/

3. А. Прядко «Система световых величин» http://rus.625-net.ru/625/2004/03/light.htm

3.1. Цвет и длина волны.

3.2. Чувствительность органов зрения человека.

3.3. Максимумы ночного и дневного зрения.

4. «Освещение теплиц. Освещение и люди.» http://www.lighting.philips.com/ru_ru/trends/light/lightandhumans.php?main=ru_ru&parent=ru_r…

5. П.В. Яньшин, «Семантика цветового образа. К вопросу о „биологической целесообразности“ цветового зрения», Провинциальная ментальность России в прошлом, настоящем и будущем. Материалы III международной конференции по исторической психологии российского сознания. Ежегодник Российского психологического общества. Т. 3, вып. 2. Самара, СамГПУ, 1999. С. 200-217.

5.1. Взято по адресу: http://colormind.narod.ru/_private/YanshinOnColorSemantics.htm

6. Евгений, «О зрении животных», «LiveJournal» http://eugenebo.livejournal.com/45235.html

6.1. http://www.life.illinois.edu/ib/426/handouts/Yokoyama%20celacanth%20PNAS99.pdf

7. Черноризов Александр Михайлович. Нейронные механизмы цветового зрения : Дис. … д-ра психол. наук : 19.00.02 : Москва, 1999 227 c. РГБ ОД, 71:99-19/41-8

7.1. http://www.lib.ua-ru.net/diss/cont/124401.html

Автор: Саваченко Григорий

Статья с сайта http://www.sportfishing.ua

Лекция 3. Физика и биология цвета. Цветовой круг/Французский институт моды/Стиль/RENDEZ-VOUS DAILY

Фиалки – бесцветные, ваша помада оттенка bordo – бесцветная и даже любимое желтое платье не имеет цвета. Мир вообще бесцветен и был бы таким в наших глазах, если бы не свет.

Свет – это излучение, которое испускает нагретое тело или вещество в возбужденном состоянии, а цвет – характеристика этого света. Предметы сами по себе бесцветны, а мы видим цвет, когда их поверхность отражает электромагнитные волны видимого диапазона, то есть свет. То, как человек воспринимает цвет, зависит от степени освещенности предмета, источника света, а также физиологических особенностей и психологического состояния каждого из нас в конкретный момент.

Физика цвета

Главный цветоприниматель человеческого организма – сетчатка глаза. Чтобы глаз увидел какой-либо предмет и его цвет, свет сначала должен упасть на этот предмет, отразиться от него, а затем попасть на сетчатку. Люди видят предметы, потому что они отражают свет, и различают цвета этих предметов в зависимости от характеристик их поверхности: какие лучи она поглощает, а какие отражает, отдавая сетчатке на анализ. Свет, поглощенный предметом, глаз увидеть не может.

Черная кожа, например, поглощает почти все излучение и кажется нам черной, потому что не отражает никакие волны. Снег, наоборот, равномерно отражает почти весь свет и поэтому выглядит для нас белым. Человек видит предмет в том цвете, лучи которого отражаются от поверхности и попадают на сетчатку. В случае с красной помадой на сетчатку попадут только лучи красного спектра, а остальные поглотятся, создав в сознании человека представление о красном цвете.

Человеческий глаз воспринимает электромагнитное излучение в узком диапазоне длин волн, от 380 до 740 нанометров. Этот видимый свет излучает фотосфера – тонкая оболочка Солнца, меньше 300 километров в толщину. В бесцветном для нашего глаза солнечном свете заключен весь видимый спектр волн, который при разложении дает цвета радуги: от красного до фиолетового. На уроках физики разложение света на спектр демонстрируют с помощью призмы, в жизни это можно увидеть на примере радуги, где функцию преломителя играют капли воды в воздухе.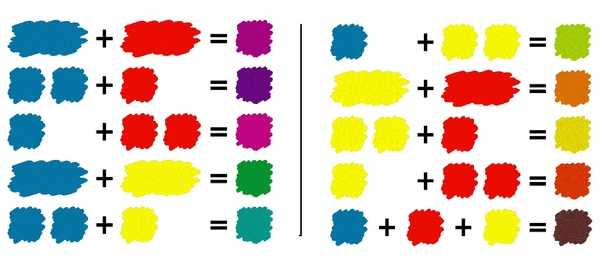


Как мы различаем цвета

Сетчатка образована светочувствительными клетками двух типов – палочками и колбочками, которые называются так из-за своей формы. Колбочки дают нам возможность видеть мир в красках, так как они чувствительны к световым волнам различной длины в видимом спектре. Колбочки бывают трех типов: первые различают волны красно-оранжевого участка спектра, вторые – зеленого, третьи – сине-фиолетовые. Палочки более чувствительны к свету, поэтому вступают «в бой» в сумерках и темноте. Палочки не способны определить цвет предмета, но благодаря им мы не спотыкаемся в темной комнате.

Запомнить назначение колбочек и палочек легко с помощью ассоциации: колбочки – как химические емкости, в которых происходят реакции и получаются яркие вещества, а палочки – буквально палки-трости, которые мы использовали бы, окажись мы в полной темноте. 

Цветовой круг

Цветовой круг – это способ представить весь видимый спектр света в условной форме круга. Секторы круга представляют цвета, размещенные в том порядке, который условно передает расположение их волн в спектре видимого света. Для связывания круга в его палитру добавлен пурпурный цвет (маджента), который соединяет крайние спектральные цвета (красный и синий) и получается из их условного смешения. 

​

Свойствами цветового круга пользуются художники, физики, дизайнеры, инженеры, стилисты. Мы с помощью цветового круга можем разграничивать холодные и теплые цвета, дополняющие цвета, оттенки и аналогичные цвета. Эти понятие станут инструментом для дальнейшей работы с образом. Вкус, который многие считают врожденным, можно развивать, и правила сочетаемости цветов – отличное для этого начало.

→ Хроматический круг: теплые и холодные тона

Теплые и холодные тона расположены в разных частях цветового круга. К теплым относятся желтый, оранжевый и красный, к холодным – зеленые, синие и фиолетовые. Вопрос о каждом пограничном цвете (например, между желтым и зеленым) стоит рассматривать в каждом случае отдельно. Смешанный желто-зеленый цвет может относиться как к теплой, так и к холодной части круга. У стилистов также есть представление о том, что теплыми и холодными версиями обладают все цвета, кроме оранжевого (он всегда теплый). Даже голубой и зеленый могут быть теплыми, но это представление основано на психологическом восприятии цвета и ассоциациях, а не на объективных характеристиках цветового круга.

→ Хроматический круг: дополняющие цвета

Дополняющие цвета – это пара тонов, расположенных в круге напротив друг друга. Получить пару цветов можно, проведя прямую линию через центр круга. Получаем желтый + фиолетовый, синий + оранжевый, зеленый + красный. 

→ Хроматический круг: аналогичные цвета

Аналогичные цвета расположены по соседству в одном цветовом семействе: желтый-оранжевый-красный, синий-голубой, зеленый-салатовый и так далее. Часто мы называем такие цвета оттенками, но это не совсем верное определение.

​

→ Хроматический круг: оттенки

Оттенки (фр. camaieu) – это варианты одного цвета, которые получаются путем добавления в него белой или черной краски. Увидеть визуальное представление оттенков можно на усовершенствованном круге с градацией цветов к белом в центре и черному – по краям. Таким представлением цвета пользуются дизайнеры, работая в Photoshop и аналогичных программах. Оттенки одного цвета – это градиентная шкала от бело-желтого до черного с желтым подтоном, от бело-голубого до иссиня-черного, где началом и концом шкалы являются белый и черный цвета.

Этих четырех свойств хроматического круга достаточно, чтобы создавать двух, трех и четырехцветные образы, не ошибаясь в оттенках. Благодаря правилам круга даже непривычные для вашего взгляда сочетания будут выглядеть гармонично.

В следующей лекции IFM мы расскажем о том, как выстраивать образ с использованием цветового круга и рассмотрим классические сочетания и современные цветовые тренды. Добавив к знаниям о цвете представление о стилях, а также информацию о типах фигур, линиях кроя и гармонизации силуэта, вы сможете самостоятельно создавать идеальные образы. Лекции IFM плюс немного практики – и никто не сможет оспорить наличие у вас вкуса. Ежедневно исследуя возможности своего гардероба, со временем вы обретете собственный стиль, самое ценное и неподвластное моде понятие. Следите за новостями Rendez-Vous Daily по хештегу #IFM4rendezvous, чтобы не пропустить полезные лекции.

• IFM4rendezvous
• мирrendezvous
• цвет
• франция
• париж

18 полезных ресурсов для работы с цветом

• Дизайн
• 3 мин на чтение
• 3158

Если вы дизайнер, то наверняка у вас возникает потребность в том, чтобы подобрать гармоничные цвета для того или иного проекта.

По теме цвета существует масса книг и курсов, но задача остается задачей, тем более когда проект горит и нужно срочно все сдать.

Так вот, специально для этих целей существуют онлайн сервисы, которые помогут вам в подборе цветов.

Сайт дает много полезной информации по любому цвету: разложение на базовые цвета, коды в разных системах кодировки, базовые цветовые схемы, альтернативные цвета, примеры текста с этим цветом, оттенки, тона и даже то, как видят этот цвет люди с расстройствами зрения.

Дизайнер Эрика Шунмейкер поделилась дизайнерским лайфхаком. Чтобы добиться связности и гармоничности любой цветовой схемы, она предлагает наложить поверх схемы цвет (оранжевый, например), и подобрать его прозрачность.

Ресурс HTML Color Codes предоставляет вам весь набор инструментов для работы с цветами в Web: переводы из одного цветового представления в другое, color picker, color chart и даже много туториалов про цвета. Очень круто.

Роскошный онлайн-инструмент для работы с цветом! Палитры, цвета, паттерны, все настраивается, выкладывается, делится и вычисляется из заданной картинки! Удобнее colorlovers в некоторых аспектах, более гибкий, чем kuler! Восторг, господа!)

Социальная сеть, куда можно прийти за вдохновением при выборе цвета, а также чтобы узнать о нынешних цветовых трендах как для личных, так и для профессиональных проектов. Общество талантливых и полных энтузиазма разработчиков COLOURlovers создает цвета, палитры и шаблоны, используя инструменты доступные онлайн.

24 сочных градиента от дизайнера Luke Davies.

Полезнейший Web-инструмент проще которого сложно что-либо придумать. Данный ресурс позволяет подбирать цветовые гармоники просто водя мышкой по экрану. Если Вас удовлетворил цвет, просто нажмите левую кнопку мышки, экран разделится на двое и вы сможете продолжить подбор второго цвета. третьего и так далее.

Отличный ресурс, который анализирует цветопалитру любого сайта и выдает вам ее с головой, цветовым кругом и гистограммой. Не первой пикче — главная страница, на второй — анализ моего бложика (да, мелочью он тоже не брезгует:)

Это один из инструментов, который всегда должен быть под рукой у дизайнера, а на Color by Hailpixel определенно стоит обратить внимание. Открывшийся сайт покажет вам пустой экран с единственной ссылкой на черный цвет (#000000). Перемещая курсор по экрану, вы будете видеть, как изменяется цвет фона, а окошко в центре будет показывать соответствующий hex-код этого цвета. Клик мышью создаст полоску текущего цвета с цифровым значением этого цвета.

Используя приложение, вы можете быстро увидеть многоаспектный характер цветов и отношения между цветами. Цвета палитрый представлены в 3d виде. Созданные палитры могут быть импортированы или экспортированы в Adobe Swatch Exchange (ASE). В ColoRotate есть свое сообщество, где можно просмотреть темы, созданные другими пользователями.

Kuler это веб-приложение, которое позволяет создавать и просматривать ваши цветовые палитры, а также палитры созданные другими пользователями.

Этот сервис пригодится особенно веб-дизайнерам. Он позволяет подобрать цветовую модель для будущего сайта.

COLOURlovers предусматривает нечто большее, чем просто способ найти цветовые палитры. Это также место для взаимодействия с другими людьми для обсуждения тем, связанных с цветом. Там же можно прочитать интересные статьи о цвете.

Тут можно создавать свои цветовые схемы. Можно также загрузить фото и разложить его на цветовые пиксели, чтобы взять образцы цветов. А после сохранить и загрузить себе в удобном формате.

Абсолютно бесплатно и, что наиболее важно – онлайн, позволяет создавать и сохранять гармоничные цветовые сочетания, как автоматически, так и вручную. Пользуясь тремя ползунками RGB или HSV вы автоматически получаете гармоничное сочетание из шести цветов и затем можете настраивать их в соответствии со своим вкусом. Цвета автоматически представляются в виде цветового HTML кода и кода RGB, а также могут быть экспортированы в виде цветовых таблиц Photoshop (.ACT) и Illustrator (.EPS). Кроме того, есть функция сравнения цвета со стандартным понтонным. Свои палитры можно хранить прямо на сайте, задавая им удобные вам имена. Также на сайте можно найти массу готовых палитр на разные случаи жизни.

ColorMunki дает возможность поиска цвета из встроенного в библиотеках, а так же с помощью ключевых слов.

Полезный сервис, который помогает подобрать правильные цвета и оттенки. Интерфейс интуитивно понятен, сложностей возникнуть не должно.

Простой, приятный интерфейс. Существуют встроеные библиотеки цветов и есть возможность создавать свои. Хорошо организован набор функций.

Фото на обложке: ShutterStock

• #веб
• #дизайн
• #онлайн
• #сервис
• #цвет
• 0

8.16. Разложить

8.

16. Разложить

8.16.1. Обзор

Рисунок 15.153. Разложение на изображения (RGB)

Исходное изображение

Применена команда «Разложить» (разложение RGB) с Разложить на слои без флажка.




Рисунок 15.154. Разложение по слоям (RGB)

Исходное изображение

Применена команда «Разложить» (разложение RGB) с Разложить по слоям отмечено.




Эта команда разделяет каналы (RGB, HSV, CMYK…) изображения. на отдельные изображения или слои.

8.16.2. Активируйте команду

8.16.3. Опции

Рисунок 15.155. Опции команды «Разложить»




Извлечение каналов

Следующие параметры описаны с помощью Разложить на слои проверены.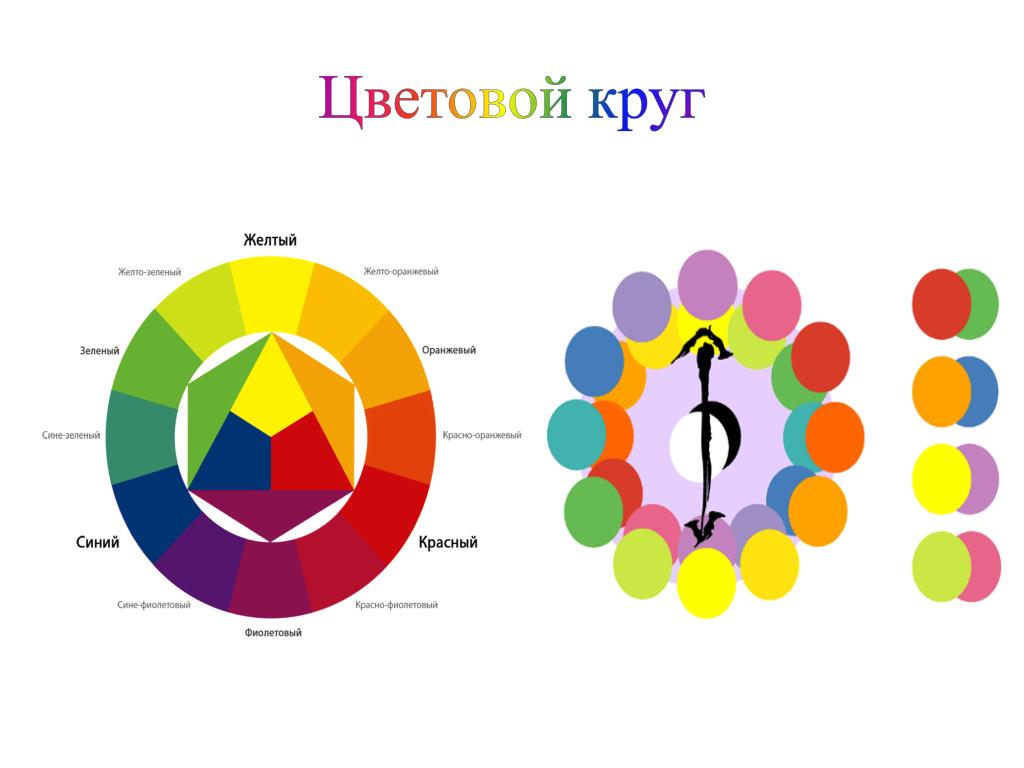

Цветовая модель

RGB

Если щелкнуть радиокнопку RGB, отображается изображение с уровнем серого. создан с тремя слоями (красный, зеленый и синий) и двумя каналы (серый и альфа).

Эта функция интересна при использовании инструмента Threshold. Ты также может выполнять такие операции, как вырезание, вставка или перемещение выделения в одном канале RBG. Вы можете использовать извлеченные оттенки серого как выделение или маска, сохранив их в канал (щелкните правой кнопкой мыши>Выбрать>Сохранить в канал).

RGBA

Если щелкнуть радиокнопку RGBA, изображение будет создано аналогично при разложении RGB с дополнительной альфой слой, заполненный значениями прозрачности источника изображение. Полностью прозрачные пиксели черные, а полный непрозрачные пиксели белые.

ВПГ

Этот параметр разбивает изображение на три слоя в оттенках серого, один для оттенка, один для насыщенности и еще один для значения.

Хотя оттенок имеет оттенки серого, он представляют оттенки. В цветовом круге белый и черный точки отправления и прибытия и накладываются друг на друга. Они представляют красный цвет в верхней части круга. Серый промежуточный уровни соответствуют промежуточным оттенкам на окружности: от темно-серого до оранжевого, от средне-серого до зеленого и от светло-серого до пурпурный.

Насыщенность и Значение: белый — максимальная насыщенность. (чистый цвет) и максимальное значение (очень яркий). Черный минимальная насыщенность (белый) и минимальное значение (черный).

ВСЛ

Этот вариант похож на HSV. Вместо из V алюминий, третий слой содержит компонент изображения L .

CMY

Этот параметр разбивает изображение на три слоя в оттенках серого, один для желтого, один для пурпурного и еще один для голубого.

Эта опция может быть полезна для передачи изображения на печать. программное обеспечение с возможностями CMY.

CMYK

Эта опция аналогична CMY Decomposing с дополнительным слоем для черного.

Эта опция может быть полезна для передачи изображения на печать. программное обеспечение с возможностями CMYK.

Альфа

Эта опция извлекает прозрачность изображения, хранящуюся в Альфа-канал в Диалог канала на отдельном изображении. Полностью прозрачные пиксели черные полностью непрозрачные пиксели белые. Серые тона гладкие переходы прозрачности в исходном изображении.

ЛАБОРАТОРИЯ

Этот параметр разбивает изображение на три слоя в оттенках серого, слой «L» для яркости, слой «A» для цветов между зеленым и красным, слой «B» для цветов между синим и желтым.

LAB Decomposing представляет собой цветовую модель Luminance-Color. семья. Канал используется для Luminosity, в то время как два других каналы используются для цветов. Цветовая модель LAB используется Photoshop.

YCbCr

В GIMP есть четыре YCbCr разложения с разными значениями. Каждая опция разбивает изображение на три слоя в оттенках серого, слой для Luminance и два других для голубизны и красноты.

Цветовая модель YCbCr, также называемая YUV, теперь используется для цифровое видео (первоначально для аналогового видео PAL). Он основан на идее, что человеческий глаз наиболее чувствителен к яркость, рядом с цветами. Разложение YCbCr использует матрица преобразования и различные варианты различные значения, рекомендованные ITU (International Телекоммуникационный союз) применяется к матрице .

Разложить на слои

Если этот параметр отмечен, создается новое изображение в оттенках серого, где каждый слой представляет один из каналов выбранного режим. Если этот параметр не отмечен, каждый канал представлен с определенным изображением, автоматически и четко названным в названии бар.

Передний план в качестве регистрационного цвета

Этот вариант для специалистов. Это связано с печатью CMYK. Когда этот флажок установлен, каждый пиксель текущего цвета переднего плана будет быть черным в каждом компоненте разложенных изображений/слоев. Этот позволяет сделать метки обрезки видимыми на всех каналах, обеспечивая полезная ссылка для выравнивания. Тонкий крест, напечатанный в Регистрационный черный цвет также можно использовать для проверки правильности печати. тарелки выстраиваются в ряд.

Обработка цветных изображений

Типы цветных изображений

Цветные изображения бывают трех различных форм: псевдоцвет, 24-битное изображение RGB или цветное составное изображение.

Псевдоцвет

Псевдоцветное изображение имеет одноканальное (т. е. серое) изображение, которому приписывается цвет с помощью «Поисковой таблицы» или LUT (также известной как палитра, таблица цветов). Это таблица значений серого (от нуля до 256 или 4095, будь то 8-битный или 12-битный серый) с соответствующими значениями красного, зеленого и синего. Вместо отображения серого цвета изображение отображает пиксель с определенным количеством каждого цвета. Различия в цвете на псевдоцветном изображении отражают различия в интенсивности объекта, а не различия в цвете образца, который был изображен. О функциях псевдоцвета см. далее.

24-битные изображения RGB

Цвета изображений RGB (24-битные с 8-битными для каждого из красного, зеленого и синего каналов) используются для отображения многоканальных изображений. Цвета предназначены для отражения подлинных цветов (т. е. зеленый цвет в изображении RGB отражает зеленый цвет в образце). На Фиджи есть несколько функций RGB.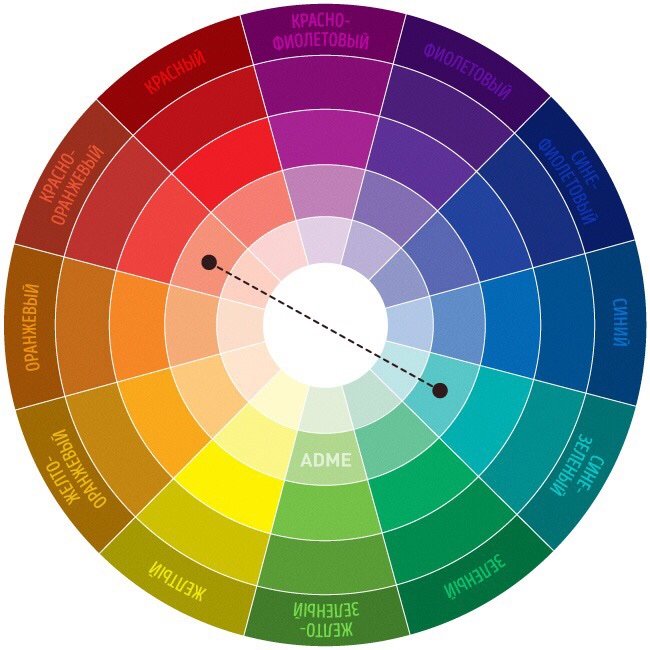 Нативные функции можно найти в Image › Color.

Цветные составные изображения

Цветные составные изображения аналогичны цветным изображениям, которые можно найти в программе обработки изображений Photoshop. В Photoshop эти изображения состоят из «слоев», а в Фиджи — из «каналов». И «слои», и «каналы» — это одна и та же идея. Преимущества использования этого типа изображения вместо изображений RGB включают в себя:

1. Каждый канал хранится отдельно от других и может быть включен или выключен с помощью «Инструмента каналов» (Изображение › Цвет › Инструмент каналов). У вас есть возможность просматривать изображение как совокупность всех или некоторых различных каналов, как отдельные каналы или как отдельные каналы в оттенках серого. В нижней части окна есть кнопка с надписью «Дополнительно», которая позволяет создавать композицию, преобразовывать изображение в RGB, объединять или разделять каналы, редактировать LUT изображения или выбирать новые цвета каналов из списка.
2. Каждый исходный канал можно оставить 16-битным.
3. Можно объединить более 3 каналов и оставить их отдельными. Каждый канал можно выбрать с помощью полосы прокрутки в нижней части окна.
4. Контрастность и яркость отдельных каналов можно регулировать после объединения.

Цветные составные изображения можно преобразовать в 24-битный формат RGB с помощью диалогового окна «Инструмент каналов».

Недостатком типа изображения Composite является то, что эта относительно недавняя разработка Фиджи не поддерживается всеми существующими плагинами. Иногда композит может вернуться к многослойному стеку. Чтобы преобразовать его обратно в композит, вы можете использовать команду меню Изображение › Цвет › Сделать композит.

Слияние многоканальных изображений

Многоканальные эксперименты с чередованием

Многоканальные эксперименты, полученные в некоторых системах, импортируются с чередованием различных каналов, т. е. срез 1 представляет собой точку времени1-канал1, а срез 2 представляет собой точку времени1-канал2. Стек должен быть «де-чередован», прежде чем его можно будет объединить в RGB. Это можно сделать с помощью Image › Stacks › Tools › Deinterleave и ввода количества каналов в диалоговом окне (обычно «2»). Вы также можете установить флажок, чтобы сохранить исходные стеки. Затем два стека можно объединить с помощью: Изображение › Цвет › Объединение RGB.

Объединение цветов RGB

Собственная функция Fiji Изображение › Цвет › Объединить каналы… может использоваться для объединения изображений красного, зеленого и/или синего канала или стеков изображений

Это уменьшает 16-битные изображения до 8-битных ( на основе текущих значений яркости и контрастности), затем генерирует 24-битное изображение RGB.

Альтернативой обычному объединению красного и зеленого является объединение изображений на основе голубого и пурпурного, голубого и желтого или любой другой комбинации цветов.

Это может помочь визуализировать колокализацию из-за нашего плохого восприятия красного и зеленого цветов. Плагин Colour_merge дает пользователю возможность использовать «разностную» арифметическую обработку для выбранных вами стеков изображений. Это не совсем слияние (при слиянии голубого и пурпурного они дают белый, а не желтый цвет), но облегчает визуализацию отдельных каналов (см. Demandolx and Davoust, J. Microscopy, 19).97 в185. стр. 21 ¹ ). Вы можете выполнить настоящее слияние, если отключите опцию «Разница».

Запустите плагин и выберите два изображения, которые нужно объединить. Выберите нужные цвета из раскрывающегося списка. использует LUT, который в данный момент имеет изображение (часто это желаемая LUT). Опция «Разность» выполняет арифметическую операцию «разность», а не «сложение». Если отмечена опция «Pre-sub 2 from 1», второе изображение вычитается из первого перед слиянием.

Объединение изображений в проходящем свете и флуоресценции

Флуоресцентные изображения и изображения в светлом поле в проходящем свете можно объединить с помощью команды Изображение › Цвет › Объединить каналы….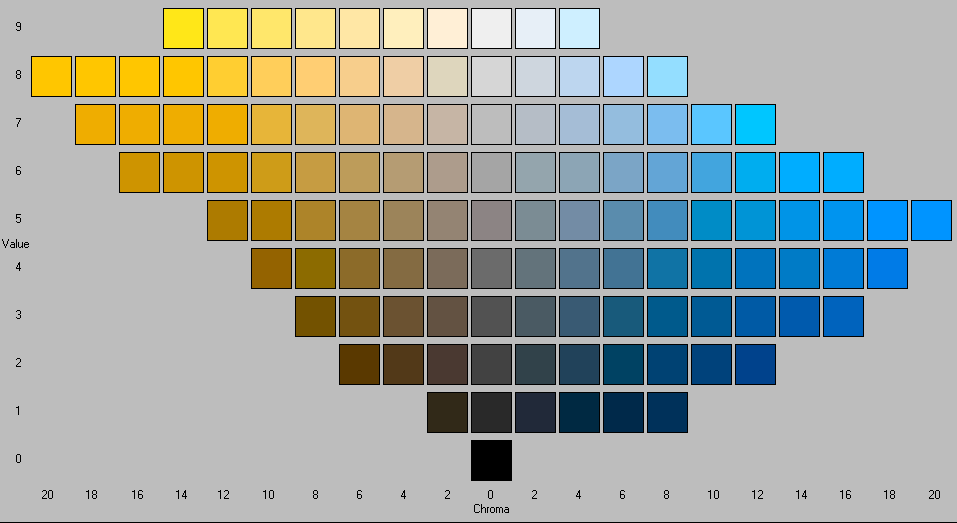 Эта инструкция позволяет вам выбрать вариант C4 (серый). Это может предотвратить «размытый» вид флуоресценции.

Это также уменьшает 16-битные изображения до 8-битных (на основе текущих значений яркости и контрастности), а затем создает 24-битное изображение RGB.

Объединение изображений в цветной композит

Команда меню Изображение › Цвет › Объединить каналы… открывает диалоговое окно для объединения каналов серого, красного, зеленого, синего, голубого, пурпурного и желтого в новое составное изображение.

Разделение многоканальных изображений

Изображение или стек RGB можно разделить на соответствующие красный, зеленый и синий компоненты изображения с помощью команды меню Изображение › Цвет › Разделить каналы.

Иногда может потребоваться отобразить объединенное изображение RGB вместе с отдельными каналами в конечном рисунке. Это можно сделать с помощью плагина «RGB to Montage».

Работает с однослойными изображениями RGB.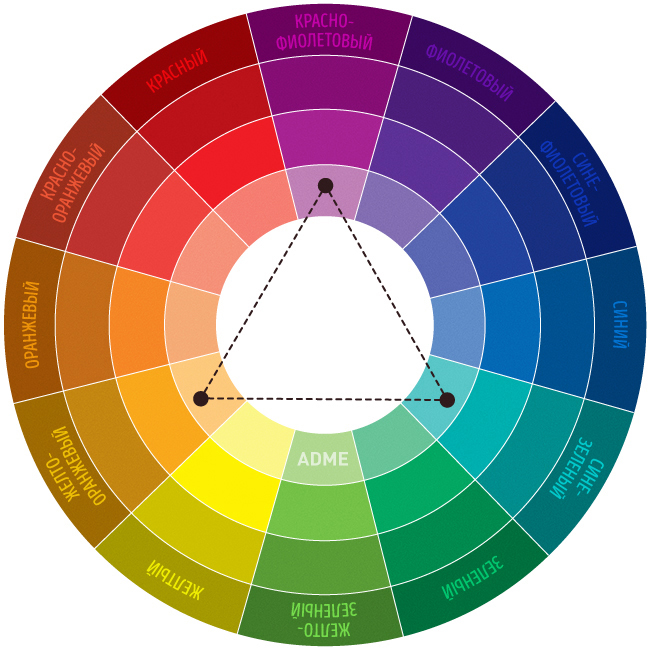 Создается новый стек RGB, канал 1 является красным каналом; 2 зеленых и 3 синих. Четвертый фрагмент является объединенным фрагментом. Если канал пуст (например, объединенное красно-зеленое изображение не будет иметь синего цвета), то срез пропускается. Затем плагин предложит вам макет монтажа. У вас есть возможность изменить ширину белой границы между панелями изображений. Если опция «Псевдоцвет» отключена, каждый канал будет в оттенках серого. Если размер линейки масштаба установлен равным нулю, линейка масштаба добавлена ​​не будет.

Цветной композит

Композит можно преобразовать в стек в оттенках серого с помощью команды меню Изображение › Гиперстеки › Гиперстеки в стек. Каналы могут быть впоследствии разделены на отдельные изображения с помощью команды меню Image › Stacks › Stack to Images.

Псевдоцвет

Разумное использование LUT может быть очень полезным для выделения нужных особенностей изображения. Человеческий глаз может воспринимать относительно небольшое количество оттенков в одном изображении. Псевдораскрашивание изображений может сделать данные более наглядными

Традиционная «зеленая» LUT

Улучшенная «зеленая горячая» LUT

Микротрубочки под ядром теперь более заметны

Поиграйте и посмотрите, какая LUT поможет проиллюстрировать особенности вашего изображения.

Монтаж, составленный из стека, сгенерированного с помощью команд меню Изображение › Цвет › Показать LUT.

Различные LUT доступны через команды меню Image › Lookup Tables.

При использовании нестандартной LUT может быть полезно добавить шкалу оттенков серого, чтобы пользователь мог определить, какой цвет представляет какое значение шкалы серого. Кривая может быть добавлена ​​с помощью встроенной функции Analyze › Tools › Calibration Bar…. Если для пандуса нет места, попробуйте увеличить холст изображения с помощью команды меню Изображение › Настройка › Размер холста….

Анализ › Инструменты › Калибровочная линейка…

1. doi:10. 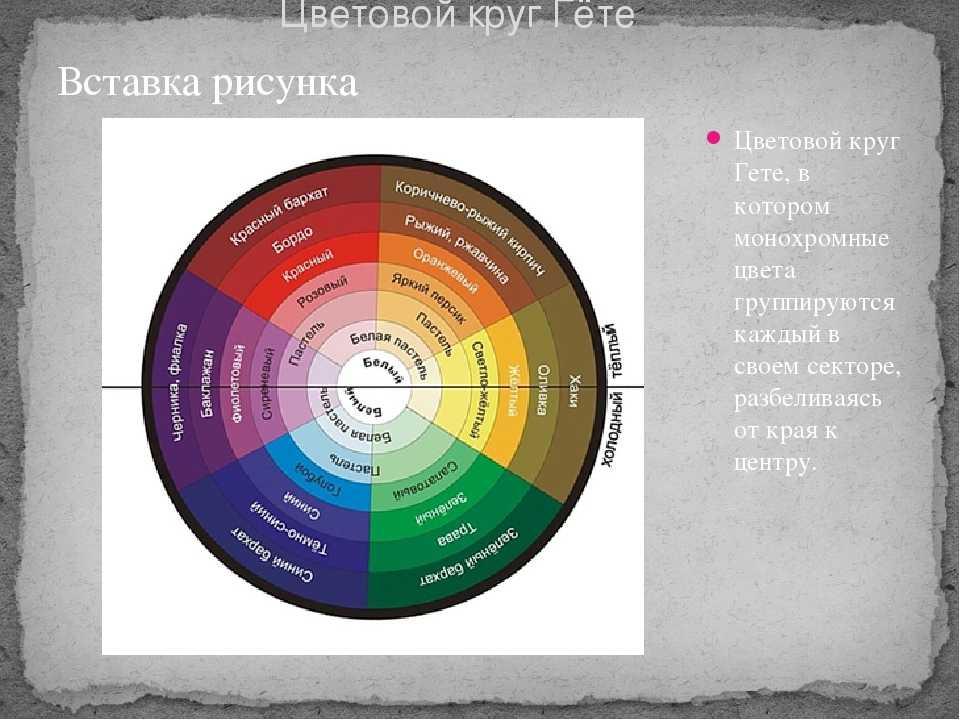1046/j.1365-2818.1997.1470704.x ↩

Визуальное разложение цвета посредством экстраполяции движения

• Опубликовано: 06 марта 1997 г.
• Роми Ниджхаван ¹  

Природа том 386 , страницы 66–69 (1997 г.)Процитировать эту статью

• 528 доступов

• 123 Цитаты

• Сведения о показателях

Abstract

Восприятие желтого цвета сыграло центральную роль в различении двух основных теорий цветового зрения. Hering предположил, что желтый цвет возникает в результате активации отдельного ретинально-нейрального механизма, тогда как, согласно представлению Young-Helmholtz-Maxwell, желтый цвет возникает в результате комбинированной активации механизмов красных и зеленых колбочек ¹ . Когда красное и зеленое изображения предъявляются отдельно к соответствующим участкам сетчатки обоих глаз, возникает ощущение желтого цвета ^1,2 . Поскольку пути от двух глаз не сходятся до коры, это предполагает, что желтый цвет действительно может возникать в результате центрального объединения отдельных красных и зеленых каналов ² . Теперь я покажу, что возможен и обратный процесс; зрительная система может разложить «желтый» стимул на составляющие его красный и зеленый компоненты. «Желтый» стимул создавался путем оптического наложения мигающей красной линии на движущуюся зеленую полосу. Если полоса видна ненадолго, мигающая линия становится желтой. Однако, если траектория зеленой полосы экспонируется в течение достаточного времени, линия неправильно воспринимается как отслеживающая полосу и становится красной. Обработка движения происходит в коре, а не в сетчатке у приматов, поэтому способность сигналов движения влиять на восприятие цвета согласуется с понятием Юнга-Гельмгольца-Максвелла о «центральном синтезе» желтого цвета.

Это предварительный просмотр содержимого подписки, доступ через ваше учреждение

Соответствующие статьи

Статьи открытого доступа со ссылками на эту статью.

• О потенциальной роли латеральной связи в ожидании сетчатки

  • Сельма Суихель
  • и Бруно Сессак

  Журнал математической неврологии Открытый доступ 09 января 2021 г.

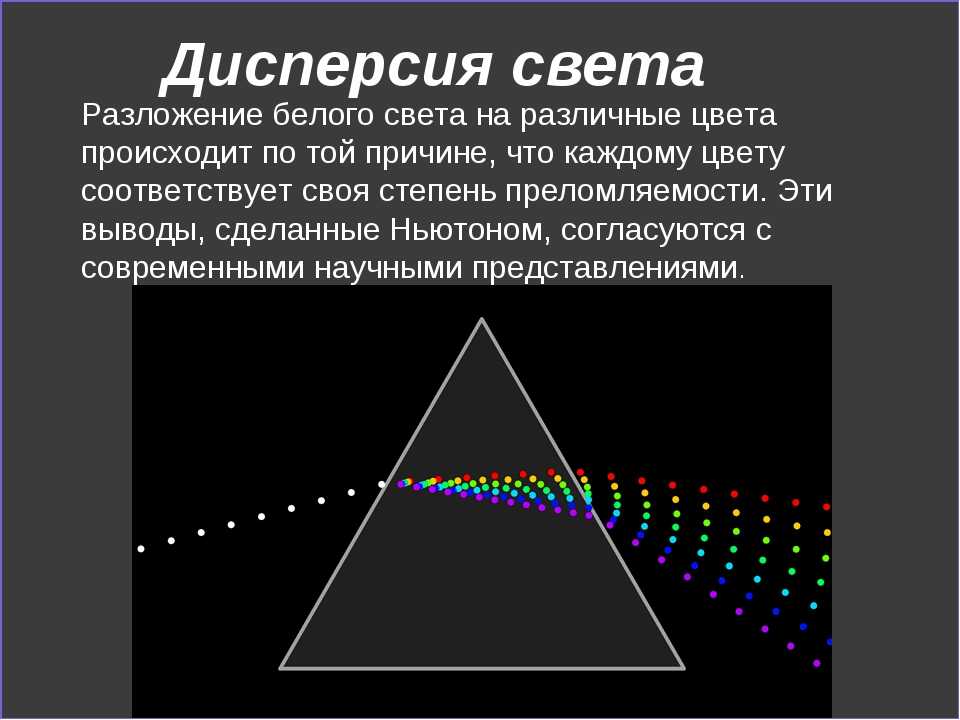
Варианты доступа

Подписаться на журнал

Получить полный доступ к журналу на 1 год

199,00 €

всего 3,90 € за выпуск

Подписаться

Расчет налогов будет завершен во время оформления заказа.

Купить статью

Получите ограниченный по времени или полный доступ к статье на ReadCube.

32,00 $

Купить

Все цены указаны без учета стоимости.

Ссылки

1. Хурвич, Л. М. и Джеймсон, Д. Бинокулярное слияние желтого в связи с теориями цвета. Science 114 , 199–202 (1951).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

2. Хехт, С. О бинокулярном слиянии цветов и его связи с теориями цветового зрения. Проц. Натл акад. науч. США 14 , 237–241 (1928).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

3. Зеки, С. М. Функциональная организация проекций от стриарной до престриарной зрительной коры у макак-резусов. 903:20 Гавань Колд-Спринг. Симп. Квант. биол. 40 , 591–600 (1975).

   Артикул Google ученый

4. Ливингстон, М.С. и Хьюбел, Д.Х. Психофизические доказательства наличия отдельных каналов для восприятия формы, цвета, движения и глубины. J. Neurosci. 7 , 3416–3468 (1987).

   КАС Статья Google ученый

5. Рамачандран, В. С. и Грегори, Р. Л. Влияет ли цвет на восприятие движения человеком? Природа 275 , 55–56 (1978).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

6. Кавана, П. , Тайлер, К.В. и Фавро, О.Е. Воспринимаемая скорость движущихся хроматических решеток. J. Опт. соц. Являюсь. 1 , 893–899 (1984).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

7. Сайто, Х., Танака, К., Изоно, Х., Ясуда, М. и Миками, А. Направленно-селективный ответ клеток в средней височной области (MT) макака на движение эквилюминесцентных цветовые стимулы противника. Экспл. Мозг Res. 75 , 1–14 (1989).

   КАС Статья Google ученый

8. Кроппер, С.Дж. и Деррингтон, А.М. Быстрое обнаружение движения по цвету в человеческом зрении. Nature 379 , 72–74 (1996).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

9. Маккей, Д. М. Стабильность восприятия стробоскопически освещенного поля зрения, содержащего самосветящиеся объекты. Природа 181 , 507–508 (1958).

   ОБЪЯВЛЕНИЕ КАС Статья Google ученый

10. Ниджхаван, Р. Экстраполяция движения при ловле. Природа 370 , 256–257 (1994).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

11. Hurvich, LM Color Vision (Sinauer, Sunderland, Massachusetts, 1981).

    Google ученый

12. Walraven, J. Пространственные характеристики хроматической индукции; выделение боковых эффектов от артефактов рассеянного света. Видение Рез. 13 , 1739–1753 (1973).

    КАС Статья Google ученый

13. Курана Б. и Ниджхаван Р. Экстраполяция или переключение внимания? Природа 378 , 565–566 (1995).

    ОБЪЯВЛЕНИЕ Статья Google ученый

14. Ахо, А.-К., Доннер, К., Хелениус, С., Олесен Ларсен, Л. и Рейтер, Т. Визуальное представление жабы ( Bufo bufo ) при низком уровне освещенности: реакция ганглиозных клеток сетчатки и точность поимки добычи. Дж. Комп. Физиол. 172 , 671–682 (1993).

    КАС Статья Google ученый

15. Richards, W. Подавление зрения при пассивном движении глаз. J. Опт. соц. Являюсь. 58 , 1159–1160 (1968).

    КАС Статья Google ученый

16. Лэнд, Э. Х. и Макканн, Дж. Дж. Легкость и теория ретинекса. J. Опт. соц. Являюсь. 61 , 1–11 (1971).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

17. Гилкрист, А. Восприятие черных и белых поверхностей. наук. Являюсь. 24 , 88–97 (1979).

    Google ученый

18. Эфрон Р. Минимальная продолжительность восприятия. Нейропсихология 8 , 57–63 (1970).

    КАС Статья Google ученый

19. Хогбен, Дж. Х. и Ди Лолло, В. Перцептивная интеграция и перцептивная сегрегация кратких визуальных стимулов. Видение Рез. 14 , 1059–1069 (1974).

    КАС Статья Google ученый

20. Заусенец, Д. Мазок движения. Природа 284 , 164–165 (1980).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

21. Морган, М. Дж. Восприятие непрерывности стробоскопического движения: временной частотный анализ. Видение Рез. 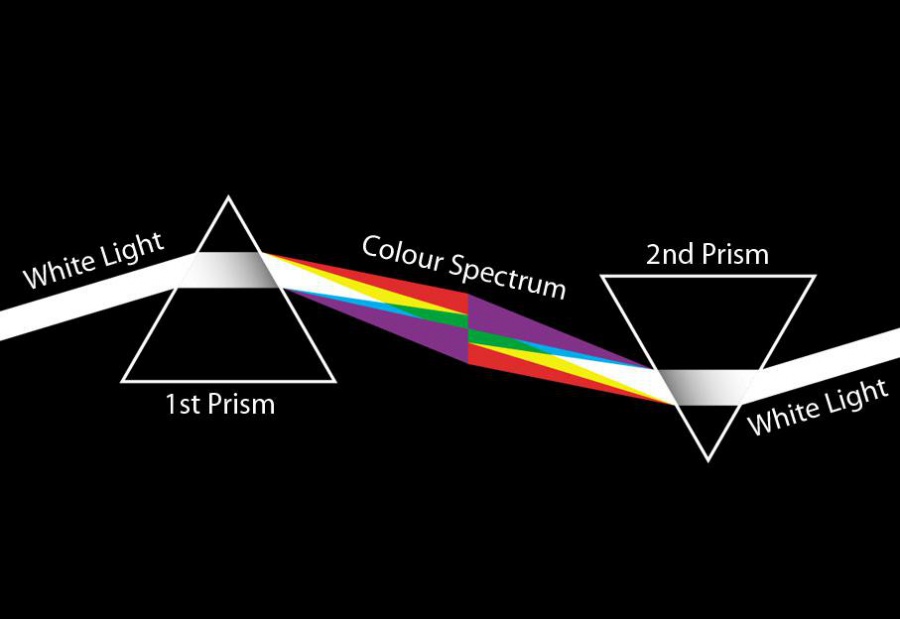19 , 491–500 (1979).

    КАС Статья Google ученый

22. Канеман, Д. Метод, результаты и теория в исследованиях визуальной маскировки. Псих. Бык. 70 , 404–425 (1968).

    КАС Статья Google ученый

23. Альперн, М. и Раштон, В.А.Х. Специфика взаимодействия колбочек в эффекте послевспышки. J. Physiol. 176 , 473–482 (1965).

    КАС Статья Google ученый

24. Йеллотт, Дж. И. и Ванделл, Б. А. Цветовые свойства эффекта контрастной вспышки: монооптическое и дихоптическое сравнение. Видение Рез. 16 , 1275–1280 (1976).

    Артикул Google ученый

25. Ди Лолло, В. и Хогбен, Дж. Х. Подавление видимого постоянства как функция пространственного разделения между вызывающими стимулами. 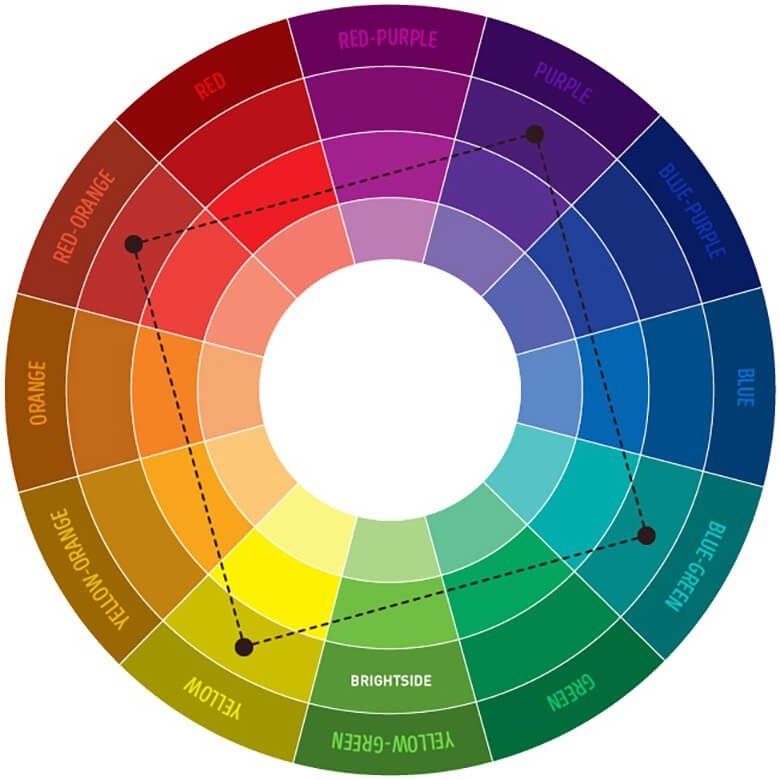Восприятие. Психофиз. 41 , 345–354 (1987).

    КАС Статья Google ученый

26. Хьюбел, Д. Х. и Визель, Т. Н. Рецептивные поля и функциональная архитектура полосатой коры обезьяны. J. Physiol. (Лондон.) 195 , 215–243 (1968).

    КАС Статья Google ученый

27. Дюамель, Дж.-Р., Колби, К.Л. и Голдберг, М.Э. Обновление представления зрительного пространства в теменной коре посредством предполагаемых движений глаз. Наука 255 , 90–92 (1992).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

28. Бойнтон, Р. М. в Визуальная психофизика и физиология (редакторы Армингтон, Дж. К., Краускопф, Дж. И Вутен, Б. Р.) 193–207 (Академический, Нью-Йорк, 1978).

    Книга Google ученый

29. Зеки, С. Представление цветов в коре головного мозга. Природа 284 , 412–418 (1980).

    ОБЪЯВЛЕНИЕ КАС Статья Google ученый

Download references

Author information

Authors and Affiliations

1. Department of Psychology, Uris Hall, Cornell University, Ithaca, New York, 14853, USA

   Romi Nijhawan

Authors

1. Romi Nijhawan

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

Права и разрешения

Перепечатка и разрешения

Об этой статье

Эту статью цитирует

• О потенциальной роли латеральной связи в ожидании сетчатки

  • Сельма Суихель
  • Бруно Сессак

  Журнал математических нейронаук (2021)

• Эффект запаздывания

  • Криштиану Челлини
  • Лиза Скоккиа
  • Кнут Рисование

  Экспериментальные исследования мозга (2016)

• Эффект мгновенного запаздывания: усложняющая экстраполяция движения движущегося эталонного стимула парадоксальным образом усиливает эффект.

  
  • Талис Бахманн
  • Каролина Мерд
  • Эндель Пыдер

  Психологические исследования (2012)

• Неправильное восприятие движения, вызванное обратными связями: нейронная модель, имитирующая эффект Фрелиха

  • Елена Карбоне
  • Марк Помплун

  Психологические исследования (2007)

• Наука, стоящая за поисками определения возраста синяков — обзор англоязычной литературы

  • Н. 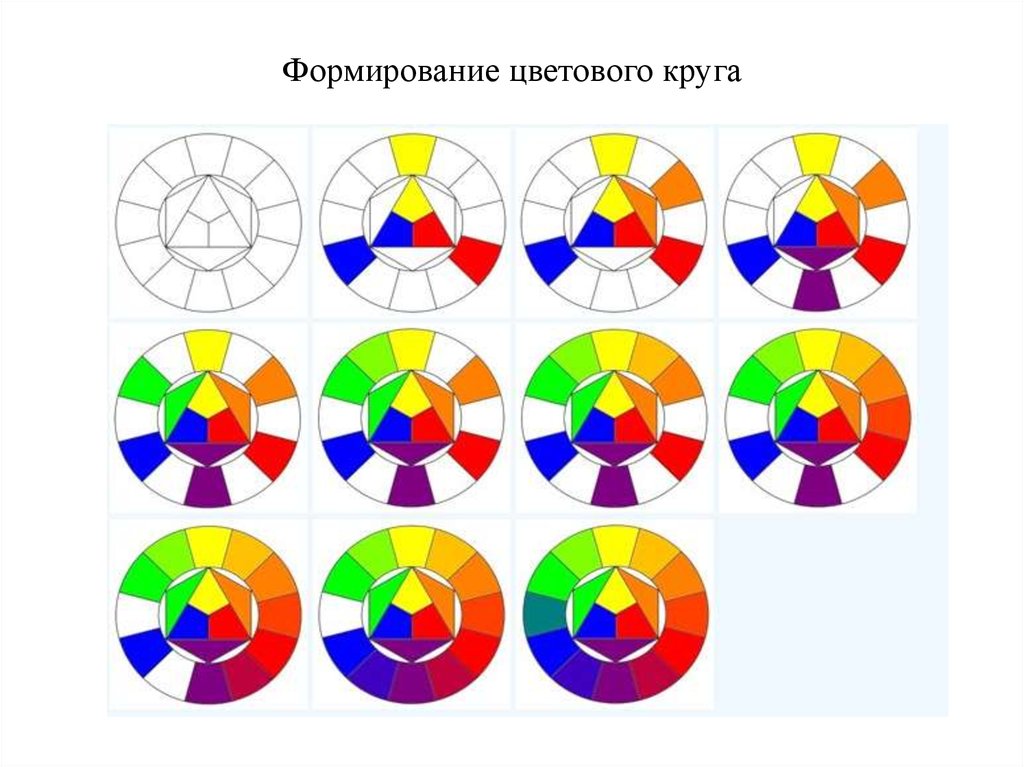Э. И. Ланглуа

  Судебно-медицинская экспертиза, медицина и патология (2007)

Комментарии

Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.

Глубокая цветовая декомпозиция на основе палитры для перекрашивания изображения с эстетическим предложением

• title={Глубокая цветовая декомпозиция на основе палитры для перекрашивания изображения с эстетическим предложением}, автор = {Чжэнцин Ли, Чжэнцзюнь Чжа и Ян Цао}, название книги={МММ}, год = {2020} }
  • Чжэнцин Ли, Чжэнцзюнь Чжа, Ян Цао
  • Опубликовано в МММ 5 января 2020 г.
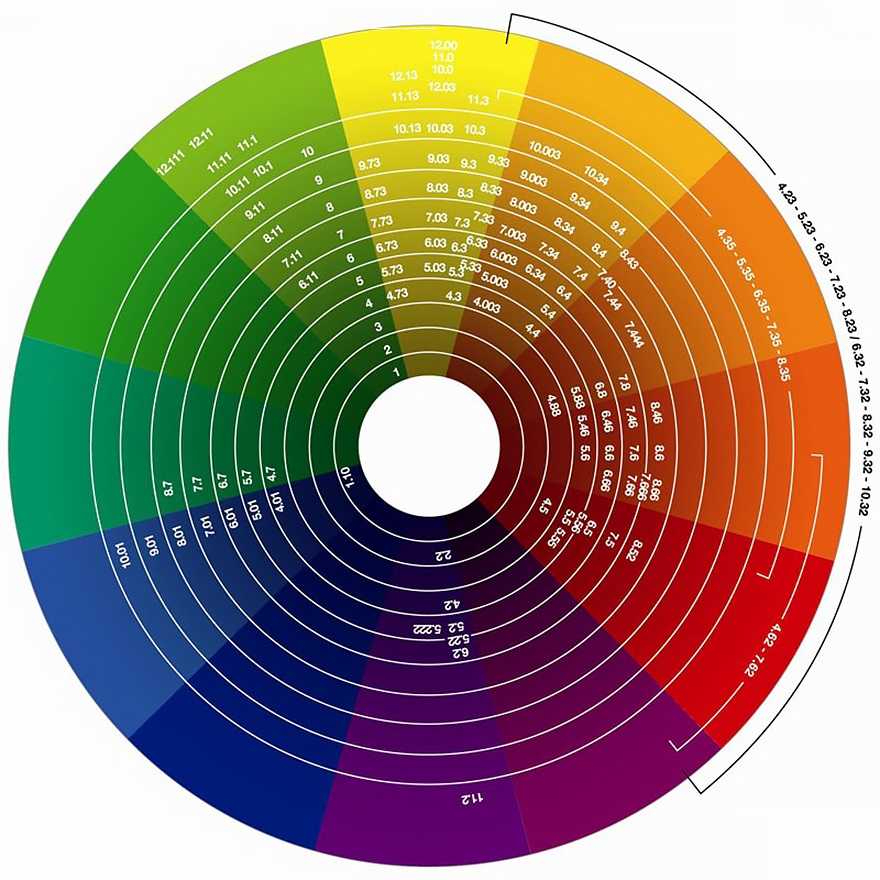
  • Art

  Цветное издание является важным вопросом при обработке изображений и графическом дизайне. В этой статье представлена ​​структура, основанная на глубокой декомпозиции цветов для перекрашивания изображений, позволяющая пользователям добиться профессионального цветного редактирования с помощью простых интерактивных операций. В отличие от существующих методов, которые выполняют генерацию палитры и цветовую декомпозицию отдельно, наш метод напрямую генерирует перекрашенные изображения с помощью облегченной CNN. Сначала мы формулируем генерацию цветовой палитры как неконтролируемую… 

  Просмотр через Publisher

  На пути к перекрашиванию изображений на основе естественных объектов

  • Menglu Cui, Zhe Zhu, Yulu Yang, Shao-Ping Lu

  • Информатика, искусство

    Comput. Вис. Медиа

  • 2022

  Подход на основе палитры для реалистичного перекрашивания изображения на уровне объекта, который превосходит существующие современные алгоритмы редактирования цвета и обеспечивает интуитивно понятный пользовательский интерфейс для эффективного управления цветом.

  Динамическое искажение ближайших цветов для сортировки и сравнения палитр

  В этом документе предлагается динамическая деформация ближайшего цвета (DCCW) для расчета минимальной суммы расстояний между цветами и графа, соединяющего цвета в другой палитре, а также демонстрируются полезные приложения, доступные с помощью DCCW, включая интерполяцию палитры, навигацию по палитре и перекрашивание изображения.

  Эстетическая передача стиля изображения

  • Zhiyuan Hu, Jia Jia, Bei Liu, Yaohua Bu, Jianlong Fu

  • Computer Science

    ACM Multimedia

  • 2020

  Новая эстетически-ориентированная модель переноса стиля на основе оптимизации модели (AAMOBST), которая может определять цветовые и текстурные особенности отдельно и может сохранять одну из них фиксированной, изменяя другую, что неприменимо. для предыдущих методов.

  Цветовая гармонизация, дегармонизация и балансировка в дополненной реальности

  • Эмануэле Марино, Ф. 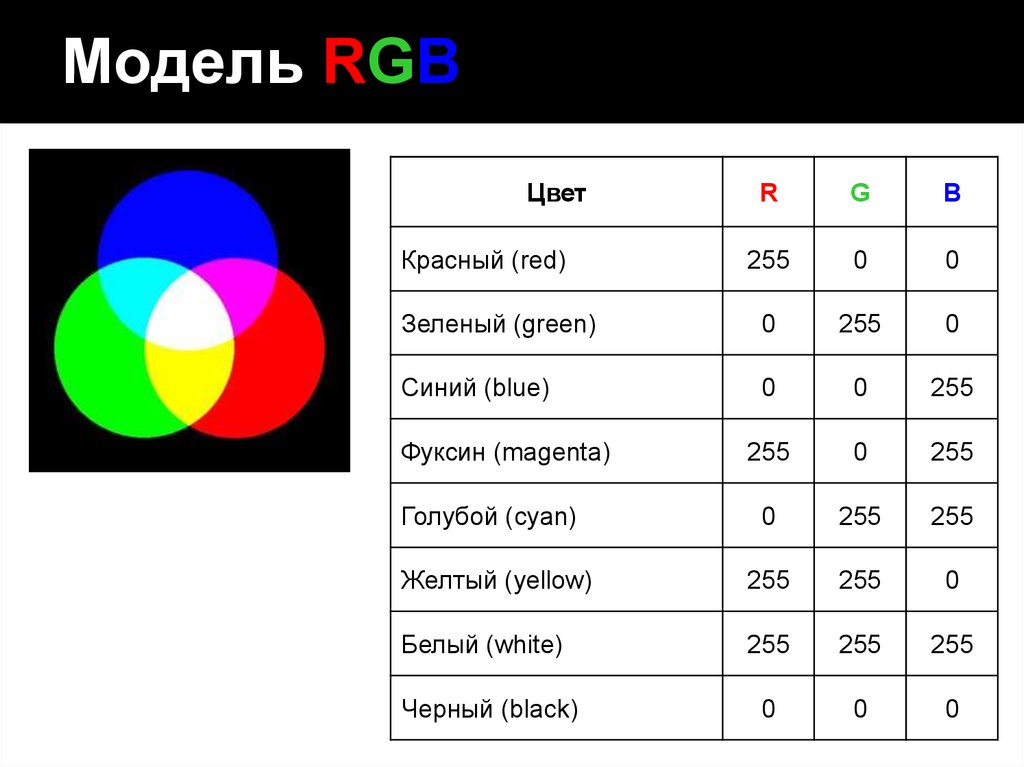Бруно, Ф. Лиарокапис

  • Информатика

    Прикладные науки

  • 2021

  Предлагается набор новых методов, основанных на методологии цветовой гармонизации, для перекрашивания содержимого дополненной реальности в соответствии с реальным фоном и достижения компромисса между гармонией и хорошей видимостью между виртуальными и реальными объектами.

  ПОКАЗАНЫ 1–10 ИЗ 24 ССЫЛОК

  СОРТИРОВАТЬ ПОРелевантностиБольше всего влияющих документовНедавность

  Перекрашивание изображения на основе палитры с использованием оптимизации цветоразложения.

  В этом документе представлен подход к редактированию цветов изображения путем настройки компактной цветовой палитры путем оптимизации разложения цветов для гибкого перекрашивания при сохранении присущих цветовых характеристик исходного изображения.

  Палитры разложения изображений, гармонизации и передачи цвета

  • Jianchao Tan, J. 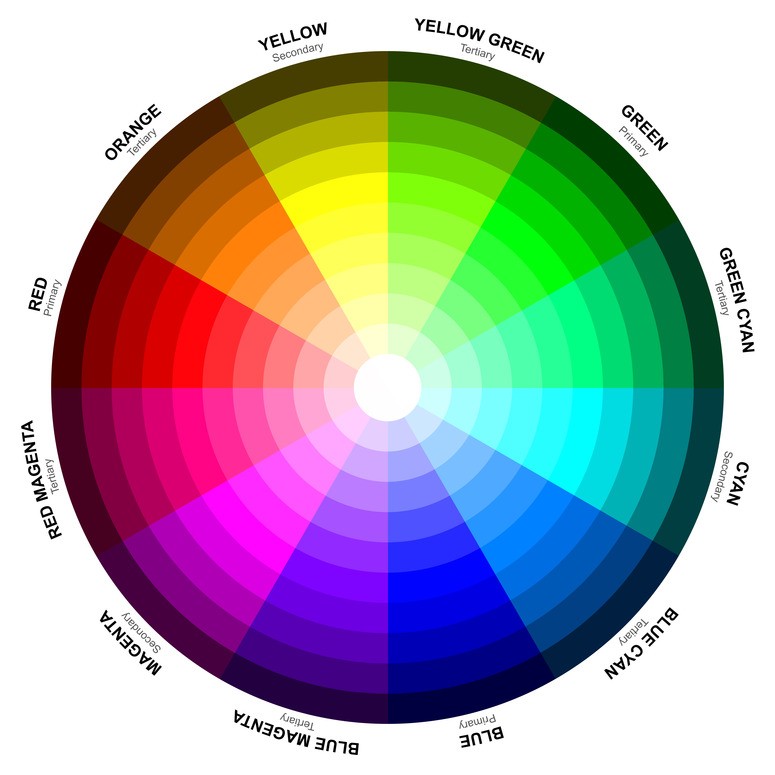Echevarria, Yotam I. Gingold

  • Art, Computer Science

    6665955955065. цвета как компактный набор осей, описывающих гармонические шаблоны на перцептивно однородных цветовых кругах, которые обеспечивают основу для различных операций с изображением с учетом цвета, таких как цветовая гармонизация и цветовая передача.

    PaletteNet: перекрашивание изображения с заданной цветовой палитрой

    Представлена ​​глубокая нейронная сеть, называемая PaletteNet, которая перекрашивает изображение в соответствии с заданной целевой цветовой палитрой, полезной для выражения концепции цвета изображения.

    LayerBuilder: декомпозиция слоев для интерактивного редактирования цветов изображений и видео

    • Шарон Лин, Мэтью Фишер, Анджела Дай, П. Ханрахан

    • Информатика

      ArXiv

    • 2017

    Представлен LayerBuilder, алгоритм, который разлагает изображение или видео на линейную комбинацию цветных слоев для облегчения приложений редактирования цвета и показывает, как это представление может принести пользу другим приложениям, таким как автоматическое предложение перекрашивания, синтез текстуры и фильтрация по цвету.

    Text2Colors: руководство по раскрашиванию изображения с помощью генерации палитры, управляемой текстом

    • Вонвун Чо, Хёджин Банг, Дж. Чу

    • Информатика

      ArXiv

    • 2018

    Эта модель может понимать форматированный текст, будь то одно слово, фраза или предложение, и генерировать из него несколько возможных палитр и может эффективно отражать заданную палитру при раскрашивании изображение.

    Эффективное разложение изображений на основе палитры и перекрашивание изображений с помощью геометрии пространства RGBXY

    • Цзяньчао Тан, Дж. Эчеварриа, Йотам И. Гинголд

    • Информатика

      АКМ транс. График

    • 2018

    Чрезвычайно масштабируемый и эффективный, но простой алгоритм декомпозиции изображений на основе палитры, который может разлагать 6-мегапиксельные изображения на слои за 20 миллисекунд, а также инструмент декомпозиции слоев в реальном времени, в котором пользователи могут интерактивно редактировать палитру для настройки слои.

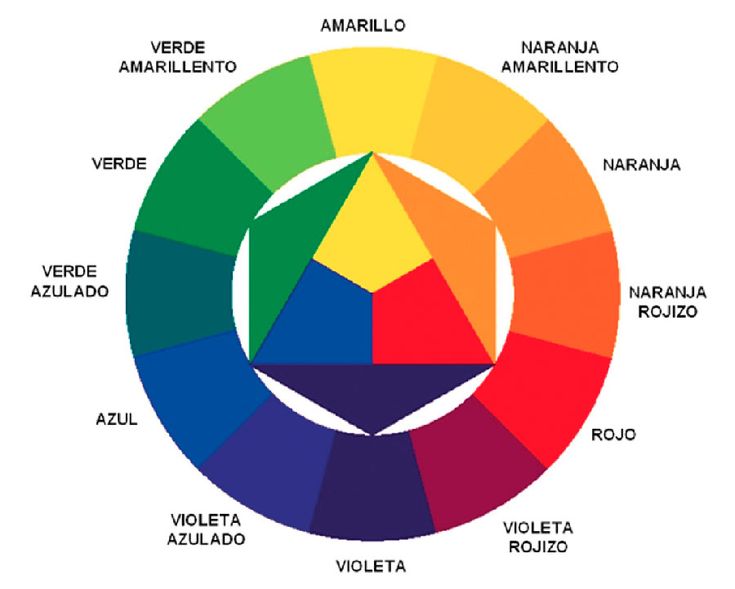
    Сегментация мягких цветов на основе разделения для обработки изображений

    • Ягиз Аксой, Т. Айдин, А. Смолич, М. Поллефейс

    • Информатика

      TOGS

    • 2017

    Мы представляем новый метод разложения изображения на набор сегментов мягких цветов, которые аналогичны цветовым слоям с альфа-каналами, которые обычно используются в современной обработке изображений…

    На основе палитры перекрашивание фотографий

    • Хуйвен Чанг, Охад Фрид, Йиминг Лю, С. ДиВерди, А. Финкельштейн

    • Информатика

      ACM Trans. График

    • 2015

    Простой, интуитивно понятный и интерактивный инструмент, который позволяет неспециалистам перекрашивать изображение путем редактирования цветовой палитры и позволяет неподготовленным пользователям достигать результатов, сравнимых с результатами экспертов, использующих профессиональное программное обеспечение.

    Окралений изображений с использованием аналогичных изображений

    • Радж Кумар Гупта, А. 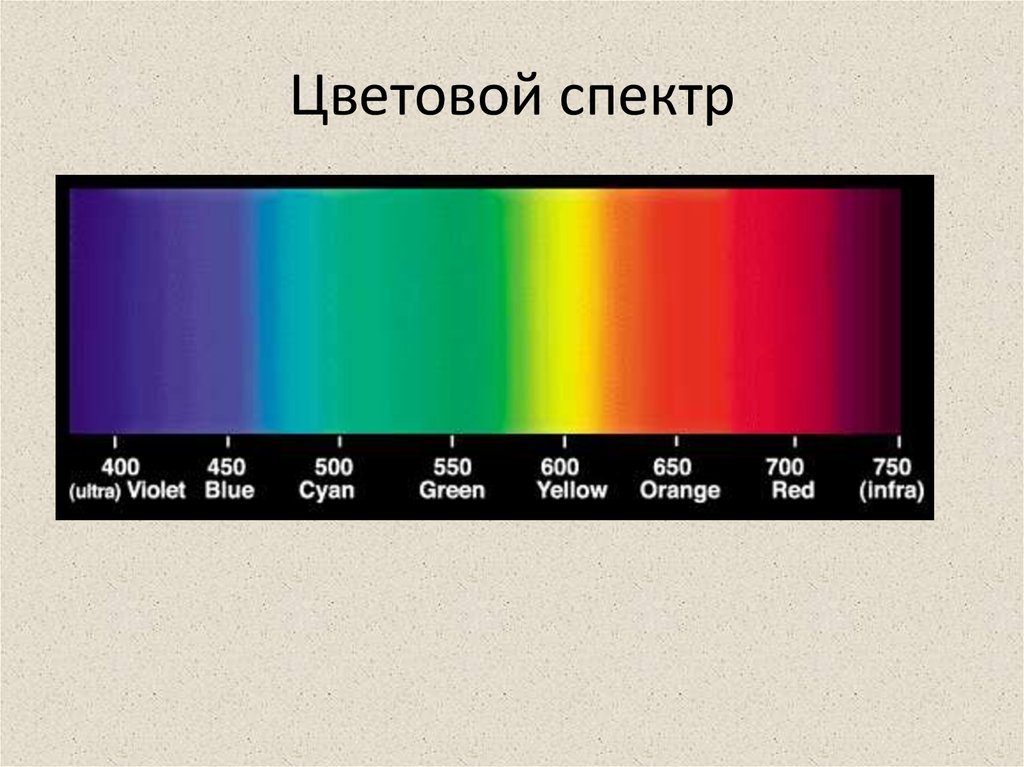Чиа, Д. Раджан, Э. С. Н.Г., Чжийонг Хуанг

    • Компьютерная наука

      Multimedia

    • 2012
    6666666666566666666665666666666666666666666666666666666666666666666666666666666656н. раскрасить серое изображение, используя схему быстрого сопоставления каскадных признаков, чтобы автоматически находить соответствия между суперпикселями эталонного и целевого изображений, что ускоряет процесс раскрашивания и позволяет раскрашиванию демонстрировать гораздо более высокую степень пространственной согласованности.

    Система поддержки цветового дизайна с учетом цветовой гармонии

    • Масатака Токумару, Н. Муранака, С. Иманиши

    • Информатика, искусство

      2002 Всемирный конгресс IEEE по вычислительному интеллекту. 2002 Международная конференция IEEE по нечетким системам. FUZZ-IEEE’02. Proceedings (Cat. No.02Ch47291)

    • 2002

    Экспериментальный результат показывает, что выполняются эффективные суждения о цветовой гармонии и цветовом изображении, и система может получить некоторые хорошие цветовые схемы с помощью системы.

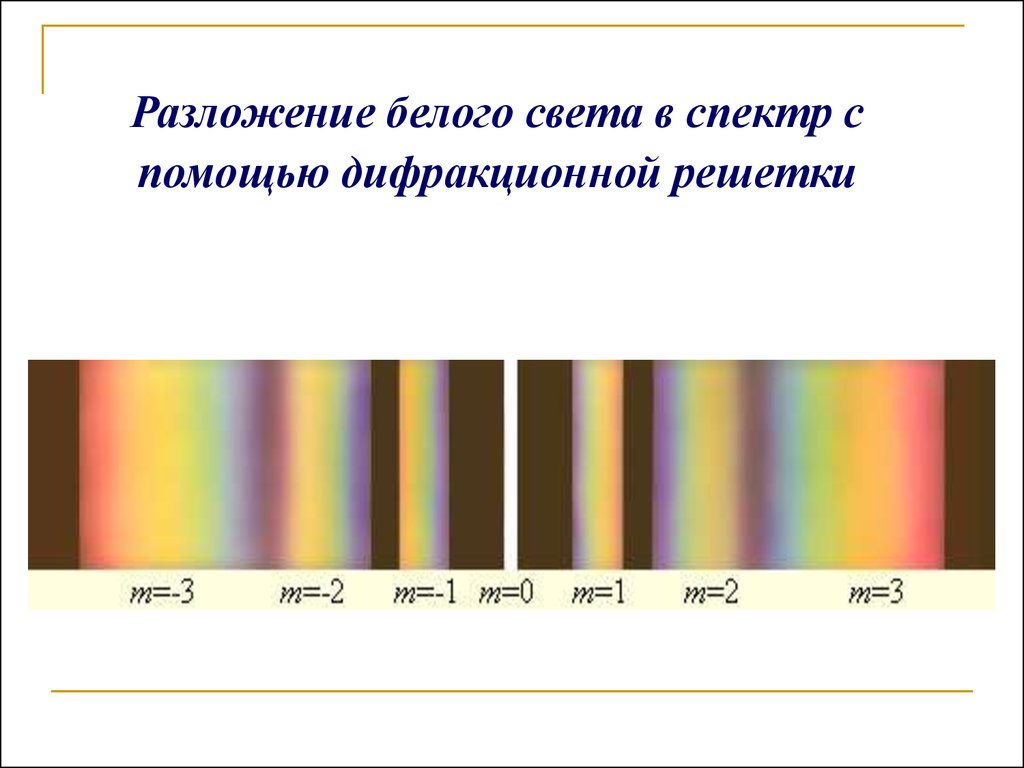
    Разложение белого света

    Разложение белого света

    Дитрих Завиша

    Контакты

    Немецкая версия

    Форматирование HTML и пользовательские инструкции отключены на этом сервере. Тот же файл с адаптированным форматированием можно найти здесь: https://farbeinf.de/static_html/whitelight.html.

    Спектр Солнца практически невозможно увидеть без подходящего аппарата «в природе». Сегодня всем известны цвета, видимые на компакт-дисках, и, глядя на свет лампы накаливания, отражаемый компакт-диском, можно увидеть зеркальное отражение лампы и, под разными углами, спектральное разложение ее света.

    
    В прежние времена это можно было наблюдать только в очень особых условиях – если, например, в темной комнате луч солнца падал на кусок граненого стекла и давал на стене разноцветную полосу, (странный) призрак в первоначальном значении этого слова. Сначала, возможно, случайно наблюдаемые условия, затем Исаак Ньютон уточнил их с помощью стеклянных призм. Ньютон описал это явление и объяснил его разной силой преломления разных цветов света. Но только Уильям Хайд Волластон (1804 г.) и независимо друг от друга Йозеф Фраунгофер (1814 г.) развили экспериментальную установку настолько далеко, что смогли увидеть и неожиданно тонкие детали в солнечном спектре: линии поглощения, длины волн которых мог измерить Фраунгофер и которые впоследствии были названы его именем.
    

    Спектр Солнца с линиями Фраунгофера. Изображение взято с почтовой марки, посвященной 200 90 269 году со дня рождения Фраунгофера.

    
    Вы можете найти в Интернете поставщиков недорогих наборов для сборки ручного спектроскопа; такие материалы, как дифракционные решетки, призмы, линзы, которые вы можете там найти, а также советы по сборке спектроскопа.
    

    Цвета радуги имеют некоторое сходство со спектром, но они далеки от спектральных цветов не только потому, что нет темного фона.

    
    Картинки, которые должны показать, как выглядит спектр света, можно найти в книгах, а также в Интернете (пример из многих : сайтов Дэна Брутона), — редко говорится, что это следует понимать в лучшем случае примерно качественно. , потому что чистые спектральные цвета не могут быть воспроизведены в печати и на экране. Это показано на следующей иллюстрации:
    

    Диаграмма CIE x y с диапазоном, отображаемым на sRGB-экране («гамма»), и линейкой спектральных цветов. Проиллюстрированы две возможности, как их можно спроецировать на край треугольника. Серые линии соединяют спектральные цвета с точками того же оттенка гаммы, стрелки указывают на цвета, которые получаются, если отрицательные значения R, G или B положить равными нулю, а положительные сохранить. Результаты представлены на следующей картинке.

    Если в дальнейшем что-то поддерживается и иллюстрируется картинками, требуется осторожность. Если под рукой есть спектроскоп, следует проверить, правильно ли здесь (и в других местах) читается.

    Как выглядит спектр?

    Воспроизведение «спектральных цветов» является суровым испытанием для любого метода воспроизведения цветных изображений, для печати, цветной пленки, электронно-лучевых трубок (цветных телевизионных и компьютерных экранов) и, в частности, для плоских экранов. (Причину неровностей и полос, видимых на некоторых TFT-экранах на следующем рисунке, я до сих пор не выяснил. На ЭЛТ-мониторах они не возникают.)
    
    

    Противостояние двух иллюстраций видимого спектра (соответствует светящемуся телу 6000К). Цвет и относительная яркость были максимально точно адаптированы к верхнему изображению, т.е. добавлен белый свет, пока не был достигнут край гаммы, а затем яркость была подогнана под реальный спектр. В нижней половине изображения отрицательные значения R, G, B были установлены равными нулю, а яркость отрегулирована заново.
    Наибольшие значения R, G или B, возникающие на изображении, не могут превышать максимальное значение 1, поэтому яркость ограничена.
    

    Где желтый свет?

    Сначала замечается, что в обоих вариантах нет настоящего желтого цвета. То, что находится между красным и зеленым, выглядит как зеленовато-оранжевый или оранжево-зеленый. Звучит странно, но посмотрите на это! Правильное обозначение цвета — оливковый.
    

    Глядя через призму на узкую белую полоску на темном фоне, мы видим, что белый (свет) разлагается на цвета; однако человек видит не семь различных цветов, как можно было бы ожидать, а только три, а именно красный, зеленый и фиолетово-синий, как уже было замечено Гёте.

    
    Также в спектроскопе не видно желтого цвета в спектре низкой интенсивности. Действительно, спектр не кажется особенно красочным, когда он тусклый; красный, зеленый и фиолетово-синий, с упомянутым «обесцвеченным» переходом между красным и зеленым. Только при достаточной яркости становятся видны тончайшие цветовые градации и спектр показывает все свое великолепие. Тогда у него также есть желтая часть.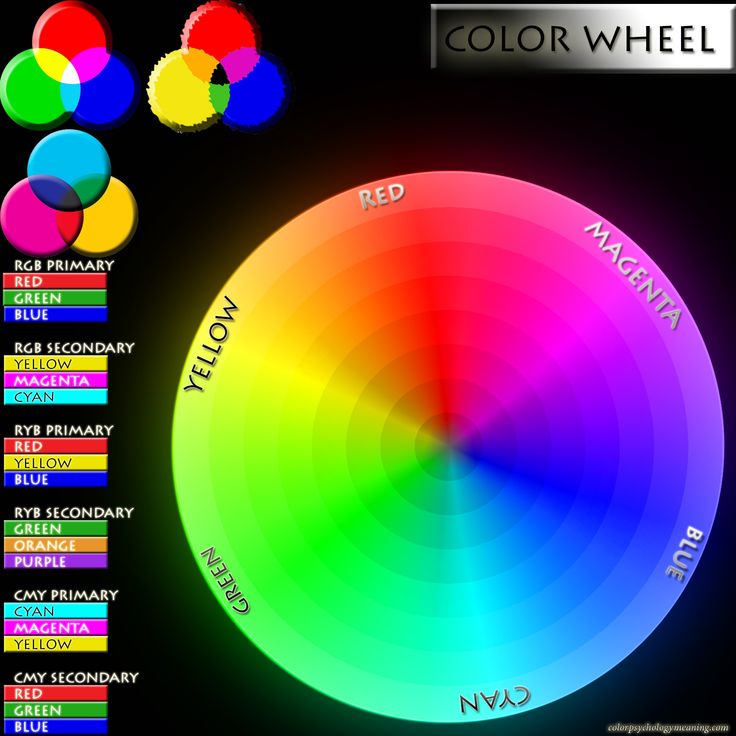 Зависимость воспринимаемого цвета от яркости известна с 19 века.го века под именем Безольда Брюке сдвига.
    Еще одним подобным эффектом является сдвиг воспринимаемого цвета при добавлении белого (света) (эффект Абни). На маленьком изображении, показанном выше, это еще не мешает; но в большом оригинале (здесь вы найдете его исходный код PostScript) темный «розово-розовый» гораздо меньше соответствует тому, что можно увидеть на красном конце спектра, чем красный в нижней части.
    Моделирование спектра, показанного в верхней половине изображения, является в определенной степени оптимумом достижимого реализма, если стремиться к как можно более точному воспроизведению цвета и яркости. «Отсутствие» желтого не исправить, лишь бы яркость соответствовала действительности. Физиологический желтый цвет ярче красного и зеленого в непрерывном спектре, однако яркость на длинах волн от 570 до 580 нм всегда близка к яркости соседних цветов. Нет действительно удовлетворительного воспроизведения спектра на экране или в печати.
    Моделирование, показанное в нижней половине, показывает более насыщенные цвета, но явные искажения оттенков: уникальный зеленый цвет, не голубоватый и не желтоватый, должен быть виден на длине волны 530 нм, но вместо этого присутствует желтовато-зеленый цвет зеленого люминофора.
    

        

    
    Рассматриваемая здесь проблема представлена ​​более подробно и тщательно обсуждена Эндрю Т. Янгом. Вы также найдете компромисс между реализмом и хорошим внешним видом желтого цвета.

    Исторический

    Исаак Ньютон открыл и описал способность солнечного света разлагаться в 1666 году и перечислил семь возникающих цветов: красный, оранжевый, желтый, зеленый, синий, индиго и фиолетовый. Однако уже из этого перечисления можно заключить, что экспериментальная установка Ньютона была довольно проста: не слишком маленькое отверстие в жалюзи, служившее для затемнения комнаты, через которое проходил солнечный луч, призма и на некотором расстоянии от нее экран , возможно, белый лист бумаги. Наблюдаемый «спектр» мог выглядеть примерно так же, как на изображении справа, но с более темным фоном.

    Справа: пятно света, брошенное на стену гранью граненого стекла.

    Если бы Ньютон видел спектр так, как это было показано выше, то для его описания ему понадобились бы только три цвета: красный, зеленый и индиго, или четыре цвета, если бы он включил оранжевый.
    Может показаться странным, что среди цветов спектра назван индиго – это звучит как удвоение синего. Но, скорее всего, Ньютон имел в виду под «синим» небесно-голубой цвет, подобный тому цвету, который сегодня в полиграфической технике принято называть цианом. Синтетический индиго используется для окраски синих джинсов – все знают их цвет, синий, как уже понятно из названия. Говоря сегодня, мы бы назвали семь цветов света красным, оранжевым, желтым, зеленым, голубым, синим и фиолетовым.

    Основные основные цвета

    Появление тусклого спектра — красного, зеленого и фиолетово-синего — естественно связано с характеристиками рецепторов сетчатки: основные основные цвета (или основные цвета колбочек) соответствуют стимуляции только одного из трех видов колбочек. Эти цвета видны в верхнем поле сравнения спектра при 630 нм, 520 нм и 450 нм. Красный цвет современных светофоров (в ясный день) в хорошем приближении соответствует физиологическому основному цвету, который некоторые авторы любят называть оранжево-красным. В темноте чувствительность колбочек повышается, тогда зеленочувствительные уже заметно раздражаются красным светом, при этом цветовосприятие смещается в сторону желтовато-красного (сдвиг Бецольда-Брюке). С цифровым фотоаппаратом кстати аналогично:

    Слева: В ясный день и на ярком небе красный свет светофора кажется чистым, насыщенным красным цветом. Справа: На рассвете на темном фоне и ночью один и тот же красный свет кажется желтоватым.

    Эстетические критерии

    Мы заканчиваем этот раздел цитатой с интересного интернет-сайта Филипа Лавена, посвященного оптике капель воды — применению теории Ми к радуге, блеску и связанным с ними явлениям. В программах для расчета этих явлений, чтобы получить цветовые координаты для представления на экране, Лавен использует очень наивную процедуру с сайта Дэна Брутона и пишет: «Алгоритм Брутона, очевидно, является упрощением сложного процесса. Более сложные алгоритмы были исследованы, например, разработанные CIE (Commission Internationale Eclairage — Международная комиссия по освещению), но ни один из них не дает эстетически приятного спектра!»
    Тот факт, что оптимально рассчитанный спектр выглядит не так красиво, как ожидалось, стал причиной использования неправильной процедуры, которая якобы дает «более красивые» результаты. Жаль. В то время как точная передача спектральных цветов невозможна, цвета радуги могут быть точно воспроизведены на экране , разумеется, с использованием данных CIE! Мораль этой истории такова: не полагайтесь слепо на эстетические критерии!

    ---

    Вернуться к разделу «Видение, измерение и передача цветов»
    или на страницу «истоки цвета»

    ---

    Многофокусное слияние цветных изображений на основе многомасштабного разложения кватернионов по сингулярным значениям

    Введение

    Слияние изображений — это процесс объединения информации из двух или более изображений в одно изображение. Он широко применяется, начиная от медицинского анализа (Jin et al., 2018a,b, 2020) и заканчивая визуализацией с помощью дистанционного зондирования и удалением искусственного тумана (Zhu et al., 2020). Важным направлением слияния изображений является многофокусное слияние изображений, при котором изображения с разными фокусными точками объединяются в полнофокусное изображение с общей четкостью и богатыми деталями. Алгоритмы многофокусного слияния изображений в основном включают методы пространственной области, методы области преобразования и методы глубокого обучения (Liu S. et al., 2020; Liu Y. et al., 2020).

    Методы пространственной области можно сгруппировать в метод на основе пикселей, метод на основе блоков и метод на основе области (Jin et al., 2018a,b; Qiu et al., 2019; Xiao et al., 2020). По сравнению с методом, основанным на пикселях, два других используют пространственную корреляцию соседних пикселей для управления слиянием изображений, чтобы избежать снижения контрастности и потери деталей в совмещенных изображениях. Сначала исходные изображения делятся на несколько блоков или областей, а затем уровень фокусировки и резкость каждого блока или области измеряются с помощью информации об интенсивности изображения. Наконец, выбирается блок или область с более высокой степенью фокусировки как часть объединенного изображения. Вишал и Винай (2018) предложили блочный метод многофокусного слияния изображений в пространственной области и использовали пространственную частоту для измерения уровня фокусировки блоков. Дуан и др. (2018) предложили схему сегментации на основе расширенного LSC, которая включает информацию о глубине пикселей в алгоритм кластеризации для слияния изображений с несколькими фокусами. Основное преимущество методов слияния, основанных на пространственной области, заключается в том, что они просты в реализации и позволяют получить фокусную меру с низкой вычислительной сложностью. Однако качество слияния изображений имеет отношение к выбору размеров блоков изображений или алгоритмов сегментации. Если размер блока изображения выбран неправильно, совмещенное изображение может создать «эффект блока». И если алгоритм сегментации не может точно сегментировать область, сфокусированная область не может быть правильно определена и извлечена.

    В подходе области преобразования различные методы многомасштабной декомпозиции (MSD) применяются для слияния многофокусных изображений. Алгоритм многомасштабной декомпозиции в основном включает пирамидальное преобразование (Burt and Kolczynski, 1993; Du et al., 2016), вейвлет-преобразование (Gonzalo and Jesús, 2002; Jaroslav et al., 2002) и многомасштабный геометрический анализ (Li et al. ., 2017, 2018; Лю и др., 2019а). По сравнению с пирамидой и вейвлет-преобразованиями, хотя метод многомасштабного геометрического анализа превосходит пирамиду и вейвлет-преобразования в представлении признаков и превосходен в сборе разнонаправленной информации и инвариантности перевода, он неэффективен по времени, когда речь идет о декомпозиции и реконструкции. . В дополнение к традиционным методам многомасштабной декомпозиции, упомянутым выше, были предложены некоторые другие методы многомасштабного слияния. Чжоу и др. (2014) предложили новую схему слияния изображений, основанную на большой и малой двухмасштабной декомпозиции. В этой схеме двухмасштабный метод используется для определения веса градиента изображения и эффективно устраняет влияние анизотропного размытия на обнаружение сфокусированной области. Ан и Ли (2019) представил новый адаптивный алгоритм декомпозиции изображений в области обработки изображений, который может быстро разлагать изображения и имеет многомасштабные характеристики. Чжан и др. (2017) предложили схему многомасштабной декомпозиции путем изменения размера структурных элементов и извлечения информации о морфологическом градиенте изображения в разных масштабах для достижения многофокусного слияния изображений. Ма и др. (2019) предложили метод слияния изображений с несколькими фокусами, основанный на прямой оценке карты фокуса с использованием мелкомасштабных и крупномасштабных измерений фокуса. Найду (2011) предложил новый метод слияния многофокусных изображений. В этом методе многомасштабный анализ и разложение по сингулярным значениям объединяются для выполнения многомасштабного разложения по сингулярным значениям на многофокусных изображениях для получения низкочастотных субизображений и высокочастотных субизображений разных масштабов. Этот метод многомасштабной декомпозиции обладает стабильностью и ортогональностью SVD. Поскольку операция свертки не требуется, скорость разложения высокая.

    Методы глубокого обучения, которые можно далее сгруппировать в методы на основе моделей классификации и методы на основе моделей регрессии (Liu Y. et al., 2020). В модели классификации Liu et al. (2017) впервые представили сверточные нейронные сети (CNN) в области многофокусного слияния изображений. С помощью этого метода измерение уровня активности и правило слияния могут быть сгенерированы совместно путем изучения модели CNN. В регрессионной модели Li et al. (2020) предложили новую сверточную нейронную сеть с глубоким регрессионным парным обучением для многофокусного слияния изображений. Этот метод напрямую преобразует все изображение в бинарную маску в качестве входных данных сети, не разделяя входное изображение на небольшие фрагменты, тем самым решая проблему оценки уровня размытия вокруг сфокусированной границы из-за разделения фрагментов. Эти методы могут извлекать больше признаков изображения посредством самообучения глубокой сети и выполнять слияние изображений на основе этих признаков. Однако трудности с обучением большому количеству параметров и больших наборов данных напрямую повлияли на эффективность и качество слияния изображений. По сравнению с методами глубокого обучения традиционные методы слияния более расширяемы и воспроизводимы, что облегчает их применение в реальных условиях. Таким образом, эта статья в основном направлена ​​на улучшение традиционных алгоритмов слияния многофокусных изображений.

    Большинство существующих алгоритмов объединения многофокусных изображений, упомянутых выше, могут обрабатывать серые и цветные многофокусные изображения. Что касается слияния цветных многофокусных изображений, каждый цветовой канал объединяется отдельно, а затем объединяется для получения окончательного слитного изображения (Найду, 2011; Лян и Хе, 2012; Аймаз и Кёсе, 2019). Эти традиционные методы слияния игнорируют взаимосвязь между цветовыми каналами, что приводит к искажению оттенков и размытию в процессе слияния изображений. Для решения вышеуказанных проблем в данной статье предлагается новая математическая модель цветных изображений, основанная на матричном анализе кватернионов. Эта модель учитывает зрительные характеристики человека и взаимодействие между пикселями в цветных изображениях и объединяет кватернион с многомасштабным разложением по сингулярным числам (MSVD) (Kakarla and Ogunbona, 2001; Naidu, 2011). В этом методе три цветовых компонента цветного изображения разлагаются как единое целое для извлечения богатой информации о цвете и деталях. Во-первых, три цветовых компонента пикселя представлены тремя мнимыми частями кватерниона.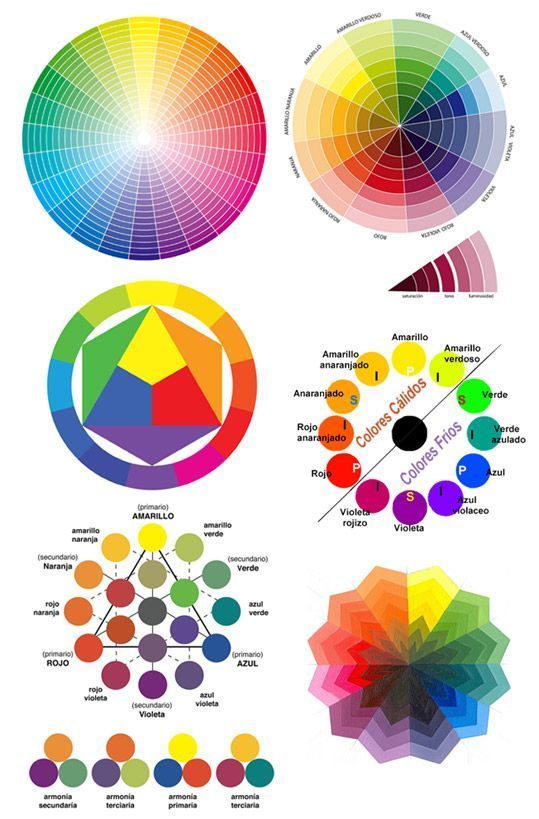 Во-вторых, многофокусное цветное изображение, представленное кватернионной матрицей, разлагается на низкочастотное субизображение и несколько высокочастотных субизображений с использованием многомасштабного разложения по сингулярным числам (MSVD). Первый содержит приблизительную информацию о структуре и цвете исходного изображения, второй содержит подробные характеристики. Затем низкочастотный компонент и высокочастотный компонент соответственно объединяются на основе разных правил слияния. Разработанное правило слияния полностью использует коэффициент разложения, представленный кватернионом, и применяет структурную информацию и информацию о цвете изображения к слиянию. Наконец, компоненты слияния используются для восстановления изображения слияния. Объединенное изображение может более точно поддерживать спектральные характеристики цветового канала. Мы определяем этот метод как кватернионное многомасштабное сингулярное разложение (QMSVD). Основные новшества этого метода перечислены ниже:

    • Комбинация кватерниона и многомасштабного разложения по сингулярным числам впервые применена к многофокусному слиянию цветных изображений. То есть цветное изображение, представленное кватернионом, подвергается разложению с помощью разложения по сингулярным числам в нескольких масштабах, а субизображения, полученные путем разложения, лучше сохраняют структуру и информацию о цвете исходного изображения.

    • Многоканальность впервые введена в QMSVD и предназначена для извлечения существенных признаков на каналах различных слоев декомпозиции для слияния изображений.

    • При слиянии низкочастотных субизображений, чтобы в полной мере использовать цветовую информацию изображения, предлагается улучшенное правило слияния максимизации локальной энергии, и правило слияния вводит цветовую разницу между пикселями и сочетает в себе местную энергию. При слиянии высокочастотных субизображений результаты слияния низкочастотных коэффициентов включаются в слияние высокочастотных субизображений, а правило слияния локального контраста основано на интеграции высокочастотных и низкочастотных фрагментов. регионов.

    Структура этого документа организована следующим образом. Раздел Многомасштабная сингулярная декомпозиция цветного изображения вводит понятие многомасштабной сингулярной декомпозиции цветного изображения. Раздел Многофокусное слияние цветных изображений на основе QMSVD предлагает модель многофокусного слияния цветных изображений на основе QMSVD. В разделе «Экспериментальные результаты и обсуждение» мы сравниваем и анализируем результаты, полученные с помощью современных методов. Наконец, выводы по данной статье сделаны в разделе Заключение.

    Многомасштабная сингулярная декомпозиция цветного изображения

    Для декомпозиции цветного изображения мы интегрируем кватернионное представление цветного изображения с многомасштабной декомпозицией. Таким образом, можно получить приблизительные и подробные части, представленные кватернионом. Две части соответственно сливаются, и объединенные компоненты используются для реконструкции объединенного изображения.

    Кватернион Представление цветного изображения

    Кватернионы были открыты в 1843 году ирландским математиком и физиком Уильямом Роуэном Гамильтоном. Это расширение обычного комплексного числа, которое расширяет обычные комплексные числа из двумерного пространства в четырехмерное пространство. Кватернион состоит из действительной части и трех мнимых частей. Операции трех мнимых частей эквивалентны, что делает его очень подходящим для описания цветных изображений и выражения внутренней связи цветовых каналов. Три цветовых канала изображения могут быть представлены тремя мнимыми частями кватерниона (Chen et al., 2014; Xu et al., 2015; Grigoryan and Agaian, 2018). Общая форма кватерниона q = q _a + q _b i + q _c j + q _d k . It contains one real part q _a and three imaginary parts q _b i , q _c j and q _c k , если действительная часть q _a кватерниона q равна нулю, то q называется чистым кватернионом. Сопряжение кватернионов определяется как:

    q*=qa-qbi-qcj-qdk    (1)

    Модуль кватерниона определяется как:

    |q|=qq*=qa2+qb2+qc2+qd2 (2)

    Теория вращения кватернионов сформулирована следующим образом:

    В трехмерном пространстве u является единицей чистого кватерниона, а модуль равен | и | = 1. Если R = e ^uθ , то RXR ^* указывает, что чистый кватернион X вращается на 2θ радиан вокруг оси. u и θ определяются как:

    u=1qb2+qc2+qd2(qbi+qcj+qbiqdk)θ={tan-1qb2+qc2+qd2/qa,qa≠0π/2qa=0

    Пусть u= (i+j+k)/3, который представляет собой трехмерную линию в градациях серого в пространстве RGB. Все три цветовых компонента пикселей на линии оттенков серого одинаковы. Пусть θ = π/2, то есть:

    RXR*=euπ/2X(euπ/2)*=(i+j+k)/3*X*(-i-j-k)/3    (3)

    Уравнение (3) означает, что X вращается вокруг серая линия u на 180 градусов. То есть X повернуто в противоположном направлении с u в качестве оси симметрии. Затем на линию оттенков серого попадает пиксель X + RXR ^* .

    Цветное изображение может быть представлено как чистый кватернион, то есть:

    f(x,y)=fR(x,y)·i+fG(x,y)·j+fB(x,y)· к    (4)

    In Equation (4), f _R ( x, y ), f _G ( x, y ), f _B ( x, y ) представляют компоненты цветовых каналов R, G и B цветного изображения соответственно. x, y представляют строки и столбцы матрицы цветного изображения, где находятся пиксели. Такое цветное изображение может быть представлено кватернионной матрицей, а обработка цветного изображения может выполняться непосредственно на кватернионной матрице. В отличие от традиционных подходов, которые преобразуют цветное изображение в изображение в градациях серого или обрабатывают каждый цветовой канал отдельно, кватернионный метод может обрабатывать цветное изображение как единое целое.

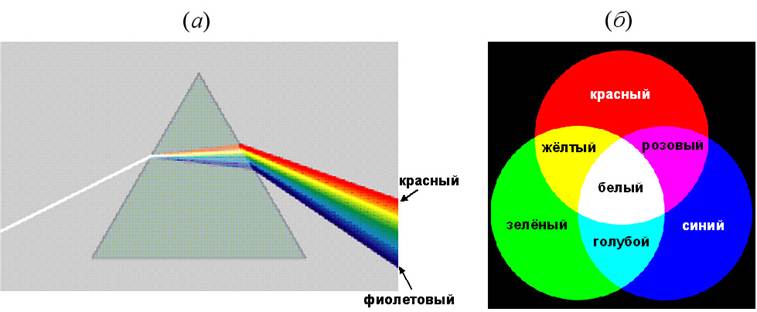
    Многомасштабное разложение цветного изображения

    Разложение по сингулярным числам является важным разложением матриц в линейной алгебре (Liu et al., 2019b) и заключается в разложении матрицы изображения по диагонали в соответствии с размером собственных значений. Среди разложенных изображений нет избыточности, и целесообразно использовать разные правила слияния для слияния каждого подизображения. В этом разделе мы распространяем декомпозицию на многомасштабную форму. С помощью мультимасштаба можно выполнять слияние изображений в разных масштабах и разных направлениях.

    X _q — матричная кватернионная форма цветного изображения f ( x, y ). Ранг кватернионной матрицы m × n X _q равен r . Given the m × m quaternion unitary matrix U _q and n × n quaternion unitary matrix V _q , we can get:

    (uq) hxqvq = [λr000] ≡λ∈Rm × n (5)

    , где суперпресс H представляет конъюгат транспонирование и λ _R = Diag {λ _{011011011071107, Diag {λ 01101101101101101101101107 гг. 2 , ⋯ , λ r }, λ i (1 ≤ i ≤ r ) is the singular value of X q , λ 1 ≥ λ 2 ≥ ⋯ ≥ λ r . Отсюда следует, что сингулярное разложение кватернионной матрицы X q равно:}

    Xq=Uq[Λr000](Vq)H    (6)

    В уравнении (6), Uq(Uq)H=Im×m,Vq(Vq)H=In ×nЕдиничная матрица.

    Многомасштабное сингулярное разложение цветного изображения, представленного кватернионом, может быть реализовано в соответствии с идеями, предложенными в Naidu (2011). Цветное изображение M × N X _q , представленное кватернионом, разделено на неперекрывающиеся m × n блоков, и каждый подблок организован в млн × 1 вектор. Комбинируя эти векторы-столбцы, можно получить кватернионную матрицу Xq’ размером . Сингулярное разложение Xq′ имеет вид:

    Xq′=Uq′Λ′(Vq′)H    (7)

    Uq′ и Vq′ — ортогональные матрицы, а Λ′ — невырожденная диагональная матрица после Xq′ разложение. Согласно уравнению (7):

    S=(Uq′)HXq′=Λ′(Vq′)H    (8)

    размер матрицы кватернионов S это мн × мн / мн .

    В соответствии с упомянутым выше разложением по сингулярным числам первый вектор-столбец Uq′ соответствует максимальному сингулярному значению. При умножении слева на матрицу Xq′ первая строка S (1, 🙂 числа S несет основную информацию из исходного изображения, которую можно рассматривать как приближенную или сглаженную составляющую исходного изображения. . Аналогично остальные строки S (2 : mn , 🙂 S соответствуют меньшим сингулярным значениям, которые сохраняют такую ​​детальную информацию, как текстура и кромка. Следовательно, посредством разложения по сингулярным значениям изображение может быть разложено на низкочастотные и высокочастотные части изображения по сингулярному значению для достижения многомасштабной декомпозиции изображения. В подходе QMSVD декомпозиция выполняется слой за слоем, повторяя описанный выше процесс. При повторной декомпозиции приблизительный компонент S (1, 🙂 верхнего слоя используется для замены следующего слоя из X _q .

    Когда исходное изображение разделено на блоки размером м × n , в соответствии с различными значениями м и n , QMSVD можно назвать ( м × n )-каналом QMSV D. For example: when m = 2 and n = 2 , it is called four-channel QMSVD when m = 2 and n = 3 or m = 3 and n = 2 , it is called six-channel QMSVD, when m = 2 and n = 4 or m = 4 and n = 2 , он называется восьмиканальным QMSVD.

    В качестве примера мы возьмем шестиканальный QMSVD, чтобы проиллюстрировать структуру декомпозиции каждого слоя. Пусть м = 2, n = 3 , а м × n = 6 :

    ,{ψh2,ψh3,ψh4,ψh5,ψH5},U}    (9)

    В уравнении (9) вектор компонентов аппроксимации с наименьшим разрешением равен ϕ _LL , векторы компонентов деталей равны {ψ _{H 1} , ψ _{H 2} , ψ _{H 3} , ψ _{H 4} , ψ _{H 5} }, а EIGECTOR — H 5 }, а EIGECTOR — H 5 }. При трансформации нижнего слоя ϕ _LL заменяется на X _q , разложение выполняется по уравнению (9), и получается разложение следующего слоя, а многослойное разложение изображения может быть получено путем повторения процесса. Поскольку процесс декомпозиции обратим, исходное изображение может быть восстановлено обратным преобразованием QMSVD.

    Метод QMSVD, предложенный в этой статье, метод MSVD (Naidu, 2011) и метод QSVD (Bihan and Sangwine, 2003) разлагают изображение посредством разложения по сингулярным числам, но у них есть свои отличительные характеристики. В Naidu (2011) MSVD в основном представляет собой метод разложения серых изображений. При разложении цветного изображения метод MSVD используется для каждого цветового канала, а затем объединяются три разложенных цветовых канала для получения разложенного цветного изображения. Этот метод декомпозиции разделения информации о канале игнорирует корреляцию между каналами и не принимает во внимание информацию о цвете изображения. Метод QMSVD преодолевает недостатки метода MSVD и может поддерживать корреляцию между цветовыми каналами при разложении цветных изображений. По сравнению с методом QMSVD, QSVD непосредственно разлагает цветные изображения для получения собственных значений и соответствующих собственных векторов. Затем, согласно опыту, мы используем метод усечения на QSVD, чтобы разделить собственные значения в порядке убывания на разные сегменты, чтобы реализовать декомпозицию изображения. Однако процесс декомпозиции, основанный на методе усечения опыта, лишен определенного физического смысла. Для придания четкого физического и геометрического смысла процессу декомпозиции вводится многоканальная КМСВД, которая непосредственно осуществляет декомпозицию изображения на низкочастотную и высокочастотную составляющие разного масштаба по размеру собственных значений.

    На рис. 1 сравниваются результаты, полученные тремя методами разложения. Видно, что: (1) Метод QMSVD непосредственно разлагает цветное изображение на низкочастотную составляющую и три высокочастотные составляющие. Низкочастотная составляющая является аппроксимацией исходного изображения, которая сохраняет характеристики исходного изображения с точки зрения структуры и цвета. Высокочастотные компоненты извлекают краевые и контурные особенности исходного изображения. (2) Метод MSVD не разлагает цветное изображение напрямую. Сначала разложите каждый цветовой канал, а затем объедините разложенные компоненты на низкочастотные и высокочастотные компоненты. По сравнению с методом QMSVD низкочастотная составляющая не сохраняет цветовые характеристики исходного изображения. Как видно из рисунка 1, основной цвет низкочастотной составляющей — синий, а основной цвет исходного изображения — красный. Высокочастотная составляющая выделяет краевые и контурные особенности исходного изображения, но не имеет мелких деталей, выделяемых методом QMSVD. Это связано с тем, что краевые элементы каждого компонента не могут полностью перекрываться при объединении компонентов. (3) По сравнению с методом QMSVD, метод QSVD не так хорош в извлечении подробных признаков.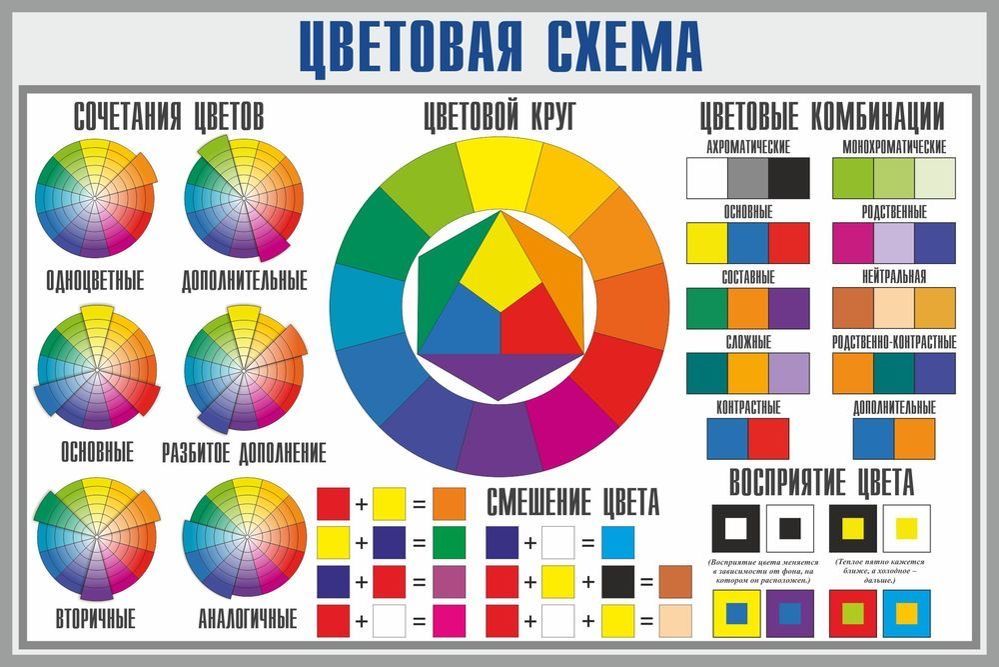 Из рисунка 1 видно, что основная информация о структуре и цвете находится в разложенном изображении, соответствующем первому значению признака, а другие значения признака усечены на три сегмента, соответствующие трем разложенным изображениям соответственно, и только эти изображения нести небольшое количество подробных функций. Поскольку метод QSVD в основном используется для сжатия изображений, в экспериментальной части сравнения мы сравниваем только QMSVD с методами MSVD.

    Рисунок 1 . На этом рисунке показано разложение цветного изображения по QMSVD, MSVD и QSVD. (A) Низкочастотное изображение исходного изображения после разложения с помощью QMSVD и (B–D) Высокочастотное изображение исходного изображения. (E) Низкочастотное изображение исходного изображения после разложения с помощью MSVD и (F–H) Высокочастотные изображения исходного изображения. (I) Изображение разложения, соответствующее первому собственному значению исходного изображения, разложенного с помощью QSVD, и (J) образ разложения, соответствующий собственному значению, усеченному со 2-го по 25-е после разложения QSVD, (K) образ разложения, соответствующий собственному значению, усеченному с 26-го по 50-е, (L) разложение изображение, соответствующее собственному значению, усеченному с 51-го до 240-го. 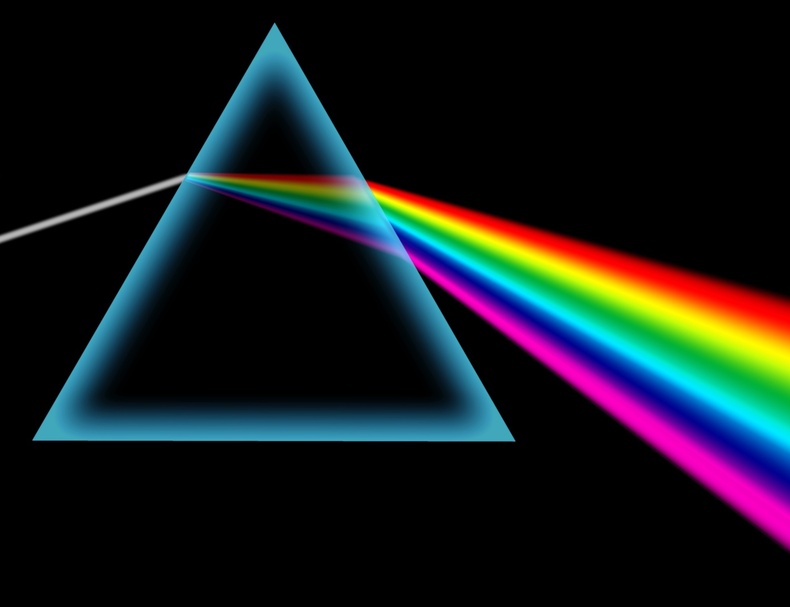Собственные значения располагаются от большего к меньшему.

    Многофокусное слияние цветных изображений на основе QMSVD

    Правила слияния низкочастотных компонентов

    Низкочастотный фрагмент изображения QMSVD отражает общие характеристики исходного цветного изображения. Обычно используемые правила слияния низкочастотных фрагментов изображения включают средневзвешенную и максимальную локальную энергию. Правило средневзвешенного значения состоит в том, чтобы получить коэффициент слияния по средневзвешенному значению низкочастотных коэффициентов в одном и том же положении изображений, что приведет к снижению контрастности совмещенного изображения. Правило максимальной локальной энергии состоит в том, чтобы сравнить энергию низкочастотных коэффициентов при одном и том же положении изображений и выбрать более высокую энергию в качестве коэффициента слияния. Это правило слияния учитывает только локальную энергию изображения и не учитывает информацию о цвете, содержащуюся в цветном изображении, поэтому визуальный эффект изображения слияния цветов нежелателен. Чтобы преодолеть несоответствие, QMSVD использует кватернион для представления цветного изображения и вычисляет цветовую разницу между двумя цветными пикселями на основе теории вращения кватерниона. Энергия окна коэффициентов используется в качестве уровня активности низкочастотного компонента, а цветовая разница между цветовыми пикселями в центре окна коэффициентов рассматривается как уровень соответствия, причем оба они совместно участвуют в отображении решения.

    Уровень активности

    Учитывая, что зрительная система человека чувствительна к локальным изменениям, в качестве измерения уровня активности используется локальная энергия окна. Локальные области с большей дисперсией демонстрируют больший контраст между пикселями и более высокий уровень активности окна. Напротив, значения пикселей, более однородные в локальных областях с меньшей дисперсией, отображают более слабый уровень активности окна. Поэтому в качестве результата слияния выбирается пиксель с самым высоким контрастом по низкочастотному коэффициенту.

    aSj(x,y)=|CSj(x,y)-mean(x′,y′)∈p(CSj(x+x′,y+y′))| (10)

    Где S представляет собой два цветных многофокусных изображения A и B , которые необходимо объединить, j представляет собой шкалу разложения, CSj(x,y) представляет собой низкочастотный поддиапазон коэффициент исходного изображения S в масштабе j в пикселе ( x, y ), P — диапазон окна коэффициента, aSj(x,y) — уровень активности CSj(x,y) ) в пикселях ( x, y ), а означает, что (·) представляет среднюю фильтрацию. Эксперименты показывают, что визуальный эффект после слияния изображений наиболее оптимален, когда P использует локальные окна размером 3×3.

    Уровень соответствия

    Уровень соответствия между пикселями A и B двух цветных многофокусных изображений можно измерить по цветовым различиям между ними, которые можно рассчитать с помощью теории вращения кватернионов (Jin et al. , 2013). Поскольку цветовое различие включает в себя цветность и яркость, формула для расчета уровня согласования выглядит следующим образом:

    mABj(x,y)=t|Q(q1,q2)|+(1-t)|I(q1,q2)| (11)

    In Equation (11), q ₁ = r ₁ i + g ₁ j + b ₁ k and q ₂ = R ₂ I + G ₂ J + B ₂ K — Pixles Pixles.0320 А и В соответственно. Q ( Q ₁ , Q ₂ ) и I ( Q ₁ , Q ₂ ). Деноте различия в Chracom и LUM. ₁ и q ₂ , вес t ∈ [0, 1] указывает на относительную важность цветности и яркости, а j представляет шкалу разложения. Согласно теории вращения кватернионов соотношение между q ₁ и q ₂ можно выразить как q3=q1+Rq2R*=r3·i+g3·j+b3·k, R = e ^{5π5 9269 1π5 9200 , u=(i+j+k)/3. 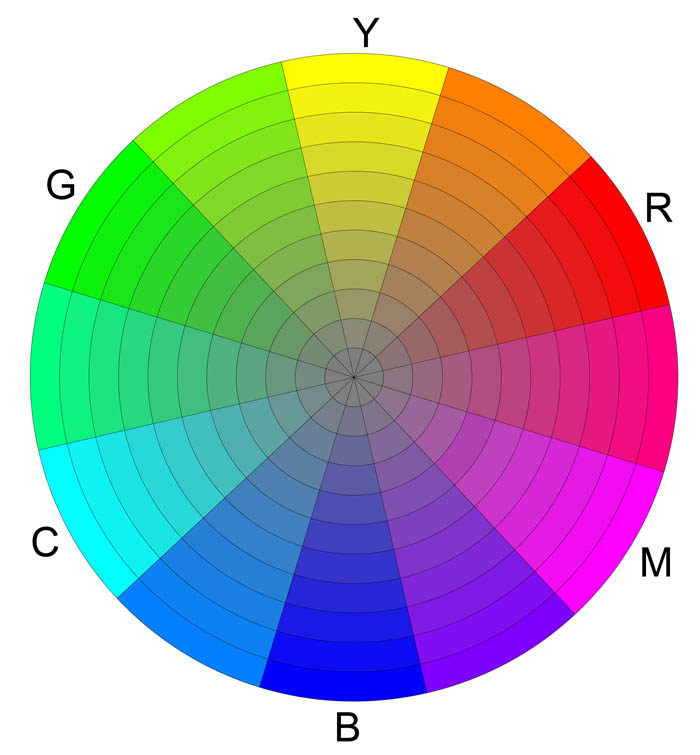If the chromaticity of q ₁ is similar to that of q ₂ , q ₃ should be near the grayscale line u , and the chromaticity difference between q ₁ and q ₂ можно выразить следующим уравнением:}

    Q(q1,q2) =(r3−(r3+g3+b3)/3)⋅i+(g3−(r3+g3                         +b3)/3)⋅j+(b3−(r3+g3+b3)/ 3)⋅k    (12)

    When Q ( q ₁ , q ₂ ) is small, the chromaticity of q ₁ and q ₂ are similar; когда Q ( q ₁ , q ₂ ) = 0, q ₁ и q 2 имеют одинаковую цветность 1. Разница в яркости между q ₁ и q ₂ можно представить как:

    I(q1,q2)=(r1-r2)/3+(g1-g2)/3+(b1-b2)/3 (13)

    Согласно уравнениям (11–13), размер mq1q2j пропорционален разнице в цвете между q ₁ и q ₂ . Следовательно, уровень соответствия между двумя пикселями можно измерить по размеру цветовой разницы.

    План принятия решения

    Значение решения оценки фокусировки цветного изображения определяется уровнем активности и уровнем соответствия локального окна. Они получаются по уравнениям (10, 11) соответственно. Значение решения рассчитывается по следующей формуле:

    dj(x,y)={1,если mABj(x,y)>T и aAj(x,y)≥aBj(x,y)0,если mABj(x,y)>T и aAj(x ,y)

    По значению решения d ^j ( x, y ) совмещенное низкочастотное изображение может быть получено с использованием FLj(x,y)=dj(x,y)*ALj(x,y)+(1-dj(x,y))*BLj(x,y), где FLj(x,y) представляет низкочастотное субизображение после слияния ALj(x,y) и BLj(x,y) в масштабе Дж . В уравнении (14) T является порогом соответствия между пикселем A и пикселем B многофокусного изображения.

    Правила объединения высокочастотных компонентов

    В уравнении (8) первая строка S представляет низкочастотный компонент исходного изображения, который несет основную информацию из изображения. Другие строки S (2 : mn , 🙂 S обозначают высокочастотные компоненты исходного изображения, представляя детали изображения. В соответствии с ортогональностью разложения по сингулярным числам каждый компонент образует ортогональное дополнение в том же масштабе. Прямая сумма каждого компонента:

    Ij=Ij+1⊕∑i=2mnS(i,:)j+1 (j=2,1,0)    (15)

    , где j представляет собой шкалу разложения; когда j = 2, самый высокий слой разложения равен 3, I ₃ = S (1, 🙂 ₃ , и каждая компонента может быть записана как:

    {I2=S(1, :)3⊕∑i=2mnS(i,:)3 j=2,I1=I2⊕∑i=2mnS(i,:)2 j=1,I0=I1⊕∑i=2mnS(i,:)1 j=0,    (16)

    Высокочастотные части изображения QMSVD отражают подробные характеристики исходного изображения. Большинство методов слияния работают в области признаков высокочастотных составляющих, не принимая во внимание влияние низких частот, что ухудшает качество слияния. Чтобы учесть влияние низкочастотных составляющих при слиянии высокочастотных компонентов, предлагается правило локального контрастного слияния, применимое как к высокочастотным, так и к низкочастотным областям. После декомпозиции исходного изображения с помощью QMSVD локальный контраст высокочастотной и низкочастотной составляющих можно получить по следующему уравнению (Pu and Ni, 2000):

    CSjk(x,y)=ISjHk(x,y)/IABjL(x,y),(Sj=AjorBj)    (17)

    В уравнении (17) IABjL представляет компонент синтеза низкочастотного сабвуфера. -изображение исходного изображения A и B в масштабе j , а ISjHk представляет собой k-ю высокочастотную составляющую исходного изображения S в масштабе j . Согласно уравнению (15), высокочастотные компоненты не накладываются на низкочастотные компоненты, и поэтому определение локального контраста, отражающего высокочастотные компоненты, справедливо. 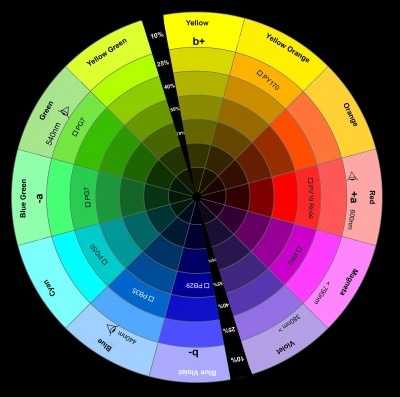Слияние высокочастотных субизображений определяется как:

    HFjk(x,y)={IAjHk(x,y),если|CAjk(x,y)|≥|CBjk(x,y)|IBjHk(x,y),иначе    (18)

    , где HFjk (x,y) представляет k -й высокочастотный компонент объединенного изображения F в масштабе j .

    Процесс слияния многофокусных цветных изображений

    На рис. 2 показана схема слияния многофокусных цветных изображений на основе QMSVD с шестью каналами, и соответствующий процесс слияния выглядит следующим образом:

    Шаг 1: Два исходных цветных мультифокуса изображения A и B разложены с помощью QMSVD. Низкочастотный субобраз A _L , B _L is represented by one channel and the high-frequency sub-images A _{H i} , B _{H i} ( H _i — i -й высокочастотный канал) представлены несколькими каналами. Ортогональные матрицы U _A и U _B , соответствующие сингулярным значениям.

    Шаг 2: Низкочастотные части изображения A _L , B _L объединяются по правилам низкочастотного объединения, а высокочастотные части изображения 7 H _i , B _{H i} сплавляются по правилам высокочастотного сплавления.

    Шаг 3: Ортогональные матрицы U _A и U _B (полученные на шаге 1) сливаются. При слиянии двух изображений после разложения QMSVD роли U _A и U _B одинаковы, поэтому правило слияния для ортогональной матрицы: = ( У _А + У _В )/2.

    Этап 4: Окончательное изображение слияния получается путем обратного QMSVD-преобразования результатов слияния на этапах 2 и 3.

    Рисунок 2 . Слияние субизображений с помощью QMSVD с шестью каналами. LL — низкочастотная составляющая разложенного изображения, h2–H5 — высокочастотные составляющие разложенного изображения, U _A и U

    B 9027 — ортогональные матрицы разложенного изображения и

    U _F = ( U _A + U _B )/2.

    Экспериментальные результаты и обсуждение

    В этом исследовании насыщенность цветовой информацией (CCM) (Yuan et al., 2011), пространственная частота (SF), показатель контрастности изображения (ICM) (Yuan et al., 2011) и границы сохранение информации (QAB/F) (Liu et al., 2012) используются для объективной оценки многофокусного изображения слияния цветов и для проверки эффективности алгоритма. Значение индекса CCM определяется цветностью цвета и градиентом цветового различия объединенного изображения. Индекс SF отражает четкость деталей изображения. Индекс ICM состоит из контраста оттенков серого и цветового контраста объединенного изображения, при этом значение обозначает контраст в объединенном изображении. Индекс QAB/F показывает, сколько информации о границах и структуре из исходного изображения сохраняется в объединенном изображении. Для приведенных выше показателей оценки большее значение оценки предполагает лучший результат слияния.

    Предлагаемый метод слияния цветных изображений QMSVD сравнивается с пятью типичными методами слияния многофокусных изображений, которые относятся к категории метода слияния с разложением по сингулярным значениям с несколькими разрешениями (MSVD) (Naidu, 2011), метод слияния на основе градиента (MWGF) (Zhou et al., 2014), метод слияния на основе форсированных случайных блужданий (RWTS) (Ma et al., 2019), метод слияния на основе управляемого фильтра (GFDF) (Qiu et al. al., 2019), метод глубокого слияния CNN (CNN) (Liu et al., 2017). Среди них MSVD, MWGF, RWTS и GFDF являются традиционными методами слияния изображений. 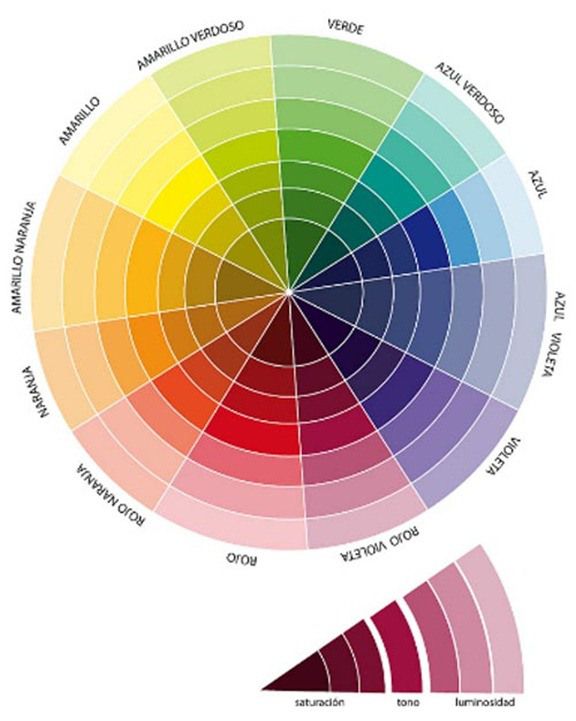CNN — это недавно предложенный метод слияния изображений, основанный на глубоком обучении. В Лю и соавт. (2017), Лю выбирает сиамцев в качестве модели CNN, а сеть имеет три сверточных слоя и один слой максимального объединения. Обучающая выборка представляет собой высококачественное естественное изображение из 50 000 из набора данных ImageNet, а размер входного фрагмента установлен на 16 × 16. Реализация Matlab пяти вышеуказанных методов слияния получена онлайн, а параметры являются заданными значениями по умолчанию. в литературе. Исходные многофокусные изображения, использованные в эксперименте, получены из нескольких наборов данных изображений. Четыре изображения (A), (B), (D), (E) на рисунке 4 и одно изображение (I) на рисунке 6 получены из набора данных Lytro (Nejati et al., 2015). Шесть изображений (A)–(F) на рис. 6 получены из набора данных Slavica (Slavica, 2011). Одно изображение (C) на рисунке 4 и два изображения (G) и (H) на рисунке 6 получены из набора данных Saeedi (Saeedi and Faez, 2015). 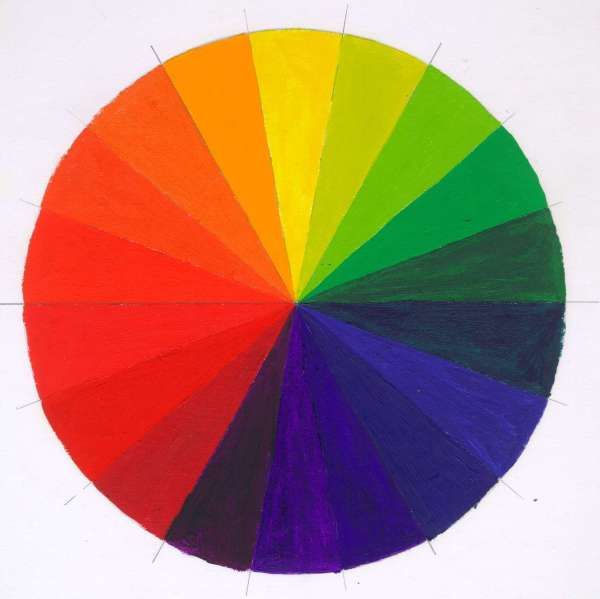Одно изображение (J) на рисунке 6 получено из набора данных Bavirisetti (Bavirisetti). В этой статье в наборах данных изображений Lytro и Saeedi выбраны пять групп цветных изображений с насыщенными цветами, и они используются в сравнительном эксперименте. Кроме того, 10 групп многофокусных изображений обычно используются в других связанных статьях, поскольку экспериментальные данные используются в сравнительном эксперименте, и они имеют разные размеры и характеристики.

    В экспериментальном процессе, во-первых, экспериментальные параметры алгоритма, установленные до начала эксперимента. Во-вторых, результаты слияния, полученные с использованием предложенного алгоритма и других алгоритмов, представлены и сравнены.

    Выбор экспериментальных параметров

    Многомасштабная сингулярная декомпозиция цветных изображений проводится через несколько независимых слоев и каналов. Декомпозиция изображения обычно делит изображение на три слоя. Канальная декомпозиция обычно делит изображение на четырехканальное, шестиканальное, восьмиканальное и девятиканальное. Разложение канала освещено в уравнении (9). На результат слияния изображений также влияет размер локального окна P, типичный размер которого составляет 3×3 или 5×5. Экспериментальное сравнение показывает, что локальное окно 5 × 5 превышает размер важной функции изображения, что подрывает оценку активности локального окна. Поэтому в этой статье мы устанавливаем локальный размер окна равным P = 3 × 3 . Как видно из уравнения (11), вес t ∈ [0, 1] указывает на относительную важность цветности и яркости, при этом t положительно связан с цветностью. В уравнении (14) T представляет собой порог совпадения уровня совпадения между пикселями двух цветных многофокусных изображений, которые должны быть объединены, и значение T напрямую влияет на значение решения 9.0320 d ( x, y ) низкочастотного слияния. Рассмотренные выше параметры в конечном итоге определяют эффект слияния изображений.

    Мы установили разные значения параметров, провели повторные сравнительные эксперименты и использовали два объективных индекса пространственную частоту (SF) и показатель цветовой красочности (CCM) (Yuan et al. , 2011) для оценки рисунка 3. Как видно из таблицы 1, SF значение уменьшается по мере увеличения числа каналов, чем больше число каналов, тем более сглажено изображение после многомасштабного разложения по сингулярным числам и тем ниже пространственная частота. Максимальное значение CCM возникает при т = 0,9. Согласно уравнению (11), значение t указывает на важность цветности. Анализ показывает, что предложенный в статье алгоритм реализуем. Из дальнейшего анализа табл. 1 можно получить предварительные параметры: P = 3, t = 0,9, T = 0,01 и P = 3, t =

    0 0,9 0,9. = 0,03 , с шестью и восемью каналами разложения.

    Рисунок 3 . Протестировано многофокусное цветное изображение. (A,B) — исходные изображения. Параметры выбраны: в (C–F) , слой = 2, P = 3, t = 0,9, T = 0,01; в (Г–Ж) , слой = 2, P = 3, t = 0,9, T = 0,03; с четырьмя, шестью, восемью и девятью каналами разложения.

    Таблица 1 . Выбор исходных параметров (1).

    На рис. 3 представлены результаты, полученные во втором слое разложения с использованием проанализированных выше предварительных параметров. Очевидно, что фьюжн-изображение, основанное на четырехканальной декомпозиции, имеет наихудший визуальный эффект, а на краях деталей появляется зигзагообразное искажение, которое возникает из-за блочного эффекта, вызванного мелкоканальной декомпозицией. Артефакты появляются на краю объединенного изображения, полученного с помощью девятиканальной декомпозиции. Это связано с большим разложением канала, которое приводит к размытию объединенного изображения. Совмещенные изображения, полученные с помощью шестиканальной и восьмиканальной декомпозиции, имеют схожие эффекты и наилучшее качество. Судя по таблице 1, можно сделать вывод, что субъективные визуальные эффекты соответствуют объективным оценочным значениям. Другими словами, значение объективной оценки положительно пропорционально субъективному визуальному эффекту.

    Из приведенного выше анализа следует, что эффекты слияния шестиканальной и восьмиканальной декомпозиции превосходят эффекты четырехканальной или девятиканальной декомпозиции. Дальнейший анализ таблицы 2 показывает, что общие результаты SF и CCM с шестью каналами лучше, чем с восемью каналами, поэтому мы, наконец, принимаем шестиканальный подход к декомпозиции. Согласно табл. 1 при шестиканальном разложении, когда P = 3, t = 0,9, T = 0,03 и слой = 1, максимальное значение SF равно 27,1624, а когда слой = 2, максимальное значение CCM равно 17,2871. Чтобы оптимизировать результат многофокусного слияния цветных изображений, мы принимаем во внимание важность индекса оценки цвета CCM при слиянии цветных изображений и используем подход с шестиканальной декомпозицией и устанавливаем P = 3, t = 0,9, T = 0,03, а слой = 2,

    Таблица 2 . Выбор исходных параметров (2).

    Субъективная оценка

    Для проверки работоспособности предлагаемого метода многофокусного слияния цветных изображений с точки зрения зрительного восприятия для нашего эксперимента выбрано 15 групп многофокусных цветных изображений. Пять групп взяты из набора данных многофокусных изображений «Lytro», а остальные 10 групп широко используются при слиянии многофокусных изображений. Между тем, предлагаемый метод слияния сравнивается с пятью типичными методами слияния многофокусных изображений, а именно MSVD, MWGF, RWTS, GFDF и CNN.

    На рисунке 4 мы выбрали пять групп изображений из многофокусного набора данных «lytro» для экспериментов. Они имеют насыщенные цвета, которые также являются экспериментальными данными, используемыми в пяти алгоритмах сравнения. Области на каждом изображении, которые необходимо сравнить, отмечены красной рамкой. Рисунок 5 представляет собой результат слияния, соответствующий пяти исходным изображениям на рисунке 4. Для лучшего сравнения области красной рамки на объединенном изображении увеличены.

    Рисунок 4 . Пять групп многофокусных цветных исходных изображений. Красные кадры — это область, которую необходимо сравнивать при слиянии изображений. (A) Женщина, (B) Ребенок, (C) Книга, (D) Девушка и (E) Ребенок. Четыре изображения (A,B,D,E) из набора данных Lytro, изображение (C) из набора данных Saeedi.

    Рисунок 5 . Соответствует результатам слияния пяти исходных изображений на рисунке 4.9.0011 A(1)–E(1) — изображения слияния, полученные методом GFDF. A(2)–E(2) — совмещенные изображения, полученные методом MWGF. A(3)–E(3) — изображения слияния, полученные методом CNN. A(4)–E(4) — изображения слияния, полученные методом RWTS. A(5)–E(5) — изображения слияния, полученные методом MSVD. A(6)–E(6) — изображения слияния, полученные методом QMSVD.

    Группа A(1)–A(6) показывает изображения «женщины» размером 208 × 208 и совмещенное изображение, полученное 6 различными методами слияния. Сравнение областей, обведенных красным, показывает, что QMSVD, RWTS, MSVD и GFDF имеют наилучшую визуальную четкость, за ними следует CNN, а MDGF является наиболее размытым. Дальнейшее сравнение показывает, что на объединенном изображении, полученном с помощью MSVD, область с красной рамкой и изображение «женщины» имеют явные цветовые искажения.

    Группа B(1)–B(6) показывает изображения «ребенка» размером 256 × 256 и совмещенное изображение, полученное шестью различными методами слияния. Сравнение областей, обведенных красными рамками, показывает, что QMSVD и MWGF имеют наилучшую визуальную четкость, а GFDF — самую нечеткую. Дальнейшее сравнение показывает, что на комбинированном изображении, полученном с помощью MSVD, яркость лица «ребенка» самая низкая.

    Группа C(1)–C(6) показывает изображения «книги» размером 320 × 240 и совмещенное изображение, полученное шестью различными методами слияния. Сравнение английских букв в красной рамке каждого изображения. С визуальной точки зрения метод на основе MSVD является наиболее размытым, а эффекты слияния, достигаемые другими методами, аналогичны.

    Группа D(1)–D(6) показывает изображения «девушки» размером 300 × 300 и совмещенное изображение, полученное шестью различными методами слияния. Сравнивая листья в красной области рамки каждого изображения, QMSVD и RWTS могут создать наилучший эффект слияния изображений, а цвет близок к исходному изображению.

    Группа E(1)–E(6) показывает изображения «ребенка» размером 360 × 360 и совмещенное изображение, полученное 6 различными методами слияния. Сравнение показывает, что QMSVD, CNN и RWTS обеспечивают наилучшие эффекты слияния изображений, за ними следуют GFDF и MSVD, а MWGF отстает.

    Чтобы еще раз доказать эффективность метода QMSVD для многофокусного слияния цветных изображений, 10 групп исходных изображений представлены на рисунке 6. На рисунке 7 показано объединенное изображение, полученное шестью различными методами слияния. На рисунках 8, 9 мы детально сравниваем две группы изображений.

    Рисунок 6 . Десять групп мультифокусных цветных изображений. (A) Размер 267×171, (B) Размер 267×175, (C) Размер 267×177, (D) Размер 267×177, (E) размер 267×174, (F) размер 320×200, (G) размер 267×174, (H) размер 390×260, (I) размер размером 222×148 и (J) размером 360×360. Шесть изображений (A–F) из набора данных Slavica, два изображения (G, H) из набора данных Saeedi, изображение (I) из набора данных Lytro и изображение (J) из набора данных Bavirisetti.

    Рисунок 7 . Десять групп многофокусных изображений слияния цветов.

    Рисунок 8 . Изображения слияния «Бутылка из-под кока-колы», полученные шестью различными методами слияния.

    Рисунок 9 . Совмещенные изображения «леса», полученные шестью различными методами слияния.

    На рис. 8 показано исходное изображение «Бутылка кока-колы» размером 320 × 200 и совмещенное изображение, полученное шестью различными методами слияния. Сравните яркие пятна в красной области кадра каждого изображения, QMSVD, CNN и GFDF обеспечивают лучшую четкость, за ними следуют MWGF и RWTS, а MSVD является наиболее неоднозначным.

    На рисунке 9 показано исходное изображение «Леса» размером 267×171 и совмещенное изображение, полученное шестью различными методами слияния. Сравните яркость листьев в красной области кадра каждого изображения, QMSVD, превосходя другие методы, позволяет получить наилучший эффект слияния изображений.

    В целом метод QMSVD сочетает в себе преимущества кватернионов и многомасштабной декомпозиции при слиянии цветных многофокусных изображений. Преимущество заключается в том, что кватернионы могут представлять и обрабатывать различные цветовые каналы цветного изображения в целом, создавая слитное многофокусное изображение с высокой точностью. Методы многомасштабной декомпозиции разлагают изображение на низкочастотную и высокочастотную составляющие на разных уровнях. Таким образом, разложенные изображения могут быть точно объединены по различным компонентам, масштабам и уровням, что позволяет получить многофокусное изображение слитного цвета с высокой четкостью и контрастностью, а также с хорошими визуальными эффектами.

    Объективная оценка

    Мы предложили метод многофокусного слияния цветных изображений. Мы классифицируем экспериментальные изображения по двум категориям. Один тип — многофокусные цветные изображения с богатой цветовой информацией, а метрики их объективной оценки различными методами представлены в таблице 3. Другой тип — обычно используемые многофокусные цветные изображения. Мы выбрали две группы, и их показатели объективной оценки различных методов подсчитываются в таблице 4. Таблица 5 представляет собой средние показатели объективной оценки различных методов на 15 группах цветных изображений. Анализ таблиц 3–5 показывает, что средние значения 15 групп, использующих показатели CCM и ICM алгоритма QMSVD, значительно выше, чем у других алгоритмов слияния. Это также показывает, что объединенное изображение имеет высокую четкость и насыщенный цвет, что согласуется с визуальными характеристиками объединенного изображения при субъективной оценке. Из всех алгоритмов слияния индекс CCM алгоритма QMSVD занимает первое место. Для индикатора QAB/F алгоритм QMSVD работает хуже, чем другие алгоритмы, в сохранении информации о границах и структуре. В целом, метод QMSVD дает наилучшие результаты по показателю CCM и хорошо работает по показателям ICM и SF. Это показывает, что метод QMSVD эффективен, а объединенное изображение имеет высокое разрешение, насыщенный цвет, меньшую потерю информации и хорошие общие визуальные эффекты.

    Таблица 3 . Значения объективной оценки многофокусных цветных изображений.

    Таблица 4 . Показатели объективной оценки многофокусных цветных изображений на рисунках 8, 9.

    Таблица 5 . Средние показатели объективной оценки различных методов на 15 группах цветных изображений.

    Заключение

    В этой статье предлагается многофокусный алгоритм слияния цветных изображений, основанный на кватернионном многомасштабном разложении по сингулярным числам. В алгоритме цветное многофокусное изображение, представленное кватернионами, подвергается многомасштабной декомпозиции в целом, что позволяет избежать потери информации о цвете, вызванной многомасштабной декомпозицией каждого цветового канала в отдельности. Кроме того, алгоритм может точно объединять информацию о декомпозированном изображении в различных компонентах, масштабах и уровнях. Чтобы проверить эффективность алгоритма, он был проанализирован качественно и количественно и сравнен с классическим алгоритмом слияния с многомасштабной декомпозицией и алгоритмами слияния, предложенными в последней литературе. Экспериментальные результаты показывают, что результат слияния этого метода сообщает о значительном улучшении субъективных визуальных эффектов. Он также хорошо работает по показателям объективной оценки, в частности, по показателю CCM насыщенности цветовой информации объединенного изображения. Поскольку алгоритм, предложенный в этой статье, основан на многофокусных цветных изображениях, представленных кватернионом, для обработки многомасштабной декомпозиции изображений требуется больше времени. Необходимо провести дальнейшие исследования, чтобы повысить эффективность алгоритма и обеспечить качество слияния изображений. Что касается настройки параметров алгоритма, то он в основном основан на эмпирических значениях, таких как выбор количества каналов, выбор размера локального окна и т. д. В будущем адаптивный выбор параметров также находится в центре нашего будущего. исследовательская работа. Кроме того, цветные изображения представлены не полными компонентами кватерниона, а чистым кватернионом в слиянии изображений. Как использовать информацию о реальной части кватерниона при обработке цветных изображений, мы сосредоточимся в будущем исследовании.

    Заявление о доступности данных

    В этом исследовании были проанализированы общедоступные наборы данных. Эти данные можно найти по адресу: https://dsp.etfbl.net/mif/; https://mansournejati.ece.iut.ac.ir/content/lytro-multi-focus-dataset.

    Вклад авторов

    HW, XT и BX задумали это исследование. HW и BX разработали алгоритм. HW выполнил компьютерное моделирование и написал первоначальный проект. HW и ZZ проанализировали данные. WL и XT пересмотрели и отредактировали рукопись. Все авторы подтвердили представленную версию.

    Финансирование

    Это исследование финансировалось Национальным фондом естественных наук Китая в рамках проекта 61673079, Фондом естественных наук Чунцина в рамках проекта cstc2018jcyjAX0160 и Фондом комиссии по образованию Чунцина Китая (гранты № KJQN201

    7 и KJ120611).

    Конфликт интересов

    Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

    Благодарности

    Авторы благодарят редакторов и рецензентов за их тщательную работу и ценные предложения для этого исследования.

    Ссылки

    Ан, Ф. и Ли, З. (2019). Алгоритм обработки изображений на основе двумерного разложения локального среднего. Дж. Матем. Визуализация VIS 61, 1243–1257. дои: 10.1007/s10851-019-00899-8

    Полнотекстовая перекрестная ссылка | Google Scholar

    Аймаз С. и Кёсе К. (2019). Новая гибридная техника на основе декомпозиции изображений с методом сверхвысокого разрешения для многофокусного слияния изображений. Инф. Фьюжн 45, 113–127. doi: 10.1016/j.inffus.2018.01.015

    CrossRef Полный текст | Google Scholar

    Бавиризетти, Д. П. Набор данных Fusion Image . Доступно в Интернете по адресу: https://sites. google.com/view/durgaprasadbavirisetti/datasets

    Bihan, N., and Sangwine, S. (2003). «Разложение цветного изображения с использованием разложения по сингулярным числам кватерниона», в Proc. 2003 Междунар. Conf.Visual Information Engineering (VIE 2003) (Суррей), 113–116.

    Google Scholar

    Берт П. и Колчински Р. (1993). «Улучшенный захват изображений посредством слияния», Четвертая международная конференция IEEE по компьютерному зрению (Берлин), 173–182.

    Google Scholar

    Чен Б., Шу Х., Коатрие Г., Чен Г. и Коатрие Дж. (2014). Анализ цветового изображения по моментам кватернионного типа. Дж. Матем. Визуализация VIS 51, 124–144. doi: 10.1007/s10851-014-0511-6

    Полный текст CrossRef | Академия Google

    Ду, Дж., Ли, В., Сяо, Б., и Наваз, К. (2016). Пирамида Union Laplacian с множеством функций для слияния медицинских изображений. Нейрокомпьютинг 194, 326–339. doi: 10.1016/j.neucom.2016.02.047

    Полный текст CrossRef | Google Scholar

    Дуан Дж. , Чен Л. и Чен К. (2018). Многофокусное слияние изображений с улучшенной линейной спектральной кластеризацией и быстрой оценкой карты глубины. Нейрокомпьютинг 318, 43–54. doi: 10.1016/j.neucom.2018.08.024

    Полный текст CrossRef | Академия Google

    Гонсало, П., и Хесус, М. (2002). Учебное пособие по слиянию изображений на основе вейвлета. Распознавание образов. 37, 1855–1872 гг. doi: 10.1016/j.patcog.2004.03.010

    Полный текст CrossRef | Google Scholar

    Григорян А. М., Агаян С. С. (2018). Обработка цветных изображений кватернионов и октонионов с помощью Matlab . Беллингем, Вашингтон: SPIE, 111–139.

    Ярослав К., Ян Ф., Варвара З. и Станислава С. (2002). Новая мера фокусировки изображения на основе вейвлета. Распознавание образов. Письмо . 23, 1785–1794. doi: 10.1016/S0167-8655(02)00152-6

    Полный текст CrossRef | Google Scholar

    Джин Л., Сонг Э., Ли Л. и Ли X. (2013). «Кватернионный оператор градиента для обнаружения края цветного изображения», в Международной конференции IEEE по обработке изображений (ICIP) (Мельбурн, Виктория), 3040–3044.

    Google Scholar

    Цзинь X., Чен Г., Хоу Дж., Цзян К., Чжоу Д. и Яо С. (2018a). Слияние мультимодальных сенсорных медицинских изображений на основе преобразования Шерлета без субдискретизации и S-PCNN в пространстве HSV. Сигнальный процесс. 153, 379–395. doi: 10.1016/j.sigpro.2018.08.002

    Полный текст CrossRef | Google Scholar

    Джин X., Цзян Q., Чу X., Сюнь Л., Яо С., Ли К. и др. (2020). Слияние медицинских изображений головного мозга с использованием функций, основанных на норме L2, и нечетко-взвешенных измерений в области EWT 2D Littlewood-Paley. IEEE Trans. Инструм. Изм. 69, 5900–5913. doi: 10.1109/TIM.2019.2962849

    Полный текст CrossRef | Google Scholar

    Цзинь, X., Чжоу, Д., Яо, С., и Ни, Р. (2018b). Метод многофокусного слияния изображений с использованием S-PCNN, оптимизированный с помощью оптимизации роя частиц. Мягкие вычисления. 22, 6395–6407. doi: 10.1007/s00500-017-2694-4

    Полный текст CrossRef | Google Scholar

    Какарла Р. и Огунбона П. (2001). Анализ сигналов с использованием формы разложения по сингулярным числам с несколькими разрешениями. IEEE Trans. Процесс изображения. 10, 724–735. doi: 10.1109/83.6

    PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

    Li, J., Guo, X., Lu, G., Zhang, B., Xu, Y., Wu, F., et al. (2020). Drpl: глубокое регрессионное парное обучение для многофокусного слияния изображений. IEEE Trans. Процесс изображения. 29, 4816–4831. doi: 10.1109/TIP.2020.2976190

    PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

    Ли С., Канг X., Фанг Л., Ху Дж. и Инь Х. (2017). Слияние изображений на уровне пикселей: обзор современного уровня техники. Инф. Фьюжн 33, 100–112. doi: 10.1016/j.inffus.2016.05.004

    Полный текст CrossRef | Google Scholar

    Li, Y., Sun, Y., Huang, X., Qi, G., Zheng, M., and Zhu, Z. (2018). Метод слияния изображений, основанный на разреженном представлении и суммарном модифицированном лапласиане в домене NSCT. Энтропия 20:522. doi: 10.3390/e20070522

    PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

    Лян, Дж., и Хе, Ю. (2012). Слияние изображений с использованием разложения по сингулярным числам более высокого порядка. IEEE Trans. Процесс изображения. 21, 2898–2909. doi: 10.1109/TIP.2012.2183140

    PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

    Лю С., Ху К., Ли П., Чжао Дж., Лю М. и Чжу З. (2019a). Подавление спеклов на основе минимизации взвешенных ядерных норм и теории Грея. IEEE Trans. Geosci. Дистанционный датчик 57, 2700–2708. doi: 10.1109/TGRS.2018.2876339

    CrossRef Full Text | Google Scholar

    Лю С., Ма Дж., Инь Л. и Ху С. (2020). Алгоритм слияния многофокусных цветных изображений, основанный на реконструкции сверхвысокого разрешения и обнаружении сфокусированных областей. Доступ IEEE 8, –

    . doi: 10.1109/ACCESS.2020.2993404

    CrossRef Full Text | Google Scholar

    Лю С. , Ван Дж., Лу Ю., Ху С., Ма X. и Ву Ю. (2019 г.)б). Многофокусное слияние изображений на основе адаптивной двухканальной модели коры головного мозга в области Шерлета без субдискретизации. Доступ IEEE 7, 56367–56388. doi: 10.1109/ACCESS.2019.2

    6

    Полный текст CrossRef | Google Scholar

    Лю Ю., Чен Х., Пэн Х. и Ван З. (2017). Многофокусное слияние изображений с помощью глубокой сверточной нейронной сети. Слияние информации. 36, 191–207. doi: 10.1016/j.inffus.2016.12.001

    PubMed Abstract | Полный текст перекрестной ссылки | Академия Google

    Лю, Ю., Ван, Л., Ченг, Дж., Ли, К., и Чен, X. (2020). Мультифокусное слияние изображений: обзор современного состояния дел. Слияние информации. 64, 71–91. doi: 10.1016/j.inffus.2020.06.013

    CrossRef Full Text | Google Scholar

    Лю З., Блаш Э., Сюэ З., Чжао Дж., Лаганьер Р. и Ву В. (2012). Объективная оценка алгоритмов слияния изображений с разным разрешением для улучшения контекста в ночном видении: сравнительное исследование. IEEE Trans. Анальный узор. Мах. Интел. 34, 94–109. doi: 10.1109/TPAMI.2011.109

    PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

    Ма Дж., Чжоу З., Ван Б., Мяо Л. и Цзун Х. (2019). Слияние изображений с несколькими фокусами с использованием усиленного алгоритма на основе случайных блужданий с двухмасштабными картами фокуса. Нейрокомпьютинг 335, 9–20. doi: 10.1016/j.neucom.2019.01.048

    Полный текст CrossRef | Google Scholar

    Найду, В. П. С. (2011). Метод слияния изображений с использованием разложения по сингулярным значениям с несколькими разрешениями. По умолчанию науч. Дж. 61, 479–484. doi: 10.14429/dsj.61.705

    Полный текст CrossRef | Google Scholar

    Неджати М., Самави С. и Ширани С. (2015). Набор данных многофокусного изображения . Доступно в Интернете по адресу: https://mansournejati.ece.iut.ac.ir/content/lytro-multi-focus-dataset

    Pu, T., and Ni, G. (2000). Слияние изображений на основе контраста с использованием дискретного вейвлет-преобразования. Опц. англ. 39, 2075–2082. doi: 10.1117/1.1303728

    Полный текст CrossRef | Академия Google

    Цю, X., Ли, М., Чжан, Л., и Юань, X. (2019). Управляемое слияние мультифокусных изображений на основе фильтров посредством обнаружения области фокусировки. Изображение процесса обработки сигналов 72, 35–46. doi: 10.1016/j.image.2018.12.004

    Полный текст CrossRef | Google Scholar

    Саиди Дж. и Фаез К. (2015). Набор данных многофокусных изображений. Технический отчет . Доступно в Интернете по адресу: https://www.researchgate.net/publication/273000238_multi-focus_image_dataset

    Slavica, S. (2011). Набор данных многофокусного изображения . Доступно в Интернете по адресу: https://dsp.etfbl.net/mif/

    Vishal, C., and Vinay, K. (2018). Слияние изображений на основе блоков с использованием многомасштабного анализа для увеличения глубины резкости и динамического диапазона. Сигнал Изображение Видеопроцесс 12, 271–279. doi: 10.1007/s11760-017-1155-y

    Полный текст CrossRef | Google Scholar

    Сяо Б., Оу Г., Тан Х., Би Х. и Ли В. (2020). Многофокусное слияние изображений с помощью разложения на основе матрицы Гессе. IEEE Trans. Мультимедиа 22, 285–297. doi: 10.1109/TMM.2019.2928516

    Полный текст CrossRef | Google Scholar

    Сюй Ю., Юй Л., Сюй Х., Чжан Х. и Нгуен Т. (2015). Векторное разреженное представление цветного изображения с использованием матричного анализа кватернионов. IEEE Trans. Процесс изображения. 4, 1315–1329. doi: 10.1109/TIP.2015.2397314

    PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar

    Юань Ю., Чжан Дж., Чанг Б. и Хань Ю. (2011). Объективная оценка качества изображения слияния цветов в видимом и инфракрасном диапазонах. Опц. англ. 50, 1–11. doi: 10.1117/1.3549928

    Полный текст CrossRef | Google Scholar

    Чжан Ю., Сян З. и Ван Б. (2017). Нахождение границ на основе многофокусного слияния изображений с помощью многомасштабной морфологической меры фокусировки.

    No related posts.