Тестирование ф: Федеральный центр тестирования — Независимое театральное объединение "Зрительские симпатии"

Содержание

СМИ: предсезонные тесты «Ф-1» пройдут в трехдневном формате в Бахрейне

https://rsport.ria.ru/20210119/formula-1-1593722924.html

СМИ: предсезонные тесты «Ф-1» пройдут в трехдневном формате в Бахрейне

СМИ: предсезонные тесты «Ф-1» пройдут в трехдневном формате в Бахрейне — РИА Новости Спорт, 19.01.2021

СМИ: предсезонные тесты «Ф-1» пройдут в трехдневном формате в Бахрейне

Предсезонные тесты «Формулы-1» в 2021 году пройдут на трассе «Сахир» в Бахрейне с 12 по 14 марта, сообщает AFP со ссылкой на «Формулу-1» и Международную… РИА Новости Спорт, 19.01.2021

2021-01-19T18:20

2021-01-19T18:32

формула-1

/html/head/meta[@name=’og:title’]/@content

/html/head/meta[@name=’og:description’]/@content

https://cdnn21.img.ria.ru/images/07e4/03/0e/1568595656_0:94:2327:1403_1920x0_80_0_0_a87c610a5cfebc4e60fb34ebb73f0246.jpg

МОСКВА, 19 янв — РИА Новости. Предсезонные тесты «Формулы-1» в 2021 году пройдут на трассе «Сахир» в Бахрейне с 12 по 14 марта, сообщает AFP со ссылкой на «Формулу-1» и Международную автомобильную федерацию (FIA). Изначально тесты намеревались провести в Барселоне, как и в предыдущие годы, но из-за переноса на ноябрь Гран-при Австралии, который должен был стать открытием сезона, выбор пал на Бахрейн. Продолжительность тестов сокращена с шести до трех дней.Чемпионат 2021 года стартует гонкой в Бахрейне 28 марта, на неделю позже, чем изначально запланированный Гран-при Австралии.

РИА Новости Спорт

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

2021

РИА Новости Спорт

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

Новости

ru-RU

https://rsport.ria.ru/docs/about/copyright.html

https://xn--c1acbl2abdlkab1og.xn--p1ai/

РИА Новости Спорт

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

https://cdnn21.

img.ria.ru/images/07e4/03/0e/1568595656_150:0:2021:1403_1920x0_80_0_0_236b1f827168bc7891e77da2e5e6404c.jpg

РИА Новости Спорт

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

РИА Новости Спорт

[email protected]

7 495 645-6601

ФГУП МИА «Россия сегодня»

https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/

МОСКВА, 19 янв — РИА Новости. Предсезонные тесты «Формулы-1» в 2021 году пройдут на трассе «Сахир» в Бахрейне с 12 по 14 марта, сообщает AFP со ссылкой на «Формулу-1» и Международную автомобильную федерацию (FIA).

Изначально тесты намеревались провести в Барселоне, как и в предыдущие годы, но из-за переноса на ноябрь Гран-при Австралии, который должен был стать открытием сезона, выбор пал на Бахрейн. Продолжительность тестов сокращена с шести до трех дней.

Чемпионат 2021 года стартует гонкой в Бахрейне 28 марта, на неделю позже, чем изначально запланированный Гран-при Австралии.

Тест по французскому языку | Французский Университетский Колледж в Москве

Даты проведения тестирования в 2021 году:

— Консультация: не проводится
— Тестирование: 3 сентября с. г.
— Тестирование (резервный день): 4 сентября с. г.

Ниже представлен образец теста по французскому языку, который сдают абитуриенты в начале учебного года. По результатам теста производится зачисление на франкоязычное отделение.

Уважаемые обладатели дипломов DALF и DELF B2! Просим при административной записи в обязательном порядке предъявить дипломы DALF или DELF B2, так как вы освобождаетесь от сдачи теста и автоматически зачисляетесь на 1-й курс франкоязычного отделения.

Partie 1 : Compréhension des écrits

25 points

Lisez le texte ci-dessous et répondez aux questions :

Admission post-bac : moins de « sans-fac » cette année

Cours de psychologie à l’Université Paul-Valéry, à Montpellier, en 2015.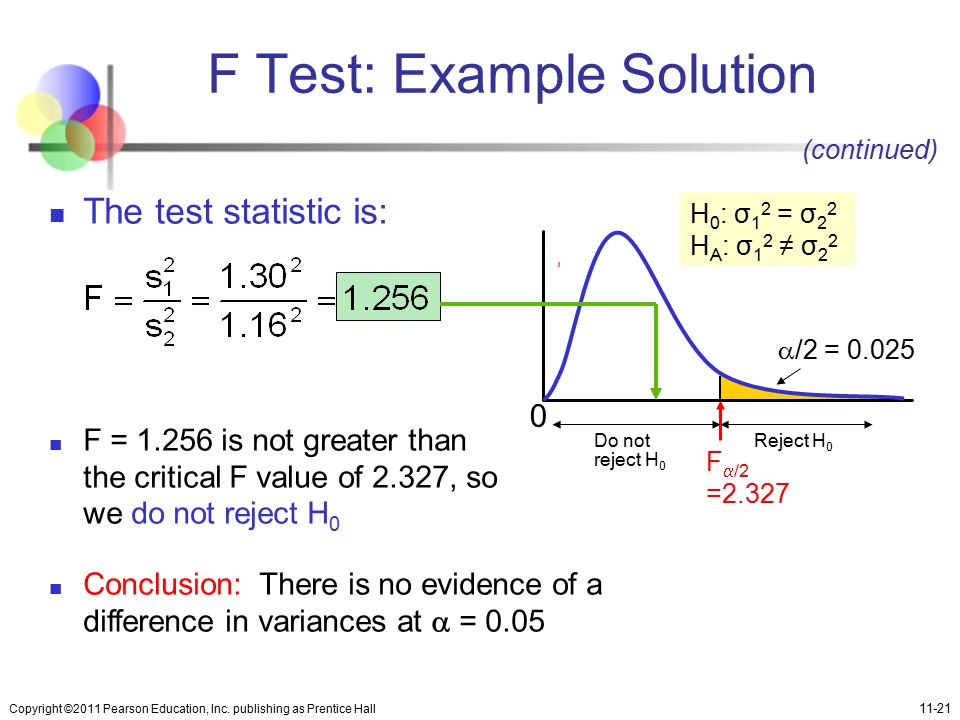 | SYLVAIN THOMAS / AFP
Le verdict est tombé. Pour les bacheliers encore en attente d’une place dans l’enseignement supérieur, la troisième phase du processus d’admission post-bac (APB) s’est achevée le 19 juillet. En 2015, à la même époque, plus de 7 000 bacheliers n’avaient pas obtenu de place dans la licence qu’ils demandaient à l’université en premier vœu, seule filière pourtant non sélective de l’enseignement supérieur. Ils ne sont que « 2 327 » cette année, assureThierry Mandon, le secrétaire d’Etat chargé de l’enseignement supérieur et de la recherche.
Face à l’afflux de générations de bacheliers toujours plus nombreuses – 38 000 étudiants de plus en 2015 –, la machine donne des signes de faiblesse, particulièrement à l’entrée des licences dites « en tension » : droit, psychologie,médecine et surtout en Staps .
Pas question de revivre, cette année, l’expérience de 2015. Des ajustements au système d’affectation APB et un effort pour mieux accompagner l’orientation des bacheliers ont permis une amélioration de la situation, assure M. Mandon.« Seuls 2 327 bacheliers n’ont pas obtenu la place qu’ils demandaient en priorité dans une filière universitaire de leur académie, assure-t-il. Soit un chiffre divisé par trois par rapport à 2015. Nous sommes sur la bonne voie. » Et parmi ces 2 327 « sans-fac », seuls 439 demeurent à ce jour sans proposition selon le ministère. Leur situation devrait être réglée avec la procédure complémentaire qui court jusqu’en septembre.
Le tirage au sort à l’entrée de certaines filières, qui fait l’unanimité contre lui, a aussi perdu du terrain. Seules 80 licences ont dû y recourir, contre 190 en 2015. « Il n’y aura aucun tirage au sort en droit et en médecine, souligne le secrétaire d’Etat. Hormis quelques exceptions, dont la psychologie à Bordeaux. Le tirage au sort concerne principalement les Staps (sciences et techniques des activités physiques et sportives). »
Cette filière reste en effet dans l’impasse, malgré 4 000 places supplémentaires ouvertes. « La situation s’aggrave, alerte Didier Delignières, à la tête de Conférence des directeurs et doyens de Staps. La demande est toujours plus forte et nous sommes démunis face aux dizaines de courriels de bacheliers ou de parents dépités. »
« Cette situation touche moins de 1 % des bacheliers »,relativise M. Mandon. Le secrétaire d’Etat ne nie pas, pour autant, la difficulté ainsi créée pour les personnes concernées, qui devront s’orienter vers une autre filière.
« Je ne comprends pas qu’on ne me laisse aucune chance, confie Line Duveau, 17 ans, qui n’a pas été retenue à l’issue des tirages au sort en Ile-de-France. Cela fait deux ans que je me prépare pour aller en Staps et je reste accrochée à l’idée. » La bachelière littéraire refuse de rejoindre la filière qu’elle a été obligée de cocher – la fac de lettres. Les bacheliers généraux doivent en effet désormais émettre au moins un vœu vers une licence « libre », c’est-à-dire qui n’est pas sous tension.

TENSIONS GEOGRAPHIQUES
Une autre nouveauté pourrait avoir un effet encore difficile à mesurer : dans ces filières où le nombre de places ne suffit pas à répondre à la demande, les bacheliers ont émis des vœux « groupés » cette année. C’est-à-dire qu’ils ont candidaté dans toutes les universités de leur académie ou de leur région proposant la filière visée. Cela permet d’accroître leur chance d’y trouver une place. Mais avec le risque de voir un phénomène s’accroître : celui des jeunes affectés dans un établissement éloigné de chez eux.
Julien, 18 ans, titulaire d’un bac économique et social, se retrouve ainsi en Staps à Epinal, alors qu’il habite Metz. « Je suis très content, confie-t-il cependant, car je sais que certains n’ont pas eu cette chance. Mais c’est vrai que je suis un peu inquiet car c’est à plus d’une heure trente de voiture. Je réfléchis à la solution la moins chère avec ma famille, peut-être en faisant du covoiturage. » Le ministère s’est engagé à accompagner, notamment avec les centres régionaux des œuvres universitaires et scolaires (Crous), les bacheliers qui se retrouveraient en difficulté pour des raisons géographiques.

INQUIETUDE POUR LA RENTREE 2016
Pourtant, si ces ajustements ont permis de diminuer les couacs dans l’affectation des bacheliers, l’inquiétude des universitaires pour la rentrée à venir demeure. Plus de 38 000 étudiants supplémentaires sont attendus, soit la même augmentation qu’en 2015.
« Le ministère a tout fait pour résoudre le problème des “sans-fac”, avec ces nouvelles règles d’APB et en demandant aux universités d’augmenter leurs capacités d’accueil, reconnaît Alexandre Leroy, président de la Fédération des associations générales étudiantes (FAGE), l’une de deux principales organisations étudiantes. Mais la rentrée va être très difficile. »
« Cela va être pire qu’en 2015 en Staps, alerte le doyen Didier Delignières. Les conditions d’études ne peuvent que se dégrader. Avec pour conséquence des taux d’échec plus importants. Nous ne pouvons pas accompagner toujours plus d’étudiants sans les moyens nécessaires. » Aujourd’hui déjà, seuls 30 % des étudiants réussissent à passer le cap de la première année de Staps, avec un fort taux d’abandon dès le premier mois.
M. Mandon se veut pourtant rassurant. « La rentrée se passera dans de meilleures conditions qu’en 2015 », promet-il. « Je m’attends bien sûr à des amphithéâtres particulièrement remplis les premières semaines, mais l’effort budgétaire que nous avons obtenu va permettre de surmonterles difficultés », juge-t-il. De fait, 850 millions d’euros supplémentaires ont été promis à l’enseignement supérieur et à la recherche dans le budget 2017, dont 100 millions pour répondre au choc démographique qui touche les universités.
Par Camille Stromboni, journaliste au Monde

1. Identifiez le type du texte lu (2 points)

texte narratif
Texte argumentatif
Texte informatif

2. Relevez la problématique du texte (3 points)

——————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————-

3. Cochez VRAI ou FAUX et justifiez votre réponse en citant un passage du texte 3 points

Le nombre des admis à la licence à l’établissement « en premier vœu » a diminué par rapport au 2015.

VRAI

FAUX

Justification :

4. Expliquez l’expression ou le mot souligné « l’afflux de générations de bacheliers » (3points

5. En ce qui concerne « le tirage au sort » à l’entrée de certaines filières les bacheliers sont plutôt (cochez la bonne réponse) / 2 points

6. Cochez VRAI ou FAUX et justifiez votre réponse en citant un passage du texte (3 points)

Les 4000 places supplémentaires ouvertes pour les Staps ont résolu les problèmes dans cette filière.

VRAI

FAUX

Justification :

7. Relevez les problèmes des bacheliers (2 réponses attendues) / 2 points
—

—

.
8. Expliquez pourquoi le président de la FAGE reconnaît que « la rentrée va être difficile » (3 points)

9. Face aux problèmes traités dans le texte, le secrétaire d’État se montre plutôt (cochez la bonne réponse) / 2 points

Optimiste
Pessimiste
Inquiêt

10. Justifiez votre réponse à la question précédante (2 points)

Partie 2 : Expression écrite.

Essai, (200 mots environ)

Exemple : « Réussir un examen, est-ce facile ? Donnez quelques conseils pour ceux qui s’y préparent.

Durée : 30-40 minutes
25 points

Attention! N’oubliez pas de construire votre texte: c’est-à-dire l’introduire, puis développer et argumenter, ensuite conclure.

Règle de décompte des mots : est considéré comme mot tout ensemble de signes placé entre deux espaces. « c’est-à-dire » = 1 mot, « un bon élève » = 3 mots, « J’ai 14 ans » = 3 mots.

Тест AF-S NIKKOR 70-200mm f/2.8E FL ED VR

В мае я побывал в Нью-Йорке, где снимал новый эпизод для моей онлайн фотошколы. И грех было не воспользоваться фактурой улиц этого бурлящего города, чтобы протестировать телеобъектив AF-S NIKKOR 70-200mm f/2.8E FL ED VR, выпорхнувший из гнезда Nikon в 2016 году. Я вооружился 70-200mm в паре с Nikon D810 и отправился снимать портреты ньюйоркцев.

Диафрагма — f/3. 5
Выдержка — 1/640, ISO 800
Фокусное расстояние — 200 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

На улицах «плавильного котла Америки» так много интересных персонажей! Мне хотелось кого-то взять крупно, кого-то в полный рост, и я быстро понял, что просто не успеваю переключать вручную выдержку и диафрагму. Поэтому воспользовался режимом приоритета диафрагмы: снимал на открытой диафрагме 3.5-2.8, а выдержка менялась автоматически. Иногда приходилось корректировать +/- ступень выдержки, но в целом автоматический режим дает достаточно хороший результат.

Диафрагма — f/3.5
Выдержка — 1/400, ISO 800
Фокусное расстояние — 200 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Поначалу я стеснялся, так как не привык снимать людей так «нагло», без спросу. Поэтому поначалу старался делать это аккуратно, незаметно, издалека. Но быстро освоился и понял, что в Нью-Йорке легко снимать, люди мало обращают внимания друг на друга. Ну, пара человек нахмурились, а многие наоборот даже немножко позировали.

Диафрагма — f/4.5
Выдержка — 1/320, ISO 400
Фокусное расстояние — 135 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Погода для объектива подобралась как специально разная: и солнце, и туман, и холод. За день я снимал несколько раз по 10-15 минут, когда было свободное время. Вся фотосессия в сумме не заняла более 40 минут, но я сделал 200 интересных, на мой взгляд, фотографий и пришел к выводу, что этот 70-200 – идеальная линза для репортажной съемки в уличных условиях: она очень резкая, очень быстрая, позволяет снимать на ходу.

Минимальное расстояние фокусировки теперь составляет 1,1 метра, что позволяет снимать в достаточно стесненных условиях, и максимальный коэффициент воспроизведения увеличился с 0,11 до 0,21.

Диафрагма — f/2.8
Выдержка — 1/800, ISO 800
Фокусное расстояние — 180 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Улучшенная система подавления вибраций позволяет снимать с выдержками гораздо длиннее обычных. Я чувствовал себя практически спортивным фотографом, снимая динамические, иногда непредсказуемые события. Мои «модели» были в движении, я сам был в движении, но улучшенные функции автофокуса в сочетании с режимом VR Sport позволили максимально быстро выбирать ракурс, кадрировать сцену и не терять фокуса на снимаемом объекте.

Диафрагма — f/2.8
Выдержка — 1/80, ISO 800
Фокусное расстояние — 170 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Нанокристаллическое покрытие повышает четкость изображения линзы, и, как следствие, позволяет снимать очень контрастные объекты без всяких искажений, уменьшает блики и засветку.

Диафрагма — f/4.5
Выдержка — 1/320, ISO 400
Фокусное расстояние — 125 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Суммируя результаты фото прогулки по улицам Нью-Йорка, скажу, что я очень доволен этим объективом. Его скорость, удобство пользования, технические характеристики легко превращают репортажные съемки в художественные.

Основные преимущества:

— великолепное боке:

Диафрагма — f/3.5
Выдержка — 1/100, ISO 800
Фокусное расстояние — 185 мм
Камера — Nikon D810

Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

— мягкое «размытие» кадра вне резко изображаемого пространства:

Диафрагма — f/5
Выдержка — 1/800, ISO 800
Фокусное расстояние — 160 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2. 8E FL ED VR

— при этом кристальная четкость и резкость автофокуса:

Диафрагма — f/3.5
Выдержка — 1/200, ISO 800
Фокусное расстояние — 200 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Все это делает этот объектив великолепным инструментом как для профессионала, так и для любителя, желающего развиваться в фотографии и не ограничивать свои творческие задачи возможностями техники.

Диафрагма — f/3.5
Выдержка — 1/320, ISO 800
Фокусное расстояние — 160 мм
Камера — Nikon D810
Объектив — AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Ifdtest2 часть F (логотип SC Reader) — (ручной тест)

10/27/2021
Чтение занимает 2 мин

В этой статье

Этот тест проверяет функциональность устройства чтения смарт-карт, проверяя тестовые карты PC/SC Workgroup.

Сведения о тесте


Характеристики	Device. input. Смарткардреадер. Суппортсинсертионандремовалмонитор Device. input. Смарткардреадер. УсбкЦидкомплиесвисусбдевицеклассспек
Платформы	Windows 10, выпуски клиента (ARM64)
Поддерживаемые выпуски	Windows 10 Windows 10 версии 1511 Windows 10, версия 1607 Windows 10 версии 1703 Windows 10 версии 1709 Windows 10 версии 1803 Windows 10, версия 1809 Windows 10 версии 1903 Следующее обновление Windows 10
Ожидаемое время выполнения (в минутах)	5
Категория	Совместимость
Время ожидания (в минутах)	300
Требуется перезагрузка	false
Требуется специальная конфигурация	false
Тип	automatic

Дополнительная документация

Тесты в этой функциональной области могут иметь дополнительную документацию, включая предварительные требования, настройки и сведения об устранении неполадок, которые можно найти в следующих разделах:

Выполнение теста

Перед выполнением теста завершите настройку теста, как описано в статье требования к тестированию: Проверка предварительных требований для средства чтения смарт-карт.

Выявлен

общие сведения об устранении неполадок тестирования хлк см. в разделе устранение неполадок Windows хлк тестов.

Сведения об устранении неполадок см. в разделе Устранение неполадок устройства. входное тестирование.

Дополнительные сведения

Синтаксис команды

Чтобы выполнить эту команду за пределами ХЛК Studio, необходимо отключить службу смарт-карт, выполнить команду и запустить службу смарт-карт.

Команда	Описание
ifdtest2.exe-SA-SB-SC-SE-SF	Выполняет тест.

Список файлов

Файл	Расположение
ifdtest2.exe	тестбинрут >\nттест\дриверстест\стораже\вдк\

Вход

Имя параметра	Описание параметра
LLU_NetAccessOnly	Учетная запись пользователя для доступа к общей папке теста.
LLU_LclAdminUsr	Учетная запись пользователя для выполнения теста.

Обзор и тест объектива Nikon NIKKOR Z 28mm f/2.8 (SE)

Когда на свет появилась камера Nikon Z fc, для неё потребовался объектив, соответствующий ей по стилистике и размеру. Им стал NIKKOR Z 28mm f/2.8 (SE) — компактный фикс с элементами ретродизайна, превращающийся на DX-камере в эквивалент 42-мм объектива.

Сам по себе NIKKOR Z 28mm f/2.8 (SE) полнокадровый, хоть и выпущен вместе с DX-моделью. Поэтому в нашем тесте вы найдёте кадры как с «кропнутого» Nikon Z fc, так и с полнокадрового Nikon Z 6.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/2000 с, 28.0 мм экв.Cкачать RAW

Особенности конструкции

NIKKOR Z 28mm f/2.8 (SE) сделан максимально компактным и простым. В отделке использован преимущественно пластик, из него же сделан и байонет. Такое техническое решение обеспечило объективу вес в 160 граммов. При толщине 43 мм и диаметре 71,5 мм его легко носить в кармане, а камера с ним помещается почти в любую сумку.

Реализовав компактность конструкции, разработчики не забыли и о пыле-влагозащите. Она здесь тоже есть.

NIKON Z fc / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F8, 1/320 с, 42.0 мм экв.Cкачать RAW

Характерное рифление фокусировочного кольца, металлический декоративный ободок и даже оригинальные шрифты — всё это отсылает нас к позапрошлому поколению оптики Nikon. Кольца управления были точно воссозданы по оригинальным чертежам, а их текстура напоминает о легендарных зеркальных фотокамерах Nikon.

Ретромотивы в отделке помогают объективу гармонировать с обликом Nikon Z fc, но и на других современных камерах он не смотрится инородным.

На корпусе NIKKOR Z 28mm f/2.8 (SE) нет выключателя автофокуса. Вероятно, он пал жертвой миниатюризации. Сам автофокус очень быстрый и беззвучный. Фокусировка внутренняя, то есть внешние элементы конструкции во время наведения на резкость не перемещаются.

Кольцо ручной фокусировки имеет нелинейный ход, позволяя наводиться с максимальной точностью. Однако нелинейность выражена не столь ярко, так что с ручной фокусировкой в видео тоже можно комфортно работать.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F4, 1/500 с, 28.0 мм экв.Cкачать RAW

В оптической схеме использовано девять элементов, объединённых в восемь групп. Две линзы — асферические. Посмотрим, как это скажется на характере рисунка? Диафрагма семилепестковая со скруглённым отверстием. Минимальная дистанция фокусировки составляет 19 см от плоскости матрицы, а масштаб съёмки при этом 0,2х.

Объектив в работе. Кроп и полный кадр

NIKKOR Z 28mm f/2.8 (SE) — объектив с секретом. Дело в том, что 28 и 42 мм — очень разные фокусные расстояния. Первое — скорее пейзажное. При установке на полный кадр объектив становится классическим тревел-фиксом для общих планов.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/3200 с, 28.0 мм экв.

Cкачать RAW

А эквивалент 42 мм — это уже про акценты в кадре, про выделение главного объекта. На кропе он именно так и будет себя вести, обладая незаурядной универсальностью и обеспечивая привычную глазу передачу перспективы.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/800 с, 28.0 мм экв.Cкачать RAW

Обладая сравнительно большой глубиной резкости, NIKKOR Z 28mm f/2.8 (SE) сможет эффектно размывать фон только на малой дистанции съёмки. Это касается и кропа, и полного кадра.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/2000 с, 28.0 мм экв.Cкачать RAW

Крупные планы с боке ему под силу, но главный объект должен быть от вас буквально на расстоянии вытянутой руки. С расстояния в метр-полтора получается лишь лёгкое отделение объекта от фона. Но есть и плюсы: главный объект почти всегда входит в глубину резкости, и о выборе диафрагмы можно не думать.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/8000 с, 28.0 мм экв.Cкачать RAW

Само качество боке не вызывает вопросов: размытие мягкое и приятное глазу. Его не портят даже два асферических элемента в конструкции, хотя часто именно они являются причиной «грязного» рисунка.

NIKON Z fc / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/25 с, 42.0 мм экв.Cкачать RAW

Съёмка в контровом свете и бликозащита

NIKKOR Z 28mm f/2.8 (SE) только выглядит будто объектив из прошлого. Оптическая схема современная, как и просветляющее покрытие. Объектив не боится яркого контрового света.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F7.1, 10 с, 28.0 мм экв.Cкачать RAW

Даже если съёмка идёт почти в полной темноте, яркие источники света не провоцируют появления артефактов. Контраст высок, бликов не образуется.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/8000 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F4, 1/5000 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F5.6, 1/2500 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F8, 1/1250 с, 28.

0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F11, 1/500 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F16, 1/320 с, 28.0 мм экв.

Вероятно, в Nikon были настолько уверены в бликозащите этой модели, что даже не предусмотрели для неё крепление бленды.

Хроматические аберрации

Этот вид искажений часто свойственен широкоугольникам. Но NIKKOR Z 28mm f/2.8 (SE) от него практически избавлен. Назойливых фиолетовых и зелёных полосок по границе контрастных объектов вы, скорее всего, не встретите на своих снимках.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F8, 1/125 с, 28.0 мм экв.Cкачать RAW

Они могут появляться при сильном увеличении только на самых провокационных сюжетах, например, когда солнце пробивается через тонкие ветви деревьев.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/1250 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F4, 1/640 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F5.6, 1/320 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F8, 1/160 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F11, 1/80 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F16, 1/40 с, 28.0 мм экв.

На «обычных» кадрах со средним или даже высоким контрастом хроматические аберрации не появляются.

Геометрические искажения

Современные камеры умеют уверенно справляться с геометрическими искажениями, присущими почти любой оптике. NIKKOR Z 28mm f/2.8 (SE) не исключение. Если открыть RAW-файлы, например, в Adobe Camera RAW, то искажений вы не встретите: их уже исправил встроенный профиль. То же касается и JPEG.

Скачать RAW

Но на самом деле искажения есть. Их можно увидеть, например, в RAW-конвертерах, не поддерживающих встроенные профили. Объектив имеет заметную бочкообразную дисторсию, программное исправление которой приводит к некоторой обрезке углов. Для большинства сюжетов это не будет играть заметной роли, ведь в момент построения кадра вы уже видите исправленное изображение. Тем не менее данную особенность объектива мы демонстрируем нашим читателям.

Виньетирование

Затемнение углов кадра хорошо заметно на открытой диафрагме, если вы снимаете на полнокадровый фотоаппарат. Для некоторых сюжетов его можно использовать как художественный приём. Но если вам важно идеальное техническое качество, то уже на f/4 виньетирование очень сильно снижается, а на f/5,6 полностью уходит.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/1600 с, 28.0 мм экв.Cкачать RAW NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F4, 1/800 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F5.6, 1/400 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F8, 1/200 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F11, 1/100 с, 28.0 мм экв. NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F16, 1/50 с, 28.0 мм экв.

Резкость

На открытой диафрагме при работе с полнокадровой камерой NIKKOR Z 28mm f/2.8 (SE) обеспечивает отличную резкость по центру и умеренно высокую по краю кадра. Лишь в самых углах заметна некоторая мягкость картинки.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/2500 с, 28.0 мм экв.Cкачать RAW

При f/4 углы добирают резкости до высокого уровня, а начиная с f/5,6 NIKKOR Z 28mm f/2.8 (SE) радует идеальной детализацией по всему полю кадра.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F4, 1/1250 с, 28.0 мм экв.Cкачать RAW NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F5.6, 1/640 с, 28.0 мм экв.Cкачать RAW NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F8, 1/320 с, 28.0 мм экв.Cкачать RAW NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F11, 1/160 с, 28.0 мм экв.Cкачать RAW NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F16, 1/80 с, 28.0 мм экв.Cкачать RAW

Если снимать на DX-камеру, то о мягких углах на открытой диафрагме и вовсе можно забыть. Ведь они буквально останутся за кадром.

Выводы

Под скромной ретровнешностью в малютке NIKKOR Z 28mm f/2.8 (SE) скрывается мощный творческий потенциал. Объектив может работать как на кроп-камерах, так и на полнокадровых, по-разному проявляя свой характер. В первом случае он — универсальный эквивалент 42 мм, объектив для любых сюжетов с естественной передачей перспективы. Во втором — лёгкий и компактный тревел-фикс для пейзажей и общих планов, классический широкоугольник.

NIKON Z fc / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F6.3, 1/400 с, 42.0 мм экв.Cкачать RAW

У объектива очень удачное соотношение веса, размера и технического качества изображения. Фотограф может рассчитывать на высокую резкость с открытой диафрагмы, уверенную работу в контровом свете, очень низкий уровень хроматических аберраций.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F5.6, 1/1000 с, 28.0 мм экв.Cкачать RAW

Из формальных минусов отметим присущую NIKKOR Z 28mm f/2.8 (SE) бочкообразную дисторсию, которая принудительно правится даже в RAW, так что фотограф вряд ли с ней столкнётся. А из мелких неудобств обращает на себя внимание отсутствие выключателя автофокуса на корпусе и пластиковый байонет.

NIKON Z 6 / NIKKOR Z 28mm f/2.8 УСТАНОВКИ: ISO 100, F2.8, 1/8000 с, 28.0 мм экв.Cкачать RAW

Плюсы:

компактность и малый вес;
высокая резкость с открытой диафрагмы даже на полном кадре;
уверенная бликозащита;
очень низкий уровень хроматических аберраций;
мягкое размытие;
бесшумная внутренняя автофокусировка;
уникальный ретродизайн;
пыле и влагозащита.

Минусы:

в сторонних RAW-конвертерах без поддержки профиля объектива будет заметна бочкообразная дисторсия;
нет выключателя автофокуса на корпусе;
пластиковый байонет.

Рейтинг Prophotos

Оценка редакции

Оправданность цены

Тест «Ф-1 (граната) — ТТХ»

Ф-1 (граната) — ТТХ

Предмет	Внеурочная деятельность
Класс	11

Вопрос №1

Граната предназначена:

A) для поражения легкой техники

B) для поражения живой силы

C) для поражения живой силы и легкой техники

Вопрос №2

Граната Ф-1 относится:

A) к ручным гранатам

B) к противопехотным гранатам

C) к ручным противопехотным

Вопрос №3

Общий вес, гр.

A) 500

B) 600

C) 700

Вопрос №4

Вес взрывчатого вещества, гр.

A) 50

B) 60

C) 70

Вопрос №5

Дальность броска, м.

A) 30-35

B) 35-40

C) 40

D) 35-45

Вопрос №6

Безопасное расстояние, м.

A) 300

B) 100

C) 200

Вопрос №7

Время замедления запала, сек.

A) 2,2-3,2

B) 3,2-4,2

Вопрос №8

Количество осколков, шт.

A) до 200

B) до 300

C) до 250

D) до 350

Вопрос №9

Три основные части гранаты Ф-1

A) запал-взрывчатое вещество-металлическая оболочка

B) ударник-детанирующая смесь-замедлитель

C) запал-взрывчатое вещество-детанирующая смесь

Вопрос №10

Длина гранаты, мм

A) 115

B) 117

C) 119

Вопрос №11

Диаметр гранаты, мм

A) 55

B) 65

C) 45

D) 75

Вопрос №12

Ударная волна, м

A) менее 0,5

B) менее 0,7

C) менее 0,9

Правильные ответы, решения к тесту:

Вопрос №1

Правильный ответ — B

Вопрос №2

Правильный ответ — C

Вопрос №3

Правильный ответ — B

Вопрос №4

Правильный ответ — B

Вопрос №5

Правильный ответ — D

Вопрос №6

Правильный ответ — C

Решение: Очень часто при описании этого типа боеприпасов указывается расстояние 200 м. Теоретически осколки гранаты могут улететь на такое расстояние, однако вероятность попадания этих осколков в цель стремится к нулю. Скорее всего, под дистанцией в 200 м понимается расстояние, на котором должен находиться наблюдатель для того, чтобы ни при каких условиях не получить ранение. В реальности о более-менее гарантированном поражении стоящего в рост человека можно говорить на дистанции не более 5—10 метров. На дистанциях более 50 м поражение человека крайне маловероятно

Вопрос №7

Правильный ответ — B

Вопрос №8

Правильный ответ — B

Решение: Опасными считаются осколки массой не менее 2 грамм. Осколки меньшей массы, даже обладая большой скоростью, не в состоянии причинить сколь-нибудь значительных повреждений. Таким образом, теоретически одна граната массой 540 г (масса заряда взрывчатого вещества 60 г) при идеальных условиях может дать до 270 осколков, обладающих убойным действием. В реальности количество и масса осколков колеблются в очень больших пределах, и число убойных осколков не превышает 150—200. В случае, если граната взрывается на земле, число убойных осколков уменьшается примерно вдвое, так как осколки, уходящие в нижнюю полусферу, не представляют опасности

Вопрос №9

Правильный ответ — A

Вопрос №10

Правильный ответ — B

Вопрос №11

Правильный ответ — A

Вопрос №12

Правильный ответ — A

Проведено тестирование кабелей Hyperline (F/UTP, SF/UTP) с удлинителями ATEN (KVM, VIDEO)

При необходимости отдалить монитор от источника видеосигнала, или установить KVM-консоль управления в удалении от компьютера/сервера – производители удлинителей интерфейсов предлагают использовать кабели типа «витая пара». Однако кабели не всех производителей способны качественно передавать сигналы. Влияющими факторами являются: качество материала токопроводящих жил (чистота меди), равномерность шага скрутки витых пар, наличие экрана из фольги и проволочной оплётки.

Проведено тестирование кабелей Hyperline (F/UTP, SF/UTP) с удлинителями ATEN (KVM, VIDEO)
Как показало тестирование, кабели Hyperline обеспечивают качественную передачу сигналов на регламентированные длины 20-100 м, а с некоторыми моделями удлинителей интерфейсов в линиях до 150 и 300 метров (с разрешением 1600х1200 и 1280×1024). Визуальные тесты качества «картинки» с различными длинами кабелей Hyperline и удлинителями ATEN представлены ниже на фотографиях 1, 2, 3, 4.

Предыстория и причины, вызвавшие необходимость тестирования
При подключении удлинителей интерфейсов ATEN монтажники оборудования столкнулись с проблемой недостаточного качества видео на приёмнике с увеличением удаления от источника сигнала. Анализ объектов монтажа выявил следующие обстоятельства:

качество кабелей не обеспечивает надлежащие характеристики;
при прокладке кабелей не всегда соблюдаются правила монтажа;
кабель не всегда удаётся прокладывать согласно нормам и правилам.

В обследуемых некачественных линиях применялись кабели сторонних производителей – не марки Hyperline

Для достижения наилучшего результата производитель удлинителей интерфейсов ATEN рекомендует использовать витую пару собственного производства – ATEN. Однако эти кабели достаточно дорогие, при этом приобрести их можно не во всех регионах России. Для проверки возможности использования кабелей другого производителя было проведено тестирование образцов марки Hyperline.

Цель проведения тестирования
Необходимо проверить качество передачи видеосигнала удлинителями интерфейсов ATEN в комплекте с кабелями Hyperline.

Тестируемые удлинители и кабели:

Для различных длин кабелей были собраны типовые схемы подключения:

Источник >> Передатчик >> Кабель витая пара (различной длины) >> Приёмник >> Монитор

VE066 (расстояние до 20 м)

CE100 (расстояние до 100 м)

VE500 (расстояние до 300 м)

Для проведения тестов регламентируемые длины кабелей были выбраны согласно рекомендациям производителя удлинителей интерфейсов ATEN. На всех собранных схемах удлинения качество видео соответствовало изображению на источнике.

В процессе тестирования была также проверена возможность применения длин кабелей, превышающих рекомендуемые расстояния. Так, в качестве эксперимента удлинитель ATEN CE100 был подключён на расстояние 305 метров, при рекомендованном удалении до 100 метров. В результате полученное изображение видео на удалённом блоке удлинителя (приёмнике) было сильно «затянуто». В этом же случае при подключении кабелей других производителей изображение полностью пропадало даже на меньших расстояниях, что однозначно говорит о хорошем качестве кабелей Hyperline и имеющемся у них запасе по характеристикам для создания более длинных линий.

ВНИМАНИЕ! Производитель и поставщик оборудования ATEN не рекомендует и не гарантирует работу оборудования при подключении на расстояниях, превышающих указанные в технической документации.

Для реализации схем удлинения интерфейсов допускается использование неэкранированной витой пары категории 5e (U/UTP). При этом производитель оборудования ATEN настоятельно рекомендует применять экранированные кабели (F/UTP, S/FTP).

Визуальные тесты качества «картинки» с различными длинами кабелей Hyperline

	Фотография 1. Тест проверки качества передачи видеосигнала с удлинителем ATEN CE100 по кабелю Hyperline F/UTP 24 AWG на расстояние 20 м. Качество видео на удалённом мониторе идеальное.
	Фотография 2. Тест проверки качества передачи видеосигнала с удлинителем ATEN VE500 по кабелю Hyperline F/UTP 24 AWG на расстояние 20 м. Качество видео на удалённом мониторе идеальное.
	Фотография 3. Тест проверки качества передачи видеосигнала с удлинителем ATEN VE500 по кабелю Hyperline F/UTP 24 AWG на расстояние 305 м. Качество видео на удалённом мониторе идеальное.
	Фотография 4. В качестве эксперимента также был проведён тест с удлинителем ATEN CE100 в комплекте с кабелем, длина которого в несколько раз превышает рекомендуемое расстояние. Качество видео на удалённом мониторе сильно искажено – эффект «затяжки» картинки. Длина кабеля была выбрана 305 м, что в 3 раза больше рекомендуемого поставщиком расстояния – 100 м, для данной модели удлинителя.

Результат последнего эксперимента с полной бухтой кабеля длиной 305 метров удивил… Поскольку данный удлинитель ATEN CE100 не предназначен для передачи сигналов на такие большие расстояния. Предусмотренное ограничение – 100 метров. В данном случае для эксперимента с длиной 305 метров брались также кабели и некоторых других производителей – изображение во всех случаях полностью отсутствовало, что однозначно подтверждает отличные характеристики кабелей Hyperline.

Выводы по результатам тестирования
Тестирование экранированных кабелей Hyperline F/UTP 24 AWG, SF/UTP 24AWG (FUTP4-C5E-S24-IN, SFUTP4-C5E-S24-IN) с различными моделями удлинителей ATEN показало стабильно высокое качество передачи видео и графических изображений. Таким образом, данные кабели Hyperline будут рекомендованы к использованию в инсталляциях с оборудованием ATEN.

По результатам проверки качества передачи сигналов кабели Hyperline не только соответствуют требованиям производителя удлинителей ATEN, но и позволяют в некоторых случаях отводить интерфейсы к оборудованию с запасом по длине.

Понимание дисперсионного анализа (ANOVA) и F-тест

Дисперсионный анализ (ANOVA) может определить, различаются ли средние трех или более групп. ANOVA использует F-тесты для статистической проверки равенства средних. В этом посте я покажу вам, как работают ANOVA и F-тесты, на примере одностороннего ANOVA.

Но подождите … Вы когда-нибудь задумывались, почему вы использовали анализ дисперсии , чтобы определить, означает ли , что разные? Я также покажу, как дисперсия дает информацию о средствах.

Как и в своих сообщениях о понимании t-тестов, я сосредоточусь на концепциях и графиках, а не на уравнениях, чтобы объяснить F-тесты ANOVA.

Что такое F-статистика и F-тест?

F-тестов названы в честь их тестовой статистики F, названной в честь сэра Рональда Фишера. F-статистика — это просто соотношение двух дисперсий. Вариации — это мера разброса или того, насколько данные разбросаны от среднего значения. Большие значения представляют большую дисперсию.

Дисперсия — это квадрат стандартного отклонения.Нам, людям, легче понять стандартные отклонения, чем отклонения, потому что они выражаются в тех же единицах, что и данные, а не в квадратах. Однако во многих анализах в расчетах фактически используются отклонения.

F-статистика основана на соотношении средних квадратов. Термин «средние квадраты» может показаться сбивающим с толку, но это просто оценка дисперсии совокупности, которая учитывает степени свободы (DF), используемые для вычисления этой оценки.

Несмотря на то, что это соотношение дисперсий, вы можете использовать F-тесты в самых разных ситуациях.Неудивительно, что F-тест может оценить равенство дисперсий. Однако при изменении дисперсий, включенных в соотношение, F-тест становится очень гибким тестом. Например, вы можете использовать F-статистику и F-тесты для проверки общей значимости регрессионной модели, для сравнения соответствия различных моделей, для проверки конкретных условий регрессии и для проверки равенства средних.

Использование F-теста в одностороннем дисперсионном анализе

Чтобы использовать F-тест, чтобы определить, равны ли средние по группе, достаточно просто включить правильные дисперсии в соотношение.В однофакторном дисперсионном анализе F-статистика — это соотношение:

F = вариация между средними значениями выборки / вариация внутри выборок

Лучший способ понять это соотношение — рассмотреть пример одностороннего дисперсионного анализа.

Мы проанализируем четыре образца пластика, чтобы определить, имеют ли они разную среднюю прочность. Вы можете скачать образцы данных, если хотите продолжить. (Если у вас нет Minitab, вы можете загрузить бесплатную 30-дневную пробную версию.) Я вернусь к результатам одностороннего ANOVA, когда объясню концепции.

В Minitab выберите Stat> ANOVA> One-Way ANOVA … В диалоговом окне выберите «Strength» в качестве ответа и «Sample» в качестве фактора. Нажмите OK, и в окне сеанса Minitab отобразится следующий вывод:

Числитель: вариация средних значений выборки

Однофакторный дисперсионный анализ ANOVA рассчитал среднее значение для каждого из четырех образцов пластика. Групповые средние значения: 11,203, 8,938, 10,683 и 8,838. Эти групповые средние значения распределены вокруг общего среднего для всех 40 наблюдений, равного 9.915. Если групповые средние значения сгруппированы близко к общему среднему, их дисперсия невысока. Однако, если групповые средние значения расходятся дальше от общего среднего, их дисперсия выше.

Понятно, что если мы хотим показать, что групповые средства различны, это помогает, если средства находятся дальше друг от друга. Другими словами, мы хотим большей изменчивости средств.

Представьте, что мы выполняем два разных односторонних дисперсионного анализа, в которых каждый анализ состоит из четырех групп. График ниже показывает разброс средств.Каждая точка представляет собой среднее значение для всей группы. Чем дальше расставлены точки, тем выше значение вариабельности числителя F-статистики.

Какое значение мы используем для измерения дисперсии между средними значениями выборки для примера пластической прочности? В выходных данных одностороннего дисперсионного анализа мы будем использовать скорректированное среднее квадратическое значение (Adj MS) для фактора, равное 14,540. Не пытайтесь интерпретировать это число, потому что оно не имеет смысла. Это сумма квадратов отклонений, деленная на коэффициент DF.Просто имейте в виду, что чем дальше друг от друга находятся групповые средние, тем больше становится это число.

Знаменатель: вариации внутри выборки

Нам также нужна оценка изменчивости внутри каждой выборки. Чтобы вычислить эту дисперсию, нам нужно вычислить, насколько далеко каждое наблюдение от его среднего значения по группе для всех 40 наблюдений. Технически это сумма квадратов отклонений каждого наблюдения от среднего значения группы, деленная на ошибку DF.

Если наблюдения для каждой группы близки к среднему по группе, дисперсия в выборках низкая.Однако, если наблюдения для каждой группы дальше от среднего по группе, дисперсия в выборках выше.

На графике панель слева показывает низкую вариацию в выборках, а панель справа показывает высокую вариацию. Чем больше отклонения наблюдений от их среднего группового значения, тем выше значение в знаменателе F-статистики.

Если мы надеемся показать, что средние значения различны, это хорошо, когда внутригрупповая дисперсия низкая.Вы можете думать о дисперсии внутри группы как о фоновом шуме, который может скрыть разницу между средними значениями.

В этом примере с односторонним дисперсионным анализом значение, которое мы будем использовать для дисперсии в пределах выборок, — это Adj MS для ошибки, равное 4,402. Это считается «ошибкой», потому что это изменчивость, которая не объясняется фактором.

F-статистика: вариации между средними значениями выборки / вариация внутри выборок

F-статистика — это статистика для F-тестов.В общем, F-статистика — это отношение двух величин, которые, как ожидается, будут примерно равны при нулевой гипотезе, что дает F-статистику приблизительно 1.

F-статистика включает обе меры изменчивости, описанные выше. Давайте посмотрим, как эти меры могут работать вместе для получения низких и высоких значений F. Посмотрите на графики ниже и сравните ширину разброса средних значений группы с шириной разброса внутри каждой группы.

График низкого F-значения показывает случай, когда средние значения группы близки друг к другу (низкая изменчивость) относительно изменчивости внутри каждой группы.График с высоким значением F показывает случай, когда изменчивость средних групповых значений велика по сравнению с изменчивостью внутри группы. Чтобы отвергнуть нулевую гипотезу о том, что средние группы равны, нам нужно высокое значение F.

Для нашего примера прочности пластика мы будем использовать Factor Adj MS для числителя (14,540) и MS корректировки ошибок для знаменателя (4,402), что дает нам F-значение 3,30.

Достаточно ли высокое значение F? Одно значение F трудно интерпретировать само по себе. Нам нужно поместить наше F-значение в более широкий контекст, прежде чем мы сможем его интерпретировать.Для этого мы будем использовать F-распределение для вычисления вероятностей.

F-распределения и проверка гипотез

Для однофакторного дисперсионного анализа отношение межгрупповой вариабельности к внутригрупповой вариабельности следует F-распределению, когда нулевая гипотеза верна.

Когда вы выполняете односторонний дисперсионный анализ для одного исследования, вы получаете одно значение F. Однако, если мы возьмем несколько случайных выборок одного и того же размера из одной и той же популяции и выполним один и тот же односторонний дисперсионный анализ, мы получим много F-значений и сможем построить распределение всех из них.Этот тип распределения известен как выборочное распределение.

Поскольку F-распределение предполагает, что нулевая гипотеза верна, мы можем поместить F-значение из нашего исследования в F-распределение, чтобы определить, насколько наши результаты согласуются с нулевой гипотезой, и вычислить вероятности.

Вероятность, которую мы хотим вычислить, — это вероятность наблюдения F-статистики, которая по крайней мере равна значению, полученному в нашем исследовании. Эта вероятность позволяет нам определить, насколько часто или редко встречается наше F-значение при предположении, что нулевая гипотеза верна.Если вероятность достаточно мала, мы можем сделать вывод, что наши данные не соответствуют нулевой гипотезе. Доказательства в выборочных данных достаточно сильны, чтобы отвергнуть нулевую гипотезу для всего населения.

Эта вероятность, которую мы вычисляем, также известна как p-значение!

Чтобы построить F-распределение для нашего примера пластической прочности, я буду использовать графики распределения вероятностей Minitab. Чтобы изобразить F-распределение, соответствующее нашему конкретному дизайну и размеру выборки, нам нужно указать правильное количество DF.Глядя на наш односторонний результат ANOVA, мы видим, что у нас есть 3 DF для числителя и 36 DF для знаменателя.

На графике показано распределение F-значений, которое мы получили бы, если бы нулевая гипотеза верна, и мы повторяем наше исследование много раз. Заштрихованная область представляет вероятность наблюдения F-значения, которое, по крайней мере, равно F-значению, полученному в нашем исследовании. F-значения попадают в эту заштрихованную область примерно в 3,1% случаев, когда нулевая гипотеза верна.Эта вероятность достаточно мала, чтобы отклонить нулевую гипотезу с использованием общего уровня значимости 0,05. Можно сделать вывод, что не все средние группы равны.

Узнайте, как правильно интерпретировать значение p.

Оценка средств путем анализа вариации

ANOVA использует F-тест, чтобы определить, превышает ли изменчивость между средними значениями групп, чем изменчивость наблюдений внутри групп. Если это соотношение достаточно велико, можно сделать вывод, что не все средства равны.

Это возвращает нас к тому, почему мы анализируем вариации, чтобы судить о средствах. Задумайтесь над вопросом: «Разве группа означает разные?» Вы неявно спрашиваете об изменчивости средств. В конце концов, если группа означает, что не отличается от или не отличается больше, чем позволяет случайный случай, то вы не можете сказать, что средства разные. Вот почему вы используете дисперсионный анализ для проверки средних значений.

1.3.5.9. F-тест на равенство двух вариантов

1.Исследовательский анализ данных
1,3. Методы EDA
1.3.5. Количественные методы

1.3.5.9.

F -Тест на равенство двух вариантов

Цель:
Проверить, равны ли дисперсии двух популяций

An F -тест (Снедекор и Кокран, 1983) используется, чтобы проверить, есть ли дисперсии двух популяции равны.Этот тест может быть двусторонним или двусторонним. односторонний тест. Двусторонняя версия тестирует альтернатива, что отклонения не равны. Односторонняя версия тестирует только в одном направлении, то есть отклонение от первой популяции либо больше или меньше (но не обоих) второй популяции дисперсия. Выбор определяется проблемой. Например, если мы тестируем новый процесс, мы можем только интересоваться, является ли новый процесс менее изменчивым чем старый процесс.{2} _ {2}} \) и являются выборочными дисперсиями. Тем более это отношение отклоняется от 1, тем сильнее доказательства неравенства дисперсия населения.

Значимость
Уровень:

Критический регион
:

Гипотеза о том, что две дисперсии равны отклоняется, если

\ (F> F _ {\ alpha, N_1 — 1, N_2 — 1} \)		для верхнего одностороннего теста
\ (F		для нижнего одностороннего теста
\ (F или \ (F> F _ {\ alpha / 2, N_1 — 1, N_2 — 1} \)		для двустороннего теста

куда F _{α , N ₁-1, N ₂-1} — это критическое значение F Распределение с N ₁-1 и N ₂-1 степени свободы и уровень значимости α .

В приведенных выше формулах для критического регионов, Справочник следует соглашению, что F _α — верхнее критическое значение из распределения F и F _{1- α} — нижнее критическое значение из F Распределение. Обратите внимание, что это противоположность обозначение, используемое в некоторых текстах и программах.

F Тестовый пример Следующий тест F был создан для Набор данных AUTO83B.DAT. Набор данных содержит 480 измерений прочности керамики для двух партий материала. Сводная статистика для каждой партии показано ниже.

ПАРТИЯ 1:
   КОЛИЧЕСТВО НАБЛЮДЕНИЙ = 240
   СРЕДНЕЕ = 688,9987
   СТАНДАРТНОЕ ОТКЛОНЕНИЕ = 65.54909
  
ПАРТИЯ 2:
   КОЛИЧЕСТВО НАБЛЮДЕНИЙ = 240
   СРЕДНЕЕ = 611,1559
   СТАНДАРТНОЕ ОТКЛОНЕНИЕ = 61,85425

Мы проверяем нулевую гипотезу о том, что дисперсии для две партии равны.

H ₀: σ ₁ ² = σ ₂ ² H _a: σ ₁ ² ≠ σ ₂ ²

Статистика теста: F = 1,123037 Числитель степеней свободы: N ₁ - 1 = 239 Знаменатель степеней свободы: N ₂ - 1 = 239 Уровень значимости: α = 0.05 Критические значения: F (1- α /2, N ₁-1, N ₂-1) = 0,7756 F ( α /2, N ₁-1, N ₂-1) = 1,2894 Область отклонения: отклонить H ₀, если F F> 1,2894

Тест F показывает, что недостаточно доказательств для отклонить нулевую гипотезу о том, что два варианта пакетного доступа равны при 0.05 уровень значимости. вопросов Тест F может быть использован для ответа на следующие вопросы: вопросов:

Бывают ли две выборки из популяций с равными variancess?
Выполняет новый процесс, лечение или тест уменьшить вариативность текущего процесса?

Связанные методы График квантиль-квантиль
Бигистограмма
Тест хи-квадрат
Тест Бартлетта
Тест Левена Пример использования Данные по прочности керамики. Программное обеспечение F -тест на равенство двух дисперсий: доступны во многих статистических программное обеспечение. Оба Код Dataplot и Код R можно использовать для генерации анализы в этом разделе. Эти скрипты используют Файл данных AUTO83B.DAT.

Статистика: F-Test

F-распределение образовано соотношением двух независимых хи-квадратов. переменные, разделенные на их соответствующие степени свободы.

Поскольку F образовано хи-квадрат, многие свойства хи-квадрат несут к распределению F.

Все значения F неотрицательны
Распределение несимметричное
Среднее значение примерно 1
Есть две независимые степени свободы, одна для числителя, а другая для знаменатель.
Существует множество различных F-распределений, по одному для каждой пары степеней свободы.

F-тест

F-тест разработан, чтобы проверить, равны ли две дисперсии генеральной совокупности.Это делается путем сравнения соотношение двух дисперсий. Таким образом, если дисперсии равны, отношение дисперсий будет равно 1.

Вся проверка гипотез выполняется в предположении, что нулевая гипотеза верна

Если нулевая гипотеза верна, то приведенная выше статистика F-теста может быть упрощена (резко). Это соотношение дисперсий выборки будет использоваться в качестве статистики теста. Если нуль гипотеза ложна, тогда мы отвергнем нулевую гипотезу о том, что соотношение было равно к 1 и наше предположение, что они были равны.

Существует несколько различных F-таблиц. Каждый из них имеет разный уровень значимости. Итак, сначала найдите правильный уровень значимости, а затем найдите степени свободы в числителе. и знаменатель степеней свободы для нахождения критического значения.

Вы заметите, что все таблицы показывают уровень значимости только для тестов правого хвоста. Поскольку Распределение F не является симметричным, и нет отрицательных значений, вы не можете просто взять напротив правого критического значения, чтобы найти левое критическое значение.Способ найти левую критику значение состоит в том, чтобы поменять местами степени свободы, найти правильное критическое значение, а затем взять величина, обратная этому значению. Например, критическое значение 0,05 слева с числителем 12 и 15 степеней свободы знаменателя найдены путем взятия обратной величины критического значения с Справа 0,05 с 15 степенями свободы в числителе и 12 в знаменателе.

Избегание левых критических значений

Так как левые критические значения сложно вычислить, их часто вообще избегают.Это процедура, описанная в учебнике. Вы можете превратить тест F в тест на правом хвосте, поместив выборка с большой дисперсией в числителе и меньшей дисперсией в знаменателе. Это не имеет значения, какая выборка имеет больший размер, а только какая выборка имеет больший размер. дисперсия.

Числитель степеней свободы будет степенями свободы для любого образца, имеющего большая дисперсия (так как она находится в числителе), и знаменатель степеней свободы будет степени свободы для той выборки, которая имеет меньшую дисперсию (поскольку она указана в знаменателе).2

Разделите альфа на 2 для теста с двумя хвостами, а затем найдите правильное критическое значение

Если вместо отклонений указаны стандартные отклонения, они должны быть возведены в квадрат

Если степени свободы не указаны в таблице, используйте значение с большей критической значение (это меньшие степени свободы). Это сделано для того, чтобы вы с меньшей вероятностью отклонить по ошибке (ошибка типа I)

Популяции, из которых были взяты образцы, должны быть нормальными.

Образцы должны быть независимыми

Содержание

Как работают F-тесты в дисперсионном анализе (ANOVA)

Дисперсионный анализ (ANOVA) использует F-тесты для статистической оценки равенства средних, когда у вас есть три или более групп. В этом посте я отвечу на несколько распространенных вопросов о F-тесте.

Как работают F-тесты?
Почему мы анализируем отклонений , чтобы проверить означает ?

Я буду использовать концепции и графики, чтобы ответить на эти вопросы о F-тестах в контексте одностороннего примера ANOVA.Я буду использовать тот же подход, который использую, чтобы объяснить, как работают t-тесты. Если вам нужен учебник по основам, прочтите мой обзор проверки гипотез.

Чтобы узнать больше о тестах ANOVA, включая более сложные формы, прочтите мой Обзор ANOVA.

Представляем F-тесты и F-статистику!

Термин F-тест основан на том факте, что эти тесты используют F-статистику для проверки гипотез. F-статистика — это соотношение двух дисперсий, названная в честь сэра Рональда Фишера.Вариации измеряют разброс точек данных вокруг среднего. Более высокие отклонения возникают, когда отдельные точки данных имеют тенденцию отклоняться от среднего значения.

Непосредственно интерпретировать отклонения сложно, потому что они выражены в квадрате единиц данных. Если вы извлечете квадратный корень из дисперсии, вы получите стандартное отклонение, которое легче интерпретировать, поскольку оно использует единицы данных. Хотя отклонения трудно интерпретировать напрямую, некоторые статистические тесты используют их в своих уравнениях.

F-статистика — это отношение двух дисперсий или, технически, двух средних квадратов. Средние квадраты — это просто дисперсии, которые учитывают степени свободы (DF), используемые для оценки дисперсии.

Подумайте об этом иначе. Отклонения — это сумма квадратов отклонений от среднего. Если у вас более крупная выборка, нужно сложить больше квадратов отклонений. В результате сумма становится все больше и больше по мере того, как вы добавляете больше наблюдений. За счет включения DF средние квадраты учитывают различное количество измерений для каждой оценки дисперсии.В противном случае дисперсии несопоставимы, и соотношение для F-статистики не имеет смысла.

Учитывая, что F-тесты оценивают соотношение двух дисперсий, вы можете подумать, что он подходит только для определения того, равны ли дисперсии. На самом деле, он может это и многое другое! F-тесты на удивление гибкие, потому что вы можете включать различные вариации в соотношение для тестирования самых разных свойств. F-тесты могут сравнивать соответствие различных моделей, проверять общую значимость в регрессионных моделях, проверять конкретные термины в линейных моделях и определять, все ли наборы средних равны.

Связанное сообщение : Измерения изменчивости: диапазон, межквартильный размах, дисперсия и стандартное отклонение

F-тест в одностороннем дисперсионном анализе

Мы хотим определить, все ли средства равны. Чтобы оценить это с помощью F-теста, нам нужно использовать правильные отклонения в соотношении. Вот коэффициент F-статистики для одностороннего дисперсионного анализа.

Чтобы увидеть, как работают F-тесты, рассмотрим пример одностороннего дисперсионного анализа. Вы можете скачать файл данных CSV: OneWayExample.Числовые результаты приведены ниже, и я буду ссылаться на них, когда проиллюстрирую, как работает тест. Этот односторонний ANOVA оценивает средние значения четырех групп.

Связанные сообщения : Как выполнить односторонний дисперсионный анализ в Excel и как выполнить двухсторонний анализ дисперсионного анализа в Excel

Числитель F-теста: межгрупповая дисперсия

Односторонняя процедура ANOVA вычисляет среднее значение каждой из четырех групп: 11,203, 8,938, 10,683 и 8,838. Средние значения этих групп разбросаны вокруг глобального среднего (9.915) из всех 40 точек данных. Чем дальше группы от глобального среднего, тем больше становится дисперсия в числителе.

Проще сказать, что групповые средства различаются, когда они находятся дальше друг от друга. Это само собой разумеющееся, правда? В нашем F-тесте это соответствует более высокой дисперсии числителя.

Точечный график показывает, как это работает, путем сравнения двух наборов групповых средних. На этом графике среднее значение каждой группы обозначено точкой. Разница между группами увеличивается по мере того, как точки расходятся.

Оглядываясь назад на результат одностороннего дисперсионного анализа, какую статистику мы используем для межгрупповой дисперсии? Используемое нами значение является скорректированным средним квадратом для фактора (Adj MS 15.540). Значение этого числа не интуитивно понятно, потому что это сумма квадратов расстояний от глобального среднего, деленная на коэффициент DF. Важным моментом является то, что это число увеличивается по мере того, как группа распространяется дальше друг от друга.

Знаменатель F-критерия: внутригрупповая дисперсия

Теперь мы переходим к знаменателю F-критерия, который учитывает дисперсию внутри каждой группы.Эта дисперсия измеряет расстояние между каждой точкой данных и ее средним значением по группе. Опять же, это сумма квадратов расстояний, деленная на ошибку DF.

Это отклонение невелико, когда точки данных в каждой группе ближе к их среднему значению по группе. По мере того, как точки данных в каждой группе расходятся дальше от их среднего значения по группе, внутригрупповая дисперсия увеличивается.

График сравнивает низкую внутригрупповую изменчивость с высокой внутригрупповой изменчивостью. Распределения показывают, насколько сильно точки данных в каждой группе кластеризуются вокруг среднего значения группы.Знаменатель F-статистики или дисперсия внутри группы выше для правой панели, потому что точки данных имеют тенденцию быть дальше от среднего по группе.

Чтобы сделать вывод о том, что средние по группе не равны, вам нужна низкая внутригрупповая дисперсия. Почему? Дисперсия внутри группы представляет собой дисперсию, которую модель не объясняет. Статистики называют это случайной ошибкой. По мере увеличения ошибки становится более вероятным, что наблюдаемые различия между средними значениями групп вызваны ошибкой, а не фактическими различиями на уровне популяции.Очевидно, вам нужно меньше ошибок!

Давайте снова обратимся к результатам дисперсионного анализа. Внутригрупповая дисперсия отображается в выходных данных как скорректированные средние квадраты ошибки (Adj MS for Error): 4,402.

F-статистика: отношение межгрупповых различий к внутригрупповым

F-статистика — это отношение двух дисперсий, которые имеют примерно одно и то же значение, когда нулевая гипотеза верна, что дает F-статистику около 1.

Мы рассмотрели две различные дисперсии, использованные в одностороннем F-тесте ANOVA.Теперь давайте объединим их, чтобы увидеть, какие комбинации дают низкую и высокую F-статистику. На графиках посмотрите, как разброс средних значений группы соотносится с разбросом точек данных внутри каждой группы.

График низкого F-значения : Группа означает кластеризацию более плотно, чем внутригрупповая изменчивость. Расстояние между средними значениями мало по сравнению со случайной ошибкой внутри каждой группы. Нельзя сделать вывод, что эти группы действительно различны на уровне населения.
График высокого F-значения : Группа означает разброс больше, чем изменчивость данных внутри групп. В этом случае становится более вероятным, что наблюдаемые различия между средними значениями групп отражают различия на уровне популяции.

Как рассчитать значение F

Возвращаясь к нашему примеру вывода, мы можем использовать числитель и знаменатель F-отношения для вычисления нашего F-значения следующим образом:

Чтобы сделать вывод о том, что не все групповые средние равны, нам нужно большое F-значение, чтобы отвергнуть нулевую гипотезу.Наш достаточно большой?

Сложность F-значений заключается в том, что они представляют собой статистику без единиц измерения, что затрудняет их интерпретацию. Наше F-значение 3,30 указывает на то, что дисперсия между группами в 3,3 раза превышает размер дисперсии внутри группы. Значение нулевой гипотезы состоит в том, что дисперсии равны, что дает значение F, равное 1. Достаточно ли велико наше значение F, равное 3,3, чтобы отклонить нулевую гипотезу?

Мы не знаем точно, насколько необычно наше F-значение, если нулевая гипотеза верна.Чтобы интерпретировать отдельные F-значения, нам нужно поместить их в более широкий контекст. F-распределения обеспечивают этот более широкий контекст и позволяют вычислять вероятности.

Как F-тесты используют F-распределения для проверки гипотез

Один F-тест дает одно F-значение. Однако представьте, что мы выполняем следующий процесс.

Во-первых, предположим, что нулевая гипотеза верна для населения. На уровне популяции все четыре средние группы равны. Теперь мы повторяем наше исследование много раз, отбирая множество случайных выборок из этой популяции, используя тот же односторонний дизайн ANOVA (четыре группы по 10 выборок в группе).Затем мы выполняем односторонний дисперсионный анализ для всех образцов и строим график распределения значений F. Это распределение известно как выборочное распределение, которое представляет собой тип распределения вероятностей.

Связанное сообщение : Общие сведения о распределении вероятностей

Если мы будем следовать этой процедуре, мы создадим график, который отображает распределение F-значений для популяции, в которой верна нулевая гипотеза. Мы используем выборочные распределения, чтобы вычислить вероятности того, насколько маловероятна наша выборочная статистика, если нулевая гипотеза верна.F-тесты используют F-распределение.

К счастью, нам не нужно собирать множество случайных выборок для создания этого графика! Статистики понимают свойства F-распределений, поэтому мы можем оценить распределение выборки, используя F-распределение и детали нашего одностороннего дизайна ANOVA.

Наша цель — оценить, является ли F-значение нашей выборки настолько редким, что оно оправдывает отклонение нулевой гипотезы для всей генеральной совокупности. Мы рассчитаем вероятность получения значения F, которое по крайней мере равно значению нашего исследования (3.30).

У этой вероятности есть название — значение P! Низкая вероятность указывает на то, что данные нашей выборки маловероятны, если нулевая гипотеза верна.

Построение графика F-теста для нашего примера однофакторного дисперсионного анализа

Для одностороннего дисперсионного анализа степени свободы в числителе и знаменателе определяют F-распределение для плана. Для каждого дизайна исследования существует свое F-распределение. Я создам график распределения вероятностей на основе DF, указанного в примере выходных статистических данных.В нашем исследовании 3 DF в числителе и 36 в знаменателе.

Соответствующее сообщение : Степени свободы в статистике

Кривая распределения отображает вероятность значений F для совокупности, в которой средние по четырем группам равны на уровне совокупности. Я закрасил область, которая соответствует F-значениям, большим или равным F-значению нашего исследования (3.3). Когда нулевая гипотеза верна, F-значения попадают в эту область примерно в 3,1% случаев. Используя уровень значимости 0.05, данные нашей выборки достаточно необычны, чтобы оправдать отклонение нулевой гипотезы. Данные выборки показывают, что не все средние по группе равны.

Узнайте, как правильно интерпретировать значения P и избежать распространенной ошибки.

Почему мы анализируем варианты для проверки средств

Давайте вернемся к вопросу о том, почему мы анализируем отклонения, чтобы определить, отличаются ли средние значения группы. Сосредоточьтесь на аспекте «средства разные». Эта часть явно включает изменение групповых средних.Если нет различий в средствах, они не могут быть разными, верно? Точно так же, чем больше разница между средними значениями, тем больше должно быть различий.

ANOVA и F-тесты оценивают степень вариабельности между средними значениями групп в контексте вариаций внутри групп, чтобы определить, являются ли средние различия статистически значимыми. Хотя статистически значимые результаты дисперсионного анализа показывают, что не все средние значения равны, он не позволяет определить, какие именно различия между парами средних значений являются значимыми.Чтобы сделать это определение, вам нужно будет использовать апостериорные тесты, чтобы дополнить результаты ANOVA.

Если вы хотите узнать о других проверках гипотез с использованием того же общего подхода, прочтите:

Чтобы увидеть альтернативу традиционной проверке гипотез, которая не использует распределения вероятностей и статистику тестирования, узнайте о загрузке в статистике!

Примечание: я написал другую версию этого поста, которая появилась в другом месте. Я полностью переписал и обновил его для своего блога.

Связанные

Тест

F — обзор

Сводка

Объяснение или прогнозирование одной переменной Y из двух или более переменных X называется множественной регрессией . Цели множественной регрессии: (1) описать и понять взаимосвязь, (2) спрогнозировать (спрогнозировать) новое наблюдение и (3) настроить и контролировать процесс.

Отсечка или постоянный член , a , дает прогнозируемое (или «подогнанное») значение для Y , когда все переменные X равны 0.Коэффициент регрессии b _j для переменной j th X определяет влияние X _j на Y после корректировки для других переменных X ; b _j указывает, насколько больше, по вашему мнению, Y будет для случая, который идентичен другому, за исключением того, что он будет на одну единицу больше в X _j . Взятые вместе, эти коэффициенты регрессии дают вам уравнение прогнозирования или уравнение регрессии , Прогнозируемый Y = a + b ₁ X ₁ + b ₂

6

X X ₂ +… + b _k X _k , который может использоваться для прогнозирования или управления.Эти коэффициенты ( a , b ₁, b ₂,…, b _k ) традиционно вычисляются с использованием метода наименьших квадратов , который минимизирует сумму квадратов прогноза. ошибки. Ошибки предсказания или остатков задаются как Y — (Прогнозируемое Y ).
Есть два способа резюмировать, насколько хорош регрессионный анализ. Стандартная ошибка оценки , S _e , указывает приблизительный размер ошибок прогнозирования.Коэффициент детерминации , R ², указывает процент вариации в Y , которая «объясняется» или «приписывается» переменным X .
Вывод начинается с теста F , общего теста, чтобы увидеть, объясняют ли переменные X значительную величину вариации в Y. Если ваша регрессия не является значимой для , вам не разрешается идти дальше.Если регрессия значительна, вы можете продолжить статистический вывод, используя тесты t для индивидуальных коэффициентов регрессии . Доверительные интервалы и проверки гипотез для отдельного коэффициента регрессии будут основаны на его стандартной ошибке, Sb1, Sb2,… или Sbk. Критическое значение из таблицы t будет иметь n — k — 1 степень свободы.
Вывод основан на линейной модели множественной регрессии , которая определяет, что наблюдаемое значение для Y равно отношению совокупности плюс независимые случайные ошибки, которые имеют нормальное распределение
Y = (α + β1X1 + β2X2 +… + βkXk) + ε = (Отношение совокупности) + Случайность
, где ε имеет нормальное распределение со средним значением 0 и постоянным стандартным отклонением σ, и эта случайность не зависит от одного случая к другому.Для каждого параметра совокупности ( α , β1, β2,…, βk, σ ) существует выборочная оценка ( a, b ₁, b ₂,…, b _k , S _e ).
Гипотезы теста F следующие:
H0: β1 = β2 =… = βk = 0
h2: По крайней мере, один из β1, β2,…, βk ≠ 0
Результат Тест F задается следующим образом:
Если значение R ² на меньше критического значения в таблице на , то модель не имеет значения (примите нулевую гипотезу, что X переменные не помогают предсказать Y ).
Если значение R ² на больше , чем значение в таблице, модель имеет значение (отклоните нулевую гипотезу и примите исследовательскую гипотезу, что переменные X помогают для прогнозирования Y ).
Доверительный интервал для индивидуального коэффициента регрессии b _j равен
Frombj − tSbjtobj + tSbj
, где t — из таблицы t для n — градусов k свободы.Гипотезы для теста t для j -го коэффициента регрессии:
H0: βj = 0h2: βj ≠ 0
Существует два подхода к сложной проблеме определения того, какие переменные X вносят наибольший вклад в уравнение регрессии. Стандартизированный коэффициент регрессии , biSXi / Sy, представляет ожидаемое изменение Y из-за изменения X _i , измеренное в единицах стандартных отклонений Y на стандартное отклонение X _i , сохраняя все остальные переменные X постоянными.Если вы не хотите корректировать все другие переменные X (сохраняя их постоянными), вы можете вместо этого сравнить абсолютные значения коэффициентов корреляции для Y с каждой X .
Есть некоторые потенциальные проблемы с множественным регрессионным анализом:
1.
Проблема мультиколлинеарности возникает, когда некоторые из ваших объясняющих переменных ( X ) слишком похожи друг на друга. Коэффициенты индивидуальной регрессии оцениваются плохо, потому что недостаточно информации, чтобы решить, какая из (или более) переменных объясняет.Вы можете опустить некоторые из переменных или переопределить некоторые из переменных (возможно, используя отношения), чтобы отличать их друг от друга.
2.
Проблема выбора переменной возникает, когда у вас есть длинный список потенциально полезных объясняющих переменных X и вы хотите решить, какие из них включить в уравнение регрессии. При слишком большом количестве переменных X качество ваших результатов будет снижаться, поскольку информация тратится впустую при оценке ненужных параметров.Если одна или несколько важных переменных X опущены, ваши прогнозы потеряют качество из-за отсутствия информации. Одно из решений — включить только те переменные, которые явно необходимы, используя список с приоритетами. Другое решение — использовать автоматическую процедуру, такую как все подмножества или пошаговой регрессии.
3.
Проблема неправильной спецификации модели относится к множеству различных потенциальных несовместимостей между вашим приложением и линейной моделью множественной регрессии.Изучая данные, вы можете быть предупреждены о некоторых потенциальных проблемах, связанных с нелинейностью, неравномерной изменчивостью или выбросами. Однако у вас может быть проблема, а может и не быть: даже если гистограммы некоторых переменных могут быть искажены, и даже если некоторые диаграммы рассеяния могут быть нелинейными, линейная модель множественной регрессии может по-прежнему работать. Диагностический график может помочь вам решить, когда проблема достаточно серьезна, чтобы требовать ее устранения. Другая серьезная проблема возникает, если у вас есть временной ряд; это может помочь выполнить множественную регрессию с использованием процентных изменений от одного периода времени к другому вместо исходных значений данных для каждой переменной.
Диагностическая диаграмма для множественной регрессии — это диаграмма разброса ошибок предсказания (остатков) по сравнению с предсказанными значениями, которая используется для определения того, есть ли у вас какие-либо проблемы с данными, которые необходимо исправить. Не вмешивайтесь, если диагностическая диаграмма не покажет вам четкую и определенную проблему.
Есть три способа справиться с нелинейностью и / или неравномерностью: (1) преобразовать некоторые или все переменные, (2) ввести новую переменную или (3) использовать нелинейную регрессию.При преобразовании каждая группа переменных, измеряемая в одних и тех же базовых единицах, вероятно, должна быть преобразована таким же образом. Если вы преобразуете некоторые из переменных X , но не преобразуете Y , то большая часть интерпретации результатов множественного регрессионного анализа останется неизменной. Если вы используете натуральный логарифм Y , тогда R ² и тесты значимости для отдельных коэффициентов регрессии сохранят свою обычную интерпретацию, индивидуальные коэффициенты регрессии имеют аналогичную интерпретацию, и требуется новая интерпретация для S _e .
Эластичность Y по отношению к X _i — это ожидаемое процентное изменение в Y , связанное с увеличением на 1% X _i , удерживая остальные X фиксированные переменные; эластичность оценивается с использованием коэффициента регрессии из регрессионного анализа с использованием натурального логарифма Y и X _i .
Другой способ справиться с нелинейностью — использовать полиномиальную регрессию для прогнозирования Y с использованием одной переменной X вместе с некоторыми ее степенями ( X ², X ³ и т. Д.).
Говорят, что две переменные демонстрируют взаимодействие , если изменение в обеих из них вызывает ожидаемый сдвиг в Y , который отличается от суммы сдвигов в Y , полученных путем изменения каждого X по отдельности. Взаимодействие часто моделируется в регрессионном анализе с использованием перекрестного произведения , образованного путем умножения одной переменной X на другую, что определяет новую переменную X , которая будет включена вместе с другими в вашу множественную регрессию.Взаимодействие также можно моделировать, используя преобразования некоторых или всех переменных.
Индикаторная переменная (также называемая фиктивной переменной ) — это количественная переменная, состоящая только из значений 0 и 1, которая используется для представления качественных категориальных данных в качестве объясняющей переменной X . Количество индикаторных переменных, используемых в множественной регрессии для замены качественной переменной, на меньше на , чем количество категорий.Оставшаяся категория определяет базовый уровень . Базовая категория представлена постоянным членом в выходных данных регрессии.
Вместо использования индикаторных переменных можно вычислить отдельные регрессии для каждой категории. Этот подход обеспечивает более гибкую модель с различными коэффициентами регрессии для каждой переменной X для каждой категории.
Глава 6. F-тест и односторонний дисперсионный анализ — вводная бизнес-статистика с интерактивными таблицами — 1-е канадское издание
Несколько лет назад статистики обнаружили, что, когда пары выборок берутся из нормальной совокупности, отношения дисперсий выборок в каждой паре всегда будут следовать одному и тому же распределению.2 / (n-1) [/ латекс]
Подумайте о форме, которую будет иметь F-распределение. Если s ₁ ² и s ₂ ² происходят из выборок из одной и той же совокупности, то если было взято много пар выборок и вычислены F-оценки, большинство этих F-оценок были бы близко к одному. Все F-баллы будут положительными, поскольку дисперсия всегда положительна — числитель в формуле представляет собой сумму квадратов, поэтому он будет положительным, знаменатель — размер выборки минус один, что также будет положительным.Обдумывание соотношений требует некоторой осторожности. Если с ₁ ² намного больше, чем с ₂ ² , F может быть довольно большим. Также возможно, что s ₂ ² будет намного больше, чем s ₁ ² , и тогда F будет очень близко к нулю. Поскольку F изменяется от нуля до очень большого, с большинством значений около единицы, он, очевидно, не симметричен; Справа длинный хвост, а слева крутой спуск к нулю.
В этой главе мы обсудим два использования F-распределения. Первый — это очень простой тест, позволяющий определить, происходят ли две выборки из популяций с одинаковой дисперсией. Второй — это односторонний дисперсионный анализ (ANOVA), который использует F-распределение для проверки того, происходят ли три или более выборки из популяций с одинаковым средним значением.
Простой тест: взяты ли эти две выборки из популяций с одинаковой дисперсией?
Поскольку F-распределение генерируется путем отбора двух выборок из одной и той же нормальной совокупности, его можно использовать для проверки гипотезы о том, что две выборки происходят из популяций с одинаковой дисперсией.У вас будет две выборки (одна размером n ₁ и одна размером n ₂ ) и дисперсия выборки для каждой из них. Очевидно, что если две дисперсии очень близки к равенству, две выборки легко могли быть получены из популяций с равной дисперсией. Поскольку F-статистика представляет собой отношение двух выборочных дисперсий, когда две выборочные дисперсии близки к равным, F-оценка близка к единице. Если вы вычисляете F-балл, и он близок к единице, вы принимаете свою гипотезу о том, что выборки происходят из популяций с одинаковой дисперсией.
Это основной метод F-теста. Выдвинуть гипотезу, что выборки происходят из популяций с одинаковой дисперсией. Вычислите F-оценку, найдя соотношение дисперсий выборки. Если F-оценка близка к единице, сделайте вывод, что ваша гипотеза верна и что выборки действительно происходят из популяций с равной дисперсией. Если F-оценка далека от единицы, тогда сделайте вывод, что совокупности, вероятно, имеют разные дисперсии.
Базовый метод должен быть дополнен некоторыми деталями, если вы собираетесь использовать этот тест на работе.Есть два набора деталей: во-первых, формальное написание гипотез, а во-вторых, использование таблиц F-распределения, чтобы вы могли определить, близок ли ваш F-балл к единице или нет. Формально для полноты нужны две гипотезы. Первая — это нулевая гипотеза о том, что разницы нет (отсюда null ). Обычно обозначается как H _o . Во-вторых, есть разница, и она называется альтернативой и обозначается H ₁ или H _a .
Использование F-таблиц для определения того, насколько близко к единице достаточно близко, чтобы принять нулевую гипотезу (истинно формальные статистики сказали бы «не смогли отвергнуть нулевую») довольно сложно, потому что таблицы F-распределения довольно сложны. Перед использованием таблиц исследователь должен решить, насколько он или она готовы рискнуть, что нуль будет отклонен, когда это действительно правда. Обычный выбор — 5 процентов, или, как говорят статистики, « α — 0,05 ″. Если требуется более или менее шанс, α может быть изменен.Выберите свой α и перейдите к F-таблицам. Сначала обратите внимание, что существует ряд F-таблиц, по одной для каждого из нескольких различных уровней α (или, по крайней мере, таблица для каждых двух α с F-значениями для одного α , выделенными полужирным шрифтом . , а значения для другого — обычным шрифтом). В каждой F-таблице есть строки и столбцы, и оба предназначены для степеней свободы. Поскольку для вычисления F-оценки берутся две отдельные выборки, и выборки не обязательно должны быть одинакового размера, существуют две отдельные степени свободы — по одной для каждой выборки.Для каждого образца количество степеней свободы составляет n -1, что на единицу меньше размера образца. Переходя к таблице, как вы решаете, какие степени свободы (df) выборки подходят для строки, а какие — для столбца? Хотя вы можете поместить любой из них в любое место, вы можете сэкономить один шаг, если поместите образец с большей дисперсией (не обязательно большей выборкой) в числитель , а затем df этого образца определяет столбец и df другого образца определяет строку.Причина, по которой это экономит вам шаг, заключается в том, что таблицы показывают только значения F, которые оставляют α в правом хвосте, где F> 1, изображение в верхней части большинства F-таблиц показывает это. Для поиска критического F-значения для левого хвоста требуется еще один шаг, который описан в интерактивном шаблоне Excel на рисунке 6.1. Просто измените числитель и знаменатель степеней свободы, а α в правом хвосте F-распределения в желтых ячейках.

Рисунок 6.1 Интерактивный шаблон F-таблицы в Excel — см. Приложение 6.
F-таблицы практически всегда печатаются как односторонние, показывая критическое F-значение, которое отделяет правый хвост от остальной части распределения. В большинстве статистических приложений F-распределения интерес представляет только правый хвост, потому что большинство приложений проверяют, больше ли отклонение от одного источника, чем отклонение от другого источника, поэтому исследователь заинтересован в том, чтобы найти, F-оценка больше единицы.В тесте на равные дисперсии исследователь заинтересован в том, чтобы выяснить, составляет ли F-балл , близкий к к единице, так что либо большой F-балл, либо маленький F-балл привели бы исследователя к выводу, что дисперсии не равный. Поскольку критическое значение F, отделяющее левый хвост от остальной части распределения, не печатается, а не просто отрицательное значение напечатанного значения, исследователи часто просто делят большую дисперсию выборки на меньшую дисперсию выборки и используют распечатанные таблицы. чтобы увидеть, является ли частное «больше единицы», эффективно превращая тест в односторонний формат.Для пуристов и редких случаев критическое значение левого хвоста может быть вычислено довольно легко.
Критическое значение левого хвоста для x , y степеней свободы (df) является просто обратной величиной критического значения правого хвоста (таблица) для y , x df. Посмотрев на F-таблицу, вы увидите, что значение F, которое оставляет α — 0,05 в правом хвосте, когда есть 10 , 20 df, равно F = 2,35. Чтобы найти значение F, которое оставляет α -.05 в левом хвосте с 10, 20 df, найдите F = 2,77 для α — 0,05, 20 , 10 df. Разделите единицу на 2,77, найдя 0,36. Это означает, что 5% F-распределения для 10 , 20 df ниже критического значения 0,36 и 5% выше критического значения 2,35.
Объединив все это вместе, вот как провести тест, чтобы увидеть, происходят ли две выборки из популяций с одинаковой дисперсией. Сначала соберите две выборки и вычислите дисперсию выборки для каждой, с ₁ ² и с ₂ ² .Во-вторых, напишите свои гипотезы и выберите α . В-третьих, найдите F-балл из ваших выборок, разделив большее s ² на меньшее так, чтобы F> 1. В-четвертых, перейдите к таблицам, найдите таблицу для α /2 и найдите критический (табличный) F-балл для правильных степеней свободы ( n -1 и n -1). Сравните это с F-оценкой образцов. Если выборки ‘F больше критического F, выборки’ F не «близки к единице» и H _a дисперсии совокупности не равны, что является лучшей гипотезой.Если F выборок меньше критического F, H _o , то следует принять, что дисперсии генеральной совокупности равны.
Пример # 1
Линь Сян, молодой банкир, переехала из Саскатуна, Саскачеван, в Виннипег, Манитоба, где она недавно получила повышение и стала менеджером City Bank, недавно созданного банка в Виннипеге с филиалами в прериях. Через несколько недель она обнаружила, что поддерживать правильное количество кассиров, кажется, сложнее, чем когда она была помощником управляющего филиала в Саскатуне.В некоторые дни очереди очень длинные, но в другие дни кассирам, кажется, нечего делать. Она задается вопросом, может ли количество клиентов в ее новом филиале просто более изменчиво, чем количество клиентов в филиале, в котором она раньше работала. Поскольку кассиры работают целый день или полдня (утром или днем), она собирает следующие данные о количестве транзакций за полдня из своего отделения и отделения, в котором она раньше работала:
Виннипегский филиал: 156, 278, 134, 202, 236, 198, 187, 199, 143, 165, 223
Филиал Саскатун: 345, 332, 309, 367, 388, 312, 355, 363, 381
Она предполагает:
[латекс] H_o: \ sigma ^ 2_W = \ sigma ^ 2_S [/ latex]
[латекс] H_a: \ sigma ^ 2_W \ neq \ sigma ^ 2_S [/ латекс]
Она решает использовать α -.2_S = 1828,56 / 795,19 = 2,30 [/ латекс]

Рисунок 6.2 Интерактивный шаблон Excel для F-теста — см. Приложение 6.
Используя интерактивный шаблон Excel на рис. 6.2 (и не забывая использовать таблицу α — 0,025, потому что таблица односторонняя, а тест двухсторонний), она обнаружила, что критическое значение F для 10,8 df равно 4.30. Поскольку ее F-оценка из рисунка 6.2 меньше критической, она приходит к выводу, что ее F-оценка «близка к единице», и что разброс клиентов в ее офисе такой же, как и в старом офисе.Ей нужно будет искать дальше, чтобы решить ее кадровую проблему.
Важность ANOVA
Более важное использование F-распределения заключается в анализе дисперсии, чтобы увидеть, происходят ли три или более выборки из популяций с равными средними значениями. Это важный статистический тест не столько потому, что он часто используется, сколько потому, что он является мостом между одномерной статистикой и многомерной статистикой, а также потому, что стратегия, которую он использует, используется во многих многомерных тестах и процедурах.
Односторонний дисперсионный анализ: все ли эти три (или более) образца взяты из популяций с одинаковым средним значением?
Это кажется неправильным — мы проверим гипотезу о средних с помощью анализа дисперсии . Это не неправильно, а скорее действительно умная идея, сделанная некоторыми статистиками много лет назад. Эта идея — изучение дисперсии для выяснения различий в средних — является основой для большей части многомерной статистики, используемой сегодня исследователями. Идеи, лежащие в основе ANOVA, используются, когда мы ищем отношения между двумя или более переменными, и это главная причина, по которой мы используем многомерную статистику.
Проверка того, происходят ли три или более выборки из групп населения с одинаковым средним значением, часто может быть своего рода многомерным упражнением. Если три образца были получены с трех разных заводов или подвергались разной обработке, мы эффективно видим, есть ли разница в результатах из-за разных заводов или обработок — есть ли связь между фабрикой (или обработкой) и результатом?
Подумайте о трех образцах. Собрана группа размером x , и по какой-то веской причине (кроме значения x) их можно разделить на три группы.У вас есть несколько x из группы (выборки) 1, некоторые из группы (выборки) 2 и некоторые из группы (выборки) 3. Если бы выборки были объединены, вы могли бы вычислить общее среднее значение , и общее значение . отклонение от этого большого среднего. Вы также можете найти среднее значение и (выборку) дисперсии в пределах каждой из групп. Наконец, вы можете взять три выборочных средних и найти отклонение между из них. ANOVA основан на анализе того, откуда берется общая дисперсия.Если вы выберете один x , источник его дисперсии, его расстояние от общего среднего, будет состоять из двух частей: (1) насколько далеко он от среднего значения его выборки и (2) насколько далеко среднее значение его выборки от большого среднего. Если три выборки действительно происходят из популяций с разными средними значениями, то для большинства значений x расстояние между средним значением выборки и общим средним значением, вероятно, будет больше, чем расстояние между средним значением x и его средним групповым значением. . Когда эти расстояния собираются вместе и превращаются в дисперсии, вы можете видеть, что, если средние значения генеральной совокупности различны, дисперсия между средними значениями выборки, вероятно, будет больше, чем дисперсия внутри выборок.
К этому моменту в книге вы не должны удивляться, узнав, что статистики обнаружили, что если три или более выборки взяты из нормальной совокупности, а дисперсия между выборками делится на дисперсию внутри выборок, то распределение выборки сформированный повторением этого снова и снова, будет иметь известную форму. В этом случае он будет распределен как F с m -1, n — m df, где m — количество отсчетов, а n — это размер m отсчетов в целом.Разница между найдена по:
, где x _j — это среднее значение выборки j , а x — это большое среднее.
Числитель дисперсии — это сумма квадратов расстояния между каждым средним выборочным значением x и общим средним. Это просто сумма одного из источников расхождения по всем наблюдениям.
Расхождение в пределах найдено по:
С двойными суммами нужно обращаться осторожно.Сначала (работая с внутри или вторым знаком суммы) найдите среднее значение каждого образца и сумму квадратов расстояний каждого x в образце от его среднего. Во-вторых (работая с цифрой за пределами знака суммы ), сложите результаты каждой из выборок.
Стратегия проведения одностороннего дисперсионного анализа проста. Собрать м проб. Вычислите дисперсию между выборками, дисперсию в пределах выборки и отношение между ними с точностью до F-оценки.Если F-оценка меньше единицы или ненамного больше единицы, дисперсия между выборками не превышает дисперсию внутри выборок, и выборки, вероятно, происходят из популяций с одинаковым средним значением. Если F-оценка намного больше единицы, дисперсия между ними, вероятно, является источником большей части дисперсии в общей выборке, и выборки, вероятно, происходят из популяций с разными средними значениями.
Детали проведения одностороннего дисперсионного анализа разделяются на три категории: (1) написание гипотез, (2) организация вычислений и (3) использование F-таблиц.Нулевая гипотеза состоит в том, что все средние по совокупности равны, а альтернатива состоит в том, что не все средние равны. Довольно часто, хотя для полноты действительно нужны две гипотезы, записывается только H _o :
[латекс] H_o: m_1 = m_2 = \ ldots = m_m [/ latex]
Организация расчетов важна, когда вы обнаруживаете отклонение в пределах. Помните, что внутренняя дисперсия находится путем возведения в квадрат, а затем суммирования расстояния между каждым наблюдением и средним значением для его выборки .Хотя разные люди делают расчеты по-разному, я считаю, что лучший способ сохранить все прямо — это найти средние значения выборки, найти квадраты расстояний в каждой из выборок, а затем сложить их вместе. Также важно, чтобы вычисления были организованы при окончательном вычислении F-балла. Если вы помните, что цель состоит в том, чтобы увидеть, велико ли отклонение между , тогда легко не забыть разделить отклонение на отклонение внутри.
Использование F-таблиц — третья деталь.Помните, что F-таблицы — это односторонние таблицы, а ANOVA — односторонний тест. Хотя нулевая гипотеза состоит в том, что все средние равны, вы проверяете эту гипотезу, проверяя, меньше ли дисперсия между дисперсией внутри нее или равна ей. Число степеней свободы составляет m -1, n — m , где m — количество выборок, а n — общий размер всех выборок вместе.
Пример # 2
Молодой менеджер банка из Примера 1 все еще пытается найти лучший способ укомплектовать свой филиал.Она знает, что по пятницам у нее должно быть больше кассиров, чем в другие дни, но она пытается выяснить, остается ли потребность в кассирах постоянной в течение остальной части недели. Она собирает данные о количестве транзакций каждый день в течение двух месяцев. Вот ее данные:
Понедельник: 276, 323, 298, 256, 277, 309, 312, 265, 311
Вторник: 243, 279, 301, 285, 274, 243, 228, 298, 255
Среды: 288, 292, 310, 267, 243, 293, 255, 273
Четверг: 254, 279, 241, 227, 278, 276, 256, 262
Она проверяет нулевую гипотезу:
[латекс] H_o: m_m = m_ {tu} = m_w = m_ {th} [/ latex]
и решает использовать α -.05. Она находит:
м = 291,8
tu = 267,3
Вт = 277,6
-е = 259,1
и среднее значение = 274,3
Она вычисляет дисперсию в пределах:
[(276-291,8) 2+ (323-291,8) 2 +… + (243-267,6) 2 +… + (288-277,6) 2 +… + (254-259,1) 2] / [34-4] = 15887,6 / 30 = 529,6
Затем она вычисляет отклонение между:
[9 (291,8-274,3) 2 + 9 (267,3-274,3) 2 + 8 (277,6-274,3) 2 + 8 (259,1-274,3) 2] / [4-1]
= 5151,8 / 3 = 1717,3
Она вычисляет свой F-балл:

Рисунок 6.3 Интерактивный шаблон Excel для одностороннего дисперсионного анализа — см. Приложение 6.
Вы можете ввести количество транзакций каждый день в желтые ячейки на Рисунке 6.3 и выбрать α . Как вы можете видеть на Рисунке 6.3, вычисленное значение F равно 3,24, тогда как F-таблица (F-Critical) для α — 0,05 и 3, 30 df составляет 2,92. Поскольку ее F-балл больше критического F-значения или, альтернативно, поскольку p-значение (0,036) меньше α — 0,05, она приходит к выводу, что среднее количество транзакций не равно в разные дни неделя, или хотя бы один день отличается от других.Она захочет скорректировать свой штат так, чтобы в одни дни у нее было больше кассиров, чем в другие.
F-распределение — это выборочное распределение отношения дисперсий двух выборок, взятых из нормальной генеральной совокупности. Он используется непосредственно для проверки того, происходят ли две выборки из популяций с одинаковой дисперсией. Хотя вы иногда будете видеть, что он используется для проверки равенства дисперсий, более важным является использование дисперсионного анализа (ANOVA). ANOVA, по крайней мере, в его простейшей форме, представленной в этой главе, используется для проверки того, происходят ли три или более выборки из популяций с одинаковым средним значением.Проверяя, происходит ли дисперсия наблюдений в большей степени из-за отклонения каждого наблюдения от среднего его выборки или из-за изменения средних значений выборок из общего среднего, ANOVA проверяет, происходят ли выборки из популяций с равные средства или нет.
ANOVA имеет более элегантные формы, которые появляются в последующих главах. Он формирует основу для регрессионного анализа, статистического метода, который имеет множество бизнес-приложений; он рассматривается в следующих главах. F-таблицы также используются для проверки гипотез о результатах регрессии.
Это тоже начало многомерной статистики. Обратите внимание, что в одностороннем дисперсионном анализе каждое наблюдение относится к двум переменным: переменной x и группе, частью которой является наблюдение. В последующих главах наблюдения будут иметь две, три или более переменных.
F-тест на равенство дисперсий иногда используется перед использованием t-теста на равенство средних, потому что t-тест, по крайней мере в форме, представленной в этом тексте, требует, чтобы выборки происходили из совокупностей с равными дисперсиями.Вы увидите, что его используют вместе с t-тестами, когда ставки высоки или исследователь немного компульсивен.
F-Test: сравните два варианта R — Easy Guides — Wiki
F-тест используется для оценки того, равны ли отклонения двух популяций (A и B).
Когда вам использовать F-тест?
Сравнение двух отклонений полезно в нескольких случаях, в том числе:
Если необходимо выполнить t-тест для двух выборок, чтобы проверить равенство дисперсий двух выборок
Если вы хотите сравнить изменчивость нового метода измерения со старым.2} \]
Степени свободы: \ (n_A — 1 \) (для числителя) и \ (n_B — 1 \) (для знаменателя).
Обратите внимание, что чем больше это соотношение отклоняется от 1, тем сильнее доказательства неравной дисперсии совокупности.
Обратите внимание, что F-тест требует, чтобы две выборки были распределены нормально.
Вычислить F-тест в R
R функция
Функция R var.test () может использоваться для сравнения двух отклонений следующим образом:
# Метод 1 var.тест (значения ~ группы, данные, альтернатива = "two.sided") # или метод 2 var.test (x, y, alternate = "two.sided")

x, y : числовые векторы
альтернатива : альтернативная гипотеза. Допустимое значение: «двусторонний» (по умолчанию), «больше» или «меньше».
Импортируйте и проверяйте свои данные в R
Для импорта данных используйте следующий код R:
# Если файл вкладки .txt, используйте это my_data
Здесь мы будем использовать встроенный набор данных R под названием ToothGrowth:
# Сохраняем данные в переменной my_data my_data
Чтобы иметь представление о том, как выглядят данные, мы начинаем с отображения случайной выборки из 10 строк с помощью функции sample_n () [в пакете dplyr ]:
библиотека ("dplyr") sample_n (my_data, 10)
len supp доза 43 23.6 OJ 1.0 28 21,5 ВК 2,0 25 26,4 ВК 2,0 56 30,9 OJ 2,0 46 25,2 OJ 1.0 7 11,2 VC 0,5 16 17,3 ВК 1.0 4 5,8 VC 0,5 48 21,2 ОДж 1,0 37 8,2 OJ 0,5
Мы хотим проверить равенство дисперсий между двумя группами OJ и VC в столбце «supp».
Предварительный тест для проверки допущений F-теста
F-тест очень чувствителен к отклонениям от нормального допущения. Перед использованием F-теста необходимо проверить, нормально ли распределяются данные.
Тест Шапиро-Уилка можно использовать для проверки правильности нормального предположения. Также можно использовать график Q-Q (график квантиль-квантиль) для графической оценки нормальности переменной. График Q-Q показывает корреляцию между данным образцом и нормальным распределением.
Если есть сомнения относительно нормальности, лучшим выбором будет использовать тест Левена или тест Флиннера-Киллина , которые менее чувствительны к отклонениям от нормального предположения.
F-тест вычислений
# F-тест res.ftest
F-тест для сравнения двух дисперсий данные: len от supp F = 0,6386, число df = 29, номинал df = 29, значение p = 0,2331 Альтернативная гипотеза: истинное соотношение дисперсий не равно 1 95-процентный доверительный интервал: 0,3039488 1,3416857 примерные оценки: соотношение отклонений 0,6385951
Интерпретация результата
Значение p для F-теста равно p = 0.2331433, что выше уровня значимости 0,05. В заключение отметим, что между двумя вариантами нет значительной разницы.
Доступ к значениям, возвращаемым функцией var.test ()
Функция var.test () возвращает список, содержащий следующие компоненты:

статистика : значение статистики F-теста.
параметр : степени свободы F-распределения тестовой статистики.
p.value : p-значение теста.
conf.int : доверительный интервал для отношения дисперсий генеральной совокупности.
оценка : отношение дисперсий выборки
Для получения этих значений используется следующий формат кода R :
# отношение отклонений res.ftest $ оценка
коэффициент отклонений 0,6385951
# p-значение теста рез.ftest $ p.value
[1] 0,2331433
.
No related posts.

СМИ: предсезонные тесты «Ф-1» пройдут в трехдневном формате в Бахрейне

Тест по французскому языку | Французский Университетский Колледж в Москве

Partie 1 : Compréhension des écrits

Lisez le texte ci-dessous et répondez aux questions :

Partie 2 : Expression écrite.

Тест AF-S NIKKOR 70-200mm f/2.8E FL ED VR

Ifdtest2 часть F (логотип SC Reader) — (ручной тест)

В этой статье

Сведения о тесте

Дополнительная документация

Выполнение теста

Выявлен

Дополнительные сведения

Синтаксис команды

Список файлов

Вход

Обзор и тест объектива Nikon NIKKOR Z 28mm f/2.8 (SE)

Особенности конструкции

Объектив в работе. Кроп и полный кадр

Съёмка в контровом свете и бликозащита

Хроматические аберрации

Геометрические искажения

Виньетирование

Резкость

Выводы

Плюсы:

Минусы:

Рейтинг Prophotos

Тест «Ф-1 (граната) — ТТХ»

Ф-1 (граната) — ТТХ

Проведено тестирование кабелей Hyperline (F/UTP, SF/UTP) с удлинителями ATEN (KVM, VIDEO)

Понимание дисперсионного анализа (ANOVA) и F-тест

Что такое F-статистика и F-тест?

Использование F-теста в одностороннем дисперсионном анализе

Числитель: вариация средних значений выборки

Знаменатель: вариации внутри выборки

F-статистика: вариации между средними значениями выборки / вариация внутри выборок

F-распределения и проверка гипотез

Оценка средств путем анализа вариации

1.3.5.9. F-тест на равенство двух вариантов

1.3.5.9.

Статистика: F-Test

F-тест

Избегание левых критических значений

Как работают F-тесты в дисперсионном анализе (ANOVA)

Представляем F-тесты и F-статистику!

F-тест в одностороннем дисперсионном анализе

Числитель F-теста: межгрупповая дисперсия

Знаменатель F-критерия: внутригрупповая дисперсия

F-статистика: отношение межгрупповых различий к внутригрупповым

Как рассчитать значение F

Как F-тесты используют F-распределения для проверки гипотез

Построение графика F-теста для нашего примера однофакторного дисперсионного анализа

Почему мы анализируем варианты для проверки средств

F — обзор

Сводка

6

Глава 6. F-тест и односторонний дисперсионный анализ — вводная бизнес-статистика с интерактивными таблицами — 1-е канадское издание

Простой тест: взяты ли эти две выборки из популяций с одинаковой дисперсией?

Пример # 1

Важность ANOVA

Односторонний дисперсионный анализ: все ли эти три (или более) образца взяты из популяций с одинаковым средним значением?

Пример # 2

F-Test: сравните два варианта R — Easy Guides — Wiki

Когда вам использовать F-тест?

Вычислить F-тест в R

R функция

Импортируйте и проверяйте свои данные в R

Предварительный тест для проверки допущений F-теста

F-тест вычислений

Интерпретация результата

Доступ к значениям, возвращаемым функцией var.test ()

Добавить комментарий Отменить ответ