Урок ИЗО в 8-м классе «Цвет — элемент композиционного пространства»
Цель урока: формирование умения использовать приемы, средства композиции, развитие эстетического вкуса на примере художественных произведений, построенных с учетом композиционных законов.
Задачи урока:
- Образовательные: познакомить учащихся с основными понятиями: цветовой круг, теплые и холодные тона, контраст.
- Развивающие: развивать познавательный интерес, способствовать формированию творческого воображения, развивать вкус и чувство композиции
- Воспитательные: воспитание интереса к искусству
Оснащение урока:
- Компьютерный класс
- Мультимедиапроектор
- Выставка полиграфической продукции
План урока:
- Организационный момент
- Показ компьютерной презентации с последующим объяснением
- Выполнение самостоятельной работы с использованием компьютера
- Подведение итогов урока
Организационный момент
Вступление.
Слайд 1. Приложение 1.
Мы с вами уже знаем, что при создании композиции художник использует различные приемы и средства для решения своих идей при создании образа, для передачи состояния или настроения в композиции.
А теперь посмотрите на произведения искусства и ответьте, чем они отличаются?
(Ответ: Эти картины отличаются цветом.)
Постановка проблемы: Какое значение имеет цвет в произведении искусства?
Ход урока
Слайд 2. Приложение 1.
Сегодня мы рассмотрим тему — она выделена цветом.
- Гармония, контраст и выразительность плоскостной композиции
- Симметрия, асимметрия и динамическое равновесие
- Движение и статика
- Прямые линии и организация пространства
- Цвет – элемент композиционного пространства
Слайд 3. Приложение 1.
Наш мир цветной, но если мы на минуту представим себе, что было бы, если бы мир вдруг стал бесцветным? Все, что нас окружает: цветы, трава, деревья, животные и все стало бы серым, скучным, унылым.
Слайд 4. Приложение 1.
Как изменится наше настроение?
Какие чувства мы будем испытывать?
(Ответ: Люди станут печальными, будут казаться усталыми, скучно жить в сером мире)
Слайд 5. Приложение 1.
Цвет больше, чем любой другой элемент композиции, обращен к нашим чувствам.
Яркая окраска автомобиля, стильно- утонченный цвет интерьера, эффективное платье, неожиданная и броская по цвету реклама или журнал привлекают наше внимание и обостряют восприятие
Слайд 6. Приложение 1.
Цвет — элемент композиционного творчества.
Так ли верно это утверждение, давайте попробуем разобраться.
Цвет — это один из признаков видимых нами предметов, осознанное зрительное ощущение. Восприятие цвета во многом зависит от цветового тона, степени его яркости и насыщенности.
Восприятие цвета во многом зависит от цветового тона, степени его яркости и насыщенности.
Что привлекает в первую очередь наше внимание в предметах, рекламе?
(Ответ: это форма предмета и его цвет.)
Слайд 7. Приложение 1.
Цветовой круг — система цветов, в которой цветовое многообразие упорядочено на основании объективной закономерности. Он может быть использован как инструмент для ориентировочного расчета результатов смешения цветов, для определения интервалов между цветами при подборе сочетаний.
Вы знаете, что есть цвета, которые невозможно получить путем смешивания каких — либо красок.
Как называются эти цвета? Назовите их.
(Ответ: Основные цвета. Это красный, желтый, синий.)
Что означает понятие — составные цвета, как вы это понимаете?
(Ответ: Цвета, которые можно получить от смешивания основных красок.)
Слайд 8. Приложение 1.
Цветовой круг обычно делят на две части — теплую и холодную.
Взгляните на цветовой круг, и вы без труда определите. Где теплые а где холодные цвета.
Теплые цвета — (красный, желтый, оранжевый) передают силу, властность, активность, радость.
Холодные цвета — (синий, зеленый и их производные) говорят о спокойствии, нежности, апатичности, грусти и вариации этих состояний.
Слайд 9. Приложение 1.
Определите в какой гамме выполнены данные произведения?
Учащиеся выполняют задание.
Слайд 10. Приложение 1.
В конструктивных искусствах создание образа осуществляется через решение как композиционно- конструктивных, так и цветовых задач.
При составлении композиции важно не только эмоционально-чувтвенное отношение к цвету, но и знание законов цветовой композиции, основ цветоведения.
Слайд 11. Приложение 1.
Очень велика роль цвета в плоскостной композиции.
Достаточно ввести цветовое пятно, чтобы все пространство перестало быть монохромным.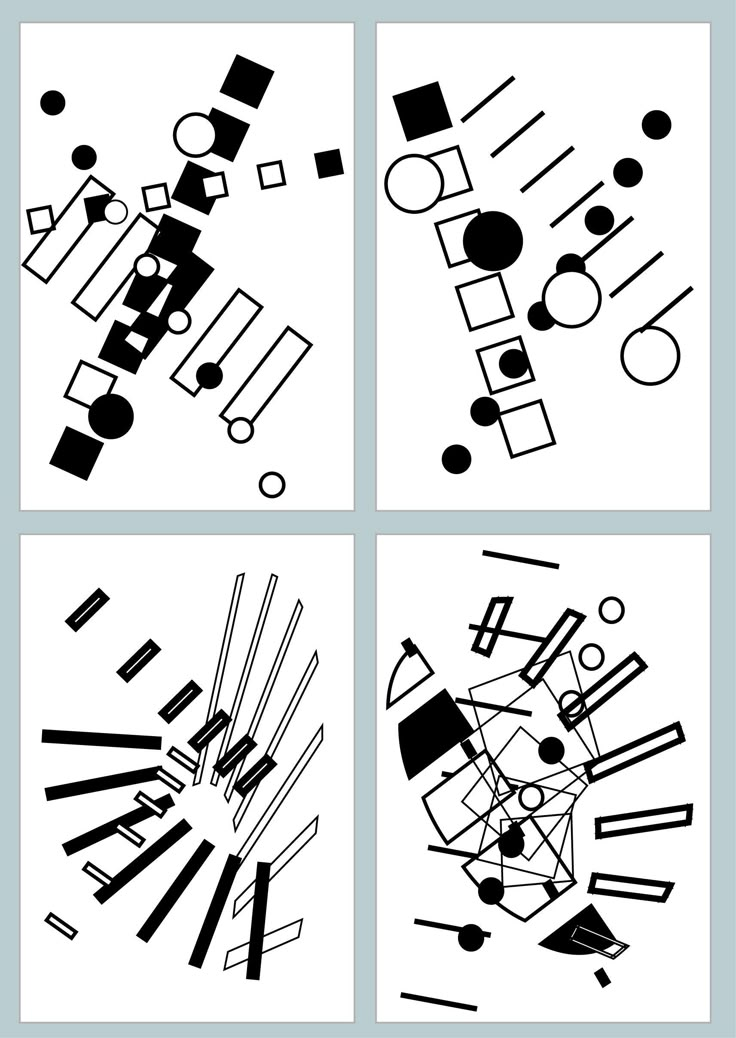
Образное впечатление движения, легкости или плотности, веселья или строгости можно создавать при помощи цветных линий и цветовыми формами.)
Слайд 12. Приложение 1.
Цветовое пятно может стать АКЦЕНТОМ, меняющим общее цветовое восприятие работы.
Особое значение для достижения выразительности в декоративной работе приобретают тоновой и цветовой контрасты. Явление цветового контраста заключается в том, что цвет изменяется под влиянием других, окружающих его цветов, или под влиянием цветов, предварительно наблюдавшихся. «Контраст как противопоставление цветов есть основной прием художественного мышления» (Н.Волков) Применение светлового и цветового контрастов повышает возможности изобразительных средств.
Слайд 13. Приложение 1.
Цвет в композиции лучше всего передает настроение и наши чувства.
Слайд 14. Приложение 1.
Задание 1
Создать композицию из 2-3 прямоугольников, 3-4 линий и небольшого круга, который должен стать доминантой в композиции.
Задание 2
Выполнить композицию из разных форм и линий передавая различное эмоцилнально- образное состояние.
- В теплой гамме
- В холодной гамме
Задание 3
Выполнить композицию из произвольного количества элементов , построенной по принципу цветового контраста.
Работу сделать на цветном фоне
Слайд 15. Приложение 1.
Свободные формы: линии и тоновые пятна
Свободная линия художественно более выразительна, богаче формами, изгибами, имеет больше оттенков и интонаций.
Свободная линия, цветовой или тональный мазок ничего не изображают, они беспредметны, абстрактны.
Слайд 16. Приложение 1.
Цветовым мазком отвлеченной формы можно передать ощущение осени, листопада, не изображая конкретный лист или лес.
Цветовыми пятнами можно вызвать ассоциации, связанные с морем, шумом набегающих волн, не изображая море и волны.
Слайд 17. Приложение 1.
Задание 4
Характером мазка, линией, цветом, ритмом в абстрактной композиции передайте событие, состояние или ощущение, предварительно сформулировав название работы (например: «Шум дождя», «Суматоха», и т.д.).
Подведение итогов урока.
С какими основными понятиями мы сегодня познакомились?
Каким приемам мы научились для передачи движения и покоя?
Как вы оцениваете свои работы и работы свои друзей?
Просмотр работ и анализ.
Список литературы
- Н.М.Сокольникова Основы композиции, Москва, Изд. «Титул», 1993г.
- А.С.Питерских, Г.Е.Гуров, Изобразительное искусство. Дизайн и архитектура в жизни человека, Москва, «Просвещение», 2008г.
Искусство композиции — презентация онлайн
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
ОСНОВЫ КОМПОЗИЦИИ В КОНСТРУКТИВНЫХИСКУССТВАХ
1. Гармония, контраст и выразительность плоскостной
Гармония, контраст и выразительность плоскостной
композиции
2.Симметрия, асимметрия и динамическое равновесие
3.Движение и статика
4.Прямые линии и организация пространства
5.Цвет – элемент композиционного пространства
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Для передачи образа чего-то
неподвижного, устойчивого
подойдет замкнутая
композиция
Основные направления линий
стягиваются к центру.
Необходимое решение дает
построение композиции по
форме круга, квадрата,
прямоугольника с учетом
симметрии.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
При изображении
большого простора,
панорамы не
следует с боков
ограничивать
какими-либо
элементами.
Такой тип
композиции
называется
открытым.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Выделяют следующие композиционные правила:
-Передача движения ( динамика)
— передача покоя ( статика)
— золотого сечения ( одной трети)
-К приемам композиции относится:
— передача ритма,
— передача симметрии и асимметрии
—равновесие частей композиции
— выделение сюжетно-композиционного центра
-Средства композиции включают:
-Формат, пространство, композиционный центр,
равновесие, Динамику и статику, симметрию и
асимметрию, открытость и замкнутость, целостность.
-Средства композиции – это все, что нужно для ее создания
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Ритм – универсальное природное свойство, которое
присутствуют во многих явлениях действительности.
Ритм всегда подразумевает движение.
Назовите примеры, связанные с ритмом из мира природы?
Ритм – это чередование каких-либо элементов в
определенной последовательности.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Ритм в жизни и в искусстве – это не одно и тоже. В искусстве
возможны перебои ритма, ритмические акценты, его
неравномерность, живое разнообразие.
В.Серов Похищение Европы
Н.Рерих Заморские гости
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Правила передачи движения:
-Использование на картине одной или нескольких диагональных
линий
—оставить свободное пространство перед движущимся объектом
—выбирать определенный момент движения, наиболее ярко
отражающий характер движения, который является
кульминацией движения
А. Рылов В голубом просторе
Рылов В голубом просторе
К.Юон Мартовское солнце
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Правила передачи покоя:
-Отсутствие диагонального направления
—отсутствие перед движущимся объектом свободного
пространства
—изображение объектов в спокойных ( статичных) позах,
отсутствие кульминации действия
—композиция является симметричной, уравновешенной или
образует простые геометрические схемы ( треугольник, круг,
овал , квадрат, прямоугольник), т.е. является статичной
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Рассмотрите картину
и определите ,какое
состояние художник
изобразил? По каким
признакам можно
определить состояние ,
изображенное на
данной картине?
В.Суриков Боярыня Морозова
К.Коровин Зимой
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Рассмотрите картину и
определите ,какое
состояние художник
изобразил? По каким
признакам можно
определить состояние ,
изображенное на данной
картине?
Володина И. П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Рассмотрим примеры создания динамичной и статичной
композиции.
Статичная
композиция
Противостояние
Динамичная
движению-его
композиция
остановка
Расположение
прямоугольника рождает
ощущение движения. А
Усиление
добавление
движения дополнительного элемента
усиливает это движение
или останавливает его.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Замкнутая или открытая композиции
Замкнутая композиция
Ритм композиции
Открытая композиция
Гармония в композиции достигается не
только формой композиционных элементов и
характером их расположения, но и балансом
черно-белых масс, чередованием
сгущенности пятен и их разряженности, так
как композиция состоит не только из
изобразительных элементов, но и из
пространства между ними,
Сгущенность и разреженность элементов
рождают ритм композиции
Володина И. П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
В работах многих художников нет
изображения реальных предметов,
но они интересны
выразительностью своей
композиции.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Доминанта – элемент создающий пластический конфликт
Доминанта
Доминанта- это центр
внимания в
композиции.
Доминанта не всегда
может быть самым
крупным элементом.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Задание 1.
Создайте из трех, пяти и более разновеликих прямоугольников :
А) фронтальную композицию
Б)глубинную композицию
Многофигурные композиции должны быть ритмически
организованы, а их элементы разнообразны по размерам и
расположению.
Работы можно выполнить как на белом, так и на черном фоне.
Задание 2.
Создайте многофигурную композицию и путем сгущенности или
разряженности кругов и точек при условии их диманического
равновесия добейтесь зрительной гармонии в композиции.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Примеры выполнения задания
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Прямые линии и организация пространства
Среди элементов
плоскостной композиции
важное место занимают
линии. Сочетание различных
прямоугольников и линий
придает композиции большее
разнообразие и зрелищность.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Среди элементов плоскостной композиции важное место
занимают линии.Сочетание различных прямоугольников и
линий придает композиции большее разнообразие и
зрелищность.
Прямая линия- простой выразительный элемент, делит плоскость
на части и одновременно усиливает взаимосвязь всех элементов
композиции, влияет на ритмическое построение композиции,
определяют движение и экспрессию всего изображения.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
РОЛЬ ЛИНИИ В КОМПОЗИЦИИ
1. Линия делит композицию на части
Линия делит композицию на части
2. Линия помогает объединить
элементы или части плоскости в
их изобразительное целое.
3. Линии, своей направленностью,
сгущенностью, пересечениями
определяют движение и
экспрессию всего изображения.
4. Линии влияют на ритмическое
построение композиции
Линия
изображенная от
края до края листа
делает композицию
открытой.
Различная
толщина и
длина линий
создает
ощущений
движения и
ритма
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
Задание 3.
Создайте композицию с использованием линий и путем расположения и
взаимным пересечением 3-4 линий разной толщины добейтесь
гармоничного членения пространства ( используйте линии навылет)
Задание 4.
Создайте композицию из 2-3 прямоугольников и 3-4 прямых линий, которые
своим расположением связывают элементы в единое композиционное целое.
Создайте:
А) фронтальную композицию
Б) глубинную композицию
Задание 5.
Из произвольного количества элементов сделайте интересную композицию,
ритмически расположив элементы на плоскости, добейтесь эмоциональнообразного впечатления :
А) полета
Б)сужения
В) замедления и т.д.
Володина И.П., учитель ИЗО, ГОУ «Центр образования» №1470, 2009г.
2.10: Процентный состав — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 158412
цели обучения
- Рассчитать массовый процентный состав отдельных атомов в соединении
- Использование состава в процентах по массе в качестве коэффициента пересчета для определения массы компонента в смеси и наоборот
- Использование состава в процентах по массе в качестве коэффициента пересчета для определения массы чистого элемента в соединении и наоборот
Процентный состав по массе
Процентный состав очень прост.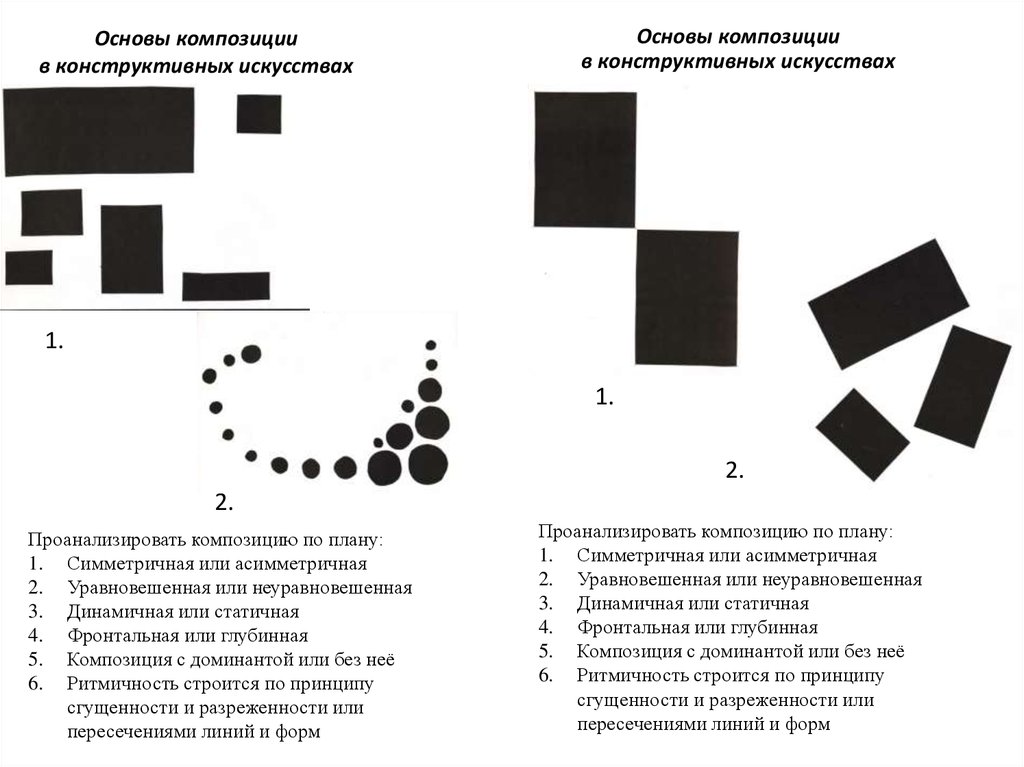 Процентный состав говорит вам по массе, какой процент каждого элемента присутствует в соединении. Химическое соединение — это комбинация двух или более элементов. Если вы изучаете химическое соединение, вы можете захотеть найти процентное содержание определенного элемента в этом химическом соединении. Уравнение для процентного состава (масса элемента/молекулярная масса) x 100. Если вы хотите узнать процентный состав элементов в соединении, выполните следующие шаги:
Процентный состав говорит вам по массе, какой процент каждого элемента присутствует в соединении. Химическое соединение — это комбинация двух или более элементов. Если вы изучаете химическое соединение, вы можете захотеть найти процентное содержание определенного элемента в этом химическом соединении. Уравнение для процентного состава (масса элемента/молекулярная масса) x 100. Если вы хотите узнать процентный состав элементов в соединении, выполните следующие шаги:
Шаги для решения:
- Найдите молярную массу все элементы в соединении в граммах на моль.
- Найдите молекулярную массу всего соединения.
- Разделите молярную массу компонента на полную молекулярную массу.
- Теперь у вас будет число от 0 до 1. Умножьте его на 100, чтобы получить состав в процентах!
Советы по решению:
- Соединения всегда дают в сумме 100%, поэтому в бинарном соединении вы можете найти % первого элемента, затем выполнить 100%-(% первого элемента), чтобы получить (% второго элемент)
- Если вы используете калькулятор, вы можете сохранить общую молярную массу в переменной, такой как «A».
 Это ускорит расчеты и уменьшит опечатки.
Это ускорит расчеты и уменьшит опечатки.
Эти шаги показаны на рисунке ниже.
Другой пример: если вы хотите узнать процентный состав соляной кислоты (HCl), сначала найдите молярную массу водорода. Н = 1,00794 г. Теперь найдем молекулярную массу HCl: 1,00794 г + 35,4527 г = 36,46064 г. Выполните шаги 3 и 4: (1,00794 г/36,46064 г) x 100 = 2,76% Теперь просто вычтите, чтобы найти процент по массе хлора в соединении: 100%-2,76% = 97,24% Следовательно, HCl составляет 2,76% водорода и 97,24%. % хлора по массе.
Процентный состав в повседневной жизни
Процентный состав играет важную роль в повседневной жизни. Это больше, чем просто количество хлора в вашем бассейне, потому что это касается всего: от денег в вашем кармане до вашего здоровья и образа жизни. Следующие два раздела описывают процентный состав применительно к вам.
Этикетки с пищевой ценностью
Этикетка с пищевой ценностью, которую можно найти на упаковке каждого кусочка обработанных пищевых продуктов, продаваемых в местном продуктовом магазине, использует идею процентного состава. На всех этикетках пищевых продуктов известный размер порции разбит на пять категорий: общий жир, холестерин, натрий, общее количество углеводов и белок. Эти категории разбиты на дополнительные подкатегории, включая насыщенные жиры и пищевые волокна. Масса для каждой категории, кроме белка, затем преобразуется в процент от дневной нормы. Только две подкатегории, насыщенные жиры и пищевые волокна, преобразуются в проценты от дневной нормы. Дневная норма основана на массе каждой категории, рекомендуемой в день на человека при диете в 2000 калорий. Масса белка не конвертируется в проценты, потому что это не рекомендуемая дневная норма белка. Ниже приведена фотография, иллюстрирующая эти идеи.
На всех этикетках пищевых продуктов известный размер порции разбит на пять категорий: общий жир, холестерин, натрий, общее количество углеводов и белок. Эти категории разбиты на дополнительные подкатегории, включая насыщенные жиры и пищевые волокна. Масса для каждой категории, кроме белка, затем преобразуется в процент от дневной нормы. Только две подкатегории, насыщенные жиры и пищевые волокна, преобразуются в проценты от дневной нормы. Дневная норма основана на массе каждой категории, рекомендуемой в день на человека при диете в 2000 калорий. Масса белка не конвертируется в проценты, потому что это не рекомендуемая дневная норма белка. Ниже приведена фотография, иллюстрирующая эти идеи.
Например, если вы хотите узнать процент по массе дневной нормы натрия, которую вы едите, когда съедаете одну порцию продукта с этой этикеткой пищевой ценности, перейдите в категорию с пометкой «Натрий». Посмотрите на ту же строку и прочитайте написанный процент. Если вы съедите одну порцию этой пищи, то вы употребите около 9% рекомендуемой дневной нормы натрия.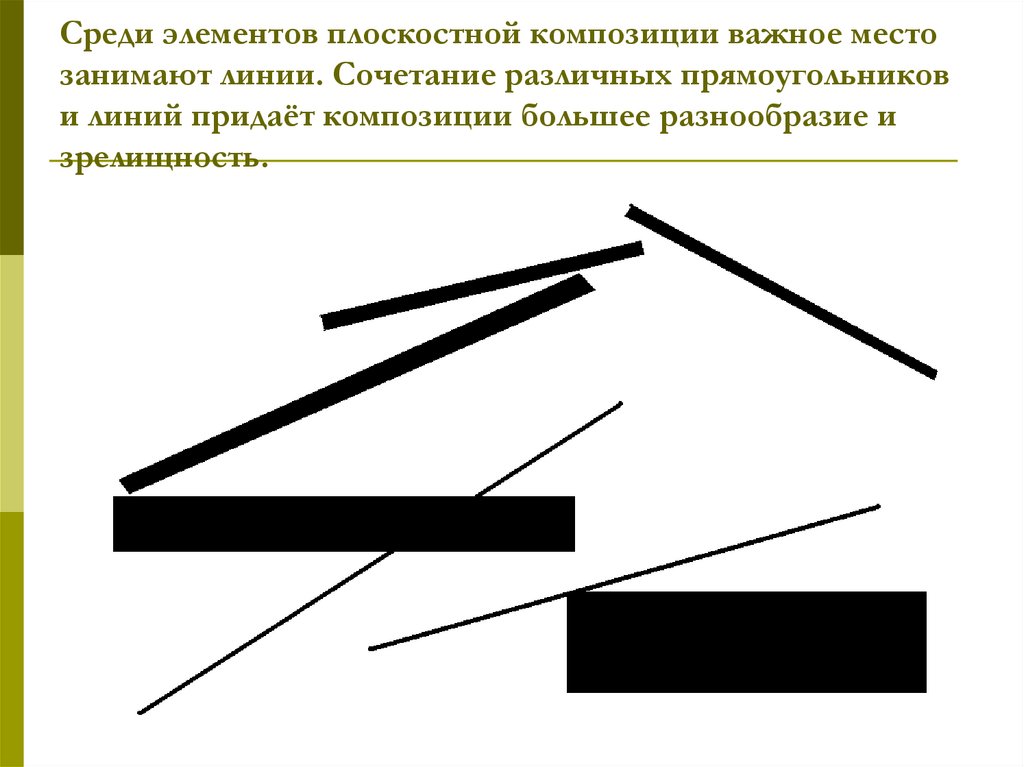 Чтобы найти массовый процент жира во всей пище, вы можете разделить 3,5 грамма на 15 граммов и увидеть, что эта закуска содержит 23,33% жира.
Чтобы найти массовый процент жира во всей пище, вы можете разделить 3,5 грамма на 15 граммов и увидеть, что эта закуска содержит 23,33% жира.
Пенни: Счастливая медная монета
Пенни следует называть «счастливая медная покрытая монета «. Пенни не делали из твердой меди с 1857 года. После 1857 года правительство США начало добавлять в смесь другие более дешевые металлы. Пенни, будучи всего лишь одним центом, буквально не стоит своего веса в меди. Люди могли плавить медные пенни и продавать медь дороже, чем стоили эти пенни. После 1857 года никель смешивали с более дорогой медью. После 1864 года пенни стали делать из бронзы. Бронза 95% меди и 5% цинка и олова. В течение одного 1943 года в пенни не было меди из-за расходов на Вторую мировую войну. Это была просто оцинкованная сталь. С 1943 по 1982 год у пенни были периоды, когда он был латунным или бронзовым.
Сегодня пенни в Америке состоит из 2,5% меди и 97,5% цинка. Медь покрывает внешнюю часть пенни, а внутренняя часть покрыта цинком. Для сравнения, пенни в Канаде состоит из 94% стали, 1,5% никеля и 4,5% меди.
Для сравнения, пенни в Канаде состоит из 94% стали, 1,5% никеля и 4,5% меди.
Процентный состав монетки может реально повлиять на здоровье, особенно на здоровье маленьких детей и домашних животных. Поскольку новые пенни сделаны в основном из цинка, а не из меди, они представляют опасность для здоровья ребенка при проглатывании. Цинк очень чувствителен к кислоте. Если тонкое медное покрытие поцарапать и соляная кислота, присутствующая в желудке, вступит в контакт с цинковым сердечником, это может вызвать язву, анемию, повреждение почек и печени, а в тяжелых случаях даже смерть. Три важных фактора при проглатывании пенни — это время, pH желудка и количество проглоченных пенни. Конечно, чем больше копеек проглочено, тем больше опасность передозировки цинка. Чем кислее среда, тем больше цинка высвобождается за меньшее время. Затем этот цинк поглощается и отправляется в печень, где начинает наносить ущерб. В такой ситуации время имеет решающее значение. Чем быстрее удаляется копейка, тем меньше цинка усваивается. Если пенни или пенни не удалить, может произойти отказ органов и смерть.
Если пенни или пенни не удалить, может произойти отказ органов и смерть.
Ниже приведено изображение поцарапанной монеты до и после того, как она была погружена в лимонный сок. Лимонный сок имеет аналогичный pH 1,5-2,5 по сравнению с нормальным человеческим желудком после употребления пищи. Прошедшее время: 36 часов.
Как видите, лимонный сок почти не повреждает медь. Вот почему пенни, изготовленные до 1982 года, в основном из меди (кроме пенни 1943 года), относительно безопасно глотать. Скорее всего, они пройдут через пищеварительную систему естественным путем, прежде чем можно будет нанести какой-либо ущерб. Тем не менее, ясно, что цинк частично растворился, хотя он находился в лимонном соке лишь ограниченное время. Поэтому процентный состав поста 1982 пенни опасны для вашего здоровья и здоровья ваших домашних животных при попадании внутрь. Чтобы узнать больше о кислотах и основаниях, проверьте здесь: wiki.
Видеоучебник: Процентный состав уксусной кислоты
видеоучебник: Процентный состав ацетилена и бензола
Примечание. Ацетилен и бензол имеют одинаковый процентный состав, однако это не так. не означает, что это одно и то же вещество.
Пример \(\PageIndex{1}\)
Масса одного пенни составляет 2,5 грамма. Сколько пенни может сделать правительство США из 20,0 кг меди, если массовый процент меди в современном пенни составляет 2,5%?
Дано: Мы знаем, что начинаем с 20,0 кг чистой меди. Нам известен массовый процентный состав чистой меди в копеечной смеси. Мы также знаем массу каждого пенни.
Стратегия: Нам нужно вычислить массу медной смеси, которую мы можем сделать из 20,0 кг чистой меди, используя массовый процентный состав меди в пенни смеси. Отсюда мы можем определить, сколько отдельных пенни мы можем сделать из этой смеси.
Отсюда мы можем определить, сколько отдельных пенни мы можем сделать из этой смеси.
Раствор
Пример \(\PageIndex{2}\)
Какова масса углерода, содержащегося в 3,0 г бутана (C 4 H 9 0143 10 ), жидкость для зажигалок?
Дано: масса всего (бутана), какова масса части (углерода)?
Стратегия: используйте формулы состава в процентах по массе для преобразования массы бутана в массу углерода:
Раствор
Практика: задачи на процентную композицию
Эти задачи имеют ту же сложность, что и задачи на плотность.
- Рассчитайте массовые проценты каждого элемента во фториде цезия (CsF).
- Рассчитайте массовые проценты каждого элемента, присутствующего в четыреххлористом углероде (CCl 4 )
- Раствор соли и воды содержит 33,0% соли по массе и имеет плотность 1,50 г/мл. Какая масса соли в граммах содержится в 5,00 л этого раствора?
- Раствор воды и HCl содержит 25% HCl по массе.
 Плотность раствора 1,05 г/мл. Если вам нужно 1,7 г HCl для реакции, какой объем этого раствора вы будете использовать?
Плотность раствора 1,05 г/мл. Если вам нужно 1,7 г HCl для реакции, какой объем этого раствора вы будете использовать? - Раствор, содержащий 42 % NaOH по массе, имеет плотность 1,30 г/мл. Какая масса в килограммах NaOH содержится в 6,00 л этого раствора?
ПРОБЛЕМА С ДОПОЛНИТЕЛЬНЫМ ГАЗОМ ПРИКРЕПЛЕНА НИЖЕ
Процентный состав Проблема Решения
1) CsF состоит из 87,5% Cs и 12,5% F по массе
2) CCl 4 содержит 92,2 % Cl и 7,8 % C по массе
3) 2480 г
4) 6,5 мл
5) 2,38 кг
Ссылки
- АВТОР, АРКИМЕД и Томас Литтл. Произведения Архимеда. Courier Dover Publications, 2002.
- Чанде, Д. и Т. Фишер (2003). «Есть пенни? Нужен пенни? Исключение одноцентовой монеты из обращения». Canadian Public Policy/Analyse de Politiques 29 (4): 511-517.
Джефферсон, Т. (1999). «Мысль за ваши гроши». JAMA 281 (2): 122.

- Петруччи, Ральф, Уильям Харвуд и Джеффри Херринг. Принципы и современное применение. девятый. Нью-Джерси: Peason Eduation, 2007. .
Rauch, F., H. Plotkin, et al. (2003). «Костная масса, размер и плотность у детей и подростков с несовершенным остеогенезом: эффект внутривенной терапии памидронатом». Журнал исследований костей и минералов 18 : 610-614.
Richardson, J., S. Gwaltney-Brant, et al. (2002). «Цинковый токсикоз от проглатывания пенни у собак». Vet Med 97 (2): 96-99.
Тейт, Дж. «Открытия Архимеда: пристальный взгляд».
Внешние ссылки
- http://en.wikipedia.org/wiki/Density
- http://www.sparknotes.com/testprep/b…section2.rhtml
- http://www.science.co.il/PTelements.asp
Авторы
- Содержание заимствовано из: 2.13: Процент композиции
- Боб Белфорд (UA of Little Rock)
- Изменено Ронией Каттум (UA из Литл-Рока)
2. 10: Процентная композиция распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована LibreTexts.
10: Процентная композиция распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- да на стр.
- Теги
6.
 4: Композиция функций — Mathematics LibreTexts
4: Композиция функций — Mathematics LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7070
- Тед Сандстром
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли 900 10
ПРОСМОТР \(\PageIndex{1}\): создание новой функции
Пусть \(A = \{a, b, c, d\}\), \(B = \{p, q, r\ }\) и \(C = \{s, t, u, v\}\). Стрелочная диаграмма на рис. 6.6 показывает две функции: \(f: A \to B\) и \(g: B \to C\). Обратите внимание, что если \(x \in A\), то \(f(x) \in B\). Поскольку \(f(x) \in B\), мы можем применить функцию \(g\) к \(f(x)\), и мы получим \(g(f(x))\), что равно элемент из \(С\).
Используя этот процесс, определите \(g(f(a))\), \(g(f(b))\), \(g(f(c))\) и \(g(f( г))\). Затем объясните, как мы можем использовать эту информацию для определения функции от \(A\) до \(C\).
Рисунок 6.6: Диаграмма-стрелка, показывающая две функции
ПРЕДВАРИТЕЛЬНОЕ ЗАДАНИЕ \(\PageIndex{1}\): Словесное описание функций
Выходные данные большинства реальных функций, которые мы изучали на предыдущих курсах математики, определялись математическими выражениями. Во многих случаях можно использовать эти выражения для пошагового словесного описания того, как вычислять выходные данные. Например, если 93\),
, мы могли бы описать, как вычислять выходы, следующим образом:
| Шаг | Устное описание | Символический результат |
|---|---|---|
| 1 | Выберите вход.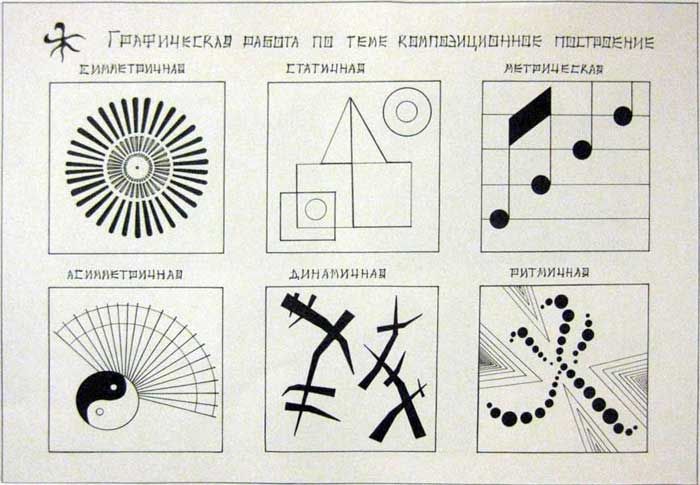 | \(х\) |
| 2 | Умножить на 3. | \(3x\) |
3 92 + 1}}\), для каждого \(x \in \mathbb{R}\).Состав функцийСуществует несколько способов объединения двух существующих функций для создания новой функции. Например, в исчислении мы узнали, как составить произведение и частное двух функций, а затем как использовать правило произведения для определения производной произведения двух функций и правило отношения для определения производной частного двух функций. . Цепное правило в исчислении использовалось для определения производной композиции двух функций, и в этом разделе мы сосредоточимся только на композиции двух функций. Затем мы рассмотрим некоторые результаты о композициях инъекций и сюръекций. 92 + 2).} \end{array}\] В этом случае \(f(x)\), выход функции \(f\), использовался как вход для функции \(g \). Определение: составная функцияПусть \(A\), \(B\) и \(C\) непустые множества, и пусть \(f: A \to B\) и \(g: B \ в С\) — функции. Композиция из \(f\) и \(g\) представляет собой функцию \(g \circ f: A \to C\), определяемую равенством \((g \circ f)(x) = g( f(x))\) для всех \(x \in A\). Мы часто называем функцию \(g \circ f\) составной функцией . Составную функцию \(g \circ f\) полезно представлять как « \(f\), за которой следует \(g\) «. Затем мы ссылаемся на \(f\) как на внутреннюю функцию и на \(g\) как на внешнюю функцию . Композиция и стрелочные диаграммы Концепция композиции двух функций может быть проиллюстрирована стрелочными диаграммами, когда область определения и область значений функций представляют собой небольшие конечные множества. Хотя термин «композиция» тогда не использовался, это было сделано в Preview Activity \(\PageIndex{1}\), и здесь приведен еще один пример. Пусть \(A = \{a, b, c, d\}\), \(B = \{p, q, r\}\) и \(C = \{s, t, u, в\}\). Стрелочная диаграмма на рис. 6.7 показывает две функции: \(f: A \to B\) и \(g: B \to C\). Если мы будем двигаться по стрелкам от множества \(A\) к множеству \(C\), мы будем использовать выходы \(f\) как входы \(g\) и получим стрелку диаграмма от \(A\) до \(C\), показанная на рис. 6.8. Эта диаграмма представляет собой композицию \(f\), за которой следует \(g\). Проверка выполнения 6.17 (композиция двух функций)Пусть \(A = \{a, b, c, d\}\) и \(B = \{1, 2, 3\}\). Определим функции \(f\) и \(g\) следующим образом: \(f: A \to B\), определяемые \(f(a) = 2\), \(f(b) = 3 \), \(f(c) = 1\) и \(f(d) = 2\). \(g: A \to B\), определяемый \(g(1) = 3\). \(g(2) = 1\) и \(g(3) = 2\). Создайте стрелочные диаграммы для функций \(f\), \(g\), \(g \circ f\) и \(g \circ g\).
Разложение функцийМы используем цепное правило в исчислении, чтобы найти производную составной функции. Первым шагом в этом процессе является признание данной функции составной функцией. Это можно сделать разными способами, но работу в Preview Activity \(\PageIndex{2}\) можно использовать для декомпозиции функции таким образом, чтобы она хорошо работала с цепным правилом. Использование терминов «внутренняя функция» и «внешняя функция» также может быть полезным. Идея состоит в том, что мы используем последний шаг процесса для представления внешней функции, а предыдущие шаги — для представления внутренней функции. Итак, для функции 93} \\ {} &= & {f(x).} \end{array}\] Мы видим, что \(g \circ h = f\) и, следовательно, мы «разложили» функцию \ (ф\). Следует отметить, что существуют и другие способы записи функции \(f\) в виде композиции двух функций, но только что описанный способ хорошо работает с цепным правилом.
Теоремы о составных функцияхЕсли \(f: A \to B\) и \(g: B \to C\), то мы можем составить составную функцию \(g \circ f: A \to C\ ). В разделе 6.3 мы узнали об инъекциях и сюръекциях. Теперь мы исследуем, каким будет тип функции \(g \circ f\), если функции \(f\) и \(g\) являются инъекциями (или сюръекциями). Проверка хода выполнения 6.19: Составы инъекций и суръекцийХотя можно использовать и другие представления функций, будет полезно использовать диаграммы со стрелками для представления функций в ходе этой проверки хода выполнения. Мы будем использовать следующие множества: \(A = \{a, b, c\}\), \(B = \{p, q, r\}\), \(C = \{u,v , w, x\}\) и \(D = \{u, v\}\).
Выполняется Проверка 6.19. Мы изучили некоторые свойства составных функций, связанные с инъекциями, сюръекциями и биекциями. Следующая теорема содержит результаты, которые должны были проиллюстрировать эти исследования. Некоторые доказательства будут включены в упражнения. Теорема 6.20.Пусть \(A\), \(B\) и \(C\) — непустые множества, и предположим, что \(f: A \to B\) и \(g: B \to C\).
ДоказательствоДоказательство части (1) — это упражнение (6). Часть (3) является прямым следствием первых двух частей. Мы обсудим процесс построения доказательства Части (2). Используя процесс «вперед-назад», мы сначала посмотрим на вывод условного оператора в части (2). Цель состоит в том, чтобы доказать, что \(g \circ f\) является сюръекцией. Поскольку \((g \circ f): A \to C\), это эквивалентно доказательству того, что Для всех \(c \in C\) существует \(a \in A\) такое, что \((g \circ f)(a) = c\). Поскольку этот оператор в обратном процессе использует универсальный квантор, мы воспользуемся методом выбора элемента и выберем произвольный элемент \(c\) в множестве \(C\). Теперь мы можем рассмотреть гипотезы. В частности, мы предполагаем, что и \(f: A \to B\), и \(g: B \to C\) являются сюръекциями. Поскольку мы выбрали \(c \in C\), а \(g: B \to C\) является сюръекцией, мы знаем, что существует такое \(b \in B\), что \(g(b) = c\). Теперь \(b \in B\) и \(f: A \to B\) является сюръекцией. Следовательно, существует \(a \in A\) такое, что \(f(a) = b\). Если теперь вычислить \((g \circ f)(a)\), мы увидим, что \((g \circ f)(a) = g(f(a)) = g(b) = с\). Теперь мы можем записать доказательство следующим образом: Доказательство теоремы 6.20, часть (2)Пусть \(A\), \(B\) и \(C\) — непустые множества, и предположим, что \ (f: A \to B\) и \(g: B \to C\) являются сюръекциями. Мы докажем, что \(g \circ f: A \to C\) является сюръекцией. Пусть \(с\) — произвольный элемент из \(С\). Мы докажем, что существует \(a \in A\) такое, что \((g \circ f)(a) = c\). существует \(b \in B\) такое, что \(g(b) = c\). Теперь \(b \in B\) и \(f: A \to B\) является сюръекцией. Следовательно, существует \(a \in A\) такое, что \(f(a) = b\). Теперь мы видим, что \[\begin{align*} {(g \circ f)(a)} &= & {g(f(a))} \\ {} &= & {g(b )} \\ {} &= & {c.} \end{align*}\] Теперь мы показали, что для каждого \(c \in C\) существует \(a \in A\) такое, что \((g \circ f)(a) = c\), и это доказывает что \(g \circ f\) является сюръекцией. Теорема 6.20 показывает нам, что если \(f\) и \(g\) являются специальными типами функций, то композиция \(f\), за которой следует \(g\), также относится к этому типу функций. следующий вопрос: «Если композиция \(f\), за которой следует \(g\), является инъекцией (или сюръекцией), можем ли мы сделать какие-либо выводы относительно \(f\) или \(g\)?» Частичный ответ на этот вопрос дан в теореме 6.21. Эта теорема будет исследована и доказана в разделе «Исследования и действия» данного раздела. Теорема 6.21Пусть \(A\), \(B\) и \(C\) — непустые множества, и предположим, что \(f: A \to B\) и \(g: B \to C \).
Упражнение 6.4
Эта страница под названием 6.4: Composition of Functions используется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
|

 Дадим теперь формальное определение композиции двух функций.
Дадим теперь формальное определение композиции двух функций.
 Не удаляйте этот текст первым.
Не удаляйте этот текст первым. 2} \end{массив}\] 92 + 1})\)
2} \end{массив}\] 92 + 1})\) Является ли в этом случае составная функция \(g \circ f: A \to C\) инъекцией? Объяснять.
Является ли в этом случае составная функция \(g \circ f: A \to C\) инъекцией? Объяснять.
 Теперь цель состоит в том, чтобы найти \(a \in A\) такое, что \((g \circ f)(a) = c\).
Теперь цель состоит в том, чтобы найти \(a \in A\) такое, что \((g \circ f)(a) = c\).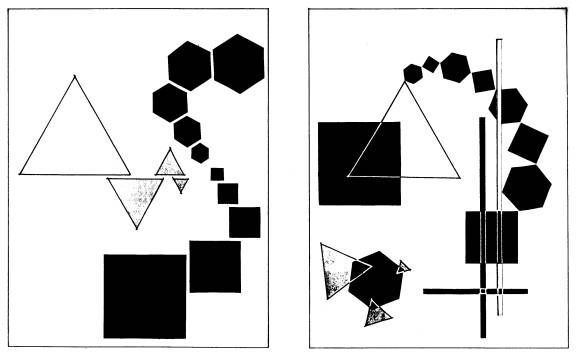 Так как \(g: B \to C\) является сюръекцией, мы заключаем, что
Так как \(g: B \to C\) является сюръекцией, мы заключаем, что См. упражнение (10).
См. упражнение (10). 3\). Определите формулы для составных функций \(g \circ h\) и \(h \circ g\). Равна ли функция \(g \circ h\) функции \(h \circ g\)? Объяснять. Что это говорит вам об операции композиции функций? 92\), пусть \(g: \mathbb{R} \to \mathbb{R}\) определяется как \(g(x) = sin x\), и пусть \(h: \mathbb{R} \ к \mathbb{R}\) определяется как \(h(x) = \sqrt[3]{x}\).
3\). Определите формулы для составных функций \(g \circ h\) и \(h \circ g\). Равна ли функция \(g \circ h\) функции \(h \circ g\)? Объяснять. Что это говорит вам об операции композиции функций? 92\), пусть \(g: \mathbb{R} \to \mathbb{R}\) определяется как \(g(x) = sin x\), и пусть \(h: \mathbb{R} \ к \mathbb{R}\) определяется как \(h(x) = \sqrt[3]{x}\).
 Пусть \(A\), \(B\) и \(C\) — непустые множества и пусть \(f: A \to B\) и \(g: B \to C\). Для этого упражнения может быть полезно нарисовать ваши стрелочные диаграммы в виде треугольника следующим образом:
Пусть \(A\), \(B\) и \(C\) — непустые множества и пусть \(f: A \to B\) и \(g: B \to C\). Для этого упражнения может быть полезно нарисовать ваши стрелочные диаграммы в виде треугольника следующим образом: 

