Векторы, графическое изображение векторов, величина вектора, направление вектора
Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.
Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.
Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют
Поэтому они представляют
В контексте векторов мы применяем = чтобы обозначить их равность.
Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.
Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.
Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √[2 — (-1)]2 + (4 — 3)2 = √9 + 1 = √10,
|| = √[0 — (-3)]2 + [0 — (-1)]2 = √9 + 1 = √10,
|w| = √(4 — 1)2 + [-1 — (-2)]2 = √9 + 1 = √10.
Отсюда
|u| = | = |w|.
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
u = = w.
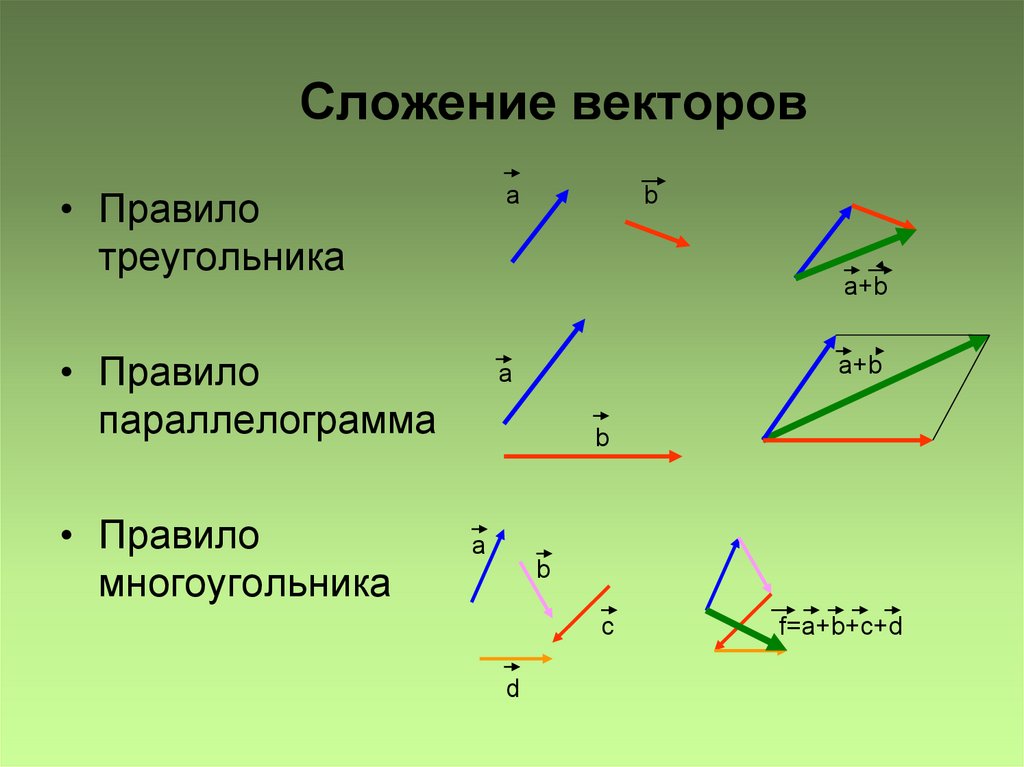
Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.
Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север.
В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.
Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v.
u + v = + =
Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.
Если две силы F1 и F2 действуют на один объект, результирующая сила есть сумма F1 + F2 этих двух отдельных сил.
Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.
Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v|2 = 152 + 252 Здесь |v| обозначает длину или величину v.
|v| = √152 + 252
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя калькулятор, мы находим θ, угол, который большая сила образует с результирующей силой:
θ = tan— 1(0,6) ≈ 31°
Результирующая имеет величину 29,2 и угол 31° с большей силой.
Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.
Пример 3. Скорость самолёта и направление. Самолёт движется по азимуту 100° со скоростью 190 км/час, в то время как скорость ветра 48 км/ч, а его азимут — 220°. Найдите абсолютную скорость самолета и направление его движения с учетом ветра.
Решение Сначала сделаем рисунок. Ветер представлен и вектор скорости самолета есть . Результирующий вектор скорости есть v, сумма двух векторов. Угол θ между v и называется угол сноса.
Обратите внимание, что величина COA = 100° — 40° = 60°. Тогда величина CBA также равна 60° (противоположные углы параллклограмма равны). Так как сумма всех углов параллелограмма равна 360° и COB и OAB имеют одну и ту же величину, каждый должен быть 120°. По правилу косинусов
Тогда величина CBA также равна 60° (противоположные углы параллклограмма равны). Так как сумма всех углов параллелограмма равна 360° и COB и OAB имеют одну и ту же величину, каждый должен быть 120°. По правилу косинусов
|v|2 = 482 + 1902 — 2.48.190.cos120°
|v|2 = 47,524
|v| = 218
Тогда, |v| равно 218 км/ч. Согласно правилу синусов, в том же самом треуголнике,
48/sinθ = 218/sin120°,
или
sinθ = 48.sin120°/218 ≈ 0,1907
θ ≈ 11°
Тогда, θ = 11°, к ближайшему целому углу. Абсолютная скорость равна 218 км/ч, и направление его движения с учетом ветра: 100° — 11°, или 89°.
Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется
Когда мы раскладываем вектор, обычно мы ищем перпендикулярные компоненты. Очень часто, однако, одна компонента будет параллельной оси x, и другая будет параллельна оси y. Поэтому, они часто называются горизонтальными и вертикальными компонентами вектора. На рисунке внизу вектор w = разложен как сумма u = и v = .
Очень часто, однако, одна компонента будет параллельной оси x, и другая будет параллельна оси y. Поэтому, они часто называются горизонтальными и вертикальными компонентами вектора. На рисунке внизу вектор w = разложен как сумма u = и v = .
Горизонтальная компонента w есть u и вертикальная компонента — v.
Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.
Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.
Из ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.
| 2.2. Геометрическое изображение вектора в R3. Линейные операции с векторами. Геометрический смысл скалярного произведения | 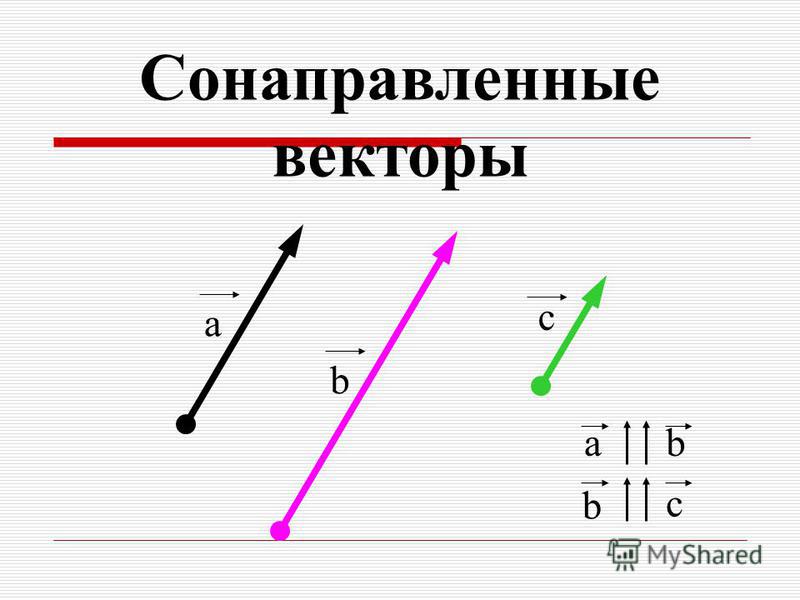 Векторная алгебра > 2.2. Геометрическое изображение вектора в R3. Линейные операции с векторами. Геометрический смысл скалярного произведения Векторная алгебра > 2.2. Геометрическое изображение вектора в R3. Линейные операции с векторами. Геометрический смысл скалярного произведения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Замечание
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| gif»> | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Что такое векторные изображения? — ВекторСток
Опубликовано
Категория
Файлы и форматы
Итак, что такое вектор?
Векторное изображение представляет собой графический файл формата . Изображение состоит из серии «Точек» с линиями, соединяющими эти точки. Используя этот метод двухточечной иллюстрации в программе векторного рисования, можно проиллюстрировать простые или сложные линейные геометрические и органические формы. Эти формы могут быть заполнены сплошными или градиентными цветами. Информация о координатах точек изображения и о том, как они связаны и окрашены, хранится в файле в виде математических данных.
Например, векторный квадрат с желтой рамкой представляет собой координаты четырех угловых точек квадрата в сочетании с данными его цвета и стиля линии.
Компьютер использует эти математические данные для визуализации векторного изображения, соединяя точки линиями, называемыми «Пути» или «Штрихи», а затем заливая фигуры цветом. С помощью программного обеспечения для векторной иллюстрации и комбинаций геометрических и органических форм, линий и цветов можно проиллюстрировать или нарисовать самые разные предметы.
Что такое формат векторного файла?
Стандартный формат файла W3C для векторного изображения — Scalable Vector Graphics ( SVG ), но чаще используются форматы Encapsulated PostScript ( EPS ) и Portable Document Format PDF (90) .
Собственный формат векторного изображения Adobe Adobe Illustrator ( Ai ) также широко используется.
Векторные изображения VectorStock доступны в форматах Vector EPS , PDF и Ai .
Узнать больше
- Масштабируемая векторная графика — W3C
- Инкапсулированный PostScript — Википедия
- Portable Document Format — Adobe
Вектор против растрового изображения
Существует два основных типа цифровых изображений
на компьютерах;
- Растровое (или растровое) изображение
- Векторное изображение
Растровые / Растровые изображения
Файлы растровых изображений — это изображения, состоящие из крошечных цветных точек, называемых «пикселями». Компьютер хранит данные о каждом пикселе в файле изображения. Количество пикселей может очень быстро составить миллионы. Например, цифровая камера, делающая фотографии с разрешением 5 мегапикселей, создает изображения, каждое из которых содержит более 5 миллионов пикселей.
Растровые изображения больше всего подходят для фотографических изображений.
Векторные изображения
Векторные изображения не содержат пикселей. Они содержат точки, которые называются «точки». Но в отличие от растрового изображения квадрата, например, которое может содержать тысячи или миллионы отдельных пикселей для отображения изображения, вектор состоит всего из нескольких точек и линии, соединяющей точки для рисования формы.
Они содержат точки, которые называются «точки». Но в отличие от растрового изображения квадрата, например, которое может содержать тысячи или миллионы отдельных пикселей для отображения изображения, вектор состоит всего из нескольких точек и линии, соединяющей точки для рисования формы.
Векторные изображения лучше всего подходят для иллюстрации.
Преимущества векторного изображения
Размеры файлов
Поскольку вектор представляет собой, по сути, список инструкций по отображению изображения, размер файла часто может быть меньше, чем у аналогичного изображения в растровой форме.
Масштабирование векторного изображения практически не влияет на размер файла. Однако изменение размера растрового изображения имеет значительный эффект, поскольку для соответствия новому размеру создаются или удаляются тысячи (а иногда и миллионы) пикселей.
Изменение размера
Возможность легко масштабировать векторные изображения до любого размера является большим преимуществом. Их размер можно изменять без потери качества изображения: изображения остаются идеально четкими при любом размере. Компьютер просто перерисовывает векторное изображение, используя математические данные в файле, до нового скорректированного масштаба.
Их размер можно изменять без потери качества изображения: изображения остаются идеально четкими при любом размере. Компьютер просто перерисовывает векторное изображение, используя математические данные в файле, до нового скорректированного масштаба.
При изменении размера растровых изображений пиксели теряются (при уменьшении масштаба) или дублируются (при увеличении), что приводит к «нечеткому» или «размытому» изображению более низкого качества.
Редактирование
С помощью приложений для редактирования векторной графики, таких как Adobe Illustrator, Corel Draw или Inkscape, файлы векторных изображений можно легко редактировать. Точки и пути отдельных объектов могут быть выбраны и изменены или удалены по мере необходимости. Цвета или заливки в изображении также можно легко выбирать и изменять.
Растровые изображения можно редактировать с помощью таких приложений, как Adobe Photoshop, но отдельные элементы изображения не всегда доступны для выбора.
Преобразование
Bitmap Vector
Растровые изображения можно преобразовать в векторные изображения с помощью таких инструментов, как «Живая трассировка» Adobe Illustrator, но этот процесс часто приводит к получению изображений низкого качества, поскольку программное обеспечение должно автоматически обводить все объекты в изображении.
Векторное растровое изображение
Преобразование векторного изображения в растровое называется «растрированием». Это простой процесс, который успешно выполняется большинством приложений для редактирования изображений.
Использование векторного изображения
Векторы обычно используются для определенных типов изображений, таких как:
- Иллюстрации
- Логотипы
- Иконки
- Инфографика
- Карты
- Шрифты
Векторы идеально подходят для печати, так как один и тот же векторный файл можно использовать для печати на небольшой открытке или гигантском рекламном щите, оставаясь при этом четким и четким в обоих случаях. Современные шрифты обычно хранятся с использованием векторной графики, что позволяет точно рисовать их любого размера.
Ниже представлено короткое видео с подробным описанием некоторых распространенных вариантов использования векторных изображений:
Программное обеспечение
Ниже перечислены некоторые часто используемые приложения для создания и редактирования векторов.
| Имя программного обеспечения | Операционная система | Лицензирование |
|---|---|---|
| Adobe Illustrator | Windows, Mac | Коммерческий |
| CorelDRAW | Windows, Mac | Коммерческий |
| Inkscape | Windows, Mac, Linux | Открытый исходный код |
| Эскиз | Mac | Коммерческий |
| Xara Фото и графический дизайнер | Окна | Коммерческий |
Примеры из повседневной жизни
Традиционно векторные изображения использовались в трафаретной печати, графическом дизайне и написании вывесок.
Сегодня использование векторов распространяется на приложения и игры, анимационную графику и архитектурные чертежи или изображения на основе CAD .
Шрифты, которые вы видите на экране своего компьютера, включая этот текст, являются векторами, и теперь, с введением векторов HTML5 SVG , изображения также могут отображаться в большинстве современных веб-браузеров. Это привело к гораздо большему использованию на повседневных веб-сайтах.
В 2012 и 2013 годах Apple, а затем Google соответственно обновили свое картографическое программное обеспечение (для Интернета и мобильных устройств), чтобы рисовать с использованием векторной графики вместо растровых изображений. Это позволяет пользователям быстро увеличивать и уменьшать масштаб без необходимости каждый раз загружать новую графику с измененным размером.
Кролик Роялти бесплатно векторное изображение
Кролик Роялти бесплатно векторное изображение — VectorStock- org/BreadcrumbList»>
- лицензионные векторы
- кролик векторов
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный / редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменять | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по запросу |
Владение Узнать больше
Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже: Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69Оплатить стандартные лицензии можно тремя способами. Цены $ долларов США.
| Оплата с | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00 Существует два способа оплаты расширенных лицензий. Цены $ $ .
Цены $ $ .
| Оплата с | Стоимость изображения |
|---|---|
| Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется. | |
| Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США). | |
Оплата
Плата за изображение $ 499Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение $ 85,00Нравится изображение, но нужны лишь некоторые модификации? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменение размера до новых размеров
- Включить логотип или символ
- Добавьте название вашей компании или компании
Включенные файлы
Подробности загрузки.

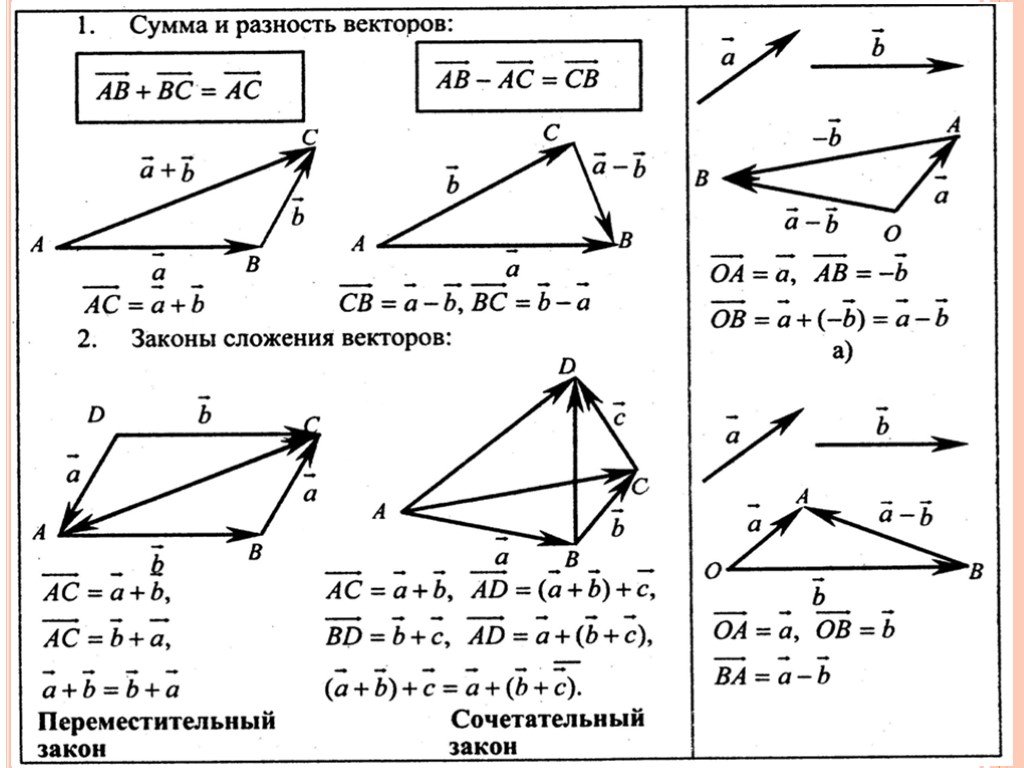 Геометрический смысл скалярного произведения
Геометрический смысл скалярного произведения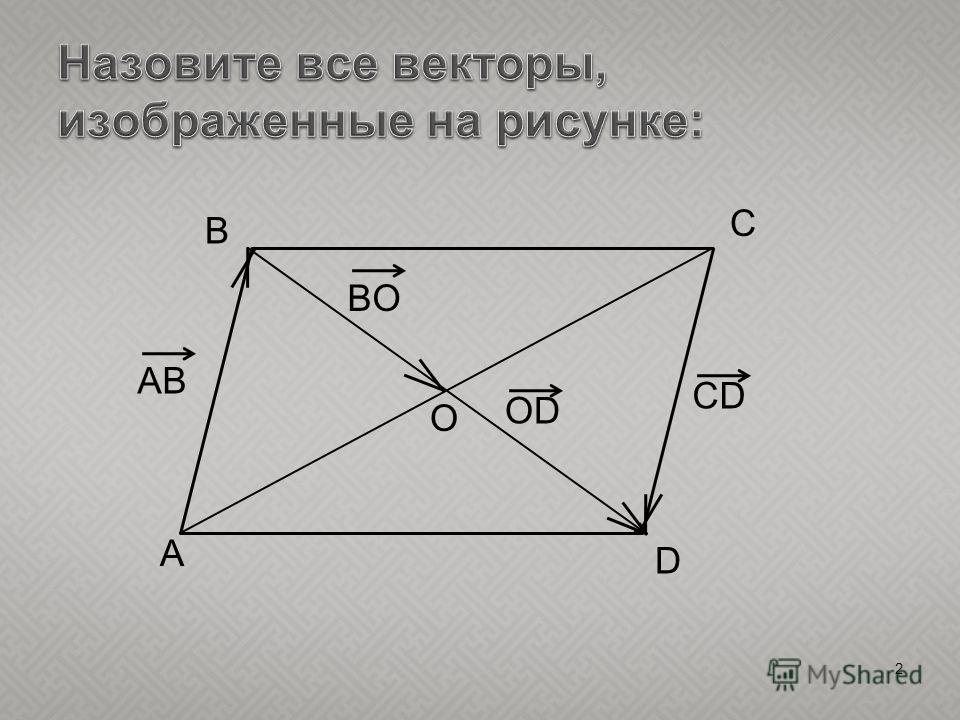
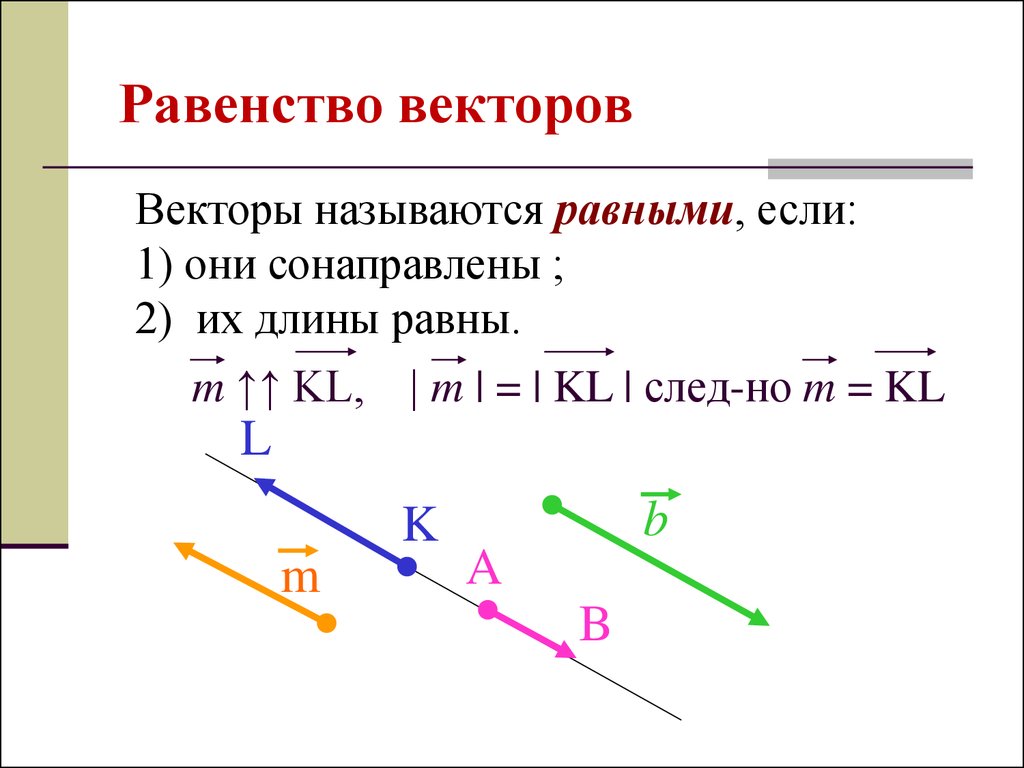
 Из этого следует, что при скалярном умножении векторов
справедливы формулы сокращенного умножения.
Из этого следует, что при скалярном умножении векторов
справедливы формулы сокращенного умножения.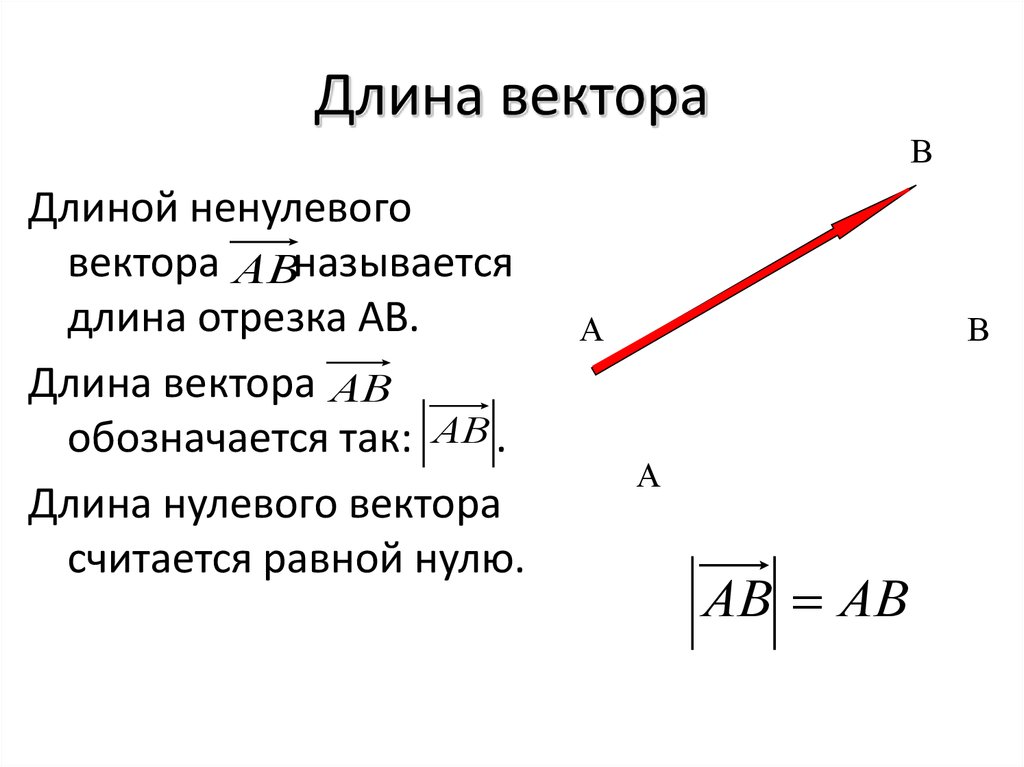 5). Такой
базис называется базисом
правой ориентации.
5). Такой
базис называется базисом
правой ориентации.