Проекция вектора онлайн
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Прab = |b|cos(a,b) или
где a•b — скалярное произведение векторов,|a| — модуль вектора a.
Инструкция. Для нахождения проекции вектора Пpab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
Заданы:две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A’B’, начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.

- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A’B’, взятая со знаком + или -, в зависимости от того, имеет ли вектор A’B’ то же направление, что и ось (вектор).
Виды проекций по системе координат
- проекции на плоскости (система координат OX,OY). Пример: a(2;-3), a=2i-3j
- проекции в пространстве (система координат OX,OY, OZ). Пример: a(2;-3;1), a=2i-3j+k
- проекции в N-мерном пространстве
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1. Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.AC’=AB’+B’C’
Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Прab = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.

- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.
| Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
|
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.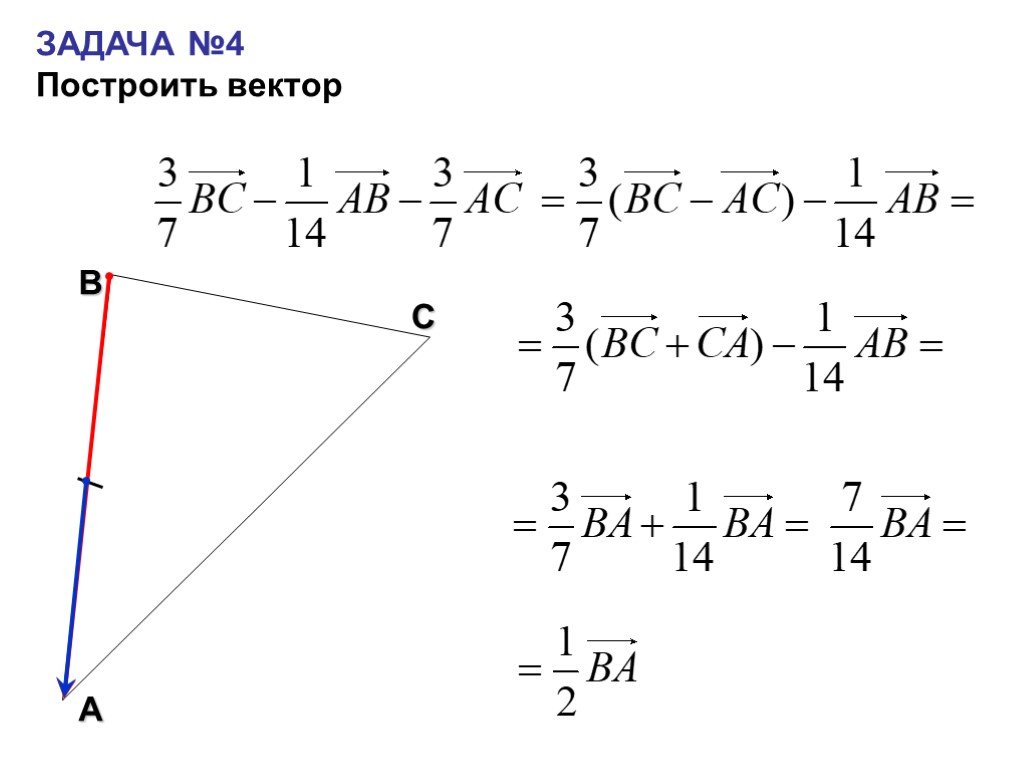
|
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.
| Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
|
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).
| Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).
| Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).
|
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора.
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Пример 3. Пусть вектор b задан через координаты точек M(1;1), N(4;5).
Координаты вектора: MN(4-1;5-1) = MN(3;4)
Тогда модуль вектора MN равен:
Направляющий вектор для оси OX равен вектору M’N’, где координаты точек M’(1;0) N’(4;0). Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.
Следовательно, вектор M’N’ имеет координаты: x = 4-1, y = 0-0 = 0.
M’N’(3;0)
с = АС = (-2;-1;3), d = CB(-5;-3;3)
Найдем проекцию вектора AC на вектор BC
Пример 5. Найти проекцию прb(-2a+4b)
где a=2m+3n и b=4m-n, |m|=k, |n|=l, угол между ∠(m,n)= π
Тогда -2a+4b = -4m+6n + 16m-4n = 12m+2n
а) Рассмотрим треугольник со сторонами a,b,c. По теореме косинусов:
a2 = b2 + c2 – 2bc∙cos(b,c), откуда
или б) Рассмотрим второй вариант решения.
Поскольку угол между векторами π, т.е. 180о, то векторы лежат на одной оси.
Таким образом, 4m-n = 4*1 – 1 = 3.
Находим проекцию.
прb(-2a+4b) = прb(12m+2n) =
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространствеВыберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и :
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж.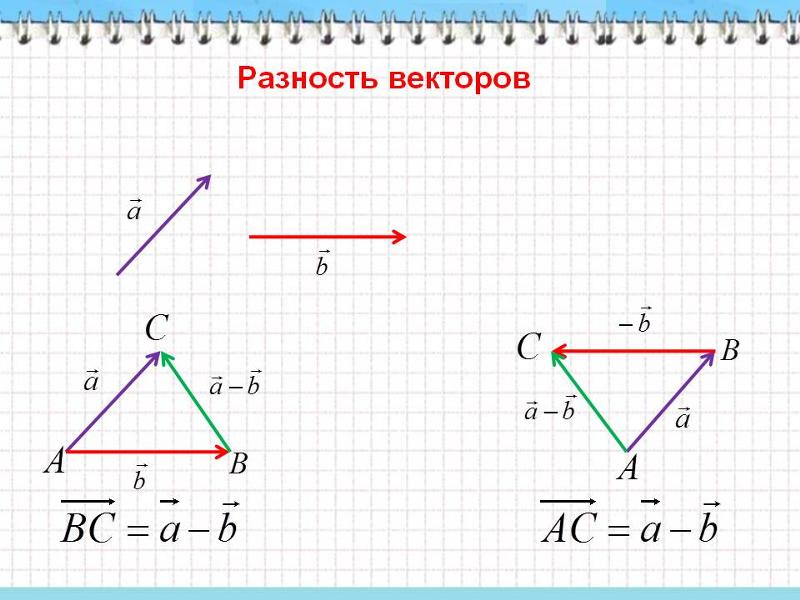 Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D».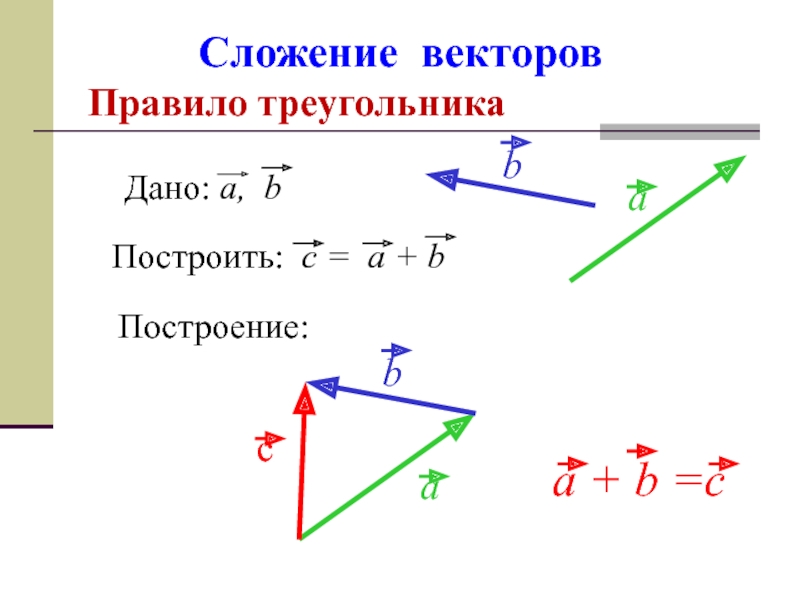 Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.05.2023
Vector Construction — Synbio Technologies
Перейти к содержимомуКонструкция Vector
Vector Constructionadmin2022-08-18T11:59:12-04:00
На базе наших платформ синтеза Syno ® 2. 0 и Syno ® 3.0 Synbio Technologies предоставит любой синтетический вектор с высокой точностью и экономичной ценой, особенно для исследований в проектах shRNA, TALENT и CRISPR-Cas9.
0 и Syno ® 3.0 Synbio Technologies предоставит любой синтетический вектор с высокой точностью и экономичной ценой, особенно для исследований в проектах shRNA, TALENT и CRISPR-Cas9.
Разработка и проверка кшРНК
РНК-интерференция (РНКи) — это быстрый, удобный и эффективный метод, который широко используется для подавления экспрессии генов. Используя кшРНК для молчания выбранного гена-мишени, РНКи чрезвычайно полезна в исследованиях вирусов, опухолей и генетических нарушений.
Разработка и проверка TALEN
TALEN (эффекторная нуклеаза, подобная активатору транскрипции) — это молекулярный инструмент, часто используемый для редактирования генома . Он точно вырезает целевые гены, что приводит к высокоточному редактированию генов. Система TALEN обеспечивает более легкий, простой и доступный метод подавления генов, чем технология нуклеазы цинковых пальцев (ZFN).
Создание и проверка CRISPR-Cas9
гРНК CRISPR-Cas9 (нуклеаза, управляемая РНК CRISPR-Cas9) — это самый последний прорыв в технологии редактирования генома после TALEN. Synbio Technologies предлагает создание и проверку системы CRISPR-Cas9 с помощью нашей запатентованной платформы Syno ® 2.0 высокоэффективным и экономичным способом.
Synbio Technologies предлагает создание и проверку системы CRISPR-Cas9 с помощью нашей запатентованной платформы Syno ® 2.0 высокоэффективным и экономичным способом.
Спецификации услуг
| Наименование услуг | Сведения об услуге | Результаты | Цена | Срок выполнения работ (рабочие дни) |
|---|---|---|---|---|
| Создание и проверка кшРНК |
|
| Цитата | Цитата |
| TALEN Строительство и проверка |
| |||
| Создание и проверка CRISPR-Cas9 |
|
Родственные
Переключить скользящую панель Область
КОНТАКТЫ
-
4250 УС-1 Люкс 3 Соединение Монмут, Нью-Джерси 08852
-
Тел.
 : +1 732-230-3003
: +1 732-230-3003 -
Факс: +1 609-228-5911
-
Справки: [email protected]
Разработка и создание вирусных векторов
Онлайн-запрос
Только для исследовательских целей. НЕ использовать у людей или животных.
- Имя
- * Телефон
- * Электронная почта
- * Заинтересованные продукты или услуги:
- Описание Проекта
Только для исследовательских целей. НЕ использовать у людей или животных.
Генная терапия — это многообещающий новый метод лечения рака и генетических нарушений путем введения чужеродных геномных материалов в клетки-хозяева для получения терапевтического эффекта.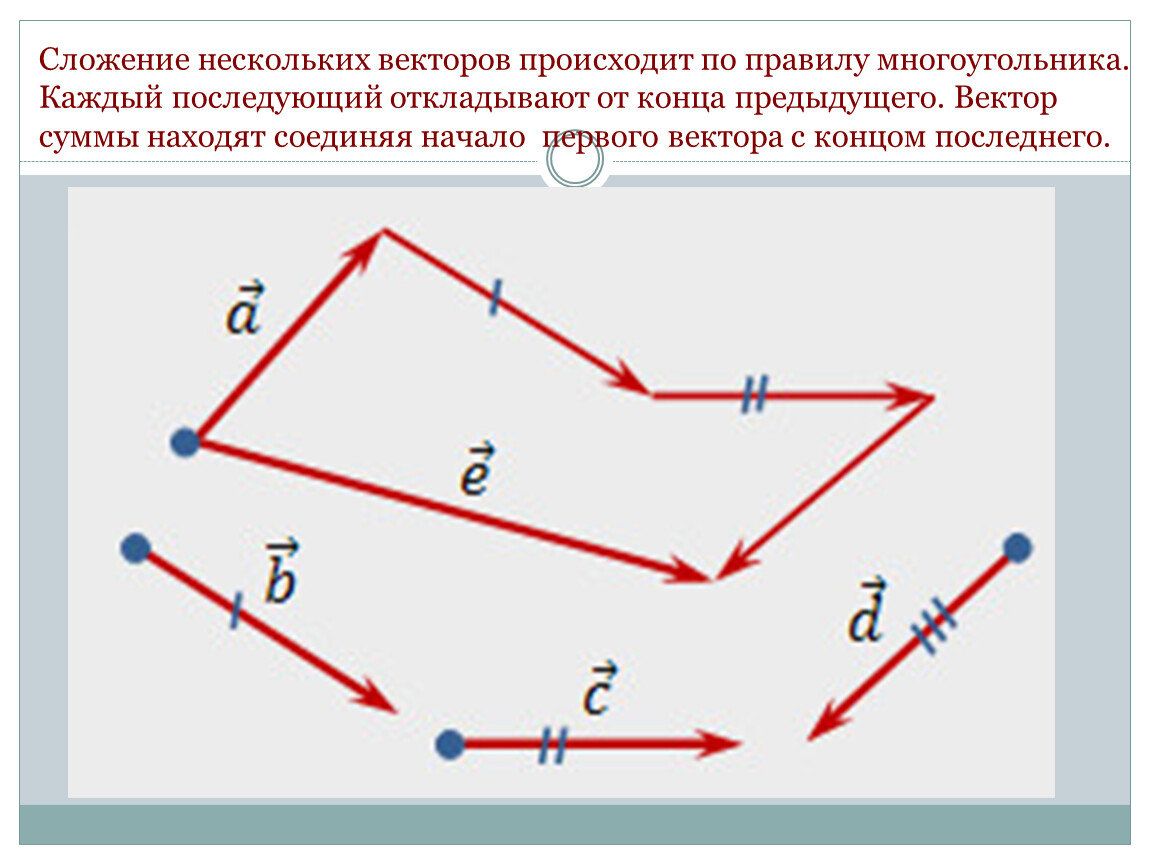 Ключом к успеху генной терапии является создание безопасных и эффективных средств доставки генов. Вирусные носители являются наиболее часто используемыми носителями для доставки ДНК из-за их высокой эффективности и безопасности. Creative Biolabs предлагает комплексные вирусные векторы и передовую технологию вирусных векторов для фундаментальных исследований и доклинических применений, включая разработку и создание подходящих вирусных векторов и производство вирусных векторов в малых и крупных масштабах.
Ключом к успеху генной терапии является создание безопасных и эффективных средств доставки генов. Вирусные носители являются наиболее часто используемыми носителями для доставки ДНК из-за их высокой эффективности и безопасности. Creative Biolabs предлагает комплексные вирусные векторы и передовую технологию вирусных векторов для фундаментальных исследований и доклинических применений, включая разработку и создание подходящих вирусных векторов и производство вирусных векторов в малых и крупных масштабах.
Потенциал доставки вирусных векторов
Вирусные векторы обладают способностью не только эффективно заражать клетки, но и переносить ДНК хозяину, не вызывая иммунного ответа. Вирусные векторы спроектированы так, чтобы быть безопасными, поскольку они неспособны к репликации. Гены, переносимые вирусными векторами, доминируют в клинических испытаниях генной терапии, потому что они более эффективны и специфичны, чем физические и химические методы. Вирусные векторы можно разделить на два типа: интегрирующиеся и неинтегрирующие вирусные векторы. Интегрированные вирусные векторы могут быть интегрированы в геном человека, включая лентивирусные, аденоассоциированные вирусные и ретровирусные векторы; неинтегрирующиеся векторы, такие как аденовирусные векторы, остаются в ядре, не интегрируясь в хромосомную ДНК, таким образом, трансген может теряться во время клеточного деления, а экспрессия чужеродных генов является временной.
Интегрированные вирусные векторы могут быть интегрированы в геном человека, включая лентивирусные, аденоассоциированные вирусные и ретровирусные векторы; неинтегрирующиеся векторы, такие как аденовирусные векторы, остаются в ядре, не интегрируясь в хромосомную ДНК, таким образом, трансген может теряться во время клеточного деления, а экспрессия чужеродных генов является временной.
Рис.1 Вирусные векторы для генной терапии
Лентивирусы представляют собой особую группу ретровирусов. Ген белка оболочки можно заменить генами из другого вирусного генома, чтобы расширить спектр клеток-мишеней. Creative Biolabs может предложить систему переноса лентивирусов, которая обеспечивает долгосрочную экспрессию и эффективный перенос, не вызывая воспалительной реакции.
Аденовирус представляет собой вирус, несущий свой генетический материал в виде двухцепочечной ДНК. Преимущество аденовирусного вектора состоит в том, что он способен сделать большинство клеток восприимчивыми к инфекции и имеет относительно высокий титр, поэтому он широко используется для лечения рака, и были одобрены продукты генной терапии на основе аденовируса.
Вирус простого герпеса (ВПГ) представляет собой нейротропный вирус человека, обладающий наибольшим потенциалом доставки генов в нервную систему и опухолевые клетки. Большой размер, непрерывная экспрессия генов и эффекты широкого спектра делают ВПГ важным вирусом-кандидатом для доставки генов.
Осповакцина (VACV или VV) представляет собой крупный вирус со сложной оболочкой, принадлежащий к семейству поксвирусов. Отсутствие интеграции вируса в клеточный геном хозяина и превосходная иммунная стимуляция делают вирус коровьей оспы привлекательным иммунотерапевтическим средством для лечения рака.
Аденоассоциированный вирус (ААВ) представляет собой небольшой вирус, проявляющий низкую иммуногенность и очевидное отсутствие патогенности. Creative Biolabs предлагает векторы AAV, характеризующиеся молекулярной инженерией и направленной эволюцией, для создания мощных векторов доставки с улучшенными свойствами для лечения заболеваний человека.
Бакуловирус представляет собой тип вируса с двухцепочечной кольцевой ДНК, который специфически поражает членистоногих. Он был успешно применен для доставки чужеродных генов в клетки млекопитающих без какой-либо репликации вируса, а также имеет эффект стимуляции противовирусных иммунных ответов хозяина и обеспечения защиты от летальной вирусной инфекции.
Он был успешно применен для доставки чужеродных генов в клетки млекопитающих без какой-либо репликации вируса, а также имеет эффект стимуляции противовирусных иммунных ответов хозяина и обеспечения защиты от летальной вирусной инфекции.
Creative Biolabs также предоставляет векторы альфавирусов, флавивирусов, вирусов кори, пенистых вирусов, хелпер-зависимых аденовирусных векторов и гибридных аденовирусных векторов, и т. д. .
Рис.2 Применение вирусных векторов для генной терапии
Помимо проектирования, конструирования и клонирования индивидуальных плазмид для производства вирусных векторов, Creative Biolabs использует ряд технологий и научных талантов для предоставления комплексных консультационных услуг по выбору вирусных векторов для генной терапии. Для получения дополнительной информации, пожалуйста, свяжитесь с нами.
Каталожные номера
- Ву, Г.Ю.; и др. . (1991). Системы доставки для генной терапии.


