Вычислить проекции вектора на оси координат. Калькулятор онлайн.Вычисление проекции вектора на вектор
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b — скалярное произведение векторов , |a| — модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Заданы :две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |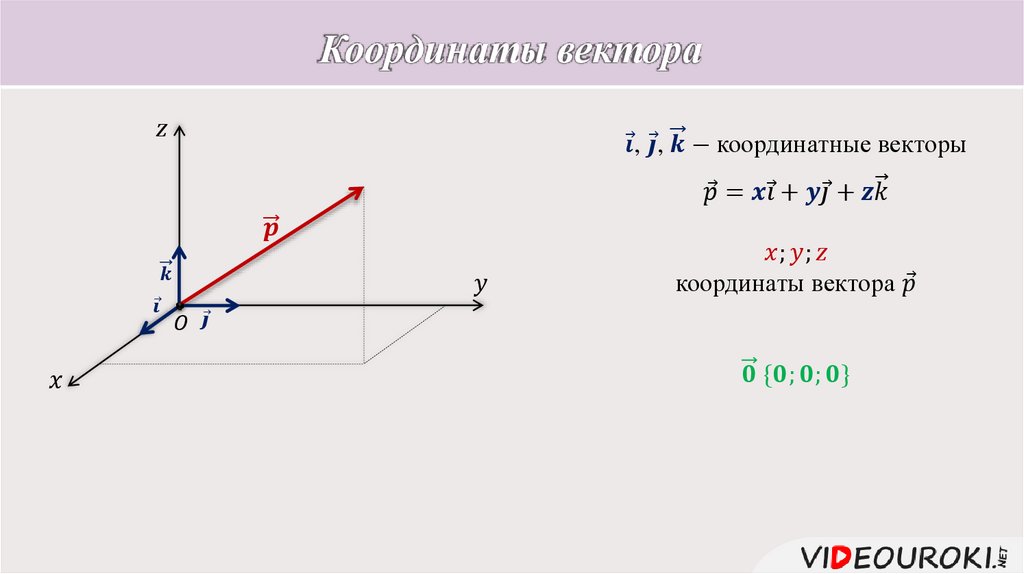
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |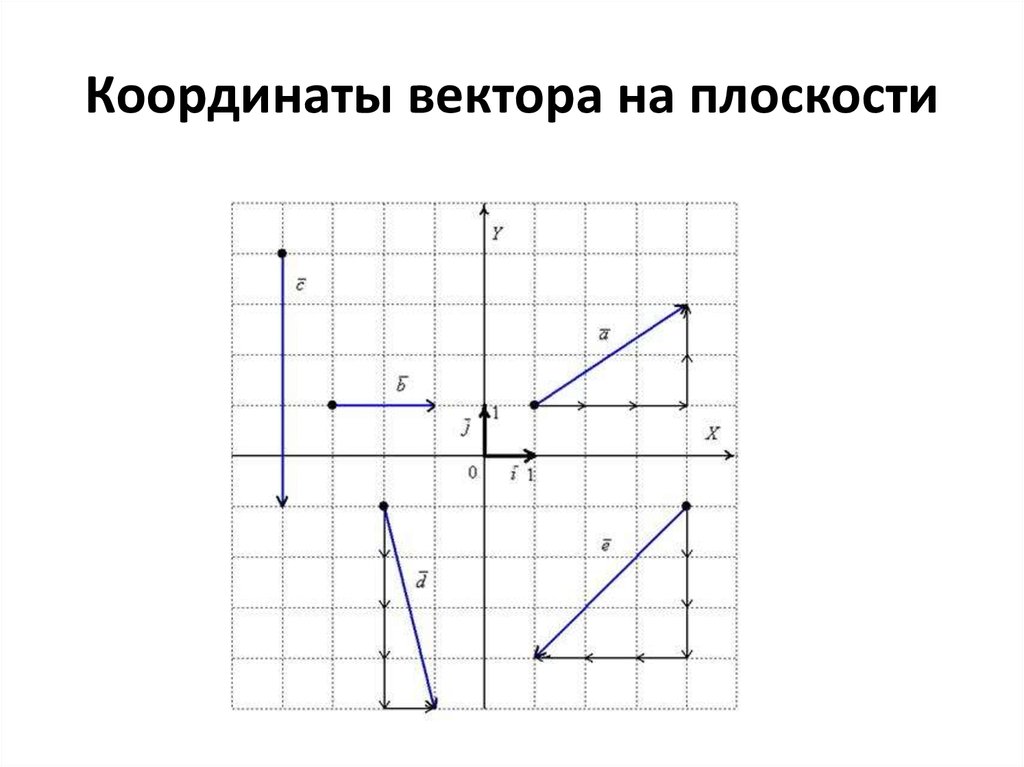
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ
Рис. 3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено.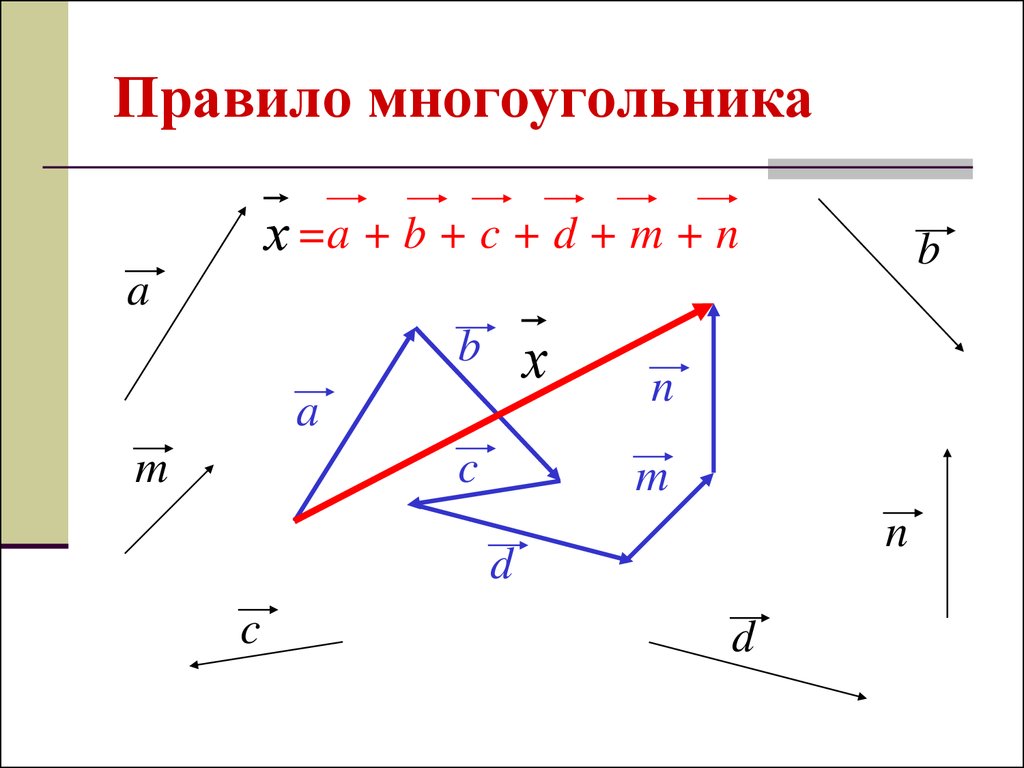
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 — вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора.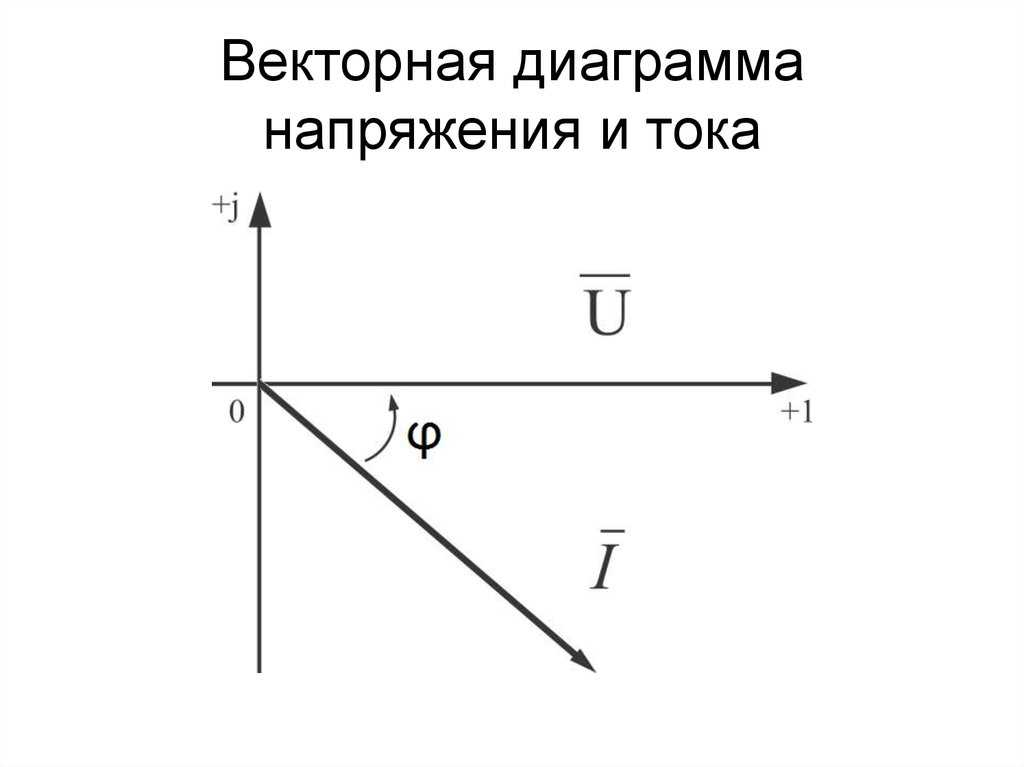
При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О — начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.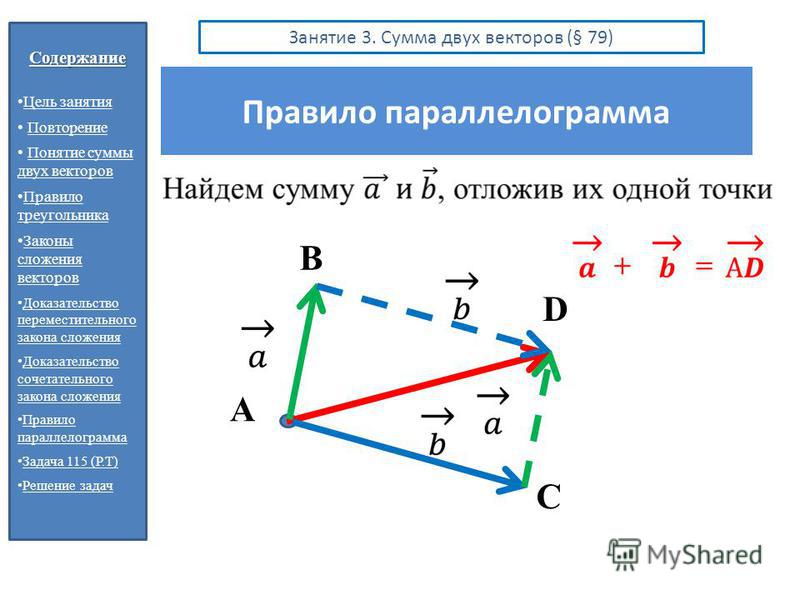
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
Таким образом, в обоих случаях справедливо утверждение теоремы.
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора.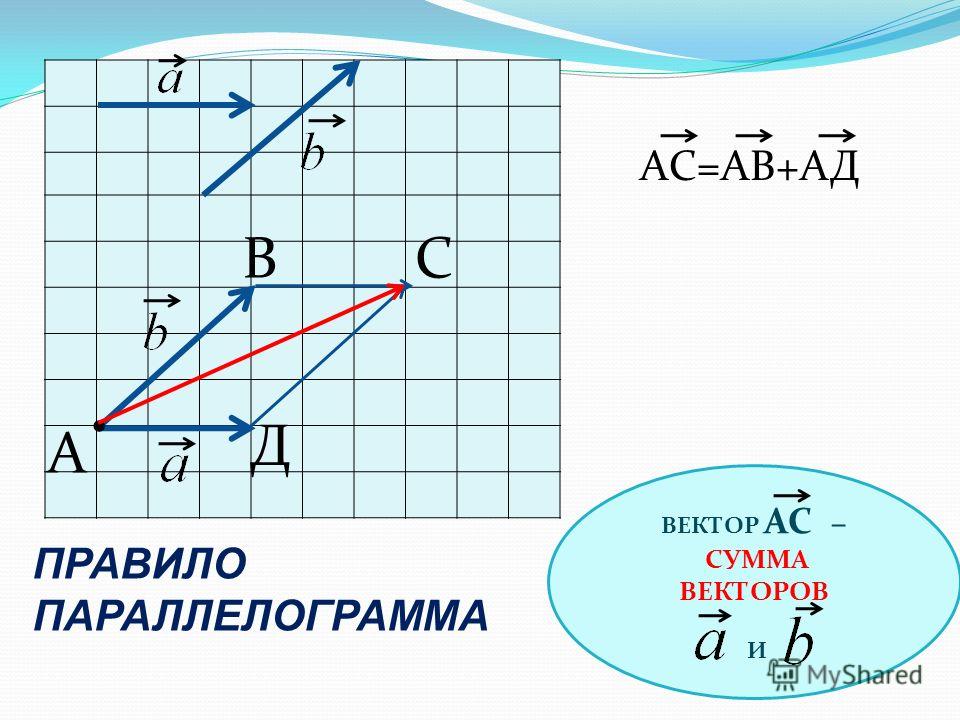
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось.
Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A»$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B»$ (рис. 7).
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O векторы и . Углом между векторами и называется наименьший из углов . Обозначается .
Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).
Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B .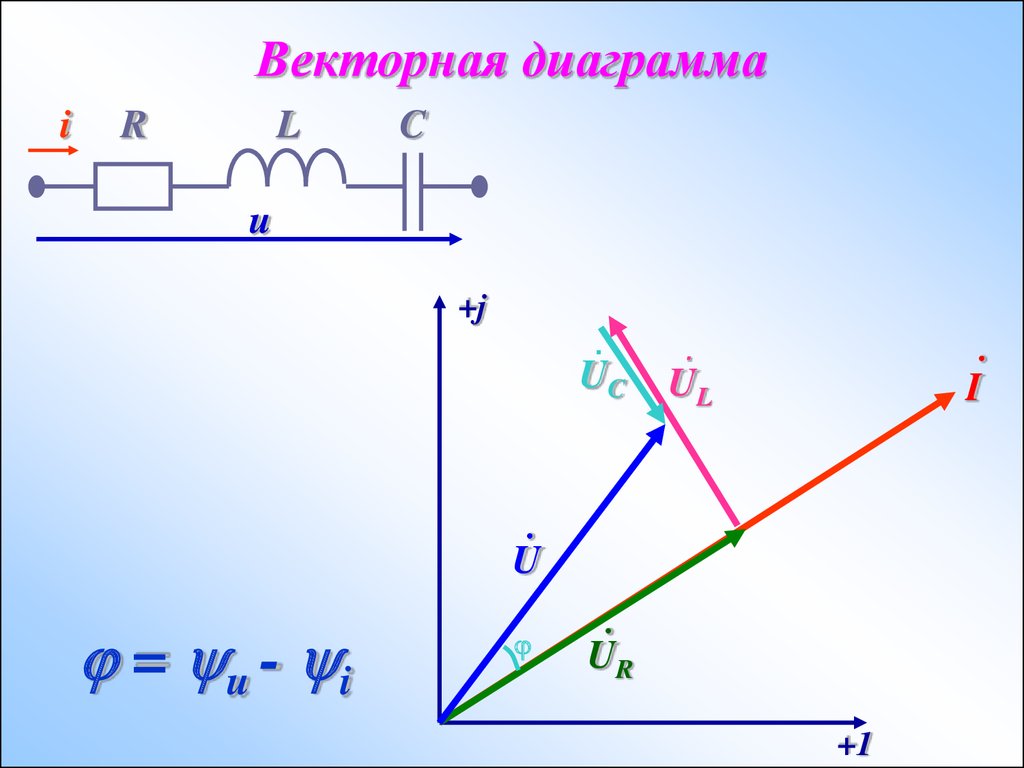
Предположим,
что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .
Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 x 1 и проекция x 2 – x 1 l , то x 2 = x 1 и x 2 – x 1 =0.
Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций .
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где — некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве их линейной комбинации можно рассматривать векторы:
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы называются линейно зависимыми , если существуют такие числа, не все равные нулю, что . Ясно, что заданные векторы будут линейно зависимыми, если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение выполняется только при , эти векторы называются линейно независимыми .
Теорема 1.
Любые два вектора линейно зависимы тогда и
только тогда, когда они коллинеарны.
Доказательство :
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство .
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема. Пусть в пространстве
задан базис . Тогда любой вектор можно представить в
виде линейной комбинации , где x , y , z – некоторые числа.
Такое разложение единственно.
Доказательство .
Таким образом, базис позволяет однозначно сопоставить каждому вектору тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой тройке чисел x, y, z при помощи базиса можно сопоставить вектор, если составить линейную комбинацию .
Если базис и , то числа x, y, z называются координатами вектора в данном базисе. Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .
Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются
осями координат – осью абсцисс, ординат и аппликат.
Плоскости, проходящие через оси координат, называют координатными плоскостями.
Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .
Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: .
Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.
Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют
единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.
Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Введение…………………………………………………………………………3
1. Значение вектора и скаляра………………………………………….4
2. Определение проекции, оси и координатой точки…………………5
3. Проекция вектора на ось………………………………………………6
4. Основная формула векторной алгебры……………………………..8
5. Вычисление модуля вектора по его проекциям……………………9
Заключение………………………………………………………………………11
Литература………………………………………………………………………12
Введение:
Физика неразрывно связана с математикой. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента или теоретических исследований.Ведь основной метод исследований в физике – экспериментальный. Это значит – вычисления ученый выявляет с помощью измерений.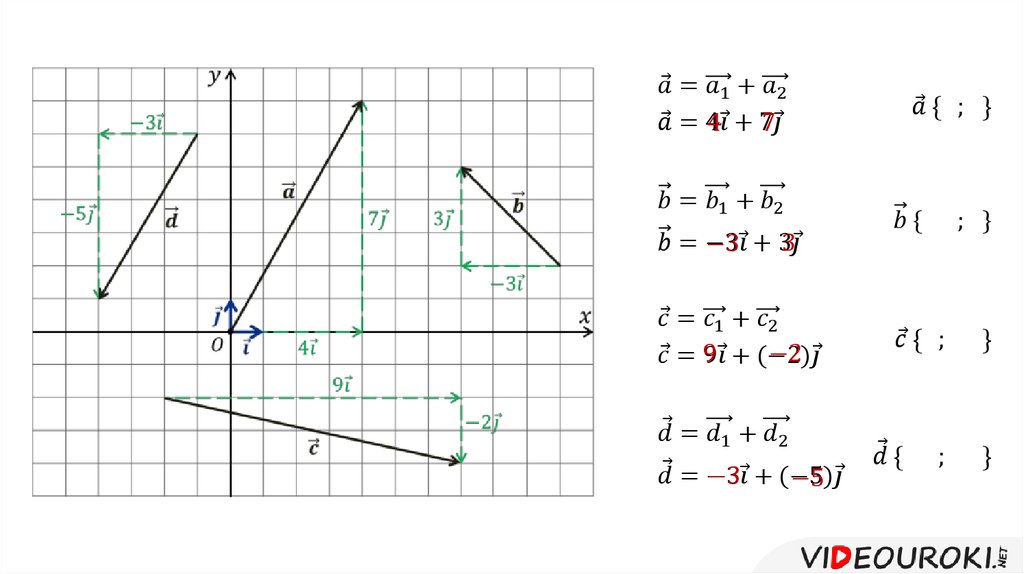
Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика — есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.
Итак, физика создает модель окружающего нас мира и изучает ее свойства. Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого — из всего многообразия выбрать главное.
Физические модели являются математическими, но не математика является их основой. Количественные соотношения между физическими величинами выясняются в результате измерений, наблюдений и экспериментальных исследований и лишь выражаются на языке математики.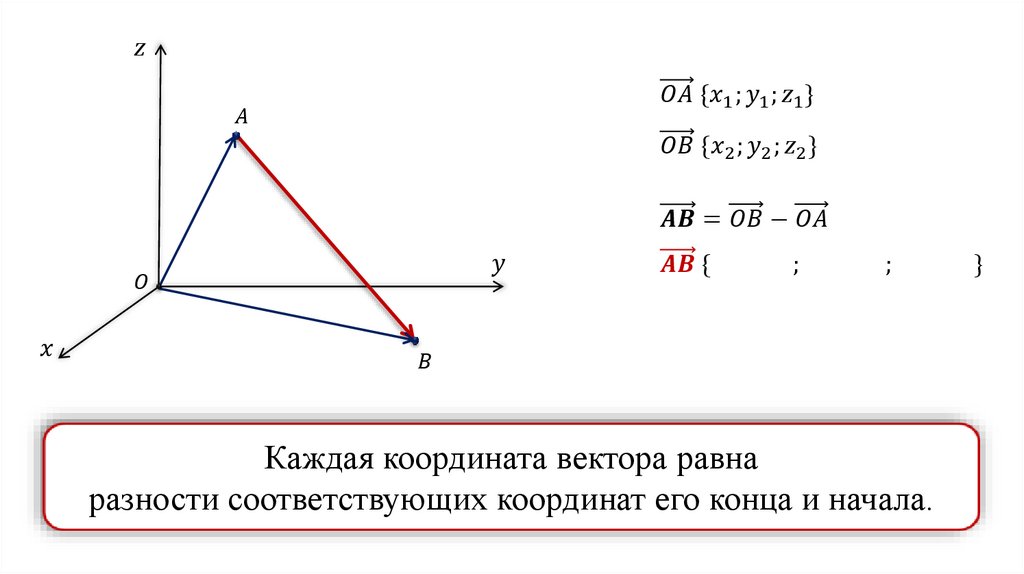
Однако другого языка для построения физических теорий не существует.
1. Значение вектора и скаляра.
В физике и математике вектор — это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами» .
Они записываются либо буквами обычного шрифта, либо цифрами (а, б, t, G, 5, −7….). Скалярные величины могут быть положительными и отрицательными. В то же время некоторые объекты изучения могут обладать такими свойствами, для полного описания которых знание только числовой меры оказывается недостаточным, необходимо ещё охарактеризовать эти свойства направлением в пространстве. Такие свойства характеризуются векторными величинами (векторами).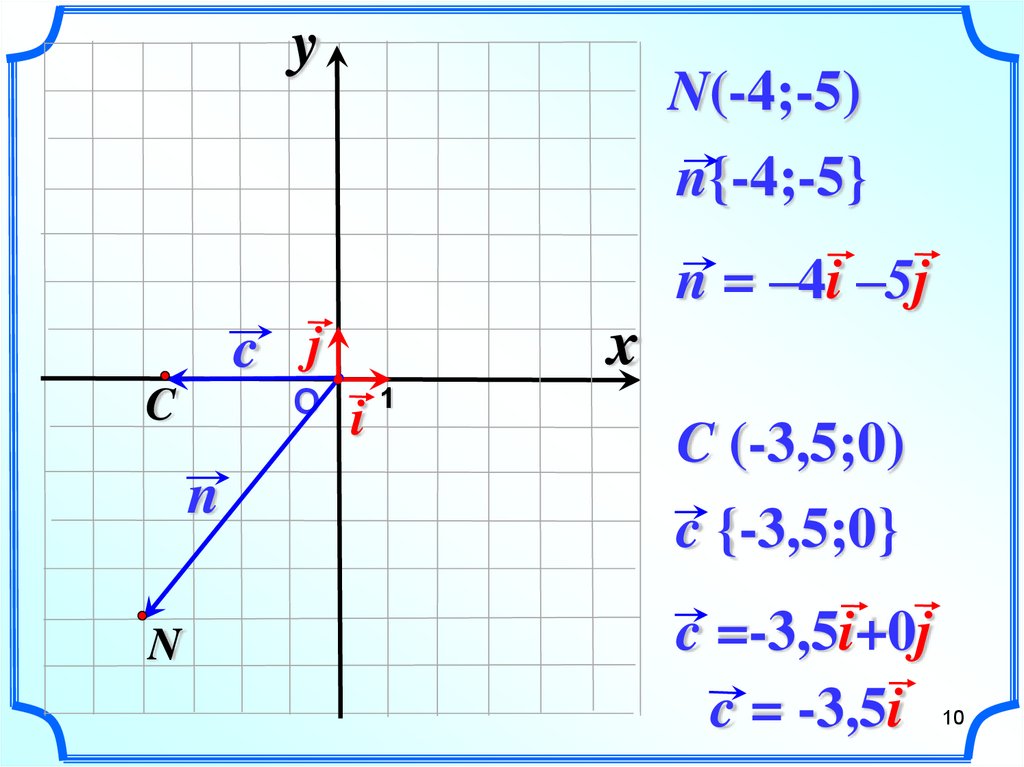
Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Нередко вектор обозначают буквой обычного (нежирного) шрифта, но со стрелкой над ней:
Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая — его конец.
Модуль вектора, то есть длину направленного прямолинейного отрезка, обозначают теми же буквами, как и сам вектор, но в обычном (не жирном) написании и без стрелки над ними, либо точно также как и вектор (то есть жирным шрифтом или обычным, но со стрелкой), но тогда обозначение вектора заключается в вертикальные черточки.
Вектор – сложный объект, который одновременно характеризуется и величиной и направлением.
Не бывает также положительных и отрицательных векторов. А вот равными между собой векторы быть могут. Это когда, например, aиb имеют одинаковые модули и направлены в одну сторону. В этом случае справедлива запись a = b.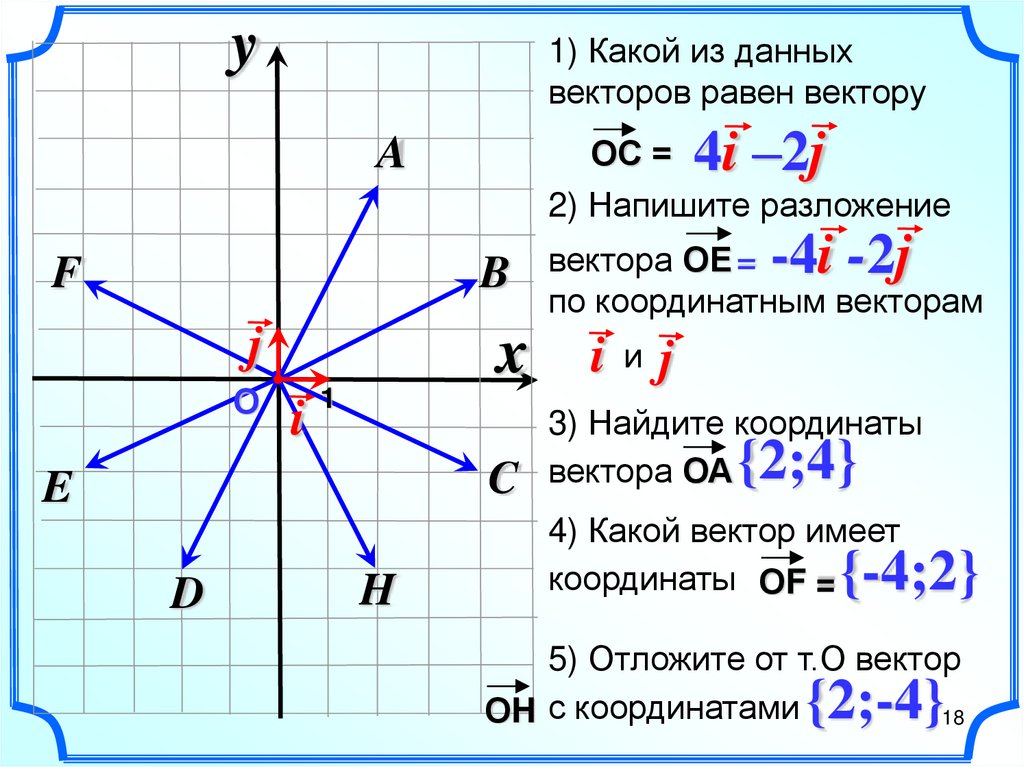
Надо также иметь в виду, что перед символом вектора может стоять знак минус, например, — с, однако, этот знак символически указывает на то, что вектор -с имеет такой же модуль, как и вектор с, но направлен в противоположную сторону.
Вектор -с называют противоположным (или обратным) вектору с.
В физике же каждый вектор наполнен конкретным содержанием и при сравнении однотипных векторов (например, сил) могут иметь существенное значение и точки их приложения.
2.Определение проекции, оси и координатой точки.
Ось – это прямая, которой придается какое–то направление.
Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.
Проекцией точки на ось называется основание перпендикуляра, опущенного из этой точки на данную ось. То есть, проекцией точки на ось является точка.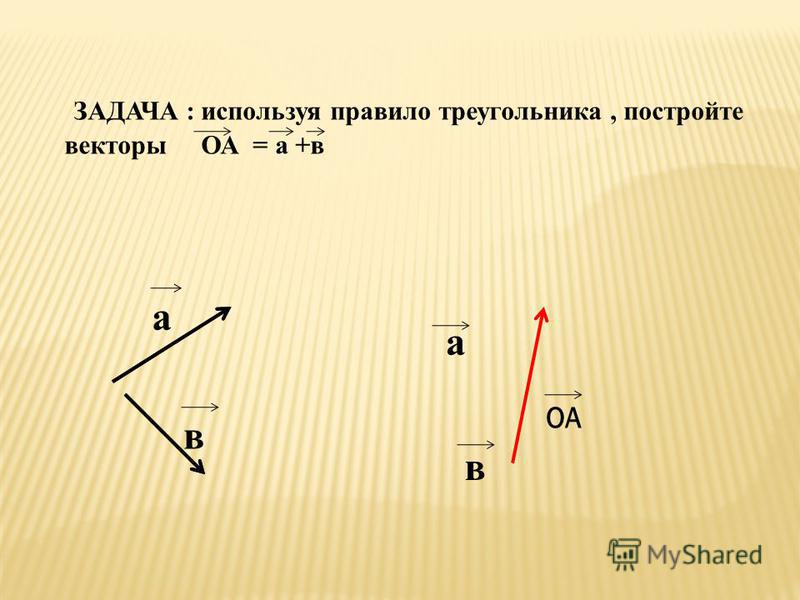
Координатой точки на данной оси называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.
3.Проекция вектора на ось.
Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а x – скалярная проекция вектора а на ось X, то а x ·i — его векторная проекция на эту ось.
Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим а x (жирная буква, обозначающая вектор и нижний индекс названия оси) или
(нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).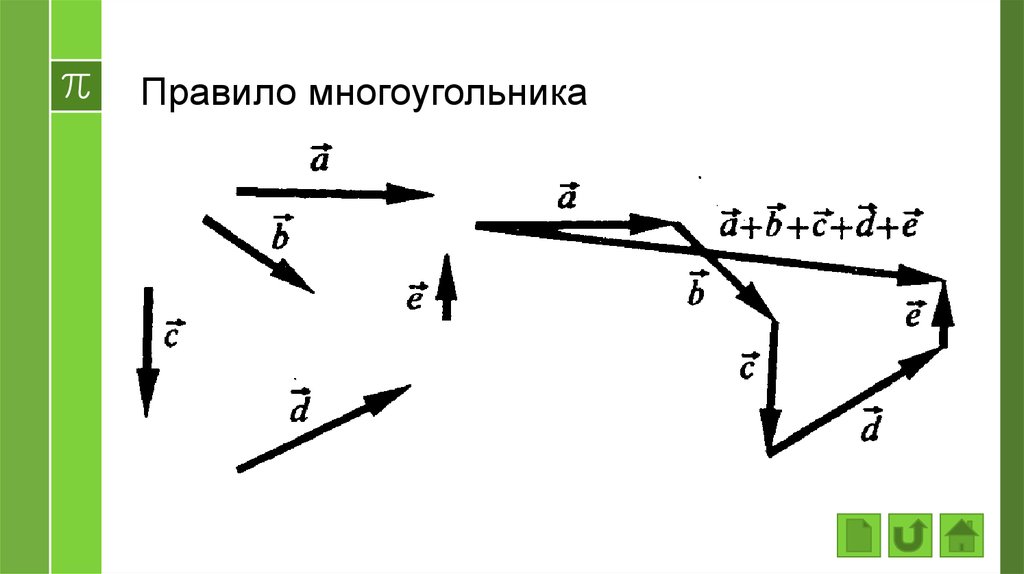
Скалярной проекцией вектора на ось называется число , абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция . Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора, то его проекция обозначается а x . При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться а y .
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
а x = х к − x н.
Проекция вектора на ось — это число. Причем, проекция может быть положительной, если величина х к больше величины х н,
отрицательной, если величина х к меньше величины х н
и равной нулю, если х к
равно х н.
Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка видно, что а x = а Cos α
То есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора . Если угол острый, то
Cos α > 0 и а x
> 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.
Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу — отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
4. Основная формула векторной алгебры.
Спроектируемвектор а на оси Х и Y прямоугольной системы координат.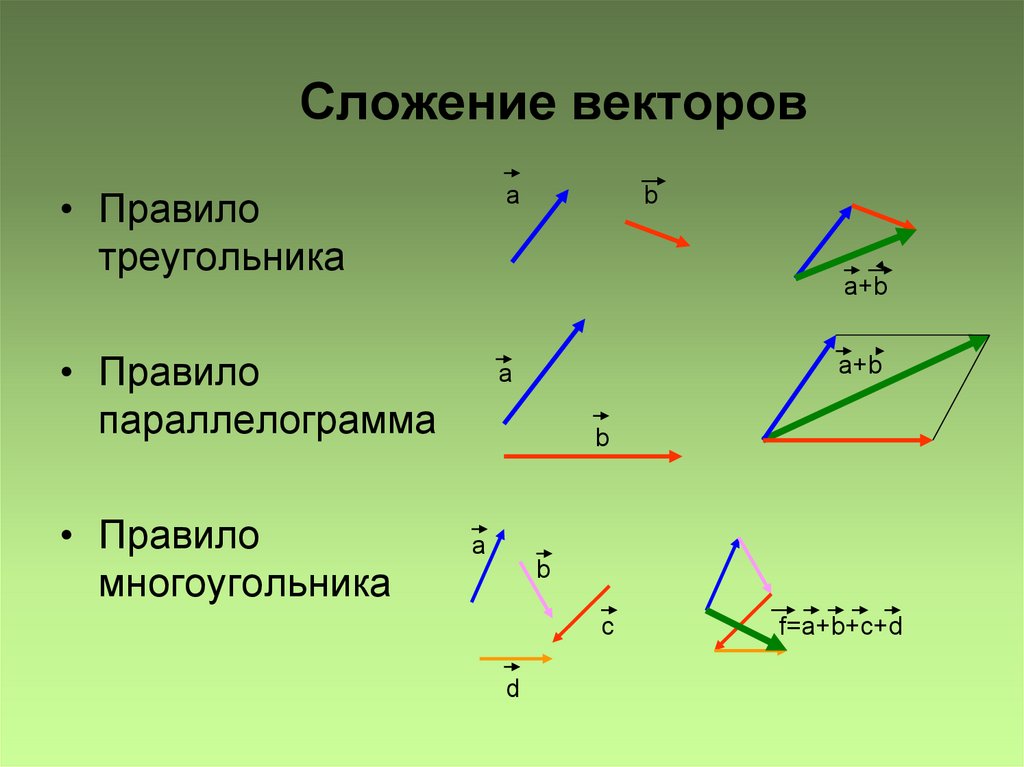
Найдем векторные проекции вектора а на эти оси:
а x = а x ·i, а y = а y ·j.
Но в соответствии справилом сложения векторов
а = а x + а y .
а = а x ·i + а y ·j.
Таким образом, мы выразили вектор через его проекции и орты прямоугольной системы координат (или через его векторные проекции).
Векторные проекции а x и а y называютсясоставляющими или компонентами вектора а. Операция, которую мы выполнили, называется разложением вектора по осямпрямоугольной системы координат.
Если вектор задан в пространстве, то
а = а x ·i + а y ·j + а z ·k.
Эта формула называется основной формулой векторной алгебры. Конечно, ее можно записать и так.
Векторное Произведение Векторов. Свойства, определение
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.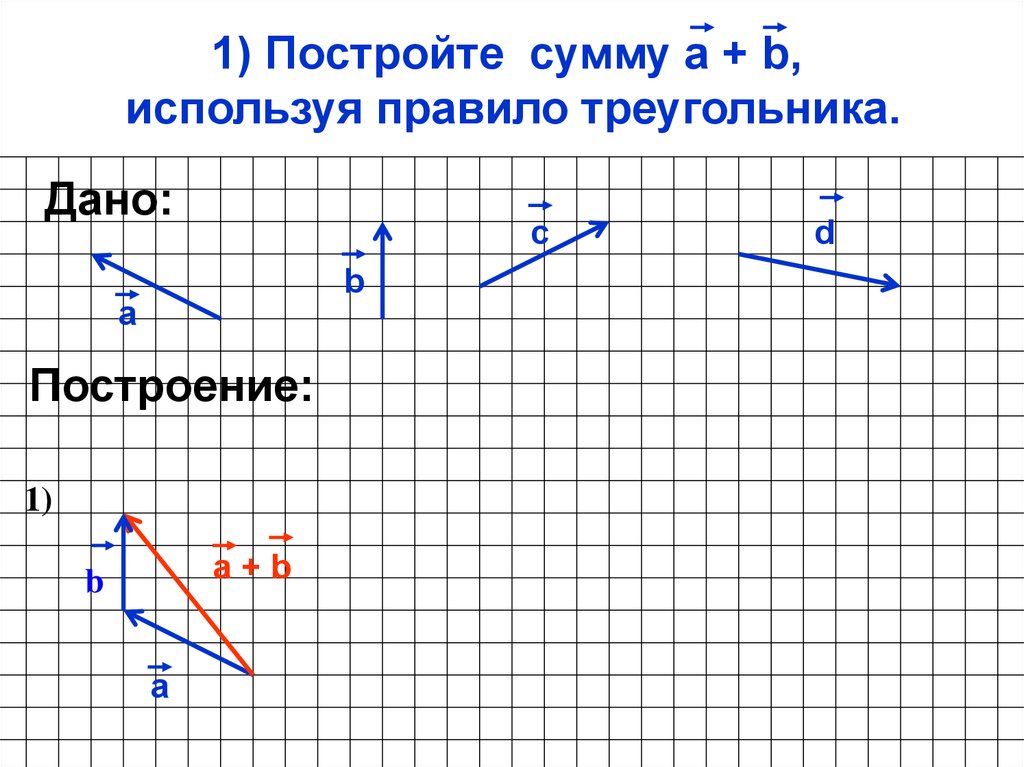
Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.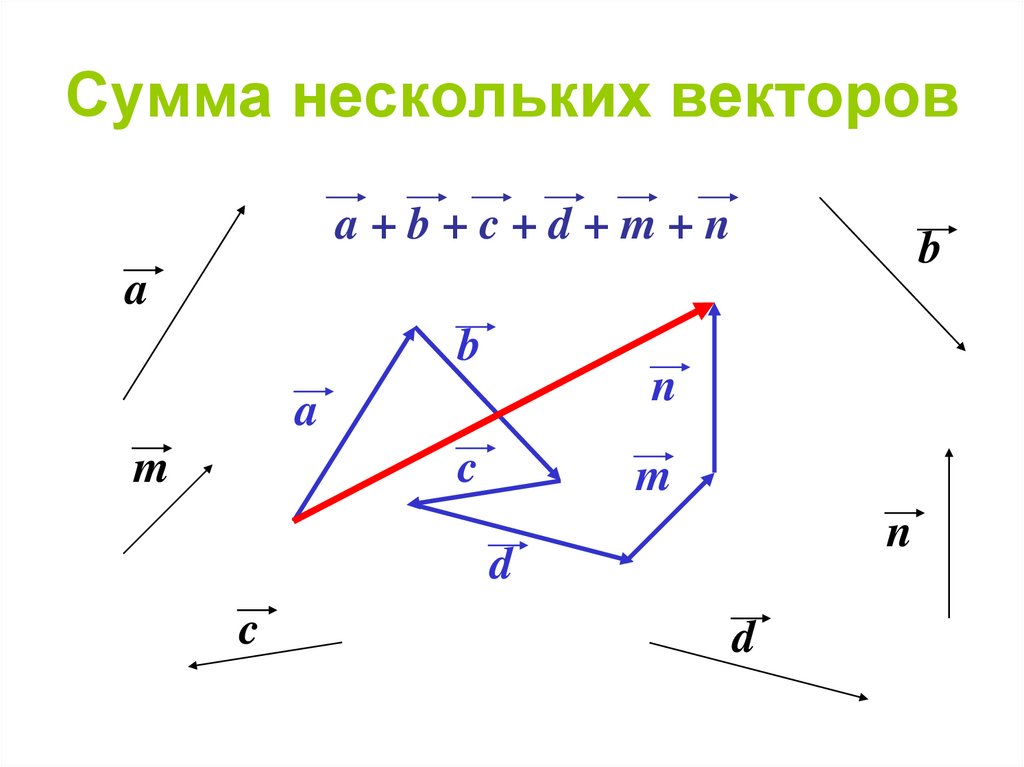
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c.
Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
, где
→i, →j, →k — координатные векторы.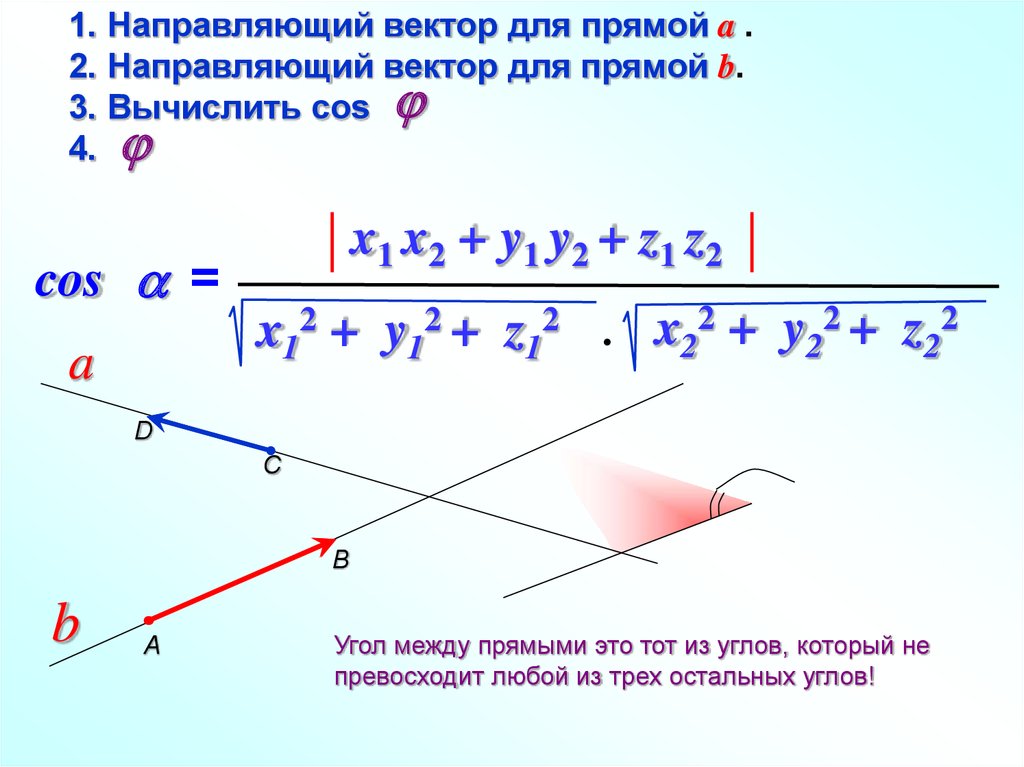
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
или
- Сочетательное свойство
или
, где λ произвольное действительное число.
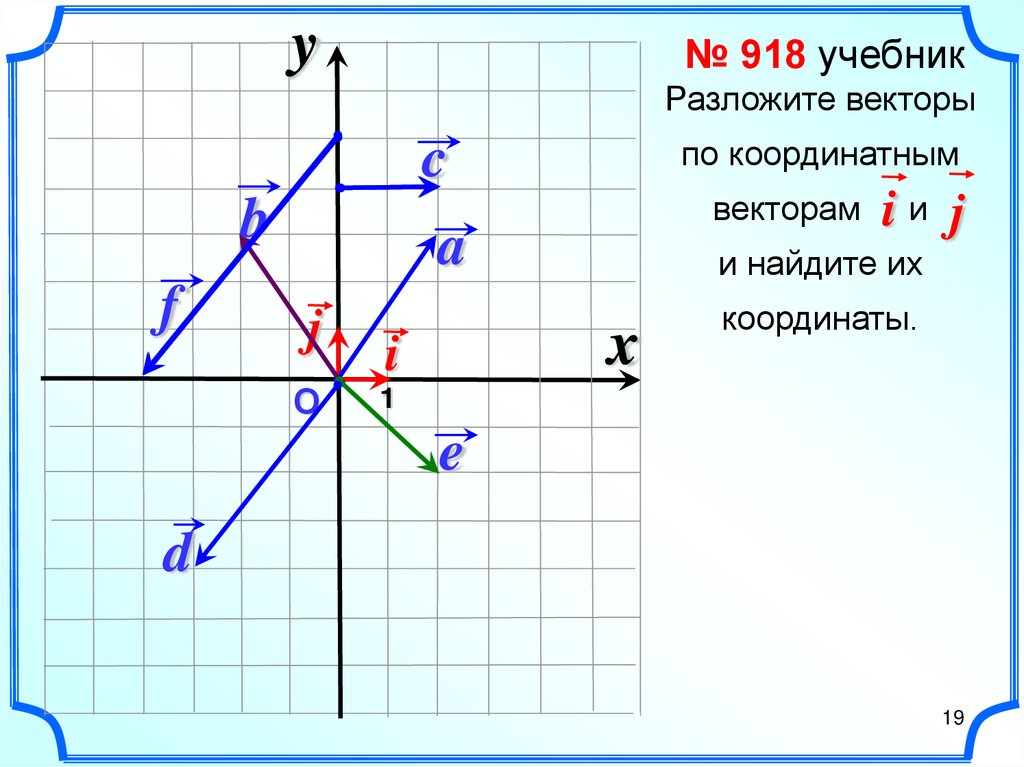
Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.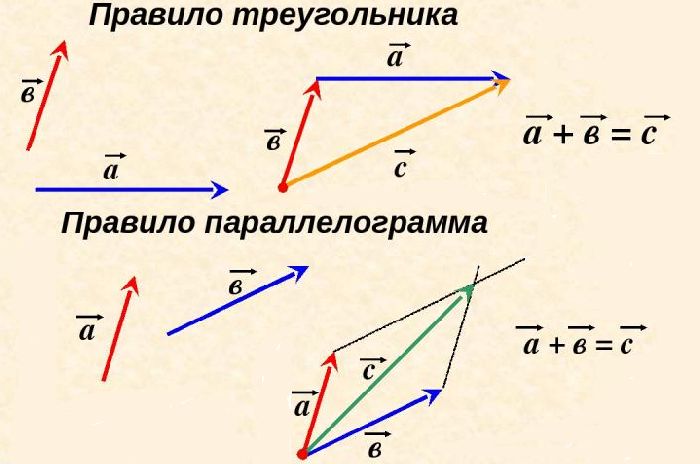
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
Как решаем:
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Ответ:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Ответ:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
Как решаем:
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Ответ:
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Как решаем:
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Ответ:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки.
Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Features — Vector Ink — Advanced SVG Editor Online
Инструмент Path Builder
Инструмент Path Builder (также известный как Shape Builder Tool) — одна из самых мощных функций в Vector Ink.
Вы можете использовать его для создания практически любой формы, которую только можете себе представить, используя только одну фигуру в качестве строительного блока. Это отлично подходит для профессиональных графических дизайнеров, но особенно для новичков, которые хотят создавать великолепные проекты, не изучая тонкости программы. Здесь нет сложных инструментов или навыков, просто выберите нужные фигуры и активируйте инструмент Path Builder, чтобы создать любое количество различных фигур.
Инструмент «Рисование»
Инструмент «Рисование» — это инструмент, который можно использовать для трассировки или рисования от руки на холсте. Стабилизатор — это функция, которая делает штрихи плавными во время рисования, поэтому вам не понадобится стилус.
В сочетании с инструментом Path Builder возможности безграничны! Вы можете уверенно рисовать и использовать инструмент «Создание контуров», чтобы обрезать штрихи до нужной формы, не мучаясь с вырезанием контуров и соединительными линиями.
Виртуальный стилус
Если вы используете сенсорный экран, но не имеете под рукой стилуса, виртуальный стилус — это встроенная функция, которая помогает вам рисовать пальцем, чтобы вы могли видеть, где вы рисуете.
Уверенно рисуйте без физического стилуса или проникайте в труднодоступные места, создавая фигуры с помощью инструмента Path Builder.
Инструмент копирования
Экономьте время, пытаясь вручную скопировать объект и расположить копии равномерно вдоль оси или вокруг другого объекта.
Используя инструмент копирования, вы можете быстро создать любое количество копий объекта слева направо, сверху вниз, в сетке или вокруг точки.
Генератор цветовых палитр
Дизайнеры и художники по всему миру используют цветовые палитры для создания и планирования своих работ и дизайнов. Однако это может быть утомительным и трудоемким процессом.
Встроенный инструмент цветовой палитры Vector Inks помогает создавать цветовые палитры, сгенерированные случайным образом, сгенерированные из фотографии, или выбрать из библиотеки встроенных цветовых палитр и добавить столько цветов, сколько вы хотите в свои палитры.
Типографика
Типографика — важный элемент дизайна, но также и один из самых эзотерических. Большинство дизайнеров хорошо разбираются в теории цвета и компоновке, но очень немногие хорошо разбираются в типографике. Часто это метод проб и ошибок.
Vector Ink поставляется со встроенными инструментами, помогающими улучшить представление текста в дизайне.
- Импорт пользовательских шрифтов и их хранение в облаке,
- Сделайте дугу и разместите текст по своему вкусу.
- Преобразуйте свой текст в векторный контур и редактируйте свои письма с помощью векторных инструментов, имеющихся в Vector Ink.
Импорт/экспорт
Экспорт проектов в форматах SVG, PNG или JPG.
Экспорт всего документа или отдельных объектов
Обрезка и экспорт фотографий в любом соотношении и любом размере без потери качества.
Импорт файлов SVG из другого редактора и возобновление работы в Vector Ink.
Импортируйте файлы JPG или JPG на холст и используйте их для трассировки или в качестве фона для вашего дизайна.
Всего просмотров: 12224 ,
Архивы практических советов — Vector Ink
Как обрисовать шрифт — конвертировать шрифт в SVG онлайн
Создание контура шрифта означает простое преобразование текстового объекта в объект векторного контура, что позволяет редактировать точки и кривые, составляющие форму текста. Это очень легко сделать в Vector Ink. Попробуйте это в живом редакторе ниже. Шаг 1. Добавьте текст в …
Как рисовать в Vector Ink
Рисовать в Vector Ink очень просто Даже если вы используете мышь или планшет без стилуса, Vector Ink упрощает рисование от руки. В этом видео я покажу вам, как рисовать с помощью инструментов «Рисование» и «Создание контуров», чтобы легко вырезать любую фигуру, которую вы хотите. Что обычно занимает …
Как использовать инструмент выделения
Инструмент «Выделение» — это основной инструмент для перемещения и преобразования объектов на холсте. Он имеет собственный набор параметров, ярлыков и элементов управления, которые помогут ускорить процесс проектирования. При активации становится доступной панель инструментов «Инструменты выделения», а также элементы управления «Преобразование» и «Объект», расположенные в …
.Как использовать инструмент «Перо»
С помощью инструмента «Перо» вы можете рисовать пути с острыми или гладкими опорными точками, а также добавлять и редактировать опорные точки на выбранном пути. При активации становится доступной панель инструментов Pen Tools, а также элементы управления Path, расположенные на панели управления. Начните с выбора инструмента «Перо» на панели инструментов …
Как использовать инструмент «Прямоугольник»
Инструментом «Прямоугольник» нарисуйте прямоугольник на холсте. Чтобы начать, щелкните инструмент «Прямоугольник» на панели инструментов, затем нажмите и перетащите прямоугольник на холст. Скругление углов Откройте панель свойств прямоугольника и установите Радиус на 20 пикселей. Теперь нарисуйте на холсте прямоугольник и углы …
Как использовать инструмент Path Builder
Инструмент создания контуров — это мощный инструмент для создания пользовательских фигур из двух или более других фигур. Для начала выберите две или более фигур на холсте, затем выберите инструмент «Создание контуров» на панели инструментов. Аккуратно перетащите между штрихами, которые вы хотите включить в новую фигуру, и штрихи будут …
Как использовать инструмент рисования
Инструмент «Рисование» — это мощный инструмент, используемый для рисования от руки. Он поставляется с параметрами, помогающими рисовать плавными штрихами, и автоматически подключается к другим контурам, чтобы вы могли поднять и продолжить рисование, не прерывая контур. Чтобы начать, выберите инструмент «Рисование» на панели инструментов, найдите место на холсте …
Как использовать инструмент копирования
Инструмент копирования используется для распределения копий объекта вокруг точки, по горизонтали слева направо, по вертикали сверху вниз или в сетке строк и столбцов. Распределение вокруг точки Это поведение по умолчанию, и после активации инструмента копирования маркер точки будет присутствовать на холсте. Это …
Как использовать инструмент «Угол»
Инструмент «Угол» используется для скругления углов контуров. При активации вы заметите, что на острых углах пути появляются ручки. Выберите нужные маркеры по отдельности и, когда будете готовы, перетащите вниз, чтобы скруглить углы сильнее, и вверх, чтобы скруглить углы меньше. После выпуска будут применены закругленные углы.
