Работа с векторами в с: C++ | Операции с векторами

умножение, сложение векторов по правилу многоугольника

Прежде чем приступить к тематике статьи, напомним основные понятия.

Определение 1

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Определение 2

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Определение 3

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Определение 4

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Сложение двух векторов

Определение 5

Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор

AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→. Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

Определение 6

Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Определение 7

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и — b→.

Умножение вектора на число

Определение 8

Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
— еслиk>1, то это число приведет к растяжению вектора в k раз;
— если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
— если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k=1, то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a→, b→,

c→и произвольные действительные числа λ и μ.

1. Свойство коммутативности: a⇀+b→=b→+a→ .
   
2. Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
   
3. Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
4. Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
5. Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→. Указанное свойство — очевидное.
6. Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ). Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
7. Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
8. Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
   Геометрически это свойство определяется подобием треугольников:
   

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Пример 1

Задача: упростить выражение a→-2·(b→+3·a→)
Решение
— используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
— используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
— затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→

Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Операции над n-мерными векторами

Следующая статья

Векторное пространство

• Векторное произведение
• Векторное пространство
• Векторы на плоскости и в пространстве
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Все темы по математике

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Защита данных в беспроводных сетях

Заказать такую же работу

Обратная матрицаРанг матрицы

• Вид работы:

  Реферат

• Выполнена:

  1 июля 2022 г.

• Стоимость:

  1 200 руб

Заказать такую же работу

Общие требования к автомобильным топливам и смазочным материалам Понятие о химмотологии Влияние качества автомобильных бензинов на отказы современных двигателей Свойства тормозных жидкостей гигроскопичность вязкость смазочные

Заказать такую же работу

Дизельный отопитель вебасто

Заказать такую же работу

Расчт эл и магнитных цепей постоянного и переменного тока

• Вид работы:

  Курсовая работа

• Выполнена:

  19 июня 2022 г.

• Стоимость:

  9 600 руб

Заказать такую же работу

тема примерная Интегралы

• Вид работы:

  Онлайн-помощь

• Выполнена:

  22 мая 2022 г.

• Стоимость:

  2 400 руб

Заказать такую же работу

Смотреть все работы по информационной безопасности

Операции с векторами, сложение векторов, умножение вектора на действительное число.

Рассмотрим вектор v с начальной точкой в начале координат в любой координатной системе x-y и с конечной точкой в (a,b). Мы говорим, что вектор находится в стандартном положении и ссылаемся на него как на радиус-вектор.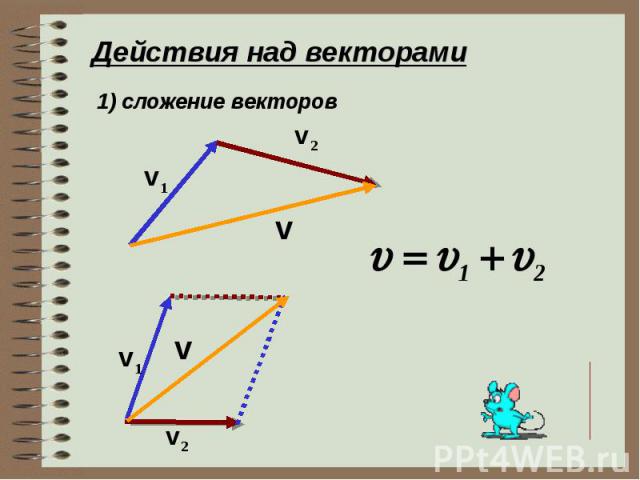 Обратите внимание, что пара точек определяет этот вектор. Таким образом, мы можем использовать это для обозначения вектора. Чтобы подчеркнуть, что мы имеем в виду вектор, и, чтобы избежать путаницы, как правило, пишут:
v = .

Координата a есть скаляром горизонтальной компоненты вектора, и координата b есть скаляром вертикальной компоненты вектора. Под скаляром мы подразумеваем численное количество, а не векторную величину. Таким образом, это рассматривается как компонентная форма v. Обратите внимание, что a и b НЕ вектора и их не надо путать с определением компонента вектора.

Теперь рассмотрим с A = (x₁, y₁) и C = (x₂, y₂). Давайте рассмотрим, как найти радиус вектор, эквивалентный . Как Вы видите на рисунке внизу, начальная точка A перемещена в начало координат (0, 0). Координаты P находятся вычитанием координат A из координат C. Таким образом, P = (x₂ — x₁, y₂ — y₁) и радиус вектор есть .

Можно показать, что и имеют одну и ту же величину и направление, и поэтому эквивалентны. Таким образом, = = 2 — x₁, y₂ — y₁ >.

Компонентная форма с A = (x₁, y₁) и C = (x₂, y₂) есть
= 2 — x₁, y₂ — y₁ >.

Пример 1 Найдите компонентную форму если C = (- 4, — 3) и F = (1, 5).

Решение Мы имеем
= = .

Обратите внимание, что вектор есть равным радиус-вектору , как показано на рисунке вверху.

Теперь, когда мы знаем, как записать вектор в компонентной форме, давайте изложим некоторые определения.
Длину вектора v легко определить, когда известны компоненты вектора. Для v = 1, v₂ >, мы имеем
|v|² = v²₁ + v²₂          Используя теорему Пифагора
|v| = √v²₁ + v²₂.

Длина, или величина ветктора v = 1, v₂ > находится как |v| = √v²₁ + v²₂.

Два вектора равны или эквивалентны, если они имеют одну и ту же величину и одно и то же направление.

Пусть u = 1, u₂ > и v = 1, v₂ >. Tогда
1, u₂ > = 1, v₂ >          только если u₁ = v₁ and u₂ = v₂.

Операции с векторами

Чтобы умножить вектор V на положительное число, мы умножаем его длину на это число. Его направление остается прежним. Когда вектор V умножается на 2, например, его длина увеличивается в два раза, но его направление не изменяется. Когда вектор умножается на 1,6, его длина увеличивается на 60%, а направление остается прежним. Чтобы умножить вектор V на отрицательное действительное число, умножаем его длину на это число и изменяем направление на противоположное. Например, Когда вектор умножается на (-2), его длина увеличивается в два раза и его направление изменяется на противоположное. Так как действительные числа работают как скалярные множители в умножении векторов, мы называем их скаляры и произведение kv называется скалярные кратные v.

Для действительного числа k и вектора v = 1, v₂ >, скалярное произведение k и v есть
kv = k.1, v₂ > = 1, kv₂ >.
Вектор kv есть скалярным кратным вектора v.

Пример 2 Пусть u = и w = . Найдите — 7w, 3u и — 1w.

Решение
— 7w = — 7. = ,
3u = 3. = ,
— 1w = — 1. = .

Теперь мы можем сложить два вектора, используя компоненты. Чтобы сложить два вектора в компонентной форме, мы складываем соответствующие компоненты. Пусть u = 1, u₂ > и v = 1, v₂ >. Тогда
u + v = 1 + v₁, u₂ + v₂ >

Например, если v = и w = , тогда
v + w = =

Если u = 1, u₂ > и v = 1, v₂ >, тогда
u + v = 1 + v₁, u₂ + v₂ >.

Перед тем, как мы определим вычитание векторов нам нужно дать определение — v. Противоположный вектору v = 1, v₂ >, изображенному внизу, есть
— v = (- 1). v = (- 1)1, v₂ > = 1, — v₂ >

Вычитание векторов, такое как u — v вовлекает вычитание соответствующих компонент. Мы покажем это представлением u — v как u + (- v). Если u = 1, u₂ > и v = 1, v₂ >, тогда
u — v = u + (- v) = 1, u₂ > + 1, — v₂ > = 1 + (- v₁), u₂ + (- v₂) > = 1 — v₁, u₂ — v₂ >

Мы можем проиллюстрировать вычитание векторов с помощью параллелограмма , как мы это делали для сложения векторов.

Вычитание векторов

Если u = 1, u₂ > и v = 1, v₂ >, тогда
u — v = 1 — v₁, u₂ — v₂ >.

Интересно сравнить суммы двух векторов с разницей тех же двух векторов в одном параллелограмме. Векторы u + v и u — v есть диагоналями параллелограмма.

Пример 3 Сделайте следующие вычисления, где u = и v = .
a) u + v
b) u — 6v
c)3u + 4v
d)|5v — 2u|

Решение
a) u + v = + = = ;
b)u — 6v = — 6. = — = ;
c) 3u + 4v = 3. + 4. = + = ;
d) |5v — 2u| = |5. — 2.| = | — | = || = √(- 29)² + 21² = √1282 ≈ 35,8

Прежде чем сформулировать свойства векторного сложения и умножения, мы должны дать определение еще одному специальному вектору — нулевому вектору. Вектор, чья начальная точка совпадает с конечной точкой, называется нулевым вектором, обозначается O, или . Его величина равна 0. В сложении векторов:
v + O = v.          1, v₂ > + = 1, v₂ >
Операции над векторами обладают те же самыми свойствами, что и операции над вещественными числами.

Свойства векторного сложения и умножения

Для всех векторов u, v, и w, и для всех скаляров b и c:
1. u + v = v + u.
2. u + (v + w) = (u + v) + w.
3. v + O = v.
4 1.v = v;          0.v = O.
5. v + (- v) = O.
6. b(cv) = (bc)v.
7. (b + c)v = bv + cv.
8. b(u + v) = bu + bv.

Орты

Вектор величиной, или длиной 1 называется орт. Вектор v = есть орт, потому что
|v| = || = √(- 3/5)² + (4/5)² = √9/25 + 16/25 = √25/25 = √1 = 1.

Пример 4 Найдите орт, который имеет то же самое направление, что и вектор w = .

Решение Найдем сначала длину w:
|w| = √(- 3)² + 5² = √34. Таким образом, мы ищем вектор, с длиной 1/√34 от w и с таким же самым направлением, что и вектор w. Этот вектор есть
u = w/√34 = /√34 = .
Вектор u есть орт, потому что
|u| = |w/√34| = = √9/34 + 25/34 = √34/34 = √1 = 1.

Если v есть вектор и v ≠ O, тогда
(1/|v|)• v,          or          v/|v|,
есть орт в направлении v.

Хотя орты могут иметь любое направление, орты, параллельные осям x и y особенно полезны. Они определяются как
i =          and          j = .

Любой вектор может быть выражен как линейная комбинация орта i и j. Например, пусть v = 1, v₂ >. Tогда
v = 1, v₂ > = 1, 0 > + 2 > = v₁ + v₂ = v₁i + v₂j.

Пример 5 Выразите вектор r = как линейную комбинацию i и j.

Решение
r = = 2i + (- 6)j = 2i — 6j.

Пример 6 Запишите вектор q = — i + 7j в компонентной форме.

Решениеq = — i + 7j = -1i + 7j =

Векторные операции могут быть также выполнены, когда векторы записаны как линейные i и j.

Пример 7 Если a = 5i — 2j и b = -i + 8j, найдите 3a — b.

Решение
3a — b = 3(5i — 2j) — (- i + 8j) = 15i — 6j + i — 8j = 16i — 14j.

Углы обзора

Конечная точка P орты в стандартной позиции есть точкой на единичной окружности, определенной (cosθ, sinθ). Таким образом, орт может быть выражен в компонентной форме,
u = ,
или как линейная комбинация орт i и j,
u = (cosθ)i + (sinθ)j,
где компоненты u есть функциями угла обзора θ измеряемого против часовой стрелки от оси x к этому вектору. Так как θ изменяется от 0 до 2π, точка P отслеживает круг x² + y² = 1. Это охватывает все возможные направления ортов и тогда уравнение u = (cosθ)i + (sinθ)j описывает каждый возможный орт на плоскости.

Пример 8 Вычислите и сделайте эскиз орта u = (cosθ)i + (sinθ)j для θ = 2π/3. Изобразите единичную окружность на эскизе.

Решение
u = (cos(2π/3))i + (sin(2π/3))j = (- 1/2)i + (√3/2)j

Пусть v = 1, v₂ > с углом обзора θ. Используя определение функции тангенса, мы можем определить угол обзора их компонент v:

Пример 9 Определите угол обзора θ вектора w = — 4i — 3j.

Решение Мы знаем, что
w = — 4i — 3j = .
Таким образом, имеем
tanθ = (- 3)/(- 4) = 3/4          и θ = tan^{— 1}(3/4).
Так как w находится в третьем квадранте, мы знаем, что θ есть углом третьего квадранта. Соответствующий угол есть
tan^{— 1}(3/4) ≈ 37°,          и          θ ≈ 180° + 37°, или 217°.

Это удобно для работы с прикладными задачами, а в последующих курсах, чтобы иметь способ выразить вектор так, чтобы его величина и направление могли быть легко определены или прочитаны. Пусть v это вектор. Тогда v/|v| есть орт в том же самом направлении, что и v. Таким образом, мы имеем
v/|v| = (cosθ)i + (sinθ)j
v = |v|[(cosθ)i + (sinθ)j]              Умножая на |v|
v = |v|(cosθ)i + |v|(sinθ)j.

Углы между векторами

Когда вектор умножается на скаляр, результатом есть вектор. Когда складываются два вектора, результатом также есть вектор. Таким образом, мы могли бы ожидать, что произведение двух векторов есть вектор, но это не так. Скалярное произведение двух векторов есть действительное число или скаляр. Этот результат полезен в нахождении угла между двумя векторами и в определении, являются ли два вектора перпендикулярными.

Скалярное произведение двух векторов u = 1, u₂ > и v = 1, v₂ > is
u • v = u₁.v₁ + u₂.v₂
(Обратите внимание, что u₁v₁ + u₂v₂ есть скаляром, а не вектором.)

Пример 10Найдите скалярное произведение, когда
u = , v = и w = .
a)u • w
b)w • v

Решение
a) u • w = 2(- 3) + (- 5)1 = — 6 — 5 = — 11;
b) w • v = (- 3)0 + 1(4) = 0 + 4 = 4.

Скалярное произведение может быть использовано для нахождения угла между двумя векторами. Угол между двумя векторами это самый маленький положительный угол, образованный двумя направленными отрезками. Таким образом, θ между u и v это тот же самый угол, что и между v и u, и 0 ≤ θ ≤ π.

Если θ есть углом между двумя ненулевыми векторами u и v, тогда
cosθ = (u • v)/|u||v|.

Пример 11Найдите угол между u = и v = .

Решение Начнем с нахождения u • v, |u|, и |v|:
u • v = 3(- 4) + 7(2) = 2,
|u| = √3² + 7² = √58, and
|v| = √(- 4)² + 2² = √20.
Tогда
cosα = (u • v)/|u||v| = 2/√58.√20
α = cos^{— 1}(2/√58.√20)
α ≈ 86,6°.

Равновесие сил

Когда несколько сил действуют на одну и ту же точку на объекте, их векторная сумма должна быть равна нуля, для того, чтобы был баланс. Когда есть баланс сил, то объект является стационарным или движется по прямой линии, без ускорения. Тот факт, что векторная сумма должна быть равна нулю вывода для получения баланса, и наоборот, позволяет решать нам многие прикладные задачи с участием сил.

Пример 12 Подвесной блок 350- фунтовый блок подвешен с помощью двух кабелей. осталось. В точке А есть три силы, действующие так: W блок тянет вниз, а R и S (два кабеля) тянут вверх и наружу. Найдите нагрузку каждого кабеля.

Решение Нарисуем диаграмму с начальными точками каждого вектора в начале кооординат. Для баланса, сумма векторов должна быть равна О:

R + S + W = О.
Мы можем выразить каждый вектор через его величину и угол обзора :
R = |R|[(cos125°)i + (sin125°)j],
S = |S|[(cos37°)i + (sin37°)j], и
W = |W|[(cos270°)i + (sin270°)j]
= 350(cos270°)i + 350(sin270°)j
= -350j          cos270° = 0; sin270° = — 1.
Заменяя R, S, и W in R + S + W + O, мы имеем
[|R|(cos125°) + |S|(cos37°)]i + [|R|(sin125°) + |S|(sin37°) — 350]j = 0i + 0j.
Это дает нам систему уравнений:
|R|(cos125°) + |S|(cos37°) = 0,
|R|(sin125°) + |S|(sin37°) — 350 = 0.
Решая эту систему, мы получаем
|R| ≈ 280 и |S| ≈ 201.
Таким образом, нагрузка на кабели 280 фунтов и 201 фунт.

Решение задач с векторами

Горячая математика

Мы можем использовать векторы для решения многих задач, связанных с физическими величинами, такими как скорость, скорость, вес, работа и так далее.

Скорость:

Скорость движущегося объекта моделируется вектором, направление которого является направлением движения, а величина — скоростью.

Пример :

Мяч брошен с начальной скоростью 70 футов в секунду, под углом 35 ° с горизонталью. Найдите вертикальную и горизонтальную составляющие скорости.

Позволять в представить скорость и использовать данную информацию, чтобы написать в в форме единичного вектора:

в «=» 70 ( потому что ( 35 ° ) ) я + 70 ( грех ( 35 ° ) ) Дж

Упрощая скаляры, мы получаем:

в ≈ 57,34 я + 40.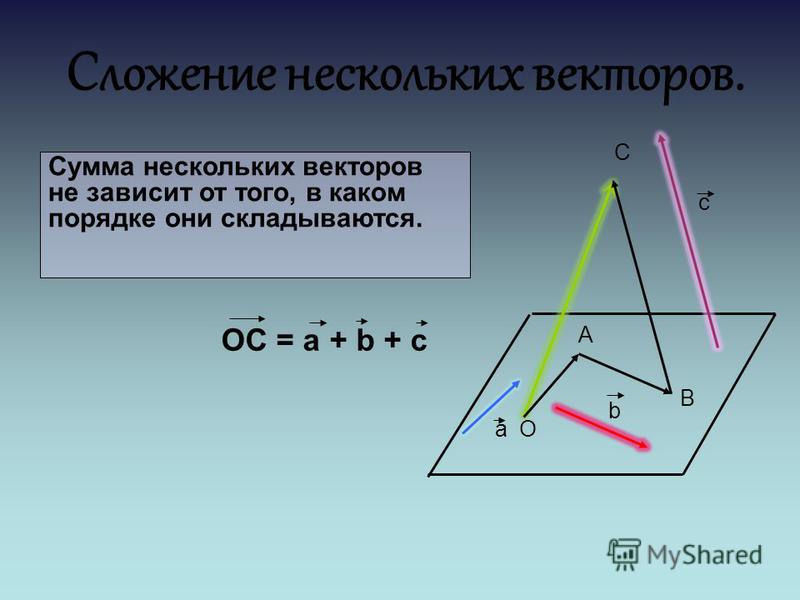 15 Дж

Поскольку скаляры являются горизонтальной и вертикальной компонентами в ,

Следовательно, горизонтальная составляющая 57,34 футов в секунду, а вертикальная составляющая 40.15 футов в секунду.

Сила:

Сила также представлена ​​вектором. Если на объект действуют несколько сил, результирующая сила, испытываемая объектом, представляет собой векторную сумму этих сил.

Пример :

Две силы Ф 1 и Ф 2 с величинами 20 и 30 фунт соответственно действуют на объект в точке п как показано. Найдите результирующие силы, действующие на п .

Сначала мы пишем Ф 1 и Ф 2 в виде компонентов:

в ≈ 57,34 я + 40.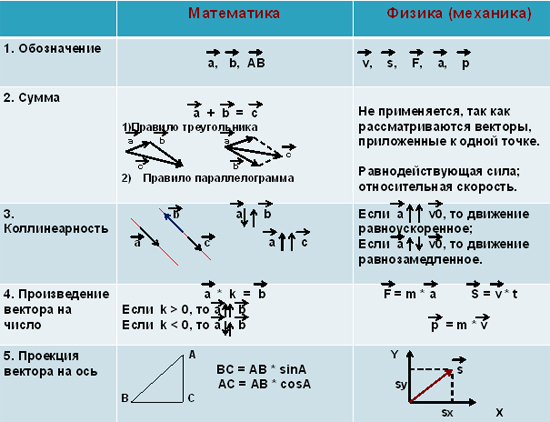 15 Дж

Упрощая скаляры, мы получаем:

Ф 1 «=» ( 20 потому что ( 45 ° ) ) я + ( 20 грех ( 45 ° ) ) Дж «=» 20 ( 2 2 ) я + 20 ( 2 2 ) Дж «=» 10 2 я + 10 2 Дж Ф 2 «=» ( 30 потому что ( 150 ° ) ) я + ( 30 грех ( 150 ° ) ) Дж «=» 30 ( − 3 2 ) я + 30 ( 1 2 ) Дж «=» − 15 3 я + 15 Дж

Итак, результирующая сила Ф является

Ф «=» Ф 1 + Ф 2 «=» ( 10 2 я + 10 2 Дж ) + ( − 15 3 я + 15 Дж ) «=» ( 10 2 − 15 3 ) я + ( 10 2 + 15 ) Дж ≈ − 12 я + 29Дж

Работа:

Работа Вт сделано силой Ф при движении по вектору Д является Вт «=» Ф ⋅ Д .

Пример :

Сила задается вектором Ф «=» 〈 2 , 3 〉 и перемещает объект из точки ( 1 , 3 ) к точке ( 5 , 9) . Найдите проделанную работу.

Сначала мы находим Displacement.

Вектор смещения

Д «=» 〈 5 − 1 , 9 − 3 〉 «=» 〈 4 , 6 〉 .

По формуле совершенная работа равна

Вт «=» Ф ⋅ Д «=» 〈 2 , 3 〉 ⋅ 〈 4 , 6 〉 «=» 26

Если единицей силы являются фунты, а расстояние измеряется в футах, то выполненная работа равна 26 фут-фунт

Объяснение урока: работа, совершаемая силой, выраженная в векторном представлении действуя на тело по вектору смещения с помощью скалярного произведения.

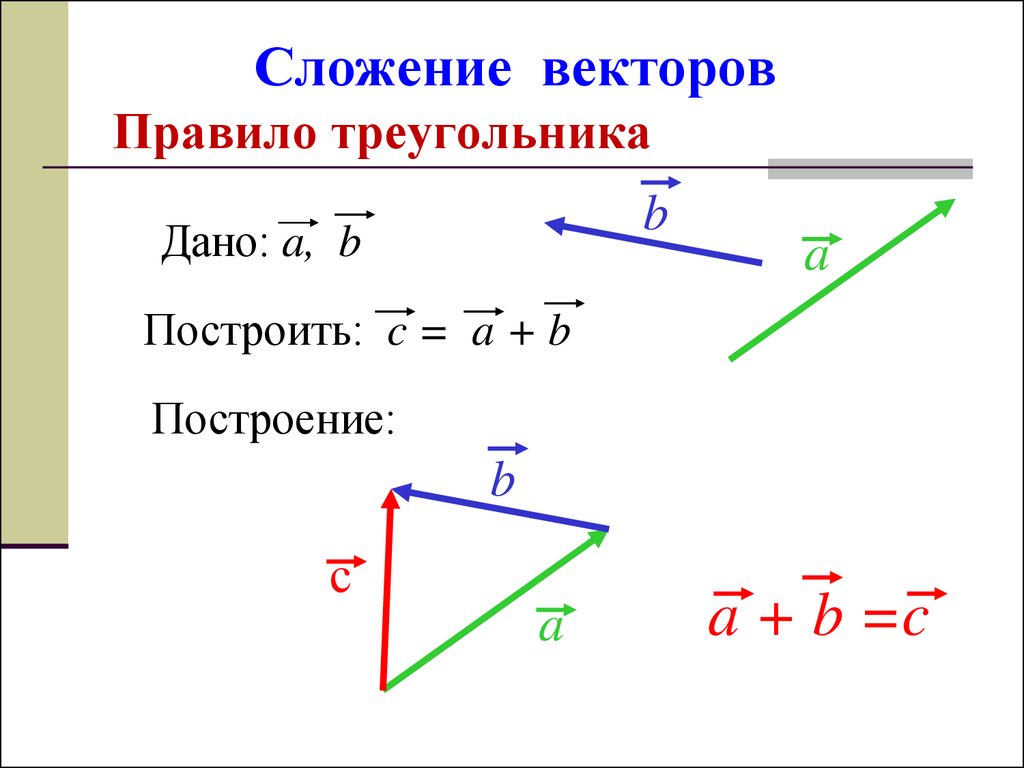
Работу, совершаемую силой над телом, можно определить следующим образом.

Определение: Работа, совершаемая силой над телом

Работа, совершаемая над телом силой, зависит от силы, действующей на тело, и расстояние, на которое тело перемещается в направлении действия этой силы по формуле 𝑊=𝐹⋅𝑑(𝜃), потому что где 𝐹 — величина силы, 𝑑 — величина перемещение тела под действием силы, а 𝜃 – угол между направлениями 𝐹 и 𝑑.

Альтернативным способом представления работы, совершаемой силой над телом, является представление сила и перемещение как векторы, а не как величины векторов.

Произведение двух векторов ⃑𝑎 и ⃑𝑏 может быть скалярным произведением векторов, которое определяется как следует.

Определение: Скалярное произведение двух векторов

Скалярное произведение двух векторов определяется выражением ⃑𝑎⋅⃑𝑏=‖‖⃑𝑎‖‖‖‖⃑𝑏‖‖(𝜃), cos где 𝜃 — угол между ⃑𝑎 и ⃑𝑏. Угол берется против часовой стрелки от от ⃑𝑎 до ⃑𝑏, как показано следующий рисунок.

Работа, совершаемая силой с величиной 𝐹 при перемещении с величина 𝑑 равна ⃑𝐹⋅⃑𝑑⃑𝐹⋅⃑𝑑=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃).cos

Графическое представление ⃑𝐹 и ⃑𝑑 показывает, что произведение величины ⃑𝐹 и величина компонента ⃑𝑑 в направлении ⃑𝐹 есть равно ‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃)cos.

Скалярное произведение двух векторов, выраженных в компонентной форме, может быть определено без речь идет об угле между векторами.

Предположим теперь, что векторы ⃑𝐹 и ⃑𝑑 перпендикулярны, как показано на следующем рисунке.

Произведение определяется как ⃑𝐹⋅⃑𝑑=(4,−3)⋅(3,4)⃑𝐹⋅⃑𝑑=(4×3)+(−3×4)=12−12=0.

Скалярное произведение двух перпендикулярных векторов равно нулю. На тело не действуют никакие силы направление перемещения, поэтому сила не действует на тело.

Давайте рассмотрим пример использования векторной записи для определения работы силы.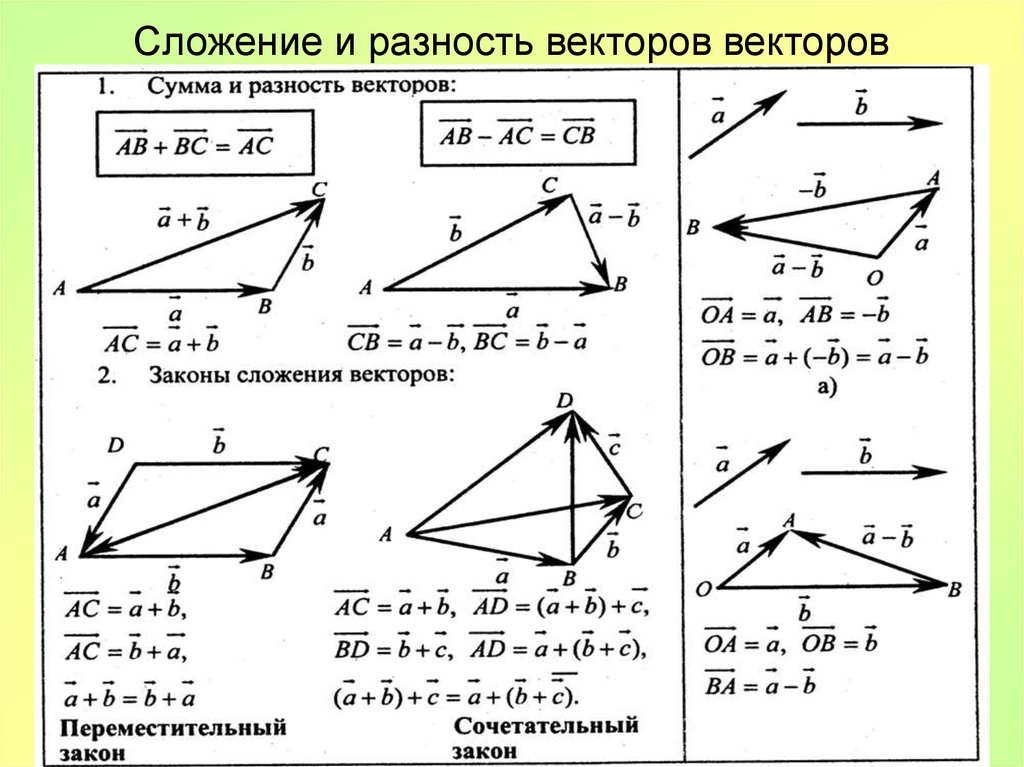

Пример 1. Расчет работы силы, действующей на частицу, где сила и положение даны в виде векторов

Частица движется в плоскости, в которой ⃑𝑖 и ⃑𝑗 — перпендикулярные единичные векторы. Сила ⃑𝐹=9⃑𝑖+⃑𝑗N действует на частицу. Частица движется из начала координат в точку с вектором положения −9⃑𝑖+6⃑𝑗 м. Найдите работу, совершенную силой.

Ответ

Работа силы равна скалярному произведению вектора силы и вектора смещения частицы. Вопрос не дает вектор смещения, однако он дает вектор положения. В вопросе также указано что частица движется в указанное положение от начала координат, поэтому вектор смещения частицы определяется выражением ⃑𝑑=(−9−0)⃑𝑖+(6−0)⃑𝑗,м который равен заданному вектору положения.

Работа силы 𝑊 определяется скалярным произведением векторов что определяется как 𝑊=(9,1)⋅(−9,6)𝑊=(9×−9)+(1×6)=−81+6=−75.

Таким образом, выполненная работа определяется выражением 𝑊=−75.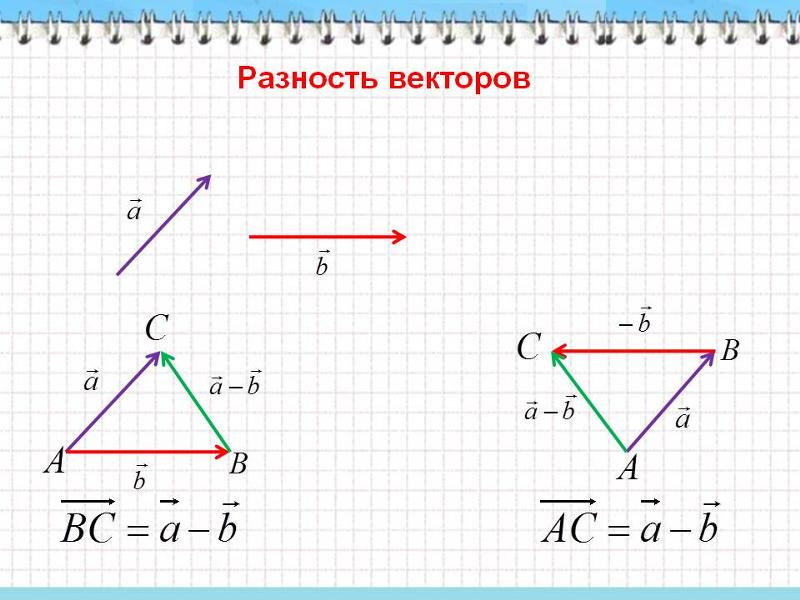 J

Проделанная работа отрицательна. Если энергия частицы сохраняется, то кинетическая энергия частицы должна уменьшаться. Если энергия частицы не сохраняется, вместо этого проделанная работа может увеличить потенциальную энергию частицы.

Теперь давайте рассмотрим пример, когда на тело действуют несколько сил, вызывающих перемещение.

Пример 2. Нахождение работы равнодействующей двух сил, действующих на тело

Тело движется в плоскости, в которой ⃑𝑖 и ⃑𝑗 — перпендикулярные единичные векторы. Две силы ⃑𝐹=9⃑𝑖−2⃑𝑗N и ⃑𝐹=9⃑𝑖−7⃑𝑗N действовать на тело. Частица движется из точки с вектором положения −6⃑𝑖+2⃑𝑗 м к точке 2⃑𝑖+3⃑𝑗 м. Найдите работу равнодействующей сил.

Ответ

На тело действуют две силы. Силы являются векторами, и равнодействующая векторов может определяется суммированием компонент векторов. 𝑥-составляющая результирующей силы определяется выражением ⃑𝐹=9⃑𝑖+9⃑𝑖=18⃑𝑖,R а 𝑦-компонента равнодействующей силы определяется выражением ⃑𝐹=−2⃑𝑗−7⃑𝑗=−9⃑𝑗. R

Следовательно, результирующая сила, действующая на тело, равна ⃑𝐹=18⃑𝑖−9⃑𝑗.RN

Конечный вектор положения тела равен 2⃑𝑖+3⃑𝑗, а вектор начального положения тела равен −6⃑𝑖+2⃑𝑗.

Таким образом, вектор смещения из начального положения в конечное положение равен ⃑𝑑=2⃑𝑖+3⃑𝑗−−6⃑𝑖+2⃑𝑗⃑𝑑=2−(−6)⃑𝑖+(3−2)⃑𝑗=8⃑𝑖+⃑𝑗.mm

.mm

.mm , у нас есть это 𝑊=⃑𝐹⋅⃑𝑑,R что дает нам 𝑊=(18,−9)⋅(8,1)𝑊=(18×8)+(−9×1)=144−9=135.J

Теперь рассмотрим пример, в котором ни одна из компонент ни вектор силы, ни компоненты вектора смещения не заданы напрямую.

Пример 3. Использование векторов для нахождения работы силы с направлением и величиной, заданными отдельно

Частица переместилась из точки 𝐴(7,−3) в точку 𝐵(−9,2) по прямой под действием силы ⃑𝐹 величины 8√10 Н действует в том же направлении, что и вектор ⃑𝑐=−3⃑𝑖−⃑𝑗.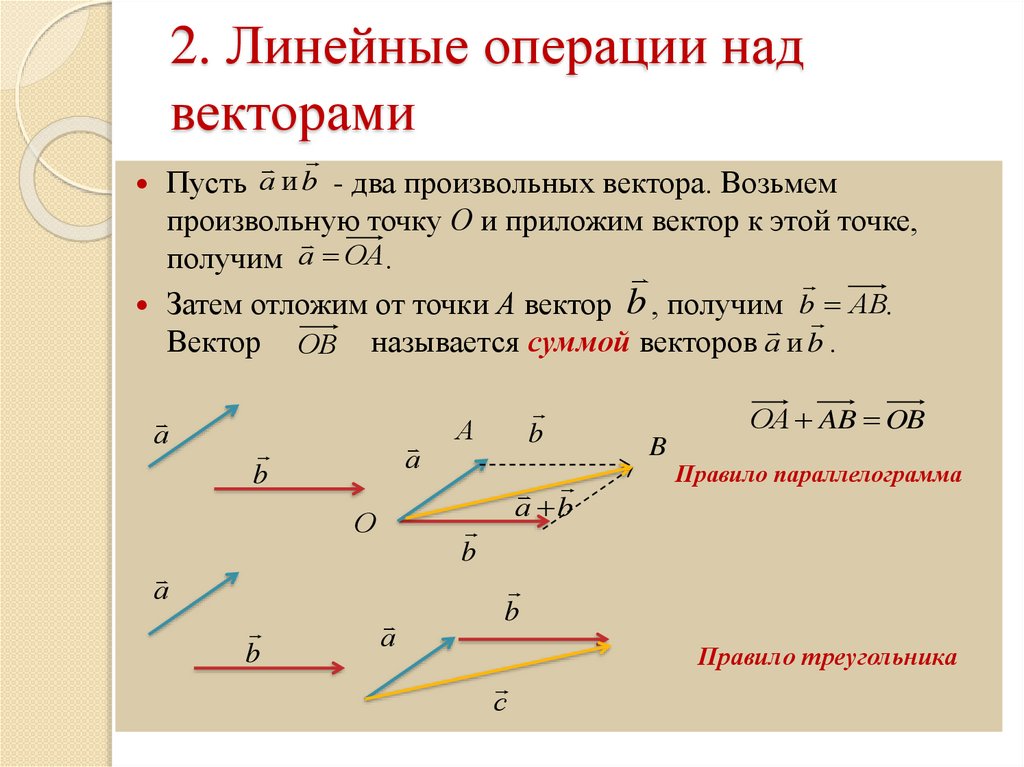 Рассчитать работу совершается силой, учитывая, что величина смещения измеряется в метрах.

Ответ

Мы можем назвать вектор смещения 𝐴𝐵, ⃑𝑑. Вектор ⃑𝑑 показан с вектором ⃑𝑐 на следующем рисунке.

Вектор ⃑𝑑 задается ⃑𝑑=(−9−7)⃑𝑖+(2−(−3))⃑𝑗=−16⃑𝑖+5⃑𝑗.m

Скалярное произведение ⃑𝑑 и ⃑𝑐 не равно скалярному произведению ⃑𝑑 и ⃑𝐹.

Величина ⃑𝐹 дана, но использовать ⃑𝐹 через точку расчет продукта, необходимо определить компоненты ⃑𝑖 и ⃑𝑗 ⃑𝐹.

Поскольку ⃑𝐹 действует по линии ⃑𝑐, ⃑𝑖 компонент ⃑𝐹 должна иметь величину, которая в три раза больше величины ⃑𝑗 компонента ⃑𝐹. Эти отношения можно выразить как 𝐹=3𝐹.

𝐹 и 𝐹 две стороны прямоугольного треугольника с гипотенузой длиной 8√10. Поэтому это в случае, когда 

И снова, так как 𝐹=3𝐹,𝐹=24.

Зная компоненты ⃑𝐹, можно выразить ⃑𝐹 как ⃑𝐹=−24⃑𝑖−8⃑𝑗.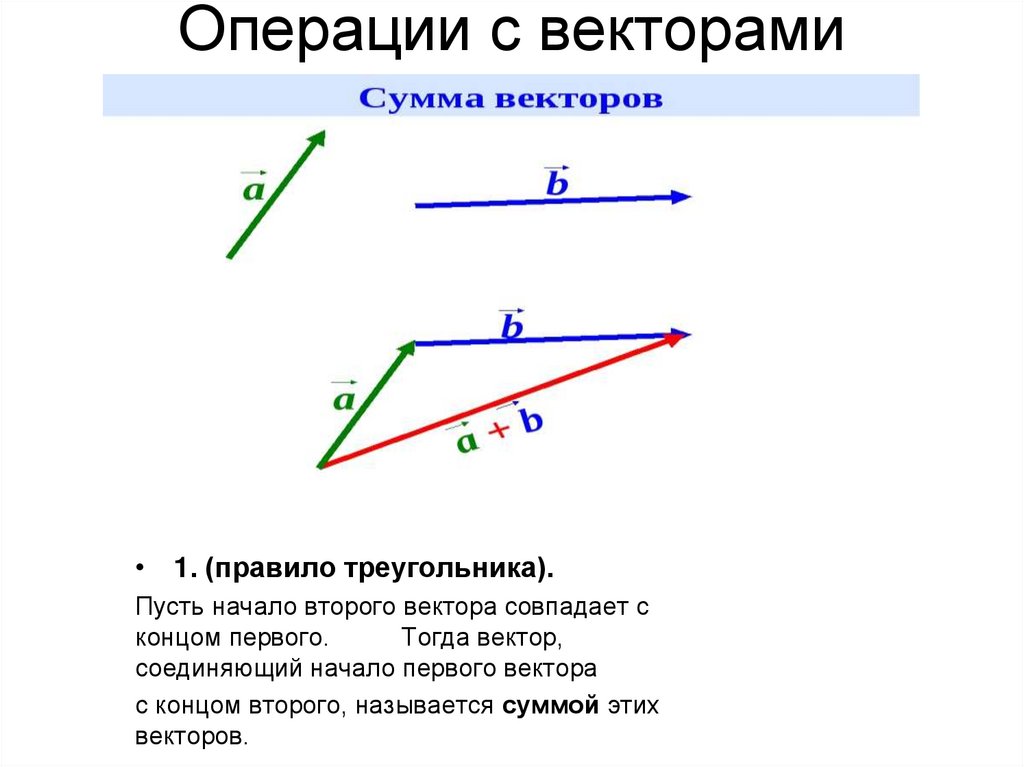 N

Таким образом, выполненная работа 𝑊 𝑊=(−24,−8)⋅(−16,5)𝑊=(−24×−16)+(−8×5)=384−40=344.J

Теперь давайте рассмотрим другой пример, где ни компоненты вектора силы, ни компоненты вектора смещения не заданы напрямую.

Пример 4. Нахождение работы векторной силы, действующей на тело, движущееся между двумя точками

Частица переместилась из точки 𝐴(−2,−2) в точку 𝐵(6,10) по прямой под действием сила ⃑𝐹=𝑘⃑𝑖−6⃑𝑗 действующий в направлении, противоположном перемещению 𝐴𝐵. Найдите работу силы ⃑𝐹.

Ответ

Вектор смещения ⃑𝑑 — это вектор, хвост которого находится в точке ⃑𝐴 и его голова в ⃑𝐵. Вектор ⃑𝑑 задается выражением ⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m

Направление ⃑𝑑 𝐴𝐵. Направление, в котором ⃑𝐹 действует противоположно 𝐴𝐵, поэтому ⃑𝐹 должен действовать вдоль прямой 𝐵𝐴𝐵𝐴=−8⃑𝑖−12⃑𝑗

Δ𝑦Δ𝑥=−12−8=32.

Чтобы ⃑𝐹 имел то же направление, что и 𝐵𝐴, доля 𝑦-компоненты над его 𝑥-компонента должна быть равна 𝐵𝐴.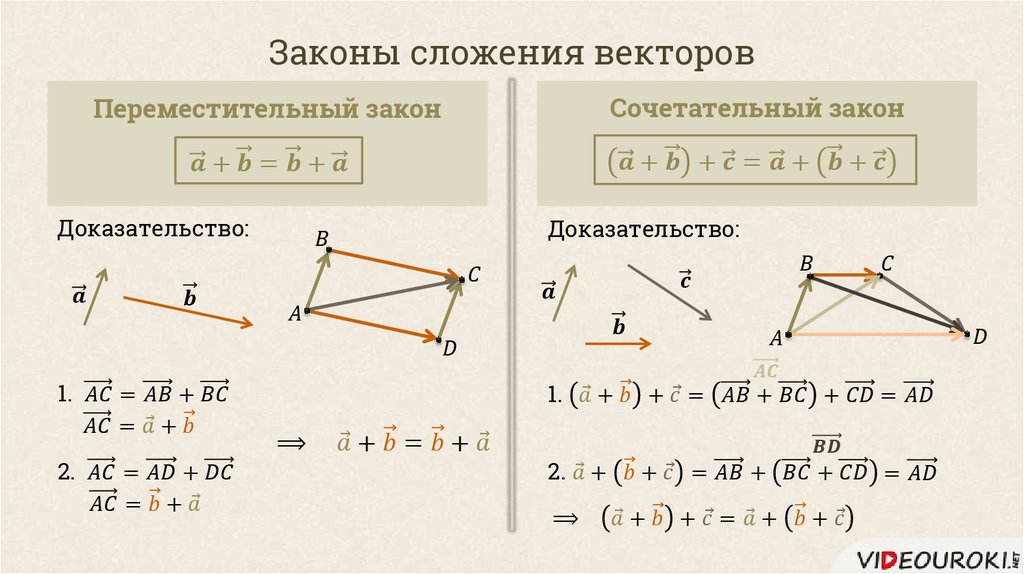 Следовательно, мы имеем это Δ𝑦Δ𝑥=−6𝑘=32.

Перестановка, чтобы сделать 𝑘 предмет уравнения дает 3𝑘=−6×2𝑘=−4.

Теперь мы можем выразить ⃑𝐹 как ⃑𝐹=−4⃑𝑖−6⃑𝑗.N

Таким образом, выполненная работа 𝑊 равна 𝑊=(−4,−6)⋅(8,12)𝑊=(−4×8)+(−6×12)=−32−72=−104.J

Неудивительно, что проделанная работа отрицательна, поскольку сила действует в направлении, противоположном перемещению.

Когда энергия частицы, на которую действует сила, сохраняется, путь, который проходит частица, чтобы сместить ее, когда на нее действует сила, не влияет на работу, совершаемую этой силой над частицей.

Теперь рассмотрим пример, в котором рассматривается работа, совершаемая силой за интервал времени.

Пример 5. Определение работы силы при задании смещения во времени

Частица движется в плоскости, в которой ⃑𝑖 и ⃑𝑗 — перпендикулярные единичные векторы. Его водоизмещение от источника в момент времени 𝑡 секунд определяется выражением ⃑𝑟=2𝑡+7⃑𝑖+(𝑡+7)⃑𝑗m и на него действует силой ⃑𝐹=6⃑𝑖+3⃑𝑗Н.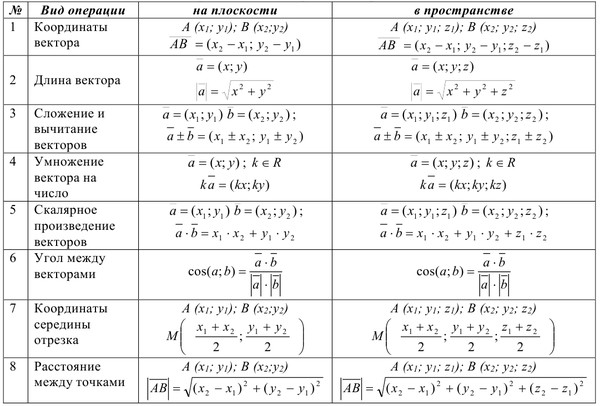 Какую работу совершает сила между 𝑡=2с и 𝑡=3s?

Ответ

Включение в этот пример не требует его решения способом, который сильно отличается от предыдущих примеров, так как скалярные произведения векторов используются таким же образом. Единственная новая особенность, обнаруженная в этом примере, заключается в том, что мы должны найти перемещения, которые соответствуют двум разным временам.

Смещение частицы при 𝑡=3 с и 𝑡=2с должны быть определены. Это делается путем замены 3 и 2 как значения 𝑡, чтобы дать ⃑𝑑 и ⃑𝑑, соответственно, что дает нам ⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм

Смещение частицы между 𝑡=3 с и 𝑡=2s равно ⃑𝑑 минус ⃑𝑑, заданный ⃑𝑑−⃑𝑑=Δ𝑑=25⃑𝑖+10⃑𝑗−15⃑𝑖+9⃑𝑗=10⃑𝑖+⃑𝑗.m

Скалярное произведение ⃐ и Δ𝑑 дает нам выполненную работу, 𝑊, между 𝑡=3s и 𝑡=2с.