Вектор построить онлайн: Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Онлайн калькуляторы векторов

Данный раздел содержит калькуляторы, позволяющие выполнять все основные действия над векторами. В частности, с помощью данных калькуляторов можно вычислять скалярное, векторное и смешанное произведения векторов, раскладывать вектора по базису, проверять их ортогональность, компланарность и др. Всего представлено 19 калькуляторов и для каждого предусмотрено подробное решение соответствующей задачи.

Сложение векторов Калькулятор позволяет складывать вектора, заданные в координатной форме.

Разность векторов Калькулятор позволяет вычитать вектора, заданные в координатной форме.

Умножение вектора на скаляр Калькулятор находит произведение вектора на скаляр.

Скалярное произведение векторов Калькулятор позволяет найти скалярное произведение двух векторов.

Векторное произведение векторов Калькулятор позволяет найти векторное произведение двух векторов.

Смешанное произведение векторов

Калькулятор находит смешанное произведение трех векторов.

Модуль (длина) вектора Калькулятор находит модуль (длину) вектора с описанием подробного решения на русском языке.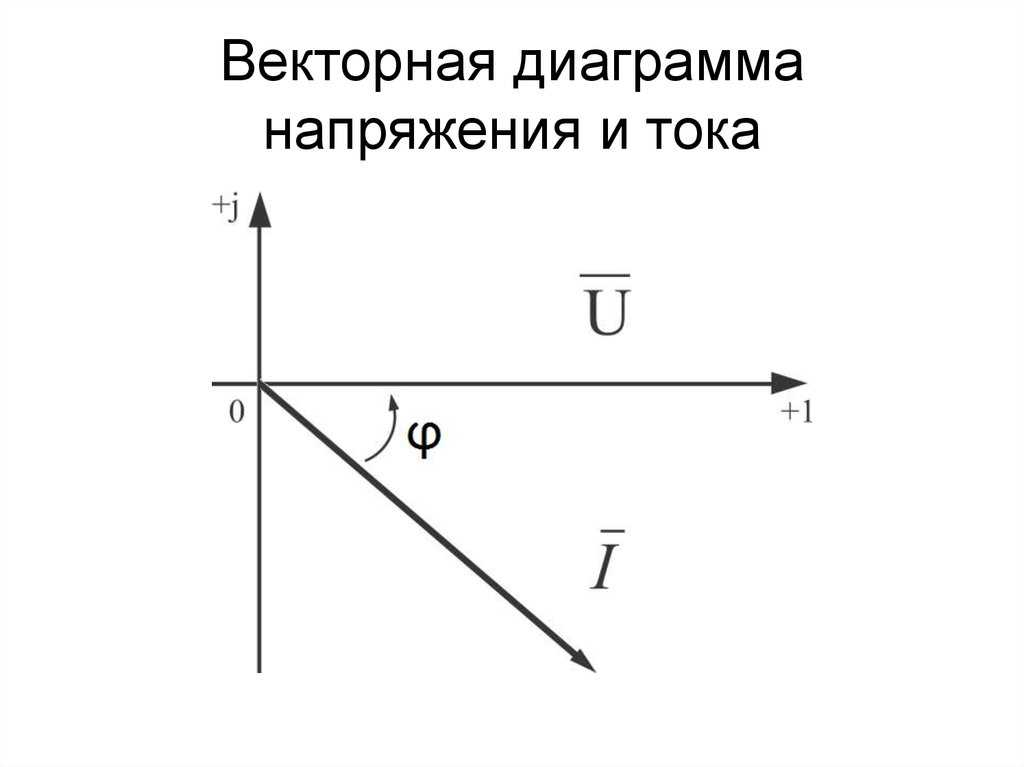

Угол между векторами Калькулятор позволяет найти угол между векторами. Подробное решение также имеется.

Направляющие косинусы вектора Калькулятор позволяет найти направляющие косинусы вектора с подробным решением на русском языке.

Проекция вектора Калькулятор вычисляет проекцию вектора на ось или на другой вектор.

Площадь треугольника, построенного на векторах Калькулятор вычисляет площадь треугольника, построенного на векторах с описанием подробного решения на русском языке.

Площадь параллелограмма, построенного на векторах Калькулятор позволяет вычислить площадь параллелограмма, построенного на векторах с описанием подробного решения на русском языке.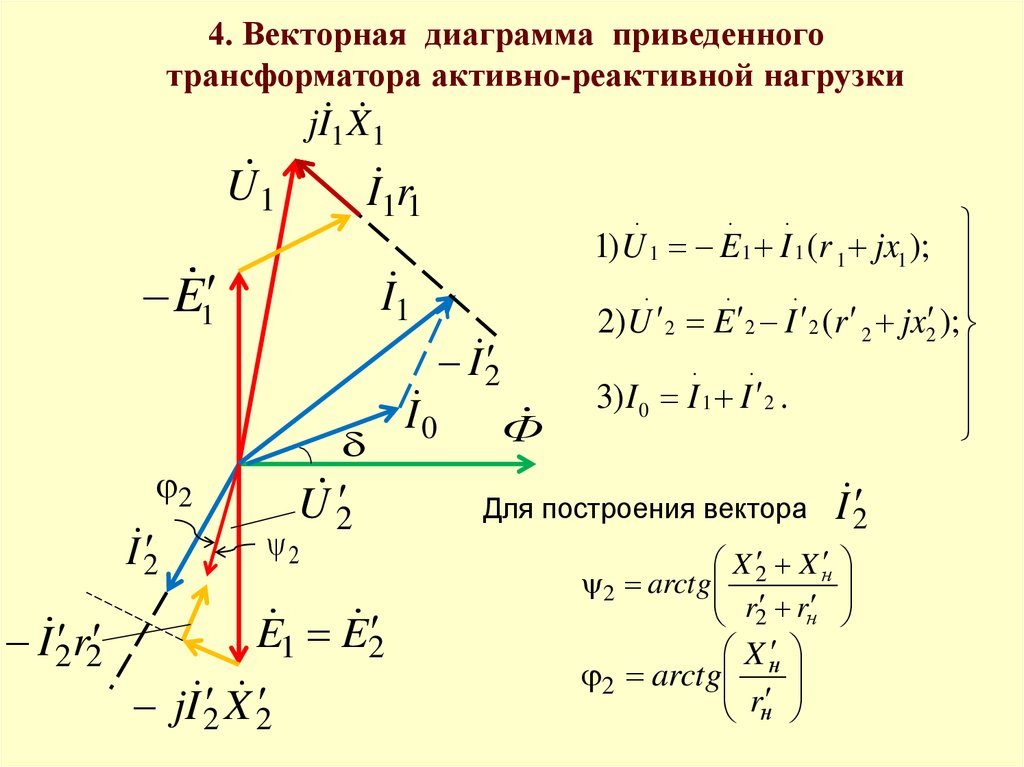

Объём параллелепипеда, построенного на векторах Калькулятор позволяет найти объём параллелепипеда, который построен на трёх векторах.

Объём треугольной пирамиды (тетраэдра), построенного на векторах Калькулятор находит объём тетраэдра, построенного на трёх векторах.

Проверить ортогональность векторов Калькулятор позволяет проверить ортогональность векторов с описанием подробного решения на русском языке.

Проверить коллинеарность векторов Калькулятор позволяет проверить коллинеарность двух векторов.

Проверить компланарность векторов Калькулятор предназначен для проверки компланарности трёх векторов.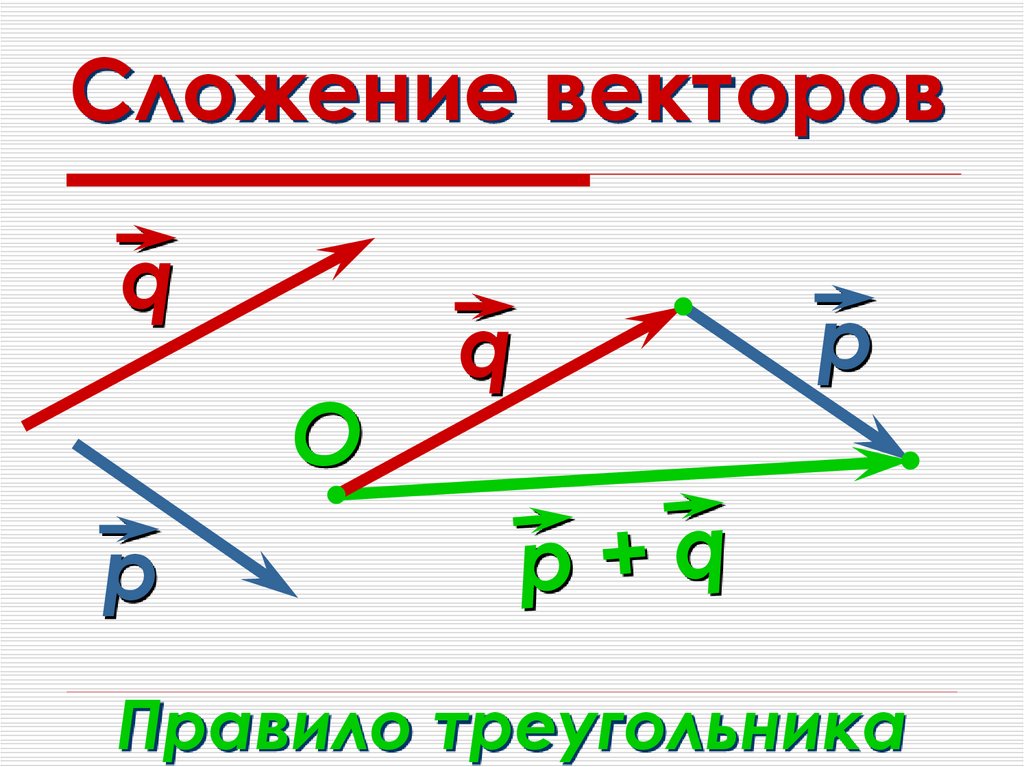

Проверить образует ли система векторов базис Калькулятор позволяет проверить образует ли система векторов базис.

Разложить вектор по базису

Калькулятор позволяет разложить вектор по базису с описанием подробного решения на русском языке.

---

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B.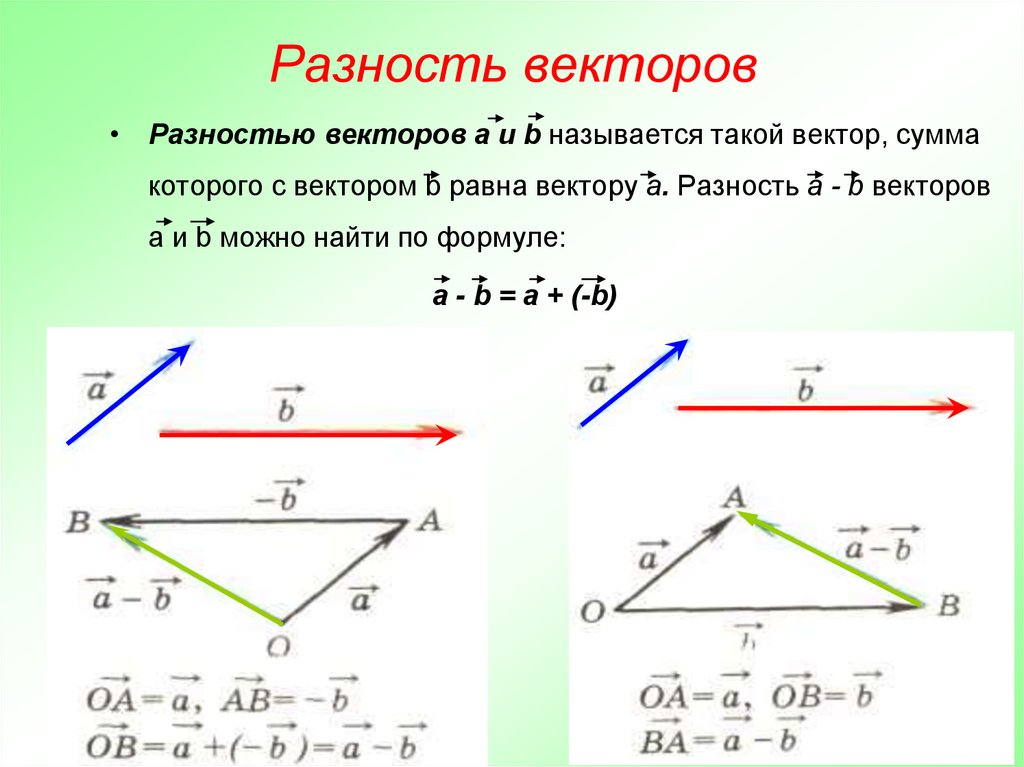 Находится как корень квадратный из суммы квадратов координат вектора:

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

Разность векторов:

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1.  В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁.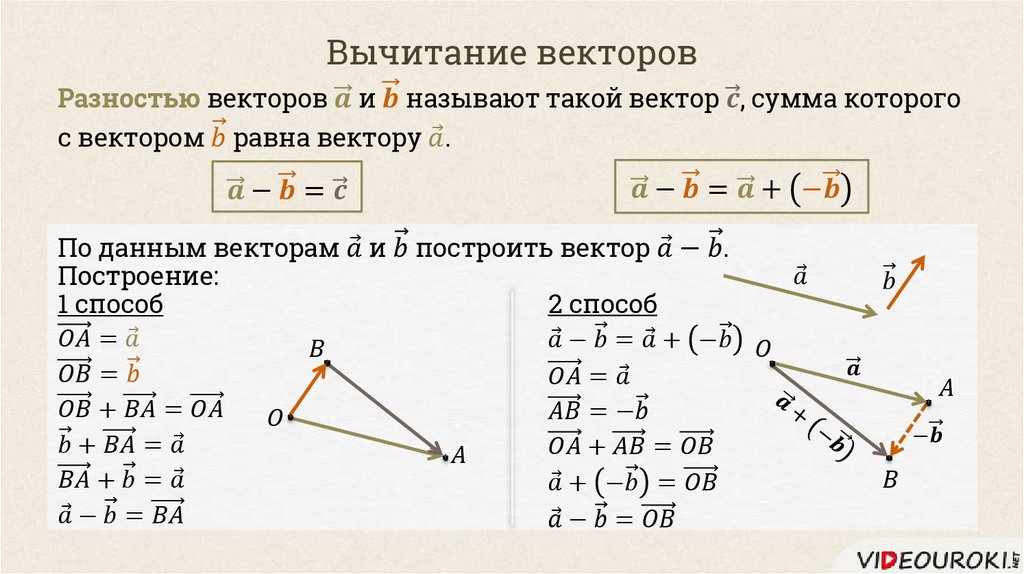 Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2.  В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и :

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми.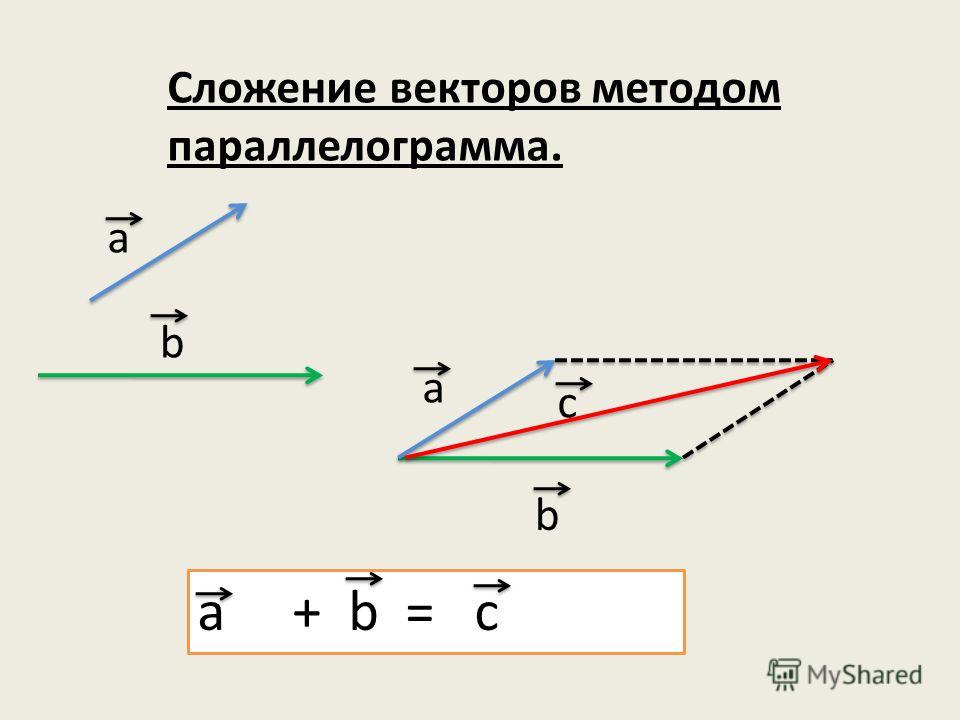 А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.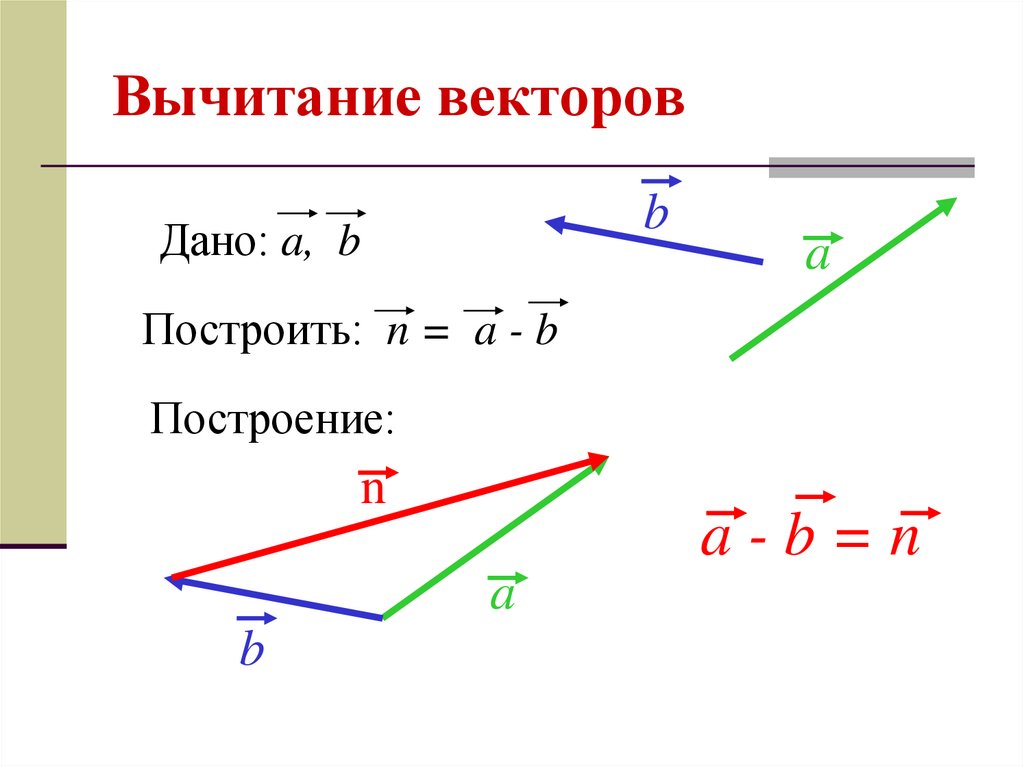

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

.

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

;

.

Выразим C и B через A и подставим в третье уравнение:

.

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Упростим систему:

.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор  или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

  

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Легкий, сверхбыстрый инструмент для построения конвейеров наблюдаемости

Vector | Легкий, сверхбыстрый инструмент для построения пайплайнов наблюдаемости. Версия Vector 0.26.0

Легкий, сверхбыстрый инструмент для создания конвейеров наблюдаемости

Быстрый старт

Язык векторного переназначения

Компоненты

---

Сбор, преобразование и маршрутизация всех простых инструментов и метрик с одним .

---

Сверхбыстрый и надежный

Построенный на Rust, Vector невероятно быстр, эффективно использует память и предназначен для обработки самых ресурсоемких рабочих нагрузок.

От начала до конца

Vector стремится быть единственным инструментом, который вам нужен для получения данных о наблюдаемости от A до B, развертывая его в качестве демона, вспомогательной машины или агрегатора.

Унифицированный

Vector поддерживает журналы и метрики, что упрощает сбор и обработку всех ваших данных для наблюдения.

Нейтральный поставщик

Компания Vector не отдает предпочтение платформам каких-либо конкретных поставщиков и поддерживает честную и открытую экосистему с учетом ваших интересов. Блокировка бесплатно и будущее.

Программируемые преобразования

Гибко настраиваемые преобразования Vector предоставляют вам всю мощь программируемых сред выполнения. Обрабатывайте сложные варианты использования без ограничений.

Четкие гарантии

Гарантии имеют значение, и компания Vector четко указывает, какие гарантии она предоставляет, помогая вам сделать правильный выбор для вашего варианта использования.

---

Разверните Vector в различных ролях в соответствии с вашим вариантом использования.
Перемещение данных из точки А в точку Б без объединения инструментов.

Узнайте больше о топологии распределенного развертывания для Vector

Узнайте больше о топологии централизованного развертывания для Vector

Узнайте больше о топологии потокового развертывания для Vector

---

Простой компонуемый формат позволяет создавать гибкие конвейеры

/etc/vector/vector.toml

Примеры конфигурации представлены в формате TOML, но Vector также поддерживает YAML и JSON

---

Упакован в виде одного двоичного файла. Никаких зависимостей, времени выполнения и безопасности памяти.

Одиночный двоичный двоичный язык

x86_64, ARM64/V7

NO Runtime

Memory Safe

Установка с одной линейкой:

• для Humans
• для машин

 Curl -proto '= HTTP'---------HTTTS----------HTTP '-------http'-----https '----http'-----http '----http'---htttps '

  
  
.  tlsv1.2 -sSf https://sh.vector.dev | bash 
 curl --proto '=https' --tlsv1.2 -sSf https://sh.vector.dev | bash -s -- -y 
 Или выберите предпочтительный метод:
 Платформы
 Менеджеры пакетов
 Операционные системы
 Руководство
 Широкий выбор источников, преобразований и приемников
 
 40
источники
 AMQP
Метрики Apache
Показатели AWS ECS
AWS Kinesis Firehose
АВС S3
АМС SQS
Агент Datadog
Демонстрационные журналы
днстап
Журналы Docker
 13
преобразовывает
 Remap с VRL
Совокупность
Метаданные AWS EC2
Дедупликация
Фильтр
Войти в метрику
Луа
Метрика для регистрации
Уменьшать
Маршрут
 50
раковины
 AMQP
Апекс
Журналы AWS Cloudwatch
Показатели AWS Cloudwatch
Журналы AWS Kinesis Data Firehose
Журналы AWS Kinesis Streams
АВС S3
АМС SQS
Аксиома
Хранилище BLOB-объектов Azure
 7. 4k+
Звезды GitHub
 150
Авторы
 30м+
Загрузки
 40
Страны
 Подпишитесь, чтобы получать электронные письма о последнем контенте Vector и новых выпусках
 Благодарим вас за подписку на нашу рассылку обновлений
 Vector Создавайте дизайны, темы, шаблоны и загружаемые графические элементы на Dribbble 
 Посмотреть примеры
 Примеры
 Посмотреть Создайте витрину своей мечты
 Создайте витрину своей мечты
 Всплывающее окно просмотра здания
 Всплывающее окно здания
 Посмотреть построить дом
 Построить дом
 Посмотреть каменную икону pt. XIV (Как создать и масштабировать команду соответствия)
 Каменная икона ч. XIV (Как создать и масштабировать группу соответствия)
 Посмотреть Банк, на котором можно построить!
 Банк, на котором можно построить!
 Просмотр JOGJAHOUSE Architect - Руководство по бренду
 JOGJAHOUSE Architect — Руководство по бренду
 Посмотреть Создать блог
 Создать блог
 Просмотр Мы создаем банк, на который вы можете положиться!
 Мы делаем банк, на котором можно строить!
 Посмотреть Дизайн карьеры!
 Дизайн карьеры!
 Посмотреть, следует ли вам создать мобильное приложение (лотереи)
 Если вам нужно создать мобильное приложение (лотереи)
 Просмотр Build Smart. Стройте с Bauhub.
 Строй умно. Стройте с Bauhub.
 Просмотр совместной работы
 Работа в команде
 Посмотреть в целости и сохранности
 в целости и сохранности
 Посмотреть дизайн логотипа xBuild
 Дизайн логотипа xBuild
 Посмотреть дизайн логотипа Buildart
 Дизайн логотипа Buildart
 Посмотреть иллюстрацию исследования - Обновите свой веб-сайт
 Иллюстрация исследования — Обновите свой веб-сайт
 Посмотреть разработку TDR
 Разработка TDR
 Посмотреть сборку
 Просмотр Build Smart.
No related posts.