Векторные диаграммы онлайн: Векторная диаграмма напряжений и токов онлайн

Содержание

Топографическая диаграмма | Электрикам

Напряжение на выводах цепи переменного тока или на любом из её участков можно выразить комплексным числом – комплексным напряжением и изобразить на комплексной плоскости вектором. Напряжение между двумя точками электрической цепи представляет собой разность потенциалов между этими точками. Следовательно, потенциалы отдельных точек цепи также можно представить комплексами – комплексными потенциалами и изображать соответствующими векторами. Вектор, изображающие комплексный потенциал, начинается в начале координат; его конец обозначают той же буквой (или цифрой), что в точке цепи, потенциал которой изображает вектор. Например, на рисунке 1 построены векторы комплексных потенциалов ϕ_а= 10 + j20 В и ϕ_б= 30 – j15 В и разность векторов или вектор напряжения U_аб = ϕ_а— ϕ_б= 10 + j20 – 30 + j15 = -20 + j35 В.

Напряжение U_абпостроено по правилу вычитания векторов, так что

ϕ_а = ϕ_б + U_абрисунок 1.

Поэтому напряжение U_абизображается вектором, направленным от точки б (второй индекс у напряжения U_аб) к точке а (первый индекс).

Напряжение U_ба = ϕ_б— ϕ_а= 30 – j15 -10 — j20 В = 20 – j35 В. Очевидно, U_ба = — U_аб и изображается вектором, направленным от точки а к точке б (штриховая линия на рисунке 1).

Рисунок 1 — Комплексные потенциалы

Такая векторная диаграмма называется топографической; она удовлетворяет двум условиям:

Каждой точке электрической цепи соответствует определенная точка на векторной диаграмме и
вектор, проведённый из начала координат в какую-либо точку диаграммы изображает комплексный потенциал соответствующей точки цепи.

При построении топографической диаграммы потенциал одной из точек цепи принимают равным нулю и на диаграмме точку нулевого потенциала совмещают с началом координат. На такой диаграмме отрезок, соединяющий любые две точки, также определяет комплексное напряжение между соответствующими точками цепи.

Рисунок 2 а — Неразветвлённая цепь

На рисунке 2, а представлена неразветвлённая цепь.

1) Для построения топографической диаграммы примем, например, потенциал точки д равным нулю, т.е. ϕ_д= 0.

2) Обходим контур в направлении, встречно току, определим потенциалы всех точек цепи. Начальную фазу общего тока примем равной нулю, т. е. I = I, поэтому вектор тока I направлен вдоль положительной полуось действительных величин.

3) Потенциал точки г или ϕ_г выше потенциала ϕ_д на падение напряжения в сопротивлении R2, т.е. на R2*I или ϕ_г = ϕ_д R2*I = 0 + R2*I = R2*I. Построив вектор R2*I, получим на диаграмме

точку г.

4) Потенциал точки в или ϕ_в больше потенциала ϕ_г,на падение напряжения на индуктивном сопротивлении X_L₂или в комплексной форме на jX_L₂*I. Построив вектор напряжения U_вг = ϕ_в— ϕ_г= jX_L₂*I, начинающийся в точке г и опережающий ток по фазе на 90 градусов (индуктивное сопротивление — вектор направлен вверх), получим

точку в.

5) Потенциал точки б или ϕ_б больше ϕ_в на падение напряжения R1*I. Построив из точки в вектор напряжения U_бв = ϕ_б— ϕ_в= R1*I, параллельный току, находим точку б.

6) Потенциал точки а или ϕ_а больше ϕ_б на падение напряжения на емкости -jXc1*I. Построив из точки б вектор напряжения U_аб = ϕ_а— ϕ_б= -jXc1*I, отстающий по фазе от тока на угол 90 градусов (емкостное сопротивление — вектор напряжения направлен вниз), получим

точку а.

Вектор, соединяющий точки д и а направленный от точки д к точке а, изображает напряжение U_ад на выходах цепи.

Необходимо учесть, что векторы напряжений на топографической диаграмме имеют по отношению к точкам цепи направления, обратные положительным направлениям напряжений относительно тех же точек цепи.

Например, напряжение U_вд = ϕ_в— ϕ_д , направленное на схеме от точки в к точке д (по направлению тока), на топографической диаграмме имеет противоположное направление относительно этих точек, что согласуется с правилом вычитания векторов, согласно которому вектор разности всегда направлен в одну сторону с уменьшаемым вектором.

25.02.2017

ТОЭ,Переменный ток,Топографическая диаграмма

Расчет цепей синусоидального тока

Векторные диаграммы. Построение векторных диаграмм

При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.

Обоснование векторной диаграммы

Предположим, что ток задан уравнением

i = I_msin(ωt +Ψ)

Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор I_m, длина которого в определённом масштабе M_i выражает амплитуду тока I_m:

I_m = I_m/M_i

Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).

Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i₀ = I_msinΨ.

Представим себе, что вектор I_m вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,

Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора I_m на вертикальную ось в этот момент времени.

Следующая статья сложение и вычитания векторов векторной диаграммы.

Например, для t = t1

i₁ = I_msin(ωt₁ +Ψ)

в общем случае

i = I_msin(ωt +Ψ)

Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.

Построение векторной диаграммы

Вращая вектор I_m‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.

При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.

В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.

Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.

Например, напряжение и ток в электрической цепи выражаются уравнениями:

u = 125 sin(ωt + 30°)

i = 12 sin(ωt — 20°).

Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока

M_u = 50 В/см; M_i = 4 А/см;

то

U_m = U_m/M_u = 125/50 = 2,5 см; I_m = I_m = i_m/M_i = 12/4 = 3 см.

Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.

Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.

Сложение и вычитание векторов

Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:

I_m = I_m1 + I_m2

Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель

но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.

Вектор I_m, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).

Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.

12.02.2014

ТОЭ,Переменный ток,Метод векторных диаграмм

Цепи синусоидального тока

Экспорт диаграмм в виде изображений SVG

Изображения SVG загружаются быстро, особенно по сравнению с загрузкой изображений диаграмм в других форматах. Вы можете встроить изображение SVG, экспортированное из диаграмм.net, в веб-сайт, документ или даже сайт WordPress, если вы установили плагин, поддерживающий загрузку файлов SVG.

SVG или масштабируемая векторная графика — это формат файла, который определяет векторную графику с использованием языка разметки XML, аналогичный формату файла .drawio , используемому для диаграмм, созданных в диаграммах.net. Изображения SVG можно увеличивать или уменьшать без потери качества или появления пикселизации, в отличие от 9.0005 .JPG , .GIF и .PNG форматы изображений. Поскольку SVG использует XML-код, в эти файлы может быть встроен код, не являющийся изображением, в результате чего они не поддерживаются на определенных платформах без сторонних подключаемых модулей.

Чтобы убедиться, что ваша диаграмма SVG отображается правильно при ее встраивании в онлайн-платформу, которая не поддерживает посторонние объекты в файлах SVG (например, WordPress), отключите Форматирование текста и Перенос слов для всех текстовых элементов диаграммы.

Подготовьте диаграмму к экспорту

Щелкните правой кнопкой мыши на пустом месте холста для рисования и выберите Выбрать все в контекстном меню, чтобы выбрать все на диаграмме (или нажмите Ctrl+A в Windows, Cmd+A в MacOS).
На вкладке Текст панели форматирования справа убедитесь, что флажок Форматированный текст снят.
Затем выберите все вершины на диаграмме — щелкните правой кнопкой мыши и выберите 9.0015 Выберите вершины (или нажмите Ctrl+Shift+I в Windows, Cmd+Shift+I в MacOS).
Снова на вкладке Текст панели форматирования убедитесь, что флажок Word Wrap снят.

Экспорт диаграммы в SVG

Теперь ваша диаграмма готова к экспорту в изображение SVG.

Щелкните Файл > Экспортировать как > SVG .
Диалоговое окно с рядом параметров позволяет настроить способ сохранения диаграммы в изображение SVG:
- Изменение масштаба Масштаб в процентах.
- Используйте прозрачный фон вместо белого фона по умолчанию.
- Если вы выбрали часть диаграммы перед ее экспортом в формате SVG, вы сможете ограничить то, что будет сохранено на диаграмме, как Только выделение и Обрезать изображение в соответствии с вашим выбором.
- Добавьте на диаграмму Shadow .
- Оставить Включить копию моей диаграммы включен, если вы хотите, чтобы другие могли беспрепятственно импортировать SVG обратно в диаграмму.net.
- Выберите способ вывода форматированных текстовых меток для более старых программ просмотра SVG, которые не поддерживают SVG 1.1 — см. примечание ниже.
- Выберите, как будут вести себя ссылки , изменив настройку в списке.
Когда вы установите нужные параметры, нажмите Экспорт и выберите место, в котором вы хотите сохранить файл SVG.

Теперь вы можете добавить версию диаграммы в формате SVG на свою веб-страницу или в запись блога, как обычный файл изображения.

Примечание: SVG 1.1 и форматированные текстовые метки

диаграммы.net и приложения draw.io экспортируют по умолчанию SVG 1.1. У некоторых старых зрителей возникают проблемы, когда текст содержит различную информацию о форматировании.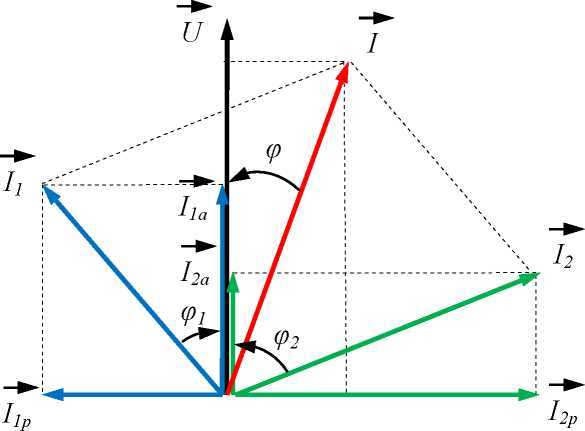

Обычно в необработанные данные SVG встроено предупреждение, которое отображается только в том случае, если ваше средство просмотра SVG не поддерживает SVG 1.1. При экспорте с использованием шагов, описанных выше, вы можете выбрать, какие Настройки текста для использования.

Подробнее о параметрах Text Settings для экспорта SVG см. в нашей последней публикации.

Следуйте за нами на GitHub, Twitter, Facebook.

Значки архитектуры AWS

Официальный набор значков AWS для создания диаграмм архитектуры

Загрузить набор инструментов для PowerPoint

Схемы архитектуры

— отличный способ рассказать о своем проекте, развертывании и топологии. На этой странице вы найдете официальную коллекцию значков архитектуры AWS (ранее — «Простые значки»), которые содержат значки продуктов AWS, ресурсы и другие инструменты, помогающие создавать диаграммы.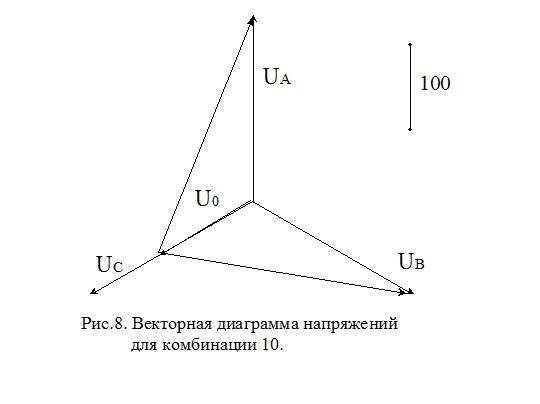

AWS разрешает клиентам и партнерам использовать указанные ниже ресурсы для создания архитектурных диаграмм. Значки сделаны простыми, чтобы вы могли легко включать их в свои диаграммы и помещать в свои технические документы, презентации, таблицы данных, плакаты или любые технические материалы.

Просмотрите схемы эталонной архитектуры AWS и узнайте, как более эффективно и результативно создавать архитектуры на AWS, используя наши экспертные рекомендации и рекомендации в Центре архитектуры AWS.

Архитектурный центр AWS

Наборы инструментов

Начните работу с одним из наших наборов инструментов.

Microsoft PowerPoint
Совместимость с Microsoft PowerPoint 2013 и новее (формат .pptx).

Скачать PPTx для темного фона Загрузить PPTx для светлого фона

Sketch

Загрузить набор инструментов Sketch

Активы

Импортируйте пакет ресурсов в свой любимый инструмент для построения диаграмм. Пакет содержит наборы как для темного, так и для светлого фона в форматах файлов PNG и SVG.

Пакет ресурсов

Инструменты для рисования и построения диаграмм

Сборка с уже существующими библиотеками на сторонних инструментах. Некоторые библиотеки могут содержать устаревшие наборы значков.

Арсентри

Cacoo