Изо 7 класс абстракция: Урок по изобразительному искусству»Абстракция»(7кл.)

Разное 

План-конспект урока «Абстрактное искусство». 7-й класс

Разделы: МХК и ИЗО

Класс: 7

Цель: осмысление абстракции как вида изобразительного искусства.

Задачи:

  • Познакомиться с абстрактным искусством на основе изучения творчества художников К.Малевича, В.Кандинского, П.Пикассо, Э.Мунка, А.Лентулова, М.Эшера, Р.Делоне, М.Ларионова, П.Филонова.
  • Осознать смысл абстрактного искусства как части искусства и культуры;
  • Выполнить индивидуальные абстрактные работы.

Ход урока (этапы):

  • Вводная беседа на тему «Творчество художников-абстракционистов» (5 мин)
  • Рассмотрение репродукций картин художников (5 мин)
  • Просмотр видеофильма «Абстракция» (5 мин)
  • Проведение игры по группам в виде «мозгового штурма » на актуальную тему «Зачем нужно абстрактное искусство?» (30 мин)
  • Выполнение индивидуальных работ в абстрактном стиле на свободные темы (20 мин)
  • Защита самостоятельных работ (15 мин)
  • Обсуждение итоговой выставки работ (самооценка) (5 мин)
  • Проведение самоанализа урока (рефлексия) (5 мин)

Оборудование:

Для учащихся:

  • листы плотной бумаги А4 и А5;
  • простой карандаш;
  • гуашевые краски;
  • жёсткие кисти;
  • палитра;
  • ёмкость для воды;
  • учебник «Изобразительное искусство. Дизайн и архитектура. 7 класс» А.С.Питерских, Г.Е.Гурова, С. 19, 26.

Для учителя:

  • специализированный кабинет;
  • компьютер;
  • интерактивная доска;
  • видеофильм «Абстракция» К.Полянского;
  • наглядный ряд – репродукции картин К.Малевича, В.Кандинского, П.Пикассо, Э.Мунка, А.Лентулова, М.Эшера, Р.Делоне, М.Ларионова, П.Филонова.
  • учебник «Искусство. 8-9 классы» Г.П.Сергеевой, И.Э.Кашековой, Е.Д.Критской, С. 12, 62, 94, 125, 128, 129, 134, 135;
  • рабочая доска;
  • музыкальный ряд – инструментальные композиции Поля Мариа;
  • электронный журнал;
  • запас художественных материалов и инструментов.

Исходя из основной цели занятия – осмысление абстракции как вида изобразительного искусства, одной из задач урока выступает проведение групповой игры на актуальную тему «Зачем нужно абстрактное искусство?» При этом применяется интерактивная педагогическая технология «мозгового штурма».

Это двухэтапная процедура решения задачи: на первом этапе выдвигаются идеи, на втором они конкретизируются и развиваются (по А.Осборну). Человек дает свободу полета своей фантазии. Важнейшей предпосылкой, на которую опирался Осборн, является представление о наличии у каждого человека двух важнейших аспектов работы мозга: творческого разума и аналитического мышления. Их чередование, по мнению Осборна, и составляет основу всех процессов творческой работы.

____________________

Нечаев М.П., Романова Г.А. Игровые педагогические технологии в организации внеурочной деятельности обучающихся.- Москва: «Перспектива», 2014.- 207 с.

Метод включает в себя два основных этапа:

  1. Этап выдвижения (генерации) идей.
  2. Этап анализа выдвинутых идей.

Работа в рамках этих этапов должна выполняться при соблюдении ряда основных правил. На этапе генерации их три:

1. Запрет критики.

2. Запрет обоснований выдвигаемых идей.

3. Поощрение всех выдвигаемых идей, включая нереальные и фантастические.

На этапе анализа основное правило: выявление рациональной основы в каждой анализируемой идее.

Во время «мозгового штурма» создается особое психологическое состояние группы, кода приветствуются шутки, смех, когда думается без особых волевых усилий и принимается во внимание все, что придет в голову, начинает работать подсознание – мощный ресурс творческого мышления.

Цель реализации данной педагогической технологии на представленном уроке – сформировать положительную мотивацию к обучению через активное взаимное общение.

Задачи:

  • пробудить интерес к изучаемому;
  • создать позитивные эмоции в учебном процессе;
  • развить творческие способности учащихся;
  • развить коммуникативные способности;
  • развить логическое мышление.

Воспитательные задачи соответственно возрасту учащихся и поставленным задачам — прогноз достижений на выходе — учащиеся:

  • активно включаются в общий учебный процесс, их интересует предмет изучения;
  • самостоятельно предлагают темы для дальнейшего изучения, планируют его;
  • намечают вектор своего личного развития;
  • учатся творить, не опасаясь отрицательной обратной связи, негативных замечаний учителя или учащихся;
  • учатся создавать вокруг себя атмосферу доброжелательности и открытости;
  • учатся радоваться своим открытиям и делиться своими победами;
  • учатся адекватно и стойко принимать, признавать поражения и находить позитивный способ для дальнейшего их неповторения;
  • учатся не падать духом, верить в себя и свои силы;
  • развивают свои творческие, креативные способности;
  • определяются в своих индивидуальных способностях, умениях и желаниях с целью дальнейшей профессионализации;
  • учатся говорить, монологизировать, высказывать грамотно и связно свои мысли;
  • учатся общаться, строить диалоги, договариваться, находить компромиссы, анализировать, выслушивать чужое мнение, проявлять терпимость и толерантность, учатся слушать, слышать и понимать, рефлексировать;
  • учатся использовать свой эмоциональный интеллект: не бояться проявлять искренние эмоции, чувства.

Организационно-методические задачи

и варианты их решений:

  1. Организовать учащихся на мероприятие – заинтересовать, заинтриговать, дать общую установку на действие, создать доброжелательную атмосферу, позитивный настрой.
    При решении данной задачи рекомендована активность со стороны учителя. Хотя учащиеся и выполняют относительно пассивную роль, но тоже могут проявлять себя. И если это по теме, то это поощряется.
  2. Осуществить наблюдение за правильным ходом мероприятия – корректировать в случае сильного отклонения от общей темы, оказывать помощь в случае существенных затруднений и непредвиденных ситуаций, следить за общей атмосферой в классе, за соблюдением санитарно-гигиенических и этических норм.
    При решении задачи учитель относительно пассивен, является внимательным наблюдателем, находится «на подхвате». Главная роль отводится детям – участникам, экспертам.
  3. Оказать помощь при подведении итогов – корректировка работы экспертной группы, помощь при обращении учащихся в спорных ситуациях и при общем оформлении протоколов.
    Роль учителя и участников-экспертов равнозначна.
  4. Организовать коллективную работу по созданию общей художественной композиции.
    Роль учителя здесь первостепенна, но учителя-советчика.
    Мнения и решения учащихся рассматриваются, учитываются и принимаются в той или иной мере.
  5. Создать условия для рефлексии – эмоционального всплеска, обмена эмоциями и мнениями, планами на будущее.
    Роли руководителя и участников не регламентированы и не строго подведены.

План проведения технологии (этапы) (30 мин):

  1. Сообщение темы, цели, правил адекватного поведения и доброжелательного сотрудничества, критериев оценки высказываний, установление заинтересованности, интриги (3 мин)
  2. Выбор научных экспертов самими учащимися или же при необходимости при подсказке учителя (2 мин)
  3. Разбивка класса на группы по желанию учащихся или же по предложению учителя в случае затруднений (2 мин)
  4. Выбор внутри группы командира для оформления общих протоколов записей-мнений (1 мин)
  5. Изложение исходной ситуации, разъяснения по объекту обсуждения (2 мин)
  6. Ответы на вопросы учащихся, возникшие по ходу общих объяснений (1 мин)
  7. Выполнение коллективных записей внутри групп (10 мин)
  8. «Атака мыслей» — выступления командиров, которые выслушиваются другими участниками без критики и без дополнений (10 мин)
  9. Работа экспертной группы – выявление наиболее многозначных ответов по группам и выделение наиболее интересных мнений (3 мин)
  10. Создание продукта экспертами в виде коллективной работы – абстрактной композиции по теме урока (2 мин).

Содержание интерактивной технологии:

Формы: индивидуальная, групповая, коллективная, совместная с учителем.

Методы: беседа, рассказ, диалоги, монологи, обсуждения, анализ.

Приёмы: мимика, голос, жесты, манера поведения, внешний вид.

Средства: наглядность, раздаточный материал, тематическое окружение.

Конспект реализации технологии «мозгового штурма»:

Сообщение темы — «Зачем нужно абстрактное искусство?»;

Постановка цели —

  • «Понять смысл абстрактных работ художников»;
  • Правил адекватного поведения – быть сдержанным в высказываниях, уважительным;
  • Правил доброжелательного сотрудничества – проявлять терпимость, терпение;
  • Критериев оценки высказываний и мнений – без критики, равные права;
  • Установление заинтересованности, интриги – «Может быть можно обойтись и без этого вида изобразительного искусства? Сейчас выясним» (3 мин)
  • Разбивка класса на группы по желанию учащихся или же по предложению учителя в случае затруднений (2 мин)
  • Выбор научных экспертов – «искусствоведов» по числу групп — самими учащимися или же при необходимости при подсказке учителя (2 мин)
  • Выбор внутри группы командира – «художника» — для оформления общих протоколов записей-мнений (1 мин)
  • Изложение исходной ситуации, разъяснения по объекту обсуждения (2 мин) – каждый предлагает максимальное количество ответов на вопрос по теме «Зачем нужна абстракция?»
  • Ответы на вопросы учащихся, возникшие по ходу общих объяснений – непредсказуемы, требуют ситуативного решения (1 мин)
  • Выполнение коллективных записей внутри групп – «художник» оформляет краткие высказывания-мысли участников группы в виде протокола — «эскиза» На выскaзывания учaстников никто не отвечaет. По их поводу не дискутируют, их не оценивaют, не aнaлизируют, a зaписывают в том виде, в кaком они излaгаются. Поощряются любые, сaмые фaнтaстические идеи. Учaстники могут выскaзанные идеи комбинировaть, видоизменять и улучшaть. Можно стaновиться на позицию другого и рaзвивать его идеи. Нельзя критиковать идеи других. Для стимулировaния мыслительной деятельности можно использовать список контрольных вопросов, которые разбираются последовательно. Можно зaдaвaть вопросы такого рода: «А если сделать нaоборот?», «А если изменить условия?» (10 мин)
  • «Атака мыслей» — выступления командиров, которые выслушиваются другими участниками без критики и без дополнений – каждому выделяется не более 2 мин. Ведущий постоянно поддерживaет «атаку мыслей» репликами, констатирующими или одобряющими зaмечаниями, которые должны стимулировaть нaпряженное и продуктивное мышление (10 мин)
  • Работа экспертной группы – «искусствоведов» – анализ выявление наиболее многозначных ответов по группам и выделение наиболее интересных мнений (3 мин)
  • Создание продукта «искусствоведами» в виде коллективной работы – абстрактной композиции по теме урока – комбинация из абстрактных фигур – «эскизов» (2 мин).

Методическое сопровождение:

Оборудование:

  • Для учащихся: ручка, лист — черновик.
  • Для «художников»: «эскизы» — абстрактные фигуры из цветной светлой бумаги, ручка .
  • Для «искусствоведов» — лист – «протокол» для фиксации результатов.
  • Для учителя: специализированный кабинет, рабочая доска, запас материалов и инструментов (листы бумаги, ножницы, клей, ручки).

Перспективы использования данной технологии:

Интерактивная педагогическая технология «мозгового штурма» актуальна и перспективна в реализации образовательных задач, так как не имеет рамок узкой специализации и может применяться на уроках, внеурочных занятиях и различных мероприятиях абсолютно любой тематики. Может быть частью большого мероприятия или же самостоятельным действом. Если говорить о специфике учебного предмета «Изобразительное искусство», в котором главное место всё-таки, на мой взгляд специалиста-предметника, является практическая составляющая, то я бы рекомендовала её как предварительную или же заключительную часть (в зависимости от поставленных целей) всего мероприятия. Я это объясняю тем, что в изобразительной деятельности умение выражаться на языке художника через выразительные возможности художественных материалов, через создание чувственных образов и яркой передачи эмоций и чувств, через рисунок, цвет и объём – является доминирующим над вербальным общением. Коммуникация же является сопутствующим компонентом, неотъемлемым и немаловажным как в изобразительной деятельности, так и в любой другой творческой активности, позволяющей личности не замыкаться в себе, а уметь контактировать с окружением. А развитие и воспитание личности – основная цель обучения.

Поэтому применение технологии «мозгового штурма» интересно, эффективно и обосновано.

Приложение

Литература

  1. Голубкова О.А. Использование активных методов обучения в учебном процессе: учебно-методическое пособие. //СПб., 1998. С.16.
  2. Гузеев В.В. К формализации дидактики: системный классификатор организационных форм обучения (уроков)// Школьные технологии. 2002. №4., С.49-58.
  3. Ибрагимова О.В., О преподавании предмета «Искусство» (8-9 классы) и «Мировая художественная культура» (10-11 классы)// Наро-Фоминск, МАОУ ДПО «Учебно-методический центр», 2014, С. 41.
  4. Ибрагимова О.В., Корнев Д.В., Переверзева И.А., Сергеева Г.П.. Чернилевская О.Н. Планируемые результаты обучения. Музыка. Изобразительное искусство. Искусство. Мировая художественная культура. Народное творчество// Балашиха, 2015, С. 46.
  5. Нечаев М.П., Романова Г.А. Игровые педагогические технологии в организации внеурочной деятельности обучающихся. – М., «Перспектива», 2014ю С. 24.
  6. Питерских А.С., Гуров Г.Е. Изобразительное искусство. Дизайн и архитектура в жизни человека. Учебник для 7 класса// М., Просвещение. 2014., С. 19,26.
  7. Рапацкая Л.А. Мировая художественная культура. Учебник для 11 класса//М., Владос, 2013. С. 369.
  8. Сергеева Г.П., Кашекова И.Э., Критская Е.Д. Искусство. Учебник для 8-9 классов// М., Просвещение, 2012. , С. 12, 62, 94, 125, 128, 129, 134, 135.
  9. Суворова Н.Г. Интерактивное обучение: новые подходы// Учитель. М., 2000., №1., С. 25-27.
  10. Чернилевская О.Н., О преподавании предмета «Изобразительное искусство» в 5-7 классах в соответствии с ФГОС ООО// Наро-Фоминск, МАОУ ДПО «Учебно-методический центр». 2014. С. 24.

Презентация по изобразительному искусству на тему Абстракция (9 класс) доклад, проект

  • Главная
  • Разное
  • Образование
  • Спорт
  • Естествознание
  • Природоведение
  • Религиоведение
  • Французский язык
  • Черчение
  • Английский язык
  • Астрономия
  • Алгебра
  • Биология
  • География
  • Геометрия
  • Детские презентации
  • Информатика
  • История
  • Литература
  • Математика
  • Музыка
  • МХК
  • Немецкий язык
  • ОБЖ
  • Обществознание
  • Окружающий мир
  • Педагогика
  • Русский язык
  • Технология
  • Физика
  • Философия
  • Химия
  • Шаблоны, фоны, картинки для презентаций
  • Экология
  • Экономика

Презентация на тему Презентация по изобразительному искусству на тему Абстракция (9 класс), предмет презентации: МХК.  Этот материал в формате pptx (PowerPoint) содержит 27 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.

Слайд 1
Текст слайда:

 Абстракция

МБОУ СОШ №72 им. Ю.В. Лукьянчикова

Выполнила учитель ИЗО Торопцева О.И.

Слайд 2
Текст слайда:

 Абстракция – отвлечение. Цель этого искусства – развитие воображения. Каждый, кто созерцает подобное творчество, ищет в нем что-то понятное для себя.

Слайд 3
Текст слайда:

Абстракционизм появился на рубеже XIX – XX в.в, поскольку именно в это время происходило брожение умов. Потребовалось создать нетрадиционный изобразительный язык, который был бы полон глубокого смысла.

Слайд 4
Текст слайда:

Кандинский Василий Васильевич (1866 -1944)
В его картинах часто встречались нетрадиционные сочетания цветов, которые Кандинский объяснял тем, что, по его мнению, каждый цвет живет отдельной, таинственной жизнью. Кандинский часто изображал на своих картинах сюжеты, которые состояли из линий, фигур, ярких цветов, свободных объектов.

Слайд 5
Слайд 6
Текст слайда:

Малевич Казимир Северинович (1878 -1935)
Написав «Черный квадрат» Малевич, долгое время говорил всем, что не может ни есть, ни спать. И сам не понимает, что такое сделал.

Слайд 7
Текст слайда:

Малевич любил изображать четкие геометрические формы в разном пространственном расположении. Линии и квадраты, овалы и круги разнообразных цветов.

Слайд 8
Текст слайда:

В абстракционизма обозначились два основных направления:  геометрическая абстракция, тяготеющая к правильным геометрическим формам и устойчивым состояниям

П.  Мондриан

К. Малевич

Слайд 9
Текст слайда:

Лирическая абстракция – это более свободные формы и динамические процессы  (Кандинский, Купка). 

В. Кандинский

Ф. Купка

Слайд 10
Текст слайда:

В 1920-е годы, во время стремительного развертывания всех авангардных направлений абстрактное искусство включало в свою орбиту кубофутуристов, беспредметников, конструктивистов, супрематистов.

А. Экстер

Л. Попова

Слайд 11
Текст слайда:

А. Родченко

В. Степанова

Слайд 12
Текст слайда:

Следующий этап в развитии русской абстракции начинается в 1970-е годы. Это время знакомства современных художников с творчеством Малевича, с супрематизмом иконструктивизмом, с традициями русского авангарда, его теорией и практикой. Современные авторы открывали для себя труды русских философов и теологов, богословов и мистиков, приобщались к неисчерпаемым интеллектуальным источникам, которые в свою очередь наполняли новым смыслом творчество.

Э. Штейнберг

Слайд 13
Текст слайда:

М. Шварцман

В. Юрлов

Слайд 14
Текст слайда:

1990-е годы подтвердили особенный «русский путь» беспредметного искусства. С точки зрения развития мировой культуры абстракционизм как стилевое направление завершился в 1958 году. Однако в: «Постперестроенном российском обществе только теперь возникла потребность в равноправном общении с абстрактным искусством, появилось желание увидеть не бессмысленные пятна, но красоту пластической игры, её ритмов, проникнуть в их значение. Услышать, наконец, звучание живописных симфоний». Художники получили возможность выражения в формах не только классических — супрематизма или абстрактного экспрессионизма, но лирической и геометрической абстракции, минимализме, скульптуре, объекте, рукотворной авторской книге, в бумажной массе, отлитой самим мастером.

Слайд 15
Слайд 16
Текст слайда:

Современный абстракционизм в живописи
Важным слагаемым современного языка абстракции стал белый цвет. Для Марины Кастальской, Андрея Красулина, Леонида Пелиха пространство белого — высшего напряжения цвета вообще наполнено бесконечными вариативными возможностями, позволяющими использовать и метафизические представления о духовном, и оптические законы отражения света.

М. Кастальская

Слайд 17
Текст слайда:

А. Красулин

Л. Пелих

Слайд 18
Текст слайда:

В современном абстракционизме развивается сюжетное направление (Геннадий Рыбалко). При сохранении беспредметности абстрактное изображение строится так, что вызывает конкретные ассоциации — разного уровня абстрагирования: от предметной ситуации до философской уровня абстрактных категорий. С другой стороны, изображение может выглядеть как картина фантастического мира — абстрактный сюрреализм.

Слайд 19
Текст слайда:

Абстракционные картины

Слайд 20
Слайд 21
Слайд 22
Слайд 23
Слайд 24
Слайд 25
Слайд 26
Слайд 27

Скачать презентацию

Что такое shareslide.
ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Конспект по изобразительному искусству на тему Гармония цета — элемент коипазиционного творчества

Поделитесь с коллегами:

Конспект урока по изобразительному искусству в 7 Б классе

« Гармония цвета элемент композиционного творчества» .

Открытый урок по изобразительному искусству в 7 Б классе

Урок — изучения творчества художников импрессионистов. Творческая мастерская.

Тема: «Гармония цвета элемент композиционного творчества».

Выполнила: Прокофьева Альфия Фатиховна

Высшая квалификационная категория,

Тема: « Гармония цвета элемент композиционного творчества».

Вид урока: творческая мастерская.

Цели и задачи:

Образовательная:

1. Расширить знания учащихся об искусстве 20 века, обучать приёмам композиционного оформления интерьера.

2. Активизировать творческое воображение, наблюдательность, художественный вкус, фантазию.

3. Помогать определению пропорции, формы предмета, его положения в пространстве

4. Закрепить знания о композиции, равновесии в композиции.

5. Развивать графические умения и навыки в изображении предметов сложной формы, от общего к деталям

Коррекционная:

Коррекция мелкой моторики рук, пальцев.

Воспитательная:

1..Воспитывать интерес любовь к всенародному искусству.

2. Передать особенности художественного сознания, направленного в поисках гармонии от частного к всеобщему.

Оборудование:

Для учителя: презентация по теме, иллюстрации, шаблоны (формы геометрических фигур), поэтапный показ, музыка С.С. Прокофьев — Симфония 7 cis-moll, op. 131 II. Allegretto

Для учеников: гуашь, акварель, кисти, баночки для воды, тряпочка, подставка для кистей.

Зрительный ряд: презентация по теме, 3 формата-А 0, справочный материал.

Ход урока.

I. Организационный момент. Мобилизующее начало.

Я постараюсь, чтобы урок для вас был интересным, а вам сегодня будет комфортно работать в мастерской.

Предлагаю к концу урока создать выставку под названием « Творчество»

Проверка подготовки учащихся к уроку.

II. Сообщение темы урока.

Вступительное слово учителя.

Всегда интересно узнать тайну искусств, тайну мастерства. У каждого художника свои секреты, мы попробуем чуть-чуть заглянуть в тайны искусств, побывав в тех местах, где красота создается своими руками.

Слайд № 2,№ 3,№ 4,№ 5,№ 6, № 7.

.Цвет и его роль в композиции.

Цвет играет важную роль в нашей жизни и деятельности. В природе нет ничего бесцветного. Человек живет в широком цветном мире. Одни цвета очень яркие и чистые, другие бледные настолько неопределенны, что порой трудно подобрать им название.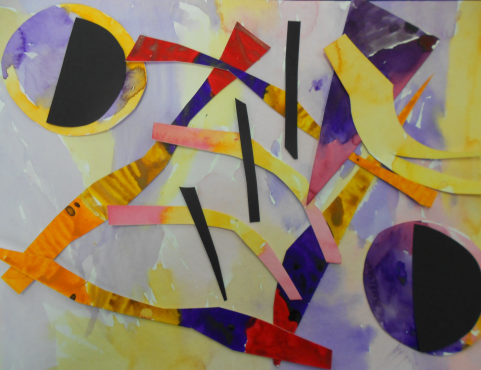

Понятие цвета и его восприятия очень сложны. Цветоведение охватывает вопросы, связанные с физикой, психологией, светотехникой, медициной, техникой, искусством.

Цвета спектра чередуются в такой последовательности: красный, оранжевый, зеленый, голубой, синий, фиолетовый.

1866 — Ньютон пропустил солнечные лучи через трехгранную призму и увидел спектральную полосу, которая состояла из гаммы (семь) различных цветов.

Все цвета делятся на две группы:

— ахроматические

— хроматические.

К ахроматических относится белый, черный и все серые цвета. К хроматическим относятся все спектральные цвета: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый, пурпурный со всеми оттенками и переходами. Цвет может успокаивать, волновать, радовать, печалить, подавлять и веселить. Вызвать чувство теплоты и холода, бодрости и усталости, расширять и сужать пространство, стимулировать зрение, мозг, нервы; помогать лечению больных.

Учащийся: Красный цвет — возбуждающий, горячий, энергичный, жизнерадостный. Сильно влияет на настроение людей.

Учащийся: Оранжевый — яркий, вызывающий радость, успокаивает или раздражает. Способствует улучшению переваривания пищи и ускорение движения крови.

Учащийся: Желтый — стимулирует зрение, мозг, нервы, создает веселье, успокаивает некоторое нервное состояние.

Учащийся: Зеленый — цвет природы, покоя, свежести, успокаивает нервную систему. Способствует понижению давления крови за счет расширенных капилляр.

Учащийся: Голубой — светлый, свежий и прозрачный. Влияет так же как и зеленый. Лечебный цвет, облегчает болезненное состояние.

Учащийся: Фиолетовый — пышный и благородный: положительно действует на сердце и легкие. Цвет усталости и грусти.

Учащийся: Коричневый — теплый; создает спокойное настроение, выражает устойчивость и прочность предметов.

Учащийся: Серый — холодный, деловой, грустный, создает апатию и грусть.

Учащийся: Белый — легкий, холодный, благородный. Символ чистоты, хорошо сочетается с другими цветами.

Учащийся: Черный — темный, тяжелый, резко снижает настроение. Он очень красивый, в небольшом количестве применяется для контраста.

Цвет в художественном контрасте рассматривается прежде всего, как средство функциональной организации предметной среды.

Слайд № 8

Учитель: Скажите, что такое композиция?

Учащийся: — Композиция /от лат./ — составление, соединение, различных частей в единое целое с какой-либо идеей.

Учитель: — Симметрично построенная композиция встречается во многих произведениях художников.

Если симметричная композиция создает впечатление покоя, тишины, торжественности, передает чувство уравновешенности, то асимметричной композиции ближе ощущение движения, беспокойства. В такой композиции составляющие части относительно центральной оси неодинаковые.

Симметрия в искусстве усвоена на реальной действительности изобилующей симметрично устроенными формами, например, симметрично устроены фигуры человека, бабочки, снежинки и т. д.

— В асимметричной композиции расположение объектов может быть самым разнообразным в зависимости от сюжета и замысла произведения, левая и правая половины неуравновешенны.

Используя закон симметрии, попробуем передать состояние покоя, устойчивости форм одной или несколько фигур.

— Но главная задача — сохранить равновесие путем подбора и расположения элементов в пространстве картины и в определениях пропорциях по форме, тону, цвету.

— При составлении соблюдайте одно условие: элементы композиции расположить ровно, без особого отклонения от вертикали либо горизонтали.

Тогда получим работу, в которой, кроме симметрии, выражено состояние статики.

Симметричные композиции — статичные /устойчивые/, левая и правая половина уравновешены.

— Теперь незаметно подошли к другому закону — статике.

Учащийся: — Статика — это покой, устойчивость.

— Ощущение движения /динамику/ можно усилить резкой сменой направления форм, линий, пятен — от горизонтальных, вертикальных к диагональным и даже спиральным.

Учащийся: — Динамика — это движение.

Учитель: — Как правило, статика и динамика неразрывно взаимосвязаны, дополняют, или усиливают друг друга, в результате работа в целом выигрывает.

Слайд № 9.

Учитель: Издавна люди пытались отобразить красоту окружающего мира, сцены из жизни в рисунках, картинах. Со временем картины наиболее талантливых людей превратились в произведения искусства. Появилось множество различных направлений в искусстве: импрессионизм, модернизм, классицизм, романтизм, натурализм, символизм, реализм, сюрреализм, абстракционизм и др. Каждое направление охватывает единство мировосприятия, эстетических взглядов, путей отображения.

Издревле беспредметное творчество существовало в виде орнамента или нонфинито, но только в новейшей истории оформилось в особую эстетическую программу — абстракционизм. Возникновение и развитие абстрактного искусства тесно связано с духовными идеями, волновавшими умы европейцев на рубеже XIX-XX веков. Увлечение метафизическими и утопическими теориями охватило не только философов, но и литераторов, музыкантов, живописцев. Стремление выразить невыразимое, передать ощущение единства души и материи потребовало от художников поиска нового, нетрадиционного изобразительного языка, полного глубокого смысла.

Вся история цивилизации последнего века построена на формулах, алгоритмах, принципах, уравнениях и правилах. Однако, человеку свойственно стремление к равновесию и гармонии. В связи с чем на заре века научно-технической революции появляется такое вот арт течение, которое не подчиняется классическим канонам рисования, а наоборот, служит своей целью дать свободу неосознанному и хаотичному, на первый взгляд лишенному смысла, но тем самым давая человеку возможность освободиться от влияния норм и догматов и сохранить внутреннюю гармонию.

Слайд № 10, № 11, № 12.

Абстракционизм (от латинского abstractus — удаленный, отвлеченный) весьма широкое направление в искусстве XX столетия, возникшее в начале 1910-х в нескольких странах Европы. Для абстракционизма характерно использование исключительно формальных элементов для отображения реальности.

В абстракционизме можно выделить два четких направления: геометрическая абстракция, основанная преимущественно на четко очерченных конфигурациях (Малевич, Мондриан), и лирическая абстракция, в которой композиция организуется из свободно текущих форм (Кандинский). Также в абстракционизме есть еще несколько крупных самостоятельных течений.

Слайд № 13

.Основоположники абстракционизма — русские художники Василий Кандинский иКазимир Малевич, голландец Пит Мондриан. В основе их метода рисования лежало стремление к «гармонизации», создание определённых цветовых сочетаний и геометрических форм, чтобы вызвать у созерцателя разнообразные ассоциации.

Слайд № 14.

Учащийся: Васи́лий Васи́льевич Канди́нский ( 1866-1944 ) — выдающийся русский живописец, график и теоретик изобразительного искусства, один из основоположнико вабстракционизма. Был одним из основателей группы «Синий всадник». Участвовал в выставках Московского товарищества художников. В 1910 и 1912 г. также участвовал в выставках художественного объединения «Бубновый валет». В эти годы он вырабатывает новаторскую концепцию «ритмического» использования цвета в живописи. Кандинский приписывал геометрическим фигурам определённые цвета и даже различия в тепловом восприятии. Горизонталь ему виделась чёрной и тёплой; вертикаль — белой, холодной; диагональ — красной, серой, зелёной; прямой угол — красным; острый — жёлтым; тупой — голубым.

Слайд № 15.

Учащийся: Пит Мондриан (1872-1944)

Пит Мондриан (наст. имя Питер Корнелис) — голландский художник. Его картины, представляющие собой сочетания прямоугольников и линий, являются примером наиболее строгой, бескомпромиссной геометрической абстракции в современной живописи. В 1917 Мондриан и Тео ван Дусбург основали авангардистский журнал «Де Стиль» и группу с таким же названием. Эстетическая теория, лежавшая в основе этого направления, была названа неопластицизмом. В соответствии с требованиями неопластицизма Мондриан еще больше сократил свои художественные средства, используя только белый, серый, черный и наиболее интенсивные тона основных цветов спектра.

К 1920 стиль Мондриана полностью сформировался. Используя прямые линии жестких контуров, он делал композиции асимметричными, достигая динамического равновесия. Благодаря отказу от частностей и деталей он надеялся достичь более ясного выражения универсальных первооснов творчества, стремясь обрести то, что он называл «чистой пластической реальностью».

Слайд № 16.

Учащийся: Малевич Казимир Северинович (1878 — 1935)

Малевич К.С. — российский живописец, график, педагог, теоретик искусства, философ. Основоположник одного из видов абстрактного искусства, так называемого супрематизма. Родился в семье управляющего заводом. С 11 лет много рисовал и писал красками. В 1894 окончил пятиклассное агрономическое училище. В 1895 — 1896 учился в рисовальной школе, потом переехал с семьей в Курск. Там он участвовал в созданном кружке любителей искусства и служил чертежником, зарабатывая деньги на жизнь и учебу в Москве. В 1904 приехал в Москву, где недолго посещал занятия в училище живописи, ваяния и зодчества и в Строгановском училище. В 1905 вернулся в Курск и самостоятельно занимался живописью. В 1907 состоялось его первое известное по каталогам участие в выставке Московского товарищества художников, где кроме работ Малевича были представлены картины В.В. Кандинского и др. . В 1928 — 1930 преподавал в Киевском художественном институте. В 1929 состоялась его персональная выставка в Государственной Третьяковской галерее. В 1930 его работы были выставлены в Австрии и Германии.

Учитель: В процессе познания природы человек открывал для себя всё новые и новые

принципы организации мира — ритм, симметрию, пропорции, контраст и др.

Этими принципами он руководствовался — сначала бессознательно, потом

осознанно, — преобразуя окружающий мир, создавая искусственную среду

обитания. Природные и созданные человеком объекты действительности породили

в его сознании устойчивые образы, сопровождаемые определёнными эмоциями.

Эти символические ассоциативные значения геометрических фигур, линий

учитываются во всех видах деятельности, связанных с созданием визуальных

форм. Вертикаль при отсутствии членений воспринимается как нечто

несоизмеримое, бесконечное, лёгкое, устремлённое ввысь. Если она имеет

утолщения в нижней части или стоит на горизонтальном основании — как нечто

более устойчивое. Горизонталь ассоциируется с надёжностью, стабильностью,

движением, развитием. Диагональ символизирует динамику. Соответственно

композиция, построенная на чётких горизонталях и вертикалях, тяготеет к

устойчивости, статичности, торжественности, а композиция, базирующаяся на

диагоналях, — к движению, изменчивости, нестабильности. Горизонтальная

композиция будет выглядеть более основательной, тяжеловесной, чем

вертикальная. Справедливость этого утверждения в большой степени зависит и

от соотношения сторон прямоугольников, и от размещения материала внутри

них.

Слайд № 17.

Вывод.

Абстракционизм — уникальное явление мировой художественной культуры. Его уникальность обусловлена особенностями переломной эпохи. XX век — это своего рода знак и не случайно он породил своеобразное искусство абстракционизма.

Искусство не терпит прямоговорения, его сила в метафоре. Реализм в искусстве бывает очень разным и это самым убедительным образом доказывает искусство абстракционизма.

Благодаря абстракционизму появилось много различных направлений в современном искусстве.

Восприятие искусства в высшей степени субъективно. Отношение к произведениям художников-абстракционистов можно выразить словами нидерландского философа XVII века Б. Спинозы: «Не плакать, не возмущаться, но понимать». Укоренившаяся глубоко привычка воспринимать сугубо реалистическую художественную форму не означает, что направление, «непохожее на жизнь», неинтересно, а тем более абсурдно. Радость искусства в том, что оно разное.

Абстракционизм можно любить и не любить, можно найти немало как сторонников, так и противников этого, как, впрочем, и любого другого вида искусства. Но любое искусство имеет право на существование, и его нельзя ни запрещать, ни очернять, ни скрывать.

Слайд № 18,№19,№20.

Произведения художников

III. Постановка Художественной Задачи

Слайд № 21

Задание № 1 Создайте композицию из 2-3 прямоугольников, 3-4 прямых линий и небольшого цветного кружка, который должен стать доминантой в композиции.

Постарайтесь добиться эмоционально-цветового преображения плоскости (её зрительного «расширения», «замкнутости» и т.д.).

Слайд № 22

Задание № 2 На чёрном или белом фоне создайте композицию из цветных линий, квадратов, прямоугольников и кругов. Выполните композицию в тёплой или холодной гамме. При помощи ритмического построения цветовых пятен постарайтесь решить в композиции различные эмоционально- образные задачи (создать, например, образ радости, строгости, печали и т.д.).

Слайд № 23

Задание № 3Создайте композицию из произвольного количества разнообразных фигур по принципу цветовой гармонии или контраста.

Работу выполните на цветном фоне, решая те же эмоционально- образные задачи

IV. Самостоятельная работа.

Задание: выполнить 1 задание на выбор используя свою фантазию.

Законченность работы — яркость и чистота цветов, чёткость и выразительность.

Проявите в работе точность, чёткость, аккуратность.

-Выбираем фон для картины.

— Используем шаблоны (формы геометрических фигур).

V. Выставка работ учащихся

VI. Итог урока.

Произведения каких художников мы изучили?

Какие направления в искусстве были в 20 веке?

Чем отличается искусство абстракционистов от современного?

Чему вы научились на уроке?

-Создавать произведение своими руками.

— Бережно относиться к культуре разных эпох.

— Беречь красоту.

Прошу всех ребят принять участие в выставке. Что мы с вами создали?

Выставку под названием « ТВОРЧЕСТВО. »

Всем мастерам за старание и желание работать « СПАСИБО!»

А самым умелым присваивается звание « МАСТЕР» ( вручается грамота)

Вот и подходит к концу наша встреча в художественной мастерской с мастерами чудесными.

И получилась у нас выставка. Пусть каждое загадочное произведение украсит интерьер вашей квартиры.

VI. Домашнее задание.

Список используемой литературы:

  1. Бердяев Н. «Кризис искусства» Репринт воспроизв. изд. 1918г.М., 1990.

  2. Волков Н.Н. Композиция живописи. С.53

  3. Гёте И.-В. Учение о цветах. С.240

  4. Деребире М. Цвет в деятельности человека. С.76-77

  5. .Ивашнев В.И. «Юный художник» №2, 2000

  6. Исмаилова Н. «Искусство» №17, 2001

  7. Исмаилова Н. «Искусство» №2, 2002

  8. Кандинский В.В. О духовном искусстве.С.46-49

  9. Словарь иностранных слов.М., 1964

  10. Энциклопедия для детей. Т.7. Ч.2 — 2 изд. испр. / Глав. ред. М.Д. Аксенова — М.: Аванта+, 1998. — 688с.: ил

Лестница абстракции — Ешьте

Лестница абстракции — одна из моих любимых концепций, помогающих написать что-то, что стоит прочитать. Пишете ли вы научную статью, пост в Facebook или стихотворение, в какой-то степени вы уже можете использовать лестницу абстракции, не улучшая свое письмо. Тем не менее, понимание концепций поможет вам пересмотреть и обдумать свое письмо по-новому.

Определение некоторых терминов

Прежде чем мы перейдем к этой лестнице, давайте определим несколько понятий. Во-первых, слово «абстрактный»: согласно онлайн-словарю Google прилагательное «абстрактный» означает «существующий в мысли или в виде идеи, но не имеющий физического или конкретного существования». Абстрактные идеи — великие. Это понятия, которые нельзя потрогать или попробовать на вкус — их нужно визуализировать. Любовь, справедливость, честь, красота, свобода, грация, богатство, доброта, истина, счастье и т. д. Если вы можете поставить перед словом «то, что есть» и написать об этом целую книгу, то это довольно абстрактно.

Во-вторых, мы должны определить антоним абстрактного, «конкретный». Опять же, согласно Google, бетон означает «существующий в материальной или физической форме; настоящий или твердый; не абстрактно». Конкретные слова — это осязаемые вещи, которые мы понимаем с помощью наших органов чувств. Клавиатура, на которой я это пишу, — это конкретный объект. Ключи в моем кармане. Пряный гамбо, который я съел на ужине, на который я ходил прошлой ночью.

Лестница абстракции

Итак, теперь Лестница абстракции, концепция, впервые предложенная С.И. Хаякавой в его книге   Язык в мыслях и действиях. Хаякава заметил, что письмо можно разбить на абстрактные и конкретные идеи, а лестница помогает показать различные уровни абстракции. Например, на картинке выше самым конкретным является конкретная осязаемая вещь: моя копия «Убить пересмешника ». Но по мере того, как вы поднимаетесь по лестнице, это становится все более и более общим и охватывает все больше и больше вещей.

Система классификации животных — хороший пример лестницы абстракции:

Домен гораздо более абстрактен, вид наиболее конкретен. Хотя если бы вы видели конкретного волка, то могли бы получить более конкретную, даже тогда систему классификации. Если бы вы хотели обсудить достоинства всех живых существ, в том числе и волков, и это было бы более абстрактно.

Допустим, я иду на прогулку к леднику Менденхолл в Джуно, Аляска, мой родной город. Год 2006. Зима, и за озером я вижу волка.

«Эй, смотри, это Ромео!» Я говорю. (Если вам интересно, читайте больше о Ромео здесь). Ромео был особенным волком, одним индивидуальным существом, самой нижней ступенью лестницы абстракции.

«Интересно, что за волк Ромео?» Я мог бы спросить себя. Я иду к периодической таблице и узнаю, что он из рода серых волков. В мире есть много других серых волков, так что это ступенька вверх по лестнице. Я вижу, что Ромео играет с соседскими собаками. Почему собаки? Что ж, на следующей ступени находится его род, canis, в который входят собаки. Они являются частью одного рода. Во всяком случае, вы получаете картину.

Поскольку абстрактное и конкретное — две противоположные стороны спектра, ваша лестница может иметь столько ступенек, сколько вы хотите. Для простоты в лестнице Хаякавы было четыре ступени.

  Четвертый уровень:   Абстракции   Примеры : Жизнь, красота, любовь, время, успех, сила, зло, добро
  Третий уровень: Широкая группа имен с небольшой спецификацией   Примеры : Люди, женщины, молодежь, промышленность, цели, вещи, телевидение
  Второй уровень:   Более определенные группы   Примеры : подростки, средний класс, швейная промышленность, университетский городок, телевизионные драмы, комнатные растения
  Первый уровень:   Конкретные, идентифицируемые существительные   Примеры : Nike Air Jordan; моя черно-белая собака Соло; Дилемма всеядного; Новый ребенок моего друга.

 

И что?

 (@drletizia)

 

Так почему я болтаю об абстракции, конкретике и этой чертовой лестнице?

По словам Яна Стревера: «Большинство текстов содержат ряд уровней абстракции, но успешных профессиональных писателей активно используют абстракции первого уровня . Изощренность мысли имеет дело с областью абстракции, но изощренность письма достигается за счет поддержки этих абстракций конкретными деталями» (Чунг).

Одной из самых больших проблем, с которыми борются студенты, является специфика. У вашего письма должна быть более крупная идея или цель — начиная с этой верхней ступени — но вы должны потратить много времени на иллюстрацию и объяснение этой идеи в деталях, в примерах . Качественное письмо касается вершины лестницы, а затем тратит большую часть своего времени на конкретные детали, объясняя большую идею.

Если вы обнаружите, что проводите слишком много времени посередине карьерной лестницы, вы начнете звучать как политик на предвыборной речи. Это может быть хорошим политиканством. Но это слишком общее для таких, как мы.

 

Процитированная работа

Чанг, Дэвид Н. «Лестница абстракции Хаякавы». Университет штата Вашингтон. факультет.wwu.edu/auer/Resources/Hayakawa-Abstraction-Ladder. pdf. По состоянию на 26 августа 2017 г.

@drletizia. «Лестница абстракции — Письменная мастерская 7-го класса TC». Twitter , 6 ноября 2015 г., 8:10, https://twitter.com/drletizia/status/662663232981700608. По состоянию на 26 августа 2017 г.

Штамм, Логан. «Как этот совет по написанию от сенатора улучшит ваш блог». SEJ. https://www.searchenginejournal.com/writing-tip-senator-will-punch-blog-posts/129100/. По состоянию на 26 августа 2017 г.

Исследование процессов математической абстракции учащихся 7-х классов средней школы

В этом исследовании изучались процессы абстрагирования учащихся 7-х классов. Кроме того, была предпринята попытка объяснить, как реализация этого процесса влияет на академические успехи студентов. Для этого были сформированы опытная и контрольная группы. В то время как текущая учебная программа была применена к контрольной группе, экспериментальная группа обучалась с помощью учебного цикла ACE, который представляет собой прикладное измерение теории, основанной на философии абстракции. Можно констатировать, что такое исследование построено по полуэкспериментальному методу. Применение было проведено в 7-м классе государственной средней школы в провинции Эрзурум в 2014-2015 учебном году, всего 31 ученик в экспериментальной группе и 32 ученика в контрольной группе. В ходе исследования были получены как количественные, так и качественные данные. В качестве инструментов сбора данных использовались тесты достижений, разработанные исследователем для количественных данных, и формы интервью, разработанные исследователем для качественных данных. Кроме того, приложение в экспериментальной группе было записано с помощью камеры для последующего просмотра, и эти записи использовались для подтверждения качественных данных. Вовлечение исследователя в качестве участника процесса давало возможность получить записи наблюдений, и эти записи наблюдений добавляли качественное измерение исследования. Поэтому в этом исследовании пытались обеспечить надежность за счет разнообразия данных. Анализ количественных данных проводился с помощью статистических тестов, а анализ качественных данных — методом описательного анализа. В конце исследования видно, что уровень абстракции учащихся по теме уравнения лучше в группе, в которой применяется учебный цикл ACE, чем в другой группе. Кроме того, видно, что обучение в процессе подачи заявок поддерживает интерес и мотивацию учащихся. По полученным результатам можно сказать, что занятия в классе, основанные на процессе абстрагирования учащихся, могут быть необходимы для качественного обучения.

В этом исследовании изучались процессы абстрагирования учащихся 7-х классов. Кроме того, была предпринята попытка объяснить, как реализация этого процесса влияет на академические успехи студентов. Для этого были сформированы опытная и контрольная группы. В то время как текущая учебная программа была применена к контрольной группе, экспериментальная группа обучалась с помощью учебного цикла ACE, который представляет собой прикладное измерение теории, основанной на философии абстракции. Можно констатировать, что такое исследование построено по полуэкспериментальному методу. Применение было проведено в 7-м классе государственной средней школы в провинции Эрзурум в 2014-2015 учебном году, всего 31 ученик в экспериментальной группе и 32 ученика в контрольной группе. В ходе исследования были получены как количественные, так и качественные данные. В качестве инструментов сбора данных использовались тесты достижений, разработанные исследователем для количественных данных, и формы интервью, разработанные исследователем для качественных данных. Кроме того, приложение в экспериментальной группе было записано с помощью камеры для последующего просмотра, и эти записи использовались для подтверждения качественных данных. Вовлечение исследователя в качестве участника процесса давало возможность получить записи наблюдений, и эти записи наблюдений добавляли качественное измерение исследования. Поэтому в этом исследовании пытались обеспечить надежность за счет разнообразия данных. Анализ количественных данных проводился с помощью статистических тестов, а анализ качественных данных — методом описательного анализа. В конце исследования видно, что уровень абстракции учащихся по теме уравнения лучше в группе, в которой применяется учебный цикл ACE, чем в другой группе. Кроме того, видно, что обучение в процессе подачи заявок поддерживает интерес и мотивацию учащихся. По полученным результатам можно сказать, что занятия в классе, основанные на процессе абстрагирования учащихся, могут быть необходимы для качественного обучения.

Ключевые слова:

___

Абельс М., де Йонг Дж. А., Деккер Т., Мейер М. Р., Шью Дж. А., Беррилл Г. и Саймон А. Н. (2006). Взлеты и падения. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.

Азиала, М., Коттрилл, Дж., Дубинский, Э., и Швингендорф, Э., К. (1997). Развитие у учащихся графического представления о производной. Журнал математического поведения, 16 (4), 399-431.

Азиала, М., Дубинский, Э., Мэтьюз, Д. М., Морикс, С., и Октак, А. (1997). Развитие у учащихся понимания смежных классов, нормальности и факторгрупп. Журнал математического поведения, 16 (3), 241-309.

Басс, Э., Дж., и Монтегю, Дж., Э. (1972). Основанные на Пиаже последовательности обучения естественным наукам. Научное образование, 56 (4), 503-512.

Биллс Л., Дрейфус Т., Мейсон Дж., Цамир П., Уотсон А. и Заславский О. (2006). Пример в математическом образовании. В Дж. Новотна (ред.), Материалы 30-й конференции Международной группы психологии математического образования. Прага, Чехия: PME.

Кули, Р. (2002). Письмо в исчислении и рефлексивной абстракции. Журнал математического поведения, 21, 255–282.

Коттрилл Дж., Дубинский Э., Николс Д., Швингендорф К., Томас К. и Видакович Д. (1996). Понимание концепции ограничения: начиная со схемы скоординированного процесса. Journal of Mathematical Behavior, 15, 167-192.

Четин, И. (2009). Понимание учащимися концепции предела: точка зрения APOS. Неопубликованная докторская диссертация. Ближневосточный технический университет, Институт педагогических наук, Анкара.

Четин, И., и Топ, Э. (2014). Programlama eğitiminde görselleştirme ile ACE döngüsü. [Цикл ACE в обучении программированию с использованием визуализации]. Турецкий журнал компьютерного и математического образования, 5 (3), 274-303.

Давыдов В. В. (1990). Виды обобщения в обучении: логические и психологические проблемы в построении школьных программ. В: Дж. Килпактрик (ред.). Советские исследования в области математического образования (стр. 2). Рестон, Вирджиния: Национальный совет учителей математики.

Динес, З., П. (1967). Об абстракции и обобщении. Гарвардское образовательное обозрение, 31, 281–301.

Дубинский, Е. (2000). Математическая грамотность и абстракция в 21 веке. Школьная наука и математика, 100 (6), 289–97.

Дубинский Э. (1991). Рефлексивная абстракция в развитом математическом мышлении. В Д. Талл (ред.), Advanced Mathematical Thinking, (стр. 95-123). Дордрехт, Нидерланды: Kluwer. Получено 18 июля 2018 г. с: http://www.math.wisc.edu/~wilson/Courses/Math9.03/ReflectiveAbstraction.pdf.

Дубинский, Э., Веллер, К., Макдональд, А., М., и Браун, А. (2005). Некоторые исторические проблемы и парадоксы, касающиеся концепции бесконечности: анализ на основе апоса: часть 1. Educational Studies in Mathematics, 58 (3), 335–359.

Фрер, П., Хаззан, О., и Манес, М. (1997). Раскрывая грани абстракции. Международный журнал компьютеров для математического образования, Американское математическое общество, 3, 234–283.

Гарсия-Крус, Дж. А., и Мартинон, А. (1997). Действия и инвариантные схемы в линейных обобщающих задачах. В: Пехконен Э. (Ред.). Конференция Международной группы психологии математического образования, 2, 289-296.

Кабаэль, Т., У., и Танышлы, Д. (2010). Cebirsel düşünme sürecinde örüntüden fonksiyona öğretim. İlköğretim Online, 9(1), 213-228.

Кэтлин, М. (1999). Активное обучение и ситуативное обучение: как пройти курс ACE. Клинические лабораторные исследования, 12(1), 35-41.

Киндт, М., Деккер, Т., и Беррилл, Г. (2006). Правила алгебры. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.

Киндт, М., Рудхардт, А., Вайерс, М., Деккер, Т., Спенс, М.С., Саймон, А.Н., Плигге, М.А., и Беррилл, Г. (2006). Узоры и фигуры. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.

Киндт, М., Виджерс, М., Спенс, М.С., Бринкер, Л.Дж., Плигге, Массачусетс, Беррилл, Дж., и Беррилл, Г. (2006). Графические уравнения. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.

Кнут, Э.Дж., Алибали, М.В., Макнил, Н.М., Вайнберг, А., и Стивенс, А.С. (2005). Понимание учащимися средней школы основных алгебраических понятий: эквивалентность и переменная. Национальный научный фонд, 37(1), 1-9.

Лю П., Х. (1996). Должны ли учителя включать историю математики в свое преподавание? Учитель математики, 96(6), 416.

Махарадж, А. (2013). APOS-анализ понимания производных студентами-естественниками. Южноафриканский журнал образования, 33(1), 458-477.

Мил, Э., Д. (2003). Модели теорий математического понимания: сравнение модели роста математического понимания Пири и Кирена и теории APOS. Проблемы CBMS в математическом образовании, 12 (2), 132-181.

Milli Eğitim Bakanlığı [MEB]. (2014). İlköğretim matematik 7 Ders Kitabı. [Элементарная математика 7 учебник]. Анкара: Ада Матбаджилик. [Анкара: Типография Ады].

Мюррей, М., А. (2002). Студенты-первокурсники, изучающие исчисление, открывают правило произведения: функция, обозначения и теория апоса (докторская диссертация). Университет в Олбани, Нью-Йорк. Носс, Р., и Хойлс, К. (1996). Окна математических смыслов: изучение культур и компьютеров. Нидерланды: Kluwer

Озмантар, М., Ф., и Монаган, Дж. (2007). Диалектический подход к формированию математических абстракций. Журнал исследований в области математического образования, 19 (2), 89–112.

Шенфельд, А. Х. (1992). Учимся мыслить математически: решение проблем, метапознание и осмысление математики. В Д. Гроувс (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр. 334-370). Нью-Йорк: Макмиллан.

Сезгин-Мемнун, Д. (2011). İlköğretim altıncı sınıf öğrencilerinin analitik geometri’nin koordinat sistemi ve doğru denklemi kavramlarını oluşturması süreçlerinin araştırılması [Исследование учеников шестого класса? построение систем координат и концепций линейных уравнений аналитической геометрии с использованием конструктивизма и реалистического математического образования]. Яинланмамыш Доктор Тези. Uludağ Üniversitesi, Eğitim Bilimleri Enstitüsü, Бурса. [Неопубликованная докторская диссертация, Университет Улудаг, Институт педагогических наук, Бурса]. Получено с https://tez.yok.gov.tr/UlusalTezMerkezi/tezSorguSonucYeni. jsp.

Сфард, А. (1991). О двойственной природе математических представлений: Размышления о процессах и объектах как о разных сторонах одной медали. Образовательные исследования по математике, 22, 1-36.

Сойлу, Ю. (2008). Yedinci sınıf öğrencilerinin cebirsel ifadeleri ve harf sembollerini (değişkenleri) yorumlamaları ve bu yorumlamada yapılan hatalar. [Интерпретация учащимися 7-го класса алгебраического выражения и символа букв при выполнении этих интерпретаций]. Selçuk Üniversitesi Ahmet Keleşoğlu Eğitim Fakültesi Dergisi [Журнал Сельчукского университета педагогического факультета Ахмета Келесоглу], 25, 237-248.

Скемп, Р. (1986). Психология обучения математике (2-е изд.). Хармондсворт: Пингвин.

Табачник, Б.Г., и Фиделл, Л.С. (2007). Использование многомерной статистики (5-е изд.). Нью-Йорк: Аллин и Бэкон.

Высокий, Д. (1999). Размышления о теории APOS в элементарном и продвинутом математическом мышлении, Труды 23-й конференции PME, Хайфа, Израиль, 1, 111–118.

Цириас, В. (2011). Теория APOS как основа для изучения концептуальных стадий проблем связанных ставок (диссертация кандидатской диссертации). Университет Конкордия, Канада.

Вачира П., Роланд Г. П. и Раймонд С. (2013). Роль учителя математики в продвижении классной речи. Международный журнал преподавания и обучения математике, 13 (1), 1–38.

Веллер, К., Арнон, И., и Дубинский, Э. (2011). Понимание учителями предварительной службы связи между дробью или целым числом и его десятичным разложением: Сила и стабильность убеждений, Канадский журнал науки, математики и технического образования, 11 (2), 129–159.

Веллер, К., Арнон, И., и Дубинский, Э. (2009 г.). Предварительное понимание учителями отношения между дробью или целым числом и его десятичным разложением. Канадский журнал науки, математики и технического образования, 9 (1), 5–28.

Вийерс, М., Рудхардт, А., Реувейк, М., Деккер, Т., Баррилл, Г., Коул, Б.Р., и Плигге, М.А. (2006). Строительные формулы. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.

Ешилдере, С., и Аккоч, Х. (2011). Matematik öğretmen adaylarının şekil örüntülerini genelleme süreçleri [Процессы обобщения визуальных паттернов учителями математики до начала работы]. Pamukkale Eğitim Fakültesi Dergisi [Педагогический журнал Университета Памуккале], 30 (2), 141–153.

Йылдырым, А., и Шимшек, Х. (2011). Nitel araştırma yöntemleri. [Качественные методы исследования]. Анкара: Seçkin Yayıncılık. [Анкара: Издательство Секин].

Йылмаз Р. (2011). Matematiksel soyutlama ve genelleme süreçlerinde görselleştirme ve rolü [Визуализация в процессах математической абстракции и обобщения и ее роль]. Яинланмамыш Доктор Тези. Uludağ Üniversitesi, Eğitim Bilimleri Enstitüsü, Бурса. [Неопубликованная докторская диссертация, Университет Улудаг, Институт педагогических наук, Бурса]. Получено с https://tez.yok.gov.tr/UlusalTezMerkezi/tezSorguSonucYeni. jsp.

Инь, Р., К. (2011). Овалитативное исследование от начала до конца. Нью-Йорк: Отдел публикаций Гилфорда.

___
APA Кылычоглу Э , Каплан А . (2019). Исследование процессов математической абстракции учащихся 7-х классов средней школы. Журнал компьютерных и образовательных исследований, 7 (13), 233-256. DOI: 10.18009/jcer.547975

Исследование математических абстракций учащихся 7-х классов средней школы

  • Абельс М., де Йонг Дж. А., Деккер Т., Мейер М. Р., Шью Дж. А., Беррилл Г. и Саймон А. Н. (2006). Взлеты и падения. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.
  • Азиала, М., Коттрилл, Дж., Дубинский, Э., и Швингендорф, Э., К. (1997). Развитие у учащихся графического представления о производной. Журнал математического поведения, 16 (4), 399-431.
  • Азиала, М., Дубинский, Э., Мэтьюз, Д.М., Морикс, С., и Октак, А. (1997). Развитие у учащихся понимания смежных классов, нормальности и факторгрупп. Журнал математического поведения, 16 (3), 241-309.
  • Басс, Э., Дж., и Монтегю, Дж., Э. (1972). Основанные на Пиаже последовательности обучения естественным наукам. Научное образование, 56 (4), 503-512.
  • Биллс, Л., Дрейфус, Т., Мейсон, Дж., Цамир, П., Уотсон, А. и Заславски, О. (2006). Пример в математическом образовании. В Дж. Новотна (ред.), Материалы 30-й конференции Международной группы психологии математического образования. Прага, Чехия: PME.
  • Кули, Р. (2002). Письмо в исчислении и рефлексивной абстракции. Журнал математического поведения, 21, 255–282.
  • Коттрилл Дж., Дубинский Э., Николс Д., Швингендорф К., Томас К. и Видакович Д. (1996). Понимание концепции ограничения: начиная со схемы скоординированного процесса. Journal of Mathematical Behavior, 15, 167–192.
  • Четин, И. (2009). Понимание учащимися концепции предела: точка зрения APOS. Неопубликованная докторская диссертация. Ближневосточный технический университет, Институт педагогических наук, Анкара.
  • Четин, И., и Топ, Э. (2014). Programlama eğitiminde görselleştirme ile ACE döngüsü. *Цикл ACE в обучении программированию с использованием визуализации. Турецкий журнал компьютерного и математического образования, 5 (3), 274-303.
  • Давыдов В. В. (1990). Виды обобщения в обучении: логические и психологические проблемы в построении школьных программ. В: Дж. Килпактрик (ред.). Советские исследования в области математического образования (стр. 2). Рестон, Вирджиния: Национальный совет учителей математики.
  • Динес, З., П. (1967). Об абстракции и обобщении. Harvard Educational Review, 31, 281–301.
  • Дубински, Э. (2000). Математическая грамотность и абстракция в 21 веке. Школьная наука и математика, 100 (6), 289-97
  • Дубинский, Э. (1991). Рефлексивная абстракция в развитом математическом мышлении. В Д. Талл (ред.), Advanced Mathematical Thinking, (стр. 95-123). Дордрехт, Нидерланды: Kluwer. Получено 18 июля 2018 г. с: http://www.math.wisc.edu/~wilson/Courses/Math9.03/ReflectiveAbstraction.pdf.
  • Дубинский, Э., Веллер, К., Макдональд, А., М., и Браун, А. (2005). Некоторые исторические проблемы и парадоксы, касающиеся концепции бесконечности: анализ на основе апоса: часть 1. Educational Studies in Mathematics, 58 (3), 335–359.
  • Фрер, П., Хаззан, О., и Манес, М. (1997). Раскрывая грани абстракции. Международный журнал компьютеров для математического образования, Американское математическое общество, 3, 234–283.
  • Гарсия-Крус, Дж. А., и Мартинон, А. (1997). Действия и инвариантные схемы в линейных обобщающих задачах. В: Пехконен Э. (Ред.). Конференция Международной группы психологии математического образования, 2, 289-296.
  • Кабаэль, Т., У., и Танышлы, Д. (2010). Cebirsel düşünme sürecinde örüntüden fonksiyona öğretim. İlköğretim Online, 9(1), 213-228.
  • Кэтлин, М. (1999). Активное обучение и ситуативное обучение: как пройти курс ACE. Клинические лабораторные исследования, 12(1), 35-41.
  • Киндт, М., Деккер, Т., и Беррилл, Г. (2006). Правила алгебры. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.
  • Киндт, М., Рудхардт, А., Вайерс, М., Деккер, Т., Спенс, М.С., Саймон, А.Н., Плигге, М.А., и Беррилл, Г. (2006). Узоры и фигуры. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.
  • Киндт, М., Вайерс, М., Спенс, М.С., Бринкер, Л.Дж., Плигге, М.А., Беррилл, Дж., и Беррилл, Г. (2006). Графические уравнения. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.
  • Кнут, Э.Дж., Алибали, М.В., Макнил, Н.М. , Вайнберг, А., и Стивенс, А.С. (2005). Понимание учащимися средней школы основных алгебраических понятий: эквивалентность и переменная. Национальный научный фонд, 37(1), 1-9.
  • Лю П., Х. (1996). Должны ли учителя включать историю математики в свое преподавание? Учитель математики, 96(6), 416.
  • Махарадж, А. (2013). APOS-анализ понимания производных студентами-естественниками. Южноафриканский журнал образования, 33(1), 458-477.
  • Мил, Э., Д. (2003). Модели теорий математического понимания: сравнение модели роста математического понимания Пири и Кирена и теории APOS. Проблемы CBMS в математическом образовании, 12 (2), 132-181.
  • Милли Эгитим Баканлыгы *MEB+. (2014). İlköğretim matematik 7 Ders Kitabı. [Элементарная математика 7 учебник]. Анкара: Ада Матбаджилик. * Анкара: Типография Ады+.
  • Мюррей, М., А. (2002). Студенты-первокурсники, изучающие исчисление, открывают правило произведения: функция, обозначения и теория апоса (докторская диссертация). Университет в Олбани, Нью-Йорк.
  • Носс Р. и Хойлс К. (1996). Окна математических смыслов: изучение культур и компьютеров. Нидерланды: Клювер
  • Озмантар, М., Ф., и Монаган, Дж. (2007). Диалектический подход к формированию математических абстракций. Журнал исследований в области математического образования, 19 (2), 89–112.
  • Шенфельд, А. Х. (1992). Учимся мыслить математически: решение проблем, метапознание и осмысление математики. В Д. Гроувс (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр. 334–370). Нью-Йорк: Макмиллан.
  • Сезгин-Мемнун, Д. (2011). İlköğretim altıncı sınıf öğrencilerinin analitik geometri’nin koordinat sistemi ve doğru denklemi kavramlarını oluşturması süreçlerinin araştırılması [Исследование учеников шестого класса? построение систем координат и концепций линейных уравнений аналитической геометрии с использованием конструктивизма и реалистического математического образования]. Яинланмамыш Доктор Тези. Uludağ Üniversitesi, Eğitim Bilimleri Enstitüsü, Бурса. *Неопубликованная докторская диссертация, Университет Улудаг, Институт педагогических наук, Бурса]. Получено с https://tez.yok.gov.tr/UlusalTezMerkezi/tezSorguSonucYeni.jsp.
  • Сфард, А. (1991). О двойственной природе математических представлений: Размышления о процессах и объектах как о разных сторонах одной медали. Образовательные исследования по математике, 22, 1–36.
  • Сойлу, Ю. (2008). Yedinci sınıf öğrencilerinin cebirsel ifadeleri ve harf sembollerini (değişkenleri) yorumlamaları ve bu yorumlamada yapılan hatalar. *Интерпретация учащимися 7-го класса алгебраического выражения и символа букв при выполнении этих интерпретаций]. Selçuk Üniversitesi Ahmet Keleşoğlu Eğitim Fakültesi Dergisi * Журнал Сельчукского университета педагогического факультета Ахмета Келесоглу], 25, 237-248.
  • Скемп, Р. (1986). Психология обучения математике (2-е изд.). Хармондсворт: Пингвин.
  • Табачник, Б.Г., и Фиделл, Л. С. (2007). Использование многомерной статистики (5-е изд.). Нью-Йорк: Аллин и Бэкон.
  • Высокий, Д. (1999). Размышления о теории APOS в элементарном и продвинутом математическом мышлении, Труды 23-й конференции PME, Хайфа, Израиль, 1, 111–118.
  • Цириас, В. (2011). Теория APOS как основа для изучения концептуальных стадий проблем связанных ставок (диссертация кандидатской диссертации). Университет Конкордия, Канада.
  • Вачира П., Роланд Г. П. и Раймонд С. (2013). Роль учителя математики в продвижении классной речи. Международный журнал по преподаванию и обучению математике, 13(1), 1-38.
  • Веллер, К., Арнон, И., и Дубинский, Э. (2011). Понимание учителями предварительной службы связи между дробью или целым числом и его десятичным разложением: Сила и стабильность убеждений, Канадский журнал науки, математики и технического образования, 11 (2), 129–159.
  • Веллер, К., Арнон, И., и Дубинский, Э. (2009). Предварительное понимание учителями отношения между дробью или целым числом и его десятичным разложением. Канадский журнал науки, математики и технического образования, 9 (1), 5–28.
  • Вийерс, М., Рудхардт, А., Реувейк, М., Деккер, Т., Баррилл, Г., Коул, Б.Р., и Плигге, М.А. (2006). Строительные формулы. В Висконсинском центре исследований в области образования и Институте Фройденталя (ред.), Математика в контексте. Чикаго: Британская энциклопедия, Inc.
  • Ешилдере, С., и Аккоч, Х. (2011). Matematik öğretmen adaylarının şekil örüntülerini genelleme süreçleri *Процессы обобщения визуальных паттернов учителями математики до начала работы]. Pamukkale Eğitim Fakültesi Dergisi *Педагогический журнал Университета Памуккале], 30 (2), 141–153.
  • Йылдырым, А., и Шимшек, Х. (2011). Nitel araştırma yöntemleri. *Качественные методы исследования+. Анкара: Seçkin Yayıncılık. * Анкара: Seckin Publishing+.
  • Йылмаз Р. (2011). Matematiksel soyutlama ve genelleme süreçlerinde görselleştirme ve rolü [Визуализация в процессах математической абстракции и обобщения и ее роль]. Яинланмамыш Доктор Тези. Uludağ Üniversitesi, Eğitim Bilimleri Enstitüsü, Бурса. [Неопубликованная докторская диссертация, Университет Улудаг, Институт педагогических наук, Бурса]. Получено с https://tez.yok.gov.tr/UlusalTezMerkezi/tezSorguSonucYeni.jsp.
  • Инь, Р., К. (2011). Овалитативное исследование от начала до конца. Нью-Йорк: Отдел публикаций Гилфорда.

APA КИЛИЧОГЛУ Э, КАПЛАН А (2019). Исследование процессов математической абстракции учащихся 7-х классов средней школы. Journal of Computer and Education Research, 7(13), 233 — 256. 10.18009/jcer.547975
Чикаго КИЛИЧОГЛУ Элиф, КАПЛАН Абдулла Исследование процессов математической абстракции учащихся 7-го класса средней школы. Журнал компьютерных и образовательных исследований 7, № 13 (2019 г.)): 233 — 256. 10.18009/jcer.547975
MLA KILIÇOĞLU Elif, KAPLAN Abdullah Исследование процессов математической абстракции учащихся 7-х классов средней школы.

No related posts.

Автор записи

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *