Изометрии построение: Построение третьего вида и изометрии с вырезом четверти

Содержание

Как начертить изометрию?

Начнем с того, что определимся с направлением осей в изометрии.

Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.

Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.

Мы получили верхнюю грань фигуры.

Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом — в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. Изображение окружностей на всех трех плоскостях я описал в

отдельном уроке, а пока лишь скажу, что в изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D.

Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b — вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм).

Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра — по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена — не хватает только прямоугольного сквозного отверстия.

Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия — по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.

На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти.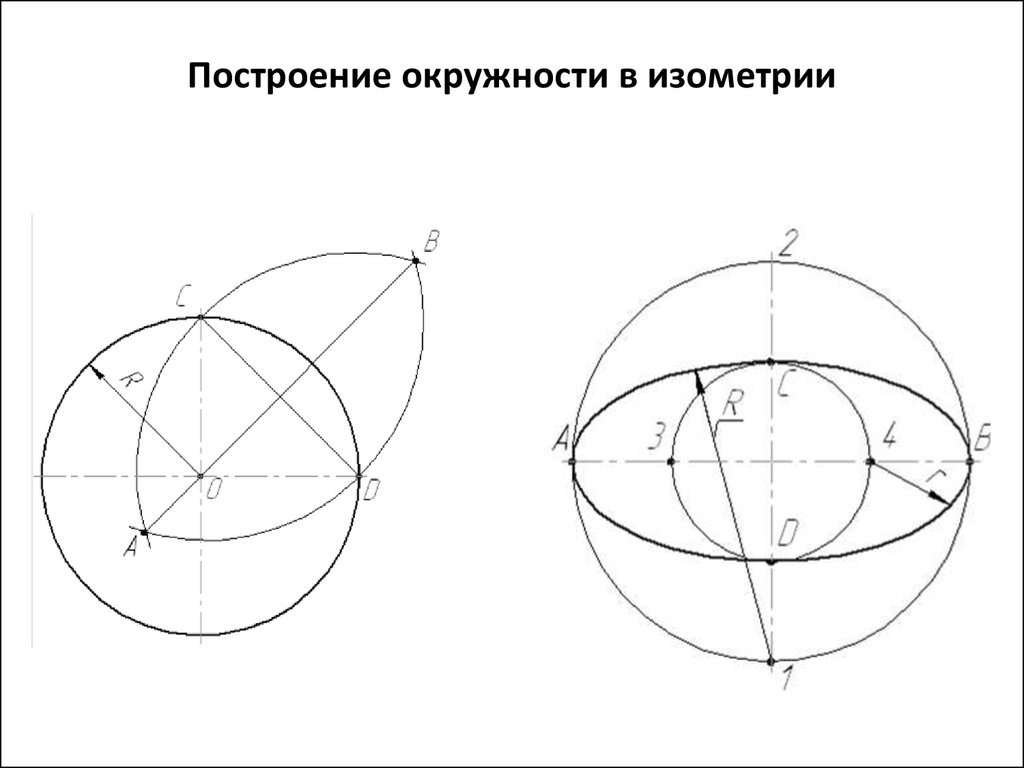 Чаще всего, это четверть нижняя левая на виде сверху — в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.

Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).

Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!

Как начертить окружность в изометрии?

Как вы наверняка знаете, при построении изометрии окружность изображается в виде эллипса. Причем вполне конкретного: длина большой оси эллипса AB=1.22*D, а длина малой оси CD=0.71*D (где D — диаметр той самой исходной окружности, которую мы хотим начертить в изометрической проекции). Как начертить эллипс зная длину осей? Об этом я рассказывал в отдельном уроке

. Там рассматривалось построение больших эллипсов. Если же исходная окружность имеет диаметр где-то до 60-80 мм, то скорее всего мы сможем начертить ее и без лишних построений, используя 8 опорных точек. Рассмотрим следующий рисунок:

Это фрагмент изометрии детали, полный чертеж которой можно увидеть ниже. Но сейчас мы говорим о построении эллипса в изометрии. На данном рисунке AB — большая ось эллипса (коэффициент 1.22), CD — малая ось (коэффициент 0.71). На рисунке половина короткой оси (ОD) попала в вырезанную четверть и отсутствует — используется полуось СО (не забудьте об этом, когда будете откладывать значения по короткой оси — полуось — имеет длину равную половине короткой оси).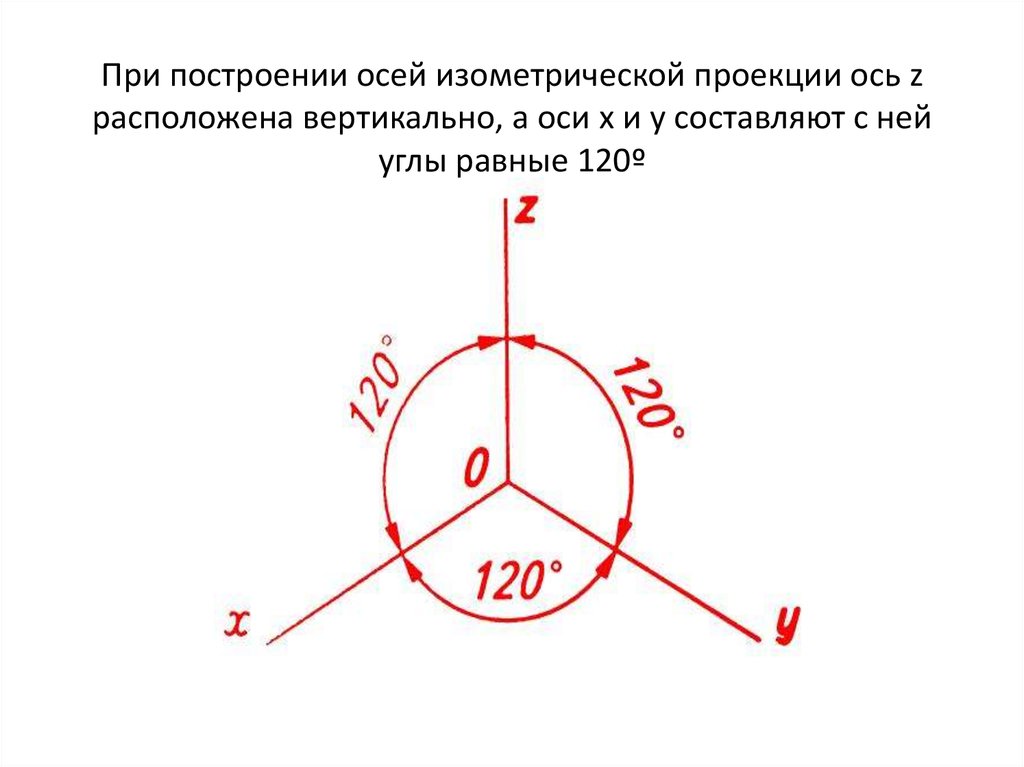

Итак, мы уже имеем 4 (3) точки. Теперь отложим по двум оставшимся изометрическим осям точки 1,2,3 и 4 — на расстоянии равном радиусу исходной окружности (таким образом 12=34=D). Через полученные восемь точек уже можно провести достаточно ровный эллипс, либо аккуратно от руки, либо по лекалу.

Для лучшего понимания направления осей эллипсов в зависимости от того, какое направление имеет циллиндр, рассмотрим три разных отверстия в детали, имеющей форму параллелепипеда. Отверстие — тот же цилиндр, только из воздуха 🙂 Но для нас это особого значения не имеет. Полагаю, что ориентируясь на эти примеры вы без труда сможете правильно расположить оси своих эллипсов. Если же обобщить, то получится так: большая ось эллипса перпендикулярна той оси, вокруг которой образован цилиндр (конус).

Инженерная графика | Лекции | Аксонометрические проекции

По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые

аксонометрическими.

Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1<>p/

Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.

В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2

Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется

диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

прямоугольные изометрические и диметрические;
косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.

Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30⁰ и 60⁰.

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.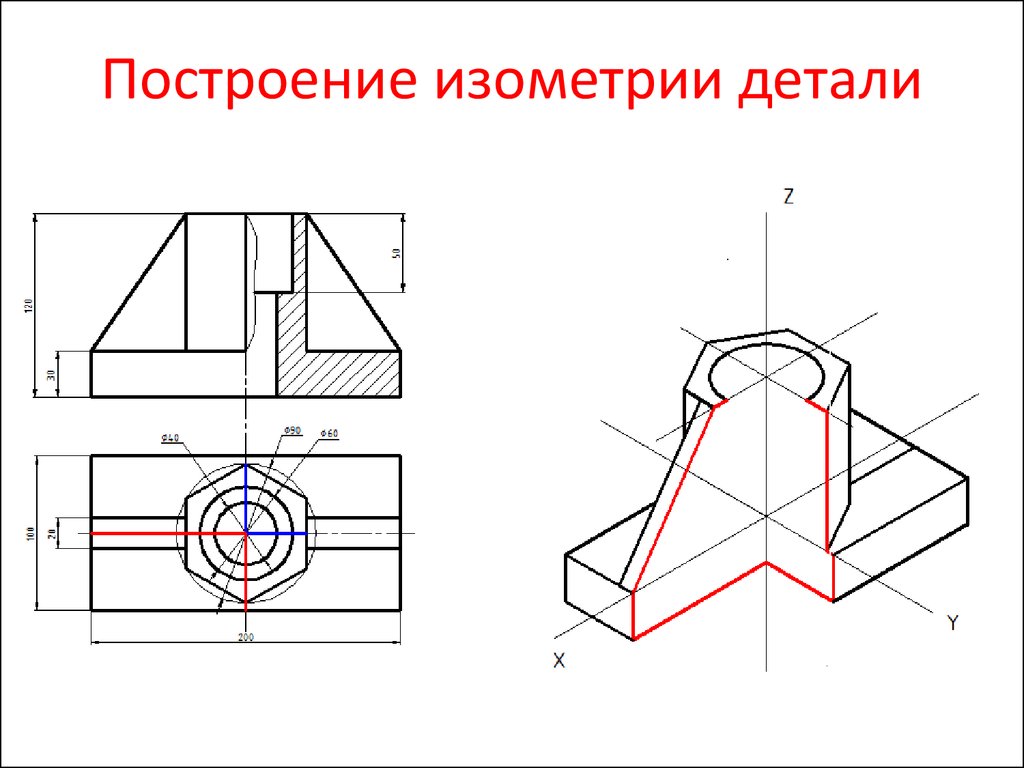

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁D₁= 0,5CD. Диаметр А ₁В₁делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Что такое изометрический рисунок? (с изображением)

Промышленность

Факт проверен

Стазе Гонсалес

Дата последнего изменения: 04 ноября 2022 г.

Изометрический рисунок — это трехмерное изображение объекта на двухмерной поверхности. Три вида одного и того же изображения объединяются для создания изометрического рисунка. Чертеж чертежа можно выполнить от руки или с помощью компьютерного программного обеспечения для черчения. Этот тип технического чертежа обычно используется в машиностроении, архитектуре и смежных областях.

Когда инженеры и архитекторы пытаются проиллюстрировать объект, они рисуют объект так, как он виден с разных сторон. Эти виды включают вид сверху, снизу, спереди, сзади, слева и справа. Размещение всех различных видов в одном чертеже называется чертежом с несколькими видами. Многоракурсные иллюстрации двумерны. Этот тип рисования помогает преобразовать эти изображения в трехмерный объект.

Людям, не имеющим инженерного или архитектурного образования, может быть трудно понять многовидовой чертеж. Проблема с несколькими представлениями заключается в том, что отдельный читатель должен уметь расшифровывать, что означают разные типы линий, и соединять различные виды, чтобы сформировать изображение. Перевод чертежа с несколькими видами требует навыков и воображения, чтобы мысленно завершить то, как выглядит изображение. Вот где изометрический рисунок становится полезным. Он объединяет три смежных вида для создания изображения с глубиной и объемом.

Изометрические рисунки — это лишь один из нескольких типов графических рисунков, используемых для иллюстрации объектов в трехмерных формах. Перспективы и изометрические проекции — это другие способы перевода чертежа с несколькими видами. Каждый тип имеет свой внешний вид и предназначение.

Этот тип рисунка отличается от перспективы тем, что перспективы используются для создания ощущения расстояния.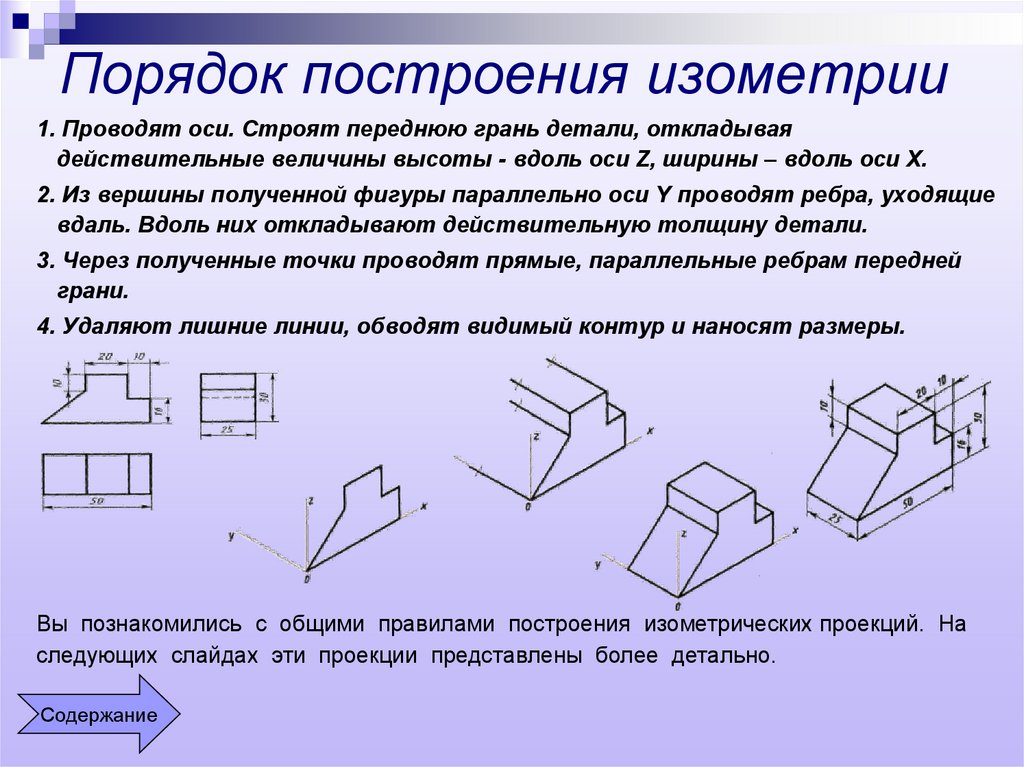 Объекты, которые находятся дальше, кажутся меньше, чем те, что ближе, даже если оба объекта имеют одинаковый размер. На этих рисунках линии остаются параллельными независимо от того, ближе или дальше находится край. В перспективных рисунках параллельные линии приближаются друг к другу, пока не сойдутся в точке схода.

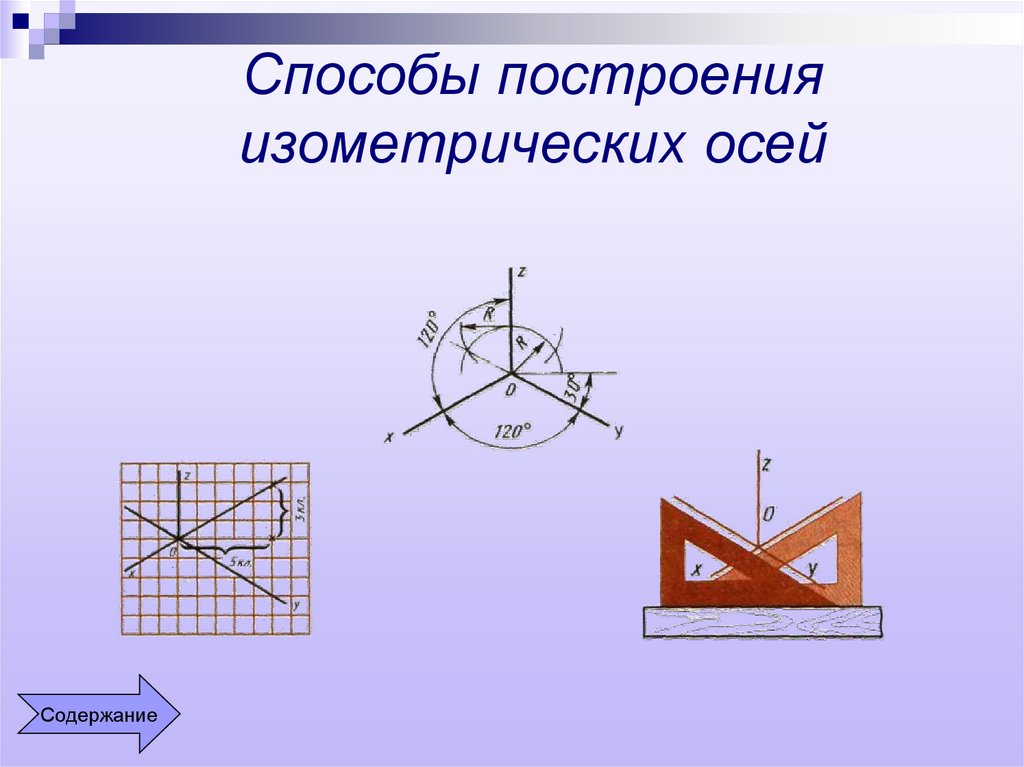
Столь же сбивает с толку термин «изометрическая проекция». И изометрический рисунок, и изометрическая проекция являются типами аксонометрических проекций, но они дают немного разные результаты. Разница в том, как нарисованы две стороны.

В изометрическом чертеже угол между двумя базовыми кромками равен 90°.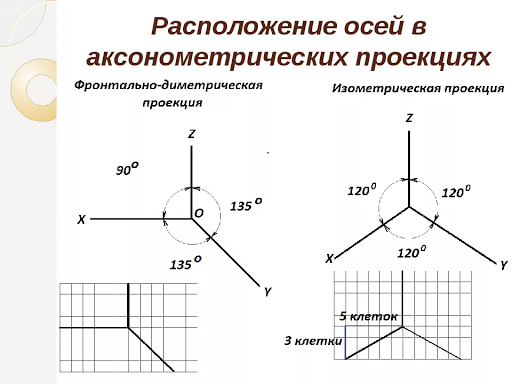 При выполнении изометрической проекции проводится базовая линия. Две соединительные базовые кромки нарисованы под углом 30°; от базовой линии, создавая угол 120° между двумя краями. В результате изометрическая проекция меньше. Размер объекта, нарисованного с использованием изометрической проекции, составляет всего 80 процентов от размера изометрического рисунка.

Что такое изометрическое рисование — Блог Bricsys

Изометрическое рисование — это особый стиль рисования, в котором угол между осями x, y и z составляет 120°, а перспектива отсутствует. Изометрический рисунок — это то, что мы, технические иллюстраторы, используем каждый день, но как часто вы останавливались, чтобы подумать о том, откуда он взялся или почему мы его используем?

Примеры различных стилей рисования

Изометрический рисунок происходит от греческого ίσο μέτρο «iso métro», что означает «равная мера». Это связано с тем, что угол между осями x, y и z равен 120°. Это форма аксонометрической перспективы (без ракурса). Другими словами: все линии лица нарисованы под одним и тем же углом.

Преимущество рисования таким образом состоит в том, что объект можно свободно вращать, перемещать и переориентировать, не перерисовывая его. Также не меняется ощущение масштаба, когда объект перемещается вперед или назад. При использовании других методов рисования, таких как вид в перспективе, наклонный вид, вид в плане или диаметральный вид, повторное использование уже нарисованных элементов невозможно. Их нужно будет перерисовывать с нуля.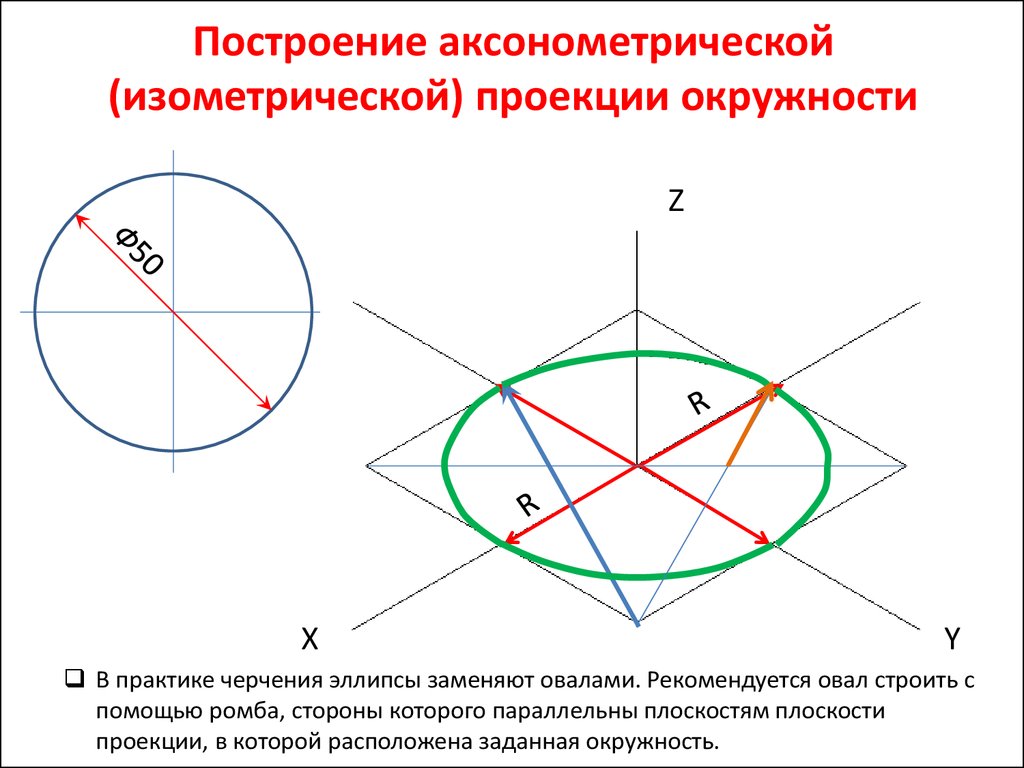

В BricsCAD виджет LookFrom автоматически выравнивает любой чертеж по изометрическому виду, если для параметра перспективы установлено значение «Выкл.» <0>. Вы также можете автоматически генерировать изометрические виды с помощью команды рисования ВИДБАЗ. Используйте панель «Свойства», чтобы изменить угол наклона линзы в виде в перспективе.

Сравнение изометрического и перспективного видов. Обратите внимание, что изометрический объект остается неизменным независимо от его положения на чертеже.

История изометрического рисования

Профессор Уильям Фариш из Кембриджского университета первым сформулировал правила изометрического рисования, когда опубликовал свою статью «Об изометрической перспективе» в 1822 году. По этой причине его часто цитируют. как создатель изометрического рисунка. Однако изометрические и аксонометрические рисунки были обычным явлением задолго до этого. Эта техника часто встречается в древнем китайском искусстве. Вдоль реки во время фестиваля Цинмин является известным примером такого рода.

Древний пример аксонометрического рисунка. Обратите внимание, что ощущение перспективы дает изменение масштаба, однако угол наклона граней остается прежним. Это приводит к некоторым интересным искажениям на лодках. Чжан Цзэдуань, «Цинмин шанхэ то». Фу Симянь, изд. Чжунго мейшу цюаньцзи, Лян Сун хуэйхуа, шан (серия, том 3). пл. 51, стр. 130-131, 134. Собрание Национального дворца-музея, Пекин. Отредактировано для цвета и контраста.

Вероятно, самое последнее и заслуживающее внимания внедрение изометрического рисунка, как и в большей части современного дизайна и архитектуры, можно проследить до Баухауза. Тео ван Дусбург и Герберт Байер широко используют аксонометрическую перспективу в своих архитектурных чертежах. В то время это несколько шокировало архитектурный мир и до сих пор не типично для архитектурного рисунка. Отсутствие перспективы превращает концептуальные рисунки в самостоятельные модернистские произведения искусства.

Аксонометрическая проекция в цвете, Частный дом, 1923 год.

Проблемы

В то время как изометрическое рисование может означать, что легко переделывать рисунки быстро. Проблема с изометрическим рисованием заключается в том, что без ощущения перспективы объект может появиться не в том месте, где он есть. Это может затруднить работу в САПР!

Использование вида в перспективе во время моделирования в САПР может оказаться выгодным, так как это позволяет пользователю САПР одновременно видеть 3 из 4 любых стен, а также пол и потолок помещения. В изометрическом и аксонометрическом видах можно просматривать только 2 из 4 стен и либо пол, либо потолок.

Слева: чистая изометрическая проекция. Видны только 3 из 6 лиц данной комнаты. Справа: вид в перспективе. Одновременно видеть 3 стороны, пол и потолок данной комнаты.

Не просто рисование линий

Если вы думали, что изометрическое рисование ограничивается черно-белыми линиями, вы ошибались!

Видеоигры часто используют изометрическую перспективу, поскольку она позволяет разработчикам игр использовать 3D-дизайн в играх без сложных расчетов, ракурсов и различных углов обзора камеры. С 8- и 16-битными графическими играми это было крайне важно. По мере совершенствования консолей в играх, где игроку требуется общий вид игрового пространства, таких как The Sims и Age of Empires, использовались изометрические виды.

Изображение предоставлено BagoGames

С появлением игровых консолей большей емкости это стало реже. Тем не менее, в последнее время стиль изометрического вида возродился на мобильных устройствах. Многие из вас знакомы с FarmVille. Мобильные игры часто используют этот стиль, потому что изометрически нарисованные объекты проще создавать, они потребляют меньше вычислительной мощности и имеют меньший заряд батареи. Консольные игры более высокого класса, такие как Shadowrun и Invisible Inc., используют псевдоизометрический вид, чтобы выделить их стилистически.

Также растет число художников, которые используют изометрические рисунки для создания инновационных и интересных произведений искусства. Они создают современные рисунки, которые оставляют линии позади.

Изображение предоставлено Германом Копытковым

Хотите использовать возможности BricsCAD для своих изометрических чертежей?

Легко попробовать, легко купить и легко владеть. Это BricsCAD. Попробуйте все наши продукты по бесплатно в течение 30 дней на сайте www.bricsys.com . Свобода выбора, а также бессрочные (постоянные) лицензии на продукты, работающие на всех языках и в любом месте. Вам понравится то, что мы создали для вас с помощью BricsCAD.

Изометрический рисунок

Изометрический рисунок происходит от греческого ίσο μέτρο «iso métro», что означает «равная мера». На рисунке нет ракурса. Профессор Уильям Фариш из Кембриджа первым установил правила изометрических рисунков в 1822 году. Используйте изометрию для свободного вращения, изменения положения и переориентации без перерисовки. Без перспективы объект может появиться в другом месте, чем то, о котором вы подумали сначала. Изометрический рисунок также широко используется в видеоиграх и современной иллюстрации.