Построение и решение графиков Функций
Понятие функции
Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие значения функции. Вот, какими способами ее можно задать:
Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы.
Словесный способ.
Область определения функции — это множество всех допустимых значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Например, для функции вида область определения выглядит так
Область значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Например, естественная область значений функции y = x
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x).
Само равенство y = f(x) называется уравнением данного графика.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия.
Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться при решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Запоминаем!
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых значение функции равно нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
Найти область определения функции.
Найти область допустимых значений функции.
Проверить не является ли функция четной или нечетной.
Проверить не является ли функция периодической.
Вычислить производную и найти критические точки, определить промежутки возрастания и убывания.
Промежутки знакопостоянства.
Асимптоты.
На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах или воспользуйтесь онлайн тренажером.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Задача 3.
Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
| x | y |
| 0 | -1 |
| 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
| x | y |
| 0 | 0 |
| 0 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, b = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 4. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 5. Построить графики функций:
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Построить графики можно при помощи элементарных преобразований.
Если построен график функции y = f(x), то при a > 0 следующие графики получаются с помощью сдвига графика f(x).
y = f(x) + a — график функции y = f(x) сдвигается на a единиц вверх;
y = f(x) − a — график функции y = f(x) сдвигается на a единиц вниз;
y = f(x + a) — график функции y = f(x) сдвигается на a единиц влево;
y = f(x − a) — график функции у = f(x) сдвигается на a единиц вправо.
Преобразование график по типу y = mf(x): y = f(x) → y = mf(x), где m — положительное число.
Если m > 1, то такое преобразование графика называют растяжением вдоль оси y с коэффициентом m.
Если m < 1, то такое преобразование графика называют сжатием к оси x с коэффициентом 1/m.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Как построить график функции
В этой статье разобран самый простой метод получения графика функции.
Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.
Итак, алгоритм по шагам:
1.
Представьте, как выглядит ваш график.
Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Пример: Построить график функции \(y=-\)\(\frac{2}{x}\)
Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:
2. Составьте таблицу точек, принадлежащих графику:
Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».
Пример: \(y=-\)\(\frac{2}{x}\)
|
при \(x=-1\) |
\(y=-\)\(\frac{2}{-1}\)\(=2\) |
|
|
при \(x=0\) |
\(y\) — не существует (делить на ноль нельзя) |
|
|
при \(x=1\) |
\(y=-\)\(\frac{2}{1}\)\(=-2\) |
|
|
при \(x=2\) |
\(y=-\)\(\frac{2}{2}\)\(=-1\) |
|
|
при \(x=3\) |
\(y=-\)\(\frac{2}{3}\) |
|
|
при \(x=4\) |
\(y=-\)\(\frac{2}{4}\)\(=-\)\(\frac{1}{2}\) |
Результат вычислений удобно представлять в виде таблицы, примерно такой:
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.
4. Постройте координатную плоскость и отметьте на ней точки из таблицы.
Пример:
5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.
Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с \(x=-2\), \(x=-4\), \(x=\)\(\frac{1}{2}\) и \(x=-\)\(\frac{1}{2}\)
|
при \(x=-2\) |
\(y=-\)\(\frac{2}{-2}\)\(=1\) |
|
|
при \(x=-4\) |
\(y=-\)\(\frac{2}{-4}\)\(=\)\(\frac{1}{2}\) |
|
|
при \(x=\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{\frac{1}{2}}\)\(=-2:\)\(\frac{1}{2}\)\(=-2 \cdot 2=-4\) |
|
|
при \(x=-\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{-\frac{1}{2}}\)\(=-2:(-\)\(\frac{1}{2}\)\()\)\(=-2 \cdot (-2)=4\) |
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(-2\) |
\(-4\) |
\(\frac{1}{2}\) |
\(-\)\(\frac{1}{2}\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
\(1\) |
\(\frac{1}{2}\) |
\(-4\) |
\(4\) |
6.
Постройте график
Теперь аккуратно и плавно соединяем точки.
Готово!
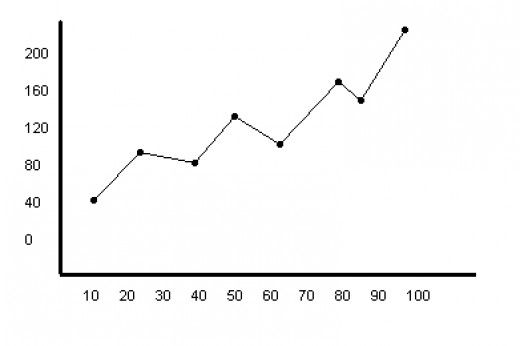
Построение графиков в Python | Набор 1
В этой серии статей вы познакомитесь с графическим представлением в Python с помощью Matplotlib, возможно, самой популярной библиотеки графического представления и визуализации данных для Python.
Установка
Самый простой способ установить matplotlib — использовать pip. Введите в терминал следующую команду:
pip install matplotlib
ИЛИ вы можете скачать ее отсюда и установить вручную.
Начало работы (построение линии)
Python
924 924 Код говорит сам за себя. Были выполнены следующие шаги: Нанесение двух или более линий на один и тот же график 9 4 Output: Настройка графиков Здесь мы обсудим некоторые элементарные настройки, применимые практически к любому графику. Output: Как видите, мы сделали несколько настроек, таких как Bar Chart Output : Histogram Output: Scatter plot Output: Pie-chart 025 slices The output of above program looks like this: Plotting curves of given equation The вывод вышеприведенной программы выглядит следующим образом: Здесь мы используем NumPy , который представляет собой пакет обработки массивов общего назначения в Python. Итак, в этой части мы обсудили различные типы графиков, которые мы можем создавать в matplotlib. Эта статья предоставлена Nikhil Kumar . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам. Уравнения в математике полезны, но они также неэффективны — для каждого значения x необходимо выполнить отдельный расчет, чтобы выяснить, что такое y. Графики берут это уравнение и превращают его в визуальное представление, на которое вы можете смотреть и сразу же видеть, что происходит при различных значениях x, как изменяется функция и многое другое! Однако, когда вы впервые изучаете графики, все сводится к запоминанию основных уравнений и того, как будут выглядеть их графики, начиная с линейных уравнений в форме пересечения наклона. - где вы должны запомнить точную настройку уравнения и то, что означает каждый член на графике, будь то вершина, наклон, точки пересечения, масштабирование, горизонтальные или вертикальные сдвиги и многое другое! Но зачем запоминать все эти а, в, к и з, если это будет полезно только в нескольких конкретных случаях?! Вместо этого в следующий раз, когда вам понадобится узнать, как должен выглядеть график функции, попробуйте выполнить эти шаги, чтобы быстро набросать любой график! Для демонстрации воспользуемся уравнением: Это похоже на полиномиальные уравнения, которые вы, возможно, видели в классе, но они кубические, поэтому у нас нет очевидных форм уравнений, которые можно было бы использовать для построения графика. Итак, как построить график этой функции? Первое, что мы хотим сделать, это получить несколько точек на нашем графике, поэтому мы хотим выбрать те, которые будет легко вычислить. Практически для любого уравнения подставить x = 0 и решить для y можно быстро и легко сделать на глаз, и почти всегда можно обойтись без калькулятора. Для нашего примера уравнения: Итак, первая точка, которую мы поместим на наш график, это (0, -4). Далее, в некоторых случаях y = 0 тоже довольно легко решить. Если вы можете быстро найти y = 0 , это еще один хороший момент, который нужно решить сразу. В данном случае: Итак, теперь у нас есть точка (-2, 0) для добавления к нашему графику! В зависимости от графика может быть легко подставить небольшие целые числа, такие как 1 или -1. Чем больше точек вы можете добавить к своему графику, тем лучше вы сможете увидеть, какую форму он в конечном итоге примет. Для этого уравнения мы получим: и Итак, теперь у нас есть четыре точки: (0,-4), (-2,0), (1,-18) и ( -1, -2). Давайте нанесем эти точки и посмотрим, как они выглядят! Мы можем начать видеть, как график обретает форму, но нам понадобится больше информации, прежде чем мы закончим. Любая линия, которую мы рисуем, должна заканчиваться стрелками на обоих концах, чтобы мы знали, что происходит по ходу движения далее по оси x как в положительном, так и в отрицательном направлении. Это то, что называется «конечным поведением». Чтобы выяснить, что это такое, мы подставим два числа в исходное уравнение — большое положительное число и большое отрицательное число. Например, подставив большое положительное число в нашу кубическую функцию, мы получим: Добавление 1 к большому положительному числу почти не изменит его — затем, когда мы возведем его в куб, оно станет действительно большим положительным числом. Однако действительно большое положительное число станет отрицательным при умножении на -2, а вычитание 2 не будет иметь большого значения, поэтому конечным результатом будет действительно большое отрицательное число. Если мы попробуем то же самое для другой стороны графика, подставив вместо x большое отрицательное число, мы получим: Большое отрицательное число в кубе — это действительно большое отрицательное число, но на этот раз, когда оно умножается на -2, оно становится действительно большим положительным числом. o, для нашего графика мы нашли, что при больших положительных x, y большие и отрицательные, а при больших отрицательных x, y большие и положительные. Давайте добавим это к нашему графику со стрелками. Некоторые уравнения имеют необычные особенности или особые точки, которые вы можете заметить, взглянув на уравнение – обратите особое внимание на любые точки, в которых большая часть уравнения может стать нулем. Это может помочь вам найти корни, асимптоты или другие места, где форма графика изменяется необычным образом. Например, в уравнении, которое мы рассматривали, Этот член интересен тем, что если x = -1, вся часть уравнения станет равной нулю. Конечно, мы уже нашли эту точку ранее, но это говорит нам о том, что x = -1 является «особой» точкой в уравнении — возможно, здесь форма графика как-то сдвинется. На данный момент мы сделали все, что могли — у нас есть несколько точек на графике, мы знаем, как он будет выглядеть на концах, и мы определили любые необычные точки или особенности. Возможно, мы до сих пор не знаем точно, какова форма графика, но здесь вы можете использовать основы для каждого основного уравнения. Мы знаем, что наша линия будет гладкой и максимально простой, но при этом будет попадать во все точки. Если мы в целом знаем, какого рода это уравнение (полиномиальное, радикальное, экспоненциальное), у нас есть хотя бы некоторое предположение, какова будет его общая форма. В нашем примере у нас достаточно точек, чтобы набросать одну сторону нашего уравнения, но отрицательная сторона немного неясна, поэтому давайте подумаем, что мы можем сказать о другом типе многочлена, квадратном уравнении. Для нашей кубической функции мы знаем, что квадратичные функции всегда симметричны относительно своей вершины, но это не совсем работает, потому что мы знаем, что в одном направлении мы получим положительное значение, а в другом нам нужно стать отрицательным. Итак, давайте предположим что-то подобное — может быть, наша «особая» точка при x = -1 — это , как вершина, но в этой точке форма графика такая же, но движется в противоположном направлении. |
plot (x, y)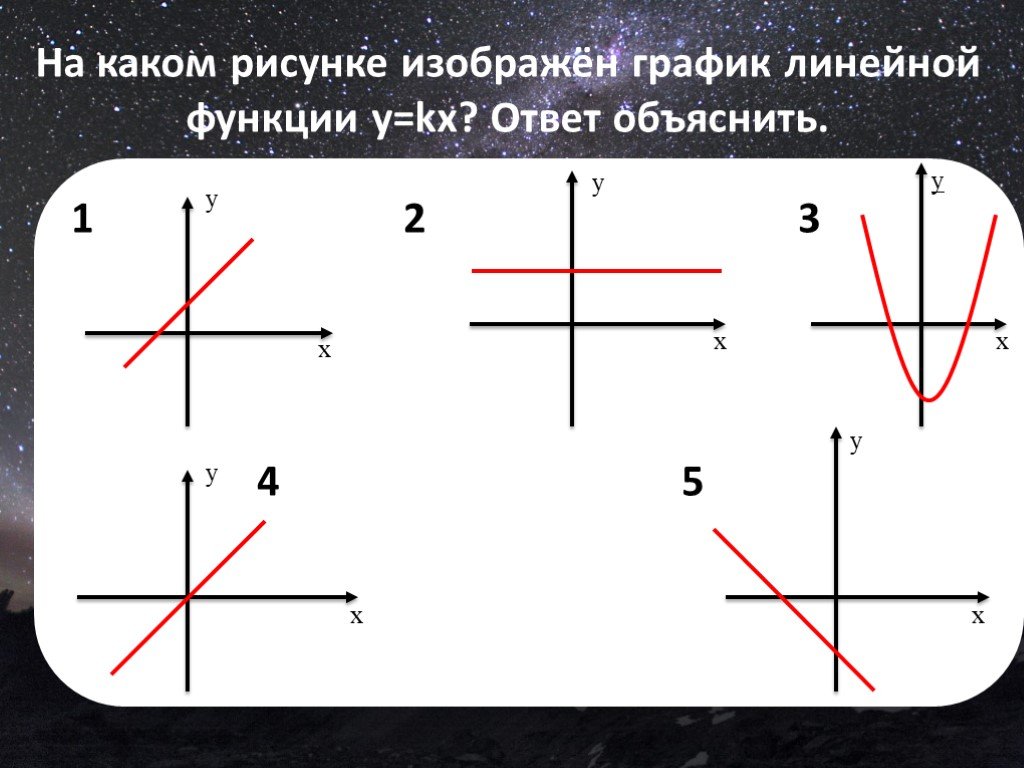 
0026 
legend() 
0026 
xlabel (
pyplot as plt 
hist(ages , Bins, 
show() 
scatter(x, г, метка 
, цвета 
show() 
Здесь мы настроили отображение процентного значения только до 1 знака после запятой.
plot(x, y)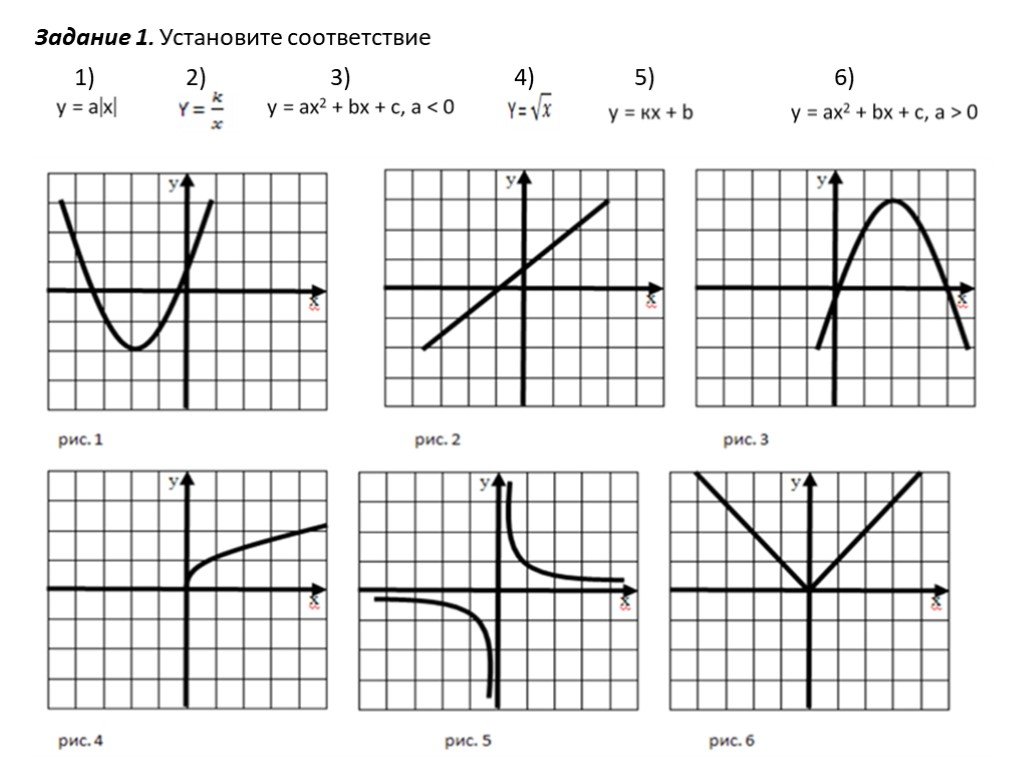 
Есть еще сюжеты, которые не были освещены, но самые важные из них обсуждаются здесь — 
Однако по мере того, как вы переходите к более сложным уравнениям, таким как квадратные уравнения и тригонометрия, вас часто просят запомнить формы таких уравнений —
График x = 0
Однако придерживайтесь точек, которые легко рассчитать. Цель этого метода — быстро найти всего несколько точек — если вы собираетесь вычислять каждую точку на графике, вы не экономите время!
Теперь мы на самом деле не собираемся выбирать число и использовать наш калькулятор, чтобы выяснить, что произойдет, мы просто посмотрим, как части уравнения повлияют на конечный результат.
Мы можем не знать точно, что это такое, но мы готовы что-то нарисовать.
