Как нарисовать фигуру в изометрии. Выполнение прямоугольной изометрии, прямоугольной диметрии по заданным видам
Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.
Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.
Рис. 109. Прямоугольная и изометрические проекции квадрата
Рис. 110. Прямоугольная и изометрические проекции треугольника
110. Прямоугольная и изометрические проекции треугольника
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
Рис. 111. Прямоугольная и изометрические проекции шестиугольника
Рис. 112. Прямоугольная и изометрические проекции круга
При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические проекции простых геометрических тел
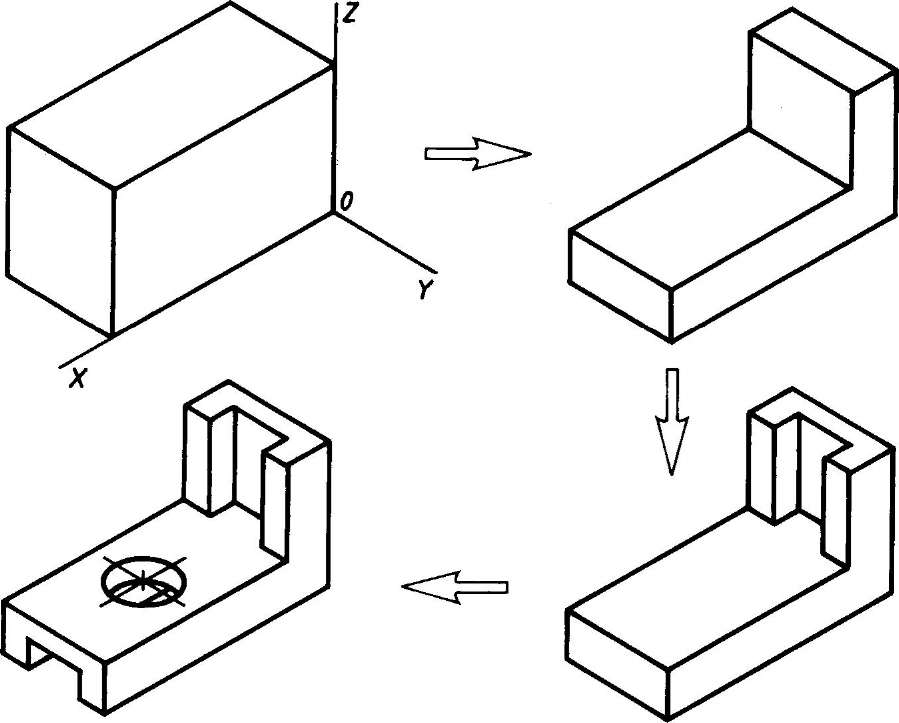
Способы построения изометрической проекции детали:
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней посредством изображения ребер модели;
Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани
4) обводка изометрической проекции (рис.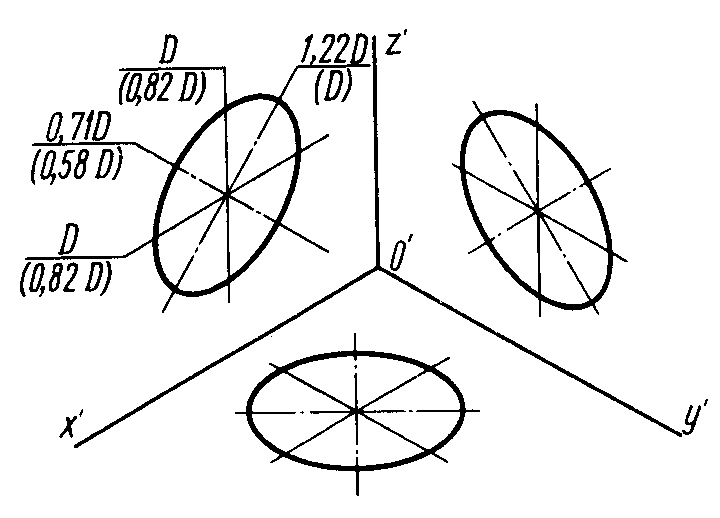
- Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
- Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
- Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов
Рис.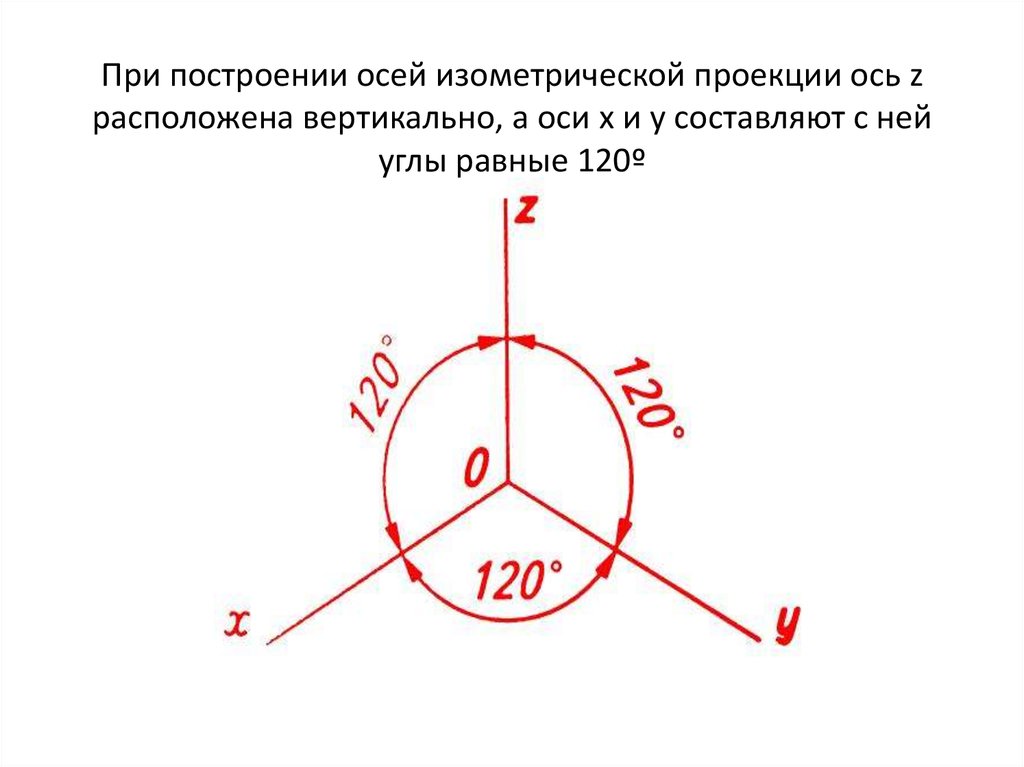 115 Построение изометрической проекции детали на основе последовательного приращения объемов
115 Построение изометрической проекции детали на основе последовательного приращения объемов
Рис. 116. Использование комбинированного способа построения изометрической проекции детали
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей
Прямоугольной изометрией называется аксонометрическая проекция, у которой коэффициенты искажения по всем трём осям равны, а углы между аксонометрическими осями 120. На рис. 1 представлено положение аксонометрических осей прямоугольной изометрии и способы их построения.
Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) циркуля; в) угольников или транспортира.
При
практических построениях коэффициент
искажения (К) по аксонометрическим осям
согласно ГОСТ 2.317- 2011 рекомендуют равный
единице. При этом изображение получают
более крупным по сравнению с теоретическим
или точным изображением при коэффициентах
искажения 0,82.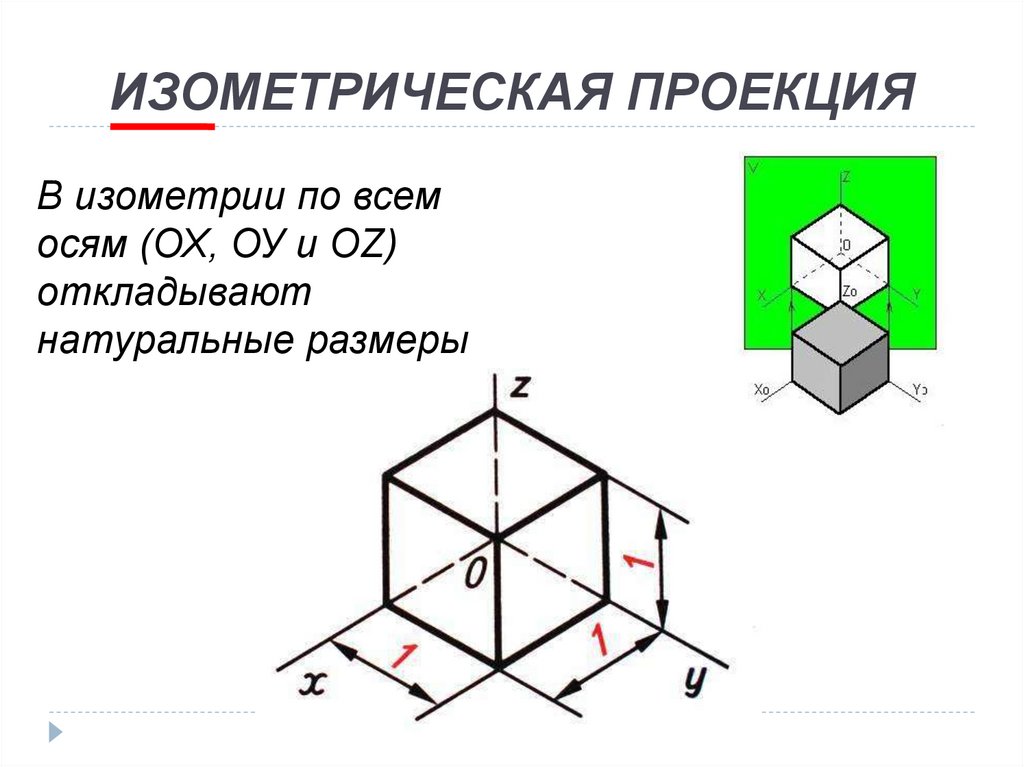
Рис. 2. Изометрия детали.
Построение в изометрии плоских фигур
Задан правильный шестиугольник АВСDЕF, расположенный параллельно горизонтальной плоскости проекций Н (П 1).
а) Строим изометрические оси (рис.3).
б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О 0 по осям откладываем натуральные величины отрезков: А 0 О 0 = АО; О 0 D 0 = ОD; К 0 О 0 = КО; О 0 Р 0 = ОР.
в) Линии, параллельные координатным осям, проводятся в изометрии также параллельно соответствующим изометрическим осям в натуральную величину.
В нашем примере стороны ВС и FЕ параллельны оси Х .
В изометрии они вычерчиваются также параллельно оси Х в натуральную величину В 0 С 0 = ВС; F 0 Е 0 = FЕ.
г)
Соединяя полученные точки, получим
изометрическое изображение шестиугольника
в плоскости Н (П 1).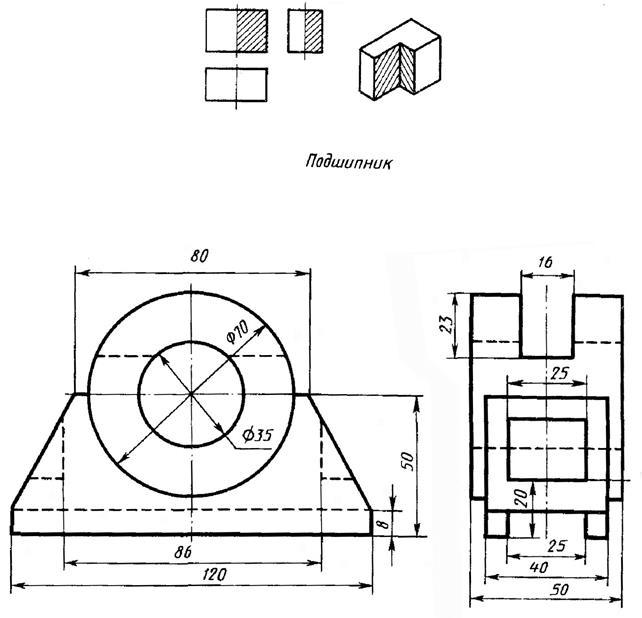
Рис. 3. Изометрическая проекция шестиугольника на чертеже
и в горизонтальной плоскости проекции
На рис. 4 представлены проекции наиболее распространенных плоских фигур в различных плоскостях проекций.
Наиболее распространённой фигурой является окружность. Изометрическая проекция окружности в общем случае представляет собой эллипс. Эллипс строят по точкам и обводят по лекалу, что в практике черчения весьма неудобно. Поэтому эллипсы заменяют овалами.
На рис. 5 построен в изометрии куб с окружностями, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается изобразить окружность. Как видно на рис. 5 большие оси овалов располагаются по большей диагонали ромбов, в которые спроецировались грани куба.
Рис. 4 Изометрическое изображение плоских фигур
а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскостиW.
Для
прямоугольной аксонометрии любого вида
правило определения главных осей эллипса
овала, в который проецируется окружность,
лежащая в какой-либо плоскости проекции,
может быть сформулировано следующим
образом: большая ось овала располагается
перпендикулярно к той аксонометрической
оси, которая отсутствует в данной
плоскости, а малая совпадает с направлением
этой оси.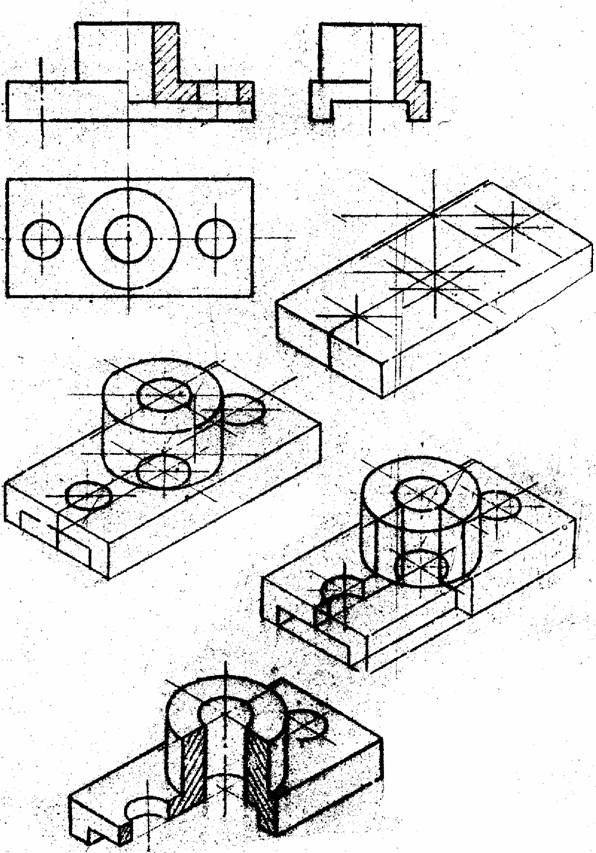
Для тoгo чтобы получить аксонометрическую проекцию предмета (рис. 106), необходимо мысленно: поместить предмет в систему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление параллельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей.
На аксонометрической плоскости проекций получают изображение — аксонометрическую проекцию предмета, а также проекции осей систем координат, которые называют аксонометрическими осями.
Аксонометрической проекцией называется изображение, полученное на аксонометрической плоскости в результате параллельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму.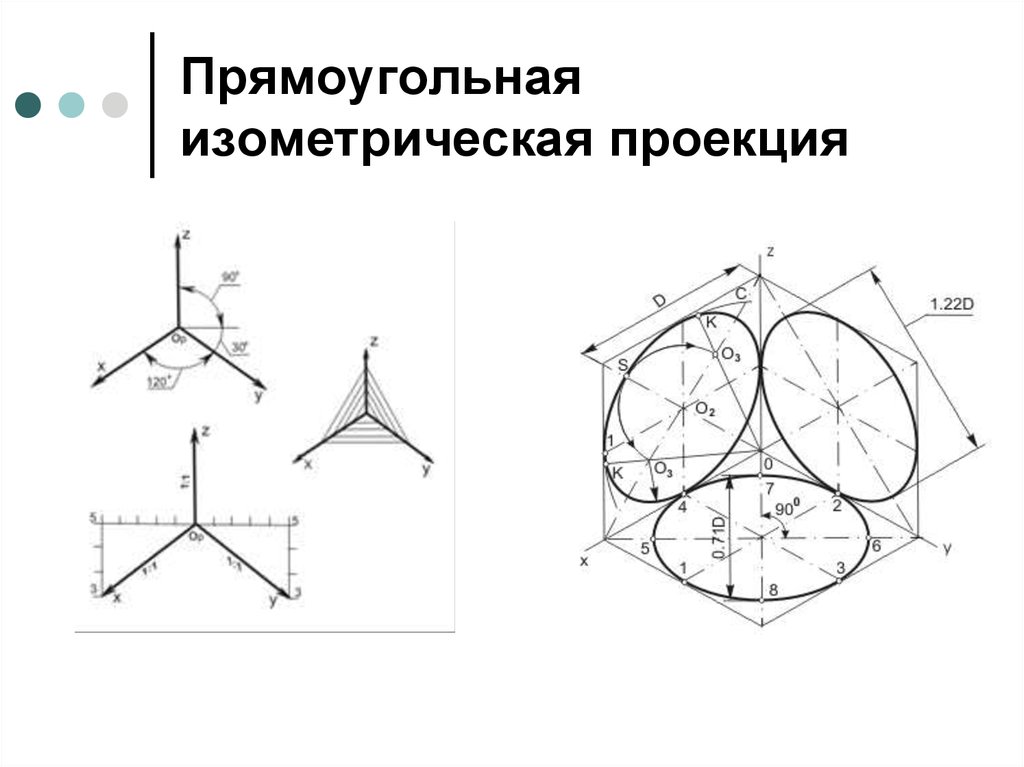
Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Система координат позволяет производить измерения по осям, определяя положение предметов в пространстве.
Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции
Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 107).
Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проекция). Изометрической проекцией (см. рис. 107, а) называется такая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью параллельного проецирования.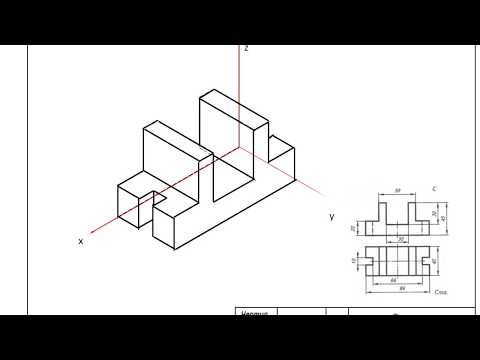
Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317-69:
а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция;
в — косоугольная фронтальная изометрическая проекция;
г — косоугольная фронтальная диметрическая проекция
Рис. 107. Продолжение: д — косоугольная горизонтальная изометрическая проекция
При этом проецирующие лучи перпендикулярны аксонометрической плоскости проекций, а координатные оси одинаково наклонены к аксонометрической плоскости проекций (cм. рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отношение размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициенты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис.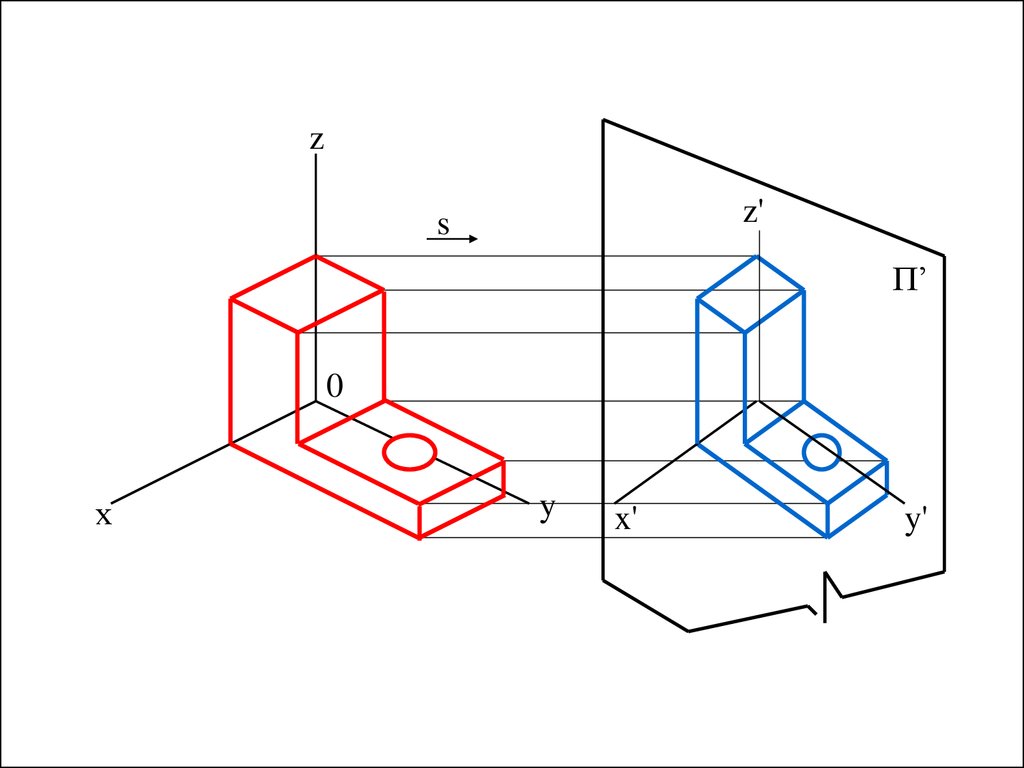 108).
108).
Рис. 108. Положение осей и коэффициенты искажения изометрической проекции
Существуют изометрические, диметрические и триметрические проекции. К изометрическим проекциям относятся такие проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковые, а величина третьего отличается от них. К триметрическим проекциям относятся проекции, у которых все коэффициенты искажения различны.
Диметрия представляет собой один из видов аксонометрической проекции. Благодаря аксонометрии при одном объемном изображении можно рассматривать объект сразу в трех измерениях. Поскольку коэффициенты искажений всех размеров по 2-м осям одинаковы, данная проекция и получила название диметрия.
Прямоугольная диметрия
При расположении оси Z» вертикально, при этом оси Х» и Y» образуют с горизонтального отрезка углы 7 градуса 10 минут и 41 градус 25 минут.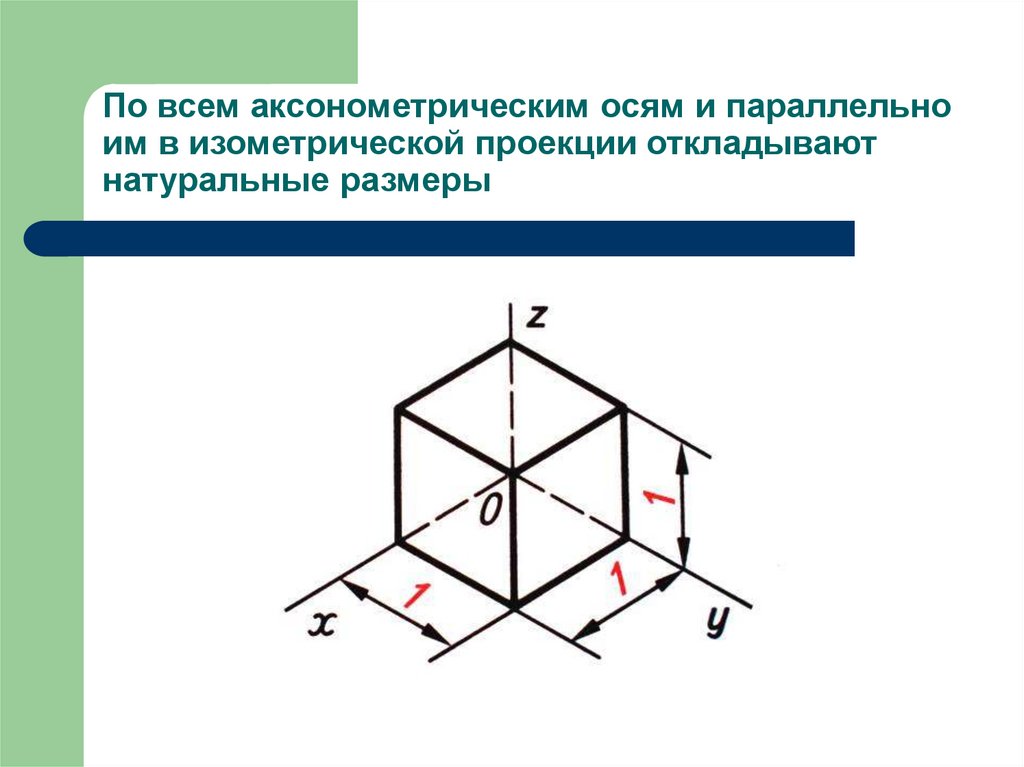 В прямоугольной диметрии коэффициент искажения по оси Y будет составлять 0,47, а по осям Х и Z в два раза больше, то есть 0,94.
В прямоугольной диметрии коэффициент искажения по оси Y будет составлять 0,47, а по осям Х и Z в два раза больше, то есть 0,94.
Чтобы осущесвить построение приближенно аксонометрические оси обычной диметрии, необходимо принять, что tg 7 градусов 10 минут равен 1/8, а tg 41 градуса 25 минут равен 7/8.
Как построить диметрию
Для начала необходимо начертить оси, чтобы изобразить предмета в диметрии. В любой прямоугольной диметрии углы, находящиеся между осями Х и Z, равны 97 градусов 10 минут, а между осями Y и Z – 131 градусов 25 минут и между Y и Х – 127 градусов 50 минут.
Теперь требуется нанести оси на ортогональные проекции изображаемого предмета, учитывая выбранное положение предмета для вычерчивания в диметрической проекции. После того, как завершите перенос на объемное ихображение габаритных размеров предмета, можете приступать к чертежу незначительных элементов на поверхности предмета.
Стоит запомнить, что окружности в каждой плоскости диметрии изображаются соответствующими эллипсами.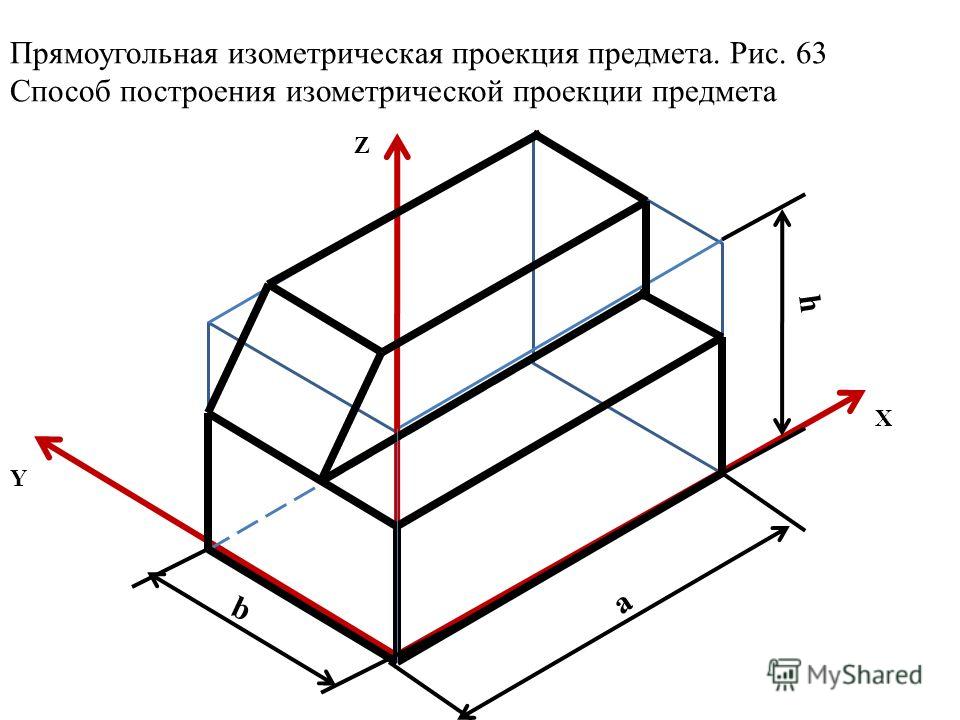 В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет составлять 1,06 диаметра нарисованной окружности. А малая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY – 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях. В плоскости ХОZ малая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.
В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет составлять 1,06 диаметра нарисованной окружности. А малая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY – 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях. В плоскости ХОZ малая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.
Чтобы получить более детально изображение, необходимо выполнить вырез через детали на диметрии. Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции выбранного квадрата на необходимую плоскость.
Что такое изометрия
Изометрия является одним из видов аксонометрической проекции, где расстояния единичных отрезков на всех 3-х осях одинаковые. Изометрическая проекция активно используется в машиностроительных чертежах, чтобы отобразить внешний вид предметов, а также в разнообразных компьютерных играх.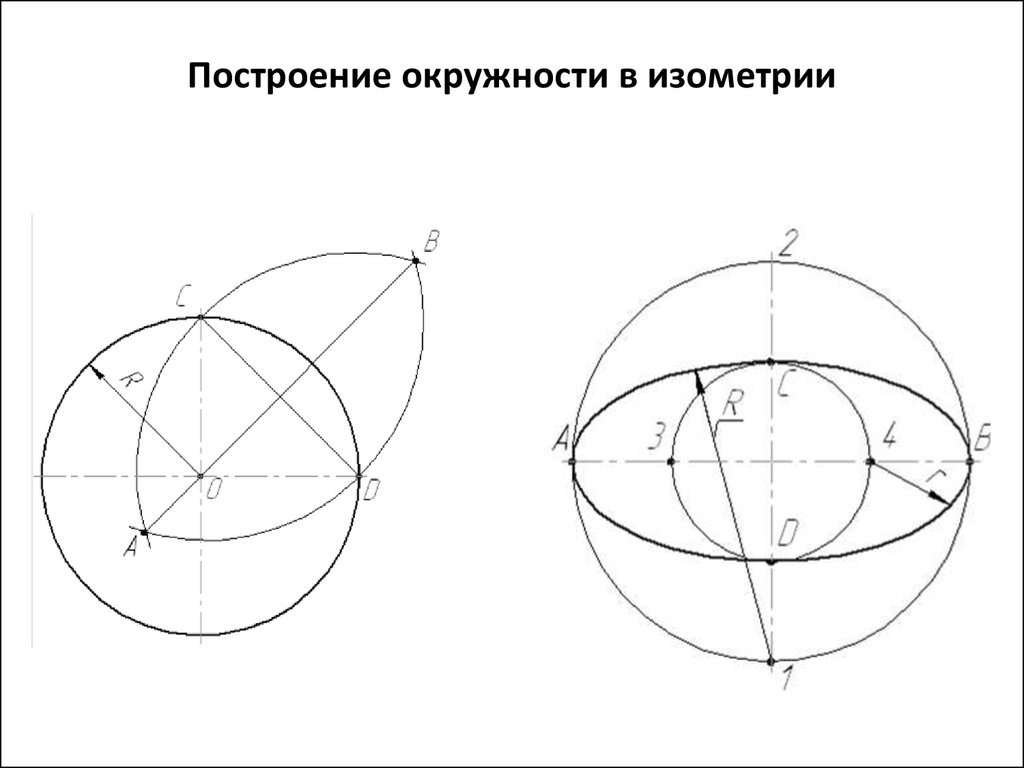
В математике изометрия известна как преобразование метрического пространства, которое сохраняет расстояние.
Прямоугольная изометрия
В прямоугольной (ортогональной) изометрии аксонометрические оси создают между собой углы, которые равны 120 градусам. Ось Z находится в вертикальном положении.
Как начертить изометрию
Построение изометрии предмета дает возможность получить наиболее выразительное представление о пространственных свойствах изображаемого объекта.
Перед тем, как начать построение чертежа в изометрической проекции, необходимо выбрать такое расположение изображаемого предмета, чтобы были максимально видны его пространственные свойства.
Теперь вам требуется определиться с видом изометрии, которую будете чертить. Существует два ее вида: прямоугольная и горизонтальная косоугольная.
Нарисуйте оси легкими тонкими линиями, чтобы изображение получилось по центру листа. Как уже раньше говорилось, углы в прямоугольном виде изометрической проекции должны составлять 120 градусов.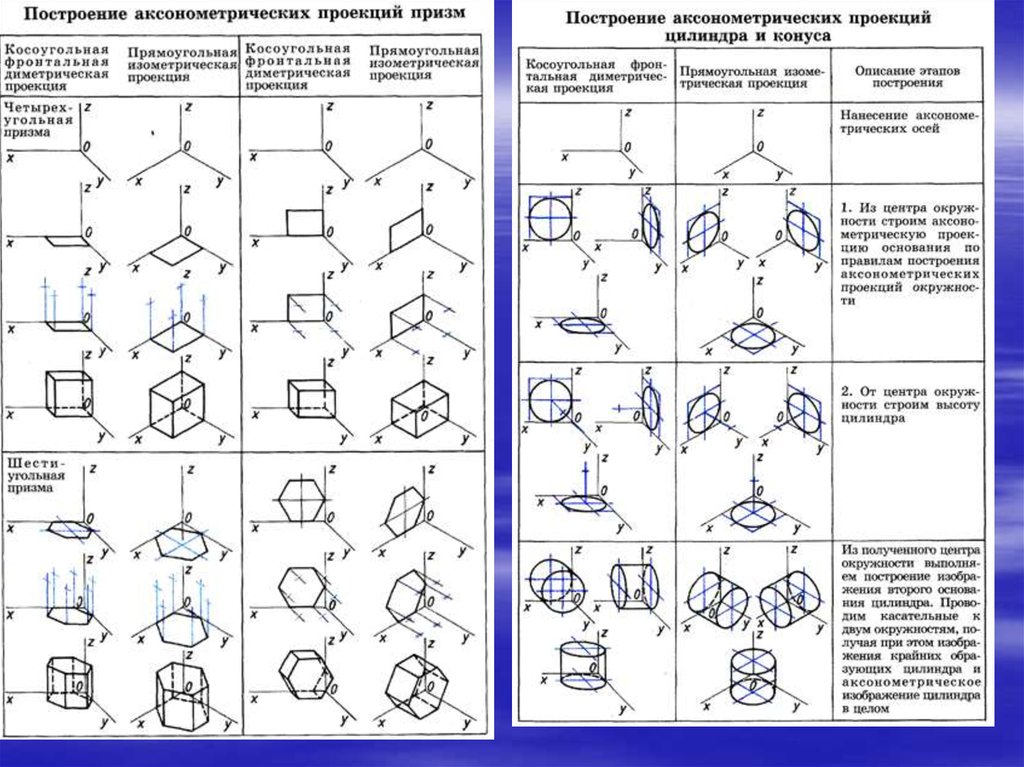
Начинайте рисовать изометрию с именно верхней поверхности изображения предмета. От углов получившейся горизонтальной поверхности нужно провести две вертикальные прямые и отложить на них соответствующие линейные размеры предмета. В изометрической проекции все линейные размеры по всех трем осям будут оставаться кратны единице. Затем последовательно требуется соединить созданные точки на вертикальных прямых. В результате получиться внешний контур предмета.
Стоит учитывать, что при изображении любого предмета в изометрической проекции видимость криволинейных деталей будет обязательно искажаться. Окружность должна изображаться эллипсом. Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.
Если изображаемый объект имеет скрытые полости ли сложные элементы, постарайтесь выполнить заштриховку. Она может быть простой либо ступенчатой, все зависит сложности элементов.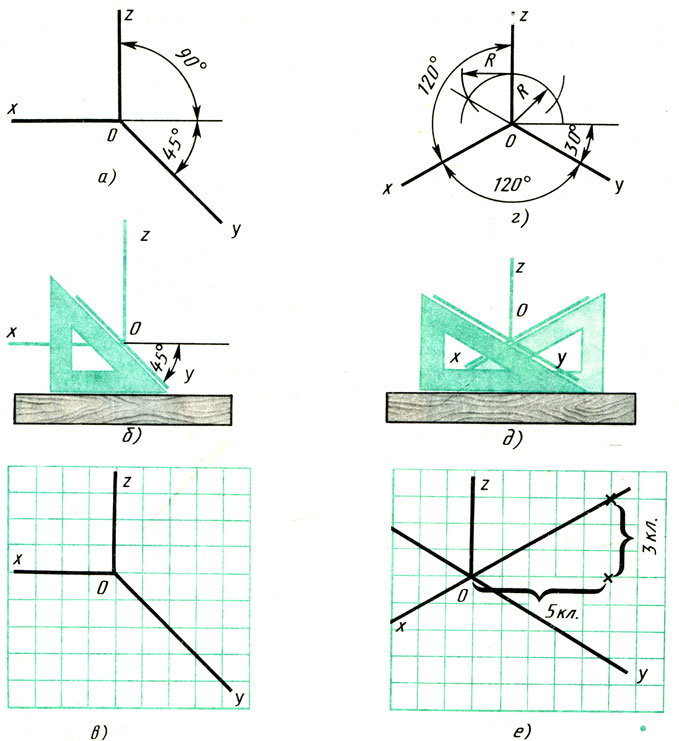
Запомните, что все построение должно выполнять строго с применением чертежных инструментов. Применяйте несколько карандашей с разными видами твердости.
Аксонометрия
Аксонометрия (от греч. axcon – ось и metreo – измеряю) дает наглядное изображение предмета на одной плоскости.
Изображение предмета в аксонометрии получается путем параллельного проецирования его на одну плоскость проекций вместе с осями прямоугольных координат, к которым этот предмет отнесен.
Коэффициенты искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине при одинаковых единицах измерения.
Натуральные коэффициенты искажения обозначают:
- по оси x – u ;
- по оси y – v ;
- по оси z – w .
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
Изометрия – все три коэффициента искажения равны между собой: u=v=w .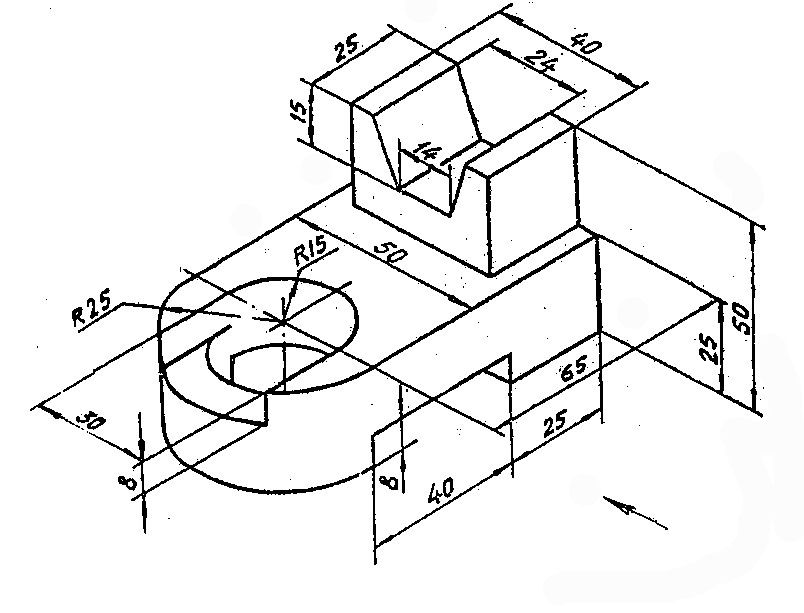
Диметрия – два коэффициента искажения равны между собой и отличаются от третьего u=v≠w ; v=w≠u ; u=w≠v .
Триметрия – все три коэффициента искажения не равны между собой: u≠v≠w .
В зависимости от направления проецирования аксонометрические проекции разделяют на прямоугольные (направление проецирования перпендикулярно плоскости аксонометрических проекций) и косоугольные (направление проецирования не перпендикулярно плоскости аксонометрических проекций).
Прямоугольные проекции
Изометрия
Положение аксонометрических осей приведено на рис.1.
Рис.1. |
Коэффициент искажения по осям x , y , z равен 0,82.
Изометрию для упрощения, как правило, выполняют без искажения по осям x , y , z , т. е. приняв коэффициент искажения равным 1.
Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т.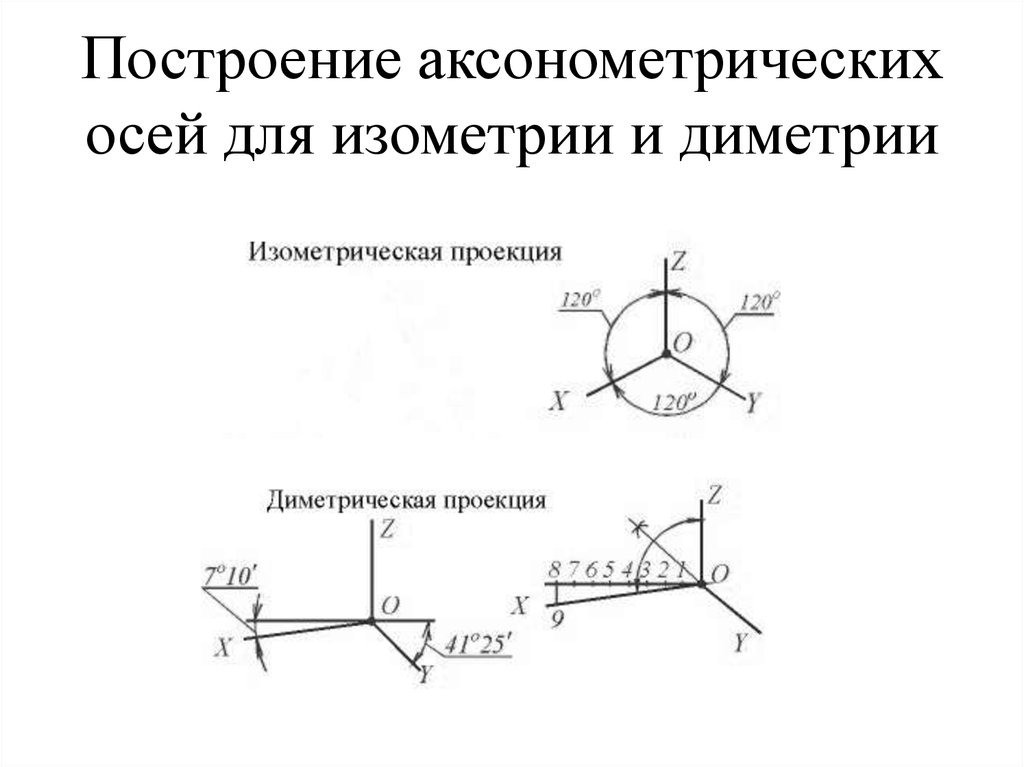 е. масштаб изображения будет М 1,22:1 .
е. масштаб изображения будет М 1,22:1 .
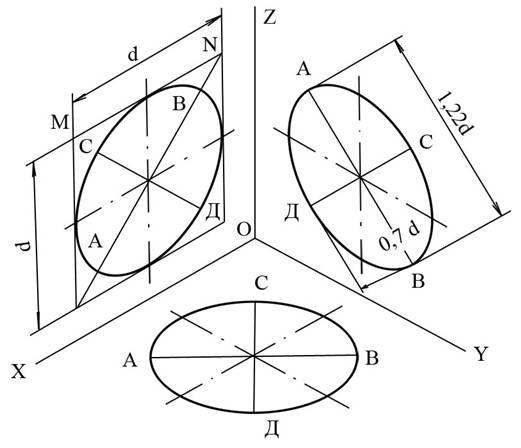
Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (рис.2). Если изометрическую проекцию выполняют без искажения по осям x , y , z , то большая ось эллипсов 1, 2, 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x , y , z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось – 0,58 диаметра окружности.
Пример изометрической проекции детали приведен на рис.3.
Диметрия
Положение аксонометрических осей приведено на рис.4.
Рис.4. |
Коэффициент искажения по оси y равен 0,47, а по осям x и z – 0,94.
Диметрическую проекцию, как правило, выполняют без искажения по осям x и z и с коэффициентом искажения 0,5 по оси y .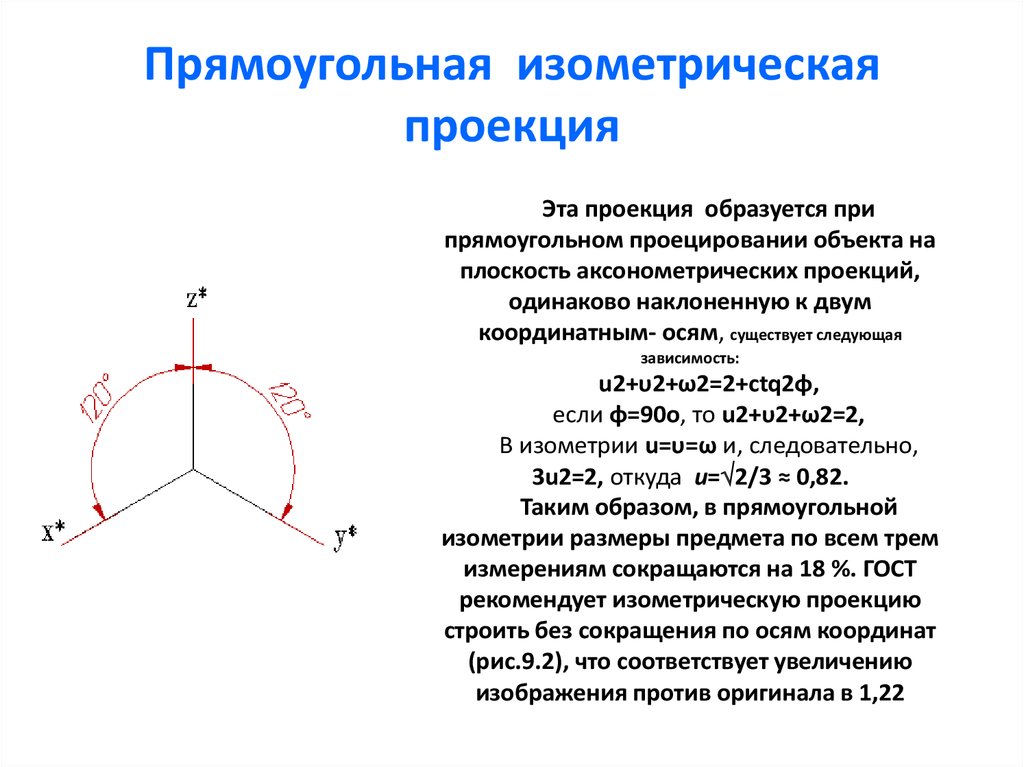
Аксонометрический масштаб будет М 1,06:1 .
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.5). Если диметрическую проекцию выполняют без искажения по осям x и z , то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95, эллипсов 2 и 3 – 0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям x и z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 – 0,9, эллипсов 2 и 3 – 0,33 диаметра окружности.
Пример диметрической проекции детали приведен на рис.6.
Косоугольные проекции
Изометрия фронтальная
Положение аксонометрических осей приведено на рис.7.
Допускается применять фронтальные изометрические проекции с углом наклона оси у 30 и 60°.
Фронтальную изометрическую проекцию выполняют без искажения по осям x , y , z .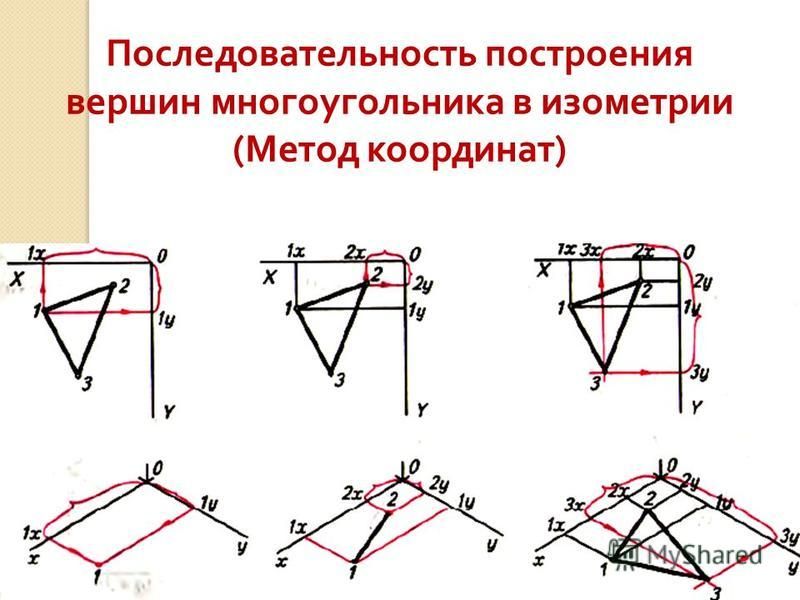
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось – 0,54 диаметра окружности.
Пример фронтальной изометрической проекции детали приведен на рис.9.
Изометрия горизонтальная
Положение аксонометрических осей приведено на рис.10.
Допускается применять горизонтальные изометрические проекции с углом наклона оси y 45 и 60°, сохраняя угол между осями x и y 90°.
Горизонтальную изометрическую проекцию выполняют без искажения по осям x , y и z .
Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций – в эллипсы (рис.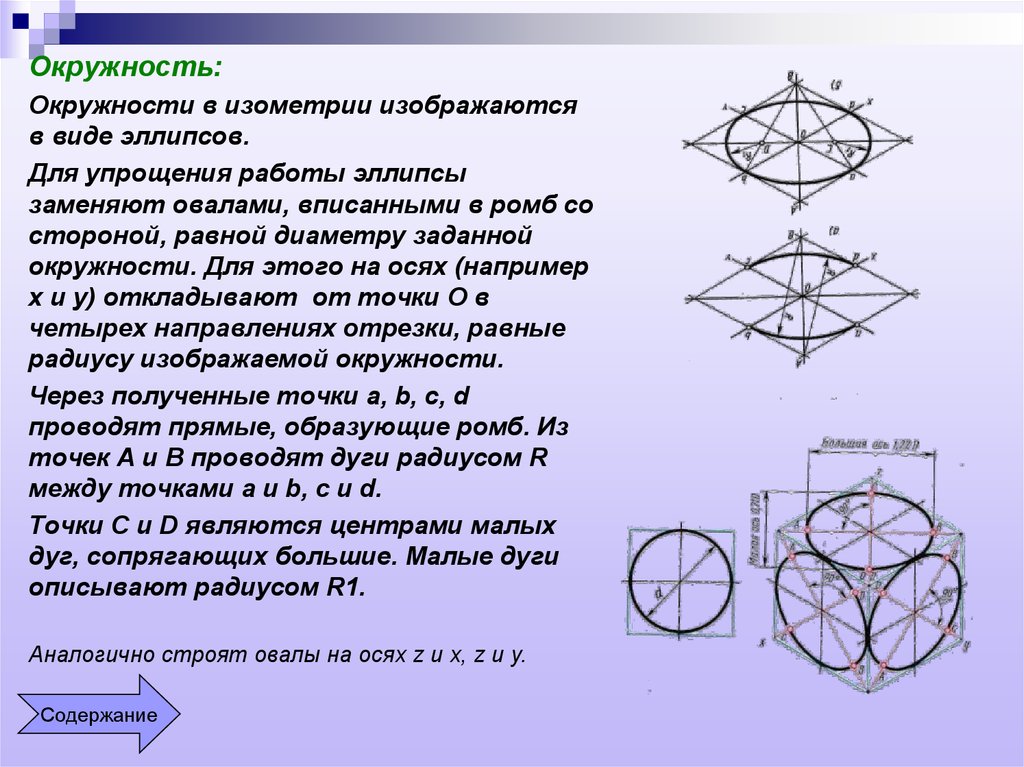 11). Большая ось эллипса 1 равна 1,37, а малая ось – 0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Оси фронтальной диметрии
11). Большая ось эллипса 1 равна 1,37, а малая ось – 0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Оси фронтальной диметрии
Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°.
Коэффициент искажения по оси y равен 0,5, а по осям x и z – 1.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось – 0,33 диаметра окружности.
Пример фронтальной диметрической проекции детали приведен на рис.15.
правила, советы, ошибки — Gamedev на DTF
Изометрия — один из самых популярных вариантов отображения игрового мира, особенно на рынке мобильного геймдева. Разбираемся, как с ней работать.
11 705 просмотров
Автор: Duncan Bell
Что такое изометрия и зачем она нужна
Изометрия — этот способ изображать предметы без перспективных искажений.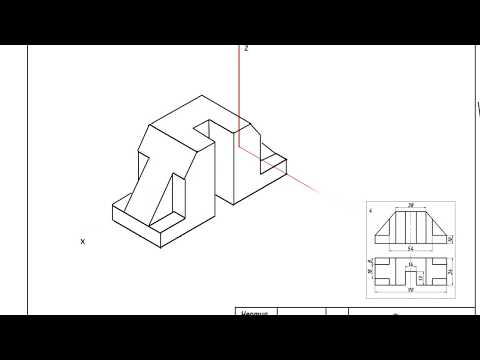 В отличие от классической реальной перспективы, где удаленные от зрителя предметы кажутся меньше, в изометрии предметы на разном расстоянии остаются одинакового размера.
В отличие от классической реальной перспективы, где удаленные от зрителя предметы кажутся меньше, в изометрии предметы на разном расстоянии остаются одинакового размера.
Перспектива (а) и изометрия (б)
Существует несколько видов изометрии: прямоугольная, косоугольная фронтальная, косоугольная горизонтальная. Они различаются положением осей X и Y и углами между ними. От этих параметров зависит изображение предмета. Это хорошо видно на примере с кубиком:
Прямоугольная (а), косоугольная фронтальная (б) и косоугольная горизонтальная (в) изометрические проекции
Чаще всего, говоря об изометрии, подразумевают прямоугольную изометрическую проекцию. В ней ось Z направлена вертикально, а оси XYZ образуют углы в 120°. Выглядит это так:
Кроме изометрии и ее разновидностей, существуют похожие на нее диметрия и триметрия. В изометрии углы между осями XYZ одинаковые и равны 120°, в диметрии равны два из трех углов, в триметрии величина всех углов между осями разная.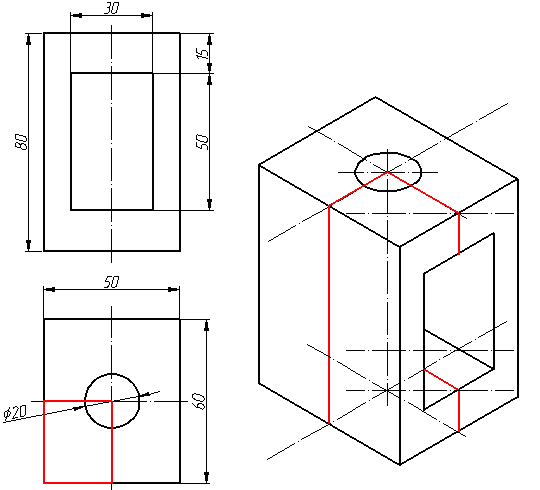 Все виды этих проекций нашли применение в геймдеве, их привычно называют одним словом — изометрия.
Все виды этих проекций нашли применение в геймдеве, их привычно называют одним словом — изометрия.
Примеры проекций, используемых в играх. Источник
Например, в игре Invisible, Inc. используется изометрическая проекция с углами 120°:
Источник
Игра Transistor — пример использования диметрии в игровой графике:
Источник
В игре Simcity 4 используется триметрическая проекция:
Источник
На заре становления изометрия позволяла создавать в играх имитацию объемного пространства с помощью плоских спрайтов. Так как объекты не меняют своих размеров в зависимости от расположения на игровом поле, компьютеру не нужно производить сложные вычисления и моделировать постоянно меняющееся окружение.
Примеры первых изометрических игр — это Zaxxon от Sega (1982), Treasure Island (1981), Q*bert (1982).
Сегодня, когда компьютеры с легкостью справляются с воспроизведением сложной графики, изометрия по-прежнему остается актуальной.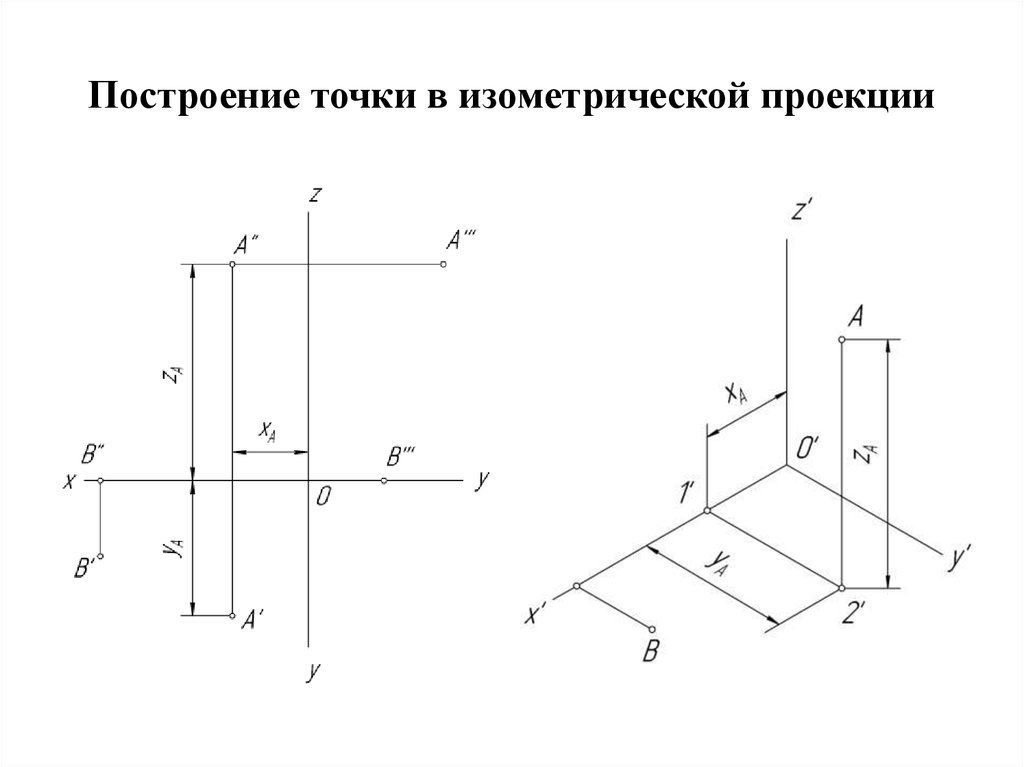 За последние несколько лет вышли такие изометрические игры как Invisible, Inc, Transistor, Disco Elysium и многие другие.
За последние несколько лет вышли такие изометрические игры как Invisible, Inc, Transistor, Disco Elysium и многие другие.
Стильная ролевая игра Disco Elysium — отличный пример современной игровой изометрии. Источник
Художественный стиль Shadowrun Returns описывают как совмещающий 2D и 3D. Источник
Изометрия остается популярной в RPG и стратегиях и повсеместно встречается в мобильных играх. Она оставляет разработчикам пространство для экспериментов и в создании визуала, и в разработке геймплея.
Mobile Legends: Bang Bang — одна из популярнейших MOBA-игр в мире. Источник
Как рисовать изометрию
Строим изометрическую сетку
В рисовании изометрии главную роль играет сетка, относительно которой художник будет выстраивать все объекты. Это может быть как классическая изометрическая сетка с углами между осями 120°, так и эксклюзивная для определенного проекта — параметры сетки могут определяться техническим заданием или самим художником.
Стандартная изометрическая сетка с углами 120°
Изометрия — отличный вариант для тех, кто не любит ломать голову над перспективными сокращениями. Нарисовав сетку один раз, вы ориентируете все горизонтали в рисунке к параллели с этой сеткой, а вертикали оставляете без изменений.
Небольшая геометрическая композиция, выстроенная по изометрической сетке. Видно, что рёбра лежат параллельно линиям сетки.
Стандартный вариант игровой изометрической сетки — диметрия с соотношением сторон 2:1.
Кадр из видео
Существует множество способов создания изометрической сетки. Можно отрисовать ее вручную, можно взять шаблон из интернета, можно настроить направляющие в Photoshop.
Один из простых и быстрых способов — строим сетку с углами 90°:
Поворачиваем ее на 45°, нажимаем «применить»:
Затем отключаем привязку высоты к ширине и меняем высоту со 100% на 50%.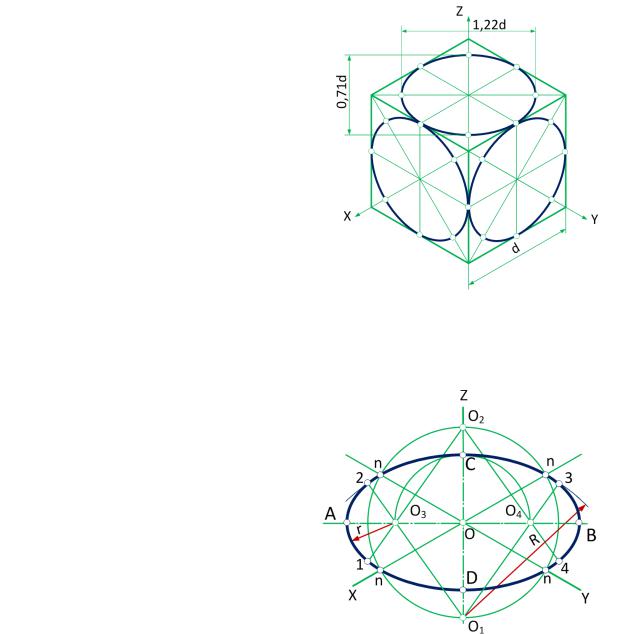 В итоге получится сетка с соотношением сторон 2:1, часто используемая в изометрических проектах:
В итоге получится сетка с соотношением сторон 2:1, часто используемая в изометрических проектах:
Процент высоты можно менять в зависимости от художественной задачи. В результате будет меняться раскрытие сетки
Важно отметить, что, чем больше сетка раскрыта, тем лучше будут видны объекты (одни не будут загораживать другие), но при этом мы можем показать меньше игрового поля. И наоборот, при небольшом раскрытии сетки видно больше игрового пространства, но объекты могут наползать друг на друга. Учитывайте этот нюанс при выборе угла сетки.
Диметрическая сетка и сетка с меньшим углом раскрытия
Строим простые фигуры по сетке
Рисование начинается с построения базовых форм. Изометрия не исключение. Ориентируемся на сетку и строим примитивные фигуры.
Если с квадратами, прямоугольниками треугольниками все понятно — их необходимо просто вписать в необходимое количество плиток, то как быть с кругом?
В случае с кругом нужно следить, чтобы крайние точки окружности с каждой стороны совпадали с углами квадратов как на картинке (отмечены точками):
Если ориентироваться по точкам сложно, можно провести через центр окружности два отрезка — своеобразную крестовину — и, ориентируясь по ней, масштабировать круг до нужных пропорций, чтобы крестовина совпала с сеткой.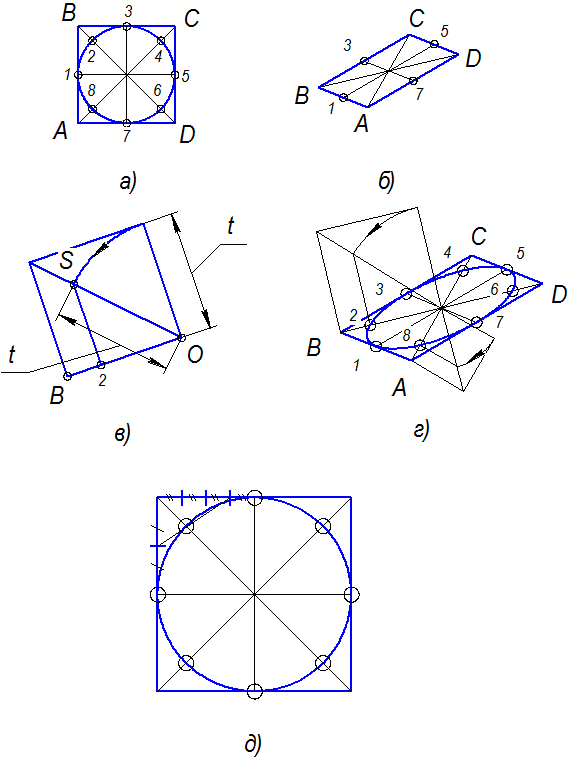
Строим объемные фигуры по сетке
Переходим к объемным фигурам. На основе квадрата строим куб. Копируем квадрат в основе на две клетки вверх и соединяем углы вертикалями. С помощью оттенков можно показать объем.
Подобным образом строим параллелепипед на основе прямоугольника.
Пирамиду также довольно легко построить на основе квадрата или прямоугольника. Проводим вертикаль из центра основания на нужную высоту и от вершины проводим прямые к углам — ребра пирамиды.
В основании цилиндра и конуса лежит круг. Копируем круг основания на нужную высоту и соединяем края вертикалями — получится цилиндр.
Проводим из центра вертикаль на нужную высоту, находим вершину и от нее проводим наклонные линии к краям круга. Получится конус.
Освоившись с базой, можно переходить к более сложным формам.
Прежде чем приступать к непосредственно построению в изометрии, пробуйте сначала свободно поскетчить, не ограничивайте воображение.
Когда найдете нужную форму — переходите к построению по сетке.
Домик в изометрии
Классический кейс казуальных игр — изометрический домик. Разбиваем концепт на простые формы и отстраиваем по сетке.
Начинаем с болванки параллелепипеда — основания домика. Его довольно легко построить по изометрической сетке.
Переходим к крыше. Проводим вертикали одинаковой длины по центрам меньших граней — получатся центральные оси, относительно которых будем строить крышу. Параллельно сетке проводим между этими осями конёк, а также боковые свесы. Соединяем свесы с коньком, чтобы получить скаты крыши.
Относительно оси строим дверь и окно. На скате крыши также строим центральную ось, опираясь на нее рисуем слуховое окошко. Вертикали остаются вертикальными, горизонтали строим по сетке.
Рисуем толщину стен в оконных проемах, добавляем детали.
Отметим, что в данном примере относительно центральных осей в обе стороны отложено одинаковое расстояние частей домика. На начальных этапах обучения так проще ориентироваться в построении и деталях.
На начальных этапах обучения так проще ориентироваться в построении и деталях.
Небольшое отступление: не всегда детали расположены симметрично относительно центральной оси, есть и примеры с асимметрией. Но чаще всего в геймдеве мы встречаем примеры симметричного построения объектов.
Завершаем лайн, добавляя финальные штрихи и детали, говорящие о характере домика.
Внутреннее убранство домика тоже можно построить примитивами по сетке, а затем дополнить мелочами.
Бэкграунд и окружение играют важную роль в изометрических играх — пользователь видит все игровое пространство или бОльшую его часть. Уделите этому особое внимание.
Дерево в изометрии
Органические объекты (деревья, кусты, камни и т.п.) с одной стороны проще нарисовать в изометрии, так как это плавные формы и там почти нет таких строгих построений. Но с другой стороны, в их изображении проще запутаться.
В этом примере в основании ствола дерева — окружности разных размеров.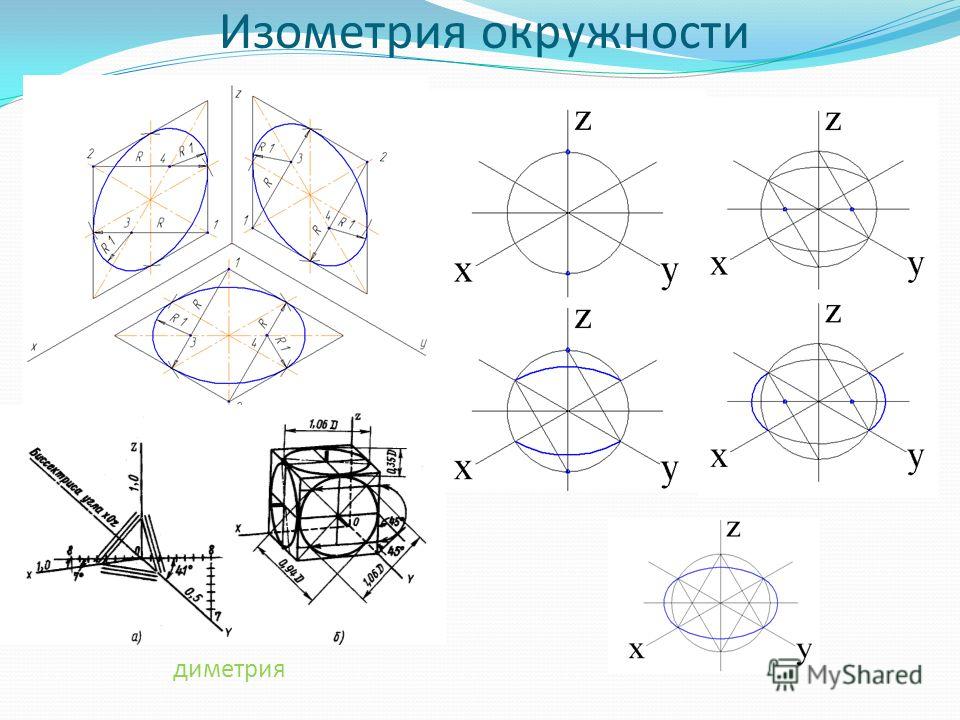
Простраиваем ствол и ветки. Важно, чтобы дерево вписывалось в 3D-пространство, чтобы ветки и крона вокруг ствола была направлены во все части света почти сферически. Поэтому, чтобы сделать дерево более объемным, направляем ветви вдоль разных линий сетки.
Простыми формами намечаем крону.
Детализируем дерево, дополняем его листьями и корнями, также направляя их в разные стороны.
Завершаем рисунок деталями.
Персонажи в изометрии
Изометрических персонажей тоже рисуют на основании примитивов. В данном случае в основании базовых частей персонажа лежат эллипсы разных размеров.
Важно, чтобы симметричные части фигуры (в данном случае, например, края прически, подол платья) находились на одном уровне. Проверяйте их линиями, параллельными сетке.
Важно следить за соотношением масштабов объектов рисунка: то есть чтобы персонаж помещался в дверь, а не был размером с дом. В этом примере объекты сомасштабны, поэтому выглядят убедительно.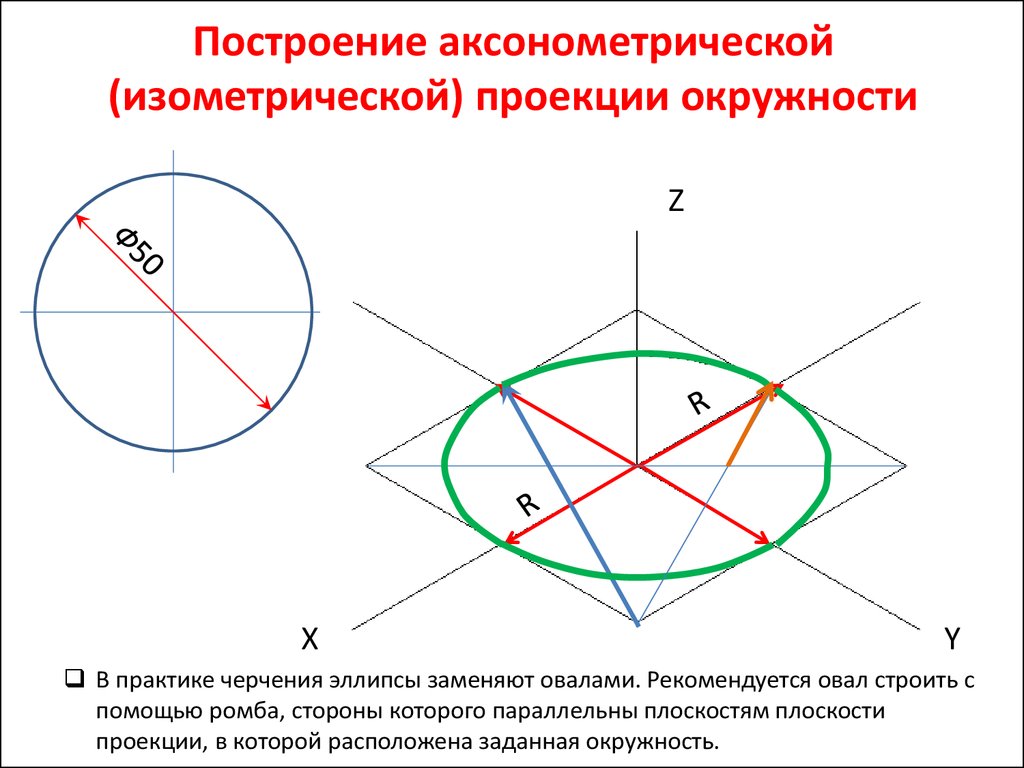
Ошибки в рисовании изометрии
Несколько типичных ошибок художников, начинающих работать с изометрией:
- Отсутствие внутреннего построения. Это происходит, когда художник берется за детали, прежде чем построить объекты примитивами. В мелочах легко запутаться и можно выбиться из изометрической сетки. Помните: сначала строим простые формы, проверяем их на соответствие сетке, а потом переходим к подробной проработке.
- Неправильное построение кривых форм. Кривые в изометрии строить несколько сложнее, чем прямые линии. Внимательно следите за правильным построением эллипсов на сетке, за расположением относительно центральной оси.
- Несоответствие объектов одной изометрической сетке. Все нарисованные объекты должны быть ориентированы одинаково. Нельзя в проекте для одних спрайтов применять одну сетку, а для других — другую.
- Разный уровень детализации. Следите, чтобы количество деталей у всех объектов было примерно одинаковым.

- Разница масштабов. Когда художник перестает соотносить объекты рисунка между собой, может получиться, что персонаж станет крупнее домика и не сможет с ним взаимодействовать (пройти в дверь, заглянуть в окно и т.п.) Важно сравнивать размеры персонажей с окружением.
Текст написала Стефания Косюг, автор в Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.
Урок изометрического рисования и бесплатная изометрическая бумага
Партнерские ссылки
Следуйте этому бесплатному уроку, пока вы и ваши ученики изучаете основы изометрического рисования. Изометрическая бумага с тремя различными размерами сетки включена, так что вы можете начать рисовать прямо сейчас!
Что такое изометрический рисунок…
Изометрический рисунок — это способ представления трехмерных объектов на двухмерной поверхности.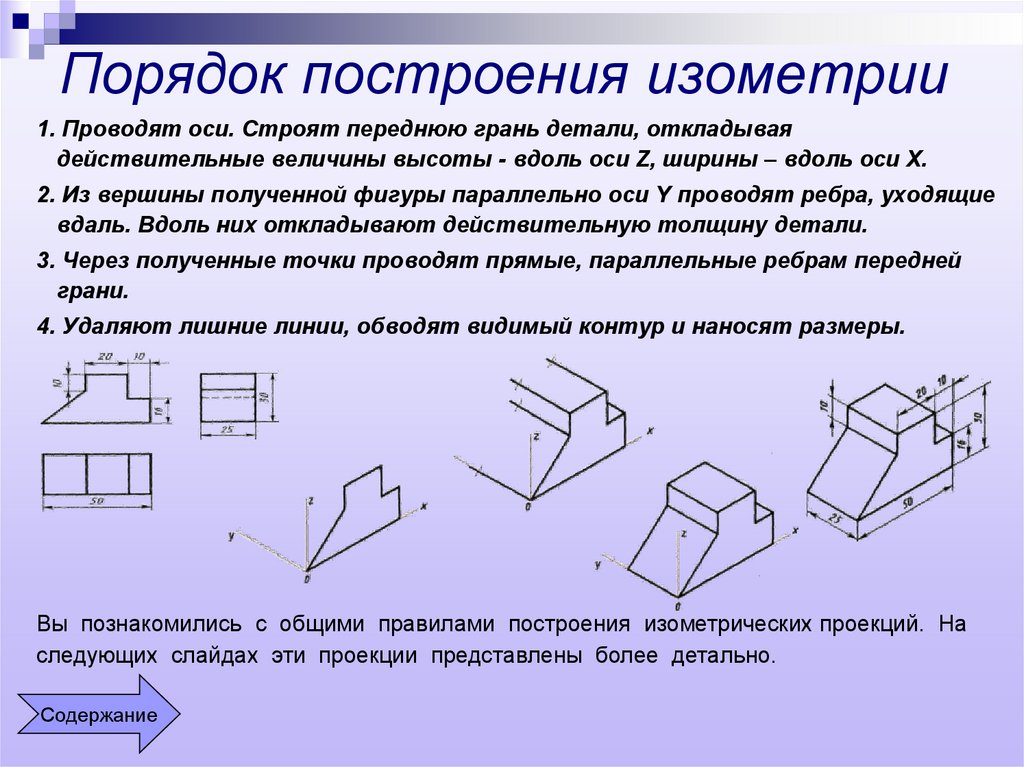 В изометрическом рисунке вы видите три стороны объекта одинаково. Как будто объект наклонен вперед на переднем углу.
В изометрическом рисунке вы видите три стороны объекта одинаково. Как будто объект наклонен вперед на переднем углу.
Изометрическое рисование отличается от рисования в одной или двух точках, потому что в изометрических рисунках отсутствует точка схода.
Что отличает изометрический рисунок от любого другого рисунка, так это использование углов. Оси изометрической сетки рисуются так, что горизонтальные оси проходят под углом 30 градусов. Как будто вертикальные оси остаются в традиционном вертикальном положении, а горизонтальные оси смещены на тридцать градусов.
Проще говоря, вертикальные линии остаются вертикальными. Горизонтальные линии сдвигаются на тридцать градусов. В изометрическом рисунке нет горизонтальных линий!
Что такое изометрическая бумага….
Изометрическая бумага — это просто бумага с изометрической сеткой, на которой можно рисовать. В то время как вы и ваши ученики всегда можете нарисовать свою собственную изометрическую сетку, эта бесплатная изометрическая бумага для печати означает, что вы можете начать рисовать сегодня!
Построение собственного изометрического рисунка на бумаге может быть полезным упражнением для старших школьников, но ваши младшие ученики могут испытать эту концепцию без разочарования!
Какова цель изометрического рисования….
Обучение детей рисованию трехмерных форм на изометрической бумаге — это еще один инструмент, который вы можете дать им, чтобы помочь им понять концепцию формы и восприятия.
Изометрические чертежи часто используются инженерами, их можно увидеть в технических иллюстрациях, инструкциях и т. д.
Как нарисовать куб в изометрической манере….
ШАГ 1- Нарисуйте две параллельные линии . Эти линии должны быть одинаковой длины. Они являются стороной куба.
ШАГ 2- Соедините верхнюю часть одной вертикальной линии с верхней частью другой вертикальной линии. Сделайте то же самое с нижней частью вертикальных линий. Это создаст параллелограмм .
ШАГ 3. Придайте кубу глубину . Решите, в какую сторону будет ориентирована ваша форма. На той стороне, которая, как вы хотите, выглядит уходящей в пространство, нарисуйте линию, которая начинается в углу и является глубиной вашей формы. Нарисуйте линию одинаковой длины на трех сторонах формы рядом с верхом и по бокам.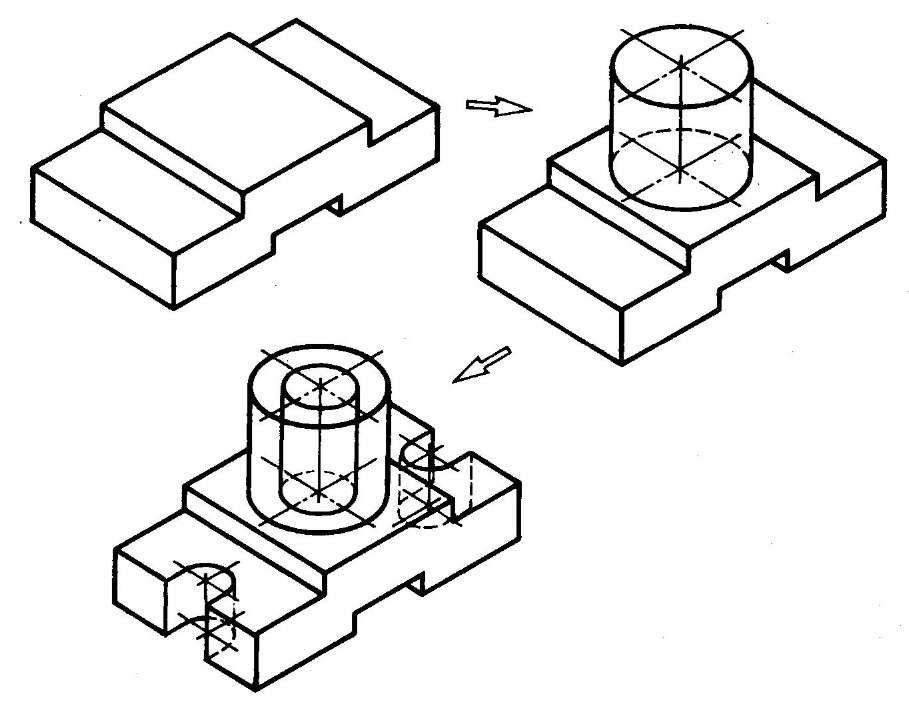 (В самом нижнем углу это не требуется.)
(В самом нижнем углу это не требуется.)
ШАГ 4- Нарисуйте линию, соединяющую заднюю часть верхней части и боковую сторону формы. Ваш куб готов.
Хотите вместе нарисовать изометрическую форму? Следуйте вместе с видео выше!
Приведение изометрического рисунка в действие….
Помимо изучения огромного словарного запаса, навыки изометрического рисования можно использовать для рисования собственных учебных пособий, передачи полезной научной информации или создания собственных натюрмортов.
Вы хотите изометрическую бумагу для печати, чтобы упростить создание собственных изометрических рисунков?
Я сделал три разных варианта изометрической бумаги для использования дома или в классе. Меньшие изометрические сетки отлично подходят для старшеклассников и более подробных рисунков. Большие изометрические сетки идеально подходят для младших школьников или начинающих!
Они абсолютно бесплатны для подписчиков My Kitchen Table Classroom. Вы можете стать абонентом KTC, используя форму ниже.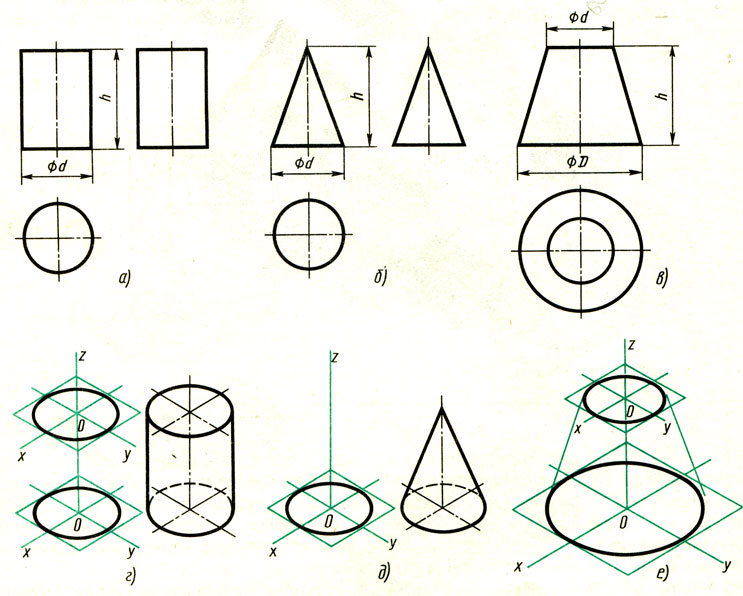 Затем перейдите в свой почтовый ящик и подтвердите, что хотите стать подписчиком. После подтверждения вы сразу же получите загрузку.
Затем перейдите в свой почтовый ящик и подтвердите, что хотите стать подписчиком. После подтверждения вы сразу же получите загрузку.
Подписавшись, вы также будете получать мой еженедельный информационный бюллетень. В нем собраны все мои лучшие новые идеи и ресурсы для печати специально для вас!
Вы уже являетесь подписчиком KTC…
Если вы уже являетесь подписчиком Kitchen Table Classroom, у вас есть два варианта получения этой изометрической сетки!
Вариант 1. Используйте форму выше. Выполните те же действия, и вы получите загрузку как можно скорее! И вы не будете получать от меня двойные электронные письма — обещаю!
Вариант 2. Когда вы станете подписчиком, вы получите специальный пароль, который даст вам доступ к моей бесплатной библиотеке ресурсов. Там вы сможете найти эти изометрические сетки и сотни других бесплатных материалов для печати! (Да, я сказал сотни!)
Вам понравился этот урок изометрического рисования и бесплатная изометрическая бумага?
Тогда поделитесь этим постом! Каждый раз, когда вы делитесь этим, это очень помогает мне!
Учебное пособие по пиксельной графике.
 Как рисовать камни в изометрическом виде
Как рисовать камни в изометрическом видеЧто такое изометрический вид?
Изометрический вид — это вид в перспективе под определенным углом, при котором все 3D-объекты имеют одинаковый масштаб и одинаковую точку обзора независимо от их местоположения и расстояния.
Изометрическая перспектива и 2 точечная перспективаИзометрический вид довольно популярен в пиксель-арте благодаря этой особенности — вы можете дублировать объект в вашей сцене без изменения его размера благодаря перспективе .
Но в Pixelart, особенно в игровой индустрии, изометрический вид немного отличается от исходной геометрии (где оси образуют угол 120°). Чтобы получить красивые диагонали в пиксель-арте, этот угол немного отличается, создавая так называемую изометрическую перспективу 2:1 .
истинная изометрия по сравнению с изометрией 2:1 Как вы можете видеть, в реальной изометрической перспективе линия выглядела бы шаткой по сравнению с прямой и обычной линией изометрии 2:1.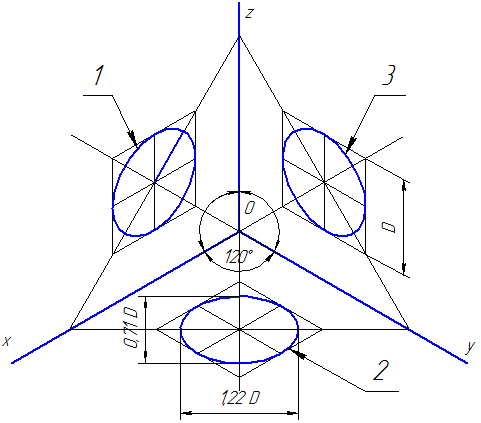
Как настроить холст
Хорошо, но как настроить холст, если угол отличается от истинной изометрической перспективы?
Не волнуйтесь, с большим количеством программного обеспечения (если не со всеми) вы можете сделать изометрический вид 2:1, а также включить сетку, чтобы помочь вам.
Вот как настроить изометрический вид в 3 разных программах:
- Photoshop (самое популярное программное обеспечение в течение долгого времени во многих областях): Ну, это самое популярное программное обеспечение, но здесь нет возможности создать сетку iso… вы должны сделать это самостоятельно. К счастью, в Интернете есть много информации и файлов, которые помогут вам или предоставят вам готовые шаблоны.
СОВЕТ: Если вы хорошо знаете Photoshop, вы можете делать кисти с диагональными линиями в разных направлениях iso 2:1.
- Aseprite (Самая популярная программа для пиксель-арта): Здесь тоже нет сетки… Но с помощью инструмента линии, зажав клавишу Shift, можно получить правильный угол для изометрической перспективы.
 Вы можете легко создать свою сетку или просто нарисовать свой объем. Очень прост в использовании. Лучшее средство, которое я знаю.
Вы можете легко создать свою сетку или просто нарисовать свой объем. Очень прост в использовании. Лучшее средство, которое я знаю.
- Affinity Photo (тот, который я использую): с помощью этого программного обеспечения вы, наконец, можете напрямую создавать идеальную сетку iso 2:1. В опции сетки вы можете создать нужный тип сетки, количество секций и т. д., а также настроить опцию магнитной сетки, чтобы ваш пиксель привязывался к этой сетке.
Используйте инструмент «Пиксель» и клавишу Shift для рисования линий.
Важность референсов
Прежде чем приступить к рисованию, я хочу уделить минуту, чтобы поговорить о важности референсных изображений. В сознании многих (в том числе и моего, не так давно) использование ссылок считается читерством. Но как ты можешь рисовать что-то хорошее, если ты не изучил реальные изображения? Как можно представить реалистичный камень, если не знаешь, как он выглядит в природе? Кроме того, существует несколько типов камней! Так что пользуйтесь ссылками, пожалуйста!
И это работает для всего! Портрет, поза, объект, пейзажи, животные.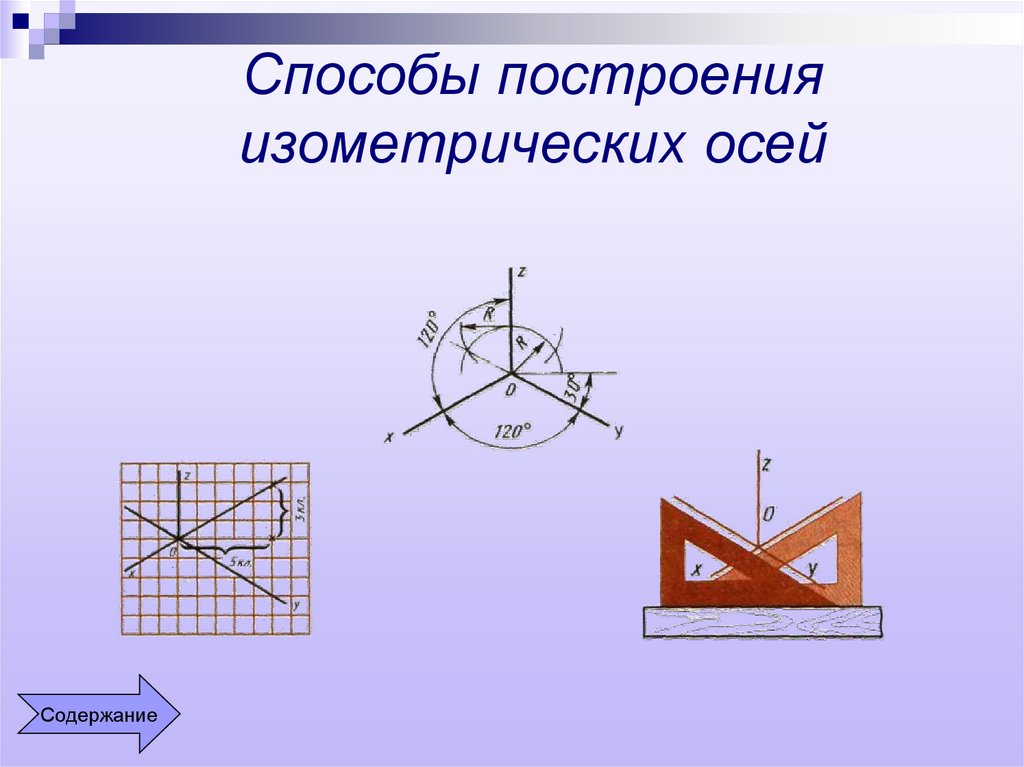 ..
..
Ваши лучшие друзья на данный момент…
СОВЕТ: Самый простой способ найти референсы? Просто выйдите на улицу и осмотритесь!
Рисование формы
Итак, изучив несколько камней и камней и получив представление о том, что вы хотите, мы можем приступить к рисованию. В пиксель-арте и в рисовании в целом есть два основных способа начать работу: нарисовать грубый набросок или нарисовать плоскими цветами (конечно, между этими двумя стилями есть несколько золотых). Проще всего начать с чернового наброска. Сделайте это прямо на компьютере или на листе бумаги; тебе решать.
В изометрической перспективе сетка представляет собой землю, а объекты всегда будут иметь три видимые стороны. Таким образом, ваш камень всегда будет показывать свою вершину и две другие стороны, в отличие от классической перспективы, где вы можете рисовать объект с разных точек зрения (в зависимости от того, где находится линия горизонта).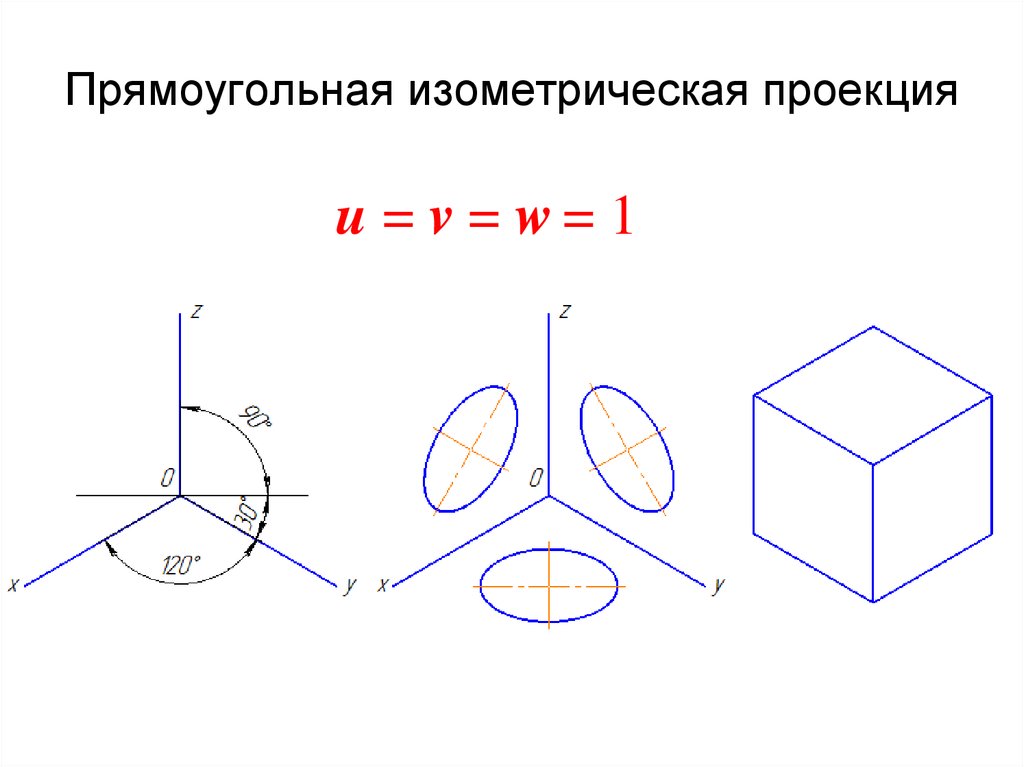
Если вы не знакомы с трехмерными объектами, не стесняйтесь создавать структуру, чтобы помочь себе. Давайте начнем с простой коробки, которая будет представлять ваш камень.
Теперь вы можете обработать эту область, чтобы создать что-то похожее на камень. Используйте зеленую структуру, чтобы разделить камень на три вида (сверху, спереди, сбоку), и попытайтесь сломать прямые линии и создать другие грани, чтобы придать камню лучший вид.
СОВЕТ: Попробуйте нарисовать что-нибудь случайное, созданное природой и временем. Если вы сделали группу камней, придайте им разные формы и направления, чтобы избежать повторения.
Как написано в совете выше, мы хотим получить что-то более рандомное. Итак, пора забыть о кубической форме. Попробуйте добавить несколько томов, чтобы получить что-то более сложное. Вы можете временно добавить новые поля, чтобы упростить создание вариантов.
Когда форма камня вас устроит, можно переходить к раскраске.
Добавление цветов
Есть несколько способов выбрать цвета! Первый и простой — получить эталонное изображение. Вы также можете найти цветовые палитры на веб-сайте Lospec.com, это хороший способ использовать ограниченные цвета в качестве традиционного пиксельного художника. Или вы можете начать с нуля и выбрать свои тона.
Вы также можете найти цветовые палитры на веб-сайте Lospec.com, это хороший способ использовать ограниченные цвета в качестве традиционного пиксельного художника. Или вы можете начать с нуля и выбрать свои тона.
СОВЕТ: Когда я выбираю более светлый или более темный цвет, я также перемещаю ползунок оттенка. После того, как вы выбрали направление для более светлых цветов, идите в противоположном направлении для более темных.
СОВЕТ: Не используйте чистый серый цвет, добавьте в него немного цвета, чтобы оживить камень.
Теперь, когда вы выбрали палитру, заполните камень средним тоном.
СОВЕТ: сделайте набросок низкой непрозрачностью, чтобы следить за общей формой и идеей.
Выберите световую точку
Свет — еще один важный элемент искусства. С хорошим знанием освещения вы получите более реалистичную сцену и, следовательно, более эффектный арт! Опять же, не стесняйтесь изучать реальный мир.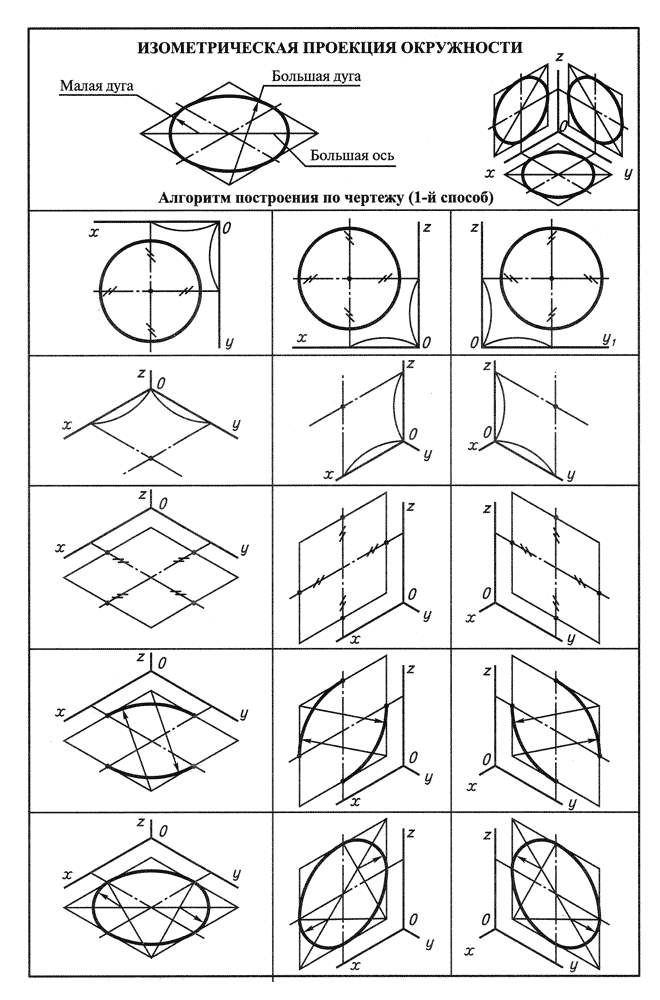 Загляните в Интернет, выйдите на улицу, поиграйте с фонариком…
Загляните в Интернет, выйдите на улицу, поиграйте с фонариком…
В изометрической проекции вы можете поместить источник света куда угодно, как и в любой другой перспективе, но наиболее естественным способом является выбор верхнего источника света, такого как солнце.
СОВЕТ: Направьте источник света вверху справа или вверху слева, чтобы создать контраст на объекте. Это будет выглядеть более трехмерно.
Теперь возьмите еще два цвета, один темнее и один светлее среднего тона. Не забывайте о своих коробках и трехстороннем виде и начинайте добавлять свет и тени, как на кубе. Все, что вверху, будет освещено, а все, что слева, будет в тени.
Нанесите на камень.
СОВЕТ: Не забудьте про тени. Объекты выше будут скрывать свет для нижележащих объектов.
Добавьте более темные тени, чтобы разграничить формы. Не забывайте избегать регулярности.
Теперь у вас есть камень!
Детали и полировка
Вы можете оставить свой камень как есть и при этом гордиться собой. Или вы можете добавить некоторые детали, чтобы придать ему больше жизни.
Или вы можете добавить некоторые детали, чтобы придать ему больше жизни.
Этот вид камня не является гладким, поэтому вы можете добавить несколько ребер, чтобы показать текстуру. Имейте в виду свет.
Вы можете добавить больше цветов, чтобы усилить контраст и придать фигурам больше объема.
Теперь идем дальше и добавляем трещины и растительность.
СОВЕТ: Попробуйте рассказать историю с помощью своего произведения. Будет легче узнать, какие детали вы можете добавить и где.
СОВЕТ: Отдайте предпочтение читабельности, а не количеству деталей, особенно в небольших пиксельных изображениях.
Заключение
Теперь у вас есть представление о том, как нарисовать камень в изометрической перспективе, или, по крайней мере, как это делаю я… потому что художников столько же, сколько и способов это сделать. Так что не стесняйтесь смотреть на разных художников и сохранять некоторые элементы, смешивать их и создавать свой собственный стиль.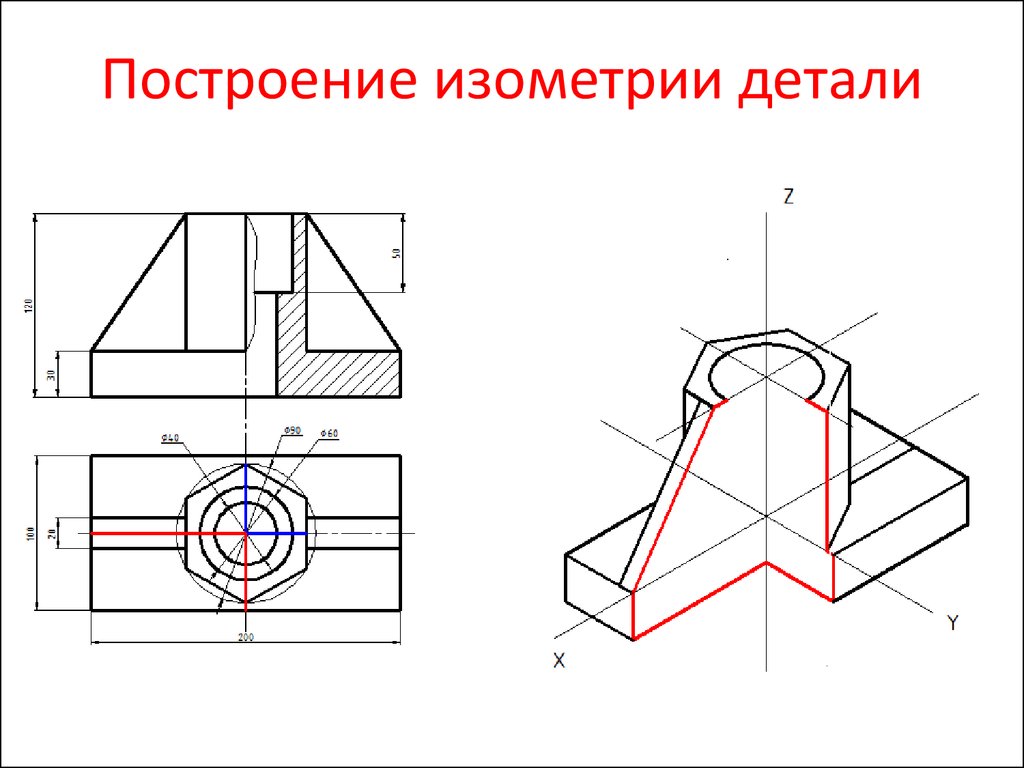

 Когда найдете нужную форму — переходите к построению по сетке.
Когда найдете нужную форму — переходите к построению по сетке.
 Вы можете легко создать свою сетку или просто нарисовать свой объем. Очень прост в использовании. Лучшее средство, которое я знаю.
Вы можете легко создать свою сетку или просто нарисовать свой объем. Очень прост в использовании. Лучшее средство, которое я знаю.