Кривая Безье — это… Что такое Кривая Безье?
Кривы́е Безье́ или Кривы́е Бернште́йна-Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Кривая Безье является частным случаем многочленов Бернштейна, описанных Сергеем Натановичем Бернштейном в 1912 году.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).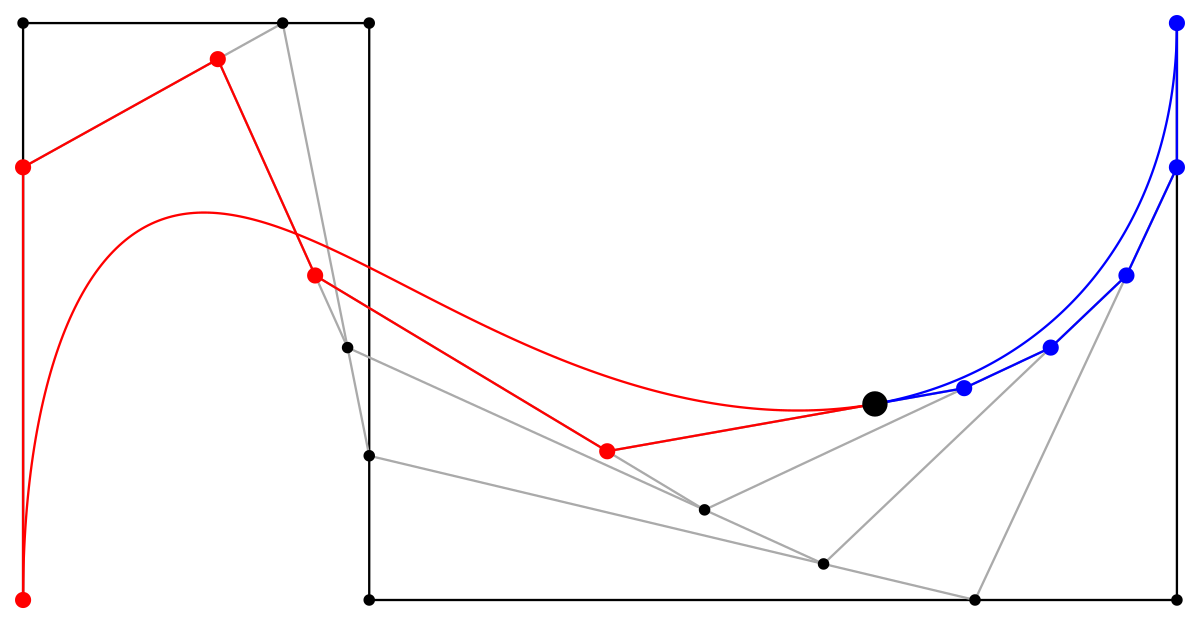
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Определение
Кривая Безье — параметрическая кривая, задаваемая выражением
где — функция компонент векторов опорных вершин, а — базисные функции кривой Безье, называемые также полиномами Бернштейна.
- ,
где — число сочетаний из по , где — степень полинома, — порядковый номер опорной вершины.
Виды кривых Безье
Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки
- .
Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1 и P2.
- .
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах (в SWF также могут использоваться кубические кривые Безье).
Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
- .
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P
В матричной форме кубическая кривая Безье записывается следующим образом:
- ,
где называется базисной матрицей Безье:
В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG), Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых. SVG также позволяет работать со сплайнами Безье 4-й степени[1].
SVG также позволяет работать со сплайнами Безье 4-й степени[1].
Построение кривых Безье
Линейные кривые
Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:
- Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.

- Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
- Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
Построение квадратичной кривой Безье | Анимация t: [0; 1] |
Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки
Построение кубической кривой Безье | Анимация t: [0; 1] |
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки
Построение кривой Безье 4-й степени | Анимация t: [0; 1] |
Свойства кривой Безье
- непрерывность заполнения сегмента между начальной и конечной точками;
- кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
- при наличии только двух контрольных точек сегмент представляет собой прямую линию;
- прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
- кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
- масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;
- изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
- степень кривой всегда на одну ступень ниже числа контрольных точек.
 Например, при трех контрольных точках форма кривой — парабола;
Например, при трех контрольных точках форма кривой — парабола; - окружность не может быть описана параметрическим уравнением кривой Безье;
- невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).
Применение в компьютерной графике
Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (
Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами .
Ссылки
Литература
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.
См. также
Примечания
Кривые Безье — это.
 .. Что такое Кривые Безье?
.. Что такое Кривые Безье?Кривы́е Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастелье было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастелье, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастелье назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастелье).
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Определение
Кривая Безье — параметрическая кривая, задаваемая выражением
где — функция компонент векторов опорных вершин, а — базисные функции кривой Безье, называемые также полиномами Бернштейна.
- , где n — степень полинома, i — порядковый номер опорной вершины
Виды кривых Безье
Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
- .
Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1 и P2.
- .
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах SWF файлах.
Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
- .

Кубическая кривая Безье
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.
В матричной форме кубическая кривая Безье записывается следующим образом:
- ,
где называется базисной матрицей Безье:
В современных графических системах, таких как GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.
Построение кривых Безье
Линейные кривые
Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.
Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.
Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:
- Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
- Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
- Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
Построение квадратичной кривой Безье
Анимация t: [0; 1]
Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
Построение кубической кривой Безье
Анимация t: [0; 1]
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
Построение кривой Безье 4-й степени
Анимация t: [0; 1]
Применение в компьютерной графике
Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии. В программах векторной графики наподобие Adobe Illustrator или path).
Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами .
Литература
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.
См. также
Wikimedia Foundation. 2010.
Для заданной последовательности точек построить кривую Безье. Кривая Безье — это параметрическая кривая n-го порядка, которая задается следующей формулой: Для построения кривой Безье необходимо задать в клиентской области окна множество точек, используя мышь. Затем, после выбора пункта меню «Draw curve» можно изменять форму кривой с помощью мыши. Пункт меню «New curve» предназначен для удаления текущей кривой и выбора точек для построения новой. #include "stdafx.h" // Заголовочный файл проекта, в который включен файл "windows.h" (#include <windows.h>). #include "Bezier curves.h" #include <vector> using namespace std; // Директива, позволяющая обращаться к // средствам пространства имен стандартной библиотеки // без квалификаторов доступа. #define MAX_LOADSTRING 100 HINSTANCE hInst; // Дескриптор экземпляра приложения. Ключевые слова: кривая Безье, построение кривой Безье, аппроксимация кривой Безье
|
Как рисовать квадратичные кривые Безье на HTML5 SVG
В моем предыдущем сообщении о SVG мы обсуждали, как создавать сложные диаграммы в SVG, используя один <путь>. У элемента есть несколько других хитростей; он предлагает три метода рисования плавных кривых, которые не требуют нездорового знания математики или навыков кодирования, подобных ниндзя. Сначала мы рассмотрим квадратичные кривые Безье.
Что такое квадратичные кривые Безье?
Пожалуйста, не ждите от меня исчерпывающего объяснения! Если вам интересно, взгляните на уравнения, вызывающие мигрень, на WolframMathWorld …
Как и любая линия, квадратичная кривая имеет начало (P 0 ) и конечную точку (P 2 ). Он также имеет одну контрольную точку (P 1 ), которая определяет кривизну линии. Это изображение из Википедии дает хорошую иллюстрацию генерации кривой.
Озадачивающие пути
Квадратичные кривые Безье определяются с помощью директивы ‘Q’ в атрибуте SVG path ‘d’:
<path d="M100,250 Q250,100 400,250" />
Начальная директива M перемещает ручку к первой точке (100,250). Две координаты следуют за «Q»; единая контрольная точка (250 100) и конечная точка, к которой мы рисуем (400 250).
Вы также можете использовать строчную букву ‘q’ для обозначения относительных, а не абсолютных координат. Следующая кривая идентична:
<path d="M100,250 q150,-150 300,0" />
Наконец, существуют сокращенные директивы «T» и «t». Они принимают одну координату, которая обозначает конечную точку. Предполагается, что контрольная точка совпадает с последней использованной, например,
<path d="M100,250 Q250,100 400,250 T250,250" />
Это рисует кривую от 100 250 до 400 250, затем 250 250. Единый контрольный пункт в 250 100 предполагается для обоих.
Единый контрольный пункт в 250 100 предполагается для обоих.
Как обычно, директива t в нижнем регистре обозначает относительные, а не абсолютные координаты.
Если вам кажется, что это немного сложно визуализировать, взгляните на интерактивную страницу демонстрации квадратичной кривой Безье в SVG — она работает во всех браузерах, кроме IE8 и ниже, которые не поддерживают SVG.
Перетащите контрольную точку или любой конец кривой, и код будет создан для вас. Нажмите на кривую, чтобы переключить эффект заливки.
В следующем сообщении SVG мы будем использовать элемент path для создания более сложных кубических кривых Безье…
Кривая Безье — Компьютерная графика
Для построения в программах векторной графики прямых и кривых линий, а также стандартных геометрических фигур используются расчеты координат точек соответствующих фигур по математическим формулам. Для построения кривой линии используются уравнения, описывающие так называемую кривую Безье. Для решения этого уравнения необходимо задать координаты 4 точек Р0, Р1, Р2 ,Р3.
Для решения этого уравнения необходимо задать координаты 4 точек Р0, Р1, Р2 ,Р3.
Р0, Р1, Р2 ,Р3 — контрольные точки.
Из четырех контрольных точек кривая Безье проходит только через две — Р0 , Р2 , поэтому эти точки называются опорными точками. В опорных точках соединяются отдельные кривые друг с другом и образуют единый сложный контур. Две другие контрольные точки — Р1, Р3 – не лежат на кривой, но их расположение на кривизну кривой, поэтому они называются управляющими точками, а линии, которые соединяют управляющие и опорные точки называются управляющими линиями.
Кривая Безье является гладкой кривой, т. е. она не имеет разрывов и непрерывно заполняет участок между начальной опорной точкой и конечной. Управляющие линии являются касательными и касаются кривой Безье в опорных точках. Это позволяет гладко соединить две кривые Безье друг с другом. Управляющие линии при этом расположены вдоль одной прямой.
Управляющие линии при этом расположены вдоль одной прямой.
Рассмотрим пример гладкого соединения двух кривых Безье. Первая кривая — Р0, Р1, Р2 ,Р3 , вторая – Т0,Т1, Т2, Т3.
Для гладкого соединения нужно конечную точку Р2 первой кривой соединить с начальной точкой Т0 второй кривой, а также необходимо управляющие линии Р3Р2 и Т0Т1 расположить на одной прямой.
Повернем управляющую линию Р2Р3 против часовой стрелки на 180 градусов:
Изменяя длину управляющих линий, можно выполнять трансформацию:
Если обе управляющие линии будут лежать на одной прямой:
Изменение положения хотя бы одной из контрольных точек ведет к изменению формы всей кривой Безье. Из множества элементов кривой Безье составляется сложный контур.
Кривая Безье — Энциклопедия по машиностроению XXL
Вид характеристического многогранника и порции аппроксимируемой поверхности показаны на рис. 1.17. Параметры аппроксимирующих поверхностей выбираются из условия не только непрерывности поверхности, но и непрерывности производных к поверхности, по крайней мере градиента поверхности при переходе от одной порции к другой. Так, из шестнадцати вершин характеристического многогранника четыре принадлежат аппроксимируемой поверхности (роо, роз, рзо и рзз). Далее, если искомая сетка является сеткой кубических кривых Безье, то еще восемь граничных вершин определяются условиями вершин характеристических ломаных кривых Безье
[c.42]
1.17. Параметры аппроксимирующих поверхностей выбираются из условия не только непрерывности поверхности, но и непрерывности производных к поверхности, по крайней мере градиента поверхности при переходе от одной порции к другой. Так, из шестнадцати вершин характеристического многогранника четыре принадлежат аппроксимируемой поверхности (роо, роз, рзо и рзз). Далее, если искомая сетка является сеткой кубических кривых Безье, то еще восемь граничных вершин определяются условиями вершин характеристических ломаных кривых Безье
[c.42]
Для ОДНОЙ кривой Безье имеются две промежуточные точки, каждая из которых лежит на касательных, проведенных в начале и конце аппроксимируемой кривой. [c.42]
П Примечание. Положением промежуточных точек на касательных можно изменять характер кривой Безье. Число вершин, координаты которых могут быть свободно выбраны, изменяется от 4 до 1 в зависимости от расположения аппроксимирующей порции па поверхности (крайнее или внутреннее). [c.42]
[c.42]
Кривая Безье, характеризующая продольное сечение, может быть построена по характеристической ломаной с вершинами Р(по, 2о), Р (а , 2 ), Рг(а2, г), Рз( з, 2з). Параметрическое уравнение кривой Безье [c.43]
Пусть труба имеет по всей длине круговое поперечное сечение площади 5, а осевая линия трубы образует произвольную плоскую кривую без самопересечений. Входное и выходное отверстия параллельны. Скорости входящего и выходящего потоков плотности р перпендикулярны сечению трубы и по величине равны V. Течение стационарное. Найти дополнительную силу, действующую на трубу со стороны потока. Указать все решения задачи. [c.441]
Отметим, что абсолютная скорость или приведенная скорость в промежуточных сечениях (см. штриховую кривую на графике рис. 7.33), а следовательно, и статическое давление р = р л Х), полученные при расчете с учетом радиальных составляющих скорости, очень близки к соответствующим значениям, получаемым из обычного уравнения расхода (105) (сплошная кривая) без поправки на угол а. [c.416]
[c.416]
| Рис. 6.4.6. Изменение длины осцил-ляционных волн Z, и их амплитуды Др1 в стационарной ударной волне с интенсивностью ре = 3,3 (остальные параметры см. рис. 6.4.4) нри различных значениях коэффициентов межфазного трения йГц и теплообмена Nu . Пунктирные кривые без указателей соответствуют расчету с учетом нестационарного сферически-симметричного раснределения температур внутри пузырька (см. 5) |
Подобно тому, как это было сделано выше для плоских кривых, предположим, что точка Ж движется по пространственной кривой I, а соответствующая ей касательная t перекатывается по кривой без скольжения. Тогда переменная точка касания получит поступательное движение по касательной прямой относительно [c.172]
Сопряжения деталей по плавным кривым без образования углов
[c. 31]
31]
На рис. 1.24 изображена кривая Безье третьего класса, второго порядка. [c.34]
Новые точки на отрезках соединяются и образовавшиеся отрезки делятся пополам. Середины являются точками сопряжения кривых Безье, а каждая кривая Безье строится описанным ранее способом (рис. 1.25). [c.34]
На фиг. 103—117 вычерчивание кривых произведено графическим способом, исходя из геометрических свойств каждой данной кривой, без вычисления координат их отдельных точек. [c.42]
[c.42]
Получив ряд точек эвольвенты, соединяют их плавной линией сначала от руки на глаз, а затем по лекалу. Любая точка прямой А- В при перекатывании этой кривой без скольжения по окружности движется по эвольвенте. На фиг. 106 тонкой линией начерчена эвольвента, описываемая точкой А. [c.45]
Наконец, м случае точки, вынужденной оставаться на кривой без трения [c.274]
Еще Гюйгенс поставил вопрос о замене, если это возможно, окружности другой кривой, тоже расположенной в вертикальной плоскости и строго изохронной, т. е. такой, чтобы время падения тяжелой точки, вынужденной двигаться по кривой без трения, действительно стало независимым от начального положения. Он нашел, что этим свойством обладает циклоида (с горизонтальным основанием и с вогнутостью, обращенной вверх). [c.49]
Для точки, находящейся под действием консервативной силы с потенциалом и и вынужденной двигаться по кривой без трения, в силу замечаний гл. I существуют соотношения
[c.77]
I существуют соотношения
[c.77]
Обратимся для определенности к плоскому движению и предположим, что S есть двухсвязная область плоскости движения (т. е. такая область, которая путем непрерывной деформации может быть превращена в круговое кольцо), ограниченная с внутренней стороны замкнутой кривой j, а с внешней замкнутой кривой с,, причем i и j представляют собою кривые без двойных точек и с непрерывно вращающейся касательной. [c.459]
Определение. Говорят, что плоское тело катится по кривой без проскальзывания, если оно касается этой кривой, и скорость той точки тела Р, которая оказалась в месте соприкосновения С, всякий раз равна нулю. Иными словами, она есть мгновенный центр скоростей. [c.199]
В результате анализа статистических данных, накопленных в результате комплексных исследований механизма привода, представляется возможность расшифровки кривых регистрируемых параметров и построения эталонных осциллограмм. Для определения оптимальных величин и характера изменения диагностических параметров на различных участках осциллограммы проводится расчет механизма аналитическим путем (в частности, с помощью методов математического моделирования). Кроме того, экспериментально определяют величины этих параметров у большого числа станков одной модели после их сборки, регулировки и обкатки. Эталонную осциллограмму выбранного параметра для каждой модели станка получают путем статистической обработки записей этого параметра у станка, изготовленного, отрегулированного и приработанного в соответствии с техническими условиями, и сравнивают полученную кривую с расчетными данными. Например, эталонная осциллограмма крутящего момента на ходовом винте привода продольной подачи (рис. 4, поз. 20) должна иметь характер периодически изменяющейся кривой без резких скачков и пиков, а максимальная величина крутящего момента не должна превышать 2,8—3,0 кгм при рабочей подаче на холостом ходу.
[c.78]
Для определения оптимальных величин и характера изменения диагностических параметров на различных участках осциллограммы проводится расчет механизма аналитическим путем (в частности, с помощью методов математического моделирования). Кроме того, экспериментально определяют величины этих параметров у большого числа станков одной модели после их сборки, регулировки и обкатки. Эталонную осциллограмму выбранного параметра для каждой модели станка получают путем статистической обработки записей этого параметра у станка, изготовленного, отрегулированного и приработанного в соответствии с техническими условиями, и сравнивают полученную кривую с расчетными данными. Например, эталонная осциллограмма крутящего момента на ходовом винте привода продольной подачи (рис. 4, поз. 20) должна иметь характер периодически изменяющейся кривой без резких скачков и пиков, а максимальная величина крутящего момента не должна превышать 2,8—3,0 кгм при рабочей подаче на холостом ходу.
[c.78]
Фиг. 39. Принципиальная схема механизма для формирования линии зуба на станках по типу п. 1 табл. 12 1 — ползун, остриё которого (соответствующее режущей кромке инструмента чертит на движущейся с постоянной скоростью пластинке 2 синусоиду 3 (поверхность пластинки соответствует плоскости производящего колеса) 4 — ползун, под воздействием которого остриё ползуна / чертит на неподвижной пластинке кривую в виде восьмёрки 5 б— кривая (без точки перегиба), получающаяся на движущейся пластинке 2 при одновременной работе ползунов 4 и 1. 39. Принципиальная схема механизма для формирования линии зуба на станках по типу п. 1 табл. 12 1 — ползун, остриё которого (соответствующее режущей кромке инструмента чертит на движущейся с постоянной скоростью пластинке 2 синусоиду 3 (поверхность пластинки соответствует плоскости производящего колеса) 4 — ползун, под воздействием которого остриё ползуна / чертит на неподвижной пластинке кривую в виде восьмёрки 5 б— кривая (без точки перегиба), получающаяся на движущейся пластинке 2 при одновременной работе ползунов 4 и 1.
|
 [c.23]
[c.23]Доказательства первых двух теорем связано с введением индекса Пуанкаре (АндрОнов и др., 1959). Доказательство последней теоремы основано на том факте, что фазовые траектории не могут пересекаться. Рис. 7 иллюстрирует это положение. Кривая, пересекающая все фазовые траектории и не касающаяся их, называется Кривой без контакта. На рис. 7 окружность R — цикл без контакта. Обнаружение предельных циклов это — основная задача в теории колебаний. Однако не существует общих аналитических методов для ее решения. Следует отметить, что если при исследовании особых точек системы обнаруживаются центры, которые нри изменении параметров превращаются в неустойчивые фокусы, то вероятность существования в этой системе предельных циклов весьма велика. [c.39]
Следовательно, в области влажного насыщенного пара изобары, являясь одновременно и изотермами, представляют собой прямые линии с угловым коэффициентом, равным из диаграммы видно, что изобары пересекают пограничные кривые без излома. Изохоры, изобары и изотермы в области перегретого пара строятся по точкам. Изобары и изохоры в области перегрева — слабо вогнутые логарифмические кривые изотермы в области перегретого пара — выпуклые кривые, поднимающиеся слева вверх направо. Вид изотерм определяется температурой, которой они соответствуют. Чем больше температура, тем выше располагается изотерма. Чем дальше от пограничной кривой х = I) проходит изотерма, тем больше она приближается к горизонтали i = onst, так как в области идеального газа энтальпия однозначно определяется температурой. На рис. 9.9 точки Л, Б, С изображают соответственно состояния влажного, сухого и перегретого пара. Причем точка А лежит на пересечении изобары (изотермы) и линии постоянной сухости, точка В лежит на пересечении изобары и верхней пограничной кривой, точка С находится на пересечении изобары и изотермы. По положению точки, соответствующей некоторому состоянию пара, можно определить на г — s-диаграмме числовые значения всех параметров в этой точке.
Изохоры, изобары и изотермы в области перегретого пара строятся по точкам. Изобары и изохоры в области перегрева — слабо вогнутые логарифмические кривые изотермы в области перегретого пара — выпуклые кривые, поднимающиеся слева вверх направо. Вид изотерм определяется температурой, которой они соответствуют. Чем больше температура, тем выше располагается изотерма. Чем дальше от пограничной кривой х = I) проходит изотерма, тем больше она приближается к горизонтали i = onst, так как в области идеального газа энтальпия однозначно определяется температурой. На рис. 9.9 точки Л, Б, С изображают соответственно состояния влажного, сухого и перегретого пара. Причем точка А лежит на пересечении изобары (изотермы) и линии постоянной сухости, точка В лежит на пересечении изобары и верхней пограничной кривой, точка С находится на пересечении изобары и изотермы. По положению точки, соответствующей некоторому состоянию пара, можно определить на г — s-диаграмме числовые значения всех параметров в этой точке. [c.118]
[c.118]
Эпюра Ми представлена на рис.9.3. дс). На тех участках, где эгпоры Мх и Му пересекают базовую линию в точках, лежащих на одной вертикали, эпюра Л/ очерчивается прямыми линиями, на остальных — кривыми без экс-rpe.vr/MOB. [c.88]
Поскольку сечения фотоэффекта и комптон-эффекта в области высоких энергий спадают практически до нуля, то рождение пар становится здесь основным механизмом поглощения уизлучения. Пропорциональность сечения величине имеет место практически при всех энергиях. График зависимости от энергии для свинца и алюминия приведен на рис. 8.8. Универсальная кривая без экранирования рассчитана в пренебрежении экранированием заряда ядра атомными электронами. [c.451]
Сплошная кривая — с учетом всех процессов поглощения пунктирная кривая — без учета рождения пар крестиком отмечен коэффициеия поглощения, найденный Ф. Жолно и И. Кюри для новаго излучения. [c.529]
Температурная зависимость тп в больщинстве выполненных до сих пор исследований подобна зависимости то(Т ), иными словами, температурная зависимость отношения тц/то представляет монотонную кривую без перегибов. Чащетп/то=сопз1 /(Г).
[c.190]
Чащетп/то=сопз1 /(Г).
[c.190]
Кривые. Для построения кривой необходимо создать определенное количество точек. Ломаная линия, соединяющая заданные точки, называется дескриптором кривой, а точки — его вершинами. Очередность создания вершин дескриптора задает направление кривой. Количество вершин в дескрипторе задает класс кривой. Порядок кривой — это количество отрезков в ее дескрипторе. Первая вершина дескриптора является начальной точкой кривой, а последняя вершина — конечной точкой. Кривая должна быть касатель-на к первому и последнему отрезкам дескриптора в начальной и конечной точках соответственно. Положение точки на кривой задается параметром и. Существуют несколько типов, кривых, такие, как кривые Безье, В-зрИпе и эквидистанты, которые различаются методами построения. [c.34]
| Рис. 1.25. В-зрИпе и кривая Безье, построенные по одинаковым дескрипторам |
Определить такую кривую, чтобы тяжелая точка, скользящая по этой кривой без трения, приобретала в каждый момент скорость, вертикальная составляющая которой имеет постоянное значение (лиценциатская, Париж). [c.405]
Геометрический объект является замкнутым точечным множеством. В ГО будем различать поверхность — множество граничных точек, и тело — множество внутренних точек, условно объединенных с множеством граничных точек. Поверхность ГО состоит из одной или нескольких граней G,, которые являются отсеками поверхностей — плоскостей, поверхностей второго порядка, вращения и т. д. Область грани G/ отделяется от остальной поверхности граничными контурами Л/,-, которые представляют собой жордановы кривые, т. е. кусочно-аналитические кривые без самопересечений. Граница грани G, задается ребрами R, проходящими через вершины V геометрического объекта в порядке обхода грани. Поскольку вводимые понятия носят топологический характер, то без потери общности будем в дальнейшем рассматривать произвольные ГО, в которых поверхности аппроксимированы кусочно-линейно. Примитивом, вслед за работой [1281, будем
[c.132]
Поверхность ГО состоит из одной или нескольких граней G,, которые являются отсеками поверхностей — плоскостей, поверхностей второго порядка, вращения и т. д. Область грани G/ отделяется от остальной поверхности граничными контурами Л/,-, которые представляют собой жордановы кривые, т. е. кусочно-аналитические кривые без самопересечений. Граница грани G, задается ребрами R, проходящими через вершины V геометрического объекта в порядке обхода грани. Поскольку вводимые понятия носят топологический характер, то без потери общности будем в дальнейшем рассматривать произвольные ГО, в которых поверхности аппроксимированы кусочно-линейно. Примитивом, вслед за работой [1281, будем
[c.132]
Для многих металлов, в частности сталей, достаточно хорошо определена взаимосвязь между коэффициентом интенсивности напряжений и скоростью роста усталостной трещины. Обычно эта связь также описывается S-образной кривой без четко выраженного плато в координатах амплитуда коэффициента интенсивности напряжений АК (или максимальное значение коэффициента интенсивности напряжений/С ) — скорость
[c. 21]
21]
Температурная зависимость предела текучести облученных металлов. Для температурно-зависимого упрочнения Я и У являются в основном функциями эффективного напряжения, и каждый процесс термически активированной деформации имеет характерные параметры активации с особыми зависимостями от напряжения. Дорн [51] рассмотрел несколько моделей преодоления дислокациями препятствий, определяющих температурную зависимость напряжения течения металлов равномерное увеличение напряжения течения во всем температурном интервале, т. е. поступательный подъем кривой без изменения величины То, изменение температурного коэффициента напряжения течения (АаМТ) в области Т Т(, без изменения величины То, что наблюдается при повышении только плотности близкодействующих барьеров изменение или сохранение значения (Да/ДТ) при Т испытаниях образцов с различной скоростью или росте прочности близкодействующих барьеров. [c.86]
Таким образом, эллипс имеет гетыре вершины (фиг. 152). Наименьшее число вершин замкнутой кривой без особых точек равно 4. [c.213]
Можно показать, что для разгонной кривой без запаздывания (кривая 2) при t = 37 i Лг/= 0,95 Аг/о, а при t=4,61 Ti Дг/ = 0,99Ауо- Для разгонной кривой с запаз-108 [c.108]
Невероятное открытие! Кривая Безье в древней полигональной кладке в Перу | Альтернативная история и путешествия
Кривая Безье — это математически описанная кривая, используемая в компьютерной графике и анимации [1].
Другими словами: этот тип отрезка очень удобен при построении плавных кривых. Что важно, так это то, что траектория такой кривой линии остается всегда гладкой. Почему это так важно, я расскажу ниже.
Поэкспериментировал с построением кривых Безье на стыках блоков полигональной кладки по фотографии стены храма Десяти Ниш (Перу, Ольянтайтамбо) в графическом редакторе. Результат превзошел все ожидания!
фото из открытого источника, коллаж авторафото из открытого источника, коллаж автора
Эксперимент выполнен при помощи программы Paint.NET. Для примера использована одна линия, которая в шаблоне редактора по умолчанию разбита на три отрезка (границы отрезков отметил красным маркером — четыре контрольные точки).
коллаж автораколлаж автора
в увеличении
коллаж автораколлаж автора
Алгоритм построения кривых Безье в редакторе практически полностью совпал с границами стыков блоков в полигональной кладке!
Пробовал для разных участков, результат похожий
коллаж автораколлаж автора
Другое фото
фото В. Жур, Ольянтайтамбо 2012. Коллаж авторафото В. Жур, Ольянтайтамбо 2012фото В. Жур, Ольянтайтамбо 2012. Коллаж автора
Особенность перуанской полигональной кладки — это очень плавные границы блоков в стыках. Именно в таких стыках, как показал эксперимент, очень комфортно чувствует себя так называемая «Кривая Безье».
В простое совпадение, как-то даже, совсем не верится…
Впрочем, если у кого-то возникли сомнения, то этот же эксперимент может повторить любой желающий. Фото прилагается:
открытый источникоткрытый источник
Вывод. Поскольку такой профиль сочленения имеет сложную криволинейную конфигурацию, а стыковка блоков (на фото) без видимых зазоров по этой конфигурации представляет собой технически сложную задачу (особенно при использовании обычного ручного инструмента каменотёса), при этом линии в местах сочленения имеют криволинейную гладкую поверхность схожую со способом построения «Кривые Безье», следовательно принцип возведения этого объекта может содержать в себе предварительный этап математического моделирования (тот же чертёж или шаблон).
Ну а предложение простое. Думаю, следует продолжить исследование в данном направлении…
Дорогие друзья, пишите ваши комментарии, делитесь своими мнением и смотрите другие интересные темы
Невероятно сложные профили стыковки блоков в древней перуанской полигональной кладке!
Прим. 1. developer.mozilla.org › docs › Словарь › Bézier_curve
Nerding Out с кривыми Безье
by Nash Vail
Последние несколько дней я пытался написать свою собственную небольшую библиотеку анимации JavaScript. Я знаю, что никого не волнует новая библиотека анимации, но дело в том, что в процессе я наткнулся на кривые Безье. Я потратил пару часов на их изучение, пытаясь понять их, во время которых наткнулся на свежую статью «Математическая интуиция за кривыми Безье», которая также послужила источником вдохновения для этой статьи.Это математика и, по-видимому, нацелена на умных людей, поэтому мне было нелегко осмыслить эту концепцию. Но, к счастью, в конце концов я это сделал, и это привело к изучению ряда интересных вещей о кривых Безье, которыми я очень рад поделиться с вами.
Что вы будете изучать
Я начну с введения в кривые, что они такое, почему они крутые, их математическое представление. Не беспокойтесь о математике, если честно, я вроде как отстой в математике, поэтому мне нужно найти способы, чтобы попытаться объяснить это самому себе, и я уверен, что «способы» сработают и для вас :).
Далее мы перейдем к кривым Безье. Что они собой представляют и чем они отличаются. Их математическая формула.
Ближе к концу мы создадим наш собственный маленький движок для рисования кривых Безье на JavaScript и SVG. Как это круто?
Кривые
Мне не нужно здесь давать формальное определение кривой, верно? Все эти линии кривые, посмотрите на них
Кривые, кривые все кривыеКривые довольно милые, они могут представлять множество вещей. Например, приведенная ниже кривая показывает количество моих подписчиков в Твиттере с течением времени.
Хорошо, ладно, это выглядит как случайно нацарапанная линия. Позвольте мне добавить контекст.
Извините, мой почеркТеперь он должен дать лучшее представление о том, что он представляет. По горизонтальной оси отложено количество дней с тех пор, как я присоединился к Twitter, а по вертикальной оси — количество подписчиков, которых я получил.
В мой первый день в Твиттере у меня было 0 подписчиков, затем он медленно увеличивался, я потерял некоторых, некоторые приобрел, а затем, во второй половине, как вы можете видеть, у меня появилось несколько новых подписчиков.Это не единственная информация, которую мы можем расшифровать по этой кривой. Я также могу узнать точное количество подписчиков, которые у меня были в любой день. Просто нужно провести две линии.
Допустим, я хотел бы знать, сколько у меня подписчиков на 60-й день.
Я провожу вертикальную линию от 60 по горизонтальной оси, затем из точки, где эта линия пересекает кривую, я рисую горизонтальную линию. Эта горизонтальная линия пересекает вертикальную ось (ось с количеством последователей) в точке.Значение этой точки на вертикальной оси дает мне точное количество подписчиков, которое у меня было на 60-й день, которое составляет 126.
Теперь, где пересекаются две красные линии, это то, что называется точкой . На двухмерном графике, таком как наш график подписчиков в Твиттере, точка однозначно идентифицируется двумя значениями: ее горизонтальной координатой ( x ) и ее вертикальной координатой ( y ). Следовательно, запись (x, y) — это все, что нужно для представления точки. В нашем случае красную точку, где пересекаются две красные линии, можно записать как (60, 126).
(60 = x / горизонтальная координата, 126 = y / вертикальная координата)
Хорошо, достаточно для того, что такое точка, вы это уже знали. Давайте поговорим о кривой, которая на самом деле представляет собой набор из множества таких точек , не так ли?
Вы берете массив данных, например, на 0-й день 0 последователей, 1-й день 50 подписчиков… 10-й день 76 подписчиков … 100-й день 500 подписчиков… и так далее. Вы конвертируете эти данные в точки (0, 0) (1, 50)… (10, 76)… (100, 500)… Вы наносите точки на график, соединяете их вместе, и вот, у вас есть кривая.
Итак, для кривой вам нужны точки, а для точек вам нужны соответствующие значения x и y. Поэтому теперь обратите внимание на то, что кривая может быть однозначно представлена чем-то, что может выдавать нам значения x и / или y. Это «нечто» мы называем в математике функцией .
В математике есть много стандартных функций. Рассмотрим функцию синус .
В таких функциях выбор x остается за нами.Мы даем ему x , это дает нам y . И вместе формируем точку (x, y). Мы даем ему еще один x, он дает нам еще один y, и так далее, мы получаем набор точек, мы строим их и получаем уникальную форму.
Источник: http://forum.kerbalspaceprogram.com/index.php?/topic/69707-sine-graphs-and-orbital-paths/Функция также может быть представлена в параметрической форме . В параметрической форме нам не нужно указывать часть координаты точки, как мы делали (x) в предыдущем примере.Вместо этого мы предоставляем параметр / переменную, обычно записываемую как t , и для каждых t мы получаем координаты x и y , короче говоря, мы предоставляем t , мы получаем точку.
Вы захотите узнать, что такое параметрическая форма, когда мы будем говорить о математике, лежащей в основе кривых Безье.
Кривые Безье
Кривые Безье — это особые кривые. Математика и идея, стоящая за ними, поразили меня, и вы тоже должны быть готовы к тому, чтобы вас поразило.
Поскольку вы читаете это, я предполагаю, что вы дизайнер или разработчик и раньше имели дело с кривыми Безье, особенно с кубическими кривыми Безье, через секунду мы узнаем, что такое кубические кривые Безье. Теперь эти кривые используются в самых разных местах, для создания векторной графики, путей анимации, кривых замедления анимации и т. Д. Только потому, что ими так легко управлять, . Вам не нужно много знать математику или совсем ничего, чтобы изменять кривые по своему вкусу. Подумайте, не существовало ли кривых Безье, и люди должны были бы придумывать уникальные математические функции для кривых, например, рисовать векторную графику, такую как шрифты, конечно, кошмар.
Математика?
Хорошо, пора немного математики. Я начну с общей формулы кривых Безье, это на первый взгляд довольно сложно, но мы справимся.
Общая формула кривой Безье степени n«Ух ты! Ого! Ого! Эйнштейн! ». Эй, погоди, не уходи. Это просто, слушай, я сделала это таким красочным?
Давайте начнем разбирать формулу. Вы можете пропустить уже знакомые вам части.
B (t)
B , потому что это кривая Эзье B .Как упоминалось ранее в статье о параметрической форме кривых, t — это параметр. Вы подключаете t и получаете x и y , точка. Скоро мы увидим, как это работает с приведенным выше уравнением. Здесь будет уместно упомянуть, что для кривых Безье значение t должно быть между 0 и 1, включая оба значения.
Σ / Sigma
Этот символ Σ в математике называется оператором суммирования. Он работает следующим образом: справа от этого символа находится выражение с переменной i, а i может содержать только целые значения.Вверху и внизу символа мы пишем пределы i. Для каждого значения i выражение справа оценивается и добавляется к сумме, пока i не достигнет n.
Вот несколько примеров.
Просто более короткое обозначение для чего-то большего.
Хорошо, похоже, с сигмой все в порядке.
nCi
Это C здесь, это C из перестановок и C комбинаций. Давайте устроим импровизированный урок комбинаций. Теперь в формуле эта часть называется биномиальным коэффициентом.Способ чтения nCi такой: n Выберите i. То есть для заданных n элементов, сколькими способами вы можете выбрать из них i элементов (n всегда больше или равно i). Хорошо, возможно, это не имело большого смысла, рассмотрим этот пример: у меня есть 3 элемента: круг, квадрат и треугольник. Следовательно, здесь n = 3. Сколько способов я могу выбрать 2 (i = 2) элемента из 3. На языке математики это будет записано как 3C2 (3 Выберите 2). Ответ: 3.
Аналогично,
И когда i равно 0, есть только один способ выбрать 0 элементов из n, 1, чтобы вообще ничего не выбрать.
Вместо того, чтобы рисовать эскизы и выяснять ответ на данное выражение Комбинации, есть эта обобщенная формула.
P sub i
Это важный бит. В общей формуле кривой Безье есть t, i и n. Мы еще не коснулись того, что такое n. n — это то, что называется степенью кривой Безье. n — это то, что определяет, будет ли кривая Безье линейной, квадратичной, кубической или чем-то еще.
Видите ли, если вы раньше использовали инструмент «Перо», вы щелкаете в двух разных местах, чтобы создать две отдельные точки, а затем управляете кривой, которая образуется между двумя точками, используя ручки.Кривая Безье всегда будет иметь как минимум две точки привязки, а остальные — это контрольные точки, которые используются для управления формой кривой. Кроме того, то, что вы называете ручками, — это просто контрольные точки, соединенные линией с точкой привязки, они нужны только для того, чтобы предоставить лучшую ментальную модель. Таким образом, когда вы настраиваете ручки, на самом деле вы просто меняете координаты контрольных точек.
Кубическая кривая БезьеИзбавимся от всех аксессуаров и сосредоточимся на ядре.
Кубическая кривая БезьеКривая, которую вы видите на изображении выше, — это Кубическая кривая Безье, или, другими словами, степень кривой Безье, показанная выше, равна 3, или в общей формуле для кривых Безье, которые вы вставляете n = 3.
n = 1 дает вам линейную кривую Безье с двумя опорными точками P0 и P1 и без контрольных точек, так что в итоге получается прямая линия.
n = 2 дает вам квадратичную кривую Безье с двумя опорными точками P0 и P2 и одной контрольной точкой P1
и аналогично n = 3 дает вам кубическую кривую Безье с двумя опорными точками P0 и P3 и двумя контрольными точками P1 и P2 .Чем выше n, тем более сложные фигуры можно нарисовать.
Теперь мы собираемся составить из общего уравнения уравнение для кубической кривой Безье, которое включает подстановку n = 3 в общую формулу. Уравнение, которое мы получим, будет в переменной t , которая, как упоминалось ранее, является параметром, значение которого варьируется от 0 до 1. Кроме того, для уравнения нам понадобится 4 Pis (читай: Pee eyes) P0, P1, P2 и P3. Выбор этих точек зависит от нас, в конце концов, когда мы рисуем векторную графику, скажем, с помощью инструмента «Перо», мы выбираем положение опорных точек, а контрольные точки не так ли? После внесения изменений наше уравнение для кубической кривой Безье выглядит примерно так.
Расширенное уравнение для кубической кривой БезьеМы используем здесь небольшую краткость, на самом деле каждая точка (P) имеет две координаты x и y, а также при переходе t к общему уравнению мы должны получить точку, которая также имеет x и координаты y. Следовательно, мы можем записать приведенное выше уравнение как
Расширенное уравнение для кубической кривой БезьеВы скоро станете свидетелями чего-то особенного в этих уравнениях.
Напомним, что упомянутое уравнение является параметрической формой кривой Безье с параметром t , который может содержать значения, варьирующиеся от 0 до 1.Кривая — это набор точек. Каждый уникальный t , который вы проходите в точку B, дает уникальную точку, которая составляет всю кривую Безье.
Магия этого уравнения заключается в том, что при t = 0, B (0) = P0 и при t = 1, B (1) = P3, поэтому крайние значения t, 0 и 1 дают наибольшее количество баллов. кривой, которые, конечно же, являются опорными точками. Это не верно только для кубических кривых Безье, для кривой степени n B (0) = P0 и B (1) = Pn.
Для любого другого значения т от 0 до 1 (например.g t = 0,2 на рисунке выше) вы получите точку, которая создает кривую.
Поскольку все уравнение зависит от положения Пис (Pee eyes), изменение их положения изменяет форму кривой. Так работают кривые Безье.
Теперь, когда мы знаем математику, лежащую в основе кривых Безье, давайте применим эти знания.
Я создал простую программу на JavaScript, которая отображает кубическую кривую Безье, нет пользовательского интерфейса для взаимодействия с ней, потому что я не хотел, чтобы логика исчезла во всем коде пользовательского интерфейса, а также из-за того, что я ленив.Но это не значит, что вы не можете с ним взаимодействовать :).
Это слишком много для восприятия? Мы начали с определения того, что такое кривые, а затем перешли к точкам и тому, как они являются строительными блоками кривой. Затем мы перешли к кривым Безье и разобрались с математикой, чтобы найти точки, которые образуют кривую Безье вверх. Надеюсь, вы что-то узнали и оставите эту статью умнее, чем когда начинали ее читать.
Код небольшого настраиваемого движка Cubic Bezier можно найти в этом репозитории GitHub.
Обновление: Генератор теперь может генерировать кривую Безье любой степени, а не только кубические кривые Безье :).
Ищете больше? Я регулярно публикую в своем блоге на nashvail.me. Увидимся там, хорошего вам дня!
Границы | Вариационная модель подгонки данных на многообразиях путем минимизации ускорения кривой Безье
1. Введение
В этой статье рассматривается проблема подгонки гладкой кривой к точкам данных d 0 ,…, d n , лежащих на римановом многообразии M и связанных с действительными параметрами t 0 ,…, т н .Кривая обеспечивает баланс между ограничением близости данных и ограничением сглаживающей регуляризации.
Несколько приложений мотивируют эту проблему в инженерии и науке. Например, аппроксимация кривой представляет большой интерес для снижения порядка одномерных динамических систем на основе проекций [1]. В этом приложении динамическая система зависит от числа Рейнольдса, а редукция модели получается путем вычисления подходящих проекторов как точек на многообразии Грассмана.Однако поиск проектора — задача, требующая много времени и памяти. На основе проекторов, предварительно вычисленных для заданных значений параметров, аппроксимация используется для аппроксимации проектора, связанного с новым значением параметра. В Gousenbourger et al. [2], та же стратегия используется для аппроксимации ориентации поля ветра, представленной в виде точек на многообразии положительных полуопределенных ковариационных матриц размера p и ранга r . Дальнейшие приложения включают движения твердого тела на SE (3), такие как приложения стержней Коссера [3] или отслеживание ориентации [4].Сферические данные также представляют интерес для многих приложений анализа данных, для отслеживания и прогнозирования штормов или для изучения миграции птиц [5].
Существуют разные подходы к решению проблемы подбора кривой. Среди прочего, мы называем здесь подход схем подразделений [6, 7] или методы алгебры Ли [8]. Однако в настоящее время наиболее популярным подходом, вероятно, является включение двух вышеупомянутых ограничений в задачу оптимизации
. minγ∈ΓEλ (γ): = minγ∈Γ∫t0tn‖D2γ (t) dt2‖γ (t) 2dt + λ2∑i = 0nd2 (γ (ti), di)), (1), где Γ — допустимое пространство кривых γ: [t0, tn] → M, t ↦γ ( t ), D2dt2 обозначает вторую ковариантную производную (Леви-Чивита), а ∥ · ∥ γ ( t ) обозначает риманову метрику в точке γ ( t ), из которой мы можем определить риманово расстояние d (·, ·).Наконец, λ∈ℝ — это параметр, который обеспечивает баланс между регуляризатором ∫t0tn∥D2γ (t) dt2∥γ (t) 2dt и подгоночным членом ∑i = 0nd2 (γ (ti), di)) . Этот подход приводит к замечательному свойству: когда многообразие M сводится к евклидову пространству, а Γ является пространством Соболева h3 (t0, tn), решением (1) является естественный кубический сплайн [9].
Оптимизация на многообразиях вызвала большой интерес в последнее десятилетие, начиная с учебника [10], который суммирует несколько методов оптимизации на матричных многообразиях.Недавно появились наборы инструментов, обеспечивающие легкий доступ к таким методам оптимизации, например, Manopt [11] и MVIRT [12]. Первые получили очень положительную отдачу во многих различных темах исследований, с приложениями, например, в низкоранговом моделировании в анализе изображений [13], уменьшении размерности [14], фазовом поиске [15] или даже в системах MIMO, подобных 5G [16]. ]. Последнее проистекает из недавнего интереса к многозначной обработке изображений и данных, сформулированной как вариационные модели на многообразии продуктов MN, где N — количество пикселей.Начиная с полной вариационной (TV) регуляризации фазозначных данных [17, 18], были разработаны различные методы для TV на многообразиях [19, 20], а также методы второго порядка [21, 22] вплоть до инфимальной свертки [23 ] и полной обобщенной вариации [23, 24]. Кроме того, различные алгоритмы были обобщены для многозначных данных, помимо предыдущих работ с использованием методов градиентного спуска или циклических проксимальных точечных методов, расщепления Дугласа – Рачфорда [25], методом наименьших квадратов с итеративным перевесом [26] и более общей полуквадратичной минимизации [ 27].
Проблема аппроксимации кривой (1) в последние несколько лет решалась по-разному. Samir et al. [28] рассмотрел случай, когда Γ является бесконечномерным соболевским пространством кривых, и использовал метрику Пале для разработки алгоритма градиентного спуска для (1) (см., Например, [29] для применения этого подхода). Другой метод состоит в дискретизации кривой γ в N точках и, следовательно, в рассмотрении Γ = MN (см., Например, [30] для результата по SO (3)). Наконец, предельный случай, когда λ → 0, уже хорошо изучен и известен как геодезическая регрессия [31–33].
Недавняя тема касается подбора кривой с помощью кривых Безье. При таком подходе пространство поиска Γ сводится к набору составных кривых Безье. Это очень универсальный инструмент для моделирования гладких кривых и поверхностей для вещественных и векторных дискретных точек данных (подробный учебник см. В [34]), но их также можно использовать для моделирования гладких кривых и поверхностей для многозначных данных. [35, 36]. Преимущество работы с такими объектами по сравнению с классическими подходами состоит в том, что (i) пространство поиска резко сокращается до так называемых контрольных точек кривых Безье (и это приводит к лучшим характеристикам времени и памяти) и (ii) очень просто наложить дифференцируемость для оптимальной кривой, что ценится в некоторых из вышеупомянутых приложений.Однако, хотя получение такой оптимальной кривой сводится непосредственно к решению линейной системы уравнений для данных, заданных в евклидовом пространстве, до сих пор не существует известной замкнутой формы оптимальной кривой Безье для многозначных данных.
В этой работе мы выводим алгоритм градиентного спуска для вычисления дифференцируемой составной кривой Безье B: [t0, tn] → M, которая удовлетворяет (1), т.е. такая, что B ( t ) имеет минимальный средний квадрат ускорение, и соответствует набору из n +1 многозначных точек данных в связанных с ними временных параметрах.Мы рассматриваем многозначное обобщение кривых Безье [36] в том же контексте, что и у Арно и др. [37] или совсем недавно в Gousenbourger et al. [38]. Мы используем (квадрат) абсолютную разность второго порядка, введенную Бачаком и др. [22], чтобы получить дискретную аппроксимацию регуляризатора из (1). Качество аппроксимации зависит только от количества точек выборки. Мы используем рекурсивную структуру алгоритма Де Кастельжау [36], чтобы получить градиент целевой функции относительно контрольных точек B ( t ).Градиент построен как рекурсия полей Якоби, которые по числовым причинам реализованы как конкатенация так называемых сопряженных полей Якоби . Кроме того, соответствующая вариационная модель зависит только от количества контрольных точек составной кривой Безье, а не от количества точек выборки. Наконец, мы получаем приближающую модель к (1), которую мы решаем с помощью алгоритма, основанного только на трех инструментах на многообразии: экспоненциальном отображении, логарифмическом отображении и определенном поле Якоби вдоль геодезических.
Работа организована следующим образом. Мы вводим необходимые предварительные сведения — кривые Безье, римановы многообразия и римановы конечные разности второго порядка — в разделе 2. В разделе 3 мы выводим градиент дискретизированного среднего квадрата ускорения составной кривой Безье относительно ее контрольных точек и, следовательно, регуляризатор (1). В разделе 4 мы представляем соответствующий алгоритм градиентного спуска, а также эффективный метод оценки градиента для решения (1) для различных значений λ.Также исследуется предельный случай, когда λ → ∞. Наконец, в разделе 5 мы проверяем, анализируем и иллюстрируем производительность алгоритма на нескольких численных примерах на сфере S 2 и специальной ортогональной группе SO (3). Мы также сравниваем наше решение с существующими методами подбора Безье. Заключение дается в разделе 6.
2. Предварительные мероприятия
2.1. Функции Безье и составной сплайн Безье
Рассмотрим евклидово пространство ℝ м .Кривая Безье степени K ∈ℕ — это функция βK: [0,1] → ℝm, параметризованная контрольными точками b0,…, bK∈ℝm и имеющая вид
βK (t; b0,…, bK): = ∑j = 0KbjBj, K (t),, где Bj, K (t) = (Kj) tj (1-t) K-j — базисные полиномы Бернштейна [34]. Например, линейная кривая Безье β 1 — это просто отрезок прямой (1- t ) b 0 + tb 1 , соединяющий две контрольные точки b 0 и b 1 .Явные формулы квадратичной и кубической кривых Безье читаются как
. β2 (t; b0, b1, b2) = b0 (1 − t) 2 + 2b1 (1 − t) t + b2t2, β3 (t; b0, b1, b2, b3) = b0 (1 − t) 3+ 3b1 (1 − t) 2t + 3b2 (1 − t) t2 + b3t3,для заданных контрольных точек b0, b1, b2∈ℝm и дополнительной точки b3∈ℝm для кубического случая.
Составная кривая Безье — это функция B : [0, n ] → ℝ m , составленная из n кривых Безье и определенная как
B (t): = {βK0 (t; b00,…, bK00), если t∈ [0,1], βKi (t − i; b0i,…, bKii), если t∈ (i, i + 1], i∈ {1,…, n − 1}, (2), где K i ∈ℕ обозначает степень i -й кривой Безье β K i из B и bji, j = 0,…, K i , являются его контрольными точками.Кроме того, B ( t ) является непрерывным, если последняя и первая контрольные точки двух последовательных сегментов совпадают [34]. Введем p i как точку на стыке двух последовательных сегментов Безье, то есть pi: = bKi-1i-1 = b0i. Дифференцируемость достигается при совмещении контрольных точек двух последовательных сегментов. Введем далее bi + 1 -: = bKi-1i и bi + 1 +: = b1i + 1 так, чтобы условие дифференцируемости читалось как pi + 1 = Kibi + 1- + Ki + 1b + i + 1Ki + Ki + 1.
Пример 1 ( C 1 условия для составных кубических кривых Безье). Мы рассматриваем случай, когда все сегменты Безье кубические, как показано на рисунке 1 . Составная кривая Безье B ( t ) — это C 1 , если pi = 12 (bi- + bi +), i = 1,…, 4 , при pi = b3i -1 = b0i, bi- = b2i-1 и bi + = b1i.
Рисунок 1 .Схематическое изображение составной кубической кривой Безье B: [0,5] → M для M = ℝ (черный) и ее контрольных точек (зеленые кружки). Непрерывная дифференцируемость достигается на стыке сегментов (синие стрелки проводят первую производную от B ).
2.2. Римановы многообразия
Мы рассматриваем полное m -мерное риманово многообразие M. Мы обращаемся к О’Нилу [39] и ду Кармо [40] за введением в римановы многообразия и к [10] за его оптимизацией.Мы будем использовать следующую терминологию и обозначения.
Обозначим через TaM (евклидово) касательное пространство к M в точке a∈M; TM: = ∪a∈MTaM — касательное расслоение к M; 〈·, ·〉 a обозначает скалярное произведение в касательном пространстве TaM в точке a , из которого мы выводим норму v∈TaM, обозначенную как ∥v∥a = 〈v, v〉 a. Для (не обязательно уникальной) кратчайшей геодезической между a и b∈M мы пишем g (·; a, b): ℝ → M, t ↦ g ( t ; a, b ), параметризованные таким образом, что g (0; a, b ) = a и g (1; a, b ) = b .Этот выбор параметризации также означает, что ковариантная производная Ddt от g по времени удовлетворяет условию ∥Ddtg (t; a, b) ∥g (t) = dM (a, b) для всех t ∈ [0 , 1], где dM (a, b) — геодезическое расстояние между a и b∈M. Риманова экспонента читается как expa: TaM → M, v↦b = expa (v), и мы обозначаем через r a ∈ℝ максимальный радиус такой, что экспоненциальное отображение биективно на Da: = {b∈M : dM (a, b)
Далее мы предполагаем, что для многообразия доступны как экспоненциальное, так и логарифмическое отображение и что их вычисление не слишком затратно для вычисления.Кроме того, мы предполагаем, что многообразие симметрично.
2.3. Составные кривые Безье на многообразиях
Один из хорошо известных способов обобщения кривых Безье на риманово многообразие M — это алгоритм Де Кастельжау [36, раздел 2]. Этот алгоритм требует только римановой экспоненты и логарифма и сохраняет свойство интерполяции первой и последней контрольных точек. Некоторые примеры интерполяции и аппроксимации кривыми Безье или поверхностями Безье, т. Е. Обобщения кривых Безье тензорного произведения, можно найти в Absil et al.[35].
Рассмотрим βK: [0,1] → M, t↦βK (t; b0, b1,…, bK), многозначную кривую Безье порядка K , управляемую K +1 контрольными точками b0,… , bK∈M. Введем точки xi [0] = bi и повторим построение дополнительных точек. Для i = 0,…, K — k , k = 1,…, K , определяем
xi [k]: = βk (t; bi,…, bi + k) = g (t; xi [k − 1], xi + 1 [k − 1]) (3)в качестве точки i -го шага k -го шага алгоритма Де Кастельжау, и получаем βK (t; b0,…, bK) = x0 [K].
Алгоритм Де Кастельжау проиллюстрирован на рисунке 2 для евклидовой кубической кривой Безье β 3 ( t ; b 0 , b 1 , b 2 , b 3 ). Общая кубическая кривая Безье может быть явно выражена на многообразии M как
β3 (t; x0 [0], x1 [0], x2 [0], x3 [0]) = g (t; g (t; g (t; x0 [0], x1 [0]), g ( t; x1 [0], x2 [0])), g (t; g (t; x1 [0], x2 [0]), g (t; x2 [0], x3 [0]))) = g (t; g (t; x0 [1], x1 [1]), g (t; x1 [1], x2 [1])) = g (t; x0 [2], x1 [2]) = x0 [3].Рисунок 2 . Построение кубической кривой Безье с помощью алгоритма Де Кастельжау.
Условия непрерывности и дифференцируемости обобщены на многообразия в Попеле и Ноуксе [36].
Лемма 2 (условия дифференцируемости [36]). Рассмотрим составную кривую Безье B: [0,2] → M , состоящую из f: [0,1] → M, t↦f (t) = βK (t; b00, b10,…, bK0) и g: [1,2] → M, t↦g (t) = βK̄ (t-1; b01, b11,…, bK̄1) , т.е.,
B (t): = {f (t) для t∈ [0,1], g (t) для t∈ (1,2].Составная кривая Безье B ( t ) является непрерывной и непрерывно дифференцируемой, если выполняются два следующих условия:
bK0 = b01 и bK0 = g (s; bK − 10, b11), s = KK + K¯. (4)Составная кривая Безье B: [0, n] → M затем определяется полностью аналогично евклидовому случаю из уравнения (2). Условия дифференцируемости (4) леммы 2 должны выполняться в каждой точке соединения p i , i = 1,…, n — 1.
Пример 3 (Составные кубические кривые Безье). Составная кубическая кривая Безье B (t): [0, n] → M — это C 1 , если pi = g (12; bi-, bi +) . См. Рисунок 1 для примера на M = ℝ с n = 5 сегментов и Рисунок 3 для примера на M = S2 с n = 3 сегментами .
Рисунок 3 . Составная кубическая кривая Безье B : [0, 3] → S 2 .Конечные точки p i , i = 0,…, 3, (голубой) и промежуточные точки bi ± (зеленый) определяют его форму; непрерывная дифференцируемость иллюстрируется логарифмическими отображениями logpibi ±, i ∈ {1, 2} (синие стрелки).
2,4. Дискретная аппроксимация среднеквадратичного ускорения
Мы дискретизируем среднеквадратичное ускорение (MSA) кривой γ: [0,1] → M, дискретизируя соответствующий интеграл
∫01‖D2γ (t) dt2‖γ (t) 2dt, (5)и.е., регуляризатор из (1). Мы аппроксимируем квадрат нормы второй (ковариантной) производной абсолютной конечной разностью второго порядка, введенной Бачаком и др. [22]. Рассмотрим три точки x, y, z∈M и набор средних точек x и z
для всех (не обязательно самых коротких) геодезических g соединяющих x и z . Многозначная абсолютная конечная разность второго порядка определяется как
d2 [x, y, z] = minc∈Cx, z2dM (c, y).(6)Это определение эквивалентно в евклидовом пространстве ∥x-2y + z∥ = 2∥12 (x + z) -y∥.
Используя точки с равным интервалом t 0 ,…, t N , N ∈ℕ, с размером шага Δt = t1-t0 = 1N, мы аппроксимируем ∥D2γ (ti) dt2∥γ ( ti) ≈1Δt2d2 [γ (ti-1), γ (ti), γ (ti + 1)], i = 1,…, N −1, и по правилу трапеций получаем
∫01‖D2γ (t) dt2‖γ (t) 2dt≈∑ k = 1N − 1Δtd22 [γ (ti − 1), γ (ti), γ (ti + 1)] Δt4.Для кривых Безье γ ( t ) = B ( t ) получаем для регуляризатора в (1) дискретизированный MSA A ( b ) , который зависит от контрольных точек b и имеет значение
. A (b): = ∑i = 1N − 1d22 [B (ti − 1), B (ti), B (ti + 1)] Δt3.(7)3. Градиент дискретизированного среднеквадратичного ускорения
Чтобы минимизировать дискретизированный MSA A ( b ), мы стремимся использовать алгоритм градиентного спуска на коллекторе MM продукта, где M — количество элементов в b. Далее мы выводим замкнутую форму градиента ∇ b A ( b ) дискретизированного MSA (7). Этот градиент получается с помощью рекурсии и цепного правила.Фактически, производная (6) уже известна [22], так что остается только вычислить производную составной кривой Безье.
Сначала введем следующие обозначения. Обозначим через Dxf [η] (x0) ∈Tf (x0) M производную по направлению от f: M → M, вычисленную как x 0 , относительно его аргумента x и в направлении η∈TxM. Мы используем сокращенную форму D x f [η] = D x f [η] ( x ) всякий раз, когда эта производная по направлению впоследствии снова оценивается как x .
Теперь мы сформулируем два следующих определения, которые имеют решающее значение для остальной части этого раздела.
Определение 4 (Градиент [10, уравнение (3.31), стр. 46]). Пусть f: M → ℝ — вещественная функция на многообразии M, x∈M и η∈TxM.
Градиент ∇Mf (x) ∈TxM f в точке x определяется как касательный вектор, который удовлетворяет
〈∇ℳf (x), η〉 x = Dxf [η] для всех η∈Txℳ. (8)Для многомерных функций f ( x, y ) мы обозначаем градиент f относительно x в ( x 0 , y 0 ) записью ∇M, xf (x0, y0).Мы сокращаем это обозначение как M, xf = ∇M, xf (x, y), когда этот градиент рассматривается как функция от x (и y ).
Определение 5 (Цепное правило на многообразиях [10, с. 195]). Пусть f: M → M, h: M → M — две функции на коллекторе M и F: M → M, x ↦ F ( x ) = ( f ° х ) ( х ) = ф ( х ( х )) , их состав. Пусть x∈M и η∈TxM .Производная по направлению D x F [η] функции F относительно x в направлении η определяется как
DxF [η] = Dh (x) f [Dxh [η]], (9), где Dxh [η] ∈Th (x) M и DxF [η] ∈TF (x) M.
Остальная часть этого раздела состоит из четырех частей. Сначала напомним теорию полей Якоби из раздела 3.1 и их связь с дифференциалом геодезических (относительно начальной и конечной точки). В разделе 3.2, мы применяем цепное правило к композиции двух геодезических, которое появляется в алгоритме Де Кастельжау. Мы используем этот результат для построения алгоритмического вывода дифференциала общей кривой Безье на многообразиях относительно ее контрольных точек (раздел 3.3). Мы распространяем результат на составные кривые Безье в разделе 3.4, включая их ограничения на точки соединения p i , чтобы обеспечить выполнение условия C 1 (4), и, наконец, собираем эти результаты для определения градиента ∇ MA (b) дискретизированного MSA (7) относительно контрольных точек.
3.1. Поля Якоби как производная геодезической модели
Далее мы представляем замкнутую форму дифференциала D x g ( t ; ·, y ) геодезической g ( t ; x, y ), t ∈ [0, 1], относительно его начальной точки x∈M. Дифференциал относительно конечной точки y∈M можно получить, взяв геодезическую g ( t, y, x ) = g (1- t ; x, y ).
Как показано на рисунке 4, мы обозначаем γ x , ξ , геодезическую, начинающуюся в γ x , ξ (0) = x и с направлением Ddtγx, ξ (0) = ξ∈ TxM. Введем ζ ( s ): = log γ x , ξ ( s ) y , тангенциальный вектор в Tγx, ξ (s) M, направленный в сторону y . Тогда геодезическая вариация Γ g , ξ ( с, t ) геодезической g (·; x, y ) относительно тангенциального направления ξ∈TxM равна
Γg, ξ (s, t): = expγx, ξ (s) (tζ (s)), s∈ (−ε, ε), t∈ [0,1],, где ε> 0.Соответствующее поле Якоби J g , ξ вдоль g тогда задается векторным полем
Jg, ξ (t): = D∂sΓg, ξ (s, t) | s = 0, который представляет направление смещения g , если x возмущается в направлении ξ.
Рисунок 4 . Схематическое изображение вариации Γ g , ξ ( s, t ) геодезической g w.r.t. направление ξ∈TxM. Соответствующее поле Якоби вдоль g и в направлении ξ является векторным полем Jg, ξ (t) = ∂∂sΓg, ξ (s, t) | s = 0.
Непосредственно получаем J g , ξ (0) = ξ и J g , ξ (1) = 0, а также Jg, ξ (t) ∈Tg (t; х, у) М. Так как Γ g , ξ ( s, t ) = g ( t ; γ x , ξ ( s ), y ) получаем по правилу цепочки
Dxg (t, ·, y) [ξ] = ddsg (t; γx, ξ (s), y) | s = 0 = ddsΓg, ξ (s, t) | s = 0 = Jg, ξ (t ). (10)Замечание . Эта связь между производной геодезических и полями Якоби представляет большой интерес для симметрических пространств, где поля Якоби могут быть вычислены в замкнутой форме, как показано в следующей лемме.
Лемма 6 . [22, предложение 3.5] Пусть M — m-мерное симметрическое риманово многообразие. Пусть g (t; x, y), t ∈ [0, 1], — геодезическая между x, y∈M, η∈TxM — касательным вектором и {ξ 1 ,… ξ m } — ортонормированным базис (ONB) TxM, который диагонализирует оператор кривизны M с собственными значениями κ ℓ , ℓ = 1,…, m. Подробнее см. Гл. 4.2 и 5 (Пример 5) из [40]. Обозначим далее через {Ξ 1 (t),…, Ξ m (t)} параллельную перемещаемую раму {ξ 1 ,…, ξ m } вдоль g.Разложив η = ∑ℓ = 1mηℓξℓ∈TxM, производная D x г [η] становится
Dxg (t; x, y) [η] = Jg, η (t) = ∑ℓ = 1mηℓJg, ξℓ (t),, где поле Якоби Jg, ξℓ: ℝ → Tg (t; x, y) M вдоль g и в направлении ξ ℓ равно
Jg, ξℓ (t) = {sinh (dg (1 − t) −κℓ) sinh (dg − κℓ) Ξℓ (t), если κℓ <0, sin (dg (1 − t) κℓ) sin (κℓdg) Ξℓ ( t), если κℓ> 0, (1 − t) Ξℓ (t), если κℓ = 0, (11)с d g = d ( x, y ) , обозначающим длину геодезической g ( t ; x, y ), t ∈ [0, 1 ].
Поле Якоби перевернутой геодезической ḡ ( t ): = g ( t ; y, x ) = g (1- t ; x, y ) получается с использованием тот же ортонормированный базис и перенесенный фрейм, но оцененный как с = 1- t . Таким образом, получаем D y g ( t ; x, y ) [ξ ℓ ] = D y g ( t; y, x ) [ξ ℓ ] = J ḡ, ξ ℓ (1− t ), где
Jg¯, ξℓ (1 − t) = {sinh (dgt − κℓ) sinh (dg − κℓ) Ξℓ (t), если κℓ <0, sin (dgtκℓ) sin (dgκℓ) Ξℓ (t), если κℓ> 0, tΞℓ (t), если κℓ = 0.Обратите внимание, что Tg (t) M = Tḡ (1-t) M. Следовательно, Ξℓ (t) ∈Tg (t) M, ℓ = 1,…, m , является ортонормированным базисом для этого касательного пространства.
3.2. Производная от связанных геодезических
Пусть M — симметрическое риманово многообразие. Мы используем результат леммы 6 для прямого вычисления производной связанных геодезических, т. Е. Функции, состоящей из g 1 ( t ): = g ( t ; x, y ) и г 2 ( т ): = г ( т ; г 1 ( т ), z ).По определению 5 имеем
Dxg2 (t) [η] = Dg1 (t) g (t; ·, z) [Dxg1 (t) [η]]и по (10) получаем
Dxg2 (t) [η] = Jg2, Dxg1 (t) [η] (t),, где направление изменения, используемое в поле Якоби, теперь является производной от g 1 ( t ) в направлении η. Точно так же мы вычисляем производную геодезической с обратной связью g 3 ( t ): = g ( t ; z, g 1 ( t )) как
Dxg3 (t) [η] = Dg1 (t) g (t; z, ·) [Dxg1 (t) [η]] = Jg¯3, Dxg1 (t) [η] (1 − t).Обратите внимание, что поле Якоби здесь перевернуто, но направление его изменения такое же, как у поля Якоби, введенного для г 2 ( t ). С вычислительной точки зрения это означает, что мы можем использовать один и тот же ONB для производных от g 3 и ḡ 3 Кроме того, в этом случае направление изменения также вычисляется полем Якоби, поскольку D x г 1 ( т ) [η] = Дж г 1 , η ( т ).
Наконец, производная от g 2 (соответственно g 3 ) на симметричных пространствах получается следующим образом. Пусть {ξ1 [1],…, ξm [1]} — ОНБ TxM для внутреннего поля Якоби вдоль g 1 , а {ξ1 [2],…, ξm [2]} — ОНБ Tg1 (t) M для внешнего поля Якоби вдоль g 2 (соответственно g 3 ). Так как η = ∑ℓ = 1mηℓξℓ [1] ∈TxM, а Jg1, ξℓ [1] (t) = ∑l = 1mμlξl [2] ∈Tg1 (t) M, производная от g 2 (соответственно . г 3 ) относительно x в направлении η∈TxM показывает
Dxg2 (t) [η] = ∑l = 1m∑ℓ = 1mJg2, ξl [2] (t) μlηℓ, (12)и соответственно для г 3 .
3.3. Производная кривой Безье
В разделах 3.1 и 3.2 представлены необходимые концепции для вычисления производной общей кривой Безье β K ( t ; b 0 ,…, b K ), как описано в уравнении (3) относительно его контрольных точек b j .Для удобства чтения рекурсивной структуры, исследуемой ниже, мы введем несколько более простые обозначения и следующую настройку.
Пусть K будет степенью кривой Безье β K ( t ; b 0 ,…, b K ) с контрольными точками b0,…, bK ∈M. Зафиксируем k ∈ {1,…, K }, i ∈ {0,…, K — k } и t ∈ [0, 1].Представляем
gi [k] (t): = g (t; gi [k − 1] (t), gi + 1 [k − 1] (t)) = βi [k] (t; bi,…, bi + k ), (13)для кривой Безье i th степени k в алгоритме Де Кастельжау, и gi [0] (t) = bi.
Кроме того, учитывая x ∈ { b i ,…, b i + k }, мы обозначаем
ηi [k]: = Dxgi [k] (t) [η], (14)его производная относительно одной из его контрольных точек x в направлении η∈TxM.
Замечание . Очевидно, что любая другая производная от gi [k] относительно x = b j , j < i или j > i + k равна нулю. Кроме того, мы имеем ηi [0] = Dxgi [0] [η] = η для x = b i и ноль в противном случае.
Теорема 7 (Производная кривой Безье). Пусть даны k ∈ {1,…, K } и i ∈ {0,…, K — k } .Производная ηi [k] = Dxgi [k] (t) [η] от gi [k] относительно своей контрольной точки x : = b j , i ≤ j ≤ i + k , а в направлении η∈TxM определяется как
ηi [k]: = Dxgi [k] (t) [η] = {Jgi [k], ηi [k − 1] (t), если j = i, Jgi [k] k, ηi [k − 1] ( t) + Jg¯i [k], ηi + 1 [k − 1] (1 − t), если iДокажем утверждение по индукции. Для k = 1 функция gi [1] является просто геодезической. Случай i < j < i +1 не встречается, а оставшиеся первый и третий случаи следуют обозначениям, введенным для k = 0 и лемме 6.
Для k > 1 применим правило цепочки (9) к D x f [η] и получаем
Dxf [η] = Daf [Dxa [η]] + Dbf [Dxb [η]].Рассмотрим первый член D a f [ D x a [η]] и j < i + k .Согласно (10) и обозначениям из (14) непосредственно имеем
Daf [ηi [k − 1]] = Jf, ηi [k − 1] (t).Для j = i + k , ясно D x a [η] = D a f [ D ] a [η]] = 0, поскольку a не зависит от b i + k .
Аналогично доказываем второй член.Для j > i , применяя цепное правило и используя формулировку обращенного поля Якоби из леммы 6 для производной геодезической относительно ее конечной точки, получаем
Dbf [ηi + 1 [k − 1]] = Jf¯, ηi + 1 [k − 1] (1 − t).Наконец, как D x b [η] = D b f [ D x b [η для ] x = b i , предположение следует.□
На рисунке 5 представлен один уровень схематического дерева распространения для вычисления производной кривой Безье.
Рисунок 5 . Схематическое изображение случаев, когда элементы составляют цепочечную производную i -й кривой Безье порядка k в алгоритме Де Кастельжау. Сплошная линия представляет поле Якоби вдоль gi [k], а пунктирная линия представляет собой перевернутое поле Якоби . (A) Представляет случай x = b i , (B) представляет случаи, когда x ∈ { b i +1 ,…, b i + k +1 }, а (C) представляет случай x = b i + k .
Пример 8 (Квадратичная кривая Безье). Рассмотрим квадратичную кривую Безье β2: [0,1] → M , определенную как
β2 (t; b0, b1, b2) = g (t; g (t; b0, b1), g (t; b1, b2)).Используя обозначения ( 13 ), имеем
g0 [1] (t): = g (t; b0, b1), g1 [1] (t): = g (t; b1, b2), g0 [2] (t): = g (t; g0 [1], g1 [1]).Производная β 2 в точке t по отношению к b 0 в направлении η∈TboM , определяется как
Db0β2 [η] = Jg0 [2], η0 [1] (t), где η0 [1]: = Jg0 [1] 1, η (t).Производную β 2 в точке t относительно b 2 в направлении η∈Tb2M можно рассматривать как производную от первой точки после инвертирования кривой Безье, т. Е. При взгляде на β̄2 (t) = β2 (1-t) , следовательно, аналогично первому члену
Db2β2 [η] = Jg¯0 [2], η1 [1] (1 − t), где η1 [1]: = Jg¯1 [1], η (1 − t).Случай D b 1 β 2 [η], η∈Tb1M , включает цепное правило, где b 1 появляется в обоих g0 [1] (как его конечная точка) и g1 [1] (в качестве начальной точки).Используя два промежуточных результата (или поля геодезических Якоби)
η0 [1]: = Jg¯0 [1], η (1 − t) и η1 [1]: = Jg1 [1], η (t),получаем
Db1β2 [η] = Jg0 [2], η0 [1] (t) + Jg¯0 [2], η1 [1] (1 − t).Пример 9 (Кубическая кривая Безье). Рассмотрим кубическую кривую Безье β3: [0,1] → M , определенную как
β3 (t; b0, b1, b2, b3) = g (t; β2 (t; b0, b1, b2), β2 (t; b1, b2, b3)).Как и в примере 8, мы используем обозначения (13) и определяем
gj [1] (t): = g (t; bj, bj + 1), j = 0,1,2, gj [2] (t): = g (t; gj [1], gj + 1 [ 1]), j = 0,1, и g0 [3] (t): = g (t; g0 [2], g1 [2]).Получение β 3 относительно b 0 или b 3 следует той же структуре, что и в Примере 8. Случай D b 1 β 3 [η] , однако, требует двух правил цепочки. Необходимые поля Якоби соответствуют древовидной структуре, показанной на Рисунке 6B : для данного η∈Tb1M мы определяем на первом шаге рекурсии
η0 [1]: = Jg¯0 [1], η (1 − t), η1 [1]: = Jg1 [1], η (t),и на втором шаге рекурсии
η0 [2]: = Jg0 [2], η0 [1] (t) + Jg¯0 [2], η1 [1] (1 − t), η1 [2]: = Jg1 [2], η1 [1 ] (t).Обратите внимание, что и η0 [2] , и η1 [2] на самом деле являются производными от β 2 ( t ; b 0 , b 1 , b 2 ) и β 2 ( t ; b 1 , b 2 , b 3 ) соответственно относительно b 1 и направление η∈Tb1M . В итоге имеем
Db1β3 [η] = Jg0 [3], η0 [2] (t) + Jg¯0 [3], η1 [2] (1 − t).Рисунок 6 . Построение и дерево вывода кривой Безье β 3 ( t ; b 0 , b 1 , b 2 , b 3 ). Производная по переменной b i получается рекурсией полей Якоби, добавленных на каждом листе дерева. (A) Древовидное представление построения кубической кривой Безье.Толстая линия показывает распространение b 1 внутри дерева. (B) Древовидное представление конструкции η0 [3]: = Db1β3 [η]. Сплошные линии — поля Якоби, а пунктирные линии — перевернутых полей Якоби .
Случай D b 2 β 3 [η] получается симметрично, с аргументами, аналогичными b 1 .
Обратите внимание, что вычисление задействованных полей Якоби следует тому же дереву декомпозиции, что и алгоритм Де Кастельжау (рис. 6A).
3.4. Объединение сегментов и получение градиента
В этом подразделе мы выводим дифференциал составной кривой Безье B ( t ), состоящей из n сегментов, и принимаем во внимание условия C 1 . Мы упрощаем обозначения из раздела 2.1 и устанавливаем фиксированную степень равной K i = K для всех сегментов, например, K = 3 для кубической составной кривой Безье.Тогда контрольными точками будут bji, j = 0,…, K , i = 0,…, n −1. Далее обозначим через pi = bKi-1 = b0i, i = 1,…, n −1 общую точку соединения сегментов и p 0 и p n начало и конечные точки соответственно. Для упрощения записи обозначим через bi- = bK-1i и bi + = b1i, i = 1,…, n −1 две точки, необходимые для исследования условий дифференцируемости ( C 1 ), cf .Рисунок 1 для иллюстрации каркаса на M = ℝ, при K = 3.
Одна из возможностей обеспечить выполнение условия (4) C 1 — включить его в составную кривую Безье, заменив bi + на
bi + = g (2; bi−, pi), i = 1,…, n − 1. (15)Таким образом, обе производные по направлению B ( t ) относительно bi- и p i изменяются из-за дополнительного (наиболее внутреннего) правила цепочки.
Лемма 10 (Производная составной кривой Безье с условием C 1 ). Пусть B будет составной кривой Безье и pi, bi +, bi- введены, как указано выше. Замена bi + = g (2; bi-, pi) удаляет эту переменную из составной кривой Безье и сохраняет оставшиеся дифференциалы неизменными, за исключением следующего, которое теперь читается как
Dbi − B (t) [η] = {Dbi − βK (t − i + 1; pi − 1, bi − 1 +,…, ·, pi) [η] t∈ (i − 1, i], Dbi + βK (t − i; pi, bi +,…, ·, pi + 1) [Dbi − g (2; ·, pi) [η]] t∈ (i, i + 1],и
DpiB (t) [η] = {DpiβK (t − i + 1; pi − 1, bi − 1 +,…, bi−, ·) [η] t∈ (i − 1, i], DpiβK (t− i; ·, bi +,…, bi + 1−, pi + 1) [η] + Dbi + βK (t − i; pi, ·,…, bi + 1−, pi + 1) [Dpig (2; bi -, ·) [η]] t∈ (i, i + 1].В обоих случаях первый интервал включает i −1 = 0 , когда i = 1.
Доказательство. Оба первых случая являются производными кривой Безье, как и раньше, для обоих вторых случаев замена bi + = g (2; bi-, pi) дает один (для p i дополнительный) член.
Теперь выведем градиент целевой функции (7). Введем сокращение Bi = B (ti) ∈M и d2, i2 = d22 (Bi-1, Bi, Bi + 1).
Теорема 11 . Пусть M будет m-мерным коллектором , x будет одной из контрольных точек составной кривой Безье B и {ξ 1 ,…, ξ m } — соответствующий ортонормированный базис (ONB) TxM .Градиент M, xA (b) дискретизированного среднеквадратичного ускорения A ( b ) из B , относительно . x , дискретизировано в N +1 равномерных временах t 0 ,…, t N задается
∇M, xA (b) = 1∆t3∑ℓ = 1m∑i = 1N − 1∑j = i − 1i + 1 〈∇Md2, i2, DxBj [ξℓ]〉 Bjξℓ.Доказательство : Поскольку ∇M, xA (b) ∈TxM, мы ищем коэффициенты a ℓ : = a ℓ ( x ) такие, что
∇Mf (x) = ∑ℓ = 1maℓξℓ.(16)Следовательно, для любого тангенциального вектора η: = ∑ℓ = 1mηℓξℓ∈TxM имеем,
〈∇M, xA (b), η〉 x = ∑ℓ = 1maℓηℓ. (17)По определению A и Определению 4 это дает
〈∇M, xA (b), η〉 x = 1Δt3∑i = 1N − 1 〈∇Md2, i2 (x), η〉 x = 1Δt3∑i = 1N − 1Dxd2, i2 [η]. (18)Мы вычисляем Dxd2, i2 [η], используя цепное правило (определение 5) как
Dxd2, i2 [η] = ∑j = i − 1i + 1DBjd2, i2 [DxBj [η]], (19), которое, согласно определению 4, снова становится
DBjd2, i2 [DxBj [η]] = 〈∇Md2, i2, DxBj [η]〉 Bj.Термин слева от внутреннего продукта приведен в Bačák et al.[22, раздел 3], а правильный термин приведен в разделе 3.3. В то время как первое может быть вычислено с использованием полей Якоби и логарифмического отображения, второе является итеративным связыванием полей Якоби. Кроме того, дифференциал D x B j [η] может быть записан как
DxBj [η] = ∑ℓ = 1mηℓDxBj [ξℓ] ∈TBjM.Отсюда получаем
DBjd2, i2 [DxBj [η]] = ∑ℓ = 1mηℓ 〈∇Md2, i2, DxBj [ξℓ]〉 Bj,, а из (17), (18) и (19) следует
〈∇M, xA (b), η〉 x = 1∆t3∑ℓ = 1mηℓ∑i = 1N − 1∑j = i − 1i + 1 〈∇Md2, i2, DxBj [ξℓ]〉 Bj,, откуда следует утверждение (16).
4. Приложение к проблеме фитинга
В последние десятилетия проблема подбора решалась по-разному. Подход с кривыми Безье появился позже, и мы ссылаемся на Absil et al. [35], Arnould et al. [37] и Gousenbourger et al. [38] для подробного обзора этих методов.
В этом разделе мы представляем численную структуру, которую мы используем для подгонки составной кривой Безье B к набору точек данных d0,…, dn∈M, связанных с временными параметрами t 0 ,…, t n , что соответствует (1).Для простоты мы ограничиваем исследование случаем, когда t i = i , i = 0,…, n . Следовательно, задача подгонки (1) принимает вид
minb∈ΓBEλ (b): = minb∈ΓB∫t0tn‖D2B (t) dt2‖B (t) 2dt + λ2∑i = 0nd2 (pi, di), (20), где ΓB∈MM — набор контрольных точек M из B . Обратите внимание, что по сравнению с (1) оптимизация теперь выполняется на многообразии продуктов MM. Кроме того, термин подгонки теперь подразумевает расстояние между d i и p i , так как B ( t i ) = p i .
Раздел разделен на три части: коллектор MM продукта определен в разделе 4.1, где также представлен вклад члена подгонки в градиент E . Затем мы предлагаем эффективный алгоритм для вычисления градиента дискретизированного MSA на основе так называемых сопряженных полей Якоби . Наконец, мы кратко упомянем алгоритм градиентного спуска, который мы используем, а также соответствующее правило Армиджо.
4.1. Примерка и интерполяция
Поясним множество ΓB∈MM из (20).Мы явно представим вектор b и укажем его размер M . Набор Γ B — это набор из M оставшихся свободных контрольных точек для оптимизации, когда накладываются ограничения непрерывности C1. Мы различаем два случая: (i) случай подгонки, который соответствует формулам, представленным в разделе 3, и (ii) случай интерполяции (λ → ∞), где ограничение d i = p i тоже навязывается.
Для данной составной кривой Безье B: [0, n] → M, состоящей из кривой Безье степени K на каждом сегменте, и с учетом условий C 1 (4), сегменты определяются баллы
b = (p0, b0 +, b20,…, bK − 20, b1−, p1,…, bn−, pn) ∈ℳM. (21)Мы исследуем длину M. Сначала bi + задается как p i и bi- via (4). Во-вторых, для сегментов i = 2,…, n мы можем дополнительно опустить p i -1 , поскольку значение также встречается в сегменте i -1 в качестве последней записи.Наконец, первый сегмент содержит дополнительное значение b0 +, которое не зафиксировано ограничениями C 1 . Таким образом, первый сегмент состоит из K +1 контрольных точек, в то время как n -1 оставшихся сегментов определяются K -1 точек. Всего получаем M = n ( K −1) +2 контрольных точки для оптимизации.
Минимизация A ( b ) сама по себе приводит к тривиальному решению для любого набора контрольных точек b = ( x ,…, x ), x∈M, и поэтому подгоночный член из (20) важно.
Фитинг (0 <λ <∞). Если начальная и конечная точки сегмента заблокированы шумом или могут двигаться, мы используем схему подбора, чтобы сбалансировать важность, придаваемую точкам данных d 0 ,…, d n . Уравнение (20) читается как
. argminb∈ΓBA˜ (b), A˜ (b): = A (b) + λ2∑i = 0ndM2 (di, pi), (22), где λ∈ℝ + задает приоритет либо члену данных (большое λ), либо среднеквадратическому ускорению (малое λ) в пределах минимизации.Градиент члена данных дан в Karcher [41], а градиент Ã задан как
∇MM, xA˜ (b) = {∇MM, xA (b) −λlogpidi, если x = pi, i = 0,…, n, ∇MM, xA (b) в противном случае.Интерполяция (λ → ∞). Для интерполяции мы предполагаем, что начальная точка p i −1 и конечная точка p i сегментов i = 1,…, n привязаны к данным d i -1 и di∈M соответственно.Оптимизация дискретного среднеквадратичного ускорения A ( b ) показывает
argminb∈ΓBA (б) s. t.pi = di, i = 0,…, n. (23)Поскольку p i фиксированы ограничением, их можно не включать в вектор b . Получаем
b = (b0 +, b20,…, b1−, b21,…, bn−) ∈ℳM ′Поскольку существует n +1 дополнительных ограничений, минимизация выполняется на коллекторе продуктов MM ′, M ′ = M — ( n +1) = n ( K −2 ) +1.
4.2. Смежные поля Якоби
В евклидовом пространстве ℝ м , сопряженный оператор T * линейно ограниченного оператора T : ℝ м → ℝ q — оператор, выполняющий
〈T (x), y〉 ℝq = 〈x, T * (y)〉 ℝm для всех x∈ℝm, y∈ℝq.То же самое можно определить для линейного оператора S: TxM → TyM, x, y∈M, на -мерном римановом многообразии M размером м. Сопряженный оператор S *: TyM → TxM удовлетворяет условию
〈S (η), ν〉 y = 〈η, S * (ν)〉 x для всех η∈TxM, ν∈TyM.Нас интересует случай, когда S — это дифференциальный оператор D x геодезической F ( x ) = g ( t ; x, y ) для некоторые фиксированные t ∈ℝ и y∈M. Дифференциал DxF: TxM → TF (x) M можно записать как
DxF [η] = Jg, η (t) = ∑ℓ = 1m 〈η, ξℓ〉 xαℓΞℓ (t),, где α ℓ — коэффициенты поля Якоби (11), а ξ ℓ , Ξ ℓ ( t ) даны, как в лемме 6.Чтобы вывести сопряженный дифференциал (DxF) *: TF (x) M → TxM, заметим, что для любого ν∈TF (x) M имеем
〈DxF [η], ν〉 F (x) = ∑ℓ = 1m 〈η, ξℓ〉 xαℓ 〈Ξℓ (t), ν〉 F (x) = 〈η, ∑ℓ = 1m 〈Ξℓ (t), ν 〉 F (x) αℓξℓ〉 x.Следовательно, сопряженный дифференциал равен
. (DxF) * [ν] = ∑ℓ = 1m 〈ν, Ξℓ (t)〉 F (x) αℓξℓ, ν∈TF (x) M.Введем сопряженное поле Якоби JF, ν *: ℝ → TxM, ν∈TF (x) M как
JF, ν * (t) = ∑ℓ = 1m 〈ν, Ξℓ (t)〉 F (x) JF, Ξℓ (t) * (t) = ∑ℓ = 1m 〈ν, Ξℓ (t)〉 F (x ) αℓξℓ.Обратите внимание, что оценка сопряженного поля Якоби J * включает в себя тот же транспортируемый фрейм {Ξ 1 ( t ),… Ξ м ( t )} и те же коэффициенты α ℓ , что и поле Якоби J , что означает, что оценка сопряженного ни в чем не уступает самому полю Якоби.
Сопряжение D * дифференциала полезно, в частности, при вычислении градиента ∇M (h ° F) композиции F: M → M с h: M → ℝ. Полагая y: = F (x) ∈M, получаем для любого η∈TxM, что
〈∇M, x (h ° F) (x), η〉 x = Dx (h ° F) [η] = DF (x) h [DxF [η]]] = 〈∇M, yh (y), DxF [η]〉 y = 〈(DxF) * [∇M, yh (y)], η〉 x.Специально для оценки градиента составной функции h ° F получаем
∇M, x (h∘F) (x) = (DxF) * [∇M, yh (y)] = JF, ∇M, yh (y) * (t).Основное преимущество этого метода проявляется в случае составных функций, то есть формы h ° F 1 ° F 2 (обобщение на композицию с функциями K несложно) . Градиент ∇M, x (h ° F1 ° F2) (x) теперь равен
. ∇M, x (h∘F1∘F2) (x) = (DxF2) * [∇M, y2h∘F1 (y2)] = JF2, ∇M, y2h∘F1 (y2)) * (t).Рекурсивное вычисление η [3] = M, xh (x) затем дается следующим алгоритмом
η [1] = ∇M, y1h (y1), η [2] = JF1, η [1] * (t), η [3] = JF2, η [2] * (t).Пример 12 . Для h = d22: M3 → ℝ мы знаем ∇M3h по лемме 3.1 и лемме 3.2 из Бачака и др. [ 22 ]. Пусть t 1 , t 2 , t 3 ∈ [0, 1] — моменты времени, а b∈MM — заданный (под) набор контрольных точек (составная) кривая Безье B . Мы определяем F: MM → M3, b↦F (b) = (B (t1), B (t2), B (t3)) как оценки B в три заданные моменты времени.Таким образом, композиция h ° F состоит из (в порядке оценки) геодезических оценок алгоритма Де Кастельжау, функции средней точки для первой и третьей временной точки и функции расстояния .
Рекурсивная оценка градиента начинается с градиента функции расстояния. Затем для первого и третьего аргументов применяется поле Якоби средней точки. Результат вставляется в последнюю геодезическую, оцененную в «дереве» геодезических де Кастельжау. В каждой геодезической касательный вектор в точке g ( t j ; a, b ) является входом для двух смежных полей Якоби, одно отображение на TaM , другое на TbM .В любом случае эта информация доступна на всех этапах рекурсии. Обойдя это дерево в обратном направлении, можно получить требуемый градиент h ° F .
Отметим также, что даже ограничение дифференцируемости (4) дает только два дополнительных (наиболее внешних) сопряженных поля Якоби, а именно Jg (2, bi-, pi), ∇M, bi + B (tj) * (2) и Jg ~ (2, bi-, pi), ∇M, bi + B (tj) * (2). Они соответствуют вариации начальной точки bi и конечной точки p i , соответственно, как указано в (10).
4.3. Алгоритм градиентного спуска
Для решения (22) или (23) мы используем алгоритм градиентного спуска, как описано в Absil et al. [10, гл. 4]. Алгоритм для полноты приведен в алгоритме 1.
Алгоритм 1 . Алгоритм градиентного спуска на многообразии N = MM
Размеры шага задаются условиями поиска линии Armijo, представленными в Absil et al. [10, Def. 4.2.2]. Пусть N — риманово многообразие, x = x (k) ∈N — итерация градиентного спуска и β, σ∈ (0, 1), α> 0.Пусть м будет наименьшим положительным целым числом такое, что
F (x) −F (expx (−βmα∇NF (x))) ≥σβmα‖∇NF (x) ‖x. (24)Мы установили размер шага sk: = βmα в алгоритме 1.
В качестве критерия остановки мы используем максимальное количество k max итераций или минимальное изменение за итерацию dN (xk, xk + 1) <ε. На практике сначала выполняется соответствие этому последнему критерию.
Алгоритм градиентного спуска сходится к критической точке, если функция F выпуклая [10, разделы 4.3 и 4.4]. Модель средних точек (6) имеет два преимущества: (i) полная дискретизированная MSA (7) состоит из (связанных) вычислений геодезических и функции расстояния, и (ii) она сводится к классическим разностям второго порядка на евклидовой шкале. Космос. Однако на общих многообразиях эта модель не является выпуклой. Пример приведен в препринте arXiv (версия 3) Бачака и др. [22], замечание 4.6. Другая возможность (также сводящаяся к классическим различиям второго порядка в евклидовом пространстве) — это так называемая логарифмическая модель (см.г., [42])
d2, Log [x, y, z] = ‖logyx + logyz‖y.(чисто технический) недостаток логарифмической модели состоит в том, что вычисление градиента включает в себя дополнительные поля Якоби, чем представленное выше, а именно для вычисления дифференциалов логарифмической карты как по отношению к ее аргументу D x log y x , а также его базовая точка D y log y x .Тем не менее, они могут быть даны в замкнутой форме для симметричных римановых многообразий [23, Th. 7.2] [43, лем. 2.3]. Насколько нам известно, совместная выпуклость модели Log в x , y и z все еще остается открытым вопросом.
5. Примеры
В этом разделе мы приводим несколько примеров применения нашего алгоритма к задаче подгонки (20).
Сначала мы проверяем его на евклидовом пространстве и проверяем, что он возвращает естественный кубический сглаживающий сплайн.Затем мы представляем примеры на сфере S 2 и специальной ортогональной группе SO (3). Мы сравниваем наши результаты с быстрым алгоритмом Arnould et al. [37], обобщенные на подгонку, и так называемые смешанные кубические шлицы из Gousenbourger et al. [38]. Контрольные точки первого получаются путем обобщения оптимальных евклидовых условий (20) (в м , это линейная система уравнений) на многообразие; кривая впоследствии восстанавливается с помощью классического алгоритма Де Кастельжау.В последнем случае кривая получается как смешение решений, вычисленных на тщательно выбранных касательных пространствах, то есть евклидовых пространствах.
В этом разделе мы покажем, что предлагаемый метод работает так же хорошо, как и существующие методы, когда данные взяты из евлидова пространства (раздел 5.1). Это также означает, что все методы работают одинаково хорошо, когда точки данных на коллекторе достаточно локальны. Однако мы покажем на других примерах (разделы 5.2 и 5.3), что предлагаемый нами метод превосходит другие, когда точки данных разбросаны по многообразию.
Следующие примеры были реализованы в MVIRT [12], а реализации сравнения от Arnould et al. [37] и Gousenbourger et al. [38] используйте Manopt [11]. Обратите внимание, что оба набора инструментов используют очень похожую матричную структуру и реализованы в Matlab, так что результаты можно напрямую сравнивать.
5.1. Валидация в евклидовом пространстве
В качестве первого примера мы выполняем минимизацию евклидова пространства M = ℝ3. Классический результат на ℝ m состоит в том, что кривая γ, минимизирующая (1), является естественным (C2) кубическим сплайном, когда Γ является пространством Соболева h3 (t0, tn).Мы сравниваем наш подход с подходом тангенциальной линейной системы, полученным в Arnould et al. [37], чтобы проверить нашу модель. Мы используем следующие точки данных
d0 = [001], d1 = [0−10], d2 = [- 100], d3 = 182 [0−1−9], (25), а также контрольные точки p i = d i и
b0 + = expp0π82 [1−10], b1 + = expp1 − π22 [101], b1− = g (2; b1 +, p1), b2 + = expp2π22 [01−1], b3− = expp3π8 [−100], b2− = g (2; b2 +, p2), (26), где экспоненциальная карта и геодезическая на ℝ 3 на самом деле являются добавочными и линейными сегментами соответственно.Отметим, что по построению исходная кривая непрерывно дифференцируема, но (очевидно) не минимизирует (1). Параметр λ установлен на 50. MSA этой начальной кривой Ã ( b ) составляет приблизительно 18,8828.
Точки данных даны алгоритму Arnould et al. [37] для восстановления оптимальной кривой Безье B ( t ), которая является естественным кубическим сплайном C2. Результат показан на фиг. 7A вместе с разностями первого порядка вдоль кривой на фиг. 7B в виде пунктирной кривой.
Рисунок 7 . Начальная интерполирующая кривая Безье в 3 (пунктир, A ) с MSA 18,8828 оптимизирована методом линейной системы (LS) из [37] (пунктир) и предлагаемым градиентным спуском (GD, сплошной синий ). Как и ожидалось, обе кривые совпадают с MSA 4,981218. Соответствие дополнительно проиллюстрировано их разностями первого порядка в (B) .
Набор контрольных точек (p0, b0 +,…, b3-, p3) оптимизирован с помощью предлагаемого нами метода.Мы дискретизируем разницу второго порядка, используя N = 1600 точек. Результирующая кривая и графики разностей первого порядка также получаются с использованием этих значений выборки и прямой разности первого порядка. Алгоритм градиентного спуска из алгоритма 1 использует правило Армиджо (24), устанавливающее β = 12, σ = 10 −4 и α = 1. Критерии остановки: ∑i = 11600dM (xi (k), xi (k + 1)) <ϵ = 10-15 или ∥∇MnÃ∥2 <10-9, и алгоритм останавливается, когда выполняется одно из двух. Для этого примера первый критерий остановил алгоритм, в то время как норма градиента была величиной 10 -6 .
Оба метода улучшают начальное функциональное значение Ã ( b ) ≈18,8828 до значения Ã ( b min ) ≈4,981218. И линейный системный подход, и градиентный спуск работают одинаково. Разность объективных значений на 2,4524 × 10 −11 меньше для градиентного спуска, а максимальное расстояние любой точки выборки результирующих кривых имеет размер 4,3 × 10 −7 . Следовательно, в евклидовом пространстве предлагаемый градиентный спуск дает естественный кубический сплайн, как и следовало ожидать.
5.2. Примеры на Сфере
S 2Проверка геодезических . В качестве второго примера с известным минимизатором мы рассматриваем многообразие M = S2, т.е. двумерную единичную сферу, вложенную в ℝ 3 , где геодезические — большие дуги. Мы используем точки данных
d0 = [001], d1 = [010], d2 = [00−1]выровнен по геодезической, соединяющей северный полюс p 0 и южный полюс p 2 , и проходит через точку p 1 на экваторе.Определим контрольные точки кубической кривой Безье следующим образом:
x0 = 16 [112], b0 + = expp0 (3logp0 (x0)), b1− = 16 [121], x2 = 16 [−11−2], b1 + = 16 [−12−1], b2− = expp2 ( 13logp0 (x2)),, где x 0 и x 2 — временные точки, а p i = d i . Получаем два гладко связанных отрезка, так как logp1b1 — = — logp1b1 +.Исходная кривая показана на фиг. 8A, где касательные векторы особенно иллюстрируют различную скорость при p i .
Рисунок 8 . Начальная кривая (пунктирная, A, ) дает геодезическую (сплошная, B ) при минимизации дискретного ускорения. Это также можно увидеть на различиях первого порядка (C) .
Контрольные точки оптимизированы с помощью нашей интерполирующей модели, т.е. мы фиксируем начальную и конечную точки p 0 , p 1 , p 2 и минимизируем A (b).
Кривая, а также разности второго и первого порядков дискретизируются с помощью N = 201 равноотстоящих точек. Параметры правила Армийо снова устанавливаются на β = 12, σ = 10 −4 и α = 1. Критерии остановки немного ослаблены до 10 −7 для расстояния и 10 −5 для расстояния. градиент из-за синусов и косинусов, участвующих в экспоненциальном отображении.
Результат показан на рисунке 8B. Поскольку минимизатор — это геодезическая, идущая от p 0 до p 2 до p 1 , мы сначала измеряем производительность, глядя на результирующую разность первого порядка, которая постоянна, как это может быть видно на Рисунке 8C.В качестве второй проверки мы наблюдаем, что максимальное расстояние полученной кривой до геодезической составляет 2,2357 × 10 −6 . Эти оценки снова подтверждают качество градиентного спуска.
Действие термина данных . В качестве третьего примера мы исследуем влияние λ в подгоночной модели. Считаем данные точки
d0 = [001] T, d1 = [0−10] T, d2 = [- 100] T, d3 = [00−1] T,, а также контрольные точки p i = d i и
b0 + = expp0 (π82 [1−10] T), b1 + = expp1 (−π42 [−101] T), b2 + = expp2 (π42 [01−1] T), b3− = expp3 (−π82 [- 110] Т).Остальные контрольные точки b1- и b2- задаются условиями C1 (4). Соответствующая кривая B ( t ), t ∈ [0, 3], показана на рисунке 9 пунктирной линией черного цвета. При вычислении минимальной кривой MSA, которая интерполирует B ( t ) в точках p i , i = 0,…, 3, ускорение не так сильно уменьшается, см. Синюю кривую на рисунке 9A.
Рисунок 9 .Составные кривые Безье состоят из трех сегментов. Начальная кривая (пунктирная, A ) оптимизирована с помощью интерполяционной модели (сплошной синий, A ), а также с помощью аппроксимирующей модели для континуума значений λ от λ = 10 (фиолетовый, B ) до λ = 0,01 (желтый, B ). Предельный случай, когда λ = 0, дает неограниченную геодезическую (сплошной черный цвет, A ).
Для подгонки рассмотрим разные значения λ и те же параметры, что и в последнем примере.Оптимизированная кривая приближает точки данных все ближе и ближе по мере роста λ, а предел λ → ∞ дает случай интерполяции. С другой стороны, меньшие значения λ дают меньшее соответствие, но также меньшее значение среднего квадрата ускорения. В предельном случае, т.е. λ = 0, кривая (точнее, контрольные точки кривой Безье) просто следует градиентному потоку к геодезической.
Результаты собраны на рисунке 9. На рисунке 9A исходная кривая (пунктирная линия) показана вместе с решением интерполяционной модели (сплошной синий цвет) и результатом градиентного потока, т.е.е., решение аппроксимирующей модели (сплошной черный цвет) с λ = 0. Рисунок 9B еще больше иллюстрирует влияние λ с непрерывным изменением λ от большого значения λ = 10 до небольшого значения λ = 0,01. Изображение создается путем выборки из этого диапазона 1000 эквидистантных значений, окрашенных в цветовую карту viridis . Кроме того, контрольные точки также отображаются тем же цветом.
Несколько соответствующих функциональных значений, см. Таблицу 1, дополнительно иллюстрируют, что с меньшими значениями λ дискретизированная MSA также все больше и больше сводится к геодезической.При λ = 0 связь с точками данных отсутствует, и, следовательно, алгоритм не ограничивает положение геодезической. Другими словами, любой выбор контрольных точек, дающий геодезическую, является решением. Обратите внимание, что градиентный поток по-прежнему выбирает геодезическую, достаточно близкую к исходным данным (рис. 9A, сплошной черный цвет).
Таблица 1 . Функциональные значения для трехсегментной составной кривой Безье на сфере и различные значения λ.
Сравнение с тангенциальным решением .В евклидовом пространстве метод, представленный в Arnould et al. [37] и Gousenbourger et al. [38] и предложенный здесь градиентный спуск дают ту же кривую, то есть естественный кубический сплайн. Однако на римановых многообразиях все подходы приближают оптимальное решение. Действительно, их метод обеспечивает решение, работая в различных касательных пространствах, а наш минимизирует дискретизацию целевого функционала.
В этом примере мы берем те же точки данных d i , что и в (25), теперь интерпретируемые как точки на M = S2.Обратите внимание, что контрольные точки, построенные в (26), по-прежнему соответствуют сфере, поскольку каждая bi ± построена с вектором в TpiM и с использованием соответствующего экспоненциального отображения. Результат показан на рисунке 10А. Норма разностей первого порядка представлена на рисунке 10Б. Начальная кривая (пунктирная черная) имеет объективное значение 10,9103. Тангенциальная версия (пунктирная) уменьшает это значение до 7,3293. Предлагаемый метод (сплошной синий) дает значение 2,7908, независимо от того, является ли начальная кривая исходной или уже рассчитанной Арноулдом и др.[37]. Обратите внимание, что когда p3 = [0,0, -1] T, касательная версия даже не может вычислить какой-либо результат, так как построение выполняется в касательном пространстве p 0 и поскольку log p 0 p 3 не определено.
Рисунок 10 . Исходная составная кривая Безье на S 2 (штриховая, A ) имеет MSA 10,9103. Кривая, полученная с помощью линейной системы (LS, пунктирная) из [37], имеет MSA 7.3293. Решение, полученное с помощью предлагаемого нами метода (GD, сплошной синий), превосходит их все с MSA 2,7908. Это дополнительно иллюстрируется производной первого порядка, аппроксимированной разностями первого порядка в (B) .
5.3. Пример ориентации
Наконец, мы сравниваем наш метод со смешанными сплайнами, представленными в Gousenbourger et al. [38] для ориентаций, т. Е. Данных, приведенных на SO (3). Пусть
Rxy (α) = [cosαsinα0 − sinαcosα0001], Rxz (α) = [cosα0sinα010 − sinα0cosα], Ryz (α) = [1000cosαsinα0 − sinαcosα]обозначают матрицы вращения в плоскостях x — y , x — z и y — z соответственно.Мы вводим три точки данных
d0 = Rxy (4π9) Ryz (−π2), d1 = Rxz (−π8) Rxy (π18) Ryz (−π2), d2 = Rxy (5π9) Ryz (−π2).Эти точки данных показаны в первой строке рисунка 11 голубым цветом.
Рисунок 11 . От верхнего ряда к нижнему ряду: (1) точки исходных данных (голубой), (2) контрольные точки, вычисленные смешанным подходом Безье из Gousenbourger et al. [38], (3) 17 точек на соответствующей кривой, где высота представляет собой абсолютную разницу первого порядка, а кривая сравнения представляет собой различия первого порядка от нашей модели, (4) 17 точек вдоль результирующей кривой от градиентного спуска, и (5) полученные контрольные точки кривой в (4).
Мы устанавливаем λ = 10 и дискретизируем (20) с N = 401 равноотстоящими точками. Эта выборка также используется для генерации конечных разностей первого порядка. Параметры алгоритма градиентного спуска устанавливаются на те же значения, что и в примерах на сфере.
Выполняем подгонку смешанных шлицев с двумя сегментами и кубическими шлицами. Полученные контрольные точки показаны зеленым во втором ряду рисунка 11. Объективное значение Ã ( b ) = 0,6464., масштабированный до той же величины. Линия выпрямляется специально для первого сегмента Безье. Тем не менее, линия все же немного изогнута и, следовательно, не геодезическая. Это можно увидеть в четвертой строке, которая представляет 17 образцов минимизирующей кривой по сравнению с ее контрольными точками в последней строке, которые нарисованы на прямой линии.
6. Заключение и дальнейшая работа
В этой статье мы представили метод решения задачи аппроксимации кривой для точек данных на многообразии с использованием составных кривых Безье.Мы аппроксимируем среднеквадратичное ускорение кривой подходящей разностью второго порядка и правилом трапеции и выводим соответствующий градиент по отношению к его контрольным точкам. Градиент вычисляется в закрытой форме с использованием рекурсивной структуры алгоритма Де Кастельжау. Таким образом, мы получаем формулу, которая сводится к конкатенации присоединенных полей Якоби.
Оценка полей Якоби — единственное дополнительное требование по сравнению с предыдущими методами, которые оценивают исключительно экспоненциальные и логарифмические карты.Для них доступны замкнутые формы на симметричных многообразиях.
В евклидовом пространстве наше решение сводится к естественному сглаживающему сплайну, уникальной полиномиальной кривой, минимизирующей ускорение. Численные эксперименты дополнительно подтверждают, что метод, представленный в этой статье, превосходит подходы, основанные на касательном пространстве (ах), по функциональному значению.
Остается открытым вопрос, существует ли на многообразии абсолютная конечная разность второго порядка, которая является совместно выпуклой.Тогда сходимость будет следовать стандартным аргументам градиентного спуска. Для такой модели еще один интересный момент для будущей работы — выяснить, достаточно ли для сходимости только приближенной оценки полей Якоби. Это означало бы, что на многообразиях, где поле Якоби может быть оценено только приближенно, решая ОДУ, представленный подход все равно будет сходиться.
Авторские взносы
Оба перечисленных автора внесли равный вклад в содержание данной работы и одобрили ее к публикации.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Работа поддержана следующими фондами: РБ благодарит за поддержку грантом DFG BE 5888 / 2–1; P-YG с благодарностью признает поддержку Fonds de la Recherche Scientifique — FNRS и Fonds Wetenschappelijk Onderzoek — Vlaanderen в рамках проекта EOS № 30468160 и Французского сообщества Бельгии — Actions de Recherche Concertées (контракт ARC 14 / 19-060).Рисунок 9A основан на идее Розан И. Розанди.
Сноски
Список литературы
1. Пыта Л., Абель Д. Интерполяционные модели Галеркина для уравнений Навье-Стокса. IFAC-PapersOnLine (2016) 49 : 204–9. DOI: 10.1016 / j.ifacol.2016.07.442
CrossRef Полный текст | Google Scholar
3. Зандер О. Геодезические конечные элементы для стержневых стержней. Int J Numer Methods Eng . (2010) 82 : 1645–70. DOI: 10.1002 / Nme.2814
CrossRef Полный текст | Google Scholar
4. Парк Дж. Интерполяция и отслеживание ориентации твердого тела. В: ICCAS , Кенги-до (2010). п. 668–73. DOI: 10.1109 / ICCAS.2010.5670237
CrossRef Полный текст | Google Scholar
5. Су Дж, Куртек С., Классен Э., Шривастава А. Статистический анализ траекторий на римановых многообразиях: миграция птиц, отслеживание ураганов и видеонаблюдение. Ann Appl Stat . (2014) 8 : 530–52.DOI: 10.1214 / 13-AOAS701
CrossRef Полный текст | Google Scholar
6. Дын Н. Линейные и нелинейные схемы деления в геометрическом моделировании. В: Cucker F, Pinkus A, Todd MJ, редакторы. FoCum. Vol. 363 Лондонской математики. Soc. Лекционная записка Ser . Гонконг: Издательство Кембриджского университета (2009). п. 68–92. DOI: 10.1017 / CBO97811368.004
CrossRef Полный текст | Google Scholar
7. Валлнер Дж., Нава Яздани Э., Грос П. Свойства гладкости схем подразделений групп Ли. Мультимасштабная модель Simulat . (2007) 6 : 493–505. DOI: 10.1137 / 060668353
CrossRef Полный текст | Google Scholar
13. Чжоу X, Ян Ц., Чжао Х., Ю. В. Моделирование низкого ранга и его приложения в анализе изображений. ACM Comput Surveys (2015) 47 : 36. DOI: 10.1145 / 2674559
CrossRef Полный текст | Google Scholar
15. Sun J, Qu Q, Wright J. Геометрический анализ восстановления фазы. Вычислительная Математика .(2017) 8 : 1131–98. DOI: 10.1007 / s10208-017-9365-9
CrossRef Полный текст | Google Scholar
16. Ю Икс, Шен Дж. К., Чжан Дж., Летаев КБ. Чередующиеся алгоритмы минимизации для гибридного предварительного кодирования в системах MIMO миллиметрового диапазона. IEEE J Selected Top Signal Process . (2016) 10 : 485–500. DOI: 10.1109 / JSTSP.2016.2523903
CrossRef Полный текст | Google Scholar
17. Стрекаловский Э., Кремерс Д. Полная вариация для циклических структур: выпуклая релаксация и эффективная минимизация.В: Конференция IEEE по компьютерному зрению и распознаванию образов (2011). п. 1905–11.
Google Scholar
18. Стрекаловский Э., Кремерс Д. Полная циклическая вариация и обобщения. J Mat Imaging Vis . (2013) 47 : 258–77. DOI: 10.1007 / s10851-012-0396-1
CrossRef Полный текст | Google Scholar
19. Леллманн Дж., Стрекаловский Э., Кёттер С., Кремерс Д. Регуляризация полной вариации для функций со значениями в многообразии.В: Международная конференция IEEE по компьютерному зрению . Сидней, Новый Южный Уэльс (2013). п. 2944–51. DOI: 10.1109 / ICCV.2013.366
CrossRef Полный текст | Google Scholar
20. Вайнманн А., Демарет Л., Сторат М. Регуляризация полной вариации для многозначных данных. SIAM J Imaging Sci . (2014) 7 : 2226–57. DOI: 10.1137 / 130951075
CrossRef Полный текст | Google Scholar
21. Бергманн Р., Лаус Ф., Стейдл Г., Вайнманн А. Различия второго порядка циклических данных и приложения в вариационном шумоподавлении. SIAM J Imaging Sci . (2014) 7 : 2916–53. DOI: 10.1137 / 140969993
CrossRef Полный текст | Google Scholar
22. Бачак М., Бергманн Р., Стейдл Г., Вайнманн А. Негладкая вариационная модель второго порядка для восстановления многозначных образов. SIAM J Comput . (2016) 38 : 567–97. DOI: 10.1137 / 15M101988X
CrossRef Полный текст | Google Scholar
23. Бергманн Р., Фитшен Дж. Х., Перш Дж., Стейдл Г. Приоры со связанными разностями первого и второго порядка для многозначной обработки изображений. J Math Imaging Vis. (2017) 60 : 1459–81. DOI: 10.1007 / s10851-018-0840-y
CrossRef Полный текст | Google Scholar
24. Бреди К., Холлер М., Сторат М., Вайнманн А. Полная обобщенная вариация для многозначных данных. SIAM J Imaging Sci . (2018) 11 : 1785–48. DOI: 10.1137 / 17M1147597
CrossRef Полный текст | Google Scholar
25. Бергманн Р., Перш Дж., Стейдл Г. Параллельный алгоритм Дугласа – Рачфорда для восстановления изображений со значениями в симметричных многообразиях Адамара. SIAM J Imaging Sci . (2016) 9 : 901–37. DOI: 10.1137 / 15M1052858
CrossRef Полный текст | Google Scholar
26. Гросс П., Спречер М. Регуляризация полной вариации на римановых многообразиях путем итеративно переназначенной минимизации. Информационный вывод (2016) 5 : 353–78. DOI: 10.1093 / imaiai / iaw011
CrossRef Полный текст | Google Scholar
27. Бергманн Р., Чан Р., Хильшер Р., Перш Дж, Стейдл Г. Восстановление многозначных образов с помощью полуквадратичной минимизации. Inverse Prob Imaging (2016) 10 : 281–304. DOI: 10.3934 / ipi.2016001
CrossRef Полный текст | Google Scholar
28. Самир К., Абсил П.А., Шривастава А., Классен Э. Метод градиентного спуска для подбора кривой на римановых многообразиях. Вычислительная Математика . (2012) 12 : 49–73. DOI: 10.1007 / s10208-011-9091-7
CrossRef Полный текст | Google Scholar
29. Су Дж, Драйден И.Л., Классен Э., Ле Х., Шривастава А. Подгонка сглаживающих сплайнов к индексированным по времени шумным точкам на нелинейных многообразиях. Image Vis Comput. (2012) 30 : 428–42. DOI: 10.1016 / j.imavis.2011.09.006
CrossRef Полный текст | Google Scholar
30. Бумаль Н, Абсил ПА. Метод дискретной регрессии на многообразиях и его приложение к данным на SO (n). В: Сборник материалов МФБ (IFAC-PapersOnline) . Vol. 18. Милан (2011). п. 2284–89. DOI: 10.3182 / 20110828-6-IT-1002.00542
CrossRef Полный текст | Google Scholar
31. Ким К.Р., Драйден Иллинойс, Ле Х.Сглаживание сплайнов на римановых многообразиях с приложениями к трехмерному пространству форм. (2018). arXiv [Препринт] : 1801.04978.
Google Scholar
32. Fletcher PT. Геодезическая регрессия и теория наименьших квадратов на римановых многообразиях. Int J Comput Vis . (2013) 105 : 171–85. DOI: 10.1007 / s11263-012-0591-y
CrossRef Полный текст | Google Scholar
33. Rentmeesters Q. Градиентный метод аппроксимации геодезических данных на некоторых симметричных римановых многообразиях.В: Decision and Control and European Control Conference (CDC-ECC), 2011 50-я конференция IEEE по . Орландо, Флорида (2011). п. 7141–6. DOI: 10.1109 / CDC.2011.6161280
CrossRef Полный текст | Google Scholar
35. Абсил П.А., Гузенбургер П.Ю., Стревски П., Вирт Б. Дифференцируемые кусочно-Безье поверхности на римановых многообразиях. SIAM J Imaging Sci . (2016) 9 : 1788–828. DOI: 10.1137 / 16M1057978
CrossRef Полный текст | Google Scholar
36.Попель Т., Ноукс Л. Кривые Безье и C2-интерполяция в римановых многообразиях. J Приблизительная теория (2007) 148 : 111–27. DOI: 10.1016 / j.jat.2007.03.002
CrossRef Полный текст | Google Scholar
37. Арноулд А., Гузенбургер П.Ю., Самир С., Абсил П.А., Канис М. Подгонка гладких путей на римановых коллекторах: реконструкция поверхности эндометрия и предоперационная навигация на основе МРТ. В: Нильсен Ф., Барбареско Ф., редакторы. GSI2015 . Издательство Springer International Publishing (2015).п. 491–8.
Google Scholar
38. Gousenbourger PY, Massart E, Absil PA. Аппроксимация данных на коллекторах с составными кривыми типа Безье и смешанными кубическими сплайнами. J Math Imaging Vis . (2018). DOI: 10.1007 / s10851-018-0865-2
CrossRef Полный текст | Google Scholar
39. О’Нил Б. Элементарная дифференциальная геометрия . Лондон: Academic Press Inc. (1966).
Google Scholar
40. do Carmo MP. Риманова геометрия .Vol. 115. Базель: Биркхойзер; 1992. Tranl. пользователя F. Flatherty.
Google Scholar
41. Керхер Х. Сглаживание риманова центра масс и смягчителя. Коммунальное чистое приложение Math . (1977) 30 : 509–41. DOI: 10.1002 / cpa.3160300502
CrossRef Полный текст | Google Scholar
42. Бумаль Н. Интерполяция и регрессия матриц вращения. В: Нильсен Ф., Барбареско Ф., редакторы. Геометрическая наука об информации . Берлин; Гейдельберг: Springer.(2013). п. 345–52.
Google Scholar
43. Перш Дж. Методы оптимизации в многозначной обработке изображений [Диссертация] . Технический университет Кайзерслаутерна (2018).
Google Scholar
Месье Безье и его элегантные формы | Автор: Ева Шикер
Основы дизайна: кривые Безье
Мы все слышали о кривой Безье. Но действительно ли мы знаем, как его нарисовать, как применить в приложениях, как написать в коде или кто открыл эту концепцию? Давайте разберемся.
Кривая Безье состоит из двух узлов с прикрепленными маркерами управления. Значения этих управляющих маркеров используются компьютерным программным обеспечением для визуализации кривой. Ручки управления определяют форму кривой в ее начальной и конечной точках, и пользователь может ими управлять в программном обеспечении.
Простая кривая Безье, показывающая гладкую горизонтальную форму слезной капли.Многое написано о пионере кривых, Пьере Этьене Безье. Короче говоря, месье Безье жил с 1910 по 1999 год и был выдающимся французским инженером.Он был одним из основателей области твердотельного, геометрического и физического моделирования, а также области представления кривых, особенно в САПР * и производственных системах. Он стал инженером в компании Renault cars, где он усовершенствовал, популяризировал и запатентовал концепцию кривой Безье. **
Кривые Безье — это векторные траектории, и как таковые они являются основой геометрического дизайна. Кривые Безье и поверхности Безье используются в приложениях и средах САПР.
Более глубокое и детальное применение кривой Безье позволяет создавать плавные и многофункциональные конструкции.Кривые Безье позволяют нам упростить сложные векторные пути до измеримых кривых через ручки, что дает нам возможность генерировать немедленные изменения кривой.
Например, если мы рисуем птицу, мы можем упростить ее форму линии до пути из 5 узлов или точек с соответствующими ручками. Каждый сегмент между двумя узлами представляет собой кривую Безье. Манипуляции с ручками определяют вариации формы птицы.
Форма птицы, нарисованная 5 составными кривыми Безье. Иллюстрация справа показывает адаптацию иллюстрации слева.Регулируя ручки на некоторых узлах, птица имеет более округлое тело и плавный, похожий на перо хвост.Как показано на приведенном выше рисунке, фигуры, нарисованные линиями Безье, просты в работе и обеспечивают плавные линии. Изменения формы можно быстро отобразить с помощью тонких настроек ручки.
Если количество узлов в форме остается постоянным, составная форма Безье на основе векторов становится идеальным инструментом в проекте motion . Программы анимационного дизайна (After Effects) полагаются на кривые Безье.
Кривые Безье создают плавные кривые от узла к узлу.
Векторные кривые Безье можно легко анимировать как пути, если количество узлов остается постоянным. Регулировка ручек определяет вариации формы, которые переходят друг в друга в анимации.
Развивающиеся векторные формы с постоянным числом узлов и скорректированными сегментированными кривыми Безье.В этом примере векторные фигуры птиц анимируются за 5-секундный цикл. Переходы кривых Безье отображаются плавно и безупречно.
Рисунок 1
Вариации кривой Безье в последовательности
Рисунок 1. Векторная анимация состоит из вариаций формы птиц для создания движения. Анимация птицы установлена на одно положение, т.е. не имеет линейного движения.Кривые Безье и помощник по ключевым кадрам Easy Ease
Easy Ease — это функция, интегрированная в программы векторного графического дизайна (AE, Xd). По определению Easy Ease регулирует входящую и / или исходящую скорость движущегося объекта с любой конечной точки.Функция Easy Ease определяется принципом кривой Безье. Траекторией линейного движения, определяемой как постоянное движение во времени, можно манипулировать, отрегулировав его ручки начальной и конечной точки и, таким образом, преобразовав ее в кривую Безье. Кривая переводит скорость движения, увеличивая или уменьшая скорость в любой точке.
Easy Ease скорость движения
Рис. 1a: Регулировка движения кривой Безье
На этом рисунке показана сегментированная траектория движения AE с регулировкой скорости между сегментами формы.Настройки скорости отображаются в виде кривых Безье и помогают визуализировать настройки скорости. Адаптировано из Adobe After Effects.Скорость формы между сегментами формы регулируется с помощью настройки времени кривой Безье. Движение птицы становится более органичным и плавным.
Рис. 1b: Нет корректировок движения
Напротив, если время сегментированного движения не регулируется, то траектория движения будет линейной. Это позволит передать движение птицы без каких-либо нюансов скорости.
На этом рисунке показана траектория непрерывного движения AE без каких-либо корректировок скорости между сегментами формы. Адаптировано из Adobe After Effects.Ода кривой Безье. Как математическое уравнение может формировать… | by Takashi Wickes
Изменения в истории искусства были вызваны культурными революциями и полными сдвигами в человеческом мышлении; редко их связывают с математическим уравнением.
Но, возможно, алгоритм с четырьмя переменными сформировал современную эстетику иллюстративного дизайна.От коробок для хлопьев до пространства галереи, он обеспечивает эстетику простых форм, четких цветовых палитр и делает упор на визуальную функциональность. Его эффективность и оптимизированный формат сегодня заслужили свое место в арсенале каждого цифрового художника. И хотя это может быть уловка для произношения, она способствует большинству визуальных произведений, с которыми мы взаимодействуем каждый день, даже буквы, которые вы сейчас читаете, не были бы такими чистыми и гладкими без этого.
Рис. 1 — Явная форма кубической кривой БезьеРедко можно приписать математическое уравнение катализатору нового момента в художественном языке.Но редко удается создать такие простые и элегантные решения, как кривая Безье.
Рис. 2 — Построение кубической кривой БезьеКривые Безье — это кривые, созданные с помощью алгоритма де Кастельжау. Требуется всего лишь четыре точки, и алгоритм создает гладкие органические линии или многочлены, которые нашли применение во многих программных приложениях. В анимации он создает плавные переходы между точкой A и точкой B; и далее в этом эссе мы увидим, как эти линии стали такими же универсальными в искусстве, как использование кисти.
История кривых Безье, в отличие от самих кривых, имела относительно плоское начало в 1912 году. Вопреки названию, математическая концепция нашего плавно изогнутого многочлена была первоначально разработана Сергеем Натановичем Бернштейном в 1912 году: когда Пьер Безье было всего 2 года. [1] Без изобретения компьютеров основа Бернштейна не могла найти сильного промышленного применения, пока чуть более 50 лет спустя математик и инженер двух конкурирующих французских производителей автомобилей не столкнулись с проблемой снасти.
В то время как Соединенные Штаты наслаждались роскошью низких цен на газ в середине 60-х годов, европейские производители автомобилей были вынуждены искать новые способы повышения топливной экономичности своих автомобилей. [2] Математик Поль де Кастельжау из Citroen и инженер Пьер Безье из Renault, оба независимо друг от друга, рассматривали базис Бернштейна как решение, сочетая математическую базисную функцию с Computer Aided Design для моделирования гладкого, извилистого автомобиля. тела. И хотя де Кастельжау открыл это приложение для основы Бернштейна в 1959 г. [3] , на несколько лет раньше, чем Безье, Citroen не разрешил ему опубликовать его работу.Поскольку Безье имел возможность публично патентовать и публиковать свои открытия, наш замечательный многочлен получил чуть менее трудное для произношения название: кривая Безье.
Как уже упоминалось, кривая Безье с тех пор использовалась в ряде программных приложений. Но наиболее наглядно он был представлен в программном обеспечении в то время, когда программное обеспечение предназначалось для офисной работы и обработки текстов.
В 1982 году трое компьютерных ученых из исследовательского центра Xerox в Пало-Альто были разочарованы до такой степени, что бросили свою работу.В то время компания Xerox PARC была сосредоточена на том, чтобы с помощью компьютерных программ изобрести офис будущего. Они изобрели текстовые редакторы, сети, лазерные принтеры и, к разочарованию Джона Варнока, не уделяли должного внимания графике. После отказа Xerox коммерциализировать новый язык управляемой графики для печати, Warnock вместе с Гешке и Путманом решили покинуть Xerox и основать собственную компанию в Кремниевой долине под названием Adobe. [4]
Рис. 3 — Джон Варнок рисует кубическую кривую БезьеИх первым продуктом была технология PostScript, эквивалентная Interpress.Это был универсальный язык, на котором печатники могли интерпретировать текстовые документы и печатать правильное содержание. Но вместо того, чтобы быть языком, основанным на растровых изображениях, PostScript был языком, основанным на контрольных точках и алгоритме, который соединял эти контрольные точки с плавными органическими кривыми.
«Я, , уже знакомился с математикой Безье, но не с чудесными геометрическими конструкциями, которые с ней связаны, и с очень, очень простыми компьютерными реализациями, связанными с Безье.И однажды я узнал об этом, потому что это очень естественно, очень легко программировать, очень легко работать на компьютере. После этого я думал, что все другие подходы были глупыми! » — Соучредитель Adobe Джон Варнок в 2004 году. Интервью [5]
Реализация Adobe кривых Безье для отображения текста букв была революционной. Тексты могут быть любого размера, большие или маленькие, сжатые или растянутые. PostScript был масштабируемым, выведен на рынок в 1985 году через лазерные принтеры Apple и стал универсальным графическим языком для визуализации шрифтов на принтерах и настольных компьютерах любой марки и любой модели.
Он мог делать изображения и печатать, но поскольку PostScript был графическим языком, вам все равно нужно было быть компьютерным программистом, чтобы создавать эту графику. Поэтому в 1985 году Adobe начала разработку продукта, который выводил код PostScript из интерфейса рисования. Поскольку PostScript основан на векторах и кривых, пользователь может щелкнуть мышью, чтобы создать опорные точки, а затем перетащить, чтобы установить вторую контрольную точку, которая будет определять кривую. Конечным результатом стал Adobe Illustrator.
«… после того, как PostScript установился, мы сказали:« Ну и дела, нам действительно нужна программа для рисования шрифтов.Я сказал, давайте будем очень прямолинейны и попросим людей поставить контрольные точки и позволить им управлять контрольными точками и управлять кривыми таким образом, и вот откуда это взялось. Майк Шустер создал небольшой прототип под названием Пикассо, которое было именем-предшественником. У него было несколько названий: одним из них была ArtiFactory. Это сработало очень хорошо. Когда люди привыкли к этому, они могли контролировать это, а затем мы начали использовать это для шрифтового дизайна ». — Джон Варнок в 2004 году. Интервью [5]
Illustrator далек от того, чтобы использовать его для шрифтового дизайна.До иллюстратора графический дизайн как профессия был трудоемкой задачей. Это была карьера, которая зависела от технического образования и терпения. Представьте себе, что современная графика создается полностью вручную. Аналогичный процесс включал в себя листы и листы букв Letraset с сухим переводом для переноса текста на лист бумаги для дизайна. Иллюстраторы и другие графические элементы были выполнены с помощью ручек Rapidograph, которые требовали постоянного обслуживания, доливки и мытья рук от взрывов чернил.
«В свое время процесс создания артов для фотоаппаратов был довольно сложным. У вас было несколько элементов … Текст был выплюнут из наборного устройства, который был вырезан и наклеен на доску ». — Цифровой художник Берт Монрой [6]
«Одна страница заданного шрифта, на это может уйти день или два дня». — Иллюстратор Рон Чан [6]
Графический дизайн был классическим обученным видом искусства, ориентированным на точность и аккуратность для создания работ, которые можно было обрабатывать с помощью камеры и распространять через печать.Варнок, чья жена Марва была классическим тренером графического дизайнера, сосредоточился на этих проблемах, которые были у графических дизайнеров. Радиальные углы, разные размеры штриха, идеальные кривые: он определил эти проблемы, чтобы перенести графический дизайн из специализированного ручного процесса в процесс, который можно было бы выполнить с помощью компьютерной программы.
Компьютерная программа была быстро принята в полиграфической промышленности, заменив способ создания новых иллюстраций, обложек, печатных объявлений — все они переняли эту новую форму рисунка.Благодаря прямому влиянию классического графического дизайна, многие функции напрямую переведены из терминологии графического дизайнера. И задача, которая раньше требовала идеального хода французской кривой, теперь стала точной, регулируемой и требовала двух щелчков мышью.
«Меня действительно поразила эта способность манипулировать кривыми, потому что кривые очень важны, особенно если вы разрабатываете шрифт. Традиционно мне нужна была эта кривая, и я хотел придать ей немного больше кривой, и если бы она была неправильной, мне пришлось бы вычеркнуть ее и начать все сначала, тогда как в Illustrator я мог просто взять ее и переместить Это.”- Digital Painter Берт Монрой [6]
С принятием традиционных графических дизайнеров, были некоторые опасения, насколько это упростило торговлю графическим дизайном. Торговля, которая требовала многолетнего обучения и образования, надлежащего оборудования и опыта, быстро превратилась в необходимость сидеть перед экраном компьютера и копией Adobe Illustrator. В отрасли возникли опасения, что графический дизайн сам по себе уменьшится. Поскольку количество обучения больше не требуется, качество дизайнера также будет следствием Illustrator.
«Все говорили, что мы [Adobe] собираемся испортить хороший дизайн, потому что теперь это может сделать каждый. Но сливки поднимаются наверх ». — Соучредитель Adobe Джон Варнок в 2004 г. Интервью
Доступность часто играет роль угрозы традиционным практикам и мышлению. Существует опасение разрешить публичный доступ к традиции, поскольку исключительность и необходимость тех, кто уже принимает в ней участие, потенциально могут идентифицировать себя как устаревшие.
А в истории искусства пространство галереи является прочной параллелью этой традиции. В прошлом посещение выставок в пространстве галереи требовало многих лет образования, чтобы понимать произведения искусства. Без твердого понимания произведений Гомера книга «Избиение женихов в конце» «Одиссеи» лишена смысла и просто превращается в старинный гончарный сосуд.
В пространстве галереи использовался барьер входа через образование, предметы в зависимости от их интертекстуальности и отсылки к концепциям и рассказам, читаемым в высших учебных заведениях.Эта концепция получила широкую популярность благодаря движению Lowbrow art, которое способствовало стиранию границ между пространством галереи и массовым контентом. Интертекстуальность и отсылки к произведениям относятся не к высшему образованию, а к поп-культуре или интуитивным человеческим знаниям. Для сравнения, Adobe Illustrator добился аналогичного эффекта, но вместо того, чтобы убрать входной барьер для понимания искусства, он удалил входной барьер для создания произведений искусства для массового потребления.
Благодаря своему вкладу в печатную рекламу, большая часть работы по графическому дизайну, которую взял на себя Illustrator, была ориентирована на массовую аудиторию.Полиграфические агентства и компании были сосредоточены на эффективности и стоимости, и компьютерное программное обеспечение по сравнению с оборудованием для традиционного графического дизайна было несложной задачей, чтобы перевести своих штатных дизайнеров в Adobe Illustrator. С этим сдвигом, происходящим в компаниях, движимых прибылью, а не художественным стимулом, Illustrator превратился в торговлю инструментами, даже несмотря на то, что он заимствовал большую часть своего дизайна и функций из классически обученного вида искусства. Эта комбинация доступных инструментов изобразительного искусства создала интересный феномен; где время на создание становится меньше, а влияние инструмента, а не художника приобретает большее значение.
Благодаря повышенной эффективности, которую обеспечивает программное обеспечение, переход от первоначальной идеи к конечному производству превращается из поездки в поездку на самолете.
Перед поездкой вы должны разбираться в картах, планировать остановки и проводить больше часов за рулем. Необходимость собственного контроля имеет первостепенное значение, и поэтому поездка требует от путешественника большей дальновидности и подготовки.
Перед полетом на самолете действия, необходимые после того, как вы знаете, куда хотите отправиться, менее сложны.После покупки билета подготовка не включает знание промежутка между посадкой в самолет и приземлением. Как и в случае с графическим дизайном, промежуток между обдумыванием идеи и отправкой окончательного дизайна больше не требует знания того, как рисовать пером на бумаге и печатать на пленке. Способ путешествия требует меньше, сокращая два фактора: общее время путешественника и потребность путешественника в подготовке.
Когда время на создание искусства сокращается, спектр влияния смещается.Этот спектр определяется двумя сторонами: влияние искусства и влияние самой среды. Два противоположных примера эффекта этого спектра — французский художник-историк Теодор Жерико и поп-художник из Кутцтауна, штат Пенсильвания, Кейт Харинг.
Эти два художника прочно вошли в канон истории искусства, находясь на двух противоположных сторонах истории.
Рис. 4 — Плот Медузы — Теодор ЖерикоДо изобретения фотографии живопись была средством записи исторических событий.Самая известная работа Жерико, Плот Медузы , изображает последствия крушения французского военно-морского корабля. Произведение Жерико запомнилось своей блестящей композицией, которая радует глаз, запоминающимся тоном, который оставляет навязчивое ощущение, и огромным размером произведения. Но вряд ли картину можно описать как свидетельство использования краски. Огромный размер картины требует многих лет работы, чтобы устранить визуальные побочные эффекты использования кисти и стать больше похожим на гигантскую фотографию.Время, проведенное на холсте, уменьшало влияние средства массовой информации, и, кроме того, подготовка Жерико была попыткой создать изображение, максимально точно соответствующее тому, что может дать фотография.
«Художник проделал огромную подготовительную работу и исследования: взял интервью у выживших и фактически сконструировал в своей мастерской масштабную модель плота. Он ходил в местные больницы и морги, где воочию наблюдал за цветом и текстурой кожи умирающих и мертвых пациентов.Он также создал бесчисленное количество этюдов и рисунков маслом ». — Цитата о процессе подготовки Жерико [7]
Тот факт, что Жерико использовал масляную живопись в качестве среды, не полностью определил эстетику его последнего произведения. С затраченным количеством времени медиум склонился бы к своей чистой воле, чтобы воссоздать образ, который он столько лет создавал в своем уме.
Сотни лет спустя через Атлантический океан Кейт Харинг будет ездить в метро Нью-Йорка в 1982 году.С палкой мела в руке Харинг искал пустой рекламный плакат. Буквально через пару минут он рисовал мультяшную картинку на черной подложке пустого плаката, оставляя ее для миллионов посетителей метро. Он должен был действовать быстро, поскольку то, что он делал, было технически незаконным граффити, что несколько раз требовало его ареста. [8]
Рис. 5 — Рисунок Кейта Харинга на станции метро«Скачок от поездов метро к пустой рекламе в метро, другими словами, был коротким, и техника Харинга — быстрая, публичная, импровизационная, виртуозная — определенно во многом обязана ранним граффити. … Это и темпоральный — мел, разумеется, подлежащий стиранию, особенно в таком общественном месте — и «тактильный», то есть его линия более решительно указана на его собственный акт творения (его создатель, его время и место изготовления).Это строка, которая требует, чтобы ее понимали как (пишет Харинг) «мгновенный отклик на чистую жизнь». — Тезис Чарли Гайлара об искусстве Харинга в метро [9]
Его стиль стал легендарным в истории современного искусства, его помнят по персонажам, сделанным из простых форм и единообразных. размерный ход. И когда мы отточим его мел и пустые рекламные щиты, мы сможем сделать вывод, откуда взялся этот стиль. Эстетика и среда более тесно связаны.И хотя в метро Харинг развил свой особый стиль, он созрел в его картинах, по-прежнему сохраняя соответствие с очерченными персонажами и равномерным штрихом.
И, конечно же, следует отдать должное Харингу за его мысли и идеи, лежащие в основе его работ, но по сравнению с предусмотрительностью Жерико для работы Харинга требовалось гораздо меньше. Харинг работал с тем, что у него было: время и мелом наброски, в то время как Жерико работал годами и исследованиями. Харинг мог определить, как он формировал эти линии, но не совсем то, как они выглядели.Он работал с самыми грубыми формами, которые мог создать его среда, и поэтому его среда определяла его эстетику.
А теперь вернемся к истории Illustrator. Ряд штатных дизайнеров вынуждены соблюдать сроки для создания печатной рекламы и графического искусства. Кроме того, для торговли графическим дизайном теперь требовалось меньше технического образования и опыта, что позволяло свежим умам вносить свой вклад в отрасль без багажа идей, который приходит с классическим обучением. Так же, как Харинг, но в промышленном масштабе, работа стала более тесно связанной с носителем, и в данном случае этим носителем был Adobe Illustrator.
Инструмент «Перо» поддерживает чистые края, естественные кривые и прямые линии, подобно тому, как мел создает жирные однородные линии и примитивные формы. Можно создать такую детализированную работу, как Жерико, с мелкими деталями, которые потребовали бы большого увеличения, чтобы увидеть острые края инструмента «Перо». Эта работа потребует времени, подробного плана выполнения и глубоких знаний программного обеспечения.
Я не утверждаю, что Illustrator произвел революцию в мире искусства, выдвинув на первый план острые края и естественные кривые.Посмотрите на работы таких художников, как Пит Мондриан и Мемфисская группа, и убедитесь, что использование примитивных форм с острыми краями изучается в области изобразительного искусства на протяжении многих лет. Illustrator не выдвигал эти идеи; было много художников и движений, которые произвели революцию в этих идеях в области искусства, дизайна и архитектуры. Учитывая это, я пришел к выводу, что особенности Illustrator оживили актуальность именно этих движений, чтобы оказать большее влияние на эстетику современного графического дизайна.
Эстетика современного графического дизайна, о которой я говорю, — это стили графического дизайна, которые используются в таких областях, как печать и визуальные эффекты программного обеспечения, которые я буду называть «цифровым дизайном».
Рис. 6 — Duolingo People Грегори ХартманаРаботы таких иллюстраторов, как Грегори Хартман, Райан Патнэм и Ник Слейтер, являются примерами этого определения эстетики цифрового дизайна. Все изображения имеют невероятно разные стили, но все они сильно зависят от использования Adobe Illustrator.Воспроизведение радиальных изгибов модели Duolingo People Грегори Хартмана с помощью любой другой техники не позволило бы добиться такой точности взгляда.
Рис. 7 — Dropbox Иллюстрация Райана ПатнэмаСоздание готовой к производству версии логотипа Dropbox Райана Патнэма не потребовало бы никаких ошибок, и даже при этом невозможно было бы воссоздать его одинаковую ширину линии, цвет и палитру непрозрачности. В работах Ника Слейтера эстетика еще больше отклоняется от математических корней Illustrator, но это достигается за счет более сложного использования кривых Безье.Стиль по-прежнему определяется ограниченной цветовой палитрой и резкими линиями.
Рис. 8 — События Ника СлейтераКаждый из этих художников создавал цифровые иллюстрации для ведущих технологических компаний Duolingo, Dropbox и Asana / Slack. Роль иллюстратора в технологических компаниях связана с большим творчеством, но также требует согласованности бренда и служит целям рекламных идей компании.
Цифровой дизайн — это отличительный стиль, и хотя художники, использованные в примере, являются художниками с меньшими временными ограничениями и большей творческой свободой, этот стиль развивался с момента создания Illustrator, и на момент создания этих иллюстраций он определил навыки и приемы использования инструмента для создания особой эстетики.
Рис. 9 — Торговый автомат Гарри Кэмпбелла (стиль BauHaus)Цифровой дизайн в основном связан с художественными движениями Bauhaus и Memphis Group, характеризующимися острыми краями и плоским дизайном.
Рис. 10 — Обложка МАГАЗИНА Лорен Роулинг (стиль Memphis Group)Тем не менее, такие движения, как Bauhaus и Memphis Group, имели в масштабе невероятно короткую продолжительность жизни — 14 и 8 лет соответственно. Их влияние на современный дизайн неоспоримо.Образовательные концепции Баухауза сформировали идеи современной школы дизайна с упором на функциональность, а не на эстетику. Изометрическую форму Баухауза, основанную на архитектурных и инженерных чертежах, можно быстро стилистически воспроизвести с помощью инструмента «Перо и сетка перспективы» в Adobe Illustrator. Проект «Мемфис» возродился в рекламе и дизайне интерфейсов с яркими цветами и узорами, которые многие называют «эстетикой 80-х». Формы и яркая, но ограниченная цветовая палитра проекта «Мемфис» могут добавить изюминку векторным изображениям, созданным в Illustrator, особенно с возможностью изменения цвета нескольких элементов с помощью инструмента «Цветовая палитра».
Оба движения обладают эстетическими характеристиками, которые хорошо подходят для среды Illustrator. Их можно быстро воссоздать, оставив при этом площадку для творческих идей и концепций. Расширение этой идеи может выявить причины, по которым минимализм, ар-деко, конструктивизм, модерн и модернизм сохраняют актуальность в современном графическом дизайне. [10] И поскольку эти движения были обновлены с учетом визуальной значимости, они несут в современную эпоху свои идеи и дополнительные идеи.Эти идеи в дальнейшем перенимаются нашими художниками, графическими дизайнерами, которые создают визуальные работы для массовой аудитории.
Вот где важность этого влияния. Это влияние не влияет напрямую на эстетику визуального искусства в галерее. Если бы это было так, эстетикой торговали бы те, кто рискнул войти в пространство галереи, и те, кто создает искусство для пространства галереи.
Концепция доступности искусства, которая возникла из художественного движения Lowbrow, определяет, что искусство, созданное для массового потребления, может иметь большее, унаследованное влияние на современную культуру в целом.Дизайн — это искусство, созданное для общественного потребления, вместо того, чтобы сосредотачиваться на границах галерейного пространства, и вместе с тем несет в себе идеи этих возрожденных художественных движений. Визуальное искусство также несет в себе идеи этих художественных течений, которые обладают огромной силой влиять на то, как культура думает, ведет себя и создает искусство.
Эти направления в искусстве были выбраны с помощью современного инструмента для иллюстрации: Adobe Illustrator. Adobe Illustrator был создан, чтобы продвинуть область графического дизайна за пределы пера и бумаги, опираясь на основу кривой Безье.Кривая Безье была изобретена для интерполяции гладких кривых с использованием четырех контрольных точек. Сдвиг в индустрии графического дизайна Illustrator вызвал возрождение старых течений в искусстве, которые стали упоминаться и переиздаваться для публики. Эта связь четырехточечного уравнения с установлением сегодняшнего фундаментального понимания изображений и искусства — это то, как простое математическое уравнение изменило ход истории искусства.
Безье
Инструмент Bezier позволяет создавать кривую, определяемую контрольными вершинами.Этот инструмент работает так же, как инструмент «Перо». Кривые Безье — это подмножество кривых неоднородного рационального B-сплайна (NURBS), которые состоят из двух типов управляющих вершин: , якоря, и касательные. Якоря лежат на кривой и определяют начало касательных. Касательные определяют форму кривой, ведущей к соседнему якорю. В зависимости от опции Mode в интерфейсе отображаются немного разные компоненты.
Каждый раз, когда вы щелкаете в окне просмотра с активированным инструментом Кривая Безье, вы создаете привязку, которая не имеет касательных, и на вашей кривой создается острый угол.Когда вы продолжаете щелкать мышью в области просмотра, к кривой добавляются дополнительные точки.
Когда вы щелкаете и перетаскиваете в окне просмотра, создаются привязка и пара касательных. Перетаскивание перемещает касательные для формирования кривой. По умолчанию обе стороны касательной перемещаются вместе.
Следующая анимация иллюстрирует рабочий процесс.
Для активации инструмента Безье прямого моделирования:
• На дополнительной вкладке Basic панели инструментов моделирования щелкните правой кнопкой мыши инструмент «Перо», чтобы открыть дополнительные параметры, и выберите Кривая Безье .
• Либо на дополнительной вкладке Кривая панели инструментов моделирования в разделе Инструменты щелкните Безье .
| 1. | Щелкните макет Model на панели переключателей в верхней части пользовательского интерфейса. |
| 2. | На панели инструментов откройте дополнительную вкладку Basic . |
| 3. | Щелкните правой кнопкой мыши инструмент «Перо» и выберите Кривая Безье . |
| 4. | Щелкните и перетащите в окне просмотра, чтобы определить первую привязку для вашей кривой. |
При этом угловая привязка разбивается на две точки, которые перемещаются вдоль сегментов, чтобы создать участок закругленной кривой между прямыми сегментами.
| 5. | Щелкните и удерживайте в другом месте и растяните касательные маркеры, чтобы сформировать кривую. Повторите, чтобы добавить дополнительные точки на вашу кривую. |
Щелкните изображение ниже, чтобы просмотреть анимацию.
Чтобы изменить угол касательной в точке привязки, включите режим выбора Многоугольники , щелкните маркер касательной и перетащите его в новое положение.Меняется резкость угла. Чтобы изменить положение привязки, включите режим выбора Многоугольники , щелкните привязку и перетащите ее в новое положение.
Во время рисования вы можете навести указатель мыши на любую точку или ручку, где она станет желтой. Затем вы можете щелкнуть и перетащить привязку или маркер для дальнейшего редактирования кривой.
Чтобы переместить только одну сторону касательной, щелкните ручку касательной и перетащите ее в другое положение.
После того, как вы уроните инструмент, нажав клавишу Space , интерактивное редактирование будет потеряно, но вы можете повторно активировать возможность редактирования, выбрав кривую в режиме выбора Polygons .
Для снятия якоря:
| 1. | На правой панели щелкните Свойства инструмента . |
Откроется панель инструментов Свойства .
| 2. | Установить режим на Удалить . |
| 3. | Щелкните любую из контрольных точек, чтобы удалить их. |
Вы можете изменить кривые Безье на кривые B-сплайна или стандартные кривые в зависимости от того, чего вы хотите достичь в своей сцене. Операция Curve Convert mesh позволяет преобразовать выбранные кривые в другой заданный тип кривой.
Для получения дополнительной информации см. Преобразование кривой.
Пример
Для изменения типа кривой:
| 1. | В макете Model откройте вкладку Curve на левой панели и щелкните Bezier . |
| 2. | В трехмерном окне просмотра щелкните в нескольких местах, чтобы создать кривую Безье, и нажмите клавишу Пробел , чтобы отпустить инструмент. |
| 3. | Откройте вкладку Mesh Ops на правой панели и нажмите Добавить оператора > Curves > Curve Convert . |
Совет: Если вкладка Mesh Ops не отображается на правой панели, щелкните значок Дополнительные вкладки или Новая вкладка и выберите Новая вкладка > Списки данных > Mesh Ops .
| 4. | Выберите тип исходной и целевой кривой, которую вы хотите преобразовать.В этом примере на вкладке Properties установите From to Bezier и To to B-Spline . |
Кривая Безье преобразуется в B-сплайновую кривую.
После того, как вы уроните инструмент, интерактивное редактирование будет потеряно, но вы можете снова активировать его, выбрав кривую в режиме выбора Полигоны .
Для получения дополнительной информации см. Режим выбора многоугольника
f
Режим | Задает режим кривой Безье.Доступны следующие варианты: • Добавить — добавляет якоря вдоль кривой. Это режим «по умолчанию». • Редактировать — Свободно щелкните и перетащите любой из якорей вдоль кривой, чтобы изменить внешний вид на желаемую форму. • Удалить — Щелкните любой из якорей вдоль кривой, чтобы удалить его. |
Точка X , Y , Z | Позволяет более тонкое управление точками, назначая определенные значения X, Y и Z в этих полях ввода для текущей выбранной привязки. |
дюйм X , Y , Z | Позволяет более тонкое управление дескриптором путем назначения определенных значений X, Y и Z в этих полях ввода In для текущей выбранной (выделенной) привязки. |
Выход X , Y , Z | Обеспечивает более точное управление ручкой путем назначения определенных значений X, Y и Z в этих полях ввода Out для текущей выбранной (выделенной) привязки. |
Закрыто | Добавляет автоматический сегмент кривой между первой и последней позициями привязки, создавая замкнутую кривую. Совет: В качестве альтернативы, чтобы создать замкнутую кривую, щелкните правой кнопкой мыши первую привязку в окне просмотра. |
Заполнено | Когда включена опция Closed , вы можете дополнительно включить опцию Filled для создания визуализируемой плоской поверхности, которая определяется самой контурной кривой.Результирующая поверхность может быть помечена как многоугольник для добавления определений материалов. |
Сделать UVs | Активирует автоматическое создание координат текстуры UV вдоль кривой.Сгенерированные значения UV представляют собой одну вертикальную линию (ось V в UV), располагая все вершины привязки равномерно между 0 и 1. Например, это может быть полезно для применения градиента к визуализированной кривой (опция Render Curves доступен в свойствах элемента сетки. |
Геометрическое моделирование и приложения обобщенных смешанных тригонометрических кривых Безье с параметрами формы | Успехи в разностных уравнениях
Чен, К., Ван, Г.: Класс кривых, подобных Безье. Comput. Помощь Geom. Des. 20 , 29–39 (2003)
MATH Статья Google ученый
Орук, Х., Филлипс, Дж .: Полиномы Q-Бернштейна и кривые Безье. J. Comput. Прил. Математика. 151 , 1–12 (2003)
MathSciNet МАТЕМАТИКА Статья Google ученый
Фарин, Г.E .: Кривые и поверхности для компьютерного геометрического проектирования: Практическое руководство. Academic Press, Сан-Диего (2002)
MATH Google ученый
Хан, X., Ма, Y., Хуанг, X: новое обобщение кривой Безье и поверхности. J. Comput. Прил. Математика. 217 , 180–193 (2008)
MathSciNet МАТЕМАТИКА Статья Google ученый
Ян, Л.Q., Zeng, X.M .: Кривые Безье и поверхности с параметрами формы. Int. J. Comput. Математика. 86 , 1253–1263 (2009)
MathSciNet МАТЕМАТИКА Статья Google ученый
Xiang, T., Liu, Z., Wang, W., Jiang, P .: Новое расширение кривых Безье и поверхностей той же степени. J. Inf. Comput. Sci. 7 , 2080–2089 (2010)
Google ученый
Лю З., Чен X., Цзян П .: Класс обобщенных кривых Безье и поверхностей с несколькими параметрами формы. J. Comput.-Aided Des. Comput. График. 22 , 838–844 (2010)
Google ученый
Хан, X .: Класс общих сплайновых кривых четвертой степени с параметрами формы. Comput. Помощь Geom. Des. 28 , 151–163 (2011)
MathSciNet МАТЕМАТИКА Статья Google ученый
Qin, X., Hu, G., Zhang, N., Shen, X., Yang, Y .: Новое расширение полиномиальных базисных функций, описывающих кривые Безье и поверхности степени n с несколькими параметрами формы. J. Appl. Математика. Comput. 223 , 1–16 (2013)
MATH Статья Google ученый
Ахмад, А., Амат, А.Х., Али, Дж. М .: Обобщение кривой типа Безье. EDUCATUM 1 , 56–68 (2014)
Google ученый
Хошек, Дж., Лассер, Д .: Основы компьютерного геометрического проектирования. Шумакер Л.Л. Переводчик. А. К. Петерс, Натик (1993)
MATH Google ученый
Ван Г., Чен К., Чжоу М .: B-сплайновые кривые NUAT. Comput. Помощь Geom. Des. 21 , 193–205 (2004)
MathSciNet МАТЕМАТИКА Статья Google ученый
Ян, Л., Лян, Q.F .: Расширение модели Безье. J. Appl. Математика. Comput. 218 , 2863–2879 (2011)
MATH Статья Google ученый
Ху, Г., Бо, К., Ву, Дж., Вэй, Г., Хоу, Ф .: Моделирование сложных кривых произвольной формы с использованием кривых SG-Безье с ограничениями геометрической непрерывности. Симметрия 10 , 545 (2018)
MATH Статья Google ученый
БиБи, С., Аббас, М., Мисро, М.Ю., Ху, Г.: Новый подход гибридной тригонометрической кривой Безье к моделированию симметричных революционных кривых и симметричных поверхностей вращения. IEEE Access 7 , 165779–165792 (2019)
Артикул Google ученый
Максуд, С., Аббас, М., Ху, Г., Рамли, А.Л.А., Миура, К.Т .: Новое обобщение тригонометрической кривой Безье и поверхности с параметрами формы и его применения.Математика. Пробл. Англ. 2020 , идентификатор статьи 4036434 (2020)
Артикул Google ученый
Хан, X.L .: Кубические тригонометрические полиномиальные кривые с параметром формы. Comput. Помощь Geom. Des. 21 , 535–548 (2004)
MathSciNet МАТЕМАТИКА Статья Google ученый
Хан, X.A., Ма, Y.C., Хуанг, X.L .: Кубическая тригонометрическая кривая Безье с двумя параметрами формы.{2} \) рациональная квадратичная тригонометрическая кривая Безье с двумя параметрами формы с приложениями. J. Appl. Математика. Comput. 219 , 10183–10197 (2013)
MATH Google ученый
Ян Л.Л .: Алгебро-тригонометрическая смешанная кусочная кривая. J. Inf. Comput. Sci. 12 , 6491–6501 (2015)
Артикул Google ученый
Ян, Л.Л .: Кубические тригонометрические неоднородные сплайновые кривые и поверхности. Математика. Пробл. Англ. 2016 , 1–9 (2016)
MathSciNet МАТЕМАТИКА Google ученый
Ху, Г., Ву, Дж., Львов, Д .: Условия геометрической непрерывности для кривых H-Безье степени n . В: 3-я Международная конференция IEEE по изображениям, зрению и вычислениям, стр. 706–710 (2018).
Google ученый
Харим, Н.А., Карим, С.А.А., Осман, М., Саабан, А., Гаффар, А., Нисар, К.С., Балеану, Д.: Интерполяция с сохранением положительности с использованием рационального сплайна четвертой степени. AIMS Math. 5 (4), 3762–3782 (2020)
MathSciNet Статья Google ученый
Али, Ф.А.М., Абдул Карим, С.А., Саабан, А., Хасан, М.К., Гаффар, А., Нисар, К.С., Балеану, Д .: Построение треугольных фрагментов кубического тиммера и его применение в интерполяции разбросанных данных.Математика 8 (2), 159 (2020)
Артикул Google ученый
Зулкифли, Н.А.Б., Карим, С.А.А., Сарфраз, М., Гаффар, А., Нисар, К.С.: Интерполяция изображений с использованием рационального бикубического шара. Математика 7 (11), 1045 (2019)
Артикул Google ученый
Башир У., Аббас М., Аванг, М. Н. Х., Али, Дж. М .: Класс квазиквинтичной тригонометрической кривой Безье с двумя параметрами формы.Sci. Азия 39S (2), 11–15 (2013)
Артикул Google ученый
Усман, М., Аббас, М., Миура, К.Т .: Некоторые технические приложения новых тригонометрических кубических кривых Безье для моделирования сложных кривых произвольной формы. J. Adv. Мех. Des. Syst. Manuf. 14 (4), 19-00420 (2020)
Артикул Google ученый
Ху, Г., Ли, Х.{1} \) соединение \ (S- \ lambda \) кривых и поверхностей. Математика 8 (8), 1359 (2020)
Google ученый
Ху, X., Ху, Г., Аббас, М., Мисро, M.Y .: Приближенная многостепенная редукция кривых Q-Безье с помощью обобщенных полиномиальных функций Бернштейна. Adv. Отличаются. Equ. 2020 (1), 413 (2020)
Артикул Google ученый
Маджид, А., Аббас, М., Миура, К.Т., Камран, М., Назир, Т .: Моделирование поверхности из 2D-контуров с приложением для построения черепно-лицевых переломов. Математика 8 (8), 1246 (2020)
Артикул Google ученый
Ли, Ф., Ху, Г., Аббас, М., Миура, К.Т .: Обобщенная модель Х-Безье: условия геометрической непрерывности и приложения к моделированию кривых и поверхностей. Математика 8 (6), 924 (2020)
Артикул Google ученый
Хан, К., Лобиял, Д.К .: Кривые Безье на основе Lupaş \ ((p, q) \) — аналог функций Бернштейна в CAGD. J. Comput. Прил. Математика. 317 , 458–477 (2017)
MathSciNet МАТЕМАТИКА Google ученый
Lupaş, A .: A q — аналог оператора Бернштейна. Семинар по численному и статистическому исчислению, Университет Клуж-Напока 9 , 85–92 (1987)
MathSciNet МАТЕМАТИКА Google ученый
Мурсалин, М., Ансари, К.Дж., Хан, А .: On \ ((p, q) \) — аналог операторов Бернштейна. Прил. Математика. Comput. 266 , 874–882 (2015) [Ошибка: 278, 70–71 (2016)]
MathSciNet МАТЕМАТИКА Google ученый
Студия | Кривые Безье
Кривые Безье — отличный способ плавно анимировать объекты вдоль кривой в ZapWorks Studio.
См. Также: Ссылка на сценарий Z.Bezier
Создание кривой Безье
Чтобы создать кривую Безье, щелкните правой кнопкой мыши корневой узел в Иерархии и выберите «Новый»> «Преобразования»> «Безье» и дайте ему имя.
Это создаст новый узел Безье в Иерархии. Как и узлы группы, узлы Безье могут содержать другие узлы. Эти дочерние узлы появятся в точке кривой, определенной их родительским узлом Безье.
Новые экземпляры кривых Безье начинаются без каких-либо точек, с помощью которых можно определить кривую, поэтому необходимо выделить узел Безье и нажать кнопку «ДОБАВИТЬ» на панели «Свойства», чтобы добавить 4 начальные точки в «Сегмент».
Управление кривой Безье
Расположение точек Безье
Если присутствует хотя бы один сегмент, в 3D-виде появится кривая.
Выделение узла Безье и нажатие кнопки «B» в верхней части 3D-вида откроет точки Безье (представленные маленькими квадратами) и позволит их перемещать. В одном сегменте две точки относятся к началу и концу кривой, а две относятся к дуге кривой между этими точками.
Если щелкнуть и перетащить открытые точки в 3D-виде, их положение изменится — это самый простой способ настроить кривую. Точки Безье также можно редактировать непосредственно из раздела точек на панели свойств и через точки (…) сеттер-функция З. Безье.
Добавление и удаление сегментов
Дополнительные сегменты можно добавить к кривой Безье, нажав кнопку «ДОБАВИТЬ» в нижней части раздела точек на панели «Свойства». Это расширит кривую и предоставит дополнительные точки для манипулирования.
сегментов можно удалить, щелкнув крестик рядом с их именем на панели свойств.
Разделение сегмента
В случае, если сегмент уже существует, но необходимо определить более сложную кривую, есть возможность разбить сегмент.Разделение создает дополнительный сегмент, который находится в центре одного разделения.
Сегмент можно разделить, нажав кнопку «РАЗБИВАТЬ» на панели «Свойства».
Опция разделения сегмента позволяет вернуться и точно настроить кривые Безье после того, как уже было создано несколько сегментов.
Анимация объектов по кривой Безье
Объекты можно анимировать по кривой Безье с помощью переменной расстояния . Узлы внутри или относительно узла Безье появятся на расстоянии от расстояния вдоль кривой.Лучший способ изменить переменную distance — использовать временную шкалу, однако это также возможно с помощью состояний и с помощью функции установки расстояния (…).
Пример справа показывает свойство расстояния узла Безье, переходящего от 0 к 1, где 0 представляет начало кривой, а 1 представляет конец. Этот переход приводит к анимации объекта вдоль кривой на протяжении временной шкалы.
Использование нескольких кривых
Хотя разделение сегментов может помочь точно настроить кривую анимации, оно не может изменить скорость, с которой объект движется по кривой в разных точках.Для этого несколько кривых должны быть «связаны» вместе в трехмерном виде, а свойство объекта relativeTo переключается между ними с помощью временной шкалы.
Два узла Безье, созданные в Иерархии, можно связать в цепочку, поместив начало одной из кривых в конец другой, либо вручную с помощью инструмента манипуляции Безье, либо с помощью раздела точек на панели «Свойства». Последний больше подходит для обеспечения того, чтобы начальная и конечная точки находились в одном и том же месте.
Затем необходимо создать временную шкалу, которая включает свойство distance обоих узлов Безье вместе со свойством relativeTo объекта (ов), анимируемого вдоль кривых.
На временной шкале должно происходить следующее в указанном порядке:
- Расстояние
- Свойство
relativeToобъекта (ов) переключается с первого узла Безье на второй. - Расстояние


 Например, при трех контрольных точках форма кривой — парабола;
Например, при трех контрольных точках форма кривой — парабола;
 Подобным образом задаются другие координаты.
Подобным образом задаются другие координаты. TCHAR szTitle[MAX_LOADSTRING]; // Строка, хранящая текст заголовка окна.
TCHAR szWindowClass[MAX_LOADSTRING]; // Имя класса окна.
ATOM MyRegisterClass(HINSTANCE hInstance);
BOOL InitInstance(HINSTANCE, int);
LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);
// Функция, вычисляющая значение х и у координат точки на кривой.
POINT CalcBezierCurve(vector<POINT>, const double&);
// Процедура отрисовки кривой Безье.
void DrawBezier(HDC, vector<POINT>);
// Функция, возвращающая номер точки массива,
// по которой пользователь щелкает мышью.
int GetNumberOfPoint (int, int, vector<POINT>);
// Главная функция программы, в которой запускается цикл обработки сообщений.
int APIENTRY _tWinMain(HINSTANCE hInstance,
HINSTANCE hPrevInstance,
LPTSTR lpCmdLine,
int nCmdShow)
{
UNREFERENCED_PARAMETER(hPrevInstance);
UNREFERENCED_PARAMETER(lpCmdLine);
MSG msg;
LoadString(hInstance, IDS_APP_TITLE, szTitle, MAX_LOADSTRING);
LoadString(hInstance, IDC_BEZIERCURVES, szWindowClass, MAX_LOADSTRING);
MyRegisterClass(hInstance);
if (!InitInstance (hInstance, nCmdShow)) {
return FALSE;
}
while (GetMessage(&msg, NULL, 0, 0)) {
TranslateMessage(&msg);
DispatchMessage(&msg);
}
return (int) msg.
TCHAR szTitle[MAX_LOADSTRING]; // Строка, хранящая текст заголовка окна.
TCHAR szWindowClass[MAX_LOADSTRING]; // Имя класса окна.
ATOM MyRegisterClass(HINSTANCE hInstance);
BOOL InitInstance(HINSTANCE, int);
LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);
// Функция, вычисляющая значение х и у координат точки на кривой.
POINT CalcBezierCurve(vector<POINT>, const double&);
// Процедура отрисовки кривой Безье.
void DrawBezier(HDC, vector<POINT>);
// Функция, возвращающая номер точки массива,
// по которой пользователь щелкает мышью.
int GetNumberOfPoint (int, int, vector<POINT>);
// Главная функция программы, в которой запускается цикл обработки сообщений.
int APIENTRY _tWinMain(HINSTANCE hInstance,
HINSTANCE hPrevInstance,
LPTSTR lpCmdLine,
int nCmdShow)
{
UNREFERENCED_PARAMETER(hPrevInstance);
UNREFERENCED_PARAMETER(lpCmdLine);
MSG msg;
LoadString(hInstance, IDS_APP_TITLE, szTitle, MAX_LOADSTRING);
LoadString(hInstance, IDC_BEZIERCURVES, szWindowClass, MAX_LOADSTRING);
MyRegisterClass(hInstance);
if (!InitInstance (hInstance, nCmdShow)) {
return FALSE;
}
while (GetMessage(&msg, NULL, 0, 0)) {
TranslateMessage(&msg);
DispatchMessage(&msg);
}
return (int) msg.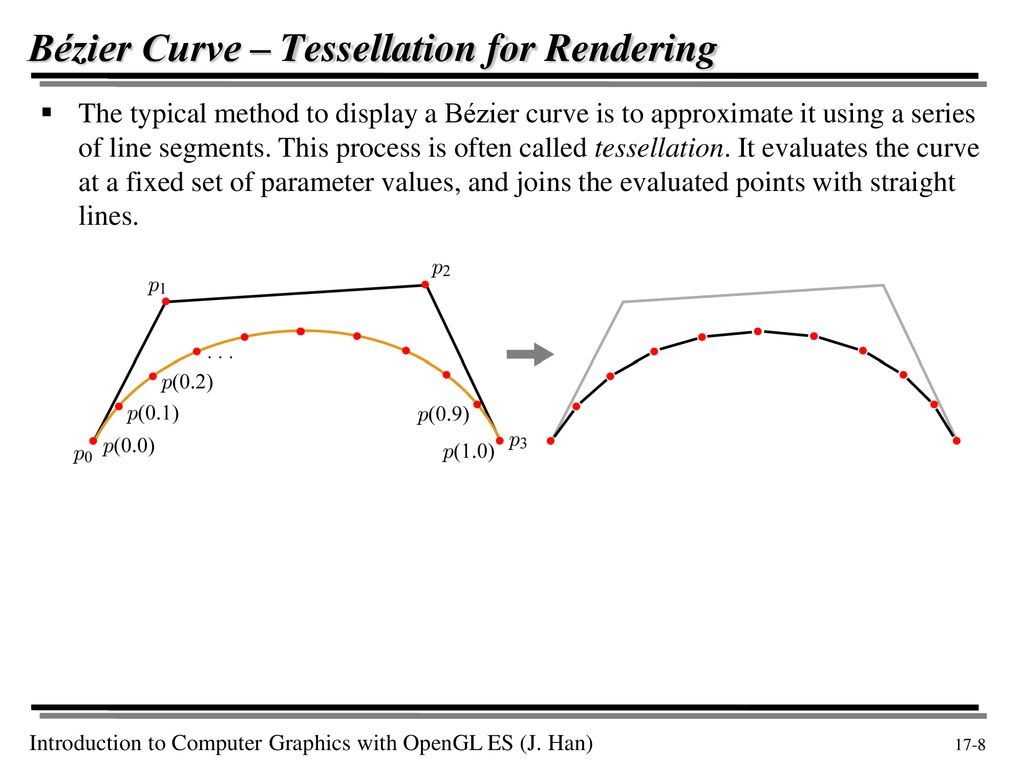 wParam;
}
// Регистрация класса окна.
ATOM MyRegisterClass(HINSTANCE hInstance)
{
WNDCLASSEX wcex;
wcex.cbSize = sizeof(WNDCLASSEX);
wcex.style = CS_HREDRAW | CS_VREDRAW;
wcex.lpfnWndProc = WndProc;
wcex.cbClsExtra = 0;
wcex.cbWndExtra = 0;
wcex.hInstance = hInstance;
wcex.hIcon = LoadIcon(hInstance, MAKEINTRESOURCE(IDI_BEZIERCURVES));
wcex.hCursor = LoadCursor(NULL, IDC_ARROW);
wcex.hbrBackground = (HBRUSH)(COLOR_WINDOW+1);
wcex.lpszMenuName = MAKEINTRESOURCE(IDC_BEZIERCURVES);
wcex.lpszClassName = szWindowClass;
wcex.hIconSm = LoadIcon(wcex.hInstance, MAKEINTRESOURCE(IDI_SMALL));
return RegisterClassEx(&wcex);
}
// Функция, сохраняющая дескриптор экземпляра приложения и
// создающая главное окно приложения.
BOOL InitInstance(HINSTANCE hInstance, int nCmdShow)
{
HWND hWnd;
hInst = hInstance;
hWnd = CreateWindow(szWindowClass, szTitle, WS_OVERLAPPEDWINDOW,
CW_USEDEFAULT, 0, CW_USEDEFAULT, 0, NULL, NULL, hInstance, NULL);
if (!hWnd) {
return FALSE;
}
ShowWindow(hWnd, nCmdShow);
UpdateWindow(hWnd);
return TRUE;
}
// Функция, вычисляющая значение х и у координат точки на кривой.
wParam;
}
// Регистрация класса окна.
ATOM MyRegisterClass(HINSTANCE hInstance)
{
WNDCLASSEX wcex;
wcex.cbSize = sizeof(WNDCLASSEX);
wcex.style = CS_HREDRAW | CS_VREDRAW;
wcex.lpfnWndProc = WndProc;
wcex.cbClsExtra = 0;
wcex.cbWndExtra = 0;
wcex.hInstance = hInstance;
wcex.hIcon = LoadIcon(hInstance, MAKEINTRESOURCE(IDI_BEZIERCURVES));
wcex.hCursor = LoadCursor(NULL, IDC_ARROW);
wcex.hbrBackground = (HBRUSH)(COLOR_WINDOW+1);
wcex.lpszMenuName = MAKEINTRESOURCE(IDC_BEZIERCURVES);
wcex.lpszClassName = szWindowClass;
wcex.hIconSm = LoadIcon(wcex.hInstance, MAKEINTRESOURCE(IDI_SMALL));
return RegisterClassEx(&wcex);
}
// Функция, сохраняющая дескриптор экземпляра приложения и
// создающая главное окно приложения.
BOOL InitInstance(HINSTANCE hInstance, int nCmdShow)
{
HWND hWnd;
hInst = hInstance;
hWnd = CreateWindow(szWindowClass, szTitle, WS_OVERLAPPEDWINDOW,
CW_USEDEFAULT, 0, CW_USEDEFAULT, 0, NULL, NULL, hInstance, NULL);
if (!hWnd) {
return FALSE;
}
ShowWindow(hWnd, nCmdShow);
UpdateWindow(hWnd);
return TRUE;
}
// Функция, вычисляющая значение х и у координат точки на кривой. // Принимает в качестве параметров вектор-массив точек и
// параметр t, характеризующий положение на кривой.
POINT CalcBezierCurve(vector<POINT> pts, const double& t)
{
int i, c;
double p;
POINT np;
int n = static_cast<int>(pts.size()) - 1;
c = 1;
for (i = 0; i <= n; i++) {
pts[i].x = pts[i].x * c;
pts[i].y = pts[i].y * c;
c = (n-i)*c/(i+1);
}
p = 1;
for (i = 0; i <= n; i++) {
pts[i].x = pts[i].x * p;
pts[i].y = pts[i].y * p;
p = p * t;
}
p = 1;
for (i = n; i >= 0; i--) {
pts[i].x = pts[i].x * p;
pts[i].y = pts[i].y * p;
p = p * (1-t);
}
np.x = 0;
np.y = 0;
for (i = 0; i <= n; i++) {
np.x = np.x + pts[i].x;
np.y = np.y + pts[i].y;
}
return np;
}
// Процедура отрисовки кривой Безье.
// Принимает в качестве параметров дескриптор контекста устройства и
// вектор-массив точек, по которым ведется построение кривой.
// Принимает в качестве параметров вектор-массив точек и
// параметр t, характеризующий положение на кривой.
POINT CalcBezierCurve(vector<POINT> pts, const double& t)
{
int i, c;
double p;
POINT np;
int n = static_cast<int>(pts.size()) - 1;
c = 1;
for (i = 0; i <= n; i++) {
pts[i].x = pts[i].x * c;
pts[i].y = pts[i].y * c;
c = (n-i)*c/(i+1);
}
p = 1;
for (i = 0; i <= n; i++) {
pts[i].x = pts[i].x * p;
pts[i].y = pts[i].y * p;
p = p * t;
}
p = 1;
for (i = n; i >= 0; i--) {
pts[i].x = pts[i].x * p;
pts[i].y = pts[i].y * p;
p = p * (1-t);
}
np.x = 0;
np.y = 0;
for (i = 0; i <= n; i++) {
np.x = np.x + pts[i].x;
np.y = np.y + pts[i].y;
}
return np;
}
// Процедура отрисовки кривой Безье.
// Принимает в качестве параметров дескриптор контекста устройства и
// вектор-массив точек, по которым ведется построение кривой. void DrawBezier(HDC hdc, vector<POINT> pts)
{
double t; // Параметр, по которому будет идти вычисление точек на кривой: t = [0,...,1].
HPEN hPen; // Дескриптор пера, которым будем пользоваться для сохранения
// разных стилей рисования линий для построения как отрезков, соединяющих
// точки массива, так и самой кривой.
POINT np = {0, 0}; // Точка, в которую будет заноситься результат выполнения функции CalcBezierCurve.
// Перемещаем текущую позицию пера в первую точку массива.
MoveToEx(hdc, pts[0].x, pts[0].y, NULL);
// Присваиваем перу характеристику: пунктирная линия, толщина - 1 пиксель, синий цвет.
hPen = CreatePen(PS_DASH, 1, RGB(0, 10, 170));
SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства.
// Строим пунктирные линии, соединяющие точки массива.
for (int i = 0; i < pts.size(); i++)
LineTo(hdc, pts[i].x, pts[i].y);
// Присваиваем перу характеристику: сплошная линия, толщина - 2 пикселя, темно-красный цвет.
hPen = CreatePen(PS_SOLID, 2, RGB(200, 50, 10));
SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства.
void DrawBezier(HDC hdc, vector<POINT> pts)
{
double t; // Параметр, по которому будет идти вычисление точек на кривой: t = [0,...,1].
HPEN hPen; // Дескриптор пера, которым будем пользоваться для сохранения
// разных стилей рисования линий для построения как отрезков, соединяющих
// точки массива, так и самой кривой.
POINT np = {0, 0}; // Точка, в которую будет заноситься результат выполнения функции CalcBezierCurve.
// Перемещаем текущую позицию пера в первую точку массива.
MoveToEx(hdc, pts[0].x, pts[0].y, NULL);
// Присваиваем перу характеристику: пунктирная линия, толщина - 1 пиксель, синий цвет.
hPen = CreatePen(PS_DASH, 1, RGB(0, 10, 170));
SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства.
// Строим пунктирные линии, соединяющие точки массива.
for (int i = 0; i < pts.size(); i++)
LineTo(hdc, pts[i].x, pts[i].y);
// Присваиваем перу характеристику: сплошная линия, толщина - 2 пикселя, темно-красный цвет.
hPen = CreatePen(PS_SOLID, 2, RGB(200, 50, 10));
SelectObject(hdc, hPen); // Выбираем объект нашего пера в контекст устройства. // Перемещаем текущую позицию пера в первую точку массива.
MoveToEx(hdc, pts[0].x, pts[0].y, NULL);
// Цикл отрисовки кривой Безье.
// Для параметра t, пробегающего от 0 до 1 с шагом 0.3 (данный шаг обеспечивает умеренную сглаженость кривой)
// вычисляем значение новой точки и строим линию, соединяющую предыдущую точку с новой.
for (t = 0.0; t < 1.0; t += 0.03) {
np = CalcBezierCurve(pts, t);
LineTo(hdc, np.x, np.y);
}
LineTo(hdc, pts.back().x, pts.back().y);
// Возвращаем стандартное перо в контекст устройства.
SelectObject(hdc, (HPEN)GetStockObject(BLACK_PEN));
// Рисуем окружности, выделяющие точки массива.
for (int i = 0; i < pts.size(); i++)
Ellipse(hdc, pts[i].x-5, pts[i].y-5, pts[i].x+5, pts[i].y+5);
}
// Функция, возвращающая номер точки массива,
// по которой пользователь щелкает мышью.
// Принимает в качестве параметров х и у координаты точки щелчка
// и вектор-массив точек, задающих кривую.
int GetNumberOfPoint (int x, int y, vector<POINT> P)
{
int lim = static_cast<int>(P.
// Перемещаем текущую позицию пера в первую точку массива.
MoveToEx(hdc, pts[0].x, pts[0].y, NULL);
// Цикл отрисовки кривой Безье.
// Для параметра t, пробегающего от 0 до 1 с шагом 0.3 (данный шаг обеспечивает умеренную сглаженость кривой)
// вычисляем значение новой точки и строим линию, соединяющую предыдущую точку с новой.
for (t = 0.0; t < 1.0; t += 0.03) {
np = CalcBezierCurve(pts, t);
LineTo(hdc, np.x, np.y);
}
LineTo(hdc, pts.back().x, pts.back().y);
// Возвращаем стандартное перо в контекст устройства.
SelectObject(hdc, (HPEN)GetStockObject(BLACK_PEN));
// Рисуем окружности, выделяющие точки массива.
for (int i = 0; i < pts.size(); i++)
Ellipse(hdc, pts[i].x-5, pts[i].y-5, pts[i].x+5, pts[i].y+5);
}
// Функция, возвращающая номер точки массива,
// по которой пользователь щелкает мышью.
// Принимает в качестве параметров х и у координаты точки щелчка
// и вектор-массив точек, задающих кривую.
int GetNumberOfPoint (int x, int y, vector<POINT> P)
{
int lim = static_cast<int>(P. size());
// Проходим по массиву точек,
for (int i = 0; i < lim; i++) {
// Если щелчок произвелся по точке или в непосредственной близости от нее, то
if ((x > P[i].x-15 && x < P[i].x+15) && (y > P[i].y-15 && y < P[i].y+15))
// возвращаем номер этой точки (индекс в массиве).
return i;
}
// Если щелчок произвелся не по точке массива, возвращаем отрицательное число.
return -1;
}
// Оконная процедура, обеспечивающая обработку сообщений для основного окна программы.
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
static bool IsSelected = false; // Булевская переменная, служащая для распознания, выбран ли набор точек
// для кривой или еще нет. Начальное значение - "ложь", не выбран.
static vector<POINT> pts; // Вектор-массив точек, по которым будем строить кривую.
PAINTSTRUCT ps;
HDC hdc; // Контекст устройства.
switch (message) // Обработка текущего сообщения.
{
case WM_LBUTTONDOWN:
// Нажата левая кнопка мыши.
size());
// Проходим по массиву точек,
for (int i = 0; i < lim; i++) {
// Если щелчок произвелся по точке или в непосредственной близости от нее, то
if ((x > P[i].x-15 && x < P[i].x+15) && (y > P[i].y-15 && y < P[i].y+15))
// возвращаем номер этой точки (индекс в массиве).
return i;
}
// Если щелчок произвелся не по точке массива, возвращаем отрицательное число.
return -1;
}
// Оконная процедура, обеспечивающая обработку сообщений для основного окна программы.
LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
static bool IsSelected = false; // Булевская переменная, служащая для распознания, выбран ли набор точек
// для кривой или еще нет. Начальное значение - "ложь", не выбран.
static vector<POINT> pts; // Вектор-массив точек, по которым будем строить кривую.
PAINTSTRUCT ps;
HDC hdc; // Контекст устройства.
switch (message) // Обработка текущего сообщения.
{
case WM_LBUTTONDOWN:
// Нажата левая кнопка мыши.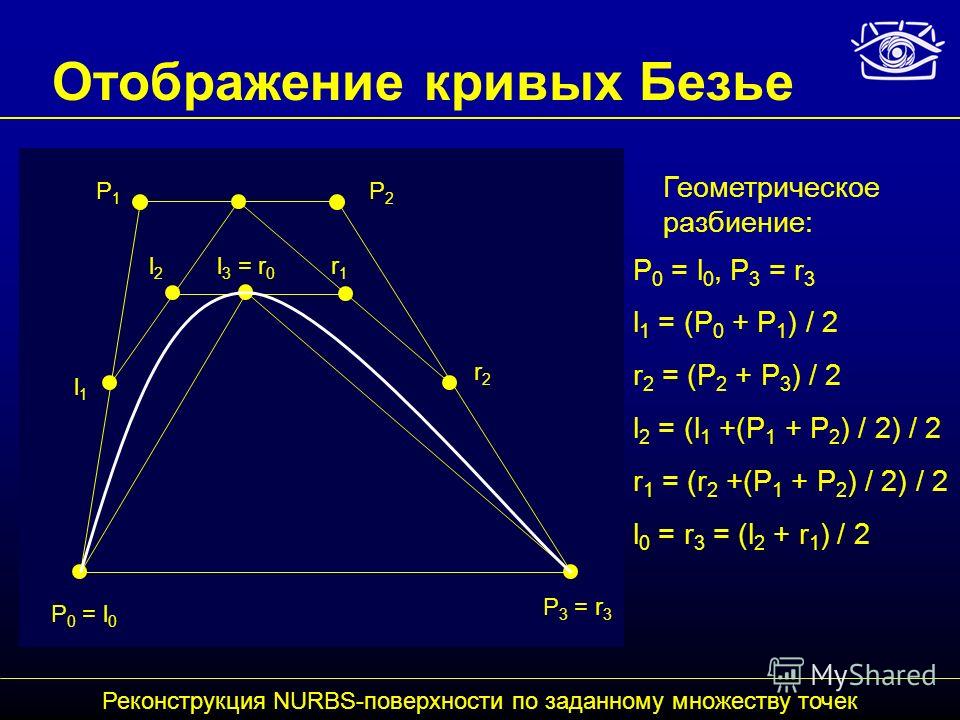 // Если точки еще не выбраны, заносим координаты точки в массив и
// рисуем окружность для выделения места нажатия.
if (!IsSelected) {
hdc = GetDC(hWnd);
POINT tmp;
tmp.x = LOWORD(lParam);
tmp.y = HIWORD(lParam);
pts.push_back(tmp);
Ellipse(hdc, pts.back().x-5, pts.back().y-5, pts.back().x+5, pts.back().y+5);
ReleaseDC(hWnd, hdc);
}
break;
case WM_MOUSEMOVE:
// Сообщение от перемещения мыши, обрабатывается только тогда, когда выбран набор точек и
// после отрисовки кривой (выбран пункт меню "Draw curve").
if (IsSelected) {
// Если при перемещении мыши нажата левая кнопка,
if (wParam && MK_LBUTTON) {
hdc = GetDC (hWnd);
// то находим номер точки массива, если щелчок произвелся по одной из его точек.
int mnp = GetNumberOfPoint(LOWORD(lParam), HIWORD(lParam), pts);
if (mnp < 0) break;
// Заносим в точку массива с номером выбранной точки новые координаты.
pts[mnp].x = LOWORD (lParam) ;
pts[mnp].
// Если точки еще не выбраны, заносим координаты точки в массив и
// рисуем окружность для выделения места нажатия.
if (!IsSelected) {
hdc = GetDC(hWnd);
POINT tmp;
tmp.x = LOWORD(lParam);
tmp.y = HIWORD(lParam);
pts.push_back(tmp);
Ellipse(hdc, pts.back().x-5, pts.back().y-5, pts.back().x+5, pts.back().y+5);
ReleaseDC(hWnd, hdc);
}
break;
case WM_MOUSEMOVE:
// Сообщение от перемещения мыши, обрабатывается только тогда, когда выбран набор точек и
// после отрисовки кривой (выбран пункт меню "Draw curve").
if (IsSelected) {
// Если при перемещении мыши нажата левая кнопка,
if (wParam && MK_LBUTTON) {
hdc = GetDC (hWnd);
// то находим номер точки массива, если щелчок произвелся по одной из его точек.
int mnp = GetNumberOfPoint(LOWORD(lParam), HIWORD(lParam), pts);
if (mnp < 0) break;
// Заносим в точку массива с номером выбранной точки новые координаты.
pts[mnp].x = LOWORD (lParam) ;
pts[mnp]. y = HIWORD (lParam) ;
// Посылаем сообщение для перерисовки клиентской обдасти окна, и, следовательно, самой кривой.
SendMessage(hWnd, WM_PAINT, NULL, NULL);
ReleaseDC (hWnd, hdc);
}
}
break;
case WM_COMMAND:
// Обработка сообщений, поступающих при выборе пунктов меню.
switch (LOWORD(wParam)) // Обработка значения идентификатора пункта меня.
{
case IDM_EXIT:
// Меню File -> Exit
// Выход.
DestroyWindow(hWnd);
break;
case ID_CURVE_DRAWCURVE:
// Меню Curve -> Draw curve
// Если размер массива точек равен нулю, т. е. пользователь не выбрал ни одной точки, то
// выводим сообщение об ошибке.
if (pts.size() == 0) {
MessageBox(hWnd, "There is necessary to put at least one point to client area of window!",
"An error occured!", NULL);
break;
}
// Иначе - присваиваем переменной IsSelected значение "истина" (означающая, что пользователь выбрал набор точек)
IsSelected = true;
// и осуществляем перерисовку.
y = HIWORD (lParam) ;
// Посылаем сообщение для перерисовки клиентской обдасти окна, и, следовательно, самой кривой.
SendMessage(hWnd, WM_PAINT, NULL, NULL);
ReleaseDC (hWnd, hdc);
}
}
break;
case WM_COMMAND:
// Обработка сообщений, поступающих при выборе пунктов меню.
switch (LOWORD(wParam)) // Обработка значения идентификатора пункта меня.
{
case IDM_EXIT:
// Меню File -> Exit
// Выход.
DestroyWindow(hWnd);
break;
case ID_CURVE_DRAWCURVE:
// Меню Curve -> Draw curve
// Если размер массива точек равен нулю, т. е. пользователь не выбрал ни одной точки, то
// выводим сообщение об ошибке.
if (pts.size() == 0) {
MessageBox(hWnd, "There is necessary to put at least one point to client area of window!",
"An error occured!", NULL);
break;
}
// Иначе - присваиваем переменной IsSelected значение "истина" (означающая, что пользователь выбрал набор точек)
IsSelected = true;
// и осуществляем перерисовку. SendMessage(hWnd, WM_PAINT, NULL, NULL);
break;
case ID_CURVE_NEWCURVE:
// Меню Curve -> New curve
// Очищаем массив точек, IsSelected присваиваем "ложь" и осуществляем перерисовку.
for (int i = pts.size(); i > 0; i--)
pts.pop_back();
IsSelected = false;
SendMessage(hWnd, WM_PAINT, NULL, NULL);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
break;
case WM_PAINT:
// Перерисовка клиенской области окна.
// Объявление всей клиентской области подлежащей перерисовке.
InvalidateRect(hWnd, NULL, TRUE);
hdc = BeginPaint(hWnd, &ps);
// Если массив точек не пуст, то рисуем кривую по данным точкам.
if (pts.size() != 0)
DrawBezier(hdc, pts) ;
EndPaint(hWnd, &ps);
break;
case WM_DESTROY:
// Выход.
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
return 0;
}
SendMessage(hWnd, WM_PAINT, NULL, NULL);
break;
case ID_CURVE_NEWCURVE:
// Меню Curve -> New curve
// Очищаем массив точек, IsSelected присваиваем "ложь" и осуществляем перерисовку.
for (int i = pts.size(); i > 0; i--)
pts.pop_back();
IsSelected = false;
SendMessage(hWnd, WM_PAINT, NULL, NULL);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
break;
case WM_PAINT:
// Перерисовка клиенской области окна.
// Объявление всей клиентской области подлежащей перерисовке.
InvalidateRect(hWnd, NULL, TRUE);
hdc = BeginPaint(hWnd, &ps);
// Если массив точек не пуст, то рисуем кривую по данным точкам.
if (pts.size() != 0)
DrawBezier(hdc, pts) ;
EndPaint(hWnd, &ps);
break;
case WM_DESTROY:
// Выход.
PostQuitMessage(0);
break;
default:
return DefWindowProc(hWnd, message, wParam, lParam);
}
return 0;
} net_Bcurves.rar
net_Bcurves.rar