Постигая кривые Безье | CAT.IN.WEB
Кривые Безье — это способ определения кривой по опорным точкам.
Для наглядности можно рассматривать их как график передвижения точки от начала до конца маршрута в зависимости от времени движения.
Время изменяется от 0 до 1 (до 100%). То есть мы изначально знаем время, за которое нужно переместиться из начальной точки (P0) в конечную (Pn) (конкретная величина не имеет значения). На основании этого времени можно вычислить точную траекторию — по формулам.
Берем все время за 100% (или за единицу). В момент 0 (0%) точка находится в точке P0, в момент 1 (100%) – в точке Pn. Положение точки в любой момент между этими моментами можно вычислить по формуле.
Порядок кривой всегда на 1 меньше количества контрольных точек. Рассмотрим построение пошагово, начиная с самой простой кривой.
Кривая Безье первого порядка
Простейшая кривая Безье — это обычная линия. Порядок первый – значит, контрольных точек две. Ее академическое уравнение выглядит так:
Порядок первый – значит, контрольных точек две. Ее академическое уравнение выглядит так:
B(t) = (1-t)*P0 + t*P1
А график — вот так:
Разберем на простейшем примере. Пусть:
- первая контрольная точка — P0 имеет координаты (0; 0),
- вторая (и последняя) – P1 – (5; 0).
Сразу же проверим формулу.
При t = 0 (в начальный момент времени) должна получиться точка P0, а при t = 1 должна получиться точка P1.
- B(0) = (1-0)*P0 + 0*P1 = P0 — (0; 0)
- B(1) = (1-1)*P0 + 1*P1 = P1 — (5; 0)
А теперь найдем несколько точек между началом и концом. Тут используется сложение и умножение векторов, но в данном случае все интуитивно понятно:
B(0.1) = (1-0.1)*P0 + 0.1*P1 = 0.9*P0 + 0.1*P1 = 0.9*(0;0) + 0. 1*(5;0) = (0.5; 0)
1*(5;0) = (0.5; 0)B(0.2) = (1-0.2)*P0 + 0.2*P1 = 0.8*P0 + 0.2*P1 = 0.8*(0;0) + 0.2*(5;0) = (1; 0)B(0.3) = (1-0.3)*P0 + 0.3*P1 = 0.7*P0 + 0.3*P1 = 0.7*(0;0) + 0.3*(5;0) = (1.5; 0)B(0.4) = (1-0.4)*P0 + 0.4*P1 = 0.6*P0 + 0.4*P1 = 0.6*(0;0) + 0.4*(5;0) = (2; 0)B(0.5) = (1-0.5)*P0 + 0.5*P1 = 0.5*P0 + 0.5*P1 = 0.5*(0;0) + 0.5*(5;0) = (2.5; 0)B(0.6) = (1-0.6)*P0 + 0.6*P1 = 0.4*P0 + 0.6*P1 = 0.4*(0;0) + 0.6*(5;0) = (3; 0)B(0.7) = (1-0.7)*P0 + 0.7*P1 = 0.3*P0 + 0.7*P1 = 0.3*(0;0) + 0.7*(5;0) = (3.5; 0)B(0.8) = (1-0.8)*P0 + 0.8*P1 = 0.2*P0 + 0.8*P1 = 0.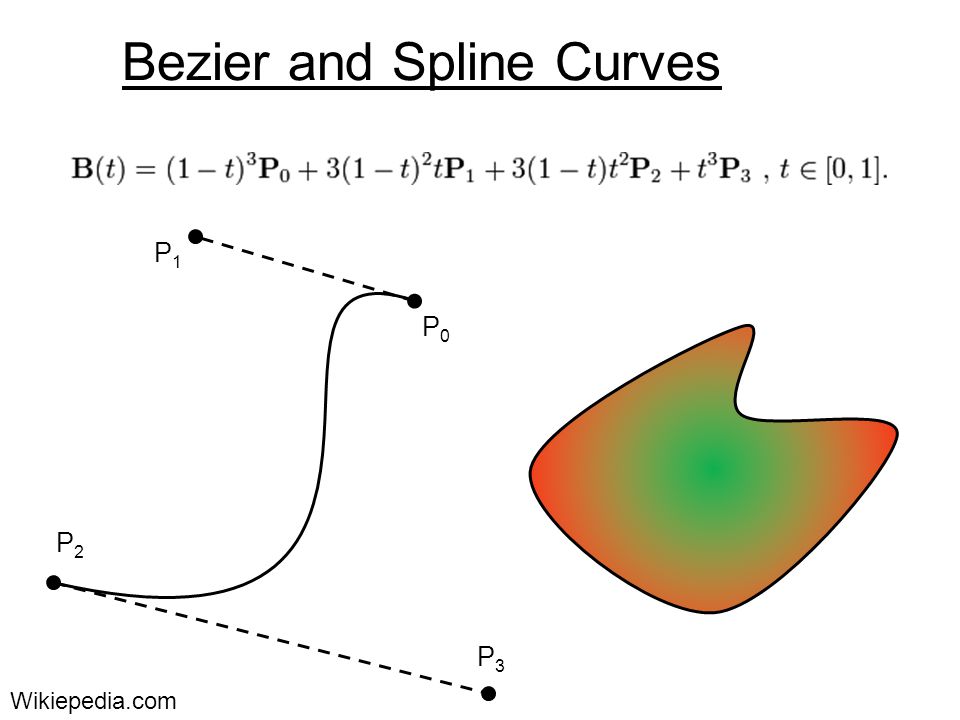 2*(0;0) + 0.8*(5;0) = (4; 0)
2*(0;0) + 0.8*(5;0) = (4; 0)B(0.9) = (1-0.9)*P0 + 0.9*P1 = 0.1*P0 + 0.9*P1 = 0.1*(0;0) + 0.9*(5;0) = (4.5; 0)
Все полученные точки лежат на одной прямой – это и есть кривая Безье первого порядка.
Время идет, точка движется от старта к финишу. И в любой момент времени мы точно знаем, где она находится.
Кривые Безье второго порядка и больше
В определении кривых Безье выше первого порядка кроме начала и конца появляются дополнительные опорные точки, смысл которых сложно понять с первого захода.
Непосредственно через них кривая не проходит, так зачем же они нужны?
На самом деле эти точки определяют направление движения (направление изгиба кривой) и крутизну этого изгиба.
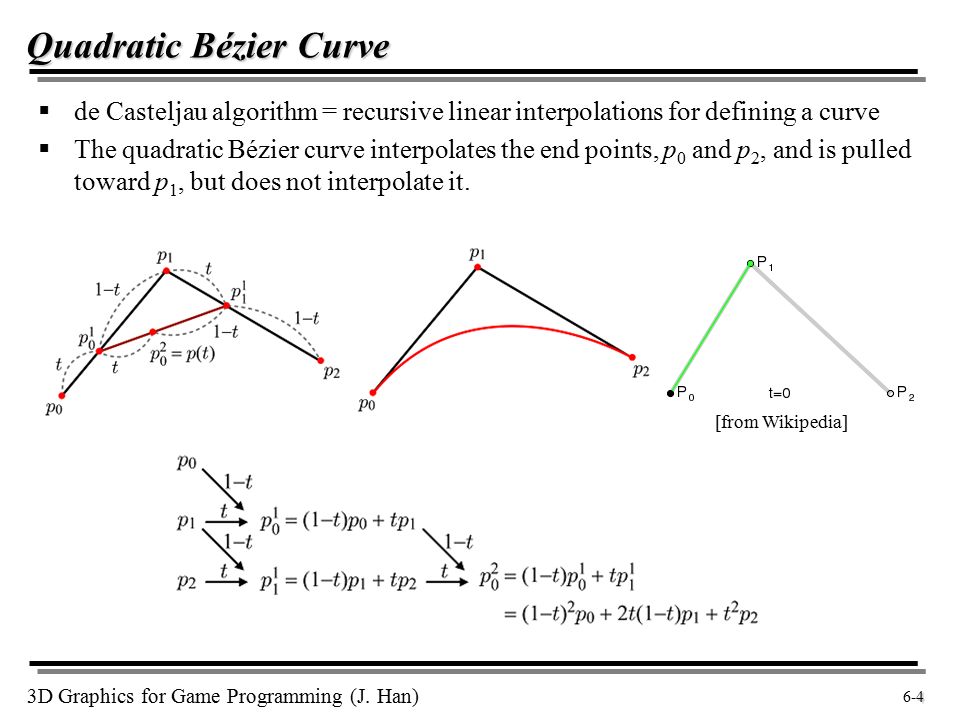
Квадратичная кривая
Кривая Безье второго порядка, или квадратичная, задается тремя контрольными точками:
- P0 – начало;
- P2 – конец;
- P1 – вспомогательная точка, определяющая изгиб кривой.

Маленький спойлер: кривая Безье второго порядка имеет форму параболы (не обязательно симметричной).
Формула у нее вот такая:
B(t) = (1 - t)2*P0 + 2t*(1 - t)*P1 + t2*P2
Проверим, что в начале и конце движения мы окажемся в точках P0 и P2 соответственно:
- B(0) = (1 — 0)2 *P0 + 2*0*(1 — 0) * P1 + 02*P2 = P0
- B(1) = (1 — 1)2 *P0 + 2*1*(1 — 1) * P1 + 12*P2 = P2
На примере:
- P0 (-1; 0)
- P2 (1; 0)
- опорная точка P1 (0; 2):
Найдем, где будет точка через половину времени t (0.5):
B(0.5) = 0.25*P0 + 0.5*P1 + 0.25*P2 = (-0.25; 0) + (0; 1) + (0.25; 0) = (0; 1)
То есть на половине временного интервала мы окажемся в точке (0; 1).
Если найти еще несколько точек, вырисуется ровная парабола. Так, в общем, и было задумано для простоты вычислений и визуальной ясности.
Рекурсивность кривых Безье
Волшебство кривых Безье заключается в том, что они рекурсивны. То есть умея строить кривую первого порядка, мы можем построить и квадратичную кривую, даже не зная ее формулы.
Вернемся к предыдущему примеру:
- P0 (-1; 0)
- P2 (1; 0)
- опорная точка P1 (0; 2):
Предположим, что мы не знаем, как построить кривую второго порядка между P0 и P2. Но мы можем построить простейшую кривую первого порядка между P0 и P1, а также между P1 и P2, пользуясь формулой:
B(t) = (1-t)*P0 + t*P1
Для каждого момента времени мы можем найти положение точки на каждой из этих кривых.
Например, в момент времени 0.25 соответствующие точки Q0 и Q1 будут в таких позициях:
Между этими точками тоже можно построить кривую первого порядка.
Магия заключается в том, что точка на этой кривой в момент времени t = 0.25 соответствует точке на искомой кривой второго порядка в этот же момент времени.
Распишем чуть подробнее.
Мы хотим найти точку на кривой второго порядка P0-P11-P2 в момент времени t.
- Этому моменту на кривой P0-P1 соответствует точка Q0;
- А на кривой P1-P2 – точка Q1.
Искомая точка – это точка на кривой Q0-Q1, соответствующая моменту времени t.
Этот рекурсивный алгоритм построения кривой Безье носит имя Поля де Кастельжо.
Кубическая кривая
Кривая Безье третьего порядка, или кубическая кривая, определяется уже четырьмя опорными точками – началом, концом и двумя вспомогательными, через которые она не будет непосредственно проходить.
Две вспомогательные точки снова определяют направление и крутизну изгибов кривой.
Формула кубической кривой еще сложнее:
B(t) = (1 - t)3*P0 + 3t*(1-t)2*P1 + 3t2*(1 - t)*P2 + t3*P3
Вы можете попробовать эту кривую рассчитать самостоятельно.
Обратите внимание, ее тоже можно получить рекурсивно!
Найти точку кривой третьего порядка в момент времени t можно по следующему алгоритму:
- Строим кривые первого порядка P0-P1, P1-P2, P2-P3
- Находим на них соответствующие t точки Q0, Q1, Q2
- Строим кривые первого порядка Q0-Q1 и Q1-Q2
- Находим на них соответствующие t точки R0 и R1
- Строим кривую первого порядка R0-R1
- Находим на ней точку, соответствующую
t.
Зачем все это нужно?
Круто, теперь мы умеем строить кривые Безье любого порядка, но зачем нам это нужно? Каково практическое применение этих построений?
Кривые Безье используются в описаниях шрифтов TrueType, в SVG, GIMP и других графических форматах, в 3D-графике. Они используются даже в CSS для описания плавности анимации.
Они используются даже в CSS для описания плавности анимации.
В общем, штука очень полезная.
Кубические кривые Безье | это… Что такое Кубические кривые Безье?
Кривы́е Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастелье было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастелье, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастелье назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастелье).
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.
Содержание
|
Определение
Кривая Безье — параметрическая кривая, задаваемая выражением
где — функция компонент векторов опорных вершин, а — базисные функции кривой Безье, называемые также полиномами Бернштейна.
- , где n — степень полинома, i — порядковый номер опорной вершины
Виды кривых Безье
Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
Кривая задаётся уравнением:
- .
Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1
- .
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах SWF файлах.
Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
- .
Кубическая кривая Безье
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки
 Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.
Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.В матричной форме кубическая кривая Безье записывается следующим образом:
- ,
где называется базисной матрицей Безье:
В современных графических системах, таких как GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.
Построение кривых Безье
Линейные кривые

Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1
- Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
- Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
- Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
Построение квадратичной кривой Безье
Анимация t: [0; 1]
Кривые высших степеней
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и
Построение кубической кривой Безье
Анимация t: [0; 1]
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
Построение кривой Безье 4-й степени
Анимация t: [0; 1]
Применение в компьютерной графике
 Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии. В программах векторной графики наподобие Adobe Illustrator или path).
Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами .
Литература
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.
См. также
- Поверхность Безье
Аппроксимация данных сплайнами Безье — Виртуальные лаборатории
Вернуться к содержанию
Сплайн (от англ. spline, – гибкое лекало, гибкая плазовая рейка – полоса металла, используемая для черчения кривых линий) – функция, область определения
которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим многочленом. Максимальная степень из использованных полиномов
называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна.
Чтобы наглядно продемонстрировать приведенные понятия сплайна, степени сплайна и дефекта сплайна, рассмотрим следующую задачу: имеется совокупность экспериментальных данных, необходимо максимально точность аппроксимировать последовательность данных полиномиальной функцией n-го порядка с достоверностью не менее 95 %. В качестве базового выбираем метод полиномиальной аппроксимации с помощью так называемого сплайна Безье. Данный метод наиболее актуален для реализации в компьютерном алгоритме.
Сплайны (кривые) Безье или Кривые Бернштейна-Безье разработаны в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной
компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей [1].
Кривая Безье относится к полиномам третьего порядка и уникально определяется четырьмя точками. Обозначим эти точки p0 (начальная), p1, p2 (две управляющие) и p3 (конечная). Обозначенные точки будут иметь координаты: (x0, y0), (x1, y1), (x2, y2) и (x3, y3). Полином третьего порядка, задающий координаты точек в двумерном пространстве, выражается параметрическими уравнениями общего вида:
где ax, bx, cx, dx, ay, by, cy и dy – константы, a параметр t меняется от 0 до 1.
Любая кривая Безье уникально определяется этими 8 константами. Их значения зависят от координат четырех точек, задающих кривую. Цель этой задачи – вывести уравнения для
расчета восьми констант по заданным координатам четырех точек.
Первое допущение для вывода этих уравнений заключается в том, что кривая Безье начинается в точке с координатами (x0, y0) при t = 0:
Даже такое простое допущение позволяет продвинуться в выводе уравнений для констант. Подставив в параметрические уравнения t = 0, получим:
Это означает, что две из констант – это просто координаты начальной точки:
Второе допущение, касающееся кривой Безье: она заканчивается в точке с координатами (x3, y3) при t = 1:
Подставив в параметрические уравнения (1) вместо t единицу, получаем:
что означает наличие следующей связи между константами и координатами конечной точки:
Остальные допущения касаются первых производных параметрических уравнений, описывающих угол наклона кривой. Первую производную параметрического уравнения общего вида, задающего
полином третьего порядка как функцию переменной t, можно записать так:
Первую производную параметрического уравнения общего вида, задающего
полином третьего порядка как функцию переменной t, можно записать так:
Нас, в частности, интересует угол наклона кривой в конечных точках. Как известно, прямая, проведенная из начальной точки через первую
управляющую точку, проходит по касательной к кривой Безье и направлена в ту же сторону, что и кривая. Обычно эту прямую задают параметрическими уравнениями:
где t изменяется от 0 до 1. Но можно задать ее иначе:
где t изменяется от 0 до 1/3.
Почему именно 1/3? Дело в том, что длина той части кривой Безье, по касательной к которой проходит прямая, проведенная из точки p0 через p1, направленная в ту же сторону, что и кривая, равна 1/3 от общей
длины кривой. Первые производные модифицированных параметрических уравнений можно записать так:
Первые производные модифицированных параметрических уравнений можно записать так:
Если нужно рассчитать по этим уравнениям угол наклона кривой Безье при t = 0, то:
Подставив t = 0 в уравнение первой производной полинома третьего порядка, получим:
Это позволяет записать равенство:
Последнее допущение таково: прямая, проведенная из второй управляющей точки через конечную, является касательной к кривой
Безье в ее конечной точке и направлена в ту же сторону, что и кривая. Иначе говоря:
Из уравнений общего вида следует, что:
поэтому:
Выражения (2), (4), (6) и (8) дают четыре уравнения с четырьмя неизвестными, которые можно решить относительно ax, bx, cx и dx, выразив их через x0, x1, x2 и x3. Выполнив ряд алгебраических преобразований, получаем:
Выполнив ряд алгебраических преобразований, получаем:
Выражения (3), (5), (7) и (9) позволяют сделать то же самое для коэффициентов y. После этого
можно подставить константы обратно в параметрическое уравнение общего вида для полинома третьего порядка:
В сущности, на этом можно было бы закончить. Но лучше раскрыть скобки и привести подобные слагаемые. В итоге получатся более элегантные
параметрические уравнения, с которыми проще работать:
Уравнения (10) и (11) позволяют построить кривую Безье в декартовых координатах.
На первом этапе разработки компьютерного алгоритма аппроксимации экспериментальных данных мы будем задавать кривую Безье
визуальным способом, перемещая ее узловые точки в декартовой системе координат графической области экрана. Пример графического представления кривой Безье представлен на рисунке 1. Точки P0 и P3 – начальная и конечная точки
кривой соответственно, P1 и P2 –
управляющие точки (или точки направляющих отрезков).
Пример графического представления кривой Безье представлен на рисунке 1. Точки P0 и P3 – начальная и конечная точки
кривой соответственно, P1 и P2 –
управляющие точки (или точки направляющих отрезков).
Рисунок 1 – К построению кривой Безье
В качестве средства разработки выбираем среду программирования Microsoft Visual Basic 6.0. На рисунке 2 представлена форма графического интерфейса, включающая графическое поле для построения кривых, и панель параметров, расположенную в левой части формы.
Рисунок 2 – Графический интерфейс пользователя программы математической аппроксимации кривой Безье
С помощью указателя мыши пользователем задаются положения точек P0, P1, P2 и P3 сплайна Безье. Центр системы координат можно смещать, перемещая указатель мыши в графической области при нажатой правой кнопке мыши.
Центр системы координат можно смещать, перемещая указатель мыши в графической области при нажатой правой кнопке мыши.
Далее проведем кривую полиномиальной функции n-го порядка по кривой построенного сплайна Безье. Целью данной процедуры является переход от параметрических уравнений сплайна Безье к аналитической функции вида y=f(x) при аппроксимировании данных. На панели параметров в левой части экрана пользователем выбирается степень n полиномиальной функции. От данного параметра зависит, сколько опорных точек будет выделено на сплайне Безье, через которые проходит полиномиальная кривая, и, следовательно, точность приближения полиномиальной кривой к сплайну, также будет зависеть от выбранной степени полинома.
Принцип построения полиномиальной кривой базируется на вычислении коэффициентов полинома:
где n – число точек на сплайне Безье, через которые проходит полиномиальная кривая.
Для вычисления коэффициентов Ci необходимо задать опорные точки на сплайне Безье, координаты которых вычисляются по известным параметрическим уравнениям Безье (10 и 11), и подставить координаты опорных точек (xi, yi) в уравнение (12). В таком случае мы получаем систему линейных уравнений с n неизвестными:
где ai – коэффициенты системы уравнений, а0 – свободные члены.
В представленном алгоритме система линейных уравнений вида (13) решается методом Крамера, подразумевающем преобразование системы уравнений в матрицы 3×3, 4×4, 5×5 и 6×6 для
полиномиальной функции 2, 3, 4 и 5-го порядков, соответственно. Программно вычисления производятся с использованием двумерных массивов, в которые записываются столбцы основной и
вспомогательных матриц Крамера, после чего производится вычисление их определителей, и находятся коэффициенты полиномиального уравнения.
В программе реализован алгоритм автоматической корректировки коэффициентов уравнения полинома. Сущность алгоритма заключается в цикличной проверке максимального расхождения полиномиальной кривой и кривой Безье в направлении оси Y (рисунок 3). Степень сплайна Безье es равна 3, а степень полиномиальной кривой ep выбирается пользователем (2, 3, 4 или 5). Теоретически, при ep ≥ es расхождение кривых сводится к нулю.
Рисунок 3 – К определению степени достоверности аппроксимации (до пересчета координат опорных точек)
С заданным шагом (по оси абсцисс) вычисляются длины вертикальных отрезков, соединяющих кривую полинома и кривую Безье (закрашенная область на рисунке 3). Длины указанных отрезков
записываются в одномерный массив, после чего определяется и фиксируется наибольшая длина отрезка (максимальная величина расхождения кривых Δ). С помощью генератора случайных чисел
задаются новые координаты опорных точек на кривой Безье, тем самым происходит их случайное смещение по сплайну, при этом каждая итерация заканчивается пересчетом величины Δ. Если после
новой итерации величина Δ уменьшилась по сравнению с предшествующей, то полиномиальная кривая перестраивается. Визуально мы наблюдаем сближение полиномиальной кривой со сплайном Безье
(рисунок 4).
С помощью генератора случайных чисел
задаются новые координаты опорных точек на кривой Безье, тем самым происходит их случайное смещение по сплайну, при этом каждая итерация заканчивается пересчетом величины Δ. Если после
новой итерации величина Δ уменьшилась по сравнению с предшествующей, то полиномиальная кривая перестраивается. Визуально мы наблюдаем сближение полиномиальной кривой со сплайном Безье
(рисунок 4).
Рисунок 4 – К определению степени достоверности аппроксимации (максимальное приближение аппроксимирующей кривой к сплайну Безье)
Разработанный алгоритм является эффективным инструментом для обработки эмпирических данных с использованием сплайнов. К
примеру, если речь идет об интегральных кривых распределения, сплайном Безье можно задавать аппроксимирующую
функцию, которая будет проходить через экспериментальные точки. При этом, конфигурация сплайна может задаваться не только ручным способом с помощью конечных и управляющих точек, а процедурно,
путем проверки расходимости координат экспериментальных точек и точек, выделенных на сплайне с равной абсциссой. В конечном итоге мы получаем полиномиальную функцию n-й степени, которая
будет максимально точно описывать последовательность эмпирических данных (например, как на рисунке 5).
При этом, конфигурация сплайна может задаваться не только ручным способом с помощью конечных и управляющих точек, а процедурно,
путем проверки расходимости координат экспериментальных точек и точек, выделенных на сплайне с равной абсциссой. В конечном итоге мы получаем полиномиальную функцию n-й степени, которая
будет максимально точно описывать последовательность эмпирических данных (например, как на рисунке 5).
Рисунок 5 – Схематичное представление процесса аппроксимации эмпирических данных
В случае аппроксимации интегральных кривых распределения на выходе работы алгоритма мы получаем функцию y(x), дифференцирование которой позволит построить закономерную дифференциальную гистограмму распределения dy(x) (например, как на рисунке 6).
Рисунок 6 – Построение дифференциальной гистограммы распределения по аппроксимирующей полиномиальной кривой
Библиографические ссылки:
[1] – Кривая Безье: Материал из Википедии – свободной
энциклопедии: Версия 64994710, сохраненная в 23:11 UTC 22 августа 2014 // Википедия, свободная энциклопедия.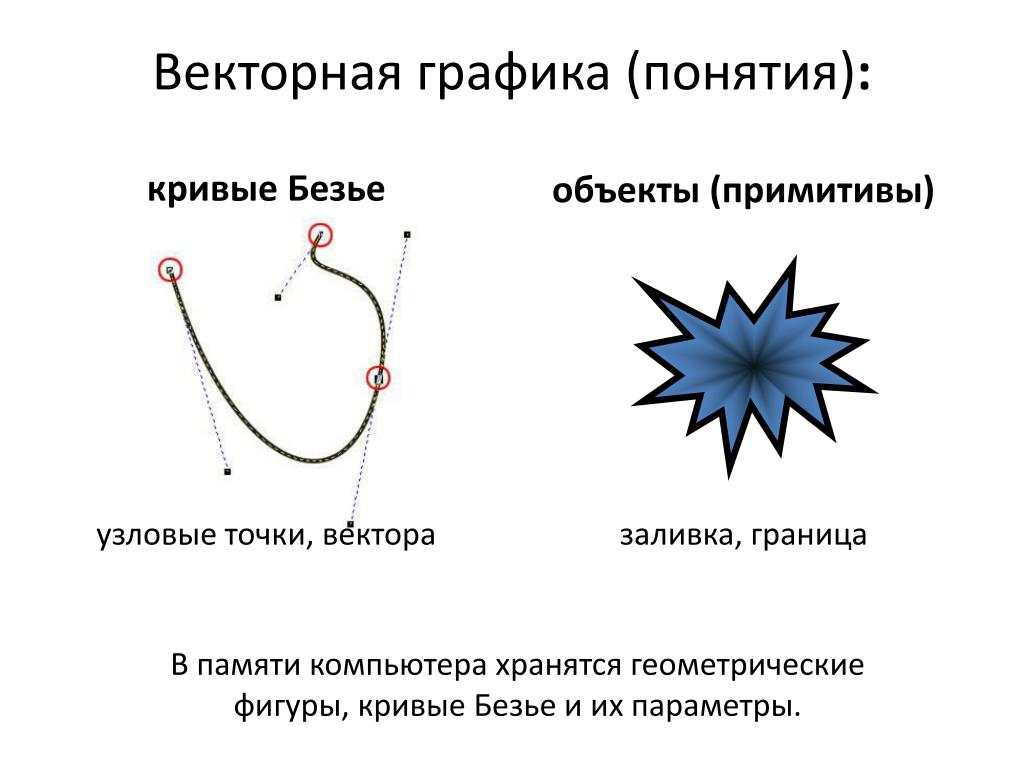 – Электрон. дан. – Сан-Франциско: Фонд Викимедиа, 2014.
– Электрон. дан. – Сан-Франциско: Фонд Викимедиа, 2014.
Вернуться к содержанию
При копировании материалов ссылка на сайт www.sunspire.ru обязательна. Также, вы можете использовать библиографическую ссылку на учебное пособие:
«Белов, В.В. Компьютерная реализация решения научно-технических и образовательных задач: учебное пособие / В.В. Белов, И.В. Образцов, В.К. Иванов, Е.Н. Коноплев // Тверь: ТвГТУ, 2015. 108 с.»
Инструкция по методу горизонтальных и вертикальных направляющих кривых Безье — Оди. О дизайне
Было интересно, почему и зачем их кривые Безье так аккуратно расставлены?
Мы постараемся пролить свет на этот загадочный процесс, выглядящий так бессмысленно.
Важно: эта заметка предполагает хорошее понимание и владением инструментом Перо в Иллюстраторе.
Опорные точки, точки привязки
До недавнего времени я, определенно, принадлежал к клубу «Нафига-это-надо?», и, в тайне, к клубу «Как-они-это-делают?». Однако, я решил узнать, в чем фишка, и, оказывается, соблюдение перпендикулярного расположения направляющих экономит кучу времени и усилий.
Однако, я решил узнать, в чем фишка, и, оказывается, соблюдение перпендикулярного расположения направляющих экономит кучу времени и усилий.
Вот надпись, которую мы нарисовали при подготовке этой инструкции:
Рис. 01
Вот просмотр кривых (outline preview) (⌘Y) в Иллюстраторе:
Рис. 02
На заметку: Чтобы настроить просмотр кривых так, как на рисунке, вам потребуется включить опцию «Показать…» (Show handles…, см. скриншот) в настройках Иллюстратора (⌘K). Теперь вы будете видеть направляющие кривых, когда вы выделяете рисунок.
Рис. 03
Заметьте, что что направляющие кривых Безье (за исключением нескольких особых случаев, которые рассмотрим позже) аккуратно выровнены по вертикальным и горизонтальным осям. Давайте посмотрим, почему такой подход — отличная практика.
Меньше вариантов для размещения узлов
Звучит, как нечто не очень крутое, верно? Но это реально удобно. Ходили когда-нибудь в ресторан, меню в котором настолько обширное и исчерпывающее, что оно практически нуждается в собственном ISBN? Я такое ненавижу. Иногда выбор места для узлов может заставить вас чувствовать себя также сложно, как и такое меню. Ваш скетч загружен в Иллюстратор и ждет трассировки, ваш пен тул (Pen Tool) бродит по кривым также, как палец по тому меню — откуда бы начать? Не знаю, как вы, но я чаще всего выбирал блюдо дня, или, как в нашем случае, самую дальнюю точку кривых. Давайте поговорим об этом.
Иногда выбор места для узлов может заставить вас чувствовать себя также сложно, как и такое меню. Ваш скетч загружен в Иллюстратор и ждет трассировки, ваш пен тул (Pen Tool) бродит по кривым также, как палец по тому меню — откуда бы начать? Не знаю, как вы, но я чаще всего выбирал блюдо дня, или, как в нашем случае, самую дальнюю точку кривых. Давайте поговорим об этом.
Размещение узлов
Вот вам секретный соус. Единственный метод, при котором направляющие размещаются аккуратно под углами в 0° и 90° — это размещать узлы с определенной стратегией. Метод может звучать сложно, но однажды поняв его, применять его супер-просто.
Фишка: зажимайте Shift когда тащите направляющие, чтобы они располагались точно вертикально или горизонтально.
Посмотрите на упрощенную схему на рисунке 4. Красными точками обозначены горизонтальные узлы, синими — вертикальные. Заметьте, что каждая точка размещается на самой дальней точке каждой кривой.
Рис. 04
Рис. 05 поясняет эту модель чуть более детально , и показывает оптимальное место для размещения вашего узла.
05 поясняет эту модель чуть более детально , и показывает оптимальное место для размещения вашего узла.
Рис. 05
Вы узнаете, что разместили узел неправильно, когда получите вот такую проблему:
Рис. 06 – Перемещение точки в красном кружке (по направлению стрелки) сделает кривую лучше подходящей под эскиз.
Теперь мы знаем, что размещение узлов не носит случайный характер. Ограничение самого себя в технике размещения узлов, описанное выше, позволяет вам думать чуть меньше во время векторизации и передать тяжелую работу от мозга вашей мышечной памяти. Теперь поговорим о направляющих кривых Безье.
Делаем классные кривые с направляющими кривых Безье
Теперь, когда мы разобрались с узлами, пришло время уделить внимание направляющим. Посмотрите на этот GIF:
Рис. 07
Если вы хоть раз векторизировали леттеринг, иллюстрацию или что-то в этом роде, картинка выше кажется вполне привычным зрелищем. Вы потратите большую часть времени, цепляя эти маленькие красные кружочки на конце направляющих, уговаривая их составить правильную кривую. Здесь нет магии, и чем больше вы практикуетесь, тем лучше будет получаться.
Здесь нет магии, и чем больше вы практикуетесь, тем лучше будет получаться.
Фантастика с этими ГВНКБ (горизонтальными и вертикальными направляющими кривых Безье) начинается, когда вы ограничиваете их (ага, снова). Ваш мизинец никогда не должен отпускать Shift во время выбора оптимальной длины направляющих. Такое линейное ограничение вариантов очень освежает. Я, буквально, чувствую себя гораздо лучше, когда мне приходит проект с векторизацией.
Итак, в чем подвох?
Звучит всё это очень клёво, конечно, но есть несколько моментов, к которым нужно присмотреться при использовании ГВНКБ.
Иногда вам не удастся найти самую дальнюю точку кривой для размещения узла.
Иногда линия заканчивается до того, как она достигает подходящей точки (как на Рис.5). Абсолютно нормально в этом случае отпустить Шифт и просто повернуть направляющую на тот угол, который кажется подходящим. Не нужно становиться фашистом Безье, нужно чтобы ваш дизайн настолько круто, насколько возможно.
Продолжай держать свои узлы на привязи.
Этот метод является гораздо более требовательным чем случайное размещение узлов. Если узлы начали сбиваться с правильного пути, ваши кривые становятся всё меньше похожими на Монро, и всё больше — на Человека-слона. Если кривая просто не желает работать (см. Рис.7), попробуйте немного сдвинуть узел.
Размещение может показаться тесным или неуклюжим.
Иногда та самая «дальняя точка» (ДТ) находится очень близко к другой ДТ. Посмотрите на этот бардак:
Рис. 08 – Это часто будет происходить в конечных штрихах букв. Например, вверху «s» в нашем слове ‘Beziers’.
Но не волнуйтесь, это всё часть веселья. Достаточный зум поможет точно настроить все детали, смотрите:
Рис. 09
Это реально стоит немного дополнительного времени в таких местах, как это, когда вы понимаете все остальные выгоды метода.
В итоге, вот почему мы будем использовать ГВНКБ в будущих проектах.
Мы поговорили об упрощении размещения узлов. Если это сохраняет и экономит ваше время, почему бы и нет. ГВНКБ также уменьшает общее количество узлов, которое приходится делать, а это — упрощает работу и уменьшает размер файлов. Кроме этого, ваши кривые в итоге получаются более плавными. И, наконец, из-за меньшего количества решений, которые приходится принимать, весь процесс векторизации ощущается чуть более автоматическим, оставляя вам больше времени, чтобы взять настоящие инструменты и нарисовать больше букв.
Если это сохраняет и экономит ваше время, почему бы и нет. ГВНКБ также уменьшает общее количество узлов, которое приходится делать, а это — упрощает работу и уменьшает размер файлов. Кроме этого, ваши кривые в итоге получаются более плавными. И, наконец, из-за меньшего количества решений, которые приходится принимать, весь процесс векторизации ощущается чуть более автоматическим, оставляя вам больше времени, чтобы взять настоящие инструменты и нарисовать больше букв.
И, будем честными, это своего рода развлекуха 🙂
И ещё, вы выглядите как кто-то, кто знает то, что не знают другие дизайнеры, когда публикуете свои работы на Дриббле 😉
Вот несколько примеров применения ГВНКБ различными дизайнерами.
Dave Foster:
Рис. 10
Рис. 11
Рис. 12
…и другие.
Рис. 13 Okay Type
Рис. 14 Neil Secretario
Рис. 15 Luke Dorny
Рис. 16 Алексадр Иванов
Оригинал на английском языке
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.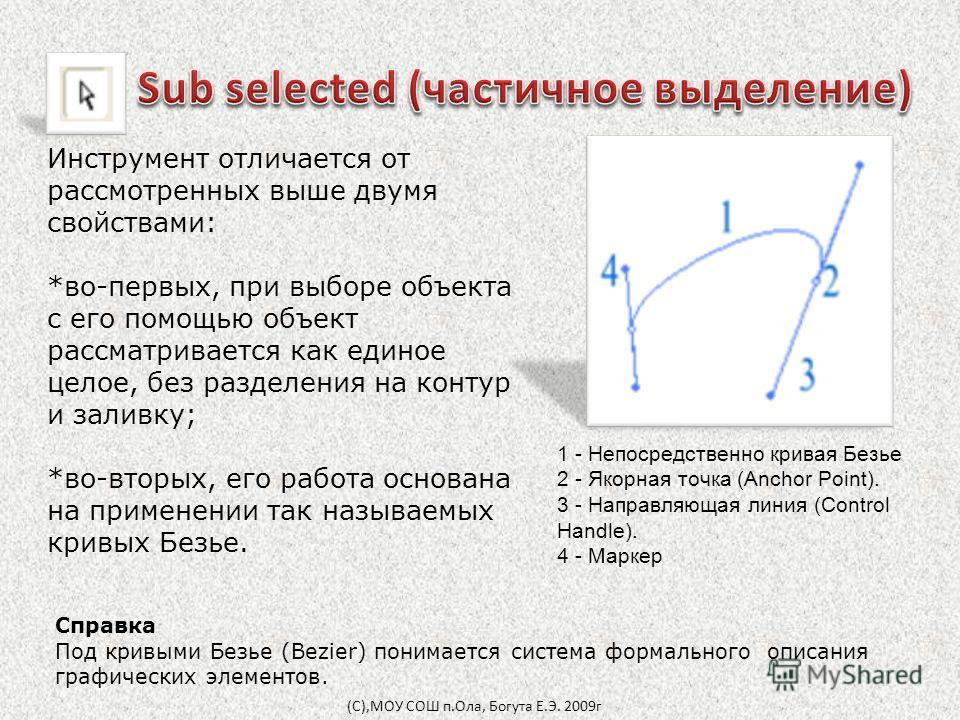
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton. mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных.
 Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума. - Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG. Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
Как работают Кривые Безье в Sketch 3
В цифровой графике компьютеры прорисовывают векторные формы, используя набор точек. Это своего рода “соединение в одно целое”, и большинство программ используют Кривые Безье для создания изогнутых линий, соединяя эти точки вектора. Вы, наверняка, видели такую функцию в инструментах для дизайна статической и анимированной графики. Однако понять, как она работает, чтобы добиться конкретной формы, не так просто. Эта статья поможет пролить свет на магию кривых Безье. Как работают Кривые Безье Хотя есть разные типы кривых Безье (они отличаются способами управления кривой и сложностью построения), “кубическая кривая Безье” (кривая Безье третьего порядка) используется чаще других в разработке графики — и это единственный метод, доступный в Sketch. Так как же работает кубическая кривая Безье? Кривые Безье создаются рычагами, которые выходят из каждой точки вектора. На конце каждого такого рычага есть точка управления. Эти рычаги вытягивают форму по отношению к себе, подобно магниту. Если вам интересно, как работают эти волшебные магниты, загляните в это коротенькое видео: http://vimeo.com/106757336 Графика создавалась с использованием Sketch, SVG Animation и еще парочки ловких инструментов. Вы можете ознакомиться с упрощенным кодом на CodePen. Если вам не интересно, как компьютеры рисуют Кривые Безье, просто перейдите к следующим разделам статьи, в которых описаны практические советы для всех уровней.
Как работают Кривые Безье Хотя есть разные типы кривых Безье (они отличаются способами управления кривой и сложностью построения), “кубическая кривая Безье” (кривая Безье третьего порядка) используется чаще других в разработке графики — и это единственный метод, доступный в Sketch. Так как же работает кубическая кривая Безье? Кривые Безье создаются рычагами, которые выходят из каждой точки вектора. На конце каждого такого рычага есть точка управления. Эти рычаги вытягивают форму по отношению к себе, подобно магниту. Если вам интересно, как работают эти волшебные магниты, загляните в это коротенькое видео: http://vimeo.com/106757336 Графика создавалась с использованием Sketch, SVG Animation и еще парочки ловких инструментов. Вы можете ознакомиться с упрощенным кодом на CodePen. Если вам не интересно, как компьютеры рисуют Кривые Безье, просто перейдите к следующим разделам статьи, в которых описаны практические советы для всех уровней.
Использование рычагов управления Безье на практикеЯ настоятельно рекомендую использовать последнее обновление Sketch 3, версия 3.1.
Пример на видео выше основывается на двух точках (прямой), в то время как большинство других векторных форм строятся из значительно большего количества точек. Фактически, чаще всего из одной точки на кривой Безье выходит два рычажка управления — по одному с каждой стороны. Ниже показано несколько способов создания кривой вокруг векторной точки в Sketch: “Mirrored” (Зеркальный способ) выбран по умолчанию, является самым простым способом управления кривой Безье. В данном подходе используется два рычага, которые равноудалены от векторной точки и находятся под одинаковым углом. Рычаги как будто формируют прямую линию, “касательную” к кривой. Опция Mirrored основывается на следующем принципе: если оба рычага под одним углом, кривая будет иметь абсолютно гладкую форму; другими словами, в форме не будет никаких видимых углов/точек, как в случае с опцией Disconnected.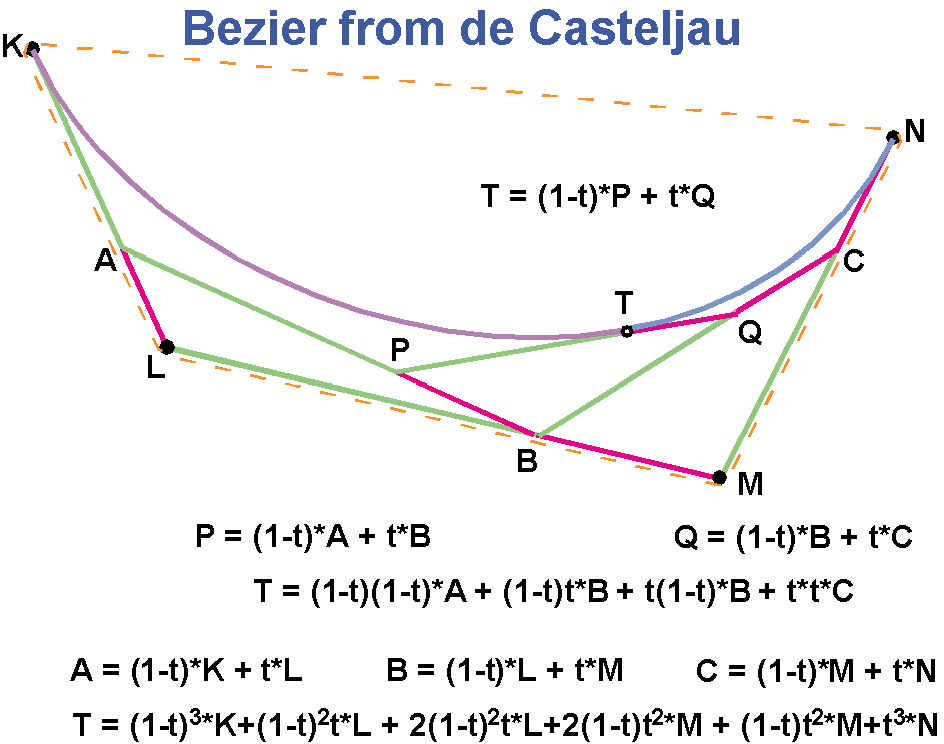 “Asymmetric” (Асимметричный) способ похож на Mirrored, так как ручки управления также находятся под одним углом, но края ручки удалены от векторной точки на разное расстояние. Эта опция особенно полезна, когда нужно придать более заостренную форму кривой на одной из сторон. “Disconnected” (Разомкнутый способ) позволяет управлять каждой ручкой независимо от другой. Такая опция необходима в двух случаях:
“Asymmetric” (Асимметричный) способ похож на Mirrored, так как ручки управления также находятся под одним углом, но края ручки удалены от векторной точки на разное расстояние. Эта опция особенно полезна, когда нужно придать более заостренную форму кривой на одной из сторон. “Disconnected” (Разомкнутый способ) позволяет управлять каждой ручкой независимо от другой. Такая опция необходима в двух случаях:
- Вам бы хотелось переломить ход кривой в векторной точке, сменить угол ее направления.
- Вам необходимо избавиться от одного рычага; иметь контроль над кривой только с одной стороны от точки, и вообще не продолжать кривую с другой стороны. Если вы выбираете такой вариант, кликните на том рычаге, который вы хотите удалить, и нажмите кнопку “delete”.
Точки с прямым углом и закругленные углы:
Когда выбрана опция Straight (прямой), у векторной точки вообще нет ручек управления, и через нее не проходит кривая.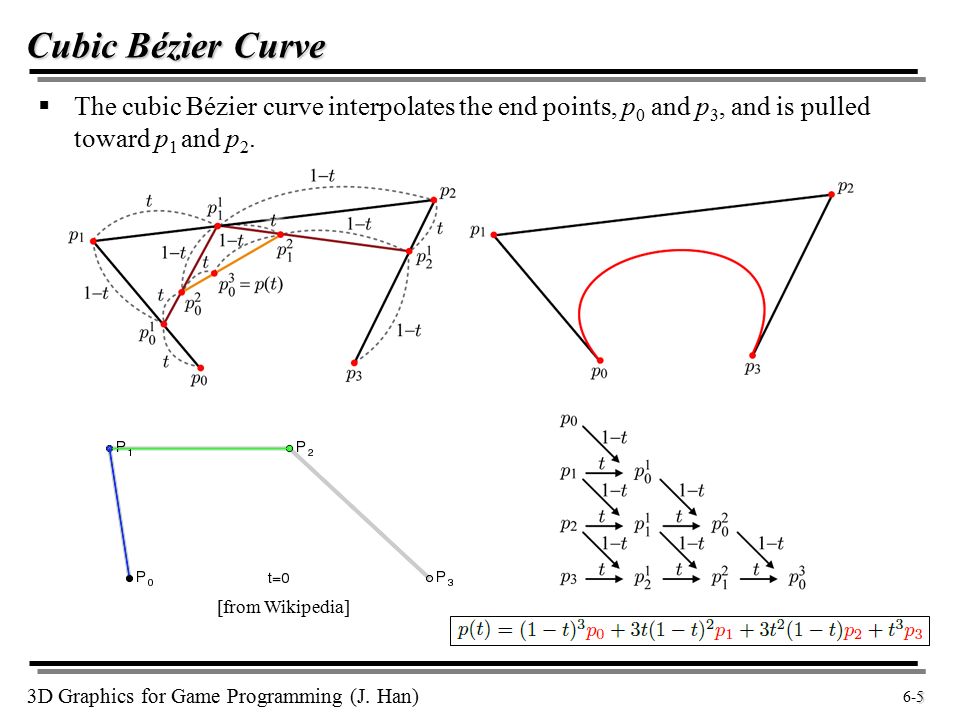 Если на двух соседних векторных точках выбрана эта опция, их будет соединять простая прямая линия. Sketch предоставляет вам возможность закруглить угол любой точки Straight (по типу border radius). И хотя в Sketch можно скруглить любой угол в два счета с помощью точки и значения радиуса, сама программа реализует это расчетом кривых Безье. Если вы желаете увидеть эти Кривые Безье, просто объедините слои вашей формы.
Если на двух соседних векторных точках выбрана эта опция, их будет соединять простая прямая линия. Sketch предоставляет вам возможность закруглить угол любой точки Straight (по типу border radius). И хотя в Sketch можно скруглить любой угол в два счета с помощью точки и значения радиуса, сама программа реализует это расчетом кривых Безье. Если вы желаете увидеть эти Кривые Безье, просто объедините слои вашей формы.
В построении кривых Безье многим не понятно, как разместить векторные точки для достижения желаемой формы. Дизайнер и художник-шрифтовик Дэйв Коулмен из AGSC недавно написал отличную статью. Я выделю основные ее моменты: Если вы подойдете к расстановке векторных точек по кривой стратегически, вы сможете значительно сократить количество точек для достижения необходимой формы. Чем проще построены формы, тем проще их будет изменять, и тем меньшим будет размер файла. Дэйв рекомендует найти “самую отдаленную” точку на кривой и сделать ее векторной. Когда все точки расставлены по своим местам, пора поиграться с рычагами. Выравнивание рычагов Безье вертикально или горизонтально в большинстве случаев смягчит переходы по кривой, делая ее более совершенной. Так как вам необходимо двигать рычаги только вдоль одной оси, весь процесс построения кривых значительно упрощается. Кроме тех случаев, когда почему-то так не происходит. Иногда кривую нельзя никак полностью воспроизвести, если рычаги Безье не под углом, или когда векторная точка не находится в самой выступающей точке. Это НОРМАЛЬНО. Как и в любом другом руководстве, здесь бывают исключения. Изучайте правила, следуйте им, понимайте — и при необходимости — ломайте. Вам, наверняка, будет приятно узнать, что существует быстрый способ установить рычаги Безье под углом 90°: просто держите нажатой кнопку “shift”, пока двигаете контрольную точку рычага. Если эта функция не работает должным образом, как показано на графике ниже, проверьте, выключен ли режим “округления”.
Когда все точки расставлены по своим местам, пора поиграться с рычагами. Выравнивание рычагов Безье вертикально или горизонтально в большинстве случаев смягчит переходы по кривой, делая ее более совершенной. Так как вам необходимо двигать рычаги только вдоль одной оси, весь процесс построения кривых значительно упрощается. Кроме тех случаев, когда почему-то так не происходит. Иногда кривую нельзя никак полностью воспроизвести, если рычаги Безье не под углом, или когда векторная точка не находится в самой выступающей точке. Это НОРМАЛЬНО. Как и в любом другом руководстве, здесь бывают исключения. Изучайте правила, следуйте им, понимайте — и при необходимости — ломайте. Вам, наверняка, будет приятно узнать, что существует быстрый способ установить рычаги Безье под углом 90°: просто держите нажатой кнопку “shift”, пока двигаете контрольную точку рычага. Если эта функция не работает должным образом, как показано на графике ниже, проверьте, выключен ли режим “округления”. Если вы используете округление до полного пикселя (“Round to full pixel edges”) или до полупикселя (“half pixel edges”), и векторная точка находится не в точной пиксельной или полупиксельной позиции, рычаги не будут точно поворачиваться на угол 90°. Одним из решений является отключение закругления, хотя бы на время настройки рычажков. Кроме того, можно вручную задать координаты для каждого рычага, как показано в следующем разделе.
Если вы используете округление до полного пикселя (“Round to full pixel edges”) или до полупикселя (“half pixel edges”), и векторная точка находится не в точной пиксельной или полупиксельной позиции, рычаги не будут точно поворачиваться на угол 90°. Одним из решений является отключение закругления, хотя бы на время настройки рычажков. Кроме того, можно вручную задать координаты для каждого рычага, как показано в следующем разделе.
Работая над созданием логотипа, я обнаружил важную, но почему-то спрятанную функцию в Sketch: свои координаты есть не только у векторных точек, каждый рычаг управления кривой Безье тоже имеет их. И это вполне логично: эти координаты очень нужны компьютеру, чтобы прорисовать кривую. Но то, что в Sketch есть возможность установить их вручную, сразу обнаружить тяжело. Эту функцию легко упустить, потому что вид рычагов не меняется при клике на них — меняются только значения X и Y позиции в инспекторе.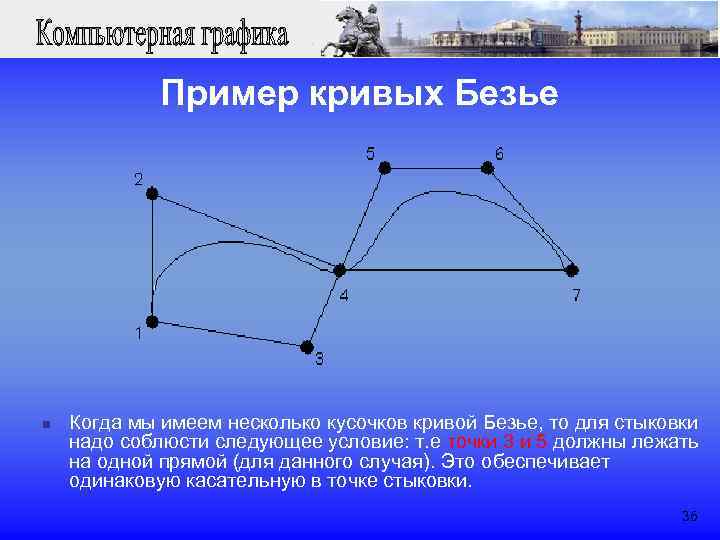 Имея возможность настраивать координаты рычагов, я успешно решил все эти головоломки и поставил рычаги Безье точно туда, куда хотел. Более того, стало легче производить мелкие настройки (измеряемые долями пикселя). Попробуйте эту опцию сами; изменяйте кривую Безье, двигая рычаги, а затем установите их позицию вручную в инспекторе.
Имея возможность настраивать координаты рычагов, я успешно решил все эти головоломки и поставил рычаги Безье точно туда, куда хотел. Более того, стало легче производить мелкие настройки (измеряемые долями пикселя). Попробуйте эту опцию сами; изменяйте кривую Безье, двигая рычаги, а затем установите их позицию вручную в инспекторе.
Двойной клик по векторной точке будет переключать режимы Straight и Mirrored. Может быть, вы уже знакомились с такой опцией в других приложениях. При редактировании формы, вы можете выбрать следующую векторную точку на кривой, нажав “tab” на клавиатуре. “Shift” + “tab” поможет выбрать предыдущую точку. Будет ли “следующая точка” по часовой или против часовой стрелки зависит от направления формы. Когда векторная точка выбрана, нажимайте клавиши 1, 2, 3 и 4 на клавиатуре, чтобы переключаться между режимами straight, mirrored, disconnected и asymmetric. Если удерживать клавишу “Command” (⌘), двигая векторную точку, Sketch будет игнорировать “smart guides”, что поможет вам выровнять точку по вертикали или горизонтали с остальными. Если удерживать клавишу “Command” (⌘), двигая рычаг Безье, вы сможете менять позицию этого рычага свободно и независимо от другого, как если бы векторная точка находилась в режиме Disconnected. Помните, если точка находится в режимах Mirrored или Asymmetrical, передвижение рычага без удержания клавиши Command сбросит результаты в режиме Disconnected. Попробуйте и посмотрите, как все это работает! И последнее. Не унывайте, если поначалу не найдете логики в кривых Безье. Просто помните: Как и любой навык, создание идеально изогнутых векторных форм требует много практики. Отличный способ попрактиковаться — отрисовка шрифтов. Возьмите фотографию или рисунок красивой буквы (что-то изогнутое, вроде “G”, “Q”, “R”, или другой символ рукописного шрифта), перенесите это изображение в Sketch, и используйте векторный инструмент для отрисовки контура этой буквы. Постарайтесь разместить векторные точки в самых выступающих местах объекта, используйте вертикальные или горизонтальные рычаги и настройте их вручную, используя координаты.
Если удерживать клавишу “Command” (⌘), двигая рычаг Безье, вы сможете менять позицию этого рычага свободно и независимо от другого, как если бы векторная точка находилась в режиме Disconnected. Помните, если точка находится в режимах Mirrored или Asymmetrical, передвижение рычага без удержания клавиши Command сбросит результаты в режиме Disconnected. Попробуйте и посмотрите, как все это работает! И последнее. Не унывайте, если поначалу не найдете логики в кривых Безье. Просто помните: Как и любой навык, создание идеально изогнутых векторных форм требует много практики. Отличный способ попрактиковаться — отрисовка шрифтов. Возьмите фотографию или рисунок красивой буквы (что-то изогнутое, вроде “G”, “Q”, “R”, или другой символ рукописного шрифта), перенесите это изображение в Sketch, и используйте векторный инструмент для отрисовки контура этой буквы. Постарайтесь разместить векторные точки в самых выступающих местах объекта, используйте вертикальные или горизонтальные рычаги и настройте их вручную, используя координаты.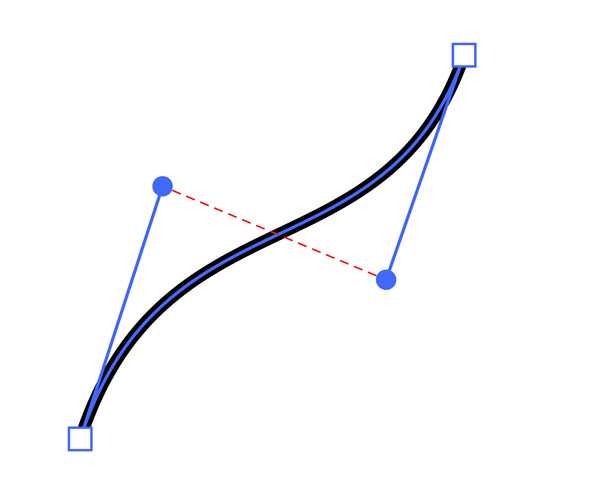 И не забудьте поделиться своими шедеврами! Используйте #sketchbezier в Twitter и Instagram. Я тоже опубликую некоторые свои наработки. Мир остро нуждается в красивых кривых! #sketchbezier
И не забудьте поделиться своими шедеврами! Используйте #sketchbezier в Twitter и Instagram. Я тоже опубликую некоторые свои наработки. Мир остро нуждается в красивых кривых! #sketchbezier
Перевод статьи Peter Nowell
Кривая Безье. Поймите математику Безье… | by Omar Aflak
Понимание математики кривых Безье
Кривые Безье широко используются в компьютерной графике, часто для создания плавных кривых, и тем не менее они являются очень простым инструментом. Если вы когда-либо использовали Photoshop, вы могли наткнуться на инструмент под названием «Якорь», где вы можете ставить опорные точки и рисовать с их помощью какие-то кривые… Да, это кривые Безье. Или, если вы использовали векторную графику, SVG, они тоже используют кривые Безье. Посмотрим, как это работает.
Учитывается N+1 очки (P0,…, PN) называется Контрольные точки , Кривая Bézier определяется этими точками, определено как:
EQ.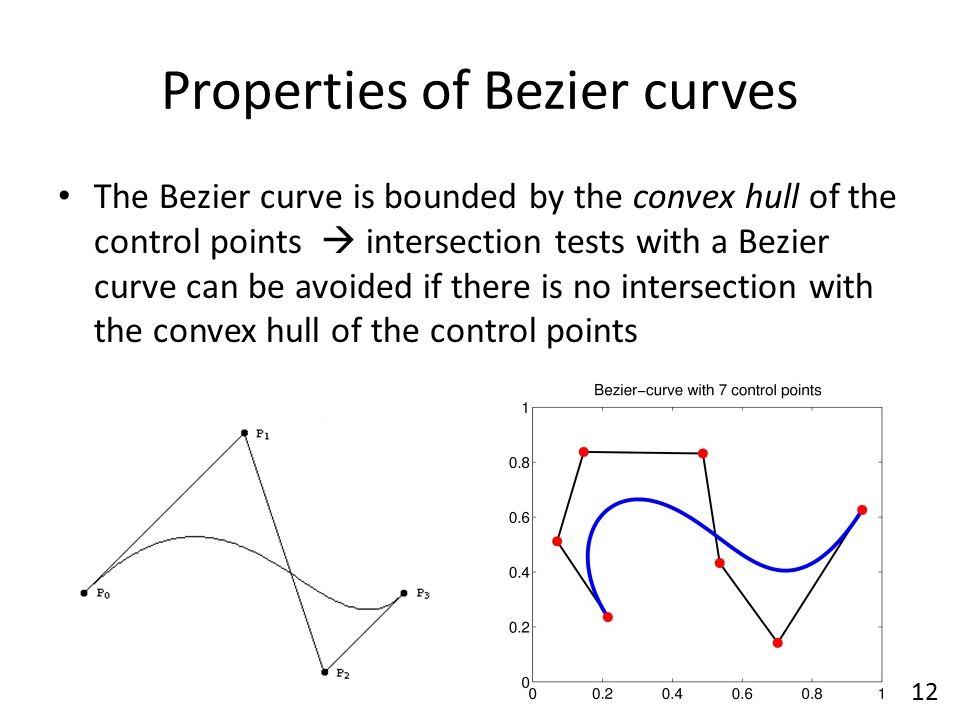 1
1Где B(t) — полином Бернштейна, а:
экв. 2Вы заметите, что этот многочлен Бернштейна очень похож на член k(th) в биномиальной формуле Ньютона:
экв. 3На самом деле многочлен Бернштейна есть не что иное, как 9n = 1. Вот почему, если вы суммируете все Bi до n , вы получите 1 . В любом случае.
Квадратичная кривая Безье — это то, как мы называем кривую Безье с 3 контрольными точками, поскольку степень P(t) будет равна 2. Давайте рассчитаем кривую Безье с учетом 3 контрольных точек и исследуем некоторые свойства, которые мы можем найти! Помните, экв. 1 соответствует n+1 точек, поэтому в нашем случае n=2.
Имейте в виду, что P(t) возвращает не число, а точку на кривой. Теперь нам осталось выбрать три контрольные точки и оценить кривую в диапазоне [0, 1] . Мы можем сделать это в Python довольно легко.
Мы можем сделать это в Python довольно легко.
Вы можете заметить, что кривая начинается и заканчивается в первой и последней контрольных точках. Этот результат будет верным для любого количества точек. Поскольку t находится в диапазоне от 0 до 1 , мы можем доказать это, оценив P(t) в t=0 и t=1 . Используя экв. 1 :
Поскольку кривая идет от P0 до P2 , в этом случае P1 полностью определяет форму кривой . Перемещаясь P1 вокруг вы можете кое-что заметить:
Кривая Безье всегда содержится в многоугольнике, образованном контрольными точками. Этот многоугольник поэтому называется контрольный многоугольник , или многоугольник Безье. Это свойство также сохраняется для любого количества контрольных точек, что делает управление ими интуитивно понятным при использовании программного обеспечения.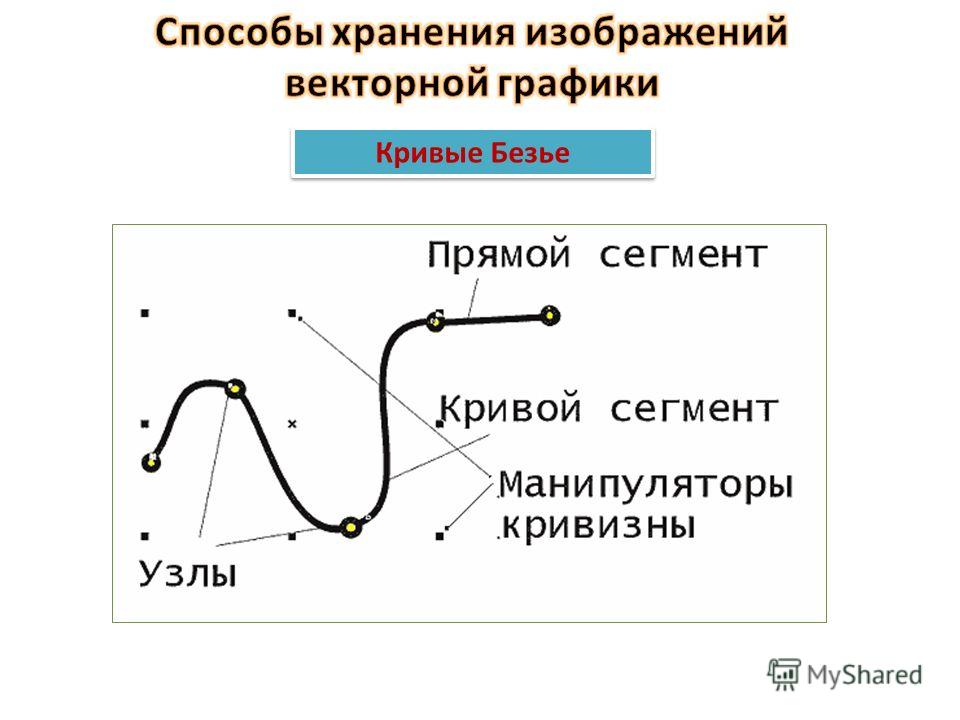
На самом деле мы можем представить формулу Безье, используя умножение матриц, что может быть полезно в других случаях, например, для разделения кривой Безье. Если мы вернемся к нашему примеру, мы можем переписать P(t) следующим образом:
экв. 6 Итак, вся информация о квадратичной кривой Безье сжата в одну матрицу, М . Теперь мы можем захотеть найти коэффициенты этой матрицы, не выполняя все эти шаги и легко программируемым способом. Поскольку коэффициенты матрицы — это просто коэффициенты полинома перед каждым Pi , то, что мы ищем, — это расширенная форма полинома Бернштейна экв. 2 .
Еще одна вещь: если мы расширим Bi(t) , мы получим многочлен перед Pi , что соответствует i(му) столбцу в матрице. Однако это не очень удобно, и было бы проще программировать, если бы вместо этого мы могли получать строки. Тем не менее, вы можете заметить, что i (я) строка матрицы точно такая же, как перевернутый (n-i) (th) столбец , и коэффициенты перевернутого (n-i) (th) столбца есть не что иное, как коэффициенты B(n-i)(t) , взятые в убывающей степени t .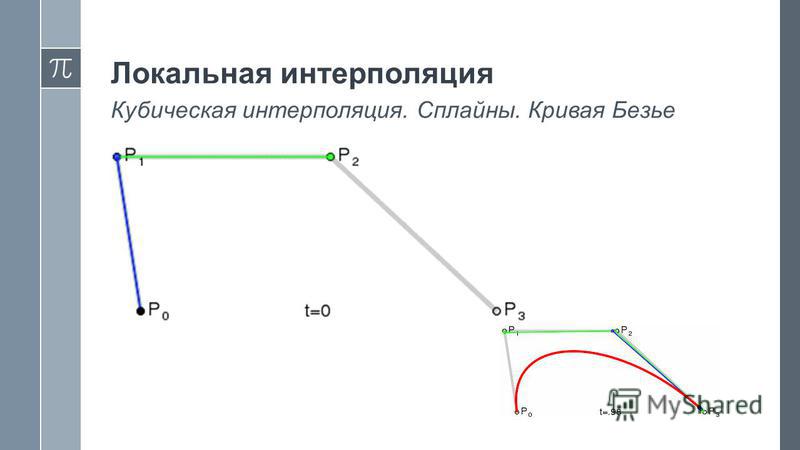
Вы можете обратиться к экв. 2 и экв. 3 , если у вас возникли проблемы.
Следовательно, коэффициенты матрицы есть не что иное, как коэффициенты перед t , что означает:
экв. 8Одним из интересных применений кривых Безье является рисование гладкой кривой, проходящей через заданный набор точек. Это интересно потому, что формула P(t) дает точек и не имеет формы y=f(x) , поэтому одно x может иметь несколько y (в основном функция, которая может «идти назад»). Например, мы могли бы нарисовать что-то вроде этого:
Однако математика для получения этого результата нетривиальна, поэтому я написал для этого специальный пост:
Интерполяция Безье
Создание гладких форм с помощью кривых Безье.
по направлению datascience.com
А пока вот как можно запрограммировать общую версию кривой Безье для любого количества контрольных точек, используя экв. . 1
1
Запустите программу, и вы получите график, отображаемый в заголовке.
Это введение в кривые Безье. Я надеюсь, что вы узнали что-то новое, и не стесняйтесь комментировать любой вопрос, который у вас может возникнуть!
Аппроксимация окружности кубическими кривыми Безье
Хорошее кубическое приближение Безье к единичной прямой дуге окружности:
, , , , где , и .
Это дает кубическую кривую Безье с центром в начале координат, начиная с и заканчивая , что практически неотличимо от дуги окружности.
Кривые Безье часто используются для создания гладких кривых, потому что они не требуют больших вычислительных затрат и дают высококачественные результаты. 3 \mathbf{P}_3″/> ,
3 \mathbf{P}_3″/> ,
Первое ограничение подразумевает, что:
И второе ограничение обеспечивает значение :
Это дает приближение:
Кубическая кривая Безье всегда остается вне круга, за исключением момента, когда она погружается внутрь, чтобы коснуться круга в его средней и конечной точках:
- Рис. 2: Радиальный дрейф в стандартном приближении.
Радиальный дрейф — это радиальное расстояние от кубической кривой Безье до окружности. В стандартном приближении максимальный радиальный дрейф равен .
Лучшее приближение
Однако возможно лучшее приближение, если мы заменим окончательное ограничение на новым ограничением :
- Концы кубической кривой Безье должны совпадать с концами единичной прямой дуги окружности, и их первые производные должны там совпадать.
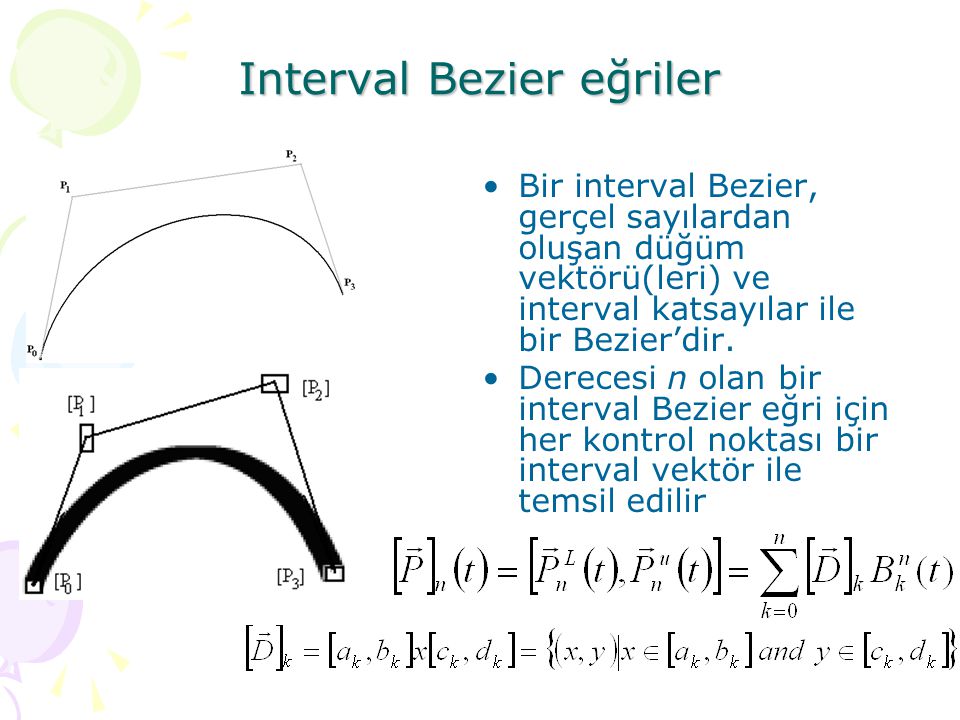 2}}{4 — 6c}»/> .
2}}{4 — 6c}»/> .Поскольку кривая Безье симметрична относительно , два максимума имеют одинаковое значение. Радиальное отклонение минимизируется, когда величина этого максимума равна величине минимума при .
Это дает лучшее значение для :
В этом приближении максимальный радиальный дрейф равен . Это на лучше стандартного приближения.
Еще лучшее приближение
Некоторое время это было в порядке вещей… пока Дэвид Эллсуорт не написал с улучшенным первым ограничением:
- Четыре контрольных точки:
, , , - Максимальный радиальный дрейф должен быть как можно меньше.
Ограничение на максимальный радиальный дрейф уже удерживает аппроксимацию Безье близкой к окружности, поэтому мы можем ослабить ограничение на конечные точки.
 2} — 1″/>
2} — 1″/>…и максимальный радиальный дрейф:
Наша задача теперь состоит в том, чтобы найти значения для , и , которые минимизируют .
Но мы можем вычислить эти значения численно:
,
и
.И вот результат:
- Рис. 4: Радиальный дрейф в еще лучшем приближении.
Концы кривой Безье больше не лежат на окружности, и там образовался излом: Ранее это решение было невозможно. Однако значительно лучше . Максимальный радиальный дрейф в этом приближении равен . Это на лучше стандартного приближения!
Результат практически неотличим от круга:
- Рис. 5: Аппроксимация Безье практически неотличима от окружности.

Окружность на рис. 5 создана с использованием кубической кривой Безье:
, , , , где
,
,
.Дополнительные усовершенствования
Больше дуг
Q. Что, если мы разделим окружность на более чем на четыре дуги?
A. Таким образом мы можем добиться сколь угодно хорошего приближения. Даже хордовое приближение может стать сколь угодно хорошим, если круг разбит на достаточное количество дуг.
Аппроксимация методом наименьших квадратов
Q. Что, если мы возьмем страницу из физики и воспользуемся эквивалентом регрессии наименьших квадратов, чтобы найти наиболее подходящую кривую Безье?
A. Аппроксимация методом наименьших квадратов почти такая же точная, как и представленная здесь наилучшая аппроксимация, но с меньшей суммой квадратов невязок.
Написано Спенсером Мортенсеном (spencer.spencermortensen.com) .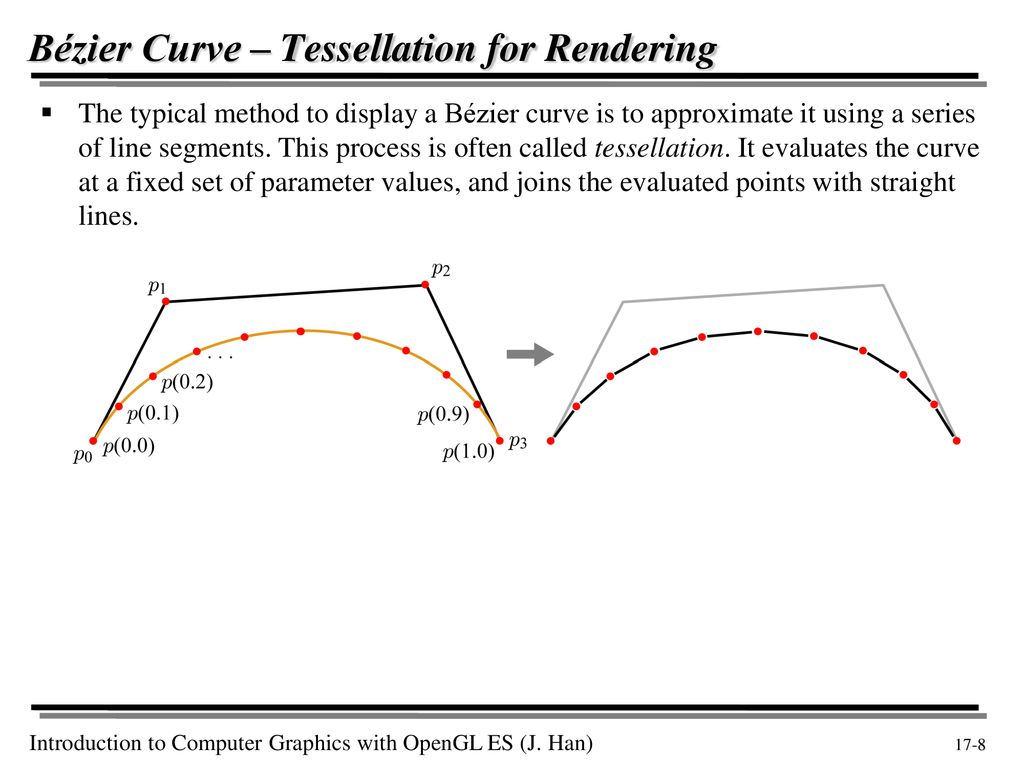
Copyright © 2012. Все права защищены.Инструмент «Перо Безье» | Профессиональная вспышка CS5
Поиск
Flash CS5 представил инструмент «Перо Безье» и инструмент «Частичное выделение» для редактирования кривых в стиле PostScript. Точки на кривых Безье меняются после определенных операций рисования или редактирования. Этот эффект является естественным и не влияет на окончательный размер файла. В следующей статье описываются технические детали этих операций с кривыми.
Формат файла SWF описывает кривые как квадратичные кривые Безье. Эти кривые немного отличаются от кубических кривых Безье, которые использует PostScript. В документации по формату файла SWF указано: «SWF использует квадратичные кривые Безье, поскольку они могут храниться более компактно и могут более эффективно отображаться».
Квадратичная кривая Безье имеет только один маркер управления для каждого сегмента кривой.
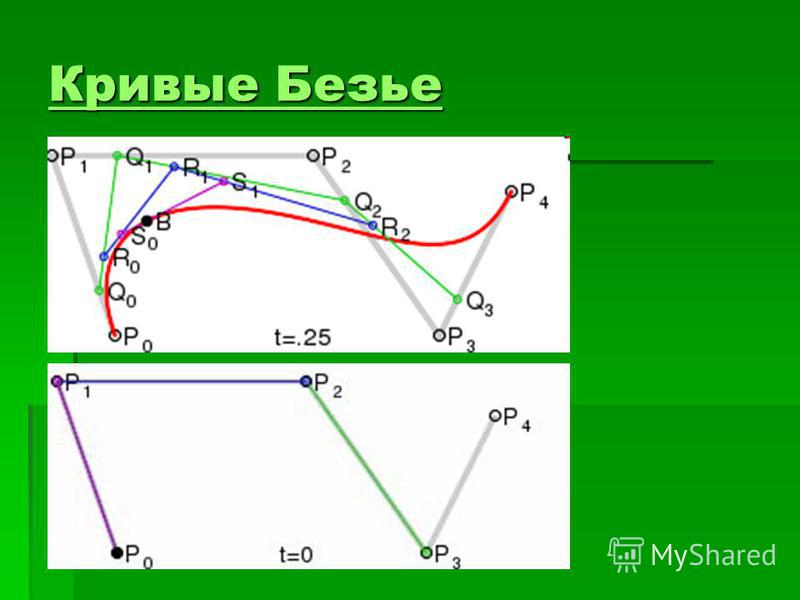 В инструменте рисования PostScript два узла на кривой и два управляющих маркера вне кривой определяют каждый сегмент кривой. Всего имеется четыре точки данных. Формат файла SWF также описывает два узла на кривой. Однако необходимо описать только одну нестандартную рукоятку управления. Следовательно, он может описать одну и ту же кривую с тремя точками данных.
В инструменте рисования PostScript два узла на кривой и два управляющих маркера вне кривой определяют каждый сегмент кривой. Всего имеется четыре точки данных. Формат файла SWF также описывает два узла на кривой. Однако необходимо описать только одну нестандартную рукоятку управления. Следовательно, он может описать одну и ту же кривую с тремя точками данных.Flash 5 представил инструмент «Перо Безье» и инструмент «Частичное выделение». Этот инструмент может создавать и редактировать альтернативные кубические представления Безье всех собственных квадратичных кривых Безье. Основным представлением остается исходная квадратичная кривая Безье. Тем не менее, кубические кривые Безье могут быть созданы по запросу, чтобы можно было рисовать пером Безье и редактировать в стиле PostScript.
Это кубическое представление Безье сохраняется в FLA-файле для использования при последующем редактировании. Во время некоторых операций редактирования новое кубическое представление Безье создается из исходного квадратичного представления Безье.
 Когда FLA-файл компилируется в файл SWF, включается только компактный Quadratic Bezier.
Когда FLA-файл компилируется в файл SWF, включается только компактный Quadratic Bezier.Подводя итог, можно сказать, что для маркеров управления в стиле PostScript требуется кривая другого типа, чем та, которую отображает Flash Player. Приложение для разработки Flash 5 может автоматически создавать эти четырехточечные кривые. Он пытается использовать их повторно, когда это возможно, но основное описание по-прежнему представляет собой квадратичную кривую Безье с тремя точками.
Авторское приложение Flash сочетает в себе методы живописного и векторного рисования, и вы можете делать то, что невозможно в других векторных программах. Некоторые из этих операций плохо обрабатываются кривыми в стиле PostScript. В таком случае приложение создает новую кубическую кривую Безье. В следующий раз, когда вы воспользуетесь ручкой Безье, вы увидите, что точки изменились.
Например, если вы импортируете векторную графику в формате Adobe Illustrator AI, она начинается с кубического представления Безье.
 Затем он преобразуется во внутренние квадратичные кривые Безье Flash. Точки Кубического Безье остаются для последующего редактирования в стиле PostScript. Но если вы используете инструмент Flash Lasso Tool, чтобы выбрать часть этой кривой и удалить ее, то будет создана совершенно новая кубическая кривая Безье. Во Flash легко захватывать и удалять части кривых. Однако для этого стиля векторного рисования, отличного от PostScript, требуется новая кривая стиля PostScript.
Затем он преобразуется во внутренние квадратичные кривые Безье Flash. Точки Кубического Безье остаются для последующего редактирования в стиле PostScript. Но если вы используете инструмент Flash Lasso Tool, чтобы выбрать часть этой кривой и удалить ее, то будет создана совершенно новая кубическая кривая Безье. Во Flash легко захватывать и удалять части кривых. Однако для этого стиля векторного рисования, отличного от PostScript, требуется новая кривая стиля PostScript.Другим примером является векторный ластик Flash. Если вы нарисуете круг и выберете его с помощью инструмента «Частичное выделение», вы увидите, что фигура имеет несколько маркеров управления Безье. Если затем провести ластиком по этой векторной фигуре, будет создано новое представление PostScript. Новые очки Bezier Pen отличаются от старых.
То же самое относится и к векторным кистям Flash, или к возможности захватывать, скручивать и лепить края фигуры, или к тому, как Flash имеет встроенные логические операции с фигурами.
 Все эти методы рисования, отличные от PostScript, могут заставить Flash отображать новое кубическое представление Безье в стиле PostScript.
Все эти методы рисования, отличные от PostScript, могут заставить Flash отображать новое кубическое представление Безье в стиле PostScript.Есть дополнительные тонкие случаи регенерации. Если вы рисуете с помощью инструмента «Перо Безье» или редактируете с помощью инструмента «Частичное выделение», то выполнение команды «Отменить» часто может привести к регенерации. В этом случае вы сможете увидеть больше точек, чем было изначально. Многие более простые кривые иногда представляют собой сложную кривую. Перемещение фигуры с помощью обычного инструмента «Стрелка» также может создать появление многих других контрольных точек инструмента «Перо Безье». Этот эффект возникает из-за того, как в настоящее время обрабатывается преобразование.
Для общего размера файла не имеет значения, сколько четырехточечных кубических точек Безье содержится на кривой. Представление Cubic Bezier не включается в окончательный SWF-файл. Все, что имеет значение, — это общая сложность правильной квадратичной кривой Безье.
 Все, что имеет значение, — это общий плавный вид кривой.
Все, что имеет значение, — это общий плавный вид кривой.Вы можете убедиться в этом сами, создав символ, содержащий простую кубическую кривую Безье, с помощью инструмента «Перо Безье». Дублируйте символ и переместите некоторые точки с помощью инструмента «Частичное выделение» и «Отменить», пока не увидите несколько более простых кривых. Эти два символа описывают одну и ту же общую кривую, но для этого используется больше четырехточечных кубических кривых Безье. Когда вы публикуете в файл SWF и проверяете отчет о размере, вы видите, что окончательные символы имеют примерно одинаковый размер.
Все, что имеет значение в окончательном SWF-файле, — это количество основных трехточечных квадратичных кривых Безье. Дополнительные узлы и маркеры, видимые с помощью инструмента «Частичное выделение» и инструмента «Перо Безье», не включены в окончательный файл.
Если вы импортируете фигуру из файла PostScript, может возникнуть другая проблема. Исходная форма могла быть слишком сложной, а исходное квадратичное преобразование Безье могло иметь больше точек, чем требовалось.
 Всякий раз, когда вы загружаете графику из приложения для печати, может быть полезно изучить каждую кривую и использовать команды Flash для сглаживания и оптимизации. Эти команды могут помочь уменьшить общий размер файла.
Всякий раз, когда вы загружаете графику из приложения для печати, может быть полезно изучить каждую кривую и использовать команды Flash для сглаживания и оптимизации. Эти команды могут помочь уменьшить общий размер файла.Во всех случаях изучайте методы естественного рисования в самом Flash. Эти методы не используют метафору четырехточечного пера, но естественные операции закрашивания, стирания и объединения могут быстро дать оптимизированные результаты.
Исходная кривая в SWF-файле — это квадратичная кривая Безье с двумя точками на кривой и одним маркером управления вне кривой. Когда вы используете инструмент «Перо Безье» или инструмент «Частичное выделение» во Flash, приложение автоматически создает кубический Безье в стиле PostScript. Кривая имеет две точки на кривой и два маркера управления вне кривой. Это кубическое представление используется только при редактировании, и точки могут изменяться во время редактирования. Только компактный формат Quadratic Bezier компилируется в окончательный SWF-файл.
Ключевые слова : tn_14765
Войдите в свой аккаунт
Войти
Управление учетной записью
Кривая Безье в компьютерной графике | Примеры
Кривая Безье-Кривая Безье может быть определена как-
- Кривая Безье — это параметрическая кривая, определяемая набором контрольных точек.
- Две точки являются концами кривой.
- Другие точки определяют форму кривой.
Понятие кривых Безье было дано Пьером Безье.
Пример кривой Bezier-Следующая кривая- пример кривой Безера-
здесь,
- КУРЕВА БЕЗЕР. 0 , б 1 , б 2 и б 3 .
- Точки b 0 и b 3 являются концами кривой.

- Точки b 1 и b 2 определяют форму кривой.
Bezier Curve Properties-Few important properties of a bezier curve are-
Property-01:Bezier curve is always contained within a polygon called as convex hull его контрольных точек.
Свойство-02:- Кривая Безье обычно повторяет форму определяющего ее многоугольника.
- Первая и последняя точки кривой совпадают с первой и последней точками определяющего многоугольника.
Свойство-03:Степень полинома, определяющего сегмент кривой, на единицу меньше, чем общее количество контрольных точек.
Степень = количество контрольных точек – 1
Свойство-04:Порядок полинома равен общему числу контрольных точек, определяющих отрезок кривой.

Порядок = количество контрольных точек
Свойство-05:- Кривая Безье обладает свойством уменьшения вариации.
- Это означает, что кривая не колеблется вокруг какой-либо прямой линии чаще, чем определяющий многоугольник.
Кривая Безера параметрически представлена
здесь,
- T IS PARAMATER, где 0 <=
- . P(t) = любая точка, лежащая на кривой Безье
- B i = i th контрольная точка кривой Безье
- n = степень кривой
- J n,i (t) = функция смешивания = C(n,i)t i (1-t) n-i где C(n,i) = n ! / я! (н-я)!
Cubic Bezier Curve-- Cubic bezier curve is a bezier curve with degree 3.
- The total number of control points in a cubic bezier curve is 4.
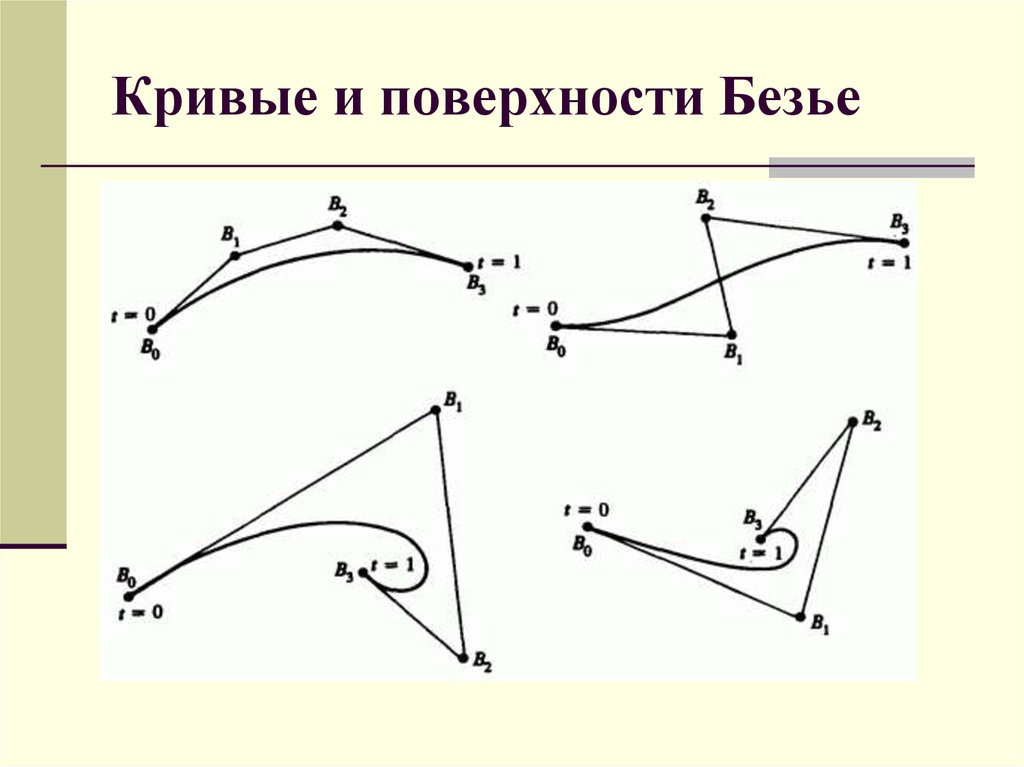
Example —Следующая кривая является примером кубической кривой Безье-
Здесь
- Эта кривая определяется 4 контрольными точками b 0 , b 1 , b 5 4 4 и 905
- Степень этой кривой равна 3.
- Итак, это кубическая кривая Безье.
Параметрическое уравнение кривой безера-
Заместитель n = 3 для Кубиса Beazier, Beazier, Beazier, Beazier, Beazier, Beazier, Beazier, Beazier, Beazier, Beazier, Beazier.0005
. + B 2 J 3,2 (T) + B 3 J 3,3 (T) ……… .. (1)
СЕЙЧАС,
. Используя (2), (3), (4) и (5) в (1), получаем: 3t(1-t) 2 + B 2 3t 2 (1-t) + B 3 t 3
5 900
Применение кривых Bezier-Кривые Безера имеют свои приложения в следующих полях-
1.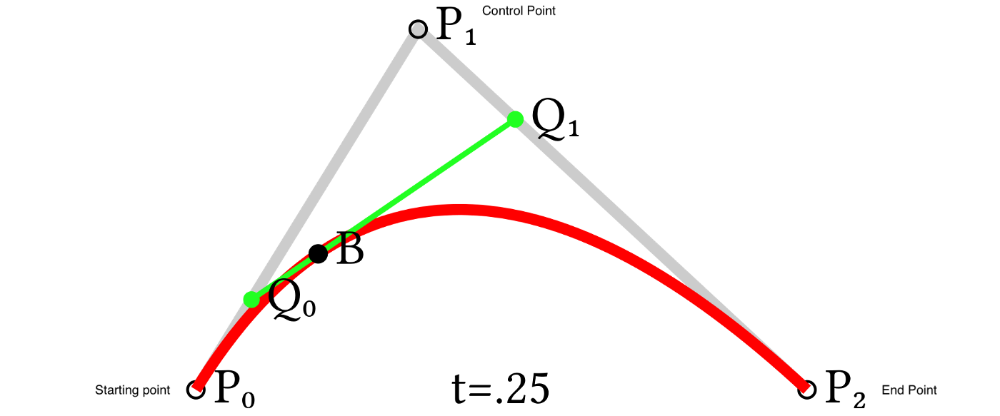 Компьютерная графика-
Компьютерная графика- - Beezier Inteclide Intectorie Intecterie Intectorie Intecterie Intectorie Intectorie Intectorie Intecterie Intearni In In Intemply Intecteries. моделировать плавные кривые.
- Кривая полностью содержится в выпуклой оболочке своих контрольных точек.
- Таким образом, точки можно графически отображать и использовать для интуитивного управления кривой.
2. Анимация-- Кривые Безье используются для описания движения в анимационных приложениях, таких как Adobe Flash и synfig.
- Пользователи обрисовывают желаемый путь кривыми Безье.
- Приложение создает необходимые кадры для перемещения объекта по траектории.
- В 3D-анимации кривые Безье часто используются для определения 3D-путей, а также 2D-кривых.
3. Шрифты-- Шрифты True Type используют составные кривые Безье, состоящие из квадратичных кривых Безье.

- Современные системы обработки изображений, такие как Postscript, Asymptote и т. д., используют составные кривые Безье, состоящие из кубических кривых Безье, для рисования изогнутых форм.
ПРАКТИЧЕСКИЕ ЗАДАЧИ НА ОСНОВЕ КРИВОЙ БЕЗЬЕ В КОМПЬЮТЕРНОЙ ГРАФИКЕ- Проблема-01:Учитывая кривую Безера с 4 контрольными точками-
B 0 [1 0], B 1 [3 3], B 2 [6 [6 3] , B 3 [8 1]
Определить любые 5 точек, лежащих на кривой. Также нарисуйте грубый набросок кривой.
Решение-Имеем-
- Данная кривая определяется 4 контрольными точками.
- Итак, данная кривая является кубической кривой Безье.
Параметрическое уравнение кубической кривой Безье:
+ B 2 3T 2 (1-T) + B 3 T 3
Заменить контрольные точки B 0 , B 1, B , B , B , B , B , B , B , B , B , B , B , B , B , B .
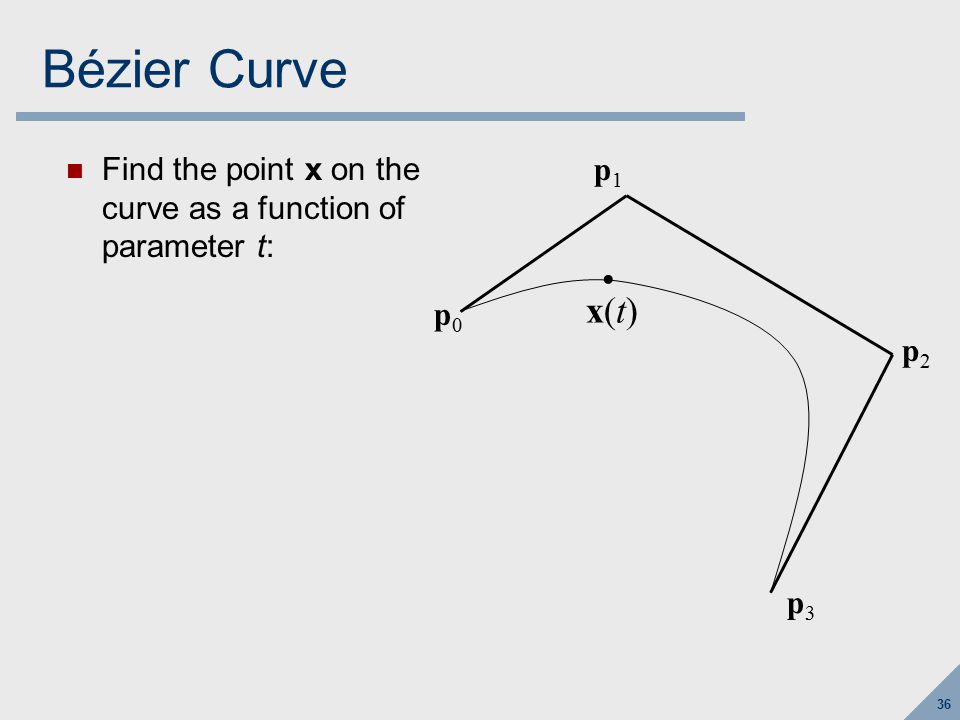 3 , получаем-
3 , получаем-P(t) = [1 0](1-t) 3 + [3 3]3t(1-t) 2 + [6 3]3t 2 (1-t) + [8 1]t 3 ……..(1)
Теперь
Чтобы получить 5 точек, лежащих на кривой, предположите любые 5 значений t, лежащих в диапазоне 0 <= t <= 1.
Пусть 5 значений t равны 0, 0,2, 0,5, 0,7, 1
Для t = 0:Подставив t=0 в (1), получим:
P(0) = [1 0](1-0) 3 + [3 3] 3(0)(1-т) 2 + [6 3]3(0) 2 (1-0) + [8 1](0) 3
P(0) = [1 0] + 0 + 0 + 0
P(0) = [1 0]
Для t = 0,2:Подставив t=0,2 в (1), получим: 0,2)(1-0,2) 2 + [6 3]3(0,2) 2 (1-0,2) + [8 1](0,2) 3
P(0,2) = [1 0]( 0,8) 3 + [3 3]3(0,2)(0,8) 2 + [6 3]3(0,2) 2 (0,8) + [8 1](0,2) 3
P(0,2) = [1 0] x 0,512 + [3 3] x 3 x 0,2 x 0,64 + [6 3] x 3 x 0,04 x 0,8 + [8 1] x 0,008
P(0,2 ) = [1 0] x 0,512 + [3 3] x 0,384 + [6 3] x 0,096 + [8 1] x 0,008
P(0,2) = [0,512 0] + [1,152 1,152] + [0,576 0,288] + [0,064 0,008]
P (0,2) = [2,304 1,448]
для t = 0,5:Замена t = 0,5 в (1), мы получаем
p (0,5) = = = = [1 0](1-0,5) 3 + [3 3]3(0,5)(1-0,5) 2 + [6 3]3(0,5) 2 (1-0,5) + [8 1](0,5) 3
P(0,5) = [1 0](0,5) 3 + [ 3 3]3(0,5)(0,5) 2 + [6 3]3(0,5) 2 (0,5) + [8 1](0,5) 3
P(0,5) = [1 0] х 0,125 + [3 3] х 3 х 0,5 х 0,25 + [6 3] х 3 х 0,25 х 0,5 + [8 1] х 0,125
P(0,5) = [1 0] х 0,125 + [3 3] х 0,375 + [6 3] x 0,375 + [8 1] x 0,125
P(0,5) = [0,125 0] + [1,125 1,125] + [2,25 1,125] + [1 0,125]
P(0,5) = [4,5 2,375]
Для t = 0,7:Подставляя t=0,7 в (1), получаем ]3t(1-t) 2 + [6 3]3t 2 (1-t) + [8 1]t 3
P(0,7) = [1 0](1-0,7) 3 + [3 3]3(0,7)(1-0,7) 2 + [6 3]3(0,7) 2 (1-0,7) + [8 1](0,7) 3
(0,7) = [1 0](0,3) 3 + [3 3]3(0,7)(0,3) 2 + [6 3]3(0,7) 2 (0,3) + [8 1](0,7) 3
P(0,7) = [1 0] x 0,027 + [3 3] x 3 x 0,7 x 0,09 + [6 3] x 3 x 0,49 x 0,3 + [8 1] x 0,343
P(0,7) = [1 0] x 0,027 + [3 3] x 0,189 + [6 3] x 0,441 + [8 1] x 0,343
P(0,7) = [0,027 0] + [0,567 0,567] + [2,646 1,323] + [2,744 0,343]
P (0,7) = [5,984 2,233]
для T = 1:Fulitutting T = 1 in (1 in (1 in (1 in (1 in (1 in (1 in (1 in (1 in (1 in (1 in (1 in (1 in (1:
), получаем —
P(1) = [1 0](1-1) 3 + [3 3]3(1)(1-1) 2 + [6 3]3(1) 2 (1-1) + [8 1](1) 3
P(1) = [1 0] x 0 + [3 3] x 3 x 1 x 0 + [6 3] x 3 x 1 x 0 + [8 1] x 1
P(1) = 0 + 0 + 0 + [8 1]
P(1) = [8 1 ]
Следующее приведено необходимый грубый набросок кривой-
, чтобы получить лучшее понимание кривых Безера в компьютерной графике,
Смотрите эту видео-лекцию
9000
Получить больше заметок и других учебных материалов по Компьютерная графика .
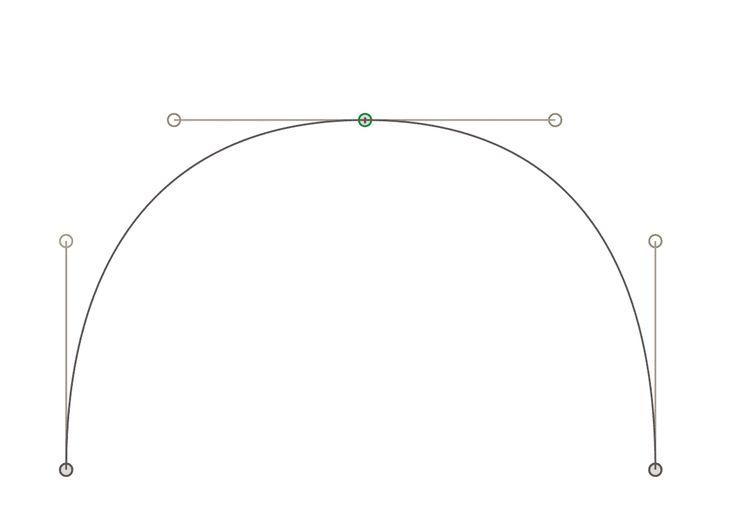
Смотрите видеолекции, посетив наш канал YouTube LearnVidFun.
Резюме
Кривые Безье в Джулии с анимацией
Я думаю, многие слышали о кривых Безье, но, возможно, некоторые из вас не слышали, и я слышал об этом, но не был уверен, что это такое и как они работают. Во время моего курса геометрического моделирования и анимации в университете у нас было несколько лекций по этому поводу, и я написал код для домашних заданий, а также чтобы немного больше понять об этом. В последние дни я публиковал свои анимации в Твиттере и спрашивал, заинтересованы ли вы в посте. Об этом было довольно много отзывов, так что вот! 9п \mathbf{b}_i \]
где \(\mathbf{b}_i\) — наши контрольные точки. Теперь второе свойство просто означает, что \(\mathbf{b}(0) = \mathbf{b}_0\) и \(\mathbf{b}(1) = \mathbf{b}_n\)
Я думаю было бы неплохо увидеть основные функции.
Здесь я использовал \(n=2\).
Теперь мы можем объединить его с нашими контрольными точками, чтобы получить:
Помимо изменения цвета, вы, вероятно, не видите разницы с первым графиком, хотя он был построен по-другому.
 9(n-i) для t в LinRange(0,1,шаги)]
конец
функция calculate_bernstein_poly (px, py; шаги = 100)
п = длина (пкс)-1
bernsteins = [compute_bernstein(i,n) для i=0:n]
x_vals = [сумма (px[k]*bernsteins[k][t] для k=1:n+1) для t=1:шаги]
y_vals = [сумма(py[k]*bernsteins[k][t] для k=1:n+1) для t=1:шаги]
вернуть x_vals, y_vals
конец
функция plot_with_bernstein (px, py; шаги = 100, подзаговор = 1)
x_vals, y_vals = calculate_bernstein_poly(px,py; steps=steps)
сюжет!(x_vals, y_vals, color=:blue, label=»»,subplot=subplot)
конец
функция основная()
px = [0, 3, 7]
ру = [2, 9, 3]
график (; размер = (700 500), axisratio =: равно, legendfont = шрифт (13))
график!(px, py, linetype=:scatter, label=»контрольные точки»)
plot_with_bernstein (px, py)
png(«использование_бернштейна»)
end
9(n-i) для t в LinRange(0,1,шаги)]
конец
функция calculate_bernstein_poly (px, py; шаги = 100)
п = длина (пкс)-1
bernsteins = [compute_bernstein(i,n) для i=0:n]
x_vals = [сумма (px[k]*bernsteins[k][t] для k=1:n+1) для t=1:шаги]
y_vals = [сумма(py[k]*bernsteins[k][t] для k=1:n+1) для t=1:шаги]
вернуть x_vals, y_vals
конец
функция plot_with_bernstein (px, py; шаги = 100, подзаговор = 1)
x_vals, y_vals = calculate_bernstein_poly(px,py; steps=steps)
сюжет!(x_vals, y_vals, color=:blue, label=»»,subplot=subplot)
конец
функция основная()
px = [0, 3, 7]
ру = [2, 9, 3]
график (; размер = (700 500), axisratio =: равно, legendfont = шрифт (13))
график!(px, py, linetype=:scatter, label=»контрольные точки»)
plot_with_bernstein (px, py)
png(«использование_бернштейна»)
end Пока довольно просто. Теперь объединим два и анимируем:
На самом деле я не совсем уверен в том, как интерпретировать цветную анимационную часть на нижнем графике с различными полиномами Бернштейна, но я думаю, что это выглядит интересно, и я никогда раньше этого не видел.
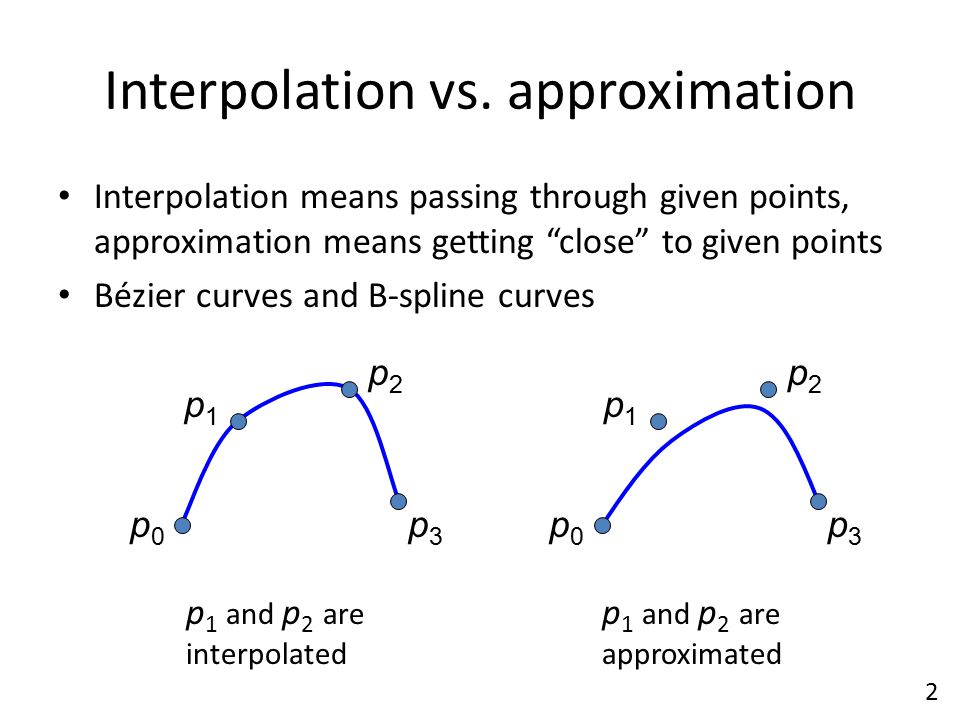 Три точки — красная, зеленая и синяя — в сумме дают черный цвет в обоих случаях. 90\), которые определяются точками Безье.
Три точки — красная, зеленая и синяя — в сумме дают черный цвет в обоих случаях. 90\), которые определяются точками Безье.Давайте посмотрим на наш основной пример в анимации:
Для второй степени у нас есть три линейных интерполяции. От одной точки Безье к другой, а затем снова от этих двух точек. Всегда интерполяция с \(t\) из предыдущей точки и \(1-t\), взвешенная со следующей точкой.
функция animate_bezier(px,py;steps=100) п = длина (пкс)-1 # сохранение всех точек между точками де Кастельжо bs = [нули (2,r) для r=n+1:-1:0] # базовый случай точек Безье бс[1][1,:] = пиксели бс[1][2,:] = ру точки = нули (шаги, 2) цвета = [:зеленый,:оранжевый,:красный,:желтый] с = 1 anim = @animate для t в LinRange (0,1, шаги) график(;размер=(700 500), axisratio=:равно, легенда=ложь) сюжет!(px,py,linetype=:scatter) для i=1:n для j=0:n-i # линейная интерполяция между точками twp new_b = (1-t)*bs[i][:,j+1]+t*bs[i][:,j+2] bs[i+1][:,j+1] = new_b # рисуем линию для линейной интерполяции, а также конкретную точку для t сюжет!(bs[i][1,j+1:j+2],bs[i][2,j+1:j+2], легенда=false, color=colors[i]) график!([new_b[1]],[new_b[2]], тип линии=:разброс, легенда=ложь, цвет=цвета[i]) если я == п точки[c,:] = [new_b[1],new_b[2]] # рисуем кривую до точки t = LinRange(0,1,steps)[c] график!(точки[1:c,1],точки[1:c,2], цвет=:черный) с += 1 конец конец конец конец gif(анимация, "bezier_d2.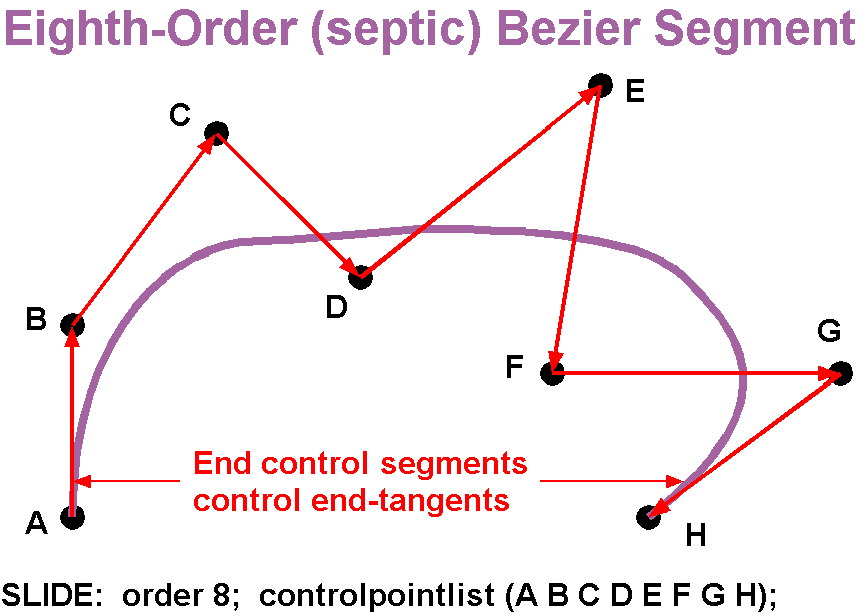 gif", кадр/с=30)
конец
gif", кадр/с=30)
конец px,py— это просто контрольные точки/точки Безье, поэтому мы можем добавить некоторые и получить это:Прежде чем мы перейдем к последней части этого поста (объединение кривых Безье), мы можем что-то сделать с этой кривой Безье степени 4. что раньше было невозможно. На самом деле существует более одной кривой Безье.
Из-за рекурсивной структуры теперь мы можем получить кривые степени 3.
Итак, последняя часть на сегодня посвящена созданию кривой, которая представляет собой комбинацию двух кривых Безье третьей степени. 9{n}(1)=n\left(\mathbf{b}_{n}-\mathbf{b}_{n-1}\right) \]
Я использовал эти точки:
px1 = [0.0,-1,3,5] ру1 = [0,0,3,5,5] px2 = [5, 8, 9] py2 = [5, 3, -1]
, поэтому для левой кривой нам нужно вычислить \(n\left(\mathbf{b}_{n}-\mathbf{b}_{n-1}\right )\) где n = 3 так:
\[ 3\влево(\mathbf{b}_{3}-\mathbf{b}_{2}\вправо) = 3 \begin{pmatrix} 5-3\5-5 \end{pматрица} = \begin{pmatrix} 6\0 \end{pматрица} \]
, тогда как для второй кривой получаем: 91\) мы хотим, чтобы параметрическое представление кривых имело непрерывность по первой производной.
 Это означает, что когда мы определяем количество шагов на первой кривой как, например, 200, а количество шагов на второй кривой равно 100, но двигаясь по кривой со скоростью 30 шагов в секунду, мы тратим больше времени на первую кривую, чем на вторую. .
Это означает, что когда мы определяем количество шагов на первой кривой как, например, 200, а количество шагов на второй кривой равно 100, но двигаясь по кривой со скоростью 30 шагов в секунду, мы тратим больше времени на первую кривую, чем на вторую. .Теперь предположим на секунду, что точка на кривой движется с постоянной скоростью по обеим кривым (что не всегда так и зависит от точек Безье), тогда в точке слияния у нас будет мгновенное изменение скорости что не всегда возможно, например, если мы перемещаем камеру по кривой. 92\) мы можем создать так называемый A-кадр:
Здесь должно выполняться следующее свойство: Соотношение между оранжевой и параллельно соединенной синей линией должно быть \(\Delta_{i+1} : \Delta_i\). Что это такое \(\Delta_i\) ? Это \(u_{i+1} — u_i\) ах ладно… Да ладно, что такое \(u\)??? Ну ладно есть проблема. \(u_i\) — это i-я компонента в векторе узла \(\mathbf{U} = (u_0,u_i, \dots, u_L)\). Ладно, клянусь, это последняя часть. Вектор узла определяет время, затрачиваемое на кривую, когда точка достигает \(u_i\).
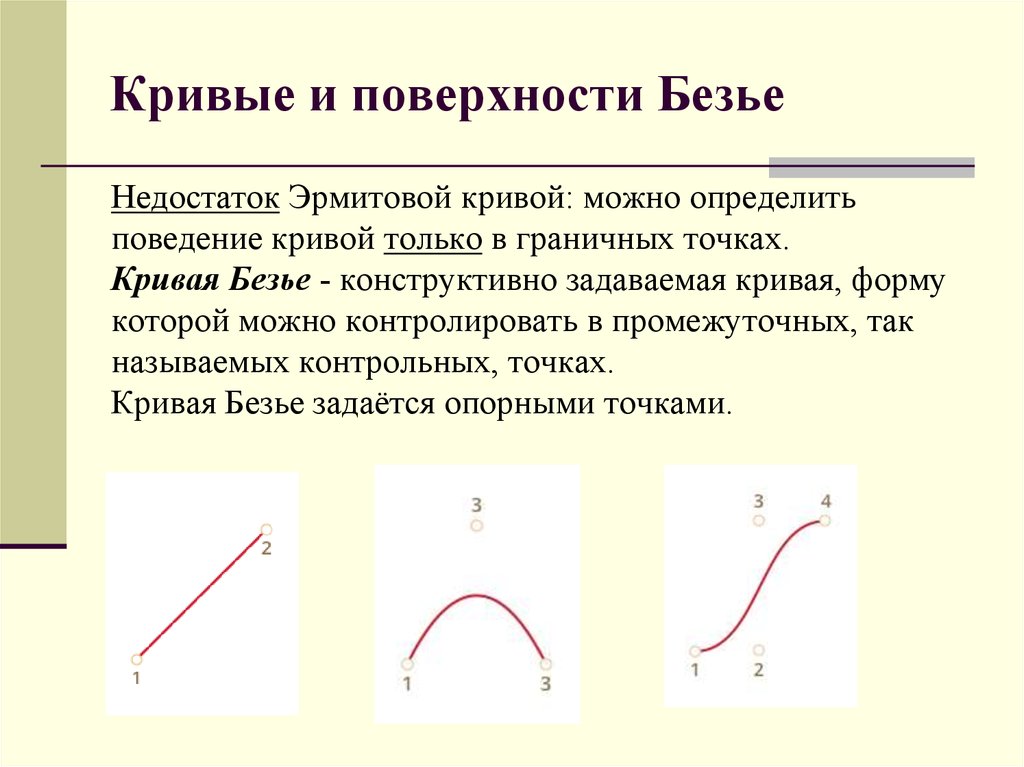 Чтобы сделать это проще, я решил иметь равноудаленный вектор узла, чтобы синие линии были такими же длинными, как оранжевые линии. (И да, желтая линия в верхнем левом углу оранжевая :D) Какая-то проблема в том, что линия не плоская и, возможно, имеет некоторые проблемы с наложением имен, или я не знаю. Однако вернемся к кривым. 92\) с другой стороны, это немного сложнее, но и у нас немного больше свободы, и я не буду доказывать, что здесь выполняются свойства. Просто график, показывающий, как это можно построить:
Чтобы сделать это проще, я решил иметь равноудаленный вектор узла, чтобы синие линии были такими же длинными, как оранжевые линии. (И да, желтая линия в верхнем левом углу оранжевая :D) Какая-то проблема в том, что линия не плоская и, возможно, имеет некоторые проблемы с наложением имен, или я не знаю. Однако вернемся к кривым. 92\) с другой стороны, это немного сложнее, но и у нас немного больше свободы, и я не буду доказывать, что здесь выполняются свойства. Просто график, показывающий, как это можно построить:Теперь у нас есть свобода выбора \(\gamma\) и \(\beta_1\). Где
\[ \gamma=\frac{(n-1)\left(1+\beta_{1}\right)}{\beta_{2}+\beta_{1}(n-1)\left(1+\beta_{ 1}\справа)} \]
можно определить как \(\beta_2\). Для последней анимации я использовал \(\beta_1 = 3\) и диапазон \(\beta_2\) от \(-30\) до \(30\).
Думаю, в этом сообщении блога есть все необходимые компоненты кода. Существуют и другие способы вычисления и рисования кривых Безье, и следующей темой будут b-сплайны.
 Если вам нравится этот пост и вы считаете разумным иметь пакет Julia или хотя бы репозиторий для этого кода, оставьте комментарий. На данный момент это не так хорошо организовано, поэтому я решил не публиковать свой код в репозиторий на этот раз. В любом случае, я думаю, что у меня достаточно открытый исходный код, чтобы каждый мог это закодировать;)
Если вам нравится этот пост и вы считаете разумным иметь пакет Julia или хотя бы репозиторий для этого кода, оставьте комментарий. На данный момент это не так хорошо организовано, поэтому я решил не публиковать свой код в репозиторий на этот раз. В любом случае, я думаю, что у меня достаточно открытый исходный код, чтобы каждый мог это закодировать;)Обновление! Я создал новый пост в этой короткой серии, посвященный B-сплайнам. Проверьте это: Визуальное понимание B-Splines
Если вы хотите получить больше таких анимаций и раньше, чем все остальные => подумайте о подписке на Patreon для поддержки этого блога.
Я буду держать вас в курсе, если будут какие-либо новости по этому поводу в Twitter OpenSourcES, а также в моем личном: Twitter Wikunia_de
Спасибо за чтение!
Если вам нравится блог в целом, подумайте о пожертвовании через Patreon. Вы можете читать мои посты раньше всех и поддерживать этот блог.
Хотите быть в курсе? Рассмотрите возможность подписки и получения почты всякий раз, когда выходит новый пост.
Введите адрес электронной почты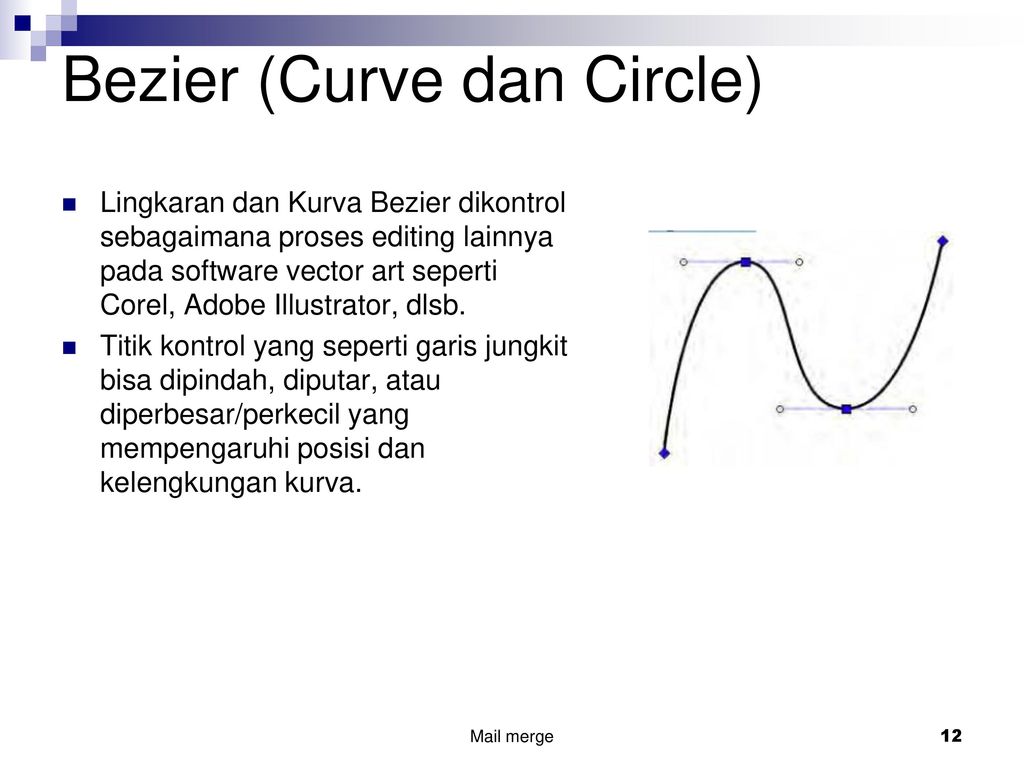
Работает на Кнопкадаун.
Подписаться на RSS
© Ole Kröger. Последнее изменение: 08 июня 2020 г. Веб-сайт создан с помощью Franklin.jl.
Как рисовать кубические кривые Безье на HTML5 SVG
HTML и CSS
- Canvas и SVGCSSHTML
Поделиться
В статье «Как создавать сложные пути в SVG» был рассмотрен элемент
Атрибут
dпредлагает несколько дополнительных приемов для рисования плавных кривых. В этой статье мы обсудим кубические кривые Безье, но вы также можете обратиться к статье «Как рисовать квадратичные кривые Безье на изображениях SVG» за несколько более простым вариантом.Что такое кубические кривые Безье?
Возможно, вы сталкивались с кубическими кривыми Безье в настольных издательских и графических пакетах.
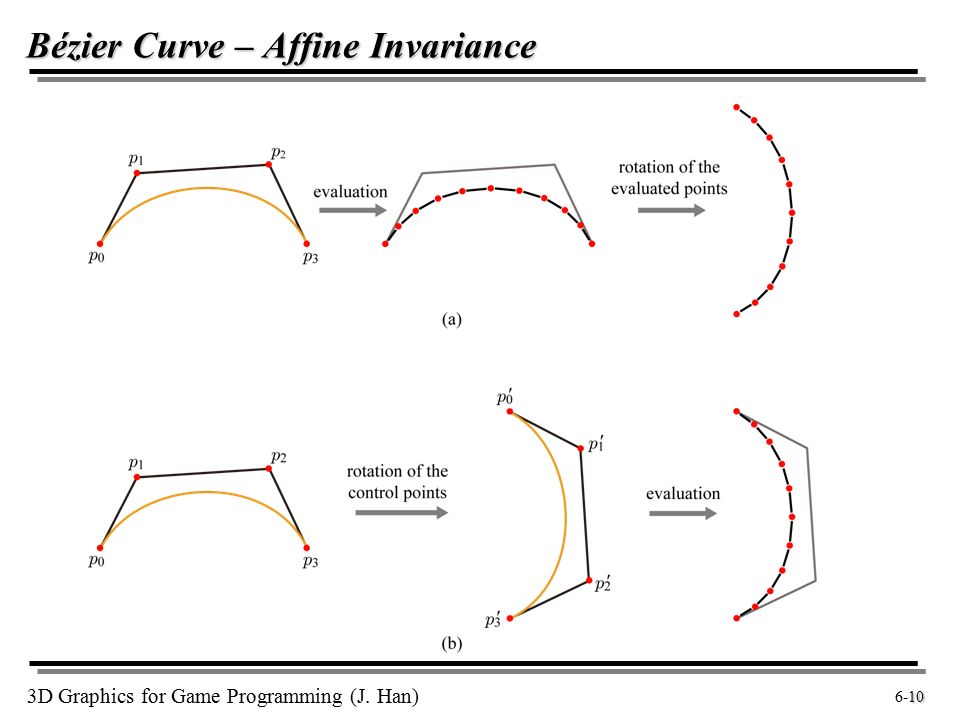 Они определяют начальную точку (
Они определяют начальную точку (P0) и конечную точку (P3). Однако, в то время как квадратичные кривые используют одну контрольную точку, кубические кривые Безье имеют две: по одной для каждого конца линии (P1иP2). Страница кривой Безье в Википедии дает хорошую иллюстрацию поколения:Источник изображения
Ужасающие уравнения также можно изучить в WolframMathWorld.
Кубические кривые Безье предоставляют дополнительные возможности. Две контрольные точки могут генерировать кривые, которые меняют направление или замыкаются сами на себя.
Головоломки с путями
Кубические кривые Безье определяются с помощью директивы
Cв атрибуте путиd:Вы также можете использовать строчные буквы
cдля обозначения относительных, а не абсолютных координат. Следующая кривая будет идентичной и, возможно, ее будет проще закодировать:Наконец, есть сокращенные директивы
Sиs(как обычно строчные буквы обозначают относительные, а не абсолютные координаты). Они принимают две дополнительные координаты для связывания нескольких кривых вместе, устанавливая еще одну конечную точку и связанную с ней контрольную точку. Предполагается, что начальная контрольная точка совпадает с конечной контрольной точкой на предыдущей кривой. Например, возьмите этот путь:Он рисует кривую от
100,250(контрольная точка100,100) до400,250(контрольная точка400,100), как указано выше. Затем строится еще одна кривая от400 250(контрольная точка без изменений400 100) до700 250(контрольная точка700 400): инструмент быстрой генерации сгенерирует<путь>код для вас:См.
 инструмент для создания кубической кривой Безье Pen
инструмент для создания кубической кривой Безье Pen
SVG от SitePoint (@SitePoint)
на CodePen.Перетащите контрольные точки на обоих концах кривой соответствующим образом. Щелкните саму кривую, чтобы переключить эффект заливки, который добавляет конечную директиву
Z.Обратите внимание, что этот инструмент должен преобразовывать координаты страницы DOM в координаты SVG, чтобы он работал на всех размерах экрана. Это может быть немного сложнее, чем вы ожидаете, поэтому обратитесь к разделу «Как преобразовать координаты DOM в координаты SVG и обратно» для получения подробной информации.
Если вам нужен более простой вариант, попробуйте создать квадратичные кривые Безье на изображениях SVG.
Поделиться этой статьей
Крейг Баклер
Крейг — внештатный веб-консультант из Великобритании, который создал свою первую страницу для IE2.0 в 1995 году. С тех пор он пропагандирует стандарты, доступность и лучшие практики HTML5.
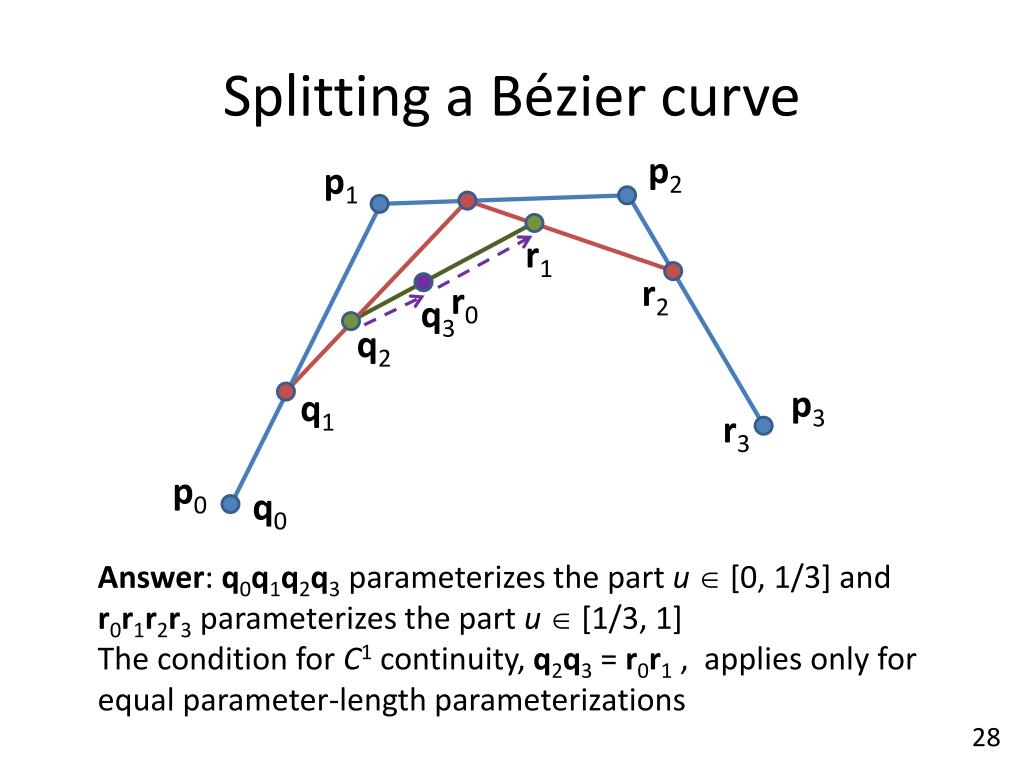
- Четыре контрольных точки:
