Кубические кривые Безье — это… Что такое Кубические кривые Безье?
Кривы́е Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Bézier) из автомобилестроительной компании «Рено» и Полем де Кастелье (de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Несмотря на то, что открытие де Кастелье было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.
Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастелье, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастелье назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастелье).
Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.![]()
Определение
Кривая Безье — параметрическая кривая, задаваемая выражением
где — функция компонент векторов опорных вершин, а — базисные функции кривой Безье, называемые также полиномами Бернштейна.
- , где n — степень полинома, i — порядковый номер опорной вершины
Виды кривых Безье
Линейные кривые
При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
- .
Квадратичные кривые
Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками:
- .
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах SWF файлах.
Кубические кривые
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:
- .
Кубическая кривая Безье
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.
Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке
В матричной форме кубическая кривая Безье записывается следующим образом:
- ,
где называется базисной матрицей Безье:
В современных графических системах, таких как GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.
Построение кривых Безье
Линейные кривые
 Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.
Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.Квадратичные кривые
Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q
- Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
- Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
- Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.
Построение квадратичной кривой Безье
Анимация t: [0; 1]
Кривые высших степеней
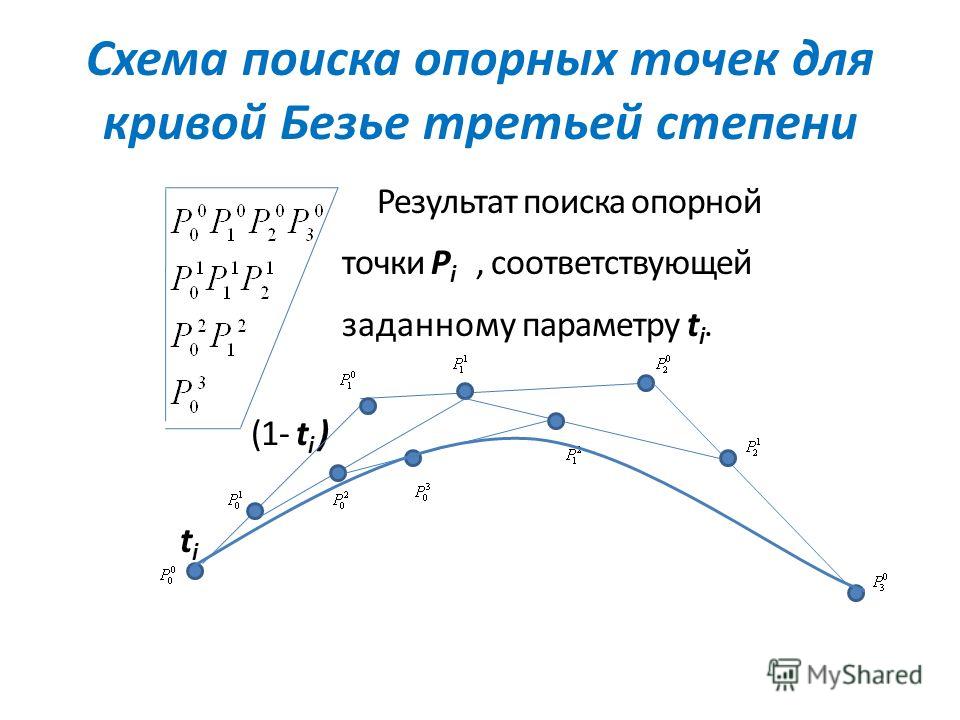
Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки
Для кубической кривой это промежуточные точки
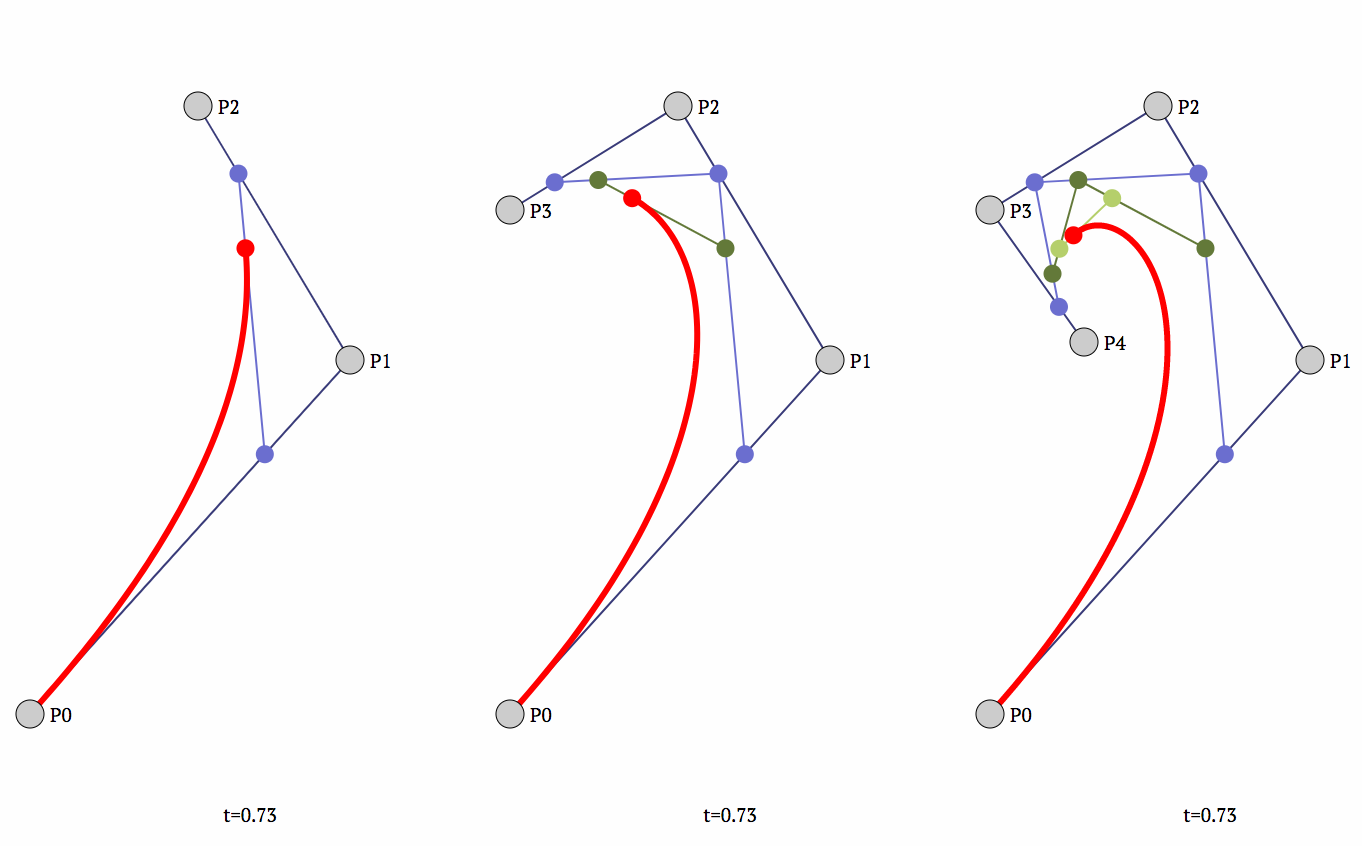
Построение кубической кривой Безье
Анимация t: [0; 1]
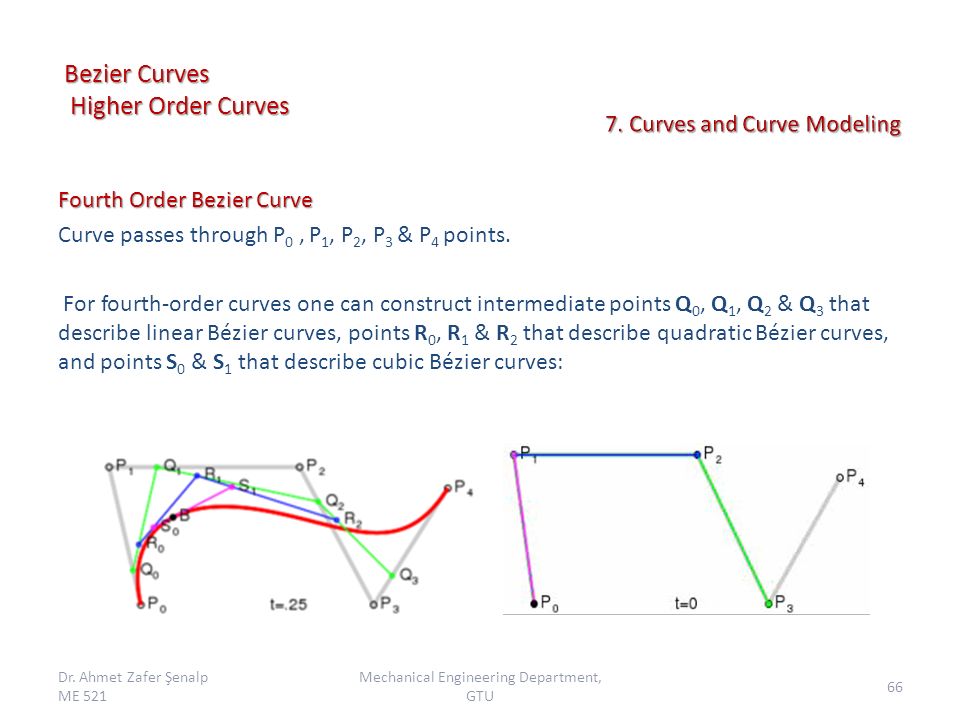
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
Построение кривой Безье 4-й степени
Анимация t: [0; 1]
Применение в компьютерной графике
Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий.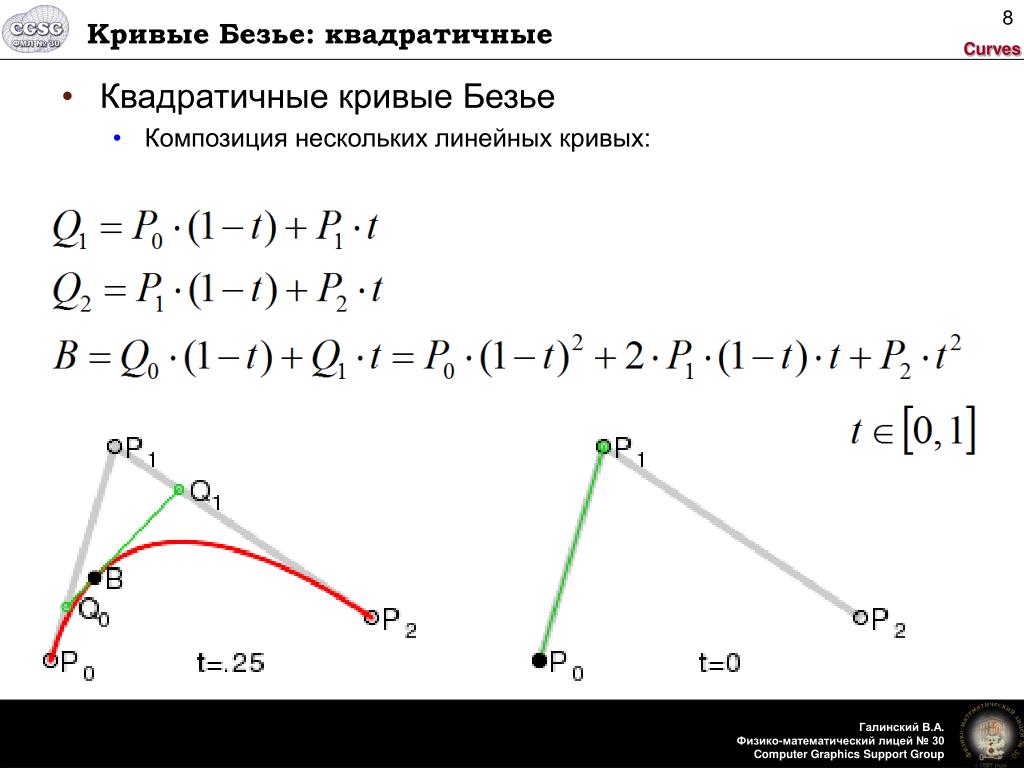 Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки, то не пересекаются и сами кривые), а с другой стороны позволяет визуализировать кривую с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.
Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, смежные опорные точки обеих кривых должны лежать на одной линии. В программах векторной графики наподобие Adobe Illustrator или path).
Преобразование квадратичных кривых Безье в кубические
Квадратичная кривая Безье с координатами преобразовывается в кубическую кривую Безье с координатами .
Литература
- Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.
См. также
Wikimedia Foundation. 2010.
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Основные преимущества формата SVG.

Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат.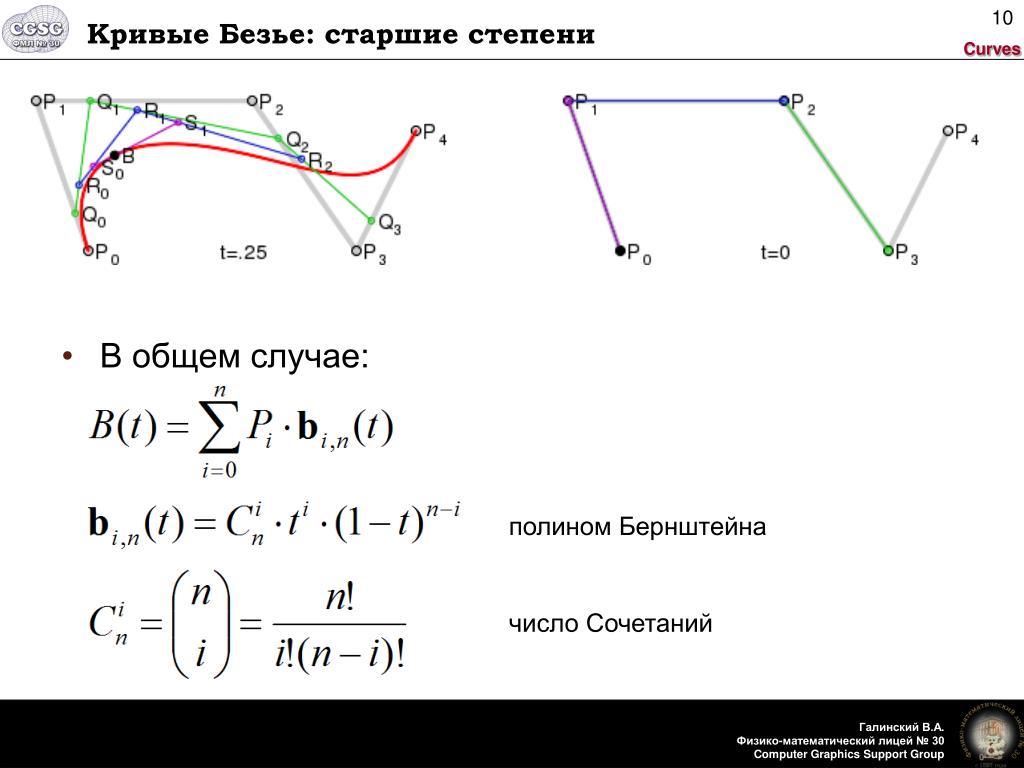
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок .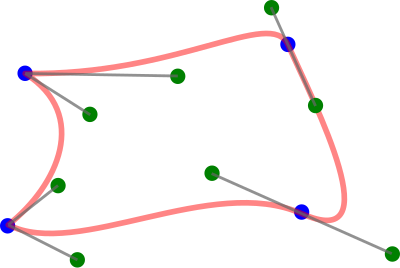 Картинка кликабельна.
Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language).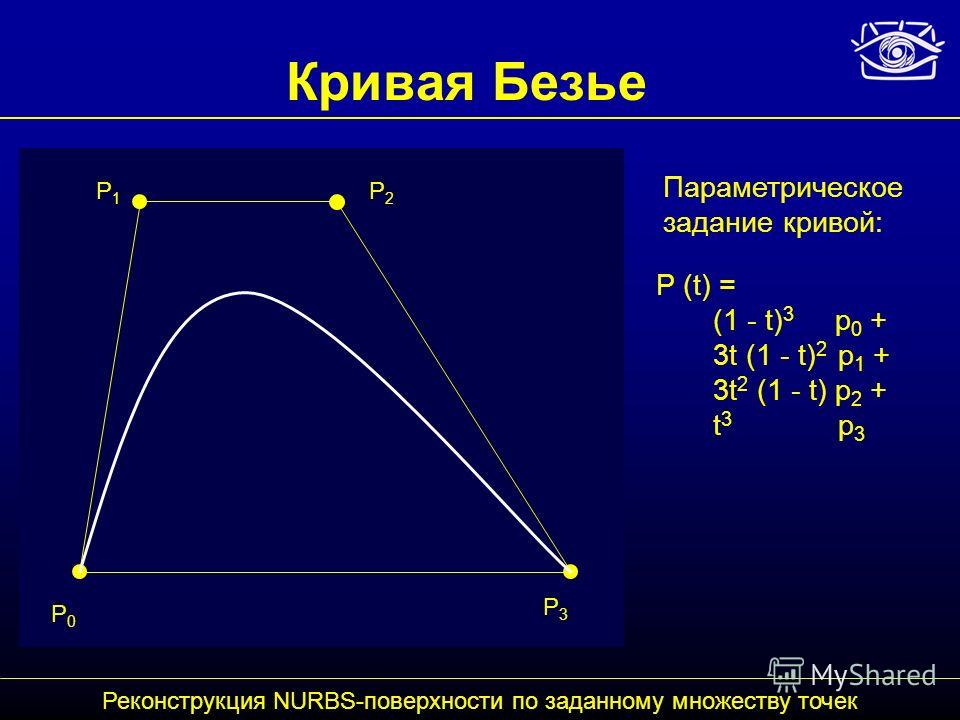 Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton.mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
- Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG. Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
Кривые Безье для ваших игр: учебник
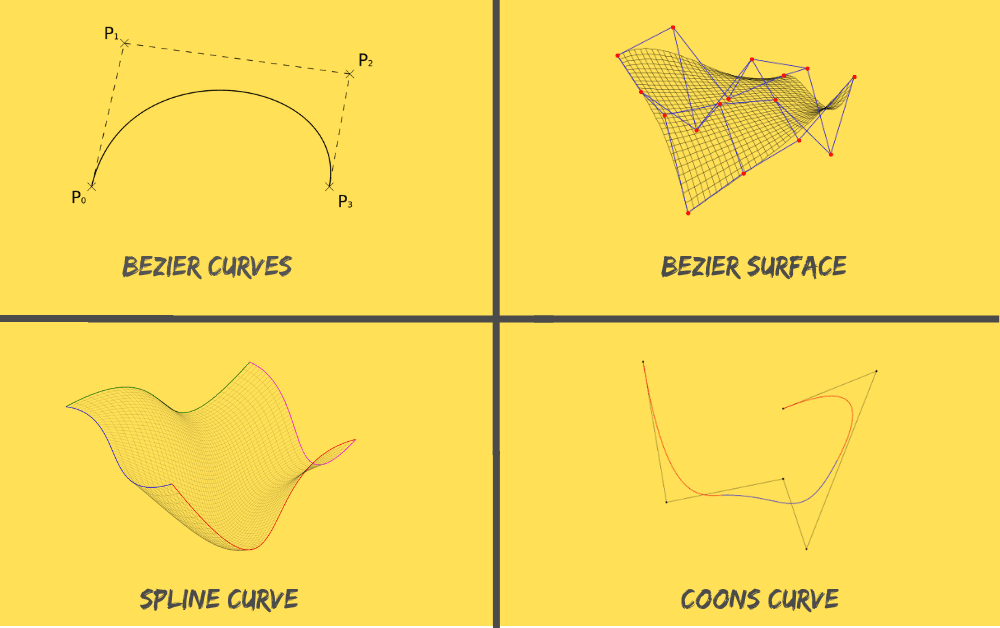
Мы все знаем что такое кривая. Вот несколько примеров.
Кривые Безье очень просты в использовании, и могут описывать многие формы. Кривые Безье широко используются для представления символов в шрифтах, и форм конструкций транспортных средств. Кривые Безье также используются в редакторах векторной графики для представления различных кривых, и в инструментах 3D-анимации для представления анимационных кривых.
В играх кривые Безье иногда полезны для описания пути: гоночный путь на трассе в гоночной игре, или линии в играх с рисованием линий, таких как Flight Control, или зацикленная траектория парения бабочки, что что живет в мире RPG.
Кривые Безье так популярны, потому что их математическое описания очень компактно, интуитивно понятно и элегантно. Их легко вычислить, легко использовать в более высоких измерениях (3D и выше), и могут быть соединены вместе, чтобы представить любую форму какую вы только можете себе представить.
В этом руководстве я дам вам инструкции, необходимые для реализации алгоритмов, чтобы вы смогли использовать кривые Безье в своих играх.
Начнем с математики. Математически мы можем описать кривую Безье на функцию. Функция принимает параметр . Значение функции есть точка на кривой; она зависит от параметра , и от множества точек, называемых контрольными точками. Первая и последняя контрольные точки являются концами кривой. Как правило, кривая не проходит через другие контрольные точки.
Значение может колебаться от 0 до 1. Значение 0 соответствует начальной точке кривой, значение 1 соответствует конечной точке кривой. Значения в промежутке соответствуют остальным точкам на кривой.
Вот пример простейшего типа кривой Безье, отрезок:
А вот сокращенное обозначение для двух уравнений, которые дают раздельные координаты:
Точки и являются контрольными точками. Когда , правая часть уравнения равна первой контрольной точке — началу отрезка. Когда , получаем точку , вторую контрольную точку — конец отрезка.
Когда , правая часть уравнения равна первой контрольной точке — началу отрезка. Когда , получаем точку , вторую контрольную точку — конец отрезка.
Для более интересных форм нам нужно больше контрольных точек. Количество контрольных точек определяет степень кривой. Две контрольные точки необходимы для линейных (первая степень) кривых, таких как отрезок выше. Для второй степени, или квадратичных кривых, нам нужны три контрольные точки.
Вот формула:
Кубические кривые (или кривые третьей степени) являются наиболее часто используюемыми, и поэтому в данном руководстве мы будем обсуждать именно кубические кривые. Для их построения требуется четыре контрольные точки, и возможно вы уже хорошо знакомы с их использованием в пакетах векторной графики (да, те самые кружочки которые используются для изменения формы кривых в программах Freehand или Inkscape и есть нашими контрольными точками).
Желтые линии протянуты в том же направлении, что и касательные на концах кривой. Чем дальше расположены эти желтые сегменты, тем сильнее «натянута» кривая по направлению касательных.
Формула для кубических кривых Безье:
Вы вряд ли будете нуждаться в более высоких степенях кривой. Если это так, то формула проста, но требует некоторых знаний биномиальные коэффициентов. Вы можете найти подробности в одном из источников в конце статьи.
В геометрии всегда найдется больше проблем, чем вы сначала могли подумать, что может привести к длительному поиску ошибок.
Вот правильные 2D кривые Безье:
Все конечные точки на одинаковом расстоянии друг от друга. 1. Кривая без перегиба, залома или петли. 2. Кривая с перегибом, без заломов или петель. 3. Кривая с заломом. 4. Кривая с петлей. 5. Прямая линия. (В точке перегиба кривая меняет направления сгиба)
Вырожденный случай 5 является самым сложным. Могут быть следующие варианты:
Могут быть следующие варианты:
- нет перекрытий
- кривая заламывается дважды на одном или обоих концах
- кривая заламывается трижды тройка где-то между концами
Существует шестой случай, когда все четыре контрольные точки совпадают: в результате кривая вырождается в одну точку. Обратите внимание, что кривая не вырождается в точку когда только конечные точки совпадают — все четыре контрольные точки должны совпадать. Кому интересны технические подробности могут почитать A Geometric Characterization of Parametric Cubic Curves (1.6 MB PDF) авторов Stone и De Rose. Статья Inflection points of a cubic Bezier объясняет, как вычислить точки перегиба, а также предоставляет интерактивные апплеты Java для наглядной иллюстрации.
В 3D, петли и переломы доставляют меньше проблем, так как они проявляются только в том случае, когда все точки лежат в одной плоскости. В 3D всегда можно изменить направление движения прямой (особенно для таких случаев как 2, 4 и 5).
При реализации алгоритмов кривых Безье, хорошо подумайте о целесообразности применения этого вида кривых к конкретному случаю, и всегда проверяйте на корректность работы алгоритма. Будьте особенно осторожны с контрольными точками — при их совпадении может возникнуть ситуация с нормализацией нулевого вектора, что в свою очередь может привести к падению программы.
Математическую формулу несложно перевести в код. Ниже приводиться реализация алгоритма, в которой уже произведена некоторая оптимизация путем сохранения и повторного использования промежуточных результатов.
Код приводится на языке C#, но перевести на Java, C + + и большинство других языков не должно принести особых проблем.
(Следующие функции будут работать и в 2D, если Vector3 заменить на Vector2.)
Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
{
float u = 1 – t;
float tt = t*t;
float uu = u*u;
float uuu = uu * u;
float ttt = tt * t;
Vector3 p = uuu * p0; //first term
p += 3 * uu * t * p1; //second term
p += 3 * u * tt * p2; //third term
p += ttt * p3; //fourth term
return p;
} |
Теперь у нас есть способ вычисления точки на кривой Безье, нам нужен способ рисования кривой.
Для изображений, самый простой подход заключается в использовании итерирования для расчета требуемых точек:
for (int i = 0; i <= SEGMENT_COUNT; ++i)
{
t = i / (float)SEGMENT_COUNT;
Vector3 pixel = CalculateBezierPoint(t, p0, p1, p2, p3);
DrawPixel(pixel); //assume this function can handle Vector3
} |
Этот подход страдает от следующих проблем:
- очень сложно угадать подходящий шаг для приращения ;
- некоторые пиксели могут быть нарисованы много раз;
- некоторые пиксели могуть быть пропущены.
Более продвинутые алгоритмы используют адаптивный прирост чтобы преодолеть эти проблемы. Сглаживание (antialiasing) кривой даст вообще класный результат, делая кривую очень гладкой и четкой. Хорошим источником для рисования кривых (и еще куча полезных тем) является Computer Graphics and Computer Modelling от David Salomon.
Более простой альтернативой является рисовать линии, а не пикселей.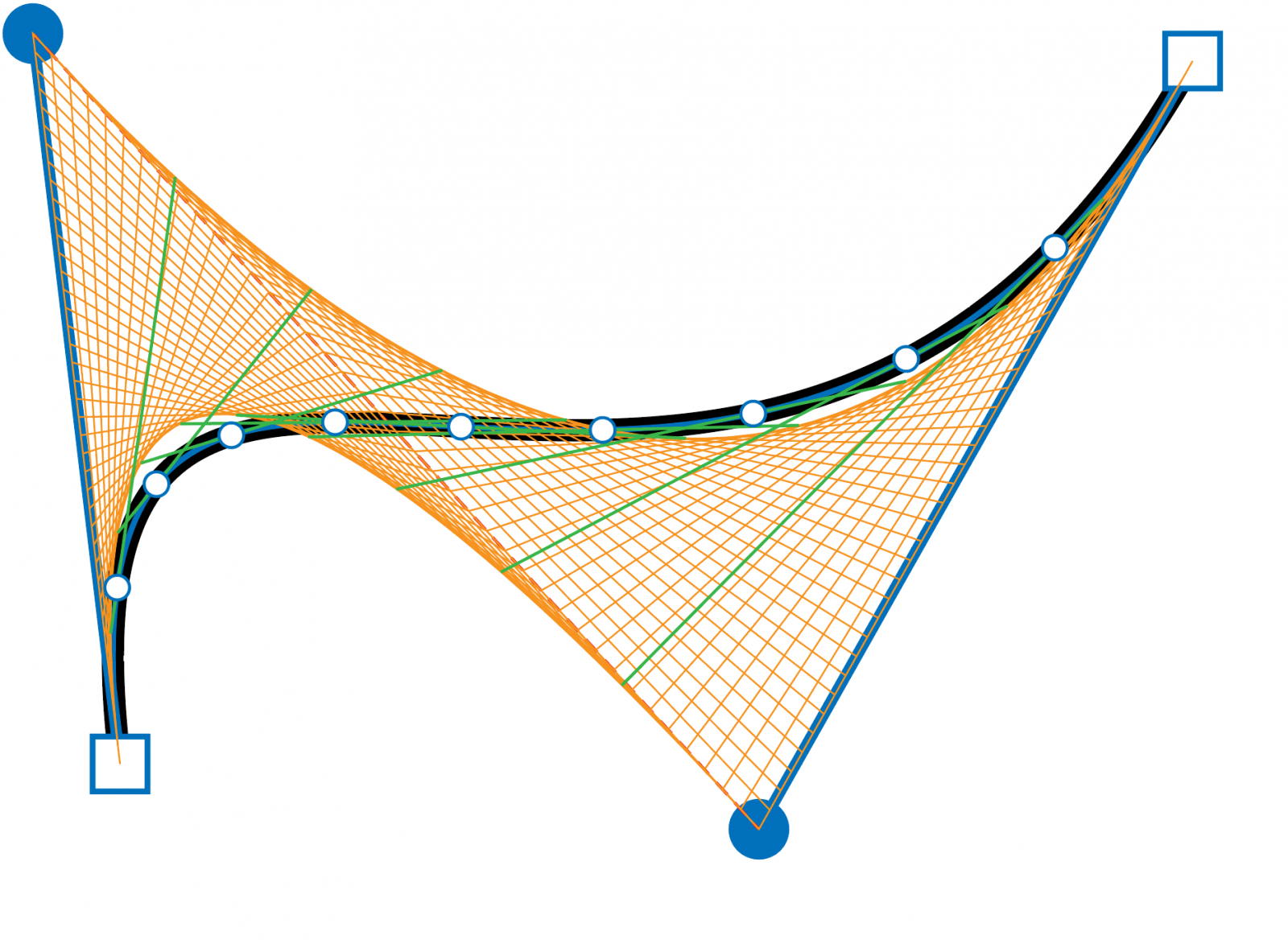 Этот метод также более подходящий для рисования кривых с помощью графического оборудования.
Этот метод также более подходящий для рисования кривых с помощью графического оборудования.
q0 = CalculateBezierPoint(0, p0, p1, p2, p3);
for (int i = 1; i <= SEGMENT_COUNT; ++i)
{
t = 1 / (float)SEGMENT_COUNT;
q1 = CalculateBezierPoint(t, p0, p1, p2, p3);
DrawLine(q0, q1);
q0 = q1;
} |
Так как теперь нам не нужно волноваться о пропуске пикселей, можно выбрать больший прирост и снизить нагрузку на отрисовку. Но все же трудно выбрать приращение должным образом.
Существует другой алгоритм, использующий рекурсивные разбиения. Как правило, он дает меньше точек отрисовок на тот же уровень точности, чем в предыдущем алгоритме. Тем не менее, он не обрабатывает все кривые с перегибами или петлями должным образом, и не должен использоваться, если возможно появление таких случаев.
Вот алгоритм:
- Стартуем в конечных точках: кривая указывает на и .
- Рассчитать точку по середине отрезка ( в первой итерации).

- Если угол между двумя получеными отрезками меньше порогового значения, тогда добавляем полученую точку в отрисовку. Дальше рекурсивно повторять для каждой половинки кривой. Алгоритм останавливается когда дальнейшее разбиение невозможно, или отрезки достигли минимальной длины.
На рисунке ниже показан рабочий пример.
1. Начнем с двух конечных точек и точкой между ними. Мы проверяем угол, образованный между двумя отрезками. Он достаточно мал, поэтому мы добавим между ними точку отрисовки. 2. Затем мы делаем то же самое для левой части кривой.В этом случае угол достаточно велик, так что мы не добавляем точку, и не разбиваем дальше. 3. Мы делаем то же самое для правой части кривой. В этом случае угол достаточно мал, поэтому мы добавляем новые точки для отрисовки, и развиваем отрезок. 4. И 5. Мы делаем то же самое для двух половинок на предыдущем шаге. В каждом случае угол достаточно велик, так что новые точки не добавляются, разбиение также не нужно. 6.Окончательный набор точек используется для рисования кривой.
В каждом случае угол достаточно велик, так что новые точки не добавляются, разбиение также не нужно. 6.Окончательный набор точек используется для рисования кривой.
Ниже приведен код рекурсивного алгоритма. Хитрость в том, чтобы вставлять точки в нужном месте в списке так, что они остаются в правильном для отрисовки порядке. Мы проверяем скалярное произведения нормированных сегментов, вместо проверки угла непосредственно. Именно поэтому для сравнения используется >, вместо < как если бы мы проверяли углы напрямую.
//returns the number of points added.
int FindDrawingPoints(float t0, float t1, int insertionIndex, List pointList)
{
tMid = (t0 + t1) / 2;
p0 = bezierCurve(t0);
p1 = bezierCurve(t1);
if (p0 – p1.sqrMagnitude < MINIMUM_SQR_DISTANCE)
{
return 0;
}
pMid = bezierCurve(tMid);
leftDirection = (p0 – pMid).Normalised;
rightDirection = (p1 – mMid).Normalised;
if (Dot(leftDirection, rightDirection) > threshold)
{
int pointsAddedCount = 0;
pointsAdded += FindDrawingPoints(t0, tMid, insertionIndex, pointList)
pointList. |
Следующая функция демонстрирует вызов рекурсивной функции:
void FindPoints()
{
List pointList = new List();
p0 = bezierCurve(0);
p1 = bezierCurve(1);
pointList.Add(p0);
pointList.Add(p1);
int pointsAdded = FindPoints(0, 1, 1, pointList);
assert(pointsAdded + 2 == pointsList.Count); //sanity check
} |
Несколько замечаний:
- Проверка на минимальное расстояние необходима для предотвращения проблем с нормализацией очень коротких векторов. Она также предотвращает ненужные вычисления.
- Пороговое значение на удивление близко к -1. Для старта неплохо начать с -0,99.
- Алгоритм не очень хорошо работает для кривых, которые содержат перегибы или петли.
 Ниже приведен пример того, что может произойти, если применить его к кривой с перегибом.
Ниже приведен пример того, что может произойти, если применить его к кривой с перегибом.
Пример, в котором алгоритм даст плохой результат. В этом случае угол превышает допустимый порог, так что никаких разбиений не будет происходить. Результат не сильно похож на желаемую кривую.
Когда мы хотим построить сложную кривую, у нас есть два варианта:
- использовать одну кривую Безье с высокой степенью;
- разделить кривую на более мелкие сегменты, и использовать кривые Безье низкой степени для каждого сегмента.
Последний тип кривой называется пути Безье. Пути Безье, как правило, более просты и эффективны в использовании, чем кривые высокой степени, поэтому именно этот метод здесь и описывается.
Приведенная здесь реализация является лишь одной из многих возможных. Мы определим класс, который создает список контрольных точек кривых Безье, которые составляют путь Безье. Поскольку сегменты связаны концом-к-концу, начальная и конечная точка соседних кривых совпадают, таким образом мы можем избежать дублирования точек.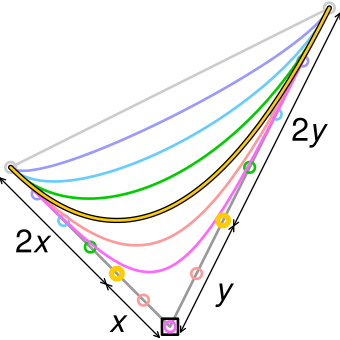 На рисунке показан пример пути Безье составленого из четырех кривых Безье. В этом случае, список содержит 13 точек, как показано на рисунке слева.
На рисунке показан пример пути Безье составленого из четырех кривых Безье. В этом случае, список содержит 13 точек, как показано на рисунке слева.
Если мы решим построить кривую с отрезками, то хорошим решением будет кешировать конечные точки отрезков, и обновлять их по мере изменения кривой. Следующий алгоритм вычисляет все точки отрисовки (конечные точки отрезков).
class BezierPath
{
List controlPoints;
Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3) {...}
List GetDrawingPoints()
{
List drawingPoints = new List();
for(int i = 0; i < controlPoints.Count - 3; i+=3)
{
Vector3 p0 = controlPoints[i];
Vector3 p1 = controlPoints[i + 1];
Vector3 p2 = controlPoints[i + 2];
Vector3 p3 = controlPoints[i + 3];
if(i == 0) //Only do this for the first endpoint.
//When i != 0, this coincides with the end
//point of the previous segment
{
drawingPoints. |
Данный рекурсивный алгоритм легко адаптируется для получения промежуточных точек. Пример вы можете найти в прилагаемом к статье коде.
При реализации путей Безье, вы можете сделать вашу жизнь намного проще, выполнив следующие действия:
- Включить отладку режимов для рисования контрольных точек, конечных точек Безье, рисование точек и касательных.
- Вывести число точек отрисовки и контрольных точек: благодаря этому вы всегда сможете проверить сколько точек генерирует алгоритм, и вменяемость этого количества.
Ну и напоследок — кривые Безье это очень круто, но не стоит использовать их везде, особенно для представления коротких, практически прямых линий.
- Большинство 3D движков требуют использовать короткие прямые линии для рендеринга кривых, поэтому вы должны точно представлять себе ценность внедрения отрисовки кривых Безье.
- Когда движение находится под контролем физики, соответственно резкие изменения скорости и направления практически отсутсвуют. Объекты, как правило, перемещаются путем изменения силы, действующей на объект, и благодаря этому их скорость не может измениться мгновенно. Таким образом, любое движение сглаживается автоматически: любой объект следующий вдоль соединенных прямых линий будет автоматически следовать сглаженому пути — в кривых Безье нет никакой надобности.
Статья является переводом, ссылка на источник — Bezier Curves for your Games: A Tutorial.
Если вы заметите какие либо неточности в переводе — просьба сообщать об этом письмом на адрес указаный внизу страницы.
Иллюстрированный самоучитель по цифровой графике › Принципы векторной графики › Свойства кривых Безье [страница — 151] | Самоучители по графическим программам
Свойства кривых Безье
Кривые Безье любой степени обладают следующими важными свойствами.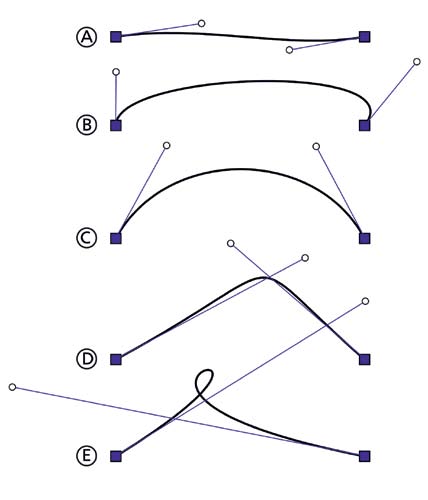
- Начальная и конечная контрольные точки лежат на кривой.
- Кривая на всем протяжении непрерывна, у нее отсутствуют разрывы. Это важнейшее свойство, без которого кривая Безье вообще бы не рассматривалась.
- Касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с другими двумя соседними контрольными точками, через которые в общем случае кривая не проходит.
- Точки на краях касательных будут располагаться на кривой только в том случае, если последняя представляет собой прямую линию.
- Поскольку кривая Безье представляет собой взвешенное усреднение всех ее контрольных точек с положительными весами, а сумма их равна единице, кривая всегда располагается внутри выпуклого многоугольника из ее контрольных точек (рис. 12.20), как и рассмотренная выше NURBS-кривая.
- Кривую Безье можно рассматривать как пошаговое уточнение формы многоугольника, получаемого последовательным соединением ее контрольных точек (рис.
 12.21-12.24). При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма определяется относительным расположением оставшихся точек, через которые в общем случае она не проходит.
12.21-12.24). При этом кривая Безье начинается и заканчивается в конечных точках данного многоугольника, а форма определяется относительным расположением оставшихся точек, через которые в общем случае она не проходит.
Рис. 12.20. Кривая в выпуклом многоугольнике
Исходя из этого можно представить канонический вид кривой Безье, который обычно используется в графических редакторах плоской графики.
Рис. 12.21. Первый этап аппроксимации кривой
Рис. 12.22. Второй этап аппроксимации кривой
Рис. 12.23. Третий этап аппроксимации кривой
Рис. 12.24. Итоговая ломаная кривая
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.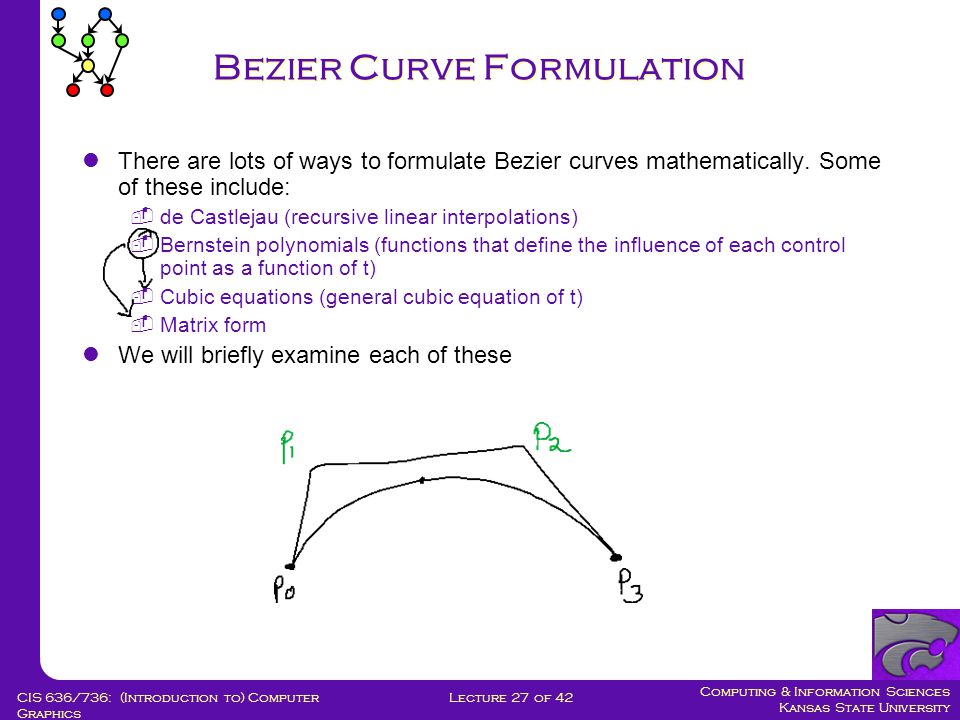 ADD_COLLECTION_DESCRIPTION}}
ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article. content_lang.display}}
content_lang.display}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}РАЗНИЦА МЕЖДУ КРИВОЙ БЕЗЬЕ И КРИВОЙ B-СПЛАЙНА | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ — НАУКА
Кривая Безье против кривой B-сплайна При численном анализе в математике и рисовании компьютерной графики используются многие типы кривых. Кривая Безье и кривая B-сплайна — две популярные модели для т
Кривая Безье и кривая B-сплайна — две популярные модели для т
Кривая Безье против кривой B-сплайна
При численном анализе в математике и рисовании компьютерной графики используются многие типы кривых. Кривая Безье и кривая B-сплайна — две популярные модели для такого анализа. У этих двух типов кривых много общего, и эксперты называют кривую B-сплайн разновидностью кривой Безье. Однако есть много отличий, которые будут обсуждаться в этой статье для удобства читателей.
Что такое кривая Безье?
Кривые Безье — это параметрические кривые, часто используемые при моделировании гладких поверхностей в компьютерной графике и многих других связанных областях. Эти кривые можно масштабировать до бесконечности. Связанные кривые Безье содержат контуры, которые представляют собой интуитивно понятные комбинации, которые можно изменять. Этот инструмент также используется для управления движениями в анимационных видеороликах. Когда программисты этих анимаций говорят о задействованной физике, они, по сути, говорят об этих кривых Безье. Кривые Безье были впервые разработаны Полем де Каслхо с использованием алгоритма Каслхо, который считается стабильным методом построения таких кривых. Однако эти кривые стали известны в 1962 году, когда французский дизайнер Пьер Безье использовал их при проектировании автомобилей.
Кривые Безье были впервые разработаны Полем де Каслхо с использованием алгоритма Каслхо, который считается стабильным методом построения таких кривых. Однако эти кривые стали известны в 1962 году, когда французский дизайнер Пьер Безье использовал их при проектировании автомобилей.
Наиболее популярные кривые Безье имеют квадратичную и кубическую природу, поскольку построение и оценка кривых более высокой степени дороги. Пример уравнения кривой Безье с двумя точками (линейная кривая) выглядит следующим образом
B (t) = P0 + t (P1 — П0) = (1 — t) P0 + tP1, tε [0,1]
Что такое кривая B-сплайна?
Кривые B-сплайна считаются обобщением кривых Безье и имеют с ними много общего. Однако у них есть более желаемые свойства, чем у кривых Безье. Кривые B-сплайна требуют больше информации, такой как степень кривой и вектор узла, и в целом требуют более сложной теории, чем кривые Безье. Однако они обладают множеством преимуществ, которые компенсируют этот недостаток.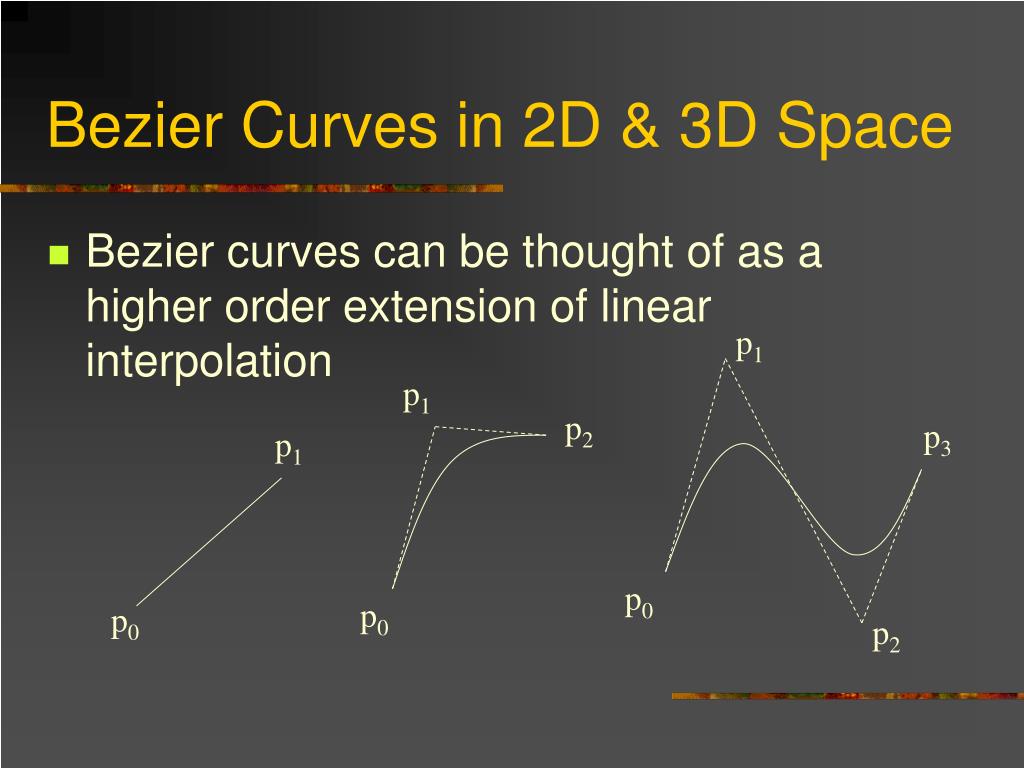 Во-первых, кривая B-сплайна может быть кривой Безье, когда программист того пожелает. Дополнительная кривая B-сплайна обеспечивает больший контроль и гибкость, чем кривая Безье. Можно использовать кривые с более низким градусом и при этом поддерживать большое количество контрольных точек. B-сплайн, несмотря на то, что он более полезен, по-прежнему является полиномиальными кривыми и не может представлять простые кривые, такие как круги и эллипсы. Для этих форм используется дальнейшее обобщение кривых B-сплайнов, известное как NURBS.
Во-первых, кривая B-сплайна может быть кривой Безье, когда программист того пожелает. Дополнительная кривая B-сплайна обеспечивает больший контроль и гибкость, чем кривая Безье. Можно использовать кривые с более низким градусом и при этом поддерживать большое количество контрольных точек. B-сплайн, несмотря на то, что он более полезен, по-прежнему является полиномиальными кривыми и не может представлять простые кривые, такие как круги и эллипсы. Для этих форм используется дальнейшее обобщение кривых B-сплайнов, известное как NURBS.
Кривые Безье и B-сплайн • Кривые Безье и B-сплайн используются для рисования и оценки гладких кривых, особенно в компьютерной графике и анимации. • B-сплайны считаются частным случаем кривых Безье. • B-Spline обеспечивает больший контроль и гибкость, чем кривые Безье. |
Построение контура кривой Безье
← →kingdom (2005-01-24 10:45) [0]
Привет всем!
Кто-нибудь занимался построение контура к кривой Безье?
Задача такая, дана кривая Безье 2 или 3 порядка, дано расстояние от кривой до контура.
Нужно построить контур из кривых Безье 2 и 3 порядка соответственно с заданной точностью.
Критерий точности можно выбра самому, главное чтобы он был разумным =)
Напомню, что контур это кривая расстояние между которой и исходной кривой константа.
Достаточно вычислить контур с одной стороны от исходной кривой.
Заранее всем спасибо!
← →
REA (2005-01-24 10:51) [1]
Сплайны рисовал, Безье не рисовал…
← →
MBo © (2005-01-24 11:52) [2]
Если имеется в виду не параллельный перенос кривой, а получение кривых, описывающих край «жирной линии», то эта задача не имеет корректного решения, т.е. эти кривые не являются кривым Безье.
Приближение — строим перпендикуляры нужной длины к кривой (с постоянным шагом по t или меняем шаг в зависимости от кривизны кривой), через полученные точки проводим какие-либо кубические сплайны (в зависимости от требуемой гладкости), переводим сплайны в базис полиномов Бернштейна.
← →
MBo © (2005-01-24 12:28) [3]
В дополнение: «плохими местами» будут те, где радиус кривизны кривой меньше офсета. По крайней мере, в точках, где эти величины совпадают, исходную кривую стоит порезать.
← →
REA (2005-01-24 12:57) [4]
А какая если не секрет предметная область?
← →
kingdom (2005-01-24 18:02) [5]
>MBo
Спасибо за ответ!
Не могу найти формулы кривизны для Кривой Безье
>REA
Пишу графическую библиотеку, нужно что-то типа StrokePath сделать
← →
MBo © (2005-01-25 08:05) [6]
>Не могу найти формулы кривизны для Кривой Безье
из дифф. 3/2
3/2
(первые и вторые производные по параметру t)
P.S. встречал упоминание о методе аппроксимации Tiller-Hanson — там, кажется, делают примерно так, как я описал, только сплайны не строят, сразу Безье по неким критериям.
Кроме того, глянь www.truetex.com, описание MetaFog.
← →
kingdom (2005-01-25 12:52) [7]
>MBo
Спасибо! Это мне очень поможет =)
Может у тебя есть ссылка на вывод этой формулы, а то у меня другая получалась.
← →
MBo © (2005-01-25 13:08) [8]
>у тебя есть ссылка на вывод этой формулы
Нет.
Примерно отсюда нужно исходить: кривизна по определению есть предел отношения угла поворота касательной к длине дуги, и
для малых углов Fi~Tan(Fi)=dy/dx
← →
MBo © (2005-01-25 13:42) [9]
вот как получается
k=dFi/dl=(ArcTan(Y»/X»))»/Sqrt(dX^2+dY^2)=(Y»/X»)»*ArcTan()»/Sqrt(dX^2+dY^2)=(Y»»X»-Y»X»»)/(X»)^2*(1/(1+(Y»/X»)^2)/Sqrt( dX^2+dY^2)=(Y»»X»-Y»X»»)/(dX^2+dY^2)^3/2
← →
kingdom (2005-01-25 14:17) [10]
Я нашел ошибку, производную неправильно взял,
спасибо!
Буду дальше разбираться =)
← →
kingdom (2005-01-25 16:57) [11]
Странная вещь получается. ..
..
Если разбить кривую пополам, то кривизна, например, в точке 0.0 для исходной и новой половинки не совпадает, она уменьшается =(
Как это можно объяснить?
← →
MBo © (2005-01-25 17:10) [12]
1. Не понял, какая точка 0.0 имеется в виду
2. Уверен, что кривую правильно разбиваешь?
← →
kingdom (2005-01-25 17:26) [13]
Подели кривую (q) на левую и правую половину (lq, rq)
q(0) = lq(0)
q(1) = rq(1)
кривизна q в точке 0 не равна кривизне lq в точке 0
← →
kingdom (2005-01-25 17:37) [14]
Короче, я тормозить начал под вечер, все нармально =)))
← →
MBo © (2005-01-25 18:15) [15]
Я попробовал — совпадает. Убедись, что правильно делишь(отрисовкой всех трех кривых) и покажи код вычисления кривизны.
Убедись, что правильно делишь(отрисовкой всех трех кривых) и покажи код вычисления кривизны.
← →
kingdom (2005-01-25 18:19) [16]
У меня осталася только один вопрос, как определить, что кривую надо разбить?
Пробую брать разницу кривизны в начале и в конце кривой. Если больше некоторого числа, то делить. Однако, на практике видно, что это не очень хороший вариант, появляется много делений на плавных участках.
← →
MBo © (2005-01-25 18:28) [17]
Тут без проб трудно посоветовать. пробеги по кривой, скажем, в 5-10 точках, оценивай кривизну. участки с большой кривизной еще подели
← →
kingdom (2005-01-25 18:36) [18]
Вот я и пробую ))
Вопрос в том какую метрику выбрать?
Экспериментировал с k(0) — k(1), плохо работает.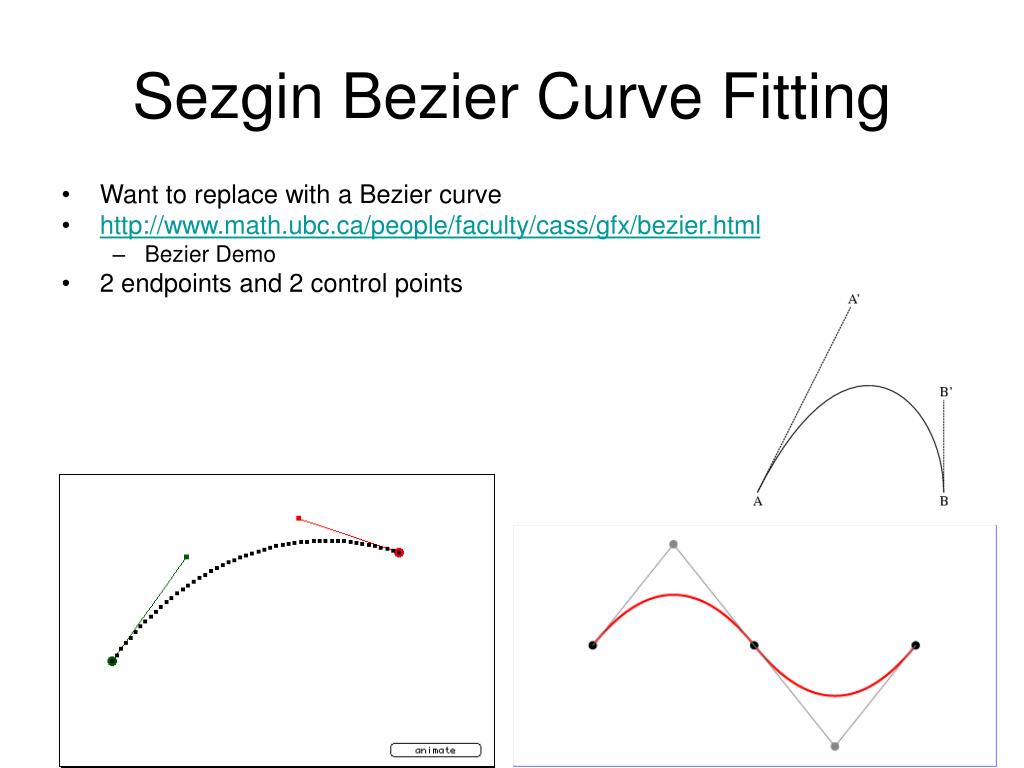
Я думаю есть метрика геометрически обоснованная, буду искать.
MBo спасибо, ты мне очень помог!
← →
Григорьев Антон © (2005-01-27 07:46) [19]
Можно подойти к этой проблеме с другого конца. Пусть для каждой точки кривой Безье мы постороили круг с центром в этой точке и радиусом, равным той самой константе, задающей расстояние от контура до кривой. Граница фигуры, которую составляют все эти круги, как раз и будет требуемым контуром.
Чтобы построить такую фигуру, нужно выполнить следующие действия:
1. Построить траекторию на основе кривой Безье (BeginPath/PolyBezier/EndPath).
2. Привести внутреннее представление траектории к ломаной, состоящей из отреков прямых (FlattenPath).
3. Получить координаты узлов этой ломаной (GetPath).
4. Пройтись по всем звеньям ломаной и с помощью LineDDA получить координаты всех промежуточных точек.
5. Для каждой из полученных точек создать регион в виде круга заданного радиуса (CreateEllipticRgn) и объединить все эти регионы в один (CombineRgn).
6. Построить контур полученного региона (FrameRgn). Всё, задача решена.
Метод работает медленно (особенно последний шаг), но даёт очень точные результаты для любой кривой.
Пример действий п. 1-4 можно посмотреть на http://www.delphikingdom.com/asp/viewitem.asp?catalogid=881
← →
kingdom (2005-01-27 15:47) [20]
>Григорьев Антон
Спасибо за ответ
Как ты правильно сказал, этот способ медленный и это не совсем то, что мне надо. Мне не надо рисовать контур, мне надо построить контур.
У меня получился такой алгоритм для кривых Безье 2 степени, берем исходную кривую и строим к ней кривую Безье, которая в точках 0 и 1 находится на заданном расстоянии от исходной и имеет такае же производные как у исходной.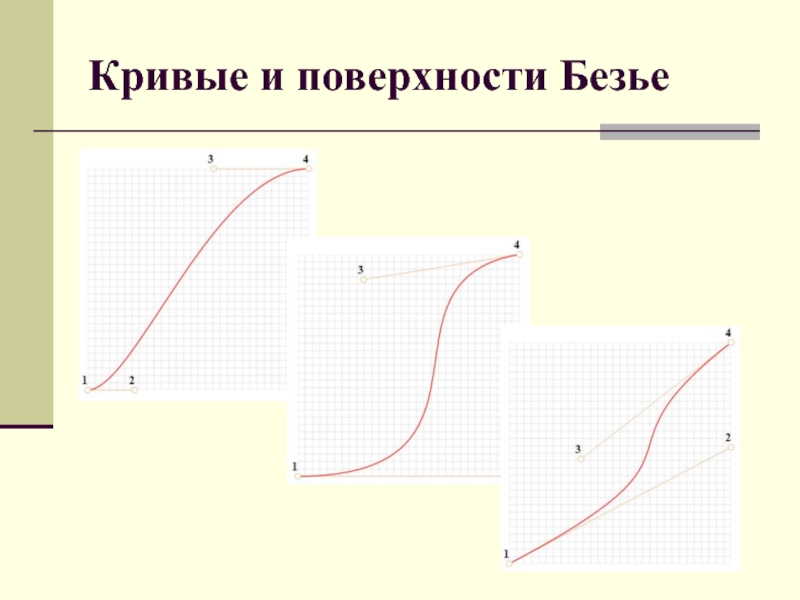 Такая кривая определяется однозначно. Расстояние между кривыми в точке 0.5 будет больше заданного, поэтому нужно иметь оценочную функцию, которая скажет велико ли отклонение. Если велико, то делим исходную кривую на две части и повторяем действия, иначе для данного участка исходной кривой контур найден.
Такая кривая определяется однозначно. Расстояние между кривыми в точке 0.5 будет больше заданного, поэтому нужно иметь оценочную функцию, которая скажет велико ли отклонение. Если велико, то делим исходную кривую на две части и повторяем действия, иначе для данного участка исходной кривой контур найден.
Вопрос в том, как выглядит эта оценочная функция?
Кривая Безье. Разберитесь в математике Безье… | Омар Афлак
Понимание математики кривых Безье
Кривые Безье часто используются в компьютерной графике, часто для создания гладких кривых, и тем не менее это очень простой инструмент. Если вы когда-либо использовали Photoshop, вы, возможно, наткнулись на инструмент под названием «Якорь», где вы можете ставить точки привязки и рисовать ими кривые… Да, это кривые Безье. Или, если вы использовали векторную графику, SVG, они тоже используют кривые Безье.Посмотрим, как это работает.
Для n + 1 точек (P0,…, Pn) называется контрольными точками , кривая Безье, определяемая этими точками, определяется как:
экв. 1
1Где B (t) — полином Бернштейна, а:
экв. 2Вы заметите, что этот многочлен Бернштейна очень похож на член k (th) в биномиальной формуле Ньютона, то есть:
экв.n = 1. Вот почему, если вы просуммируете все Bi до n , вы получите 1 . В любом случае. Квадратичная кривая Безье — это то, как мы называем кривую Безье с 3 контрольными точками, поскольку степень P (t) будет равна 2. Давайте вычислим кривую Безье для 3 контрольных точек и исследуем некоторые свойства, которые мы можем найти! Помните, экв. 1 соответствует n + 1 точек, поэтому в нашем случае n = 2.
Имейте в виду, что P (t) возвращает не число, а точку на кривой. Теперь нам просто нужно выбрать три контрольные точки и оценить кривую в диапазоне [0, 1] . Мы можем сделать это на Python довольно легко.
Мы можем сделать это на Python довольно легко.
Вы можете заметить, что кривая начинается и заканчивается в первой и последней контрольных точках. Этот результат будет верен для любого количества баллов. Поскольку t находится в диапазоне от 0 до 1 , мы можем доказать это, оценив P (t) при t = 0 и t = 1 .Используя экв. 1 :
Поскольку кривая идет от P0 до P2 , в этом случае P1 полностью определяет форму кривой . Перемещая P1 вокруг, вы можете кое-что заметить:
Кривая Безье в компьютерной графике | Примеры
Кривая Безье —Кривая Безье может быть определена как —
- Кривая Безье — параметрическая кривая, определяемая набором контрольных точек.

- Две точки — это концы кривой.
- Другие точки определяют форму кривой.
Концепция кривых Безье была дана Пьером Безье.
Пример кривой Безье —Следующая кривая является примером кривой Безье —
Здесь
- Эта кривая Безье определяется набором контрольных точек 0 , b 1 , b 2 и b 3 .
- Точки b 0 и b 3 являются концами кривой.
- Точки b 1 и b 2 определяют форму кривой.
Несколько важных свойств кривой Безье:
Свойство-01:Кривая Безье, называемая выпуклой частью многоугольника своих контрольных точек.
Property-02:- Кривая Безье обычно повторяет форму определяющего ее многоугольника.
- Первая и последняя точки кривой совпадают с первой и последней точками определяющего многоугольника.
Степень полинома, определяющего сегмент кривой, на единицу меньше, чем общее количество контрольных точек.
Степень = Количество контрольных точек — 1
Свойство-04:Порядок полинома, определяющего сегмент кривой, равен общему количеству контрольных точек.
Порядок = количество контрольных точек
Свойство-05:- Кривая Безье демонстрирует свойство уменьшения вариации.
- Это означает, что кривая не колеблется вокруг прямой линии чаще, чем определяющий многоугольник.
Кривая Безье параметрически представлена -
Здесь
- t — любой параметр, где 0 <= 1
- .
 P (t) = любая точка, лежащая на кривой Безье
P (t) = любая точка, лежащая на кривой Безье - B i = i th контрольная точка кривой Безье
- n = градус кривой
- J n, i (t) = Смешивание function = C (n, i) t i (1-t) ni где C (n, i) = n! / я! (н-я)!
- Кубическая кривая Безье — это кривая Безье со степенью 3.
- Общее количество контрольных точек в кубической кривой Безье составляет 4.
Следующая кривая является примером кубической кривой Безье —
Здесь ,
- Эта кривая определяется 4 контрольными точками b 0 , b 1 , b 2 и b 3 .
- Степень этой кривой равна 3.
- Итак, это кубическая кривая Безье.
Параметрическое уравнение кривой Безье —
Подставляя n = 3 для кубической кривой Безье
, мы получаемРасширяя приведенное выше уравнение, получаем-
P (t) = B 0 J 3,0 (t) + B 1 J 3,1 (t) + B 2 Дж 3,2 (т) + B 3 Дж 3,3 (т) ………. . (1)
. (1)
Now,
Используя (2), (3), (4) и (5) в (1), мы получаем-
P (t ) = B 0 (1-t) 3 + B 1 3t (1-t) 2 + B 2 3t 2 (1-t) + B 3 t 3
Это необходимое параметрическое уравнение для кубической кривой Безье.
Применение кривых Безье —Кривые Безье находят свое применение в следующих областях —
1.Компьютерная графика —- Кривые Безье широко используются в компьютерной графике для моделирования плавных кривых.
- Кривая полностью содержится в выпуклой оболочке своих контрольных точек.
- Итак, точки могут отображаться графически и использоваться для интуитивного управления кривой.
- Кривые Безье используются для контуров движения в анимационных приложениях, таких как Adobe Flash и synfig.

- Пользователи указывают желаемый путь в кривых Безье.
- Приложение создает необходимые рамки для перемещения объекта по траектории.
- Для 3D-анимации кривые Безье часто используются для определения 3D-контуров, а также 2D-кривых.
- Истинные шрифты используют составные кривые Безье, состоящие из квадратичных кривых Безье.
- Современные системы обработки изображений, такие как постскриптум, асимптоты и т. Д., Используют составные кривые Безье, состоящие из кубических кривых Безье для рисования изогнутых форм.
Дана кривая Безье с 4 контрольными точками. , B 1 [3 3], B 2 [6 3], B 3 [8 1]
Определите любые 5 точек, лежащих на кривой. Также нарисуйте грубый набросок кривой.
У нас-
- Данная кривая определяется 4 контрольными точками.
- Итак, данная кривая является кубической кривой Безье.
Параметрическое уравнение для кубической кривой Безье —
P (t) = B 0 (1-t) 3 + B 1 3t (1-t) 2 + B 2 3t 2 (1-t) + B 3 t 3
Замена контрольных точек B 0 , B 1 , B 2 и B 3 , получаем-
P (t) = [1 0] (1-t) 3 + [3 3] 3t (1-t) 2 + [6 3] 3t 2 (1 -t) + [8 1] t 3 …….. (1)
Теперь
Чтобы получить 5 точек, лежащих на кривой, предположим, что любые 5 значений t лежат в диапазоне 0 <= t <= 1.
Пусть 5 значений t равны 0, 0,2 , 0,5, 0,7, 1
Для t = 0:Подставляя t = 0 в (1), получаем —
P (0) = [1 0] (1-0) 3 + [3 3] 3 (0) (1-t) 2 + [6 3] 3 (0) 2 (1-0) + [8 1] (0) 3
P (0) = [1 0] + 0 + 0 + 0
P (0) = [1 0]
Для t = 0.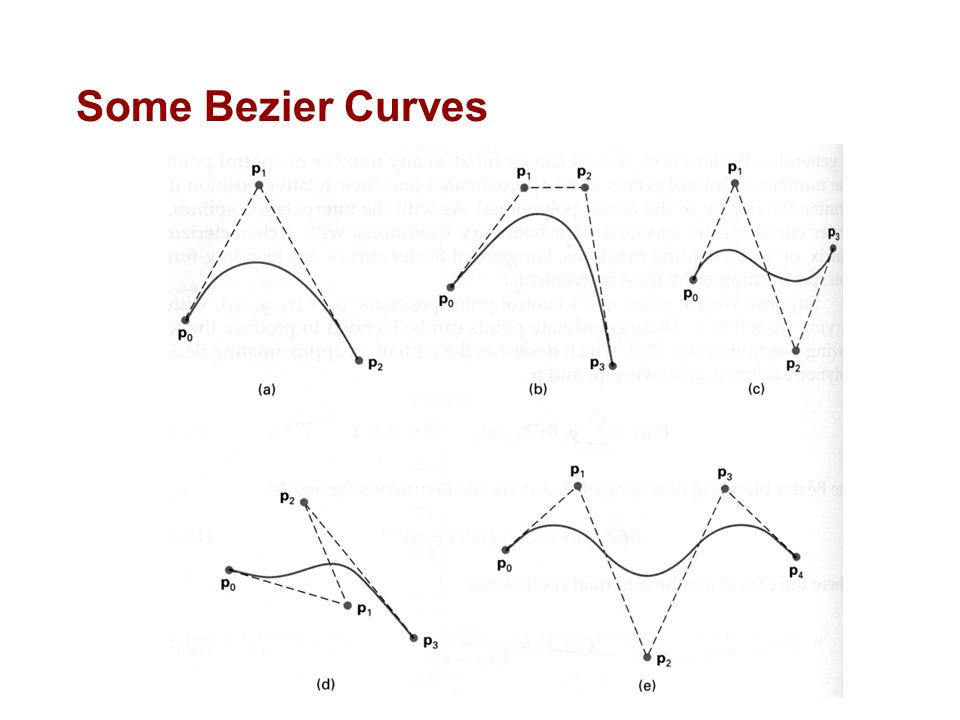 2:
2: Подставляя t = 0,2 в (1), мы получаем —
P (0,2) = [1 0] (1-0,2) 3 + [3 3] 3 (0,2) (1- 0,2) 2 + [6 3] 3 (0,2) 2 (1-0,2) + [8 1] (0,2) 3
P (0,2) = [1 0] (0,8) 3 + [3 3] 3 (0,2) (0,8) 2 + [6 3] 3 (0,2) 2 (0,8) + [8 1] (0,2) 3
P (0,2) = [1 0] x 0,512 + [3 3] x 3 x 0,2 x 0,64 + [6 3] x 3 x 0,04 x 0,8 + [8 1] x 0,008
P (0,2) = [1 0] x 0.512 + [3 3] x 0,384 + [6 3] x 0,096 + [8 1] x 0,008
P (0,2) = [0,512 0] + [1,152 1,152] + [0,576 0,288] + [0,064 0,008]
P (0,2) = [2,304 1,448]
Для t = 0,5:Подставляя t = 0,5 в (1), получаем-
P (0,5) = [1 0] (1- 0,5) 3 + [3 3] 3 (0,5) (1-0,5) 2 + [6 3] 3 (0,5) 2 (1-0,5) + [8 1] (0,5) 3
P (0,5) = [1 0] (0,5) 3 + [3 3] 3 (0.5) (0,5) 2 + [6 3] 3 (0,5) 2 (0,5) + [8 1] (0,5) 3
P (0,5) = [1 0] x 0,125 + [3 3] x 3 x 0,5 x 0,25 + [6 3] x 3 x 0,25 x 0,5 + [8 1] x 0,125
P (0,5) = [1 0] x 0,125 + [3 3] x 0,375 + [6 3 ] x 0,375 + [8 1] x 0,125
P (0,5) = [0,125 0] + [1,125 1,125] + [2,25 1,125] + [1 0,125]
P (0,5) = [4,5 2,375]
Для t = 0,7:Подставляя t = 0,7 в (1), получаем —
P (t) = [1 0] (1-t) 3 + [3 3] 3t ( 1-t) 2 + [6 3] 3t 2 (1-t) + [8 1] t 3
P (0. 7) = [1 0] (1-0,7) 3 + [3 3] 3 (0,7) (1-0,7) 2 + [6 3] 3 (0,7) 2 (1-0,7) + [8 1] (0,7) 3
7) = [1 0] (1-0,7) 3 + [3 3] 3 (0,7) (1-0,7) 2 + [6 3] 3 (0,7) 2 (1-0,7) + [8 1] (0,7) 3
P (0,7) = [1 0] (0,3) 3 + [3 3] 3 (0,7) (0,3) 2 + [6 3] 3 (0,7 ) 2 (0,3) + [8 1] (0,7) 3
P (0,7) = [1 0] x 0,027 + [3 3] x 3 x 0,7 x 0,09 + [6 3] x 3 x 0,49 x 0,3 + [8 1] x 0,343
P (0,7) = [1 0] x 0,027 + [3 3] x 0,189 + [6 3] x 0,441 + [8 1] x 0,343
P (0,7) = [0,027 0] + [0.567 0,567] + [2,646 1,323] + [2,744 0,343]
P (0,7) = [5,984 2,233]
Для t = 1:Подставляя t = 1 в (1), получаем —
P (1) = [1 0] (1-1) 3 + [3 3] 3 (1) (1-1) 2 + [6 3] 3 (1) 2 ( 1-1) + [8 1] (1) 3
P (1) = [1 0] x 0 + [3 3] x 3 x 1 x 0 + [6 3] x 3 x 1 x 0 + [8 1] x 1
P (1) = 0 + 0 + 0 + [8 1]
P (1) = [8 1]
Ниже приведен примерный эскиз кривой —
Чтобы лучше понять кривые Безье в компьютерной графике,
Посмотрите эту видеолекцию
Получите больше заметок и других учебных материалов по Computer Graphics .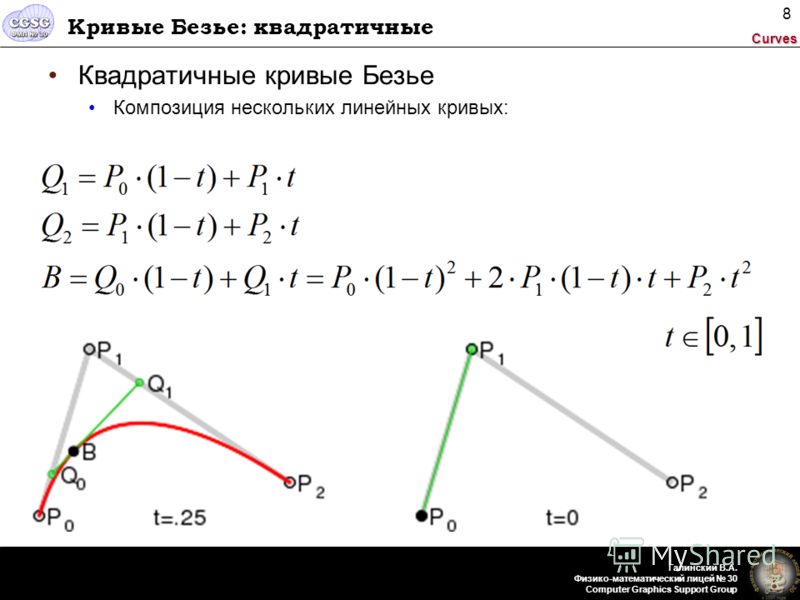
Смотрите видеолекции на нашем YouTube-канале LearnVidFun.
Резюме
Название статьи
Кривая Безье в компьютерной графике | Примеры
Описание
Кривая Безье в компьютерной графике — это параметрическая кривая, определяемая набором контрольных точек. Пример и свойства кривой Безье. Кубическая кривая Безье — это кривая Безье степени 3. Задача о кривой Безье.
Автор
Акшай Сингхал
Имя издателя
Gate Vidyalay
Логотип издателя
Создание кривых Безье — ArcGIS Pro | Документация
На панели «Создание объектов» инструменты построения линейных и полигональных объектов включают метод построения для создания кривых Безье.Он доступен на панели инструментов построения при создании объекта.
Кривые Безье — это нелинейные сегменты, определяемые четырьмя контрольными точками. Первые две контрольные точки определяют касательную в исходной точке. Вторая пара контрольных точек определяет касательную в точке To.
Длина касательных линий и положение контрольных точек определяют форму кривой. Каждая последующая пара контрольных точек, которую вы рисуете, создает кривую, касательную к кривой, определенной предыдущей парой контрольных точек.
- На панели «Каталог» выполните одно из следующих действий, чтобы добавить на карту слой полилинии или полигона:
- Разверните «Базы данных», разверните базу данных, содержащую ваши данные, и перетащите класс пространственных объектов на карту.
- Щелкните правой кнопкой мыши базу данных по умолчанию и создайте класс пространственных объектов полилинии или полигона.
Создание класса пространственных объектов или перетаскивание его на карту добавляет слой к текущей карте и создает шаблон пространственных объектов с настройками по умолчанию.
- На вкладке «Правка» в группе «Привязка» включите параметры привязки.
Совет:
Вы можете нажать и удерживать пробел, чтобы временно отключить привязку во время рисования объекта.
- Если вы работаете с объектами с поддержкой z, на вкладке «Правка» в группе «Высота» выберите способ добавления значений z к вашим объектам.
- На вкладке «Правка» в группе «Компоненты» нажмите «Создать».
Появится панель «Создать компоненты».
- На панели щелкните шаблон линейного или полигонального объекта.
- Чтобы создать вершину линии, щелкните «Линия».
- Чтобы создать вершину многоугольника, щелкните «Многоугольник».
Панель инструментов построения появляется внизу карты.
- На панели инструментов построения щелкните Кривая Безье.
- Нарисуйте первые две контрольные точки, определяющие касательную в исходной точке.
- Щелкните карту.
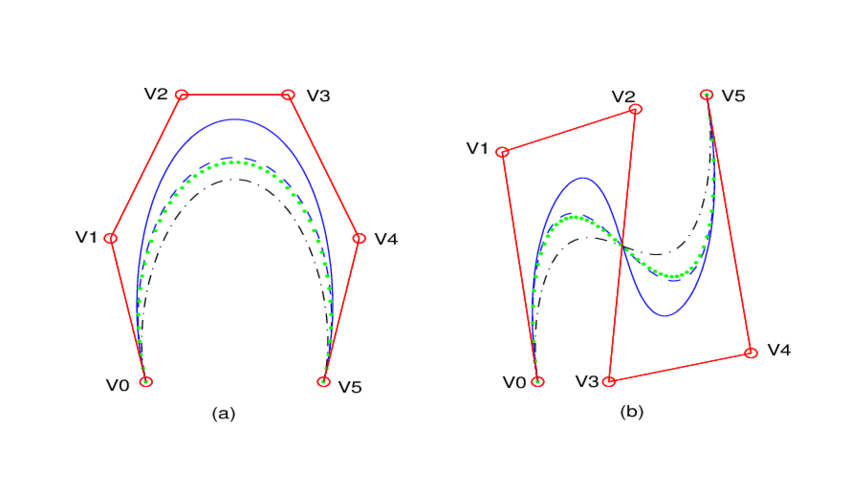
- Переместите указатель и щелкните карту.
- Щелкните карту.
- Переместите указатель и нарисуйте следующие две контрольные точки, которые определяют касательную в точке «До».
- Щелкните карту.
- Переместите указатель и щелкните карту.
Чтобы создать сплайн, продолжайте рисовать пары контрольных точек. Каждая последующая пара контрольных точек создает кривую, касательную к кривой, определенной предыдущей парой контрольных точек.
- Чтобы продолжить создание других сегментов, используйте инструменты на панели инструментов построения.
- Чтобы завершить функцию, щелкните правой кнопкой мыши и выберите «Готово» или нажмите клавишу F2.
Отзыв по этой теме?
Инструмент кривой Безье— Руководство пользователя Pyware 3D
Инструмент Кривая Безье создаст кривую Безье.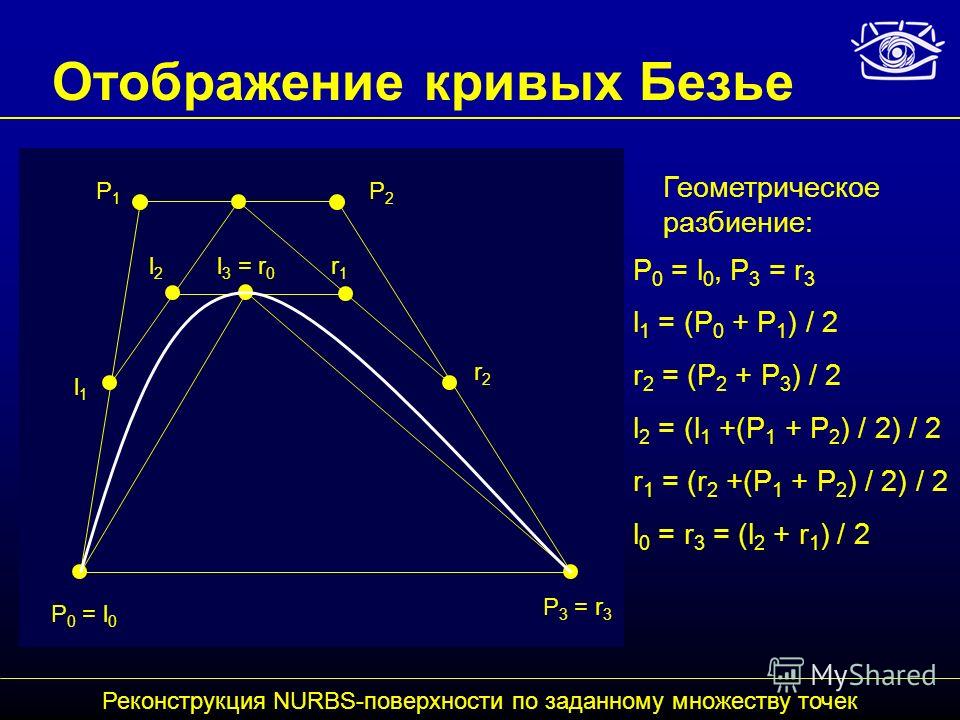 Думайте об инструменте «Кривая Безье» как о более сложном инструменте «Кривая» с большим контролем над кривизной, особенно в конечных точках.
Думайте об инструменте «Кривая Безье» как о более сложном инструменте «Кривая» с большим контролем над кривизной, особенно в конечных точках.
Для НОВЫХ исполнителей установите Red и Yellow Anchors на Дорожке счета на счет, при котором вы хотите рисовать кривую. Чтобы преобразовать СУЩЕСТВУЮЩИХ исполнителей в кривую, переместите Red Anchor на счетчик, где выбранные исполнители должны «попасть» в форму кривой. Переместите Yellow Anchor на начальный счет перехода в новую кривую.Обычно это предыдущий набор в упражнении. Выберите существующих исполнителей, которые будут двигаться по кривой, с помощью инструмента выделения. См. Обзор инструментов рисования для получения дополнительных сведений о новых исполнителях и переходе существующих исполнителей.
Если щелкнуть инструмент Кривая Безье , откроется панель управления Кривая Безье .
Рисование кривой Безье
Кривая строится щелчком по двум или более точкам на отображении поля.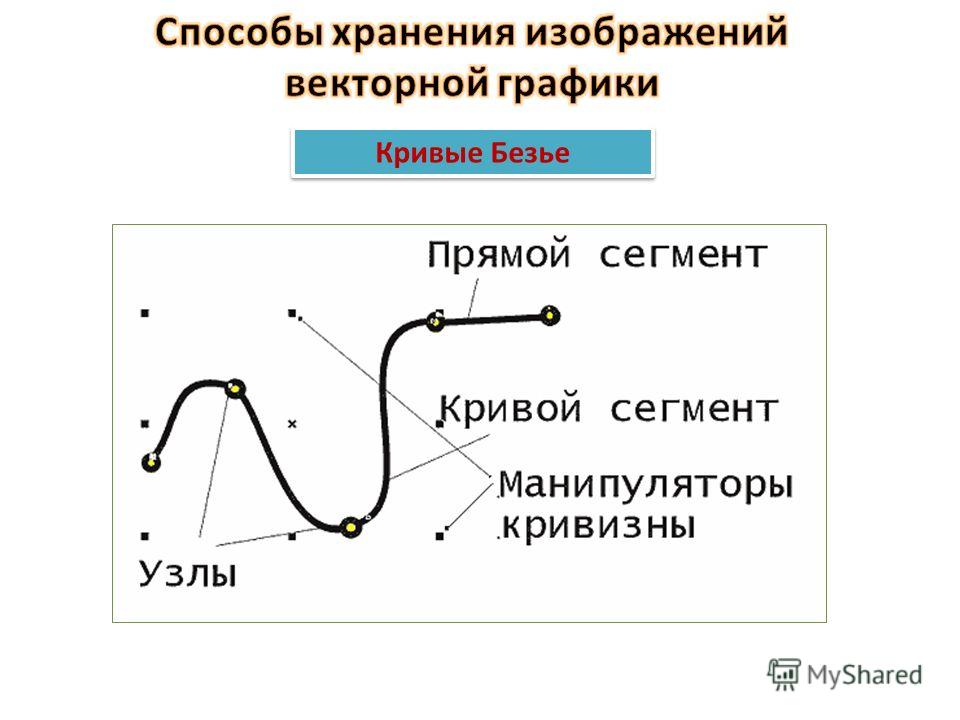 Первый щелчок по полю — это первая конечная точка кривой. При втором щелчке по полю сначала кривая отображается в виде линии. На концах строки находится ручек редактирования .
Первый щелчок по полю — это первая конечная точка кривой. При втором щелчке по полю сначала кривая отображается в виде линии. На концах строки находится ручек редактирования .
Перетаскивание красного квадрата на ручке редактирования переместит конечные точки.
Перетаскивание красного круга, выходящего за квадратную ручку, придаст форму кривой.
Ввод интервала в поле Interval заблокирует интервал, и форма будет поддерживать интервал, пока вы перемещаете его -маркеры редактирования на .Поскольку интервал между позициями заблокирован, форма будет увеличиваться или уменьшаться за счет изменения количества позиций в форме.
Смешанные интервалы также вводятся нажатием кнопки. Эта опция позволит вам иметь разные интервалы в одной форме. Смешанные интервалы чрезвычайно полезны при построении диаграмм для больших инструментов или инструментов, которые расположены близко друг к другу, но различаются по размеру (например, линии барабанов).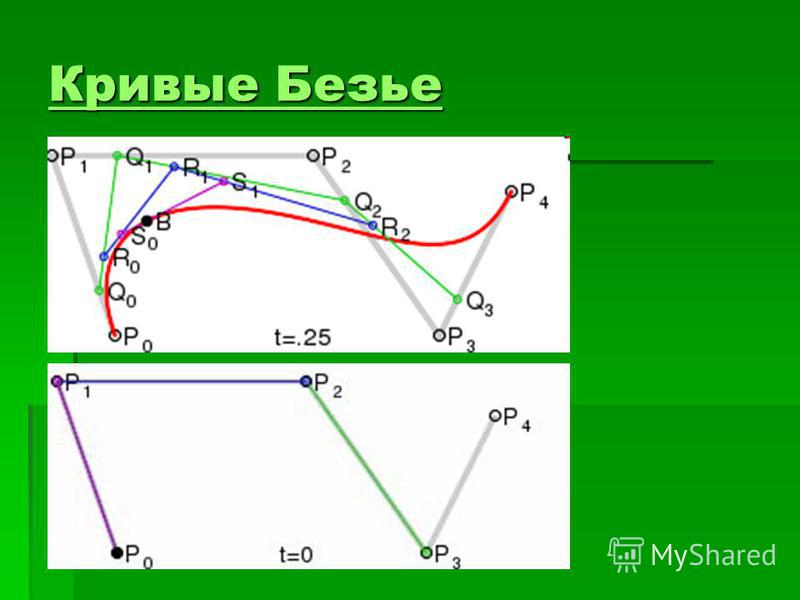
Чтобы создать смешанный интервал , введите значение интервала, затем «x» и количество позиций в этом интервале.Например, форма с 5 позициями с интервалом в 3 шага, за которыми следуют 10 позиций с интервалом в 2 шага, заканчивающаяся 5 позициями с интервалом в 3 шага, будет введена следующим образом:
5 × 3,10 × 2,5 × 3
Смешанные интервалы можно ввести до или после создания формы, но необходимо ввести до Принять форму.
Многие параметры панели управления Кривая Безье точно такие же, как параметры в инструменте «Линия».Обратитесь к инструменту Line для получения подробной информации о Clone , Alignment , Symbol , Color , Editing Handles и Reposition Handles . См. «Соответствующие строки» для объяснения функций Matching Lines .
Мы не можем найти эту страницу
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$ select.selected.display}}
LANGUAGE}}
{{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}границ | Необходимые и достаточные условия для выражения квадратичных рациональных кривых Безье
1.
 Введение
ВведениеКривые Безье находят широкое применение в компьютерном геометрическом проектировании, так как они используются для получения точно описанных точек вдоль заданной кривой [1].По сравнению с другими методами, такими как французская кривая, подходы на основе Безье более доступны с точки зрения вычислений и надежны. Кроме того, к преимуществам кривой Безье в геометрическом дизайне можно отнести ее простую, но понятную математическую функцию [2]. Например, он может включать как конические сечения, так и параметрические кубические кривые в качестве частных случаев [3]. Таким образом, можно одновременно работать с двумя разными кривыми, используя одну уникальную вычислительную процедуру. Некоторые предварительные исследования и применения кривых Безье можно найти в Lu et al.[4], Ли [5] и Хан [6].
В этой статье, чтобы лучше понять основные характеристики кривых Безье, мы проводим некоторые фундаментальные исследования. В частности, мы обсуждаем необходимые и достаточные условия для представления шести различных основных форм, включая точку, отрезок прямой, параболу, эллиптическую дугу, дугу окружности и гиперболу, с использованием кривых Безье [7, 8]. Эти результаты играют фундаментальную роль в формулировании формы и могут помочь в облегчении любого последующего компьютерного геометрического проектирования.
Эти результаты играют фундаментальную роль в формулировании формы и могут помочь в облегчении любого последующего компьютерного геометрического проектирования.
Для начала введем математическую модель квадратичной рациональной кривой Безье [1].
Определение 1 . Квадратичная рациональная кривая Безье определяется следующим образом:
p (t) = (1 − t) 2ω0P0 + 2t (1 − t) ω1P1 + t2ω2P2 (1 − t) 2ω0 + 2t (1 − t) ω1 + t2ω2, t∈ [0,1], (1)где
t = ω0μω0μ + ω2 (1-μ), μ∈ [0,1], (2)и ω 0 и ω 2 не являются нулевыми значениями одновременно .
Монотонность формулы (1.2) обсуждается ниже. Пусть μ 1 ∈ [0, 1], μ 2 ∈ [0, 1] и μ 1 ≤ μ 2 . Соответственно, в случае μ 1 = 0 имеем:
t1 = ω0μ1ω0μ1 + ω2 (1-μ1) = 0. (3) Обратите внимание, что 1 ≥ μ 2 > μ 1 ≥ 0 и t2 = ω0μ2ω0μ2 + ω2 (1-μ2) ≥0; тогда легко получить t 2 ≥ t 1 = 0.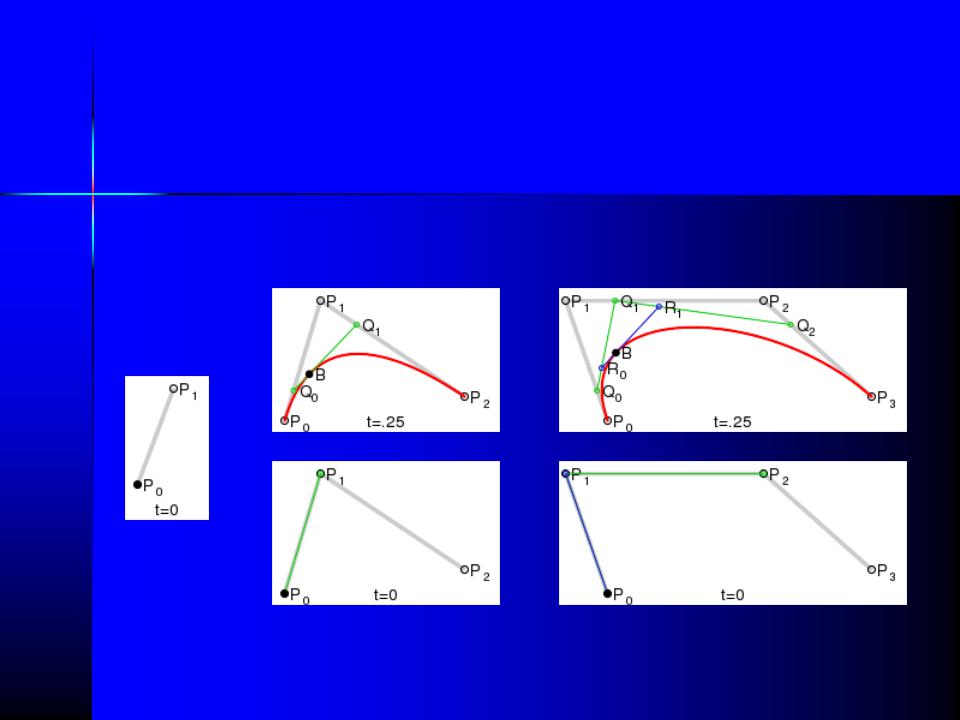
В случае μ 1 ≠ 0 и μ 2 ≠ 0 согласно формуле (1.2) имеем:
t1t2 = ω0μ1ω0μ1 + ω2 (1 − μ1) / ω0μ2ω0μ2 + ω2 (1 − μ2) = (ω0 + ω2 (1μ2−1)) / (ω0 + ω2 (1μ1−1)) ≤1. (4)Другими словами, мы имеем вывод, что t монотонно возрастает [9–11]. Кроме того, если применить линейное преобразование к формуле (1.1), легко узнать
p (μ) = ω0ω2 (1 − μ) 2P0 + 2ω0ω2ω1μ (1 − μ) P1 + ω0ω2μ2P2ω0ω2 (1 − μ) 2 + 2ω0ω2ω1μ (1 − μ) + ω0ω2μ2 = ((1 − μ) 2 Ρ0 + 2ω12ω0ω2μ (1 −μ) Ρ1 + μ2Ρ2) / ((1 − μ) 2 + 2ω12ω0ω2μ (1 − μ) + μ2). (5)Пусть ω = ω12ω0ω2 и заменим μ на t в стандартной форме квадратичной рациональной кривой Безье.С этой целью у нас есть упрощенная версия квадратичной рациональной кривой Безье, которая выражается следующим образом:
p (t) = (1-t) 2P0 + 2ωt (1-t) P1 + t2P2 (1-t) 2 + 2ωt (1-t) + t2. (6)2. Достаточные и необходимые условия для вырождения квадратичной рациональной кривой Безье в точку
Теорема 1 . Квадратичная рациональная кривая Безье вырождается в точку тогда и только тогда, когда три контрольные точки P 0 , P 1 , P 2 совпадают с .
Квадратичная рациональная кривая Безье вырождается в точку тогда и только тогда, когда три контрольные точки P 0 , P 1 , P 2 совпадают с .
Доказательство . Предположим, что квадратичная рациональная кривая Безье вырождается в точку P A . То есть
p (t) = (1-t) 2P0 + 2ωt (1-t) P1 + t2P2 (1-t) 2 + 2ωt (1-t) + t2 = PA⇔ (1-t) 2 (P0-PA) + 2t (1-t) ω (P1-PA) + t2 (P2-PA) = 0. (7) Как видно из формулы (7), при t ∈ (0, 1) имеем (1- t ) 2 ≠ 0, t 2 ≠ 0, 2 t (1- t ) ≠ 0, поэтому P 0 = P A , P 1 = P A , P П А .То есть, когда квадратичная рациональная кривая Безье вырождается в точку, P 0 , P 1 , P 2 являются той же точкой P A .
С другой стороны, когда совпадают три контрольные точки (скажем, одна и та же точка P A ), мы знаем, что:
p (t) = (1-t) 2PA + 2t (1-t) ωPA + t2PA (1-t) 2 + 2t (1-t) ω + t2 = PA. (8)Как видно из формулы (8), когда совпадают три контрольные точки P 0 , P 1 , P 2 , квадратичная рациональная кривая Безье вырождается в точку [12, 13 ].
Алгоритм 1 : вырождение квадратичной рациональной кривой Безье в точку
3. Необходимые и достаточные условия деградации квадратичной рациональной кривой Безье в линейное сечение
Теорема 2 . Квадратичная рациональная кривая Безье вырождается в отрезок прямой тогда и только тогда, когда контрольные точки P 0 , P 2 не совпадают, весовой коэффициент ω = 0 или контрольная точка P 1 находится на отрезке [14–16].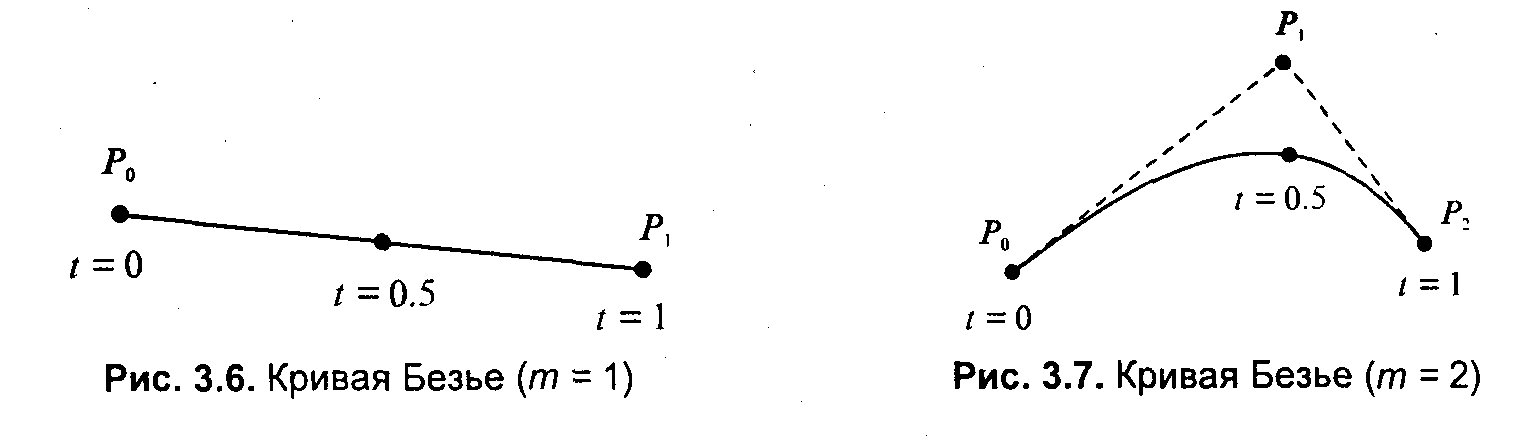
Доказательство . Во-первых, мы предполагаем, что одна точка имеет две координаты; в качестве альтернативы имеем P 0 = ( x 0 , y 0 ), P 1 = ( x 1 , y 1 и P 2 = ( x 2 , y 2 ). Таким образом, для произвольной точки p ( t ) = ( x, y ), согласно Формуле (6) легко получить:
х = (1-t) 2×0 + 2t (1-t) ωx1 + t2x2 (1-t) 2 + 2t (1-t) ω + t2, y = (1-t) 2y0 + 2t (1-t) ωy1 + t2y2 (1-t) 2 + 2t (1-t) ω + t2, (9)С другой стороны, общая форма линейной функции может быть выражена как: y = ax + b , где a , а b — константа [17].Затем, подставляя x и y с помощью формулы (12), мы можем получить:
(1-t) 2y0 + 2t (1-t) ωy1 + t2y2 (1-t) 2 + 2t (1-t) ω + t2 = a (1-t) 2×0 + 2t (1-t) ωx1 + t2x2 (1-t) 2 + 2t (1-t) ω + t2 + b, (10)Если упростить приведенную выше формулу, легко узнать:
(y0-ax0-b + y2-ax2-b-2y1ω + 2ax1ω + 2bω) t2 (11) -2 (y0-ax0-b-y1ω + ax1ω + bω) т + y0-ax0-b = 0.
Во-первых, мы предполагаем, что одна точка имеет две координаты; в качестве альтернативы имеем P 0 = ( x 0 , y 0 ), P 1 = ( x 1 , y 1 и P 2 = ( x 2 , y 2 ).Таким образом, для произвольной точки p ( t ) = ( x, y ), согласно Формуле (6) легко получить:
х = (1-t) 2×0 + 2t (1-t) ωx1 + t2x2 (1-t) 2 + 2t (1-t) ω + t2, y = (1-t) 2y0 + 2t (1-t) ωy1 + t2y2 (1-t) 2 + 2t (1-t) ω + t2, (12)Теперь контрольные точки P 0 и P 2 являются первой и последней точками кривой Безье. Поскольку все они находятся на кривой Безье, они также будут на прямой [18–20]. В качестве альтернативы у нас есть:
y0 = ax0 + b, y2 = ax2 + b.(13)Следовательно, формула (11) дополнительно упрощается:
(y1-ax1-b) (ωt-ωt2) = 0. (14)Далее формула (14) анализируется в следующих аспектах:
1. Если контрольная точка P 1 также находится на кривой Безье (или на прямой), то y 1 — ax 1 — b = 0, и формула (14) явно выполняется.
Если контрольная точка P 1 также находится на кривой Безье (или на прямой), то y 1 — ax 1 — b = 0, и формула (14) явно выполняется.
2. Если контрольная точка P 1 не находится на кривой Безье (или не на прямой), то y 1 — ax 1 — b ≠ 0, и Формулу (14) можно упростить до
Следовательно, когда t ∈ [0, 1], для выполнения формулы (15) имеем ω = 0.
Таким образом, доказано, что, когда квадратичная рациональная кривая Безье вырождается в отрезок прямой, выполняются два условия: (1) весовой коэффициент ω = 0 или (2) контрольная точка P 1 равна на отрезке с контрольной точкой P 0 , P 2 в качестве конечной точки. Ниже мы обсудим эти два условия отдельно.
1. Согласно формуле (6) при весовом коэффициенте ω = 0 имеем:
p (t) = (1-t) 2P0 + 2ωt (1-t) P1 + t2P2 (1-t) 2 + 2ωt (1-t) + t2 = (1-t) 2P0 + t2P2 (1-t) 2 + t2, (16)и
Икс = (1-t) 2×0 + t2x2 (1-t) 2 + t2 = (1-t) 2×0 (1-t) 2 + t2 + t2x2 (1-t) 2 + t2.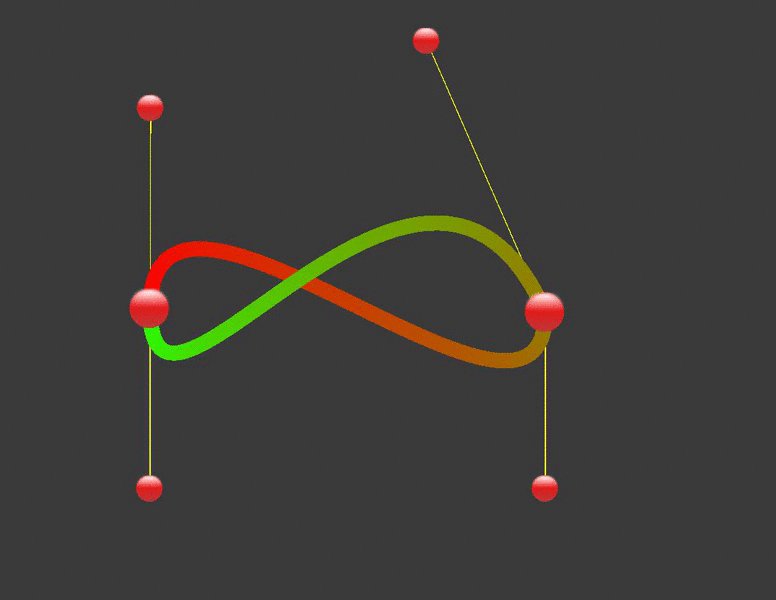 (17)
y = (1-t) 2y0 + t2y2 (1-t) 2 + t2 = (1-t) 2y0 (1-t) 2 + t2 + t2y2 (1-t) 2 + t2. (18)
(17)
y = (1-t) 2y0 + t2y2 (1-t) 2 + t2 = (1-t) 2y0 (1-t) 2 + t2 + t2y2 (1-t) 2 + t2. (18)Для упрощения процесса расчета допустим, что:
α = (1-t) 2 (1-t) 2 + t2. (19)и
1-α знак равно t2 (1-t) 2 + t2. (20)Теперь имеет место следующая формула:
x = αx0 + (1-α) x2 → x-x2 = α (x0-x2). (21) y = αy0 + (1-α) y2 → y-y2 = α (y0-y2). (22)В качестве контрольных точек P 0 , P 2 не совпадают, x 0 ≠ x 2 , y 0 ≠ y
α = y-y2y0-y2 = x-x2x0-x2 (23) yy0-y2-xx0-x2 = y2y0-y2-x2x0-x2, (24), где x 0 , x 2 , y 0 , y 2 — константы.Мы предполагаем, что 1y0-y2 = A, 1×0-x2 = B, y2y0-y2-x2x0-x2 = C (то есть A, B, C — все константы). Соответственно, мы знаем, что Ay — Bx = C — это отрезок прямой [21].
2. Пусть условная контрольная точка P 1 будет конечной точкой (на отрезке прямой с контрольными точками P 0 и P 2 ) [22]; таким образом, видно, что:
P1 = (1-v) P0 + vP2, v∈ [0,1], (25)Формулу (25) можно заменить Формулой (6), чтобы получить:
p (t) = (1 − t) 2 + 2t (1 − t) ω (1 − v) (1 − t) 2 + 2t (1 − t) ω + t2P0 + (2t (1 − t) ωv + t2 (1 — t) 2 + 2t (1 — t) ω + t2P2. (26)
(26)Затем устанавливаем:
u = (2t (1 − t) ωv + t2 (1 − t) 2 + 2t (1 − t) ω + t2. (27)Сравнивая формулу (26) с формулой (27), легко найти, что
p (t) = (1-u) P0 + uP2. (28)В заключение, формула (28) является параметрической формулой отрезка прямой. Когда контрольная точка P 1 находится на отрезке прямой с контрольной точкой ( P 0 , P 2 ) в качестве конечной точки, формулу (26) можно записать как параметрическую формулу отрезка формулы (28).Таким образом, доказано, что он вырождается в отрезок [23, 24].
Алгоритм 2 : вырождение квадратичной рациональной кривой Безье в линейный участок
Алгоритм 3 : вырождение квадратичной рациональной кривой Безье в линейный участок
4. Необходимые и достаточные условия квадратичной рациональной кривой Безье для представления сечения дуги
Теорема 3 . Квадратичные рациональные кривые Безье можно использовать для представления дуги тогда и только тогда, когда | P 0 P 1 | = | P 2 P 1 | и 0 ≤ ω ≤ 1 [25].
Доказательство . Уравнение окружности, проходящей через три коллинеарных точки Q i ( x i , y i ), ( i = 1, 2, 3), на прямоугольной координатной плоскости это:
| x2 + y2xy1x02 + y02x0y01x12 + y12x1y11x22 + y22x2y21 | = 0. (29)Учитывая три точки, которые не лежат на одной прямой, имеем:
P0 (x0, y0,0) = (- a, 0,0), A (xA, yA, 0), P2 (x2, y2,0) = (a, 0,0). (30)Кривая дуги начинается от точки P 0 и проходит через точку A до точки P 2 .Теперь найдем еще одну контрольную вершину P 1 . Для этого P 0 , A , P 2 подставляем в трехточечное уравнение общего круга 29, и мы получаем
| x2 + y2xy1x02 + y02x0y01xA2 + yA2xAyA1x22 + y22x2y21 | = 0. (31) Из формулы (30) к формуле (31) мы можем найти, что x 0 = — a, y 0 = 0, x 2 = a, y 2 = 0. Кроме того, раскрывая определитель 31 в первой строке, получаем
Кроме того, раскрывая определитель 31 в первой строке, получаем
Из них
| −a010yA1a01 | = −2ayA, | a201yA2yA1a201 | = 0, | a2 − a1yA201a2a1 | = −a3 + ayA2 + ayA2 − a3, | a2 − a0yA20yAa2a0 | = −a3yA − a3yA. (33)Наконец, приведенную выше формулу можно упростить следующим образом:
(-2ayA) (x2 + y2) + y (-a3 + 2ayA2-a3) + 2a3yA = 0.(34)Поскольку y A ≠ 0, легко узнать
x2 + (y + a2-yA22yA) 2 = a2 + (a2-yA2) 24yA2. (35)С другой стороны, поскольку x A = 0, мы можем добавить x A , чтобы получить
x2 + (y + a2- (xA2 + yA2) 2yA) 2 = a2 + (a2- (xA2 + yA2)) 24yA2. (36)Обобщая приведенную выше формулу, координаты центра окружности O равны:
xO = 0, yO = a2- (xA2 + yA2) 2yA. (37)Радиус круга равен:
г = а2 + (а2- (хА2 + уА2)) 24уА2.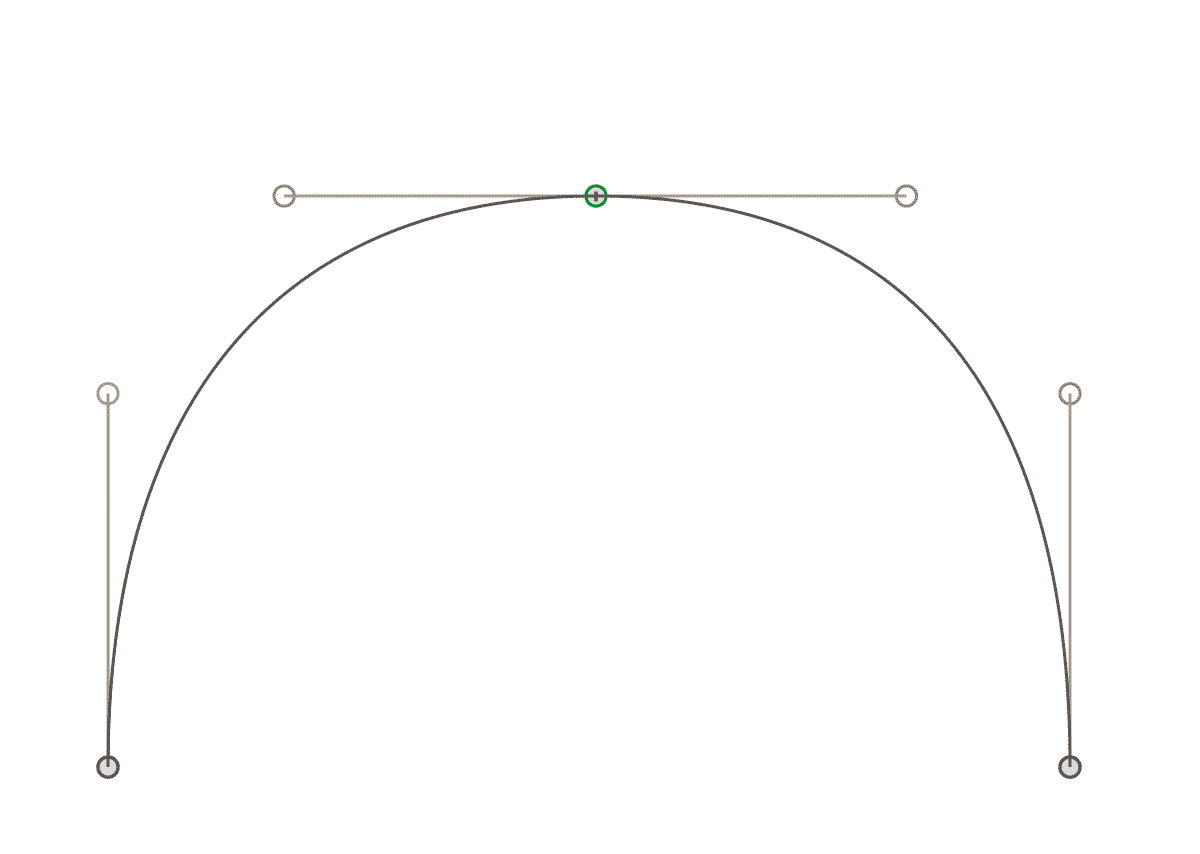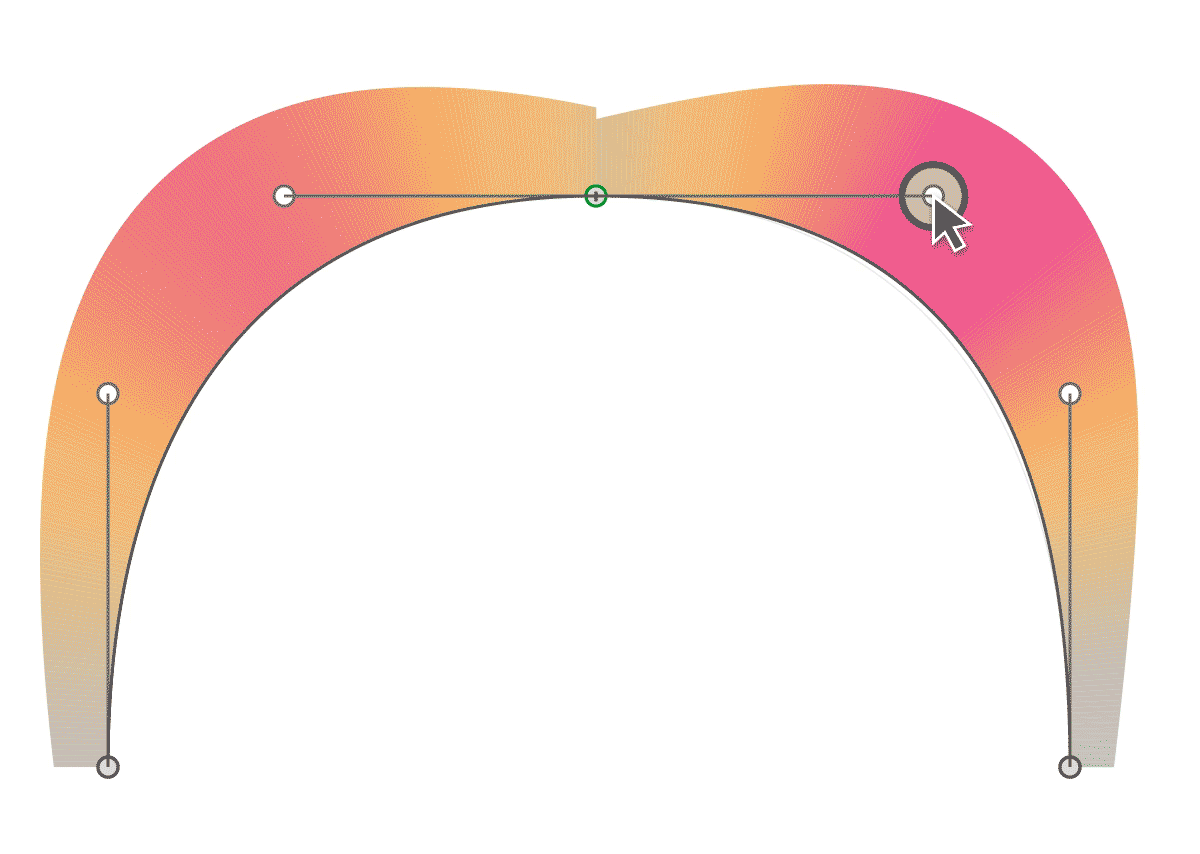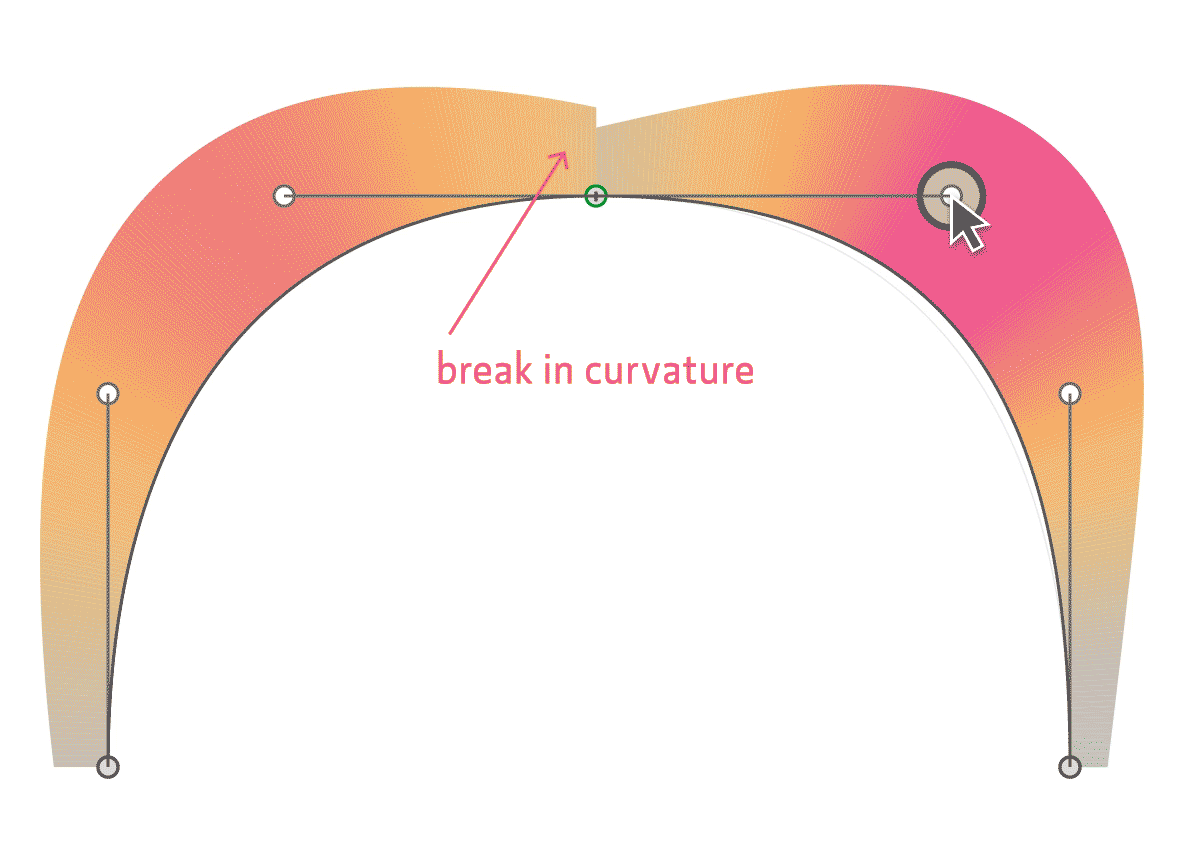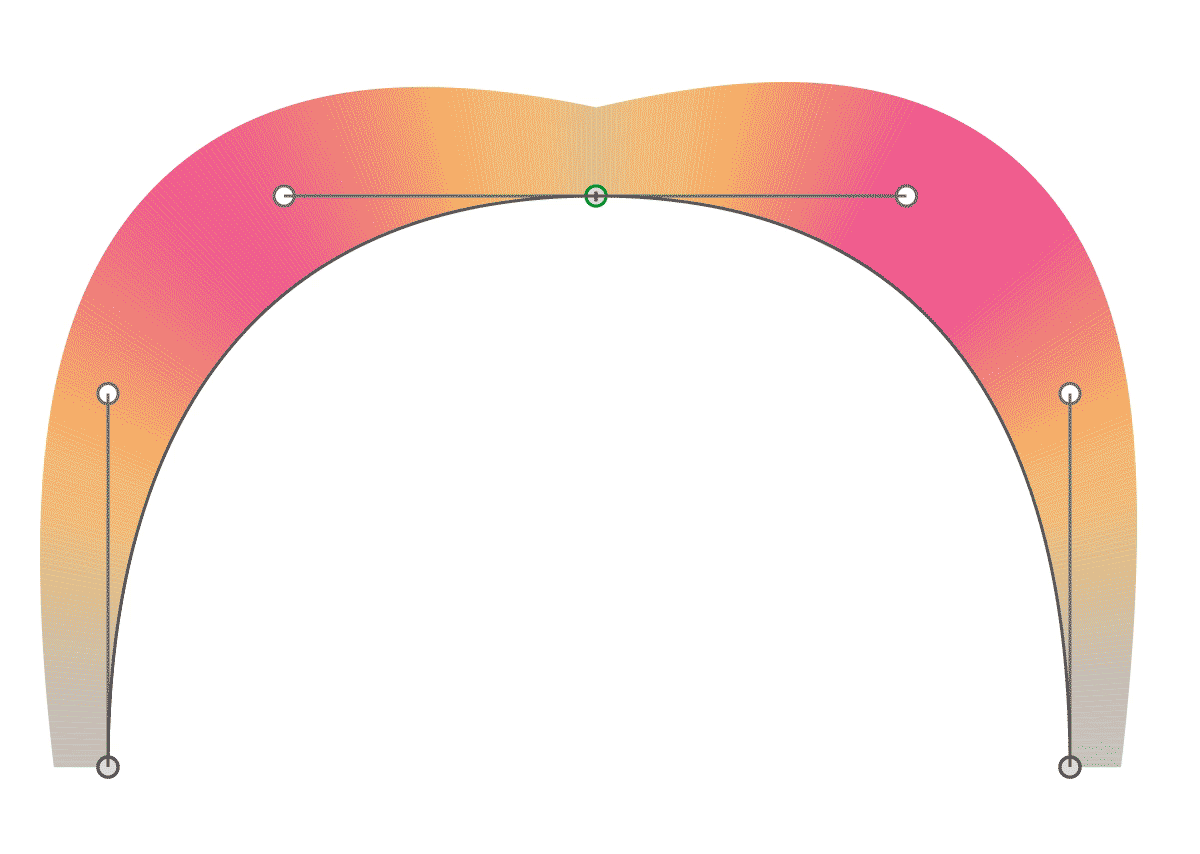 (38)
(38)Вертикальные линии OP 0 и OP 2 проходят от точек P 0 и P 2 соответственно. Согласно симметрии, если две вертикальные линии пересекаются с осью Y в точке P 1 , то точка P 1 является контрольной вершиной дугообразной кривой. То есть
y1 = 2a2yAa2- (xA2 + yA2). (39)Соответственно, координаты точки P 1 равны:
x1 = 0, y1 = 2a2yAa2- (xA2 + yA2).(40)Из определения кривой Безье в формуле (1) имеем:
x (t) = (1-t) 2ω0x0 + 2t (1-t) ω1×1 + t2ω2×2 (1-t) 2ω0 + 2t (1-t) ω1 + t2ω2, y (t) = (1-t) 2ω0y0 + 2t (1-t) ω1y1 + t2ω2y2 (1-t) 2ω0 + 2t (1-t) ω1 + t2ω2. (41)Чтобы упростить формулу (41), мы дополнительно вводим квадратичную базисную функцию Бернштейна ( B i , 2 ( t )), которая может быть выражена следующим образом:
B0,2 (t) = (1-t) 2, B1,2 (t) = 2t (1-t), B2,2 (t) = t2. (42)
(42)Таким образом, формулу (41) можно переписать, применив B i , 2 ( t ) в следующем формате:
x (t) = — aω0B0,2 (t) + aω2B2,2 (t) ω0B0,2 (t) + ω1B1,2 (t) + ω2B2,2 (t), y (t) = 2t (1-t ) ω1y1ω0B0,2 (t) + ω1B1,2 (t) + ω2B2,2 (t).(43)С другой стороны, обратите внимание, что стандартное уравнение кривой дуги окружности можно оценить как
x2 (t) + (y (t) + acotθ) 2 = a2 / sin2θ. (44)Следовательно, подставляя формулы (43) в уравнение (44), получают следующие результаты:
(−aω0B0,2 (t) + aω2B2,2 (t) ω0B0,2 (t) + ω1B1,2 (t) + ω2B2,2 (t)) 2 + (ω1y1B1,2 (t) ω0B0,2 ( t) + ω1B1,2 (t) + ω2B2,2 (t) + acotθ) 2 = a2sin2θ, (45)Обратите внимание, что
a2sin2θ-a2cot2θ = a2. (46)Таким образом, формулу (45) можно дополнительно упростить до
a2ω02B0,22 (t) + a2ω22B2,22 (t) −2a2ω0ω2B0,2 (t) B2,2 (t) + ω12y12B1,22 (t) + (2ω1y1B1,2 (t) acotθ (ω0B0,2 (t) + ω1B1,2 (t) + ω2B2,2 (t)) = a2 (ω0B0,2 (t) + ω1B1,2 (t) + ω2B2,2 (t)) 2 (47)Кроме того, согласно формуле (38) и формуле (40), мы можем иметь
y1cotθ = 2a2yAa2- (xA2 + yA2) × (a2- (xA2 + yA2)) 2ayA = a, (48), а затем
(y12 + a2) ω12B1,22 (t) -4a2ω0ω2B0,2 (t) B2,2 (t) = 0. (49)
(49)Опять же, мы рассматриваем квадратичную базисную функцию Бернштейна, и тогда приведенная выше формула (в формуле 49) может быть упрощена следующим образом:
((y12 + a2) ω12-a2ω0ω2) (1-t) 2t2 = 0. (50)Далее, согласно Формуле (40), мы знаем
(ω12sec2θ-ω0ω2) (1-t) 2t2 = 0, (51)и t ∈ (0, 1), t 2 (1 — t ) 2 ≠ 0. Таким образом, узнать
легко. ω12 = ω0ω2cos2θ. (52)Согласно стандартной форме квадратичной рациональной кривой Безье (см. Формулу 6), мы можем дополнительно оценить ω 0 = ω 2 = 1, ω 1 = cosθ и диапазон значений θ центра угол полукруга должен быть 0 ≤ θ ≤ π / 2 [26].
Таким образом, рациональные квадратичные выражения Безье для дуговых кривых, проходящих через точки P 0 , A, P 2 , следующие:
С (t) = (1-t) 2P0 + 2cos (θ) t (1-t) P1 + t2P2 (1-t) 2 + 2cos (θ) t (1-t) + t2. (53)По сравнению со стандартной формулой рационального квадратичного Безье, получены следующие результаты:
, где 0 ≤ θ ≤ π / 2, 0 ≤ ω ≤ 1. Следовательно, необходимые и достаточные условия для того, чтобы рациональная квадратичная кривая Безье представляла дугу окружности, выражаются следующим образом:
Следовательно, необходимые и достаточные условия для того, чтобы рациональная квадратичная кривая Безье представляла дугу окружности, выражаются следующим образом:
Алгоритм 4 : квадратичная рациональная кривая Безье для представления участка дуги
5. Необходимые и достаточные условия квадратичных рациональных кривых Безье для представления параболы, эллиптической дуги и гиперболы
Теорема 4 . Квадратичная рациональная кривая Безье представляет параболу, эллиптическую дугу и гиперболу тогда и только тогда, когда ω = ± 1, −1 <ω <1 и ω <−1 или ω > 1, соответственно [27].
Доказательство . В соответствии с базисной функцией Бернштейна второго порядка формулы (42) кривая Безье из формулы (1) записывается следующим образом:
p (t) = ω0B0,2 (t) P0∑j = 02Bj, 2 (t) ωj + ω1B1,2 (t) P1∑j = 02Bj, 2 (t) ωj + ω2B2,2 (t) P2∑j = 02Bj, 2 (t) ωj = ∑i = 02Ri, 2 (t) Pi, (56)где
Ri, 2 (t) = ωiBi, 2 (t) ∑j = 02Bj, 2 (t) ωj. (57)
(57)Затем мы представляем локальную наклонную систему координат P 1 , S, T , так что S = P 0 — P 1 , T = P 2 — П 1 .Поскольку точка P ( t ) находится в пределах δ P 0 P 1 P 2 для произвольных t ∈ [0, 1], P ( t ) можно переписать как
P (t) = P1 + u (t) S + v (t) T = P1 + u (t) (P0-P1) + v (t) (P2-P1) = u (t) P0 + [1-u (t) -v (t)] P1 + v (t) P2. (58)Сравнивая коэффициенты из формулы (56) и формулы (58), мы знаем, что
R0,2 (t) = u (t), R1,2 (t) = 1-u (t) -v (t), R2,2 (t) = v (t). (59)Пусть k = ω0ω2 / ω12, где k — инвариантный коэффициент формы коники, поэтому
u (t) v (t) = R0,2 (t) Ṙ2,2 (t) = 14k [1-u (t) -v (t)] 2.(60) Формула (60) представляет собой неявное уравнение квадратичной кривой в локальной наклонной системе координат P 1 , S, T . Расширение формулы (60) далее показывает, что:
Расширение формулы (60) далее показывает, что:
В декартовой системе координат изображение двоичного квадратного уравнения может представлять собой коническую кривую, и все конические кривые могут быть получены вышеупомянутым способом [1]. Уравнение имеет следующий вид [28]:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, A, B, C не все равны нулю, (62), где A, B, C, D, E, F — полиномиальные коэффициенты.Если выполняются следующие условия,
, тогда Формула (62) представляет собой эллипс; кроме того, при тех же условиях, если коника вырождается (то есть A = C, B = 0), уравнение представляет собой круг. Кроме того, если выполняются следующие условия,
, то формула (62) представляет собой параболу [29]. Наконец, если выполняются следующие условия,
, то Формула (62) представляет собой гиперболу. Коэффициенты из формулы (61) и формулы (62) могут быть получены следующим образом: A = k, B = k -2, C = k, D = −2 k, E = −2 к, F = к . Таким образом, мы можем получить:
Таким образом, мы можем получить:
Алгоритм 5 : квадратичные рациональные кривые Безье для представления параболы, эллиптической дуги и гиперболы
Затем мы проводим обсуждение и оценку формулы (66). То есть из условия формулы (63), если кривая представляет собой эллипс, то в формуле (66) мы имеем B 2 -4 AC = 1- k <0. Следовательно, когда k > 1 кривая представляет собой эллипс. Из условия (64), если кривая является параболой, то B 2 — 4 AC = 1- k = 0 (снова см. Формулу 66).Следовательно, когда k = 1, кривая представляет собой параболу. Из условия 65, если кривая является гиперболой, тогда B 2 — 4 AC = 1 — k > 0, поэтому, когда k <1, кривая является гиперболой.
Отметим, что k = ω0ω2 / ω12. Таким образом, при стандартной форме квадратичной рациональной кривой Безье мы имеем ω 0 = ω 2 = 1 и ω = ω 1 .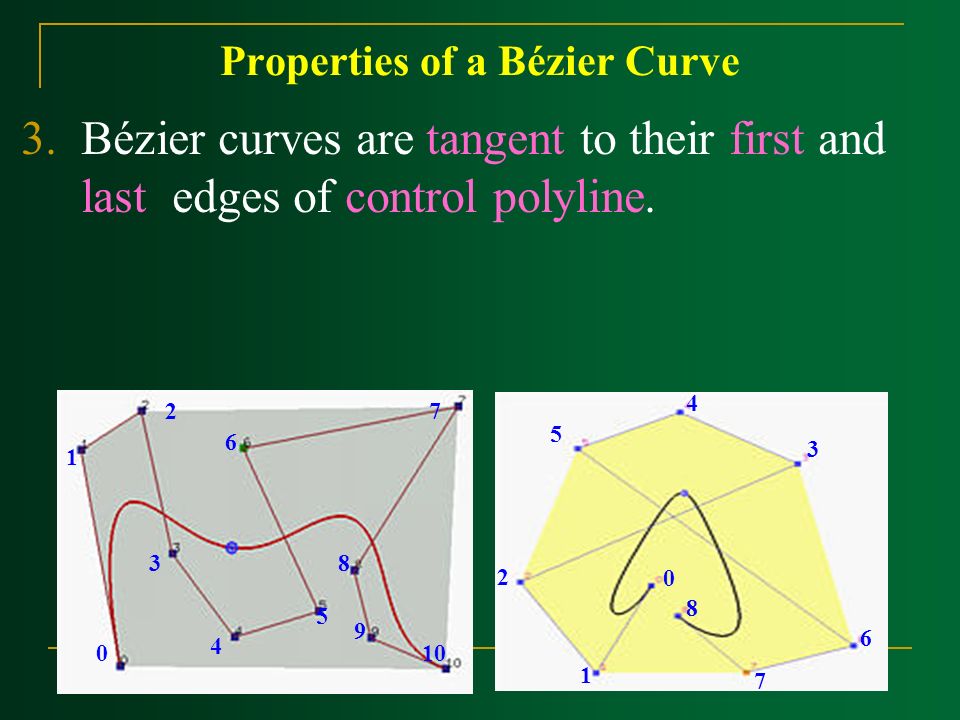 Следовательно, мы доказываем, что при −1 <ω <1 квадратичная рациональная кривая Безье является эллипсом; когда ω = ± 1, квадратичная рациональная кривая Безье является параболой; когда ω <−1, или ω > 1, квадратичная рациональная кривая Безье является гиперболой.
Следовательно, мы доказываем, что при −1 <ω <1 квадратичная рациональная кривая Безье является эллипсом; когда ω = ± 1, квадратичная рациональная кривая Безье является параболой; когда ω <−1, или ω > 1, квадратичная рациональная кривая Безье является гиперболой.
6. Заключение
В этой статье мы обсуждаем необходимые и достаточные условия для использования квадратичных рациональных кривых Безье для представления различных форм, таких как точка, отрезок прямой, парабола, эллиптическая дуга, дуга окружности и гипербола. Эти результаты могут быть далее использованы для упрощения других компьютерных геометрических разработок.
Заявление о доступности данных
Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без излишних оговорок.
Авторские взносы
CY: концептуализация, методология, программное обеспечение, проверка, исследование, визуализация и написание первоначального проекта. JY: программное обеспечение, написание — просмотр и редактирование, авторский надзор. YL: программное обеспечение, визуализация и написание — оригинальный проект. XG: написание — просмотр и редактирование, проверка и визуализация.
YL: программное обеспечение, визуализация и написание — оригинальный проект. XG: написание — просмотр и редактирование, проверка и визуализация.
Финансирование
Эта работа была поддержана Национальным фондом естественных наук Китая (грант № 61873004, 51874003) и Фондом гуманитарных и социальных наук Департамента образования Аньхой, Китай (грант №SK2017A0098). Мы также хотели бы поблагодарить JY из Университета Вуллонгонга за полезное обсуждение.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Список литературы
1. Уолтон Д. Д., Мик Д. С.. Конструкция кривой G2 с плоскими квадратичными рациональными сегментами спирали Безье. Инт Дж. Вычислительная математика . (2013) 90 : 325–40.DOI: 10.1080 / 00207160.2012.716831
CrossRef Полный текст | Google Scholar
2. Чжан Р. Улучшенные оценки производной рационально-квадратичных кривых Безье. Прикладная математика . (2015) 250 : 492–6. DOI: 10.1016 / j.amc.2014.10.120
Чжан Р. Улучшенные оценки производной рационально-квадратичных кривых Безье. Прикладная математика . (2015) 250 : 492–6. DOI: 10.1016 / j.amc.2014.10.120
CrossRef Полный текст | Google Scholar
3. Ши М. Степень редукции дисковых рациональных кривых Безье с использованием методов многокритериальной оптимизации. Int J Appl Math . (2015) 45 : 392–7.
Google Scholar
4. Лу Л., Цзян К., Сян Х. Некоторые замечания о взвешенных кривых Лупаша [формула опущена] -Безье. J Comput Appl Math . (2017) 313 : 393–6.
Google Scholar
5. Ли Э. Рациональное представление Безье для коник. Модель Geometr . (1987) 3 : 5–19.
Google Scholar
6. Хан X. Квадратичные тригонометрические полиномиальные кривые относительно локального управления. Appl Numer Math .(2006) 56 : 105–15. DOI: 10.1016 / j.apnum.2005. 02.013
02.013
CrossRef Полный текст | Google Scholar
7. Самрин С., Сарфраз М., Хусейн М.З., Ливесу М. Компьютерное проектирование с использованием рационального квадратичного тригонометрического сплайна с контролем формы интервала. В: Международная конференция по вычислительным наукам и вычислительному интеллекту, 2017 г., . Лас-Вегас, Невада: IEEE (2017). п. 246–51.
Google Scholar
8. Башир У, Аббас М.А., Али Дж. Рациональная квадратичная тригонометрическая кривая Безье G2 и C2 с двумя параметрами формы с приложениями. Прикладная математика . (2013) 219 : 10183–97. DOI: 10.1016 / j.amc.2013.03.110
CrossRef Полный текст | Google Scholar
9. Сюй Ц., Ким Т., Фарин Г.Е. Эксцентриситет конических сечений, сформулированных как рациональные квадратики Безье. Comput Aided Geometr Des . (2010) 27 : 458–60. DOI: 10.1016 / j.cagd.2010.04.001
CrossRef Полный текст | Google Scholar
10.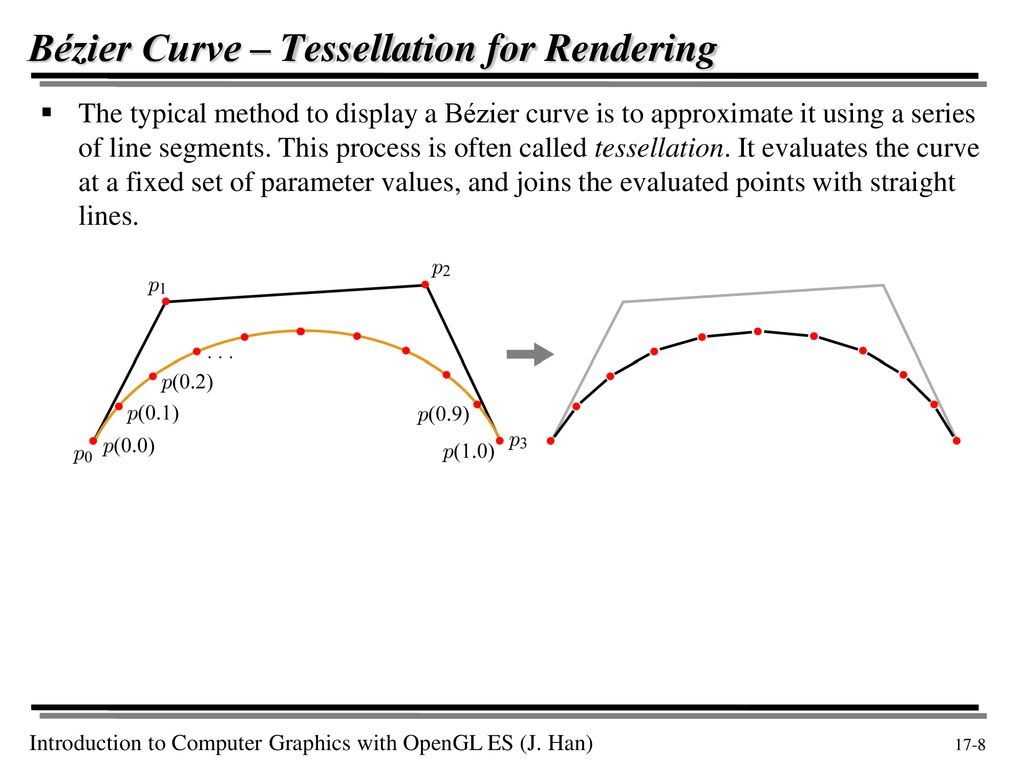 Бастл Б., Джеттлер Б., Лвицка М., Скичо Дж., Сир З. Сферические квадратичные треугольники Безье с параметризацией длины хорды и триполярными координатами в пространстве. Comput Aided Geometr Des . (2011) 28 : 127–34. DOI: 10.1016 / j.cagd.2010.11.001
Бастл Б., Джеттлер Б., Лвицка М., Скичо Дж., Сир З. Сферические квадратичные треугольники Безье с параметризацией длины хорды и триполярными координатами в пространстве. Comput Aided Geometr Des . (2011) 28 : 127–34. DOI: 10.1016 / j.cagd.2010.11.001
CrossRef Полный текст | Google Scholar
11. Хуссейн М.З., Иршад М., Сарфраз М., Зафар Н. Интерполяция сигналов дискретного времени с использованием кубических функций. В: Международная конференция IEEE по визуализации информации . Чикаго, Иллинойс: IEEE (2015). п. 454–9.
Google Scholar
12. Хан Л., Ву И, Чу Ю. Взвешенные кривые Лупаша q-Безье. J Comput Appl Math .(2016) 308 : 318–29. DOI: 10.1016 / j.cam.2016.06.017
CrossRef Полный текст | Google Scholar
13. Хань Л-В, Чу И, Цю Цзы. Обобщенные кривые и поверхности Безье, основанные на q-аналоге Лупаша оператора Бернштейна. J Comput Appl Math . (2014) 261 : 352–63.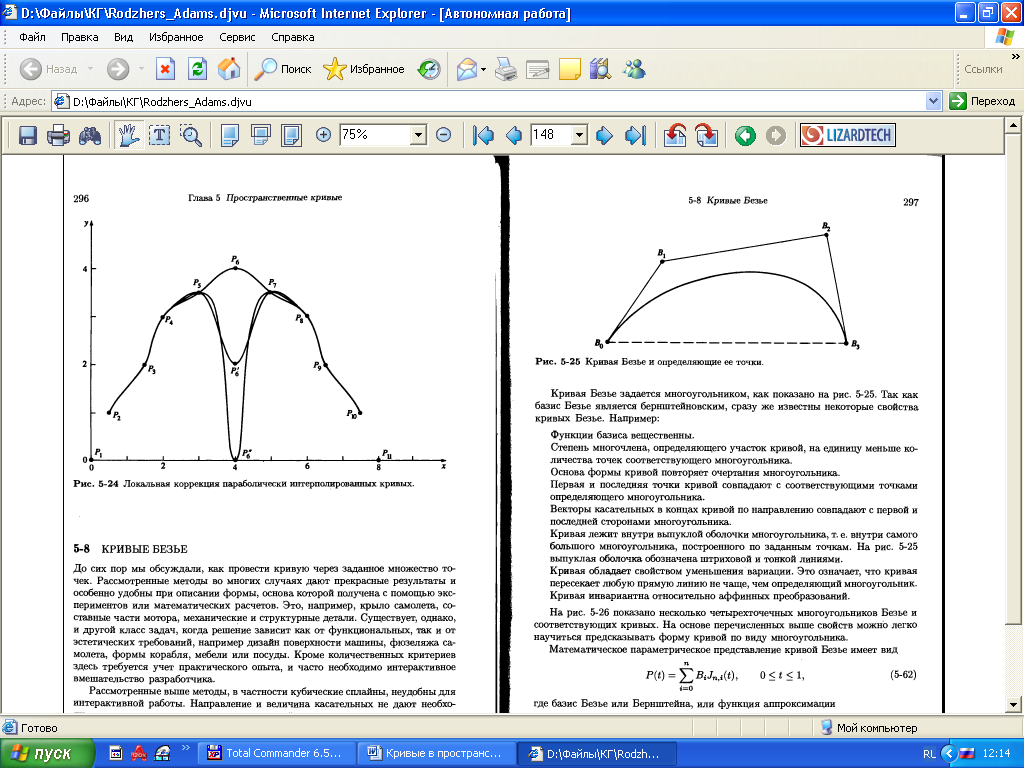 DOI: 10.1016 / j.cam.2013.11.016
DOI: 10.1016 / j.cam.2013.11.016
CrossRef Полный текст | Google Scholar
14. Каттьо-Хийяр И., Альбрехт Г., Эрнандес-Медерос В. Оптимальная параметризация рациональных квадратичных кривых. Comput Aided Geometr Des . (2009) 26 : 725–32. DOI: 10.1016 / j.cagd.2009.03.008
CrossRef Полный текст | Google Scholar
15. Хуссейн М., Салим С. C 1 рациональный квадратичный тригонометрический сплайн. Egypt Inform J . (2013) 14 : 211–20. DOI: 10.1016 / j.eij.2013.09.002
CrossRef Полный текст | Google Scholar
16. Сарфраз М., Самрин С., Хуссейн М.З. Моделирование 2D-объектов с помощью взвешенного квадратичного тригонометрического сплайна.В: 13-я Международная конференция по компьютерной графике, изображениям и визуализации. Бени Меллал (2016). п. 29–34.
Google Scholar
17. Ли Т-К, Пэк С.-Х, Чхве И-Х, О С-Й. Плавное планирование пути покрытия и управление мобильными роботами на основе представления карты сетки с высоким разрешением. Робот Auton Syst . (2011) 59 : 801–12. DOI: 10.1016 / j.robot.2011.06.002
Робот Auton Syst . (2011) 59 : 801–12. DOI: 10.1016 / j.robot.2011.06.002
CrossRef Полный текст | Google Scholar
18. Хан X. Сохраняющий форму кусочно-рациональный интерполянт с четвертым числителем и квадратичным знаменателем. Прикладная математика . (2015) 251 : 258–74. DOI: 10.1016 / j.amc.2014.11.067
CrossRef Полный текст | Google Scholar
19. Ламний А., Оумеллаль Ф. Метод локальной интерполяции с помощью тригонометрических сплайновых кривых и поверхностей натяжения. Прикладная математика . (2015) 9 : 3019–35. DOI: 10.12988 / ams.2015.52154
CrossRef Полный текст | Google Scholar
20. Ши М. Степень редукции классических дисковых рациональных кривых Безье в L 2 Норм.В: 2015 14-я Международная конференция по автоматизированному дизайну и компьютерной графике . Сиань: IEEE (2015). п. 202–3.
Google Scholar
21. Xu A, Viriyasuthee C, Rekleitis I. Эффективный полный охват известной произвольной среды приложениями для воздушных операций. Робот Auton . (2014) 36 : 365–81. DOI: 10.1007 / s10514-013-9364-x
Xu A, Viriyasuthee C, Rekleitis I. Эффективный полный охват известной произвольной среды приложениями для воздушных операций. Робот Auton . (2014) 36 : 365–81. DOI: 10.1007 / s10514-013-9364-x
CrossRef Полный текст | Google Scholar
22. Хан А., Норин I, Хабиб З.Планирование пути покрытия мобильных роботов с использованием рационального квадратичного сплайна Безье. В: Международная конференция по границам информационных технологий, 2016 г., . Исламабад: IEEE (2016). п. 319–23.
Google Scholar
23. Бакман Дж., Пийрайнен П., Оксанен Т. Создание плавной траектории поворота для сельскохозяйственных машин на поворотных полосах. Биосист Анг . (2015) 139 : 76–86. DOI: 10.1016 / j.biosystemseng.2015.08.005
CrossRef Полный текст | Google Scholar
24.Yu X, Roppel TA, Hung JY. Оптимизационный подход для планирования роботизированного покрытия поля. В: 41-я ежегодная конференция Общества промышленной электроники IEEE . Иокогама: IEEE (2015). п. 76–86.
Иокогама: IEEE (2015). п. 76–86.
Google Scholar
25. Сара Э., Питер П. Использование структур решетки в реализациях грамматики форм. АИ ЭДАМ . (2018) 32 : 147–61. DOI: 10.1017 / S08417000282
CrossRef Полный текст | Google Scholar
26. Ли И, Дэн Ц., Цзинь В., Чжао Н.О границах производной рациональных кривых Безье. Appl Math Comput. (2013) 219 : 10425–33. DOI: 10.1016 / j.amc.2013.04.042
CrossRef Полный текст | Google Scholar
27. Дэн Ц., Ли И, Му Х, Чжао Ю. Характеристическая коника рационального билинейного отображения. J Comput Appl Math . (2019) 346 : 277–83. DOI: 10.1016 / j.cam.2018.07.012
CrossRef Полный текст | Google Scholar
28. Ли Чжэн Л., Ченг Кай Дж. Некоторые замечания о взвешенных кривых Лупаша [формула опущена] -Безье. J Comput. Прил. Математика . (2017) 313 : 393–6. DOI: 10.1016 / j.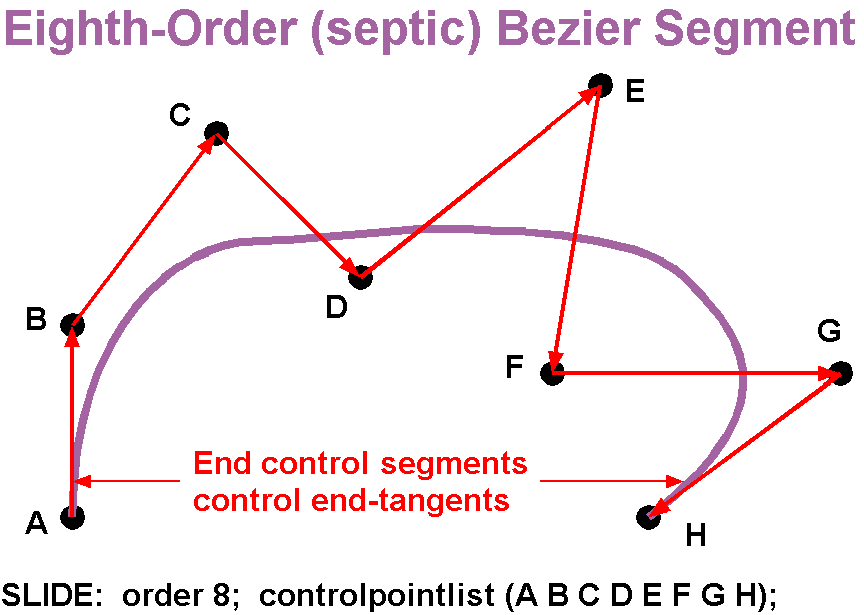 cam.2016.09.044
cam.2016.09.044
CrossRef Полный текст | Google Scholar
Инструмент кривой Безье— Руководство Krita 5.0.0 документация
С помощью этого инструмента можно рисовать кривые. Щелкните значок, чтобы указать начальную точку кривой, затем щелкните еще раз для следующих друг за другом контрольных точек кривой.
Krita покажет синюю линию с двумя маркерами, когда вы добавите контрольную точку.Вы можете перетащить эти маркеры, чтобы изменить направление кривой в этой точке.
На векторном слое вы можете щелкнуть ранее вставленную контрольную точку, чтобы изменить ее. С промежуточной контрольной точкой (то есть точкой, которая не является начальной и не конечной точкой), вы можете перемещать маркеры направления отдельно, чтобы кривая входила и выходила из точки в разных направлениях. После редактирования точки вы можете просто щелкнуть холст, чтобы продолжить добавление точек к кривой.
Нажатие клавиши Del удалит текущую выбранную контрольную точку из кривой. Дважды щелкните на любой точке кривой или нажмите клавишу Enter , чтобы закончить рисование, или нажмите клавишу Esc , чтобы отменить всю кривую. Вы можете использовать клавишу Ctrl , удерживая нажатой, чтобы переместить всю кривую в другое положение.
Дважды щелкните на любой точке кривой или нажмите клавишу Enter , чтобы закончить рисование, или нажмите клавишу Esc , чтобы отменить всю кривую. Вы можете использовать клавишу Ctrl , удерживая нажатой, чтобы переместить всю кривую в другое положение.
При рисовании клавиша Ctrl при перетаскивании сдвигает ручки в обе стороны. Клавиша Alt создаст острый угол, а клавиша Shift позволит вам сделать ручку в конце кривой.отменит последнюю добавленную точку.
Опции инструмента
Новое в версии 4.1.3:
- Autosmooth Curve
При включении этого параметра узлы будут инициализированы сглаженными кривыми вместо углов. Снимите этот флажок, если хотите создать острые углы для узла. Это повлияет на резкость кривой при перетаскивании после щелчка.
- Дельта привязки угла
Угол привязки.
- Активировать угловую привязку
Угловая привязка упростит расположение следующей линии под определенным углом к текущей.
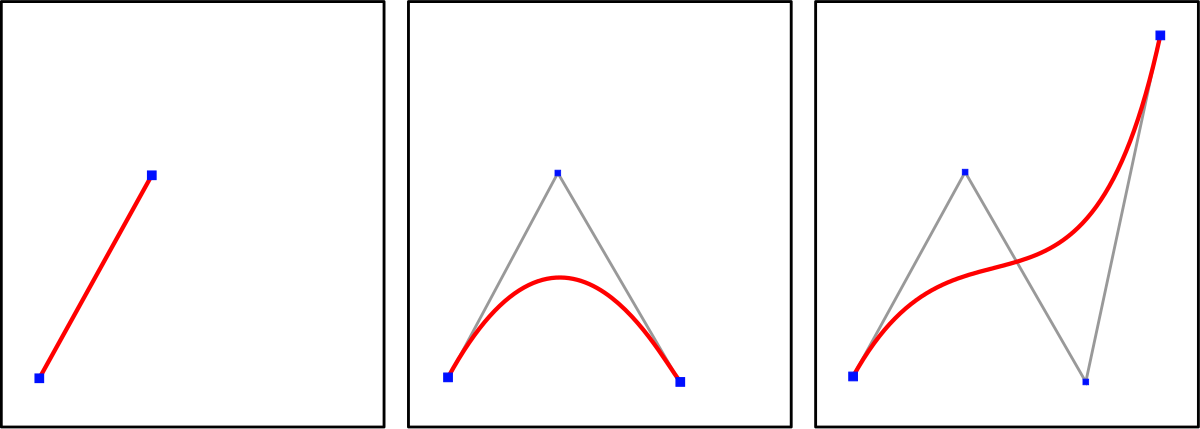

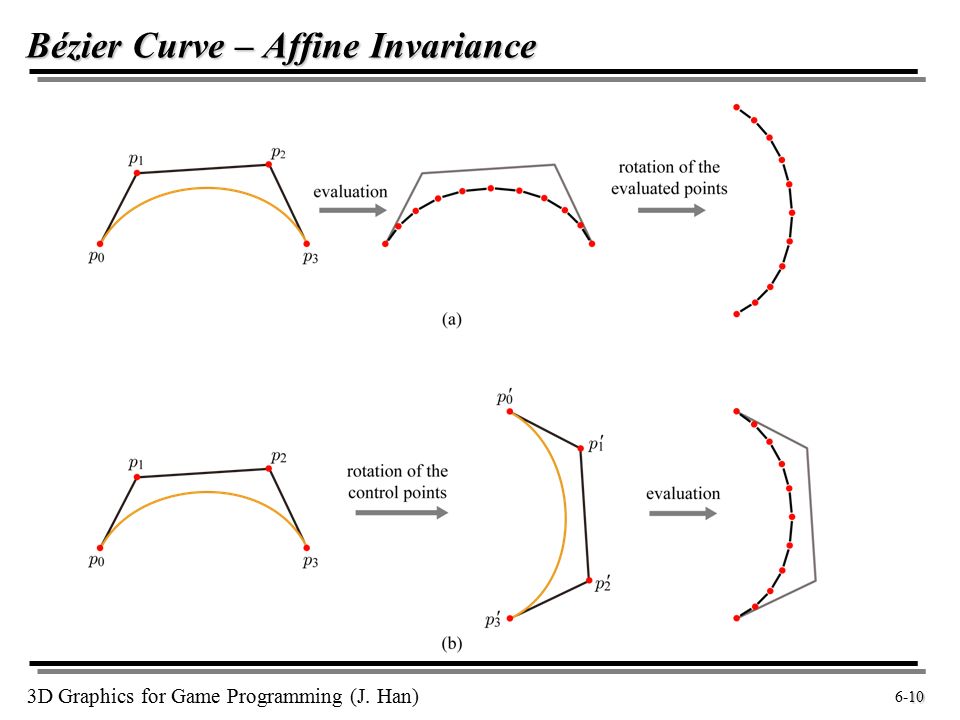 insert(insertionIndex + pointsAdded, pMid);
pointsAdded++;
pointsAdded += FindDrawingPoints(tMid, t1, insertionIndex + pointsAdded, pointList);
return pointsAdded;
}
return 0;
}
insert(insertionIndex + pointsAdded, pMid);
pointsAdded++;
pointsAdded += FindDrawingPoints(tMid, t1, insertionIndex + pointsAdded, pointList);
return pointsAdded;
}
return 0;
}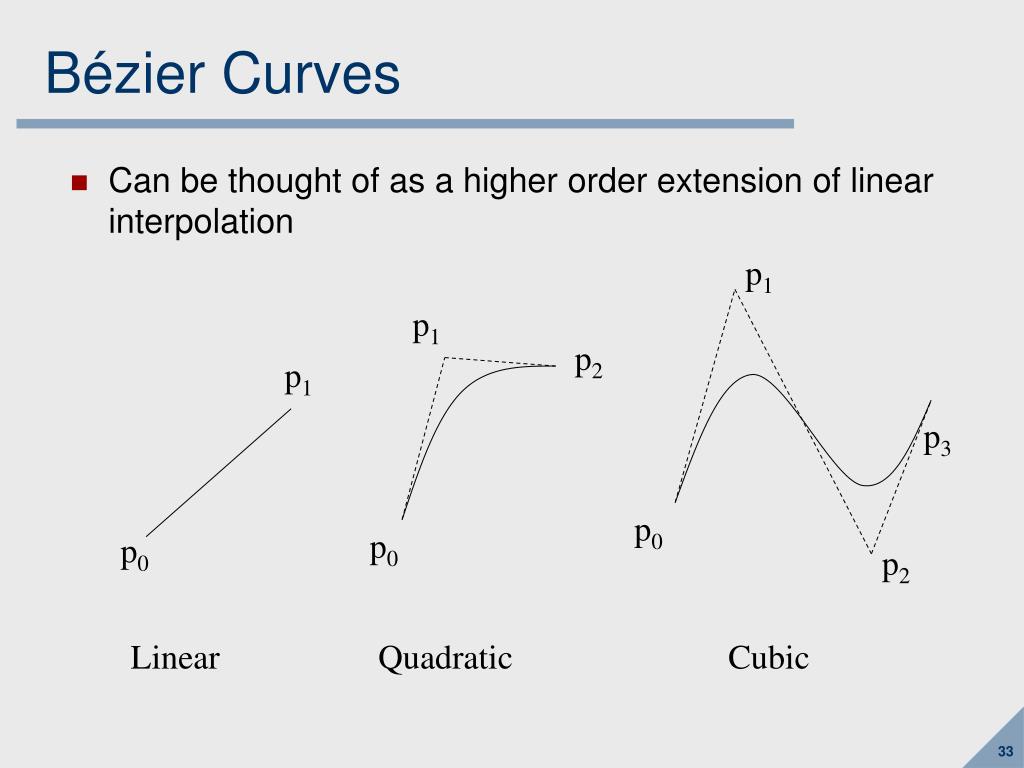 Add(CalculateBezierPoint(0, p0, p1, p2, p3));
}
for(int j = 1; j <= SEGMENTS_PER_CURVE; j++)
{
float t = j / (float) SEGMENTS_PER_CURVE;
drawingPoints.Add(CalculateBezierPoint(t, p0, p1, p2, p3));
}
}
return drawingPoints;
}
}
Add(CalculateBezierPoint(0, p0, p1, p2, p3));
}
for(int j = 1; j <= SEGMENTS_PER_CURVE; j++)
{
float t = j / (float) SEGMENTS_PER_CURVE;
drawingPoints.Add(CalculateBezierPoint(t, p0, p1, p2, p3));
}
}
return drawingPoints;
}
}