Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.
Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.
Рис. 109. Прямоугольная и изометрические проекции квадрата
Рис. 110. Прямоугольная и изометрические проекции треугольника
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
Рис. 111. Прямоугольная и изометрические проекции шестиугольника
Рис. 112. Прямоугольная и изометрические проекции круга
При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические проекции простых геометрических тел
Способы построения изометрической проекции детали:
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней посредством изображения ребер модели;
Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани
4) обводка изометрической проекции (рис. 113).
- Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
- Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
- Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов
Рис. 116. Использование комбинированного способа построения изометрической проекции детали
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей
1.2.6. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ.
ГОСТ 2.317-69
Аксонометрические проекции применяются в качестве вспомогательных к чертежам в тех случаях, когда требуется поясняющее наглядное изображение формы детали. В ГОСТ 2.317-69 стандартизованы прямоугольные и косоугольные аксонометрические проекции с различным расположением осей.
ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ
Изометрическая проекция
Положение аксонометрических осей приведено на рис. 1. Коэффициент искажения по осям x, y, z равен 0,82. Для упрощения изометрическую проекцию, как правило, выполняют без искажения, т.е. приняв коэффициент искажения равным 1.
Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям. Для изометрической проекции вариант штриховки по плоскостям приведен на рис. 2.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 3).
1, 2, 3 – эллипсы, их большые оси расположены под углом 90° к осям y, z, x соответственно и равны (при коэффициенте искажения – 1) 1,22d, а малые оси – 0,71d, где d – диаметр окружности.
Построение эллипсов в изометрической проекции окружности можно заменить построением овалов, Следует отметить, что очертание любого циркульного овала не совпадает с очертанием эллипса, имеющего такие же оси, хотя и приближается к нему. Один из способов построения овала приведен на рис. 4.
Пример изображения детали в прямоугольной изометрии приведен на рис. 5.
Рис. 5
Диметрическая проекция
Положение аксонометрических
осей приведено на рис. 6. Коэффициент искажения по оси y равен 0,47, а по осям
Штриховка сечений в прямоугольной диметрической проекции показана на рис.7, а пример изображения детали – на рис. 9.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 8).
1 – эллипс, его большая ось расположена под углом 90° к оси y и равна (при коэффициенте искажения – 1) 1,06d, а малая ось – 0,95d, где d – диаметр окружности;
2, 3 – эллипсы, их большие оси расположены под углом 90° к осям z и x соответственно и равны 1,06d, а малая ось – 0,35d (при коэффициенте искажения – 1).
КОСОУГОЛЬНЫЕ ПРОЕКЦИИ
Фронтальная изометрическая проекция
Положение аксонометрических осей приведено на рис. 10. Допускается применять проекции с углом наклона оси y 30 и 60 градусов. Фронтальную изометрическую проекцию выполняют без искажения по осям x, y, z.
Штриховка сечений в косоугольной фронтальной изометрической проекции показана на рис. 11, а пример выполнения изображения детали – на рис.13.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис. 12).
1 – окружность d; 2, 3 – эллипсы, большая ось расположена под углом 22°30¢ к осям x и z соответственно и равна 1,3d, а малая ось – 0,54d.
Горизонтальная изометрическая проекция
Положение аксонометрических осей приведено на рис.14. Допускается применять горизонтальные изометрические проекции с углом наклона оси y 45 и 60 градусов, сохраняя угол между осями x и y равным 90 градусов. Горизонтальную изометрическую проекцию выполняют без искажения по осям x, y и z.
Штриховка сечений в косоугольной горизонтальной изометрической проекции показана на рис.15, а пример изображения детали – на рис. 17.
Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций, – в эллипсы (рис.16).
1 – эллипс, большая ось расположена под углом 15° к оси z и равна 1,37d, а малая ось – 0,37d;
2 – окружность d;
3 – эллипс, большая ось расположена под углом 30° к оси z и равна 1,22d, а малая ось – 0,71d;
Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на рис. 18. Допускается применять фронтальные диметрические проекции с углом наклона оси y 30 и 60 градусов. Коэффициент искажения по оси y равен 0,5, а по осям x, z – 1.
Штриховка сечений в косоугольной фронтальной диметрии показана на рис.19, а пример изображения детали – на рис.21
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной или профильной плоскости проекций, – в эллипсы (рис.20). 1 – окружность d; 2, 3 – эллипсы, большая ось расположена под углом 7°14¢ к осям x и z соответственно и равна 1,07d, а малая ось – 0,33d.
Аксонометрические проекции — Технология Jimdo-Page!
ГОСТ 2.317—68* устанавливает прямоугольные и косоугольные аксонометрические проекции.
Построение аксонометрических проекций заключается в том, что геометрическую фигуру вместе с осями прямоугольных координат, к которым
эта фигура отнесена в пространстве, параллельным (прямоугольным или косоугольным) способами проецируют на выбранную плоскость проекций. Таким образом, аксонометрическая проекция — это проекция на
одну плоскость. При этом направление проецирования выбирают так, чтобы оно не совпадало ни с одной из координатных осей.
При построении аксонометрических проекций изображаемый предмет жестко связывают с натуральной системой координат Oxyz. В целом аксонометрический чертеж получается состоящим из параллельной проекции предмета, дополненной изображением координатных осей с натуральными масштабными отрезками по этим осям. Название «аксонометрия» и произошло от слов — аксон — ось и метрео — измеряю.
Аксонометрические проекции в зависимости от направления проецирования разделяют на:
- косоугольные, когда направление проецирования не перпендикулярно плоскости
аксонометрических проекций;
- прямоугольные, когда направление проецирования перпендикулярно плоскости
аксонометрических проекций.
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
- изометрия — все три коэффициента искажения равны между собой;
- диметрия — два коэффициента искажения равны между собой и отличаются от
третьего;
- триметрия — все три коэффициента искажения не равны между собой.
Рассмотрим построение треугольника на горизонтальной плоскости в изометрической проекции. При построении первоначально необходимо определить расположение фигуры относительно начала координат. Для этого по оси х откладывают расстояние m, равное смещению оси треугольника относительно оси у. Из найденной точки проводят прямую, параллельную оси у, и на ней откладывают отрезок, равный k — смещению основания треугольника от оси х, получили точку 1. Симметрично точке 1 по прямой, параллельной оси х, в обе стороны откладывают отрезки, равные половине основания треугольника – найдены точки 3, 4. Из точки 1 по прямой, параллельной оси у, откладывают отрезок, равный высоте треугольника – определена точка 2. Полученные точки соединяют. Аналогично строят фронтальную и профильную проекцию фигуры.
Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими.
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).
Рисунок 4.1
Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.
Рисунок 4.2
Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:
- прямоугольные изометрические и диметрические;
- косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;
Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.
4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
Направление аксонометрических осей приведено на Рисунке 4.3.
Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции
Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.
Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.
Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции
4.1.2. Диметрическая проекция
Положение аксонометрических осей проводится на Рисунке 4.5.
Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.
Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.
Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.
Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции
Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 300 и 600.
Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.
Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.
Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.
Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).
Одна из этих окружностей делится на несколько равных (или неравных) частей.
Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.
Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.
а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)
4.3.2 Построение эллипса по хордам
Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А1В1=АВ и С1 D1 = 0,5CD. Диаметр А 1В1 делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).
4.4 Штриховка сечений
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).
а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях
Как начертить изометрию? — Мегаобучалка
Автор: WebMoroz
Дата: 2010-08-02
Практически все, кому довелось изучать черчение и инженерную графику сталкивались с необходимостью произвести построение изометрической проекции детали. В этом уроке мы попробуем разобрать основные моменты, которые нужно знать, чтоб начертить изометрию. Уверен, что повторив указанные в этом уроке шаги, вы сможете самостоятельно выполнить и более сложное задание. В вашей детали может быть большее количество построений, но основные принципы останутся неизменными. Но при этом оговорюсь, что построение изометрии скорее всего будет вам не под силу, если вы еще не освоили построение третьего вида и построение простого разреза. Вы должны уже уметь хорошо ориентироваться в трех видах на чертеже.
Начнем с того, что определимся с направлением осей в изометрии.
На следующей схеме показано соответствие направлений, по которым откладываются размеры в изометрии по отношению к размерам на чертеже. Интересный момент: как показал опыт, этот рисунок кому-то помогает понять принцип построения, а кого-то — наоборот — ставит в тупик. Поэтому, если вас эта схема скорее смущает, нежели просветляет, не зацикливайтесь на нем и читайте дальше — вполне вероятно, что там все будет понятно.
На этом закончим вступительную часть и начнем непосредственно построение изометрической проекции детали. Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.
Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.
Мы получили верхнюю грань фигуры. Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом — в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. Изображение окружностей на всех трех плоскостях я описал в отдельном уроке, а пока лишь скажу, что в изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b — вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм).
Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра — по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена — не хватает только прямоугольного сквозного отверстия.
Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия — по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.
На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху — в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.
Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).
Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!
Рекомендую посмотреть урок окружность в изометрии.
Тема: «Получение и построение аксонометрических проекций ».
Тип урока: урок изучения нового материала.
Цели и задачи урока:
— познакомить с новым термином «аксонометрия»;
— сформировать понятие о косоугольной фронтальной диметрической и прямоугольной изометрической проекциях, их особенностях и различиях, расположении осей, принципах построения аксонометрических проекций;
— учить проецированию куба на фронтальную димметрическую и изометрическую проекцию, способам построения аксонометрических проекций плоских фигур;
— развивать пространственные представления и пространственное мышление;
— развитие навыков работы чертёжными инструментами;
— воспитывать аккуратность в графических построениях;
— воспитание целеустремлённость;
Оборудование: чертежные инструменты, тетрадь, учебник, таблица с изображением аксонометрии, объёмные детали.
Ход урока:
I. Организация учащихся на уроке.
Приветствие, проверка явки учащихся, проверка готовности к уроку, заполнение журнала.
II. Сообщение темы, целей урока.
III. Работа по теме урока:
1)Повторение и закрепление материала по проецированию на 3 плоскости проекций. Индивидуальные карточки – задания.
Построение третьего вида по двум данным.
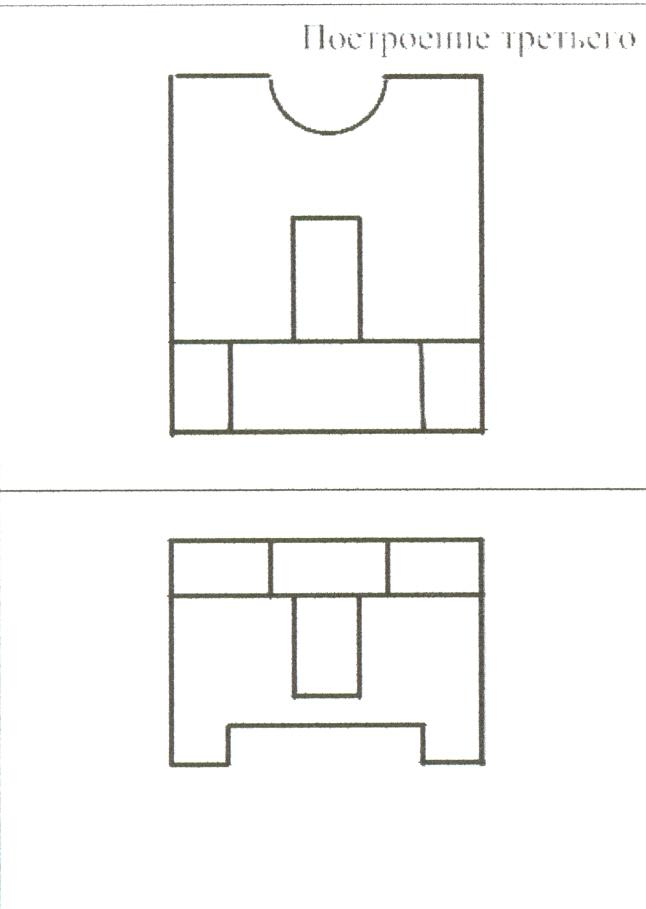
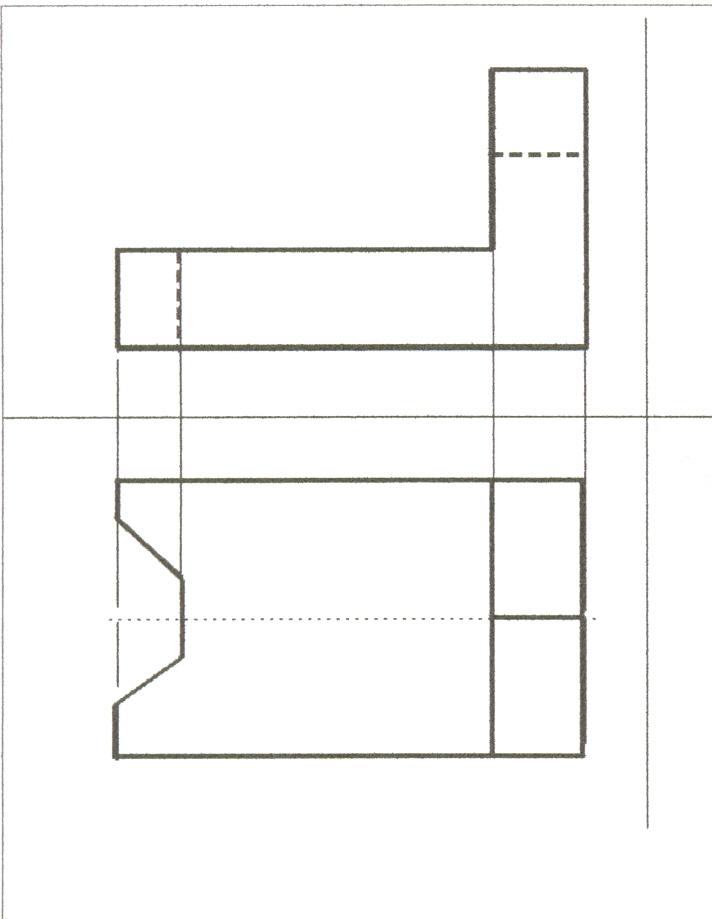
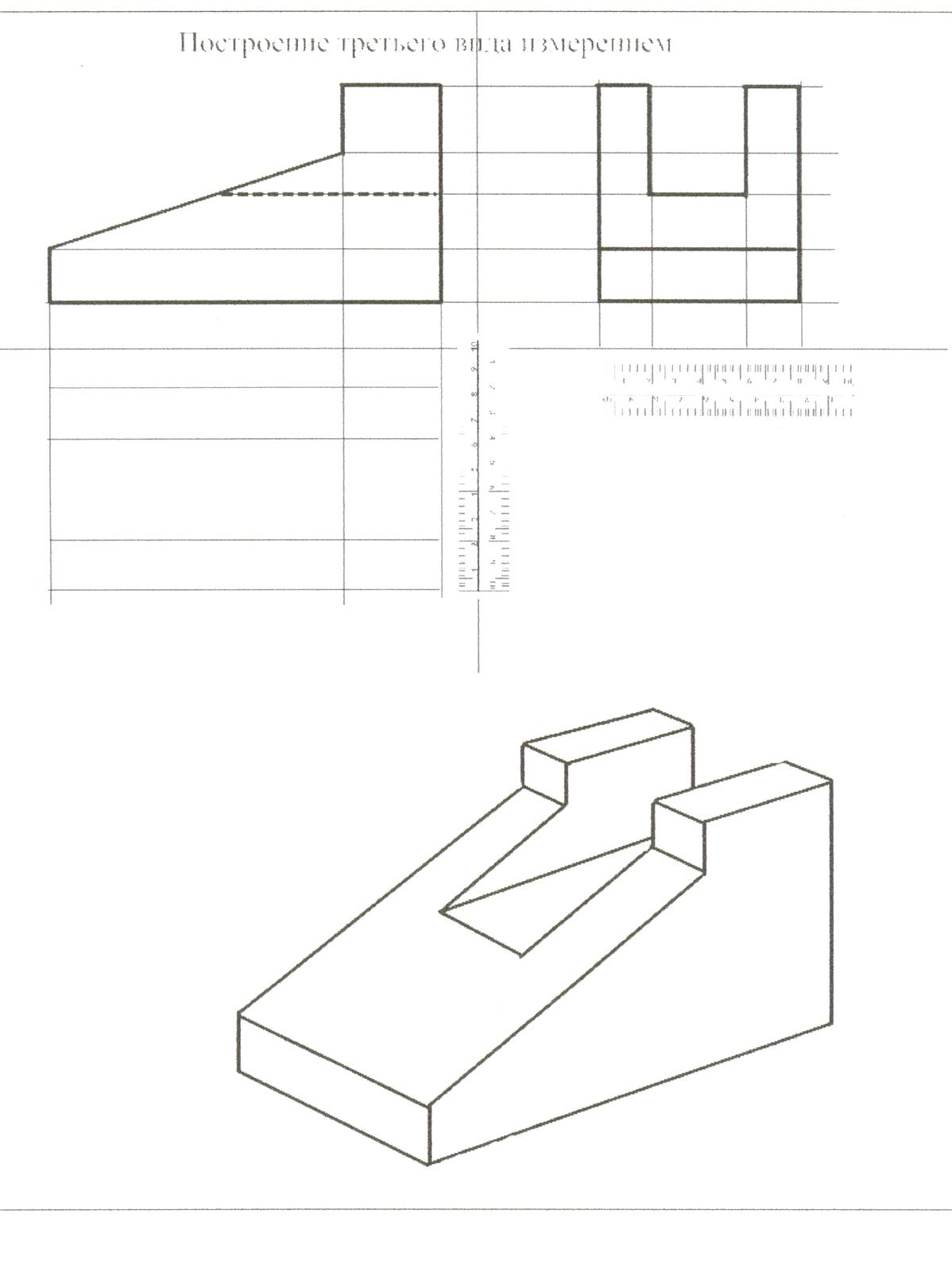
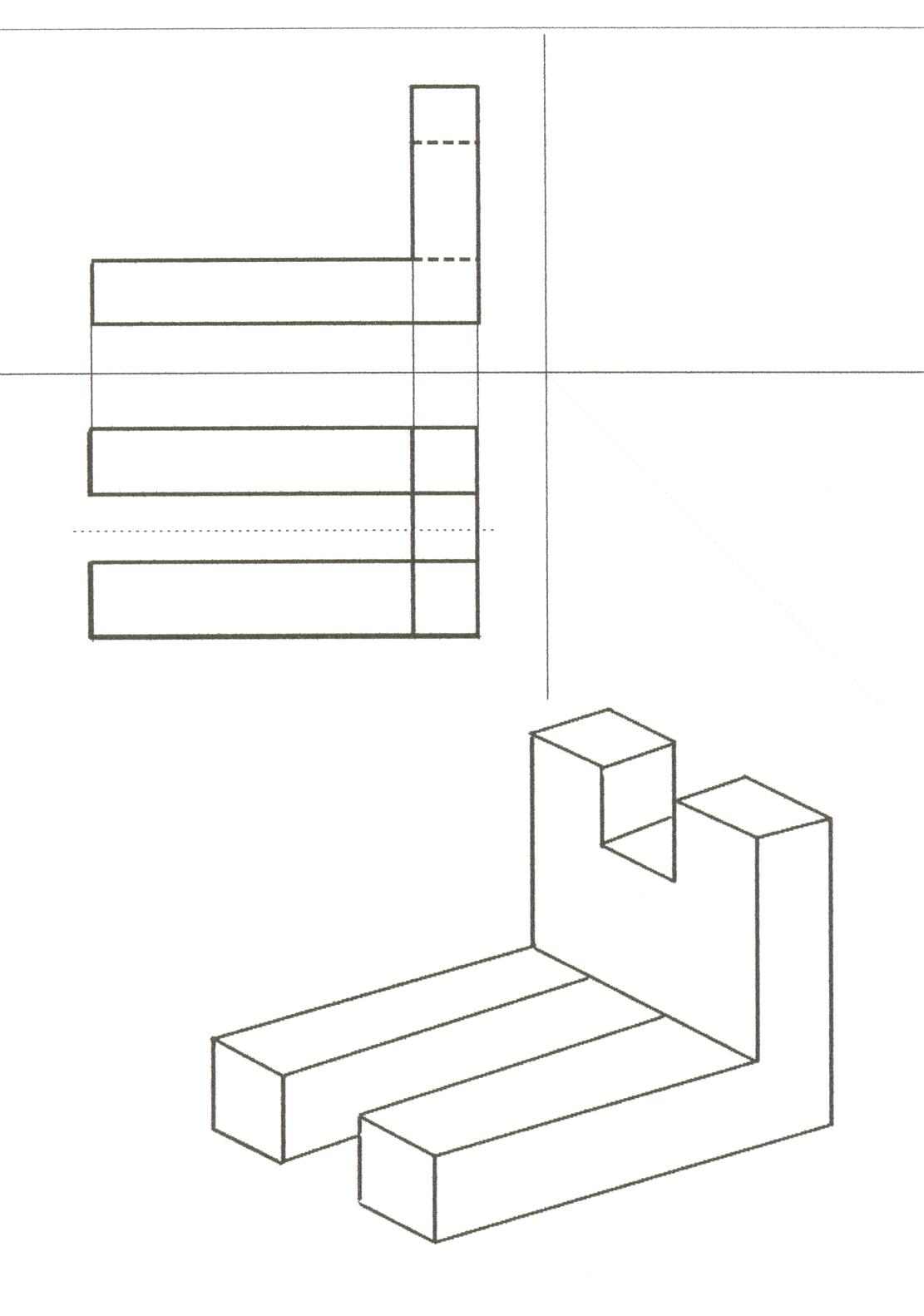
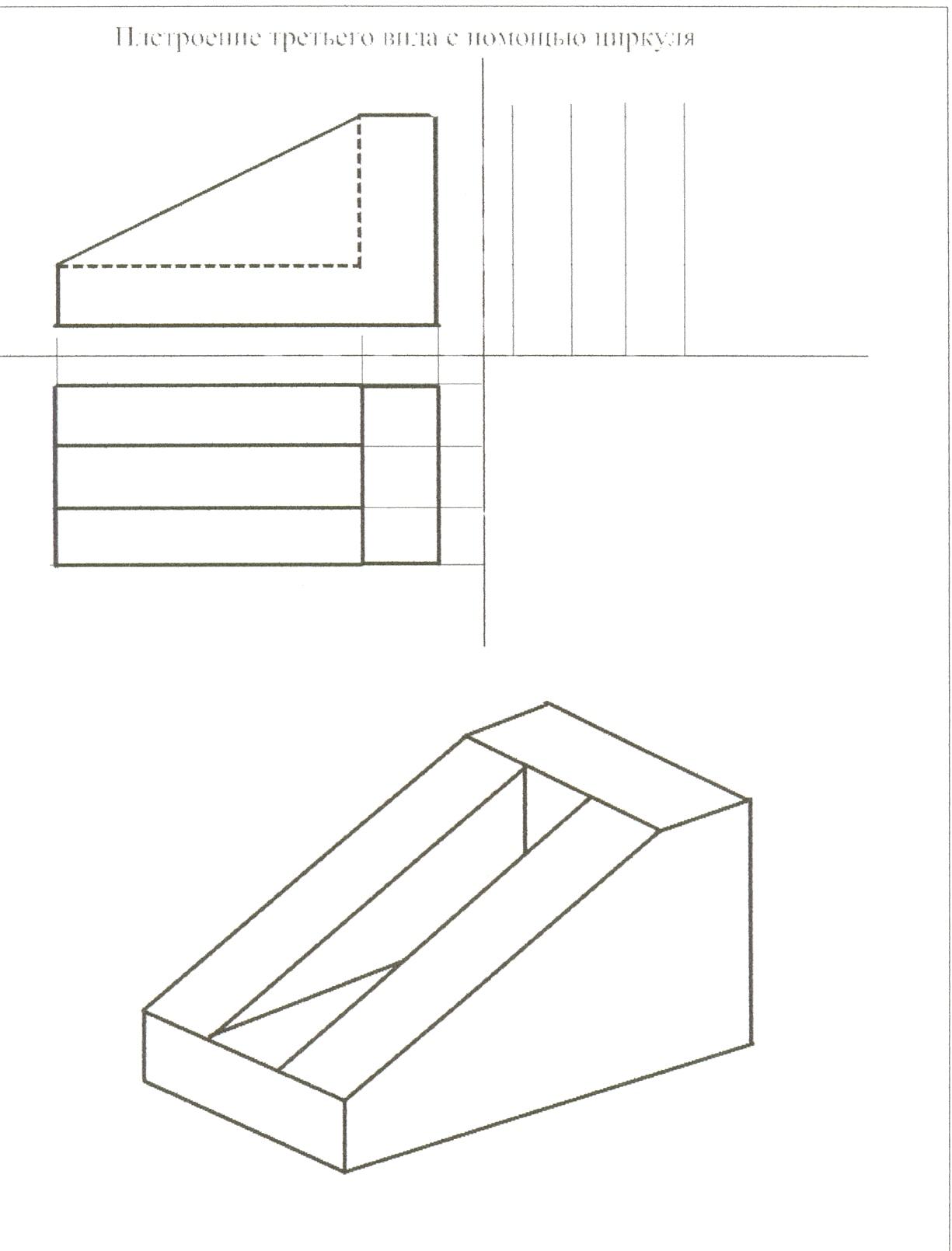

Карточки вклеиваются в тетрадь и выполняются построения в карточке.
Дополнение чертёжа недостающими линиями. 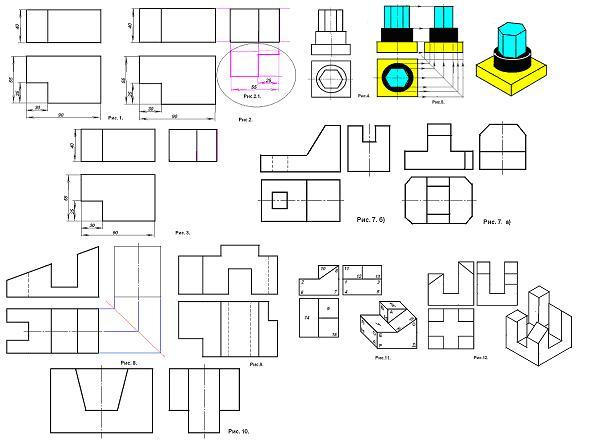
2) Аксонометрические проекции. (Изучение новых понятий с записью их в тетрадь).
Чертеж механизма или детали не дает полное представление о его форме. Поэтому чертежи сложных изделий сопровождают наглядными изображениями (аксонометрическими проекциями).
Аксонометрия — слово греческое, в переводе означает измерение по осям.
Проекции называются аксонометрическими потому, что предмет проецируется на плоскость вместе с осями координат.
При построении аксонометрических проекций размеры откладывают вдоль осей X,Y,Z — аксонометрические оси.
Аксонометрические проекции отличаются наглядностью. На аксонометрических проекциях форма предмета всегда передаётся одним изображением, позволяющим увидеть 3 его стороны.
Стандарт устанавливает несколько типов аксонометрических проекций. Мы познакомимся с 2 из них: косоугольной фронтальной диметрической и прямоугольной изометрической проекциями.
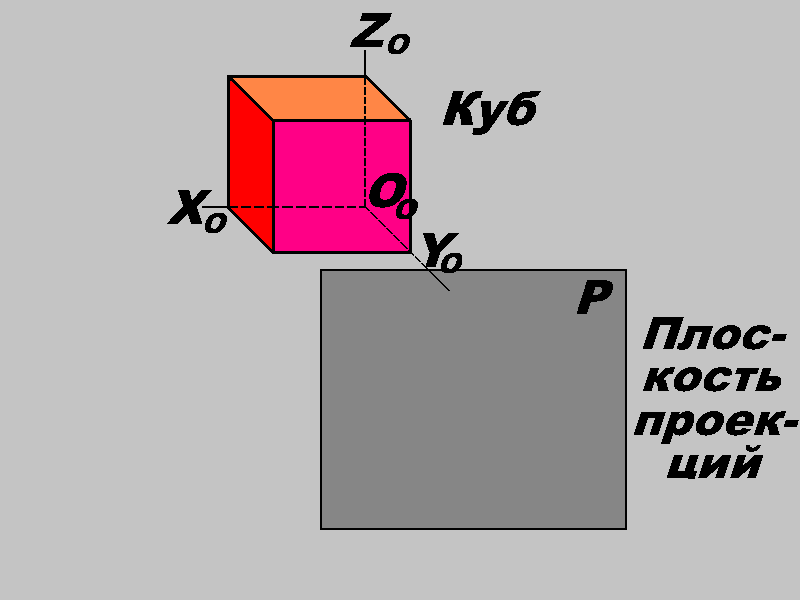
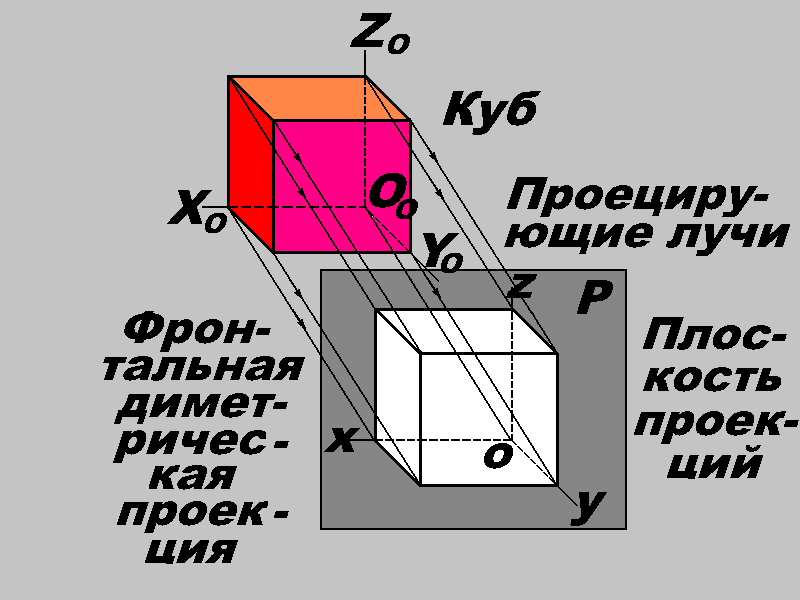
Фронтальная диметрическая проекция (диметрия).
При выполнении диметрической проекции перед плоскостью проекций предмет располагается так, чтобы его передняя грань была параллельна плоскости проекций. На аксонометрической плоскости проекций получают изображение координатных осей и косоугольную фронтальную димметрическую проекцию предмета. Оси X и Z отобразились на плоскость перпендикулярно друг другу, а ось Y под углом 45 к положению оси X.
Работа в тетрадях.
На листе в клетку отступите 8 клеток сверху и слева. Ось Z – вертикально, ось X – горизонтально, ось Y – под углом 45, по углам клеточек. Особенность данного вида проецирования в том, что мы видим без искажения переднюю сторону детали, то есть вид спереди. Однако стороны, расположенные вдоль оси Y, будут уменьшены в 2 раза по сравнению с оригиналом. Отсюда название «диметрия» — двойное измерение.
Прямоугольная изометрическая проекция.
Изометрия – это одна из аксонометрических проекций.
Изометрия (греч.) — равное измерение.
При вычерчивании изометрической проекции (изометрии) размеры по всем трем осям откладывают натуральные. Углы между аксонометрическими осями в этой проекции равны 120.
Работа в тетрадях.
На листе в клетку отступите 8 клеток сверху и слева. Ось Z – вертикально, ось X , ось Y – под углом 30 , отсчитайте 5 клеток в сторону и 3 клетки вниз.
Общие правила в выполнении аксонометрических проекций как в диметрии, так и в изометрии:
1. Ось Z всегда вертикальна.
2. Все измерения производятся только по аксонометрическим осям или по прямым, параллельным им.
3. Горизонтальные размеры отмеряются по осям X и Y.
III. Практическое закрепление пройденного материала.
1. Выполнение в тетради построения некоторых плоских геометрических фигур в аксонометрии. Начнём с квадрата со стороной 3 см (построение в диметрии и изометрии).
Теперь выполним построение простой плоскогранной фигуры (см. учебник стр. 50) .
Построение можно начинать выполнять с основания фигуры, либо с передней грани( главного вида). Обратите внимание на то, как нужно наносить размеры в аксонометрии: выносные линии являются продолжением сторон, расстояние между которыми они указывают, а размерную линию проводят параллельно той стороне детали, размер которой она указывает.
IV. Теоретическое закрепление изученного материала.
С каким видом проецирования мы сегодня познакомились?
Какие виды аксонометрических проекций узнали?
Чем они различаются?
Под каким углом оси располагаются в диметрии?
А в изометрии?
Какая ось всегда вертикальна?
Как по клеткам отложить угол 30 ?
V. Подведение итогов урока. Выставление оценок.
Домашнее задание:
§ 6,7, вопросы с. 42.
Построение третьего вида и изометрии с вырезом четверти заключается в определении и построении видимых и невидимых линий, которые необходимы для обозначения выреза данной фигуры.
Для того чтобы приступить необходимо задание. В качестве примера было выбрано это задание:
Рассмотрим более подробно шаг за шаг выполнение этого задания. Чертеж выполняется в следующей последовательности:
1.) Чертим вид спереди и вид сверху согласно заданию, указываем видимые и невидимые линии, затем переносим вспомогательные линии из вида сверху на вид слева. Вспомогательные линии строятся из крайних точек фигуры.
2.) Чертим вспомогательные линии из вида спереди на вид слева.
3.) Соединяем точки, полученные в результате пересечения вспомогательных линий.
4.) Чертим третий вид с соответствующими линиями чертежа, прочерчивая видимые и невидимые линии.
5.) Смотрим где есть пустоты в детали согласно линии на рисунке снизу и обозначаем их.
6.) Строим вырез согласно линии, указанной на рисунке. Смотрим где есть пустота и обозначаем ее.
7.) Обозначаем полую часть и неполую, т.е. чертим «штриховку».
8.) Приступаем к построению изометрии с вырезом, для этого необходимо начертить осевые линии.
9.) Как из видим из рисунка, размеры расположенные по осям на трех видах переносим на вид изометрии. Для лучшего представления следует начать с узора выреза.
10.) Применяя методы построения овала и переноса линий на вид изометрии строим остальную часть детали. 11.) Затем обводим соответствующими линиями деталь.
изометрия с вырезом четверти
12.) Указываем штриховыми линиями ту часть, которую вырезали.
Пример решения этого задания имеет общий принцип построения для всех заданий подобного вида.
В виду того что при выполнении подобных заданий студентами все равно допускаются ошибки, мои вышеперечисленные пошаговые подсказки может не каждый поймет, для таких случаев я предлагаю просмотреть видео, в котором задание решается последовательно с указанием всех линий, показано как перенести размеры из трех видовых проекций на вид изометрии.
Но все же чтобы закрепить необходимо выполнить самостоятельно подобные задания несколько раз.
Пример выполненного чертежа смотрите здесь.
Строительные инженерные расчеты и правила Thumb
перейти к содержанию- О Elsevier
- О нас
- Elsevier Connect
- Карьера
- Продукты и решения
Понимание правил и норм строительства дома
Понимание местных строительных норм и разрешений
Когда вы приобретаете планы домов у нас здесь, в The Plan Collection, это скорее всего мотивация для идеального дома мечты или мастер-ванной, которая точно соответствует вашим потребностям. Прелесть поиска нужного места в вашем следующем доме с помощью базы данных поэтажных планов заключается в том, что вы, скорее всего, найдете именно то, что ищете, с каждым элементом вашего нового дома в нужном месте.
О том, о чем вы, возможно, не задумываетесь, разрабатывая свой идеальный план, являются строительные нормы, строительные нормы и разрешения. Это естественные следующие шаги в процессе жилищного строительства, так как вам нужно будет получить соответствующие разрешения, чтобы начать строительство по идеальному плану, который вы нашли среди нашего стиля, коллекций по функциям или региональных домов.

Ваш план и IRC
Здесь, в The Plan Collection, мы хотим убрать как можно больше догадок, когда речь идет о строительстве вашего нового дома, и это включает в себя предложение только планов, которые соответствуют Международному жилому кодексу (IRC).
IRC — это автономный кодекс проживания, разработанный официальными лицами международного кодекса Совета по международному кодексу, который оценивает и устанавливает минимальные правила для жилых помещений, но он не является стандартом, установленным конкретными округами или штатами. Он основан на широко общих принципах, поэтому один IRC может или не может выполнять все правила и нормы, установленные вашим округом, муниципалитетом или штатом.

Преимущества IRC
Факторинг в постоянно меняющихся правилах каждого города и округа, в которые могут застроиться наши клиенты, будет почти невозможен, но вы можете быть удивлены степенью преимуществ, которые может предложить план, разработанный со стандартами IRC.IRC содержит собственный набор положений кодекса, которые соответствуют минимальным стандартам большинства региональных норм и охватывают все аспекты строительства вашего нового дома.
IRC уделяет особое внимание защите общественного здоровья, безопасности и благосостояния.
• Здание плана
• Энергосбережение во время и после строительства
• Правильная сантехника
• Механические элементы плана
• Обеспечение топливным газом (через Американскую газовую ассоциацию)
• Электрооборудование из Национального электротехнического кодекса.
Эффективность проектов IRC не только учитывает все элементы успешной сборки дома, но и обеспечивает гибкость для чиновника, строителя, дизайнера и архитектора кода. И не только ваш дом будет включать в себя самые современные строительные технологии, он будет безопаснее и эффективнее.
Ваш строитель поблагодарит вас
Работа с плохими или нереалистичными планами может стать кошмаром для строителя или подрядчика.Предлагая план, который соответствует стандартам IRC, вы берете на себя многие из этих рисков за счет уравнения для вашего генерального подрядчика, застройщика или разработчика.
Некоторые из элементов плана IRC включают
• Меры безопасности, имеющие проверенный послужной список для безопасных и санитарных сантехнических установок.
• Простые в использовании планы, которые предлагают тот же формат, который используется во всех I-кодах.
• Предпочтение от использования самых современных технологий, а также защиты здоровья и безопасности населения.
• Открытая и честная разработка кода в результате консенсуса сотен экспертов по сантехнике, строительству и безопасности в Северной Америке.

(Фото любезно предоставлено Михалом Джармолуком из Pixabay).
Ограничения IRC
На детальном или местном уровне строительные нормы и правила в основном регулируются штатами, округами, городами, муниципалитетами и районами.Несмотря на то, что IRC представляет собой высокий стандарт развития, он не станет «концом всех, быть всем» для вашей следующей сборки дома. Предоставление ваших разрешений и процесс строительства будет определяться вашими местными законами.

Going Local
К сожалению, однако, местные строительные нормы и правила являются немного движущейся целью. Здесь, в The Plan Collection, мы делаем все возможное, чтобы поддерживать наши стандарты на высоком уровне, чтобы у вас не было никаких сюрпризов, когда придет время подавать заявку на получение разрешения на строительство в местном строительном отделе, но строительные нормы и правила постоянно меняются и значительно различаются в зависимости от региона.
Хотя в некоторых штатах принят IRC, в таких штатах, как Мичиган, Нью-Йорк, Флорида и Калифорния, например, есть свои собственные законы и правила.И эти законы могут обновляться каждые три года, поэтому важно оценить их непосредственно перед тем, как вы планируете начать строительство своего нового дома.
Как проверить местные строительные коды
После того, как вы приобрели свои планы, поговорили с застройщиком и готовы подать заявку на получение разрешений — ознакомьтесь с местными законами, чтобы увидеть, насколько ваши планы соответствуют требованиям вашего штата или округа. Вы можете начать, связавшись с местным отделом строительной инспекции, отделом планирования и зонирования и / или отделом разрешений.Названия этих офисов также могут отличаться.
Эти офисы должны предоставить вам информацию, необходимую для начала процесса подачи заявления на получение разрешения на строительство или для изменения ваших планов по адаптации к местным законам. Они также могут сообщить вам, применяются ли к вашей собственности какие-либо государственные или федеральные требования. Например, это может войти в игру, если недвижимость, на которой вы планируете построить, является частью охраняемых водно-болотных угодий.
Вы также можете спросить о любых изменениях, которые были внесены в правила в связи с какой-либо местной юрисдикцией.Иногда местные советы или советы принимают конкретные стандарты, которых нет в местных кодексах.

Где искать онлайн
Если вы не хотите ждать в очереди в одном из своих местных офисов, чтобы начать процесс сбора информации, в Интернете имеется огромное количество информации.
Посетите страницы своего правительства штата или округа, чтобы ознакомиться с местными строительными нормами и информацией о получении необходимых лицензий, необходимых для начала строительства дома. Государственные веб-сайты можно найти в следующем формате: www.штат. (yourstateabbreviation) .us, или www. (yourstate) .gov
Чтобы продолжить изучение с уровня штата, не мешало бы проверить требования, выдвинутые вашим округом, так как вы будете придерживаться этих стандартов во время вашего проекта.
Найти местного консультанта
Если идея всего этого исследования и подачи документов вызывает у вас головную боль, всегда есть более простой вариант найти уважаемого инженера или архитектора в вашем районе, чтобы проверить ваши планы.(Возможно, вам все равно придется сделать это на каком-то этапе процесса, чтобы удовлетворить местных чиновников, занимающихся строительством.) Любой специалист в этой области, расположенный в вашем районе, будет хорошо осведомлен обо всех правилах и нормах, которые прилагаются при строительстве дома в вашем городе. или город.
Часть их работы или работы вашего подрядчика будет заключаться в том, чтобы подать правильные документы и получить соответствующие разрешения, необходимые для начала строительства. Если ваши планы не совсем соответствуют уникальным правилам, установленным вашим округом или штатом, архитектор или инженер может изменить или сделать пометки в ваших планах, чтобы у вас не было проблем с получением необходимых разрешений для начала строительства.

(Фото любезно предоставлено Лоренцо Кафаро из Pixabay)
Наше обещание
В The Plan Collection мы твердо верим, что наша ответственность заключается в том, чтобы предоставить вам планы, которые предложат вам эффективный и безопасный дом и сделают процесс строительства полезным.Хотя мы не можем учитывать детали каждого города или округа и их уникальные требования, мы можем сделать все возможное, чтобы наши планы соответствовали максимально возможному общему стандарту, и это IRC.
Благодаря инвестициям в проверенный план, подобный предлагаемому в The Plan Collection, и некоторой тщательности со стороны вас и / или вашего местного инженера / архитектора — мы не сомневаемся, что строительство дома вашей мечты будет быть удовлетворительным, полезным и продуктивным опытом для вас и вашего подрядчика.Мы не можем дождаться, чтобы увидеть ваш законченный проект! Нажмите здесь, чтобы сообщить нам, как это происходит, и прислать нам фотографии.
,Правил строительства палубы | Weiß Schwarz
■ Стандартная конструкция
Можно использовать все официально выпущенные карты.
■ Side Constructed
Вы можете использовать в своей колоде только карты «Weiß Side» или «Schwarz Side».
■ Neo-Standard Constructed
Вы можете включать в свою колоду только карты с одинаковым названием.
● Список названий
Заголовок (Weiß Side) | Титульный код |
Puella Magi Мадока Магика | MM |
Love Live! | LL |
Angel Beats! Re: Редактировать | AB |
-NISEKOI-Ложная любовь | NK |
Меланхолия Харухи Судзумии | SY |
IDOLM @ STER CINDERELLA GIRLS | IMC |
Ловеру Тьме 2-й | TL |
Love Live! Солнечный свет!! | LSS |
BanG Dream !, BanG Dream! Вечеринка группы девушек! | BD |
КОНОСУБА — Божье благословение в этом прекрасном мире! | KS |
Cardcaptor Sakura: Очистить карту | CCS |
Мошенник не мечтает о зайчихе Сэмпай | SBY |
Fujimi Fantasia Bunko | F ** |
Заголовок (сторона Шварца) | Титульный код |
Disgaea | DG |
Искусство Меча Онлайн | SAO |
Судьба | ФЗ, ФС |
Хацунэ Мику — Проект DIVA- | PD |
Серия МОНОГАТАРИ (БАКЕМОНОГАТАРИ, NISEMONOGATARI) | BM, NM |
KILL la KILL | KLK |
Персона | P4, P5 |
Fairy Tail | FT |
Kancolle | KC |
Атака на Титан | AOT |
LOG HORIZON | лв |
Детектив Опера Милки Холмс | МК |
Fate / kaleid liner PRISMA ILLYA | PI |
Accel ・ World | AW |
GURREN LAGANN | GL |
Судьба / Апокриф | АПО |
Re: Ноль — Начиная жизнь в другом мире — | RZ |
нет игры нет жизни | NGL |
SAO Альтернатива — Gun Gale Online — | GGO |
Revue Starlight | RSL |
Бэтмен ниндзя | BNJ |
Убийца гоблинов | GBS |
Причудливое приключение ДжоДжо: Золотой Ветер | JJ |
Вы можете использовать следующие карты в любом формате, если не указано иное.
Номер карты | Имя карты |
BWC2015 / WS01EN | Любит карточные игры! Shiyoko |
BWC2015 / WS02EN | После школы Shiyoko |
BWC2016 / WS01EN | Аплодисменты Shiyoko |
BWC2016 / WS02EN | Сезон приветствия Shiyoko |
WSE-CGS / WS01-PE04 PR | Shirokuro Fest 2017 Shiyoko |
● Ограничения на использование карты
Чтобы поддерживать здоровую конкурентную среду в игре Weiß Schwarz, для построения колоды в турнирах будут применяться следующие ограничения.
Персонал турнираоставляет за собой право проверять вашу колоду в любое время во время турнира, чтобы убедиться, что она соответствует списку ограничений.
Бэтмен ниндзя | ||
Ограничение выбора | Бэтмен: проникновение | |
Горилла Гродд: Приманка | ||
| Дополнительное примечание: версия «Бэтмен: Проникновение» в бустере с картой №.На BNJ / SX01-092 это правило не распространяется. | ||
■ Правила использования карты PR Judge
Пожалуйста, обратите внимание, что следующая карта судьи PR может использоваться только в турнирах после 18 октября 2019 года.
BD / W63-E054 PR PR
«Энтузиазм Хаддл» Касуми Тояма 
Пожалуйста, обратите внимание, что следующая карта судьи PR может использоваться только в турнирах после 30 ноября 2018 года.

KS / W55-E082R
«Спасение души» Aqua
Преобразования и изометрии — Концепция
Преобразование изменяет размер, форму или положение фигуры и создает новую фигуру. Преобразование геометрии является либо жестким, либо нежестким; другое слово для жесткого преобразования — «изометрия». Изометрия, такая как вращение, перемещение или отражение, не меняет размер или форму фигуры. Расширение не является изометрией, поскольку оно либо сжимает, либо увеличивает фигуру.
Преобразования в геометрии, в основном, это то, что они изменяют исходный размер, форму или положение фигуры, чтобы создать новое изображение, так что вы собираетесь начать с чего-то, и вы собираетесь изменить это каким-то образом и в итоге получить новое изображение. Сейчас есть 4 типа преобразований.
Первый тип — это расширение. И дилатация — это получение фигуры и либо ее увеличение, либо уменьшение ее и уменьшение, но вы будете сохранять размеры этих соотношений одинаковыми, поэтому вы будете создавать похожие фигуры.
Второй тип, повороты, поэтому вы начнете с фигуры, а затем выберете точку и величину, которую вы собираетесь повернуть, чтобы не изменять размер или форму.
Следующий тип — это перевод или скольжение, поэтому в основном у вас будет фигура, и вы будете двигать ее в каком-то направлении.
И последний тип преобразования — это отражение или отражение, поэтому при отражении вам понадобится линия, которую вы отражаете, так что обратите внимание, здесь я отразил этот треугольник над этой пунктирной линией.
Некоторые преобразования описаны более конкретно, и мы называем эти изометрии. Изометрия — это преобразование, при котором исходная форма и новое изображение совпадают. Другой способ сказать это — назвать это жестким преобразованием, а не «regeed», а «жестким» преобразованием, так что только 3 преобразования — это изометрии, вращения. Я собираюсь написать «I» — это переводы изометрий — это изометрии и отражения. Причина, по которой дилатации не являются изометриями, заключается в том, что вы изменяете размер фигуры, поэтому эти 2 никогда не будут конгруэнтными, когда у вас расширение, если ваш масштабный коэффициент не равен 1.
Как мы описываем переводы? Итак, мы будем использовать стрелку, чтобы показать исходное изображение, переходящее к нашему новому изображению, поэтому, если вы только что сделали одно преобразование, вы бы написали это как треугольник abc, отображающий на треугольник простое число, простое число b, простое число c, и я написал, что внизу, так что эти маленькие апострофы на самом деле означают простое число. Допустим, вы сделали еще одно преобразование, которое станет треугольником двойного простого числа, b двойного простого числа, c двойного простого числа, поэтому каждый раз, когда вы проходите преобразование, у вас будет еще одно простое число в каждой из ваших вершин, поэтому сохраняйте это в Обратите внимание, что вы можете выполнить любой тип преобразования.
