Закон золотого сечения: что это такое, пропорции, принцип, применение в архитектуре и строительстве

Золотое сечение как объяснение пропорций красоты

Главная Статьи Золотое сечение — пропорции красоты

Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.

Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?

На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.

Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.

Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.

Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».

Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

Так что же особенного в этом соотношении?

Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:

То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).

Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».

Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».

В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.

Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».

История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., известный, как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.

Так в чём же ореол таинственности «золотого сечения»?

Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.

Паук плетёт паутину по спирали, ДНК человека закручено по спирали.

А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а

Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».

Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.

Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.

А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.

Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.

Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.

Какие же пропорции в лице человека стремятся к «золотому сечению»?

Прежде всего, у людей с красивыми лицами наблюдается:

1. Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
2. Соотношение высоты верхней и нижней губы будет 1,618.
3. Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
4. Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
5. Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
6. Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
7. Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.

В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.

Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».

Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».

Вот некоторые примеры соотношений размеров и расстояний между зубами:

1. Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
2. В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
3. Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
4. Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.

И этот список можно продолжить.

Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?

Разумеется, искать применение золотых пропорций в эстетической стоматологии.

Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».

Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.

А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.

Время работы

Пн-Пт	10:00 — 22:00
Сб-Вс	10:00 — 20:00

Левковская Ольга Владимировна Врач-стоматолог терапевт

ПОСЛЕДНИЕ СТАТЬИ

Как соблюдать зубную гигиенуПротезирование зубов: металлокерамика и другие материалыПротезирование на имплантахИзготовление съемных зубных протезов и их ценаКак проходит процесс диагностики зубов

Закон «золотого сечения» и его проявление в литературе

Аннотация. В статье рассматривается история развития закона «золотого сечения». На примерах произведений А.П. Чехова, И.С. Тургенева, М.М. Зощенко проанализированы особенности проявления данного закона в литературе. Выявлено, что «золотому сечению» почти безусловно подчиняются произведения малой и средней формы.

Ключевые слова: художественная форма, конфликтосфера, композиция, хронотоп.

С античных времен философы и ученые ищут «формулы красоты» – принципы, воплощающие гармонию идеала. Исследователям удалось найти такую пропорцию – «Божественную», «золотую», или иными словами – закон «золотого сечения». Следствием этого математического принципа оказался прорыв в человеческом миропонимании, повлиявший на многие виды деятельности, в т.ч. на искусство, включая литературу.

Цель данной статьи состоит в том, чтобы проследить историю закона «золотого сечения» и рассмотреть конкретику его осуществления в классических произведениях литературы, и прежде всего в произведениях русской прозы.

Обнаружение закономерностей в математике и формулирование закона «золотого сечения»

Суть указанного закона состоит в том, что для гармонизации целого необходимы величины, когда бо́льшая часть целого так относится к меньшей его части, как целое – к бо́льшей части. Ученые установили, что величина «золотой пропорции» является иррациональным числом и близка к 1,6.

Впервые на указанную пропорцию обратили внимание древнегреческие мыслители. Еще в V в. до н. э. математик Гиппас обнаружил, что «золотое сечение» не является ни целым числом, ни дробью. Пифагорейцы не знали о существовании иррациональных чисел, поэтому открытие Гиппаса показалось им удивительным. После Гиппаса изучением данного числа занимался Евклид. В его «Началах», созданных около 300 г. до н. э., описана основа античной математики, в т.ч. там встречается задача о делении отрезка в крайнем и среднем отношении [1]. Евклид приводит несколько теорем и их доказательства с использованием «золотого сечения».

Последователем Евклида стал Платон, в диалоге которого «Тимей», созданном около 360 г. до н. э., упоминается «золотая пропорция» [8]. Эта работа посвящена математическим и эстетическим воззрениям школы Пифагора. Платон развил мысль Евклида и сформулировал собственное определение «золотого сечения». Смысл его заключается в том, что для соединения двух частей с третьей необходима пропорция, которая бы «скрепила» их в единое целое.

Интерес к закону «золотого сечения» вновь проявился в эпоху Возрождения. В 1509 г. была опубликована книга Луки Пачоли, в которой «золотая пропорция» называется «Божественной» [7]. Использование этого терминологического синонима по отношению к «золотому сечению» обосновано автором следующим образом: «золотая пропорция» ассоциируется с абсолютным идеалом и безусловной гармонией. В своей книге Пачоли писал о математической формуле и, что важно, о ее применении в искусстве. Ученый подчеркивал, что цель его работы состоит в том, чтобы раскрыть всем художникам секрет гармонических форм через использование «Божественной пропорции». Иллюстрации к книге Пачоли создал его гениальный современник – Леонардо да Винчи, который и стал в дальнейшем разработчиком и популяризатором закона «золотого сечения».

С данным законом непосредственно связан ряд чисел, открытый в XIII в. итальянским математиком Фибоначчи. Решая практическую «задачу о размножении кроликов», Фибоначчи установил последовательность, в которой каждое последующее число является суммой двух предыдущих. Более того, при делении любого последующего числа из последовательности на предыдущее всегда получается число, равное приблизительно 1,6. Первым, кто установил связь между «золотым сечением» и рядом чисел Фибоначчи, был математик Иоганн Кеплер.

Справедливо отметить, что такие понятия, как «золотое сечение» и ряд чисел Фибоначчи, «могли бы остаться только достижением математики, если бы не тот факт, что все исследователи «золотого деления» в растительном и животном мире, а также в искусстве неизменно находили его подтверждение» [2, с. 205]. Помимо этого, «золотое сечение» присуще и строению человеческого тела – этот факт доказан известным рисунком Леонардо да Винчи «Витрувианский человек».

Действие закона «золотого сечения» в музыке как временно́м виде искусства было в 1920-е гг. проанализировано А. Ф. Лосевым. Философ обратился к этому закону как к одному «из наиболее универсальных» [6, с. 67]. В систематике А.Ф. Лосева, представленной в его монографиях «Диалектика художественной формы» и «Музыка как предмет логики» (обе – 1927 года), «Божественная пропорция» в музыкальном произведении «выражает и движение, и покой» и воплощается в композиционной организации целого [6, с. 67]. Мысль философа «о композиции как «подвижном покое» <…> разделяли и русские научные формалисты», прежде всего Ю.Н. Тынянов [6, с. 67].

Опыт и практический анализ А.Ф. Лосева оказываются продуктивными и при рассмотрении произведений литературы. Однако на сегодняшний день осуществление этого закона в данном временно́м виде искусства в научно-исследовательских разработках литературоведения практически не представлено.

Обратимся к трем произведениям русской прозы, написанным на разных этапах русской литературы.

Закон «золотого сечения» на службе литературы

В литературном произведении, и прежде всего в малой и средней формах эпических произведений, закон «золотого сечения» регулирует композиционную организацию художественного целого и позволяет, в частности, актуализировать кульминационный этап в сюжетном развитии и тем самым сосредоточить внимание читателя на конфликтосфере произведения в «точке» наивысшего обострения «внешних» и «внутренних» противоречий между героями и персонажами.

Так, повесть И.С. Тургенева «Ася» (1857, опубл. 1858) выверена по принципу «золотого сечения». В основе произведения лежит драматический любовный конфликт, когда герой-рассказчик, Н.Н., и юная Ася были устремлены друг другу, но разминулись на этом пути. Герой влюбляется в Асю, ему дороги ее непосредственность, прямодушие, искренность чувств. В свою очередь и Ася не остается равнодушной к Н.Н. Конфликтосфера в данной повести сформирована автором не только как «внешнее» столкновение характеров (проявляющееся в недопонимании героями друг друга), но и как «внутренний» конфликт, возникший в сознании Н.Н., который не сразу ощущает свою любовь к Асе и вовремя не предлагает ей выйти за него замуж.

Кульминация повести приходится на главу XXI и обусловлена словом «вчера», написанном Асей. В главе 776 слов, указанное – 481-е (соответствующее границе в тексте после 62% ее объема). Ася писала, обращаясь к Н.Н.: «Вчера, когда я плакала перед вами, если б вы мне сказали одно слово, одно только слово – я бы осталась» [9, с. 193]. В этой фразе из письма Аси Тургенев сосредоточил мысль о том, что исход отношений героев зависел лишь от решения Н.Н. – жениться или нет. Однако Н.Н. не признался Асе в любви, поэтому пути влюбленных разошлись.

Ярким примером соответствия художественной формы закону «золотого сечения» также может служить рассказ А.П. Чехова «Дама с собачкой» (1899). Его композиционная организация «отличается безукоризненной отделкой» [5, с. 9]. Произведение состоит из четырех частей, в основе которых лежит история любви Дмитрия Дмитриевича Гурова и провинциалки Анны Сергеевны, в замужестве фон Дидериц. Встретившись в Ялте, Гуров не относился серьезно к развитию отношений с Анной Сергеевной – в отличие от героини, считавшей, что их свела «сама судьба» [10, с. 134]. Герой был уверен, что Анна Сергеевна уйдет из его памяти, однако этого не произошло. В результате через несколько месяцев после расставания с Анной Сергеевной Гуров решается поехать в город С., потому что «ему хотелось повидаться с Анной Сергеевной» [10, с. 140]. «Свидание» происходит в губернском театре, в антракте между действиями спектакля, когда герои мучительно ищут возможность поговорить минуту-две и поднимаются-спускаются по лестницам внутри театра.

Данная сцена, отмеченная аллегорическим знаком лестницы, выверена по закону «золотого сечения». Кульминационной «точкой» в сюжетном развитии, подтвержденной математическим расчетом, являются слова «приехал он». Глагол прошедшего времени «приехал» показывает, что чувство Гурова сопровождалось поступком: герой совершил действие, чем доказал свое трепетное отношение к Анне Сергеевне (из 5030 слов в рассказе «золотое сечение» приходится на указанное словосочетание.)

Обращаясь к малой форме, нельзя не обратиться к творчеству еще одного великого мастера малой формы рассказа – М.М. Зощенко, работавшего прежде всего в области сатиры и юмористики, в т.ч. в жанре фельетона. Последним обстоятельством фиксируется тот литературный факт, что гармоническое целое и регулирующий его закон «золотого сечения» проявляются не только в произведениях с драматическим пафосом или пафосом романтики.

Обратимся к рассказу «Аристократка» (1924). Главный герой – «маленький человек», слесарь-сантехник в жилищной конторе – активно интересуется понравившейся ему женщиной, представляющейся ему «аристократкой» уже на том основании, что у нее золотой зуб «во рте блестит» и мопсик «у ей» на руках [3, с. 29]. Ирония пронизывает всё произведение: она выражается в речи героя и всем существе его рассказа о любовной истории, случившейся в его жизни. Наиболее показательна в этом отношении сцена в театральном буфете. Во время антракта происходит событие, в полной мере демонстрирующее невежество героев как культурно-нравственный уровень их миропонимания и самоопределения: Григорий Иванович согласился угостить даму пирожными, а «аристократка» (а на деле женщина, промышляющая «древней профессией») безудержно хватает одно лакомство за другим, тогда как у героя нет на это денег.

Кульминационный взлет в сюжете, согласно закону «золотого сечения», приходится на 455-е слово («деньги») из 734-х: «Съела она с кремом, цоп другое. Я аж крякнул. И молчу. Взяла меня этакая буржуйская стыдливость. Дескать, кавалер, а не при деньгах» [3, с. 30]. Так Зощенко обличает героя и так называемой «аристократки»: Григорий Иванович – человек мелочный, глуповатый, но претендующий на то, чтобы быть значимой фигурой, чуть ли не вершителем судеб; героиня же, как всегда, уверена, что за ее прихоть будет платить мужчина. В результате слово «деньги», соответствующее расчету по «золотой пропорции», приобретает особое значение в смысловой парадигме рассказа.

Таким образом, принцип «золотого сечения» и в произведениях литературы (в частности, в классических произведениях русской прозы малой и средней формы – в рассказах и повестях) можно рассматривать как «универсальный закон художественной формы» [4, с. 361]. В отношении крупной формы этот закон не может дать очевидного результата (в частности, из-за особенностей хронотопа, когда автор вводит «стяжение» определенного объема времени в одну или несколько фраз).

The law «Golden ratio» and its revealing in the literature

Akopian S. A.,
Bachelor of 2 course of the Moscow City University, Moscow

Coauthor:
Dudchenko I.V.,
Bachelor of 2 course of the Moscow City University, Moscow

Research supervisor:
Loskutnikova Maria Borisovna,
Docent of the Department of the Russian Literature of the Institute of Humanities of the Moscow City University, Candidate of Philological Sciences, Docent

Annotation. In the article the story of the law’s «Golden ratio» development is researched. The features of the law «Golden ratio» in literature are analyzed in the compositions by A.P. Chekhov, I.S. Turgenev, M.M. Zoshchenko. Revealed that compositions of small and medium forms are fit by the law «Golden ratio» almost totally.
Keywords: art form, conflict sphere, composition, chronotope.

---

1. Евклид. Начала. М., Л.: 1948. 448 с.
2. Доберштейн В.Ю. «Золотое сечение» в поэзии // Вестник Костромского государственного университета им. Н.А. Некрасова. 2008. № 2. С. 205-206.
3. Зощенко М.М. Аристократка // Зощенко М.М. Рассказы и повести. М.: 1998. С. 28-30.
4. Лосев А.Ф. Музыка как предмет логики // Лосев А.Ф. Из ранних произведений. М.: 1990. 388 с.
5. Лоскутникова М.Б. Особенности стиля А.П. Чехова (на материале рассказов «Длинный язык» и «Дама с собачкой») // Вестник РУДН. Серия Литературоведение. Журналистика. 2009. № 4. С. 5-13.
6. Лоскутникова М.Б. Отечественное литературоведение XX века: Вопросы теории и методологии. М.: 2014. 148 с.
7. Пачоли Лука. О Божественной пропорции. М.: 2007. 252 с.
8. Платон. Тимей // Платон. Собр. соч.: в 4-х тт. Т. 3. М.: 1994. С. 421-501.
9. Тургенев И.С. Ася // Тургенев И.С. Полн. собр. соч. и писем: в 30 т. Т. 5. М.: 1983. С. 149-197.
10. Чехов А.П. Дама с собачкой // Чехов А.П. Полн. собр. соч. и писем: в 30 т. Т. 10. М.: 1977. С. 128-143.

1. Euclid. Starts. М., L.: 1948. 448 pages.
2. Doberstein V. Y. «Golden ratio» in poerty // Messenger of Kostroma State University named by N.A. Nekrasov. 2008. № 2. Page 205-206.
3. Zoshchenko М.М. Noblewoman // Zoshchenko М.М. The stories and the tales. М.: 1998. Page: 28-30.
4. Losev А.F. Music as a subject of logics // Losev А.F. From early compositions. М.: 1990. 388 pages.
5. Loskutnikova М.B. Features of style of A.P. Chekhov (on a material of stories «Long Tongue» and «The Lady with a Doggie») // Messenger RUDN. Series Literary Study. Journalism. 2009. № 4. Page: 5-13.
6. Loskutnikova М.B. Domestic Literary Study of XX century: Questions of theory and methodology. М.: 2014. 148 pages.
7. Pacioli Luka. About God Proportion. М.: 2007. 252 pages.
8. Plato. Timay // Plato. Collection of works: in 4-х tt. Т. 3. М.: 1994. Page: 421-501.
9. Turgenev I.S. Asya // Turgenev I.S. Complete set of works and letters: in 30 т. Т. 5. М.: 1983. Page: 149-197.
10. Chekhov A. P. Lady with a dog // Chekhov A.P. Complete set of works and letters: in 30 т. Т. 10. М.: 1977. Page: 128-143.

Что такое золотое сечение в фотографии?

Композиция — это то, как мы размещаем объекты и элементы на фотографии, чтобы создать визуальный интерес, произвести впечатление и рассказать историю. Несколько методов помогут вам обрамить фотографию и определить, где разместить контент.

Камеры часто показывают наложение сетки «правило третей». Золотое сечение, также известное как золотая середина, золотая спираль, золотое сечение, божественные сечения, божественные пропорции, спираль Фибоначчи или фи-сетка, представляет собой аналогичную, более эффективную композиционную директиву, основанную на древней математике и используемую в искусстве такими мастерами, как Микеланджело. , Леонардо Ди Винчи и Сальвадор Дали.

Что такое золотое сечение?

Золотое сечение указывает, где разместить объект (дерево, человека, здание и т. д.) или элемент фотографии (например, горизонт), чтобы он был наиболее приятным для глаз.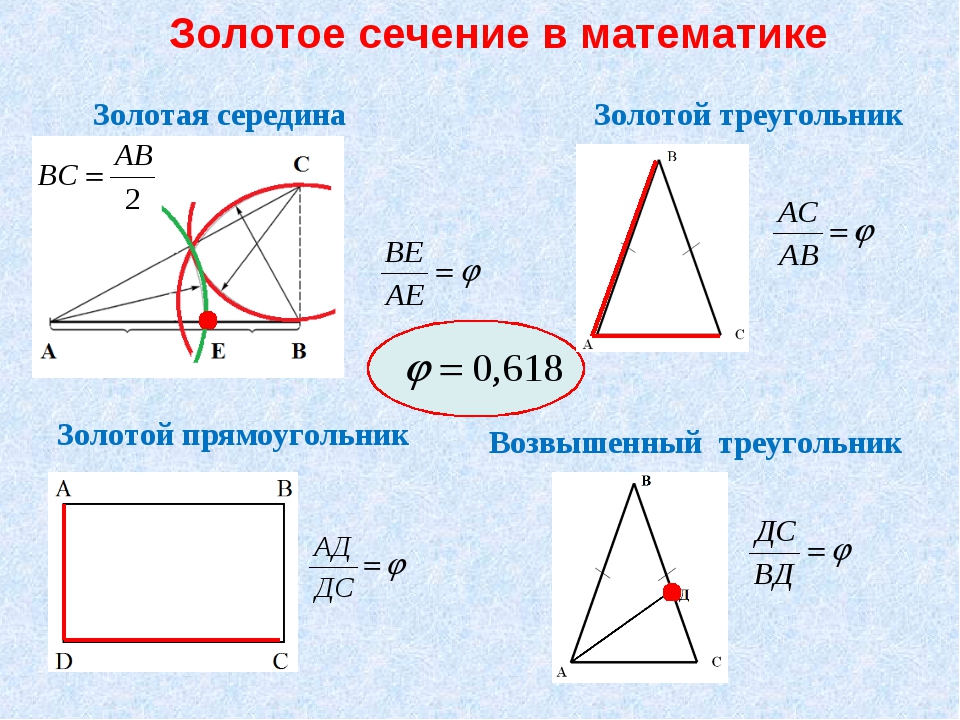 Это божественное соотношение составляет 1,618:1.

Первое записанное определение золотого сечения было дано Евклидом в 3 веке до н.э. Греческий математик Евклид был наиболее известен своими работами по геометрии, теперь известными как «евклидова геометрия». Он вычислил золотое сечение с помощью прямоугольников, что также можно объяснить с помощью линии.

Золотое сечение — это математическое правило, которое гласит, что любую линию можно разделить так, что более длинный сегмент, разделенный на более короткий сегмент, будет иметь такое же отношение, как полная линия, разделенная на более длинный сегмент.

Наглядно:

Изображение предоставлено Питером Марьяновичем/Wikimedia Commons

Первый сегмент — это a. Второй сегмент — б. Длина линии равна a+b.

Итак, уравнение: a/b = (a+b)/a = 1,6180339887498948420.

Золотое сечение — это иррациональное число, которое продолжается вечно и сокращается до 1,618. В математических кругах это уникальное число представлено греческой буквой фи.

Это уравнение полезно для фотографов, разбирающихся в математике и геометрии. Но даже если вы смотрите на числа и уравнения с затуманенными глазами, вы можете использовать золотое сечение, поскольку оно используется для создания золотой спирали и сетки Фи. Эти наложения помогают визуализировать, где разместить элементы на фотографии.

Что такое фи-сетка?

Сетка Phi похожа на сетку правила третей, которая обычно используется для принятия решения о компоновке фотографии. Правило третей — один из основных принципов фотографии. Обе сетки используют две горизонтальные линии и две вертикальные линии для разделения кадра.

Правило третей делит кадр на три строки и три столбца одинакового размера или 1:1:1 по вертикали и 1:1:1 по горизонтали. Сетка Phi аналогичным образом разделяет кадр, но делает средний ряд и средний столбец меньше в соответствии с золотым сечением. В результате получается 1,618:1:1,618 по вертикали и 1,618:1:1,618 по горизонтали.

Вот краткое сравнение:

Взгляд зрителя естественным образом притягивается к областям пересечения линий сетки. Итак, вот где расположить фокус фотографии. В этом примере Млечный Путь расположен на вертикальной линии сетки Фи с фокусом на пересечении.

Спираль Фибоначчи

Золотое сечение является основой последовательности Фибоначчи, составляющей спираль Фибоначчи. Последовательность и спираль названы в честь итальянского математика Леонардо Пизанского, позже известного как Фибоначчи (сын Боначчи). В 1202 году Фибоначчи представил эту последовательность в своей книге «Liber Abaci». Как и наложения сетки, спираль Фибоначчи указывает, где разместить самый важный объект на фотографии.

Математически последовательность Фибоначчи начинается с числа 1, добавляет предыдущее целое число и образует бесконечный ряд чисел с этим шаблоном. Итак, серия выглядит так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

Или добавьте 1+1=2 и 2+3=5 и так далее. После первых двух чисел отношение последовательных чисел очень близко к золотому сечению.

В геометрии золотое сечение также может быть выражено в виде определенного типа прямоугольника. Предположим, вы берете пример линии a+b (или x+y) и превращаете ее в прямоугольник, где ширина равна x, а длина равна x+y. Если разделить площадь этого прямоугольника на ряд квадратов, получится спираль, основанная на последовательности Фибоначчи.

Фибоначчи обнаружил, что эта «золотая спираль» появляется в нескольких местах в природе, от молекул ДНК до лепестков цветов, ураганов и Млечного Пути. Подобно тому, как золотое сечение приятно для человеческого глаза в природе, так и фотография, размещающая содержание в центре золотой спирали.

Адриан Бежан, профессор машиностроения Инженерной школы Дьюка Пратта, говорит, что золотое сечение эстетически приятно из-за эволюции человеческого зрения.

Короче говоря, наш мозг должен обрабатывать все, что видят наши глаза. Чем быстрее он может что-то обработать, тем это приятнее. Любое изображение с золотым сечением проводит зрителя через всю фотографию и быстро обрабатывается мозгом, поэтому сигнализирует о том, что такое изображение эстетично.

Как использовать спираль Фибоначчи

Независимо от того, занимаетесь ли вы простым жанром фотографии или чем-то более сложным, спираль Фибоначчи может вам помочь. Золотую спираль можно использовать при кадрировании фотографии или принятии решения об обрезке изображения. К сожалению, камеры часто предлагают наложение сетки по правилу третей, но не по спирали Фибоначчи.

Идея состоит в том, чтобы поместить объект или то место, где вы хотите, чтобы взгляд зрителя был нарисован в наименьшем завитке спирали. Это то место, куда естественно стремится глаз. Спираль может закручиваться влево или вправо вертикально или горизонтально. Важной концепцией являются пропорции, которые приводят взгляд к фокусу фотографии.

Если у вас нет наложения, вы можете оценить положение, представив цифру 9.

Как видите, спираль естественным образом направляет ваш взгляд через фотографию к фокусу или от точки фокусировки. фокус обратно за пределы изображения.

Как Lightroom, так и Photoshop предлагают наложение спирали Фибоначчи при кадрировании фотографии. В инструменте обрезки нажмите O , чтобы просмотреть наложения. Добравшись до спирали, вы можете изменить ее ориентацию, нажав Shift + O . Затем переместите инструмент обрезки или измените размер фотографии, чтобы поместить основной объект в центр спирали.

Лучшие приложения для золотого сечения

Фи-сетка и наложения золотой спирали доступны в некоторых приложениях для камеры смартфона. Lightroom Mobile имеет камеру для съемки фотографий в приложении, которое включает в себя наложение сетки Phi.

Загрузить: Lightroom для Android | iOS (бесплатно, предлагает покупки в приложении)

Приложение Golden Ratio Camera — это накладка на камеру смартфона, которая позволяет использовать руководство во время фотосъемки на телефоне.

Загрузить: Камера с золотым сечением для Android | iOS (бесплатно, предлагает покупки в приложении)

Wise Camera включает в себя различные наложения руководств по композиции с инструкциями по их использованию.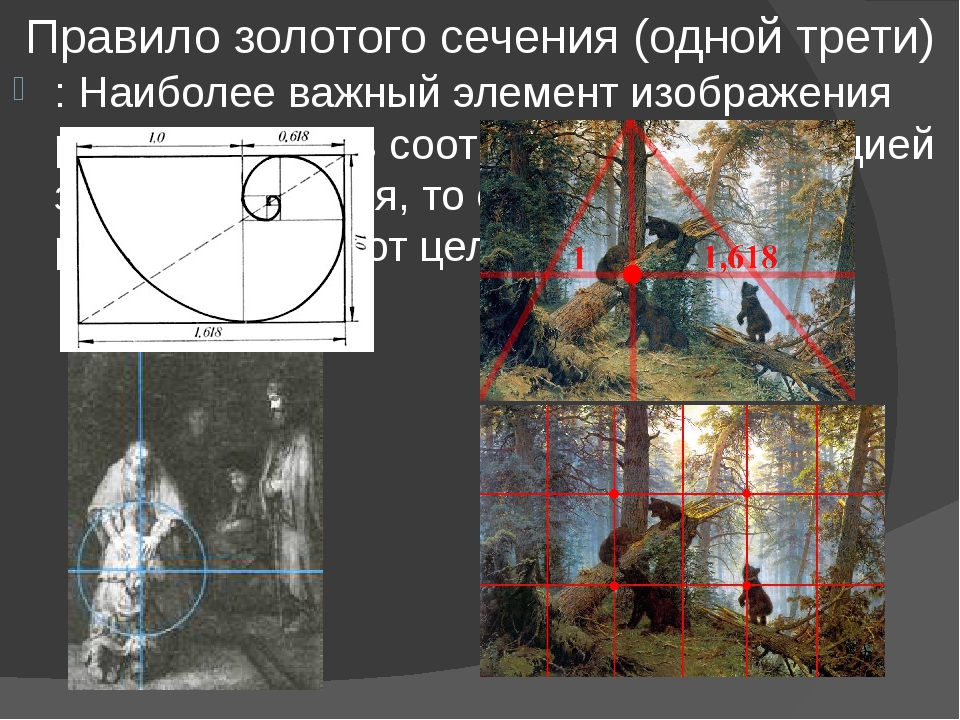 Пользователи могут переключаться между сверхширокоугольным, телеобъективом и базовым объективом iPhone.

Загрузить: Wise Camera для iOS (бесплатно, предлагает покупки в приложении)

Золотое сечение против правила третей центр фото. За исключением преднамеренно симметричного изображения, расположение объекта с той или иной стороны вызывает напряжение и визуальный интерес; зритель тратит больше времени, рассматривая фотографию и видя все, что на ней есть. Это создает поток и ощущение движения.

Основной объект смещен вправо или влево при размещении его на пересечении горизонтальной и вертикальной линий. Напротив, размещение объекта на пересечении сетки Фи или в центре золотой спирали смещает его ближе к центру фотографии. Знание этого может помочь при съемке, поскольку вы можете угадать расположение на основе наложения сетки правила третей на вашей камере.

Этот пример фотографии показывает разницу между кадрированием с использованием сетки Phi и сетки правила третей. Обратите внимание, что горизонт расположен на одной из линий сетки Phi. Получение горы (фокальной точки) на перекрестке потребовало большего кадрирования фотографии, что привело к более элегантной композиции.

Стремитесь разместить горизонт на одной из горизонтальных линий сетки Фи. Многие начинающие фотографы помещают горизонт в центр фотографии. Золотое сечение помогает расположить видимый горизонт выше или ниже на фотографии для лучшей эстетики.

Когда использовать золотую спираль и правило третей

Вот когда следует использовать золотую спираль и правило третей:

• В целом, золотая спираль создает более сбалансированное изображение в пейзажной фотографии.
• Используйте правило третей в портретах.
• Включите сетку правила третей на своей камере, чтобы ориентироваться при съемке фотографий.
• Используйте золотую спираль для точного размещения при кадрировании фотографий.

Прочитайте наше подробное руководство о том, как использовать правило третей.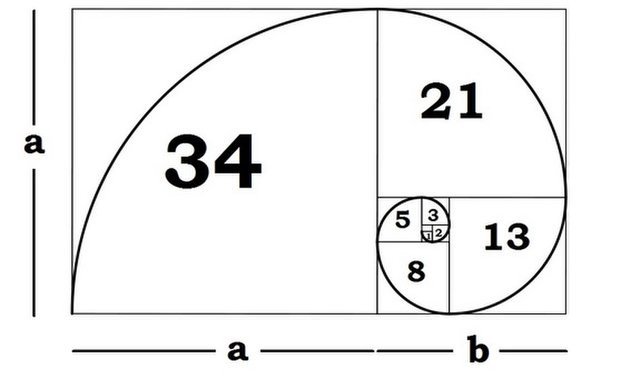

Использование золотого сечения для улучшения композиции

Золотое сечение — это просто руководство, инструмент для создания лучшей композиции, которая сделает вашу фотографию более привлекательной. Независимо от того, используете ли вы сетку Phi или золотую спираль, это может улучшить ваши фотографии естественным образом. Хотя это ценный инструмент, существует множество других композиционных приемов для создания визуально интересной, впечатляющей фотографии, рассказывающей историю.

Золотое сечение в дизайне и фотографии

Скорее всего, вы слышали о золотом сечении. Возможно, вы познакомились с ним в школе, на уроках математики, искусства или дизайна. Возможно, вы видели фильм Код да Винчи и узнали о нем. И есть множество веб-сайтов, которые могут рассказать вам больше, чем вы когда-либо хотели знать.

Что такое композиция золотого сечения и можно ли ее действительно применить в дизайне и фотографии? Должны ли мы, художники, использовать Ratio или игнорировать его? Хорошей новостью является то, что его легко наносить, и он действительно может сделать ваши работы более увлекательными и красивыми.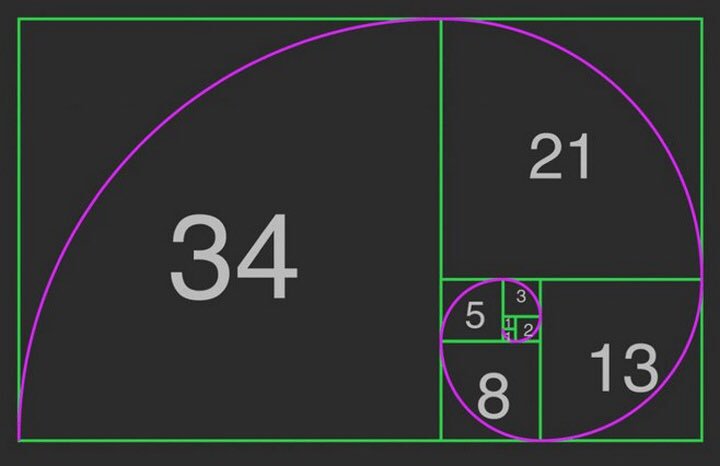 Если вам нужны реальные советы о том, как использовать его, чтобы улучшить свою работу, не ищите дальше. Читай дальше.

Что такое золотое сечение?

За расчетом золотого сечения стоит много математики. Но дизайнеры, художники и фотографы обычно не являются математиками высокого уровня. Чтобы помочь тем, кто не склонен к алгебре, давайте не будем усложнять.

Отношение приблизительно равно 1,618 к 1. Оно приблизительное, потому что это иррациональное число, продолжающееся с бесконечным числом знаков после запятой. В математике число обозначается греческой буквой φ или фи.

Отношение было впервые описано древнегреческими математиками Фидием, Платоном и Евклидом еще ок. 450 г. до н.э. Его изучали и совершенствовали в течение двух с половиной тысячелетий.

Отношение также тесно связано с последовательностью Фибоначчи. Этот математический шаблон показывает числа, которые складываются вместе, чтобы получить следующее число. Первыми числами последовательности являются 0, 1, 1, 2, 3, 5, 8, 13, 21 и т. д.

Кроме того, когда два последовательных числа в последовательности Фибоначчи делятся, их отношение очень близко к Фи. Чем больше число, тем точнее будут результаты.

Почему возник спор?

Один из самых распространенных аргументов против важности числа Фи заключается в том, что, хотя число Фи можно применить ко многим явлениям в природе, тщательный анализ показывает, что оно редко бывает математически совершенным. Когда измеряют спирали раковины наутилуса, их отношение друг к другу не точно равно 1,618.
Известные произведения искусства и архитектуры также не выдерживают тщательного изучения. Это верно от древних пирамид и знаменитых зданий от Древней Греции до Моны Лизы и других произведений искусства мастеров.

Хотя это всего лишь догадка, она выглядит педантичным и академическим аргументом. Эти работы могут не радовать математиков, но цифры чертовски близки. Достаточно близко, чтобы заставить людей задуматься и убедить случайного наблюдателя. И независимо от того, совершенна ли математика, эти работы выдержали испытание временем. Их до сих пор изучают и ими восхищаются.

Как художники, мы можем понять. Вещи в природе и произведения искусства редко бывают совершенными. И все же мы все еще можем найти их привлекательными и красивыми.
В том же духе часто утверждалось, что правило третей в фотографии является упрощением Фи. Он дает примерно такой же результат, но его легче применять в полевых условиях или на ходу. Помогает ли правило третей фотографам создавать более захватывающие изображения? Оно делает.
Должен ли он каждый раз идеально наноситься? Нет, вы можете получить отличные результаты и красивые фотографии, используя его в качестве отправной точки и изменяя по своему усмотрению.

При анализе классических произведений дизайна, архитектуры или изобразительного искусства необходимо помнить об этом. Думал ли художник явно о Фи и стоящей за ней математике, когда создавал свои шедевры? Достали ли они линейку для измерения идеальных золотых прямоугольников? Возможно, некоторые сделали. Но большинство из них просто наловчились на красивые пропорции. И, применяя свои навыки и дары, они очень близко подошли к тому, что можно доказать математически.

Почему это важно?

Подобно многим вещам в природе, узор имеет интересное подсознательное влечение. Осознаем мы это или нет, но люди не могут не находить объекты, соответствующие Фи, как внутренне красивые.

Как художники и создатели, мы можем использовать эту предрасположенность себе во благо. Включив Ratio в наш дизайн и фотографию,
, мы можем улучшить качество и красоту нашей работы.

Должен ли он быть математически совершенным? Нет, абсолютно нет. Соотношение следует рассматривать как полезное руководство; это инструмент, помогающий вашей композиции. Это не жесткие рамки, которых нужно придерживаться. Независимо от того, какую позицию вы занимаете в дебатах, твердое понимание Фи и того, как ее можно применить в своей работе, делает вас более сильным художником.

Как его применять

Уникальным свойством коэффициента является то, что его можно применять разными способами.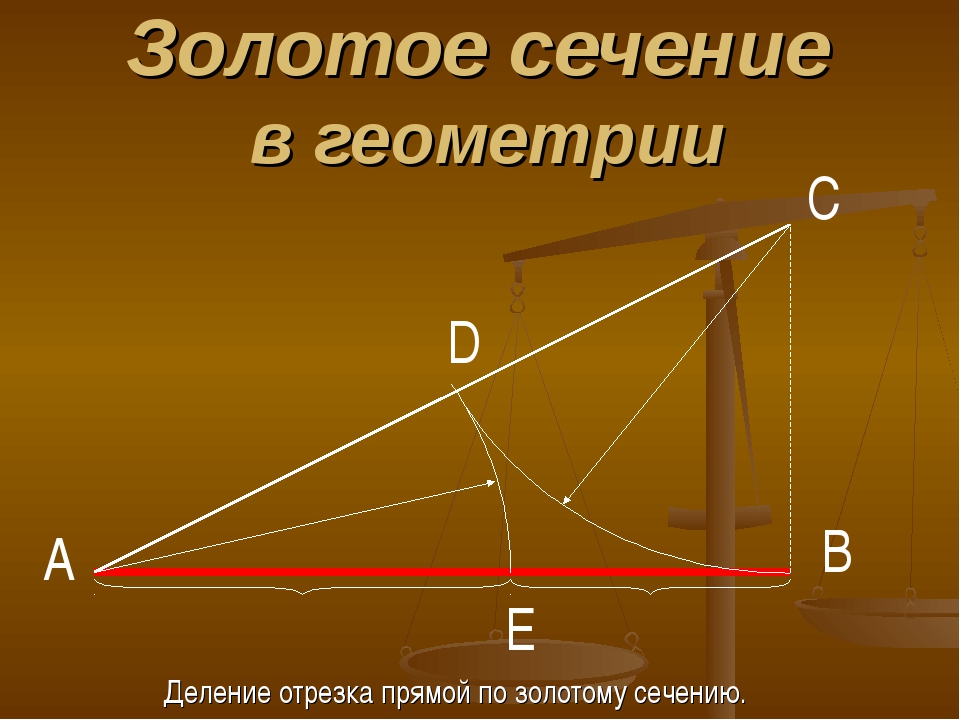 Это алгебра, обычно она отображается с помощью переменных a и b .
Но при работе с изобразительным искусством проще всего применить его геометрически. Наиболее распространенным примером является использование прямоугольников. Золотой прямоугольник — это тот, у которого короткая сторона равна 1, а длинная — 1,618. Затем прямоугольник можно разделить на себя с помощью магического числа 1,618 бесконечное количество раз.
Обычной экстраполяцией этого является Золотая Спираль. Глядя на изображение медленно уменьшающихся прямоугольников, можно нарисовать размеры спирали.

После визуального отображения вы можете найти свидетельства существования Фи повсюду в природе. Это естественное явление, которое можно наблюдать в спиралях морских раковин, полосах дождя урагана, лепестках цветов или листьях растений. Для художников естественно имитировать красоту природы.
Существуют и другие способы применения коэффициента. К любой форме можно применить соотношение. Круги, треугольники или квадраты можно разделить на узоры на основе числа 1,618.

Золотое сечение в дизайне

В дизайне макеты — идеальное место для начала применения пропорции. Двухколоночные макеты чрезвычайно распространены. Но разное взвешивание столбцов добавляет динамичности любым публикациям. Веб-страницы, в частности, используют концепцию боковой панели, чтобы придать динамическое, взвешенное ощущение, которое работает естественно.

Но какие должны быть размеры? Единицы измерения значения не имеют. Длина большего края большего прямоугольника должна быть в 1,618 раз больше длины края меньшего прямоугольника.

Например, ширина большинства веб-макетов составляет 960 пикселей. При делении на 1,618 получается 594 пикселя. Это будет высота макета проекта. Чтобы разделить его на столбцы, вы делаете то же самое снова. Большое поле, расположенное справа или слева от сетки макета, также будет иметь ширину 594 пикселя. Меньшая боковая панель будет иметь ширину 366 пикселей и высоту 594 пикселя.

Вы можете продолжать узор сколько угодно. Меньший прямоугольник можно разделить таким же образом, насколько позволяет ваш дизайн. Если вы хотите разместить дополнительные элементы внутри двухколонной структуры, которую вы создали выше, используйте для их размещения все меньшие и уменьшающиеся прямоугольники.
Вы также можете размещать элементы по спирали на основе этих прямоугольников. Детали вашего дизайна будут становиться плотнее по мере того, как взгляд зрителя будет двигаться по спирали к вершине. Это отличный способ сбалансировать пустое пространство в дизайне и сохранить приятный баланс.

Еще одним прекрасным примером применения Ratio в дизайне является дизайн логотипа. Многие знаковые логотипы можно свести к соотношению. Используя масштаб 1:1,618 для всевозможных форм, вырезов, заливок и узоров, симметрия дизайна действительно может быть достигнута. Поищите в Интернете, и вы сможете найти отличный анализ того, как некоторые из самых знаковых корпоративных брендов извлекают выгоду из использования Ratio в своих проектах.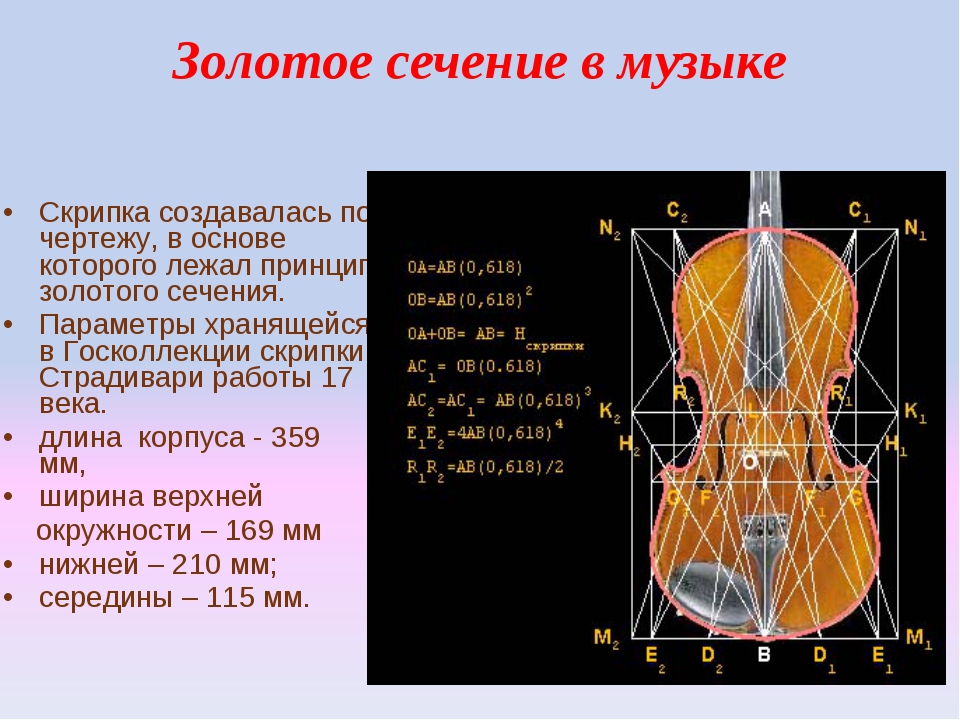
Это простые примеры, но важно понимать, что соотношение может повторяться в произведении несколько раз. Если вы разделите свой холст на прямоугольники, начиная слева, вы можете сделать это снова справа. Затем у вас есть те же пропорции центрирующих элементов, что очень похоже на правило третей в фотографии.

Чтобы сделать еще один шаг вперед, на рамке можно рисовать золотые прямоугольники как по вертикали, так и по горизонтали. Многие эксперты интерпретируют «Тайную вечерю» Леонардо таким образом, с прямоугольниками, нарисованными со всех краев.
Соотношение можно использовать даже для определения размера шрифта. Если у вас возникли проблемы с определением типографики для проекта, возьмите размер основного шрифта и умножьте его на 1,618. Итак, если основной шрифт 10 пунктов, то заголовки должны быть примерно 16 пунктов. Названия страниц над этим? Попробуйте 26 очков или около того. Правило можно применить и другим способом, если вы хотите установить заголовок или размер заголовка и определить размер основного текста.
Как только вы увидите магию пропорций, количество способов, которыми они могут быть применены к вашим проектам, станет безграничным.

Золотое сечение в фотографии

Как было сказано выше, многие фотографы используют правило третей как упрощенную форму соотношения. В правиле третей вы просто делите кадр на части по одной трети по вертикали и горизонтали. Важные элементы размещаются на пересечениях линий. Линии также можно использовать на самой фотографии. Горизонты в пейзажах обычно располагаются на горизонтальной линии в одну треть.

Размер каждого прямоугольника для традиционного изображения по правилу третей составляет 1:1:1.
Правило третей можно немного изменить, чтобы лучше применить его к Соотношению. Вместо того, чтобы размещать вертикальные и горизонтальные линии на расстоянии одной трети от края, немного измените их и разделите рамку на золотые прямоугольники. Теперь сетка будет состоять из двух одинаковых вертикальных и двух горизонтальных линий, но внутренние прямоугольники будут иметь размер 0,618 размера внешних прямоугольников. Затем сетку можно использовать так же, как традиционное правило третей, но с более близким приближением к соотношению. Таким образом, размер каждого прямоугольника для изображения с золотым сечением будет 1:0,618:1,9.0003

Оба руководства также могут быть полезны при планировании и размещении элементарных предметов и объектов в кадре. Так же, как и в дизайне, фотографы могут играть с тем, где именно лежат объекты вдоль рамки сетки или золотой спирали.
Концепция спирали особенно эффективна в фотографии. Поместив свой элементальный объект в точку спирали и распустив элементы дальше друг от друга по мере удаления, вы можете объединить концепции Фи и сетки золотого прямоугольника, описанные выше.

Кроме того, эти правила могут стать отличным руководством при создании изображений. Но они так же эффективны при кадрировании и постобработке. Многие обычные фотографии можно спасти с помощью творческой обрезки.

Еще одно применение Phi в фотографии — захват объектов, которые уже им обладают. Листья растений, далекие спиральные галактики, лепестки цветов и морские ракушки — привлекательные объекты, из которых получаются отличные сюжеты. Задача состоит в том, чтобы понять, какую роль играет золотая спираль в создании этой красоты, и запечатлеть ее на изображении. Что вы можете сделать, чтобы подчеркнуть спираль и передать эту красоту своим зрителям? Ищите объекты, которые уже используют Соотношение внутри, и используйте это в своих интересах.

Заключение

Соотношение — отличный инструмент для применения ко многим фотографиям и проектам, которые в противном случае отсутствовали бы. Понимание технической алгебры и геометрии, лежащих в основе Phi, не является самым важным выводом при изучении Ratio. Для дизайнеров и фотографов понимание того, что такое искусство золотого сечения, является первой ступенькой.

Помните, что использование Phi — это не только создание собственных изображений. Это также инструмент для оценки других изобразительных искусств, с которыми вы сталкиваетесь. Это инструмент для анализа того, что вам нравится. Изучая работы других, вы делаете свои собственные творения лучше. Учитесь у других и смотрите, как они это использовали. Использование его в вашей работе связано с композицией, а не с продвинутой математикой. Это еще один ценный инструмент в вашем наборе инструментов, который поможет вам избежать банального дизайна и скучных фотографий.

После того, как вы изучите правила и будете готовы продемонстрировать свои изображения, создайте потрясающее онлайн-портфолио с помощью Pixpa. Pixpa – это платформа для создания веб-сайтов, которой доверяют творческие профессионалы во всем мире.

Pixpa предлагает простой, но мощный конструктор веб-сайтов с возможностью перетаскивания и включает в себя клиентские галереи, инструменты электронной коммерции и блогов, которые позволяют вам полностью управлять своим присутствием в Интернете с помощью единой бесшовной платформы. Изучите все функции , которые делают Pixpa идеальным выбором для фотографов и других творческих профессионалов.